Optimal energy management of distributed generation resources in a microgrid under various load and solar irradiance conditions using the artificial bee colony algorithm

Abstract

Optimal energy management of distributed generation and storage systems in microgrids plays a critical role in minimizing operational costs, reducing environmental emissions, improving power quality, and enhancing system reliability. Achieving these objectives requires comprehensive modeling of all microgrid components, including load profiles, generation sources, and the network structure. In recent years, metaheuristic optimization techniques have gained significant traction due to their flexibility and robustness in handling complex, nonlinear, and multi-objective problems without the need for initial estimations. This study proposes the artificial bee colony algorithm as an effective tool for the optimal energy management of a hybrid microgrid system comprising photovoltaic panels, wind turbines, fuel cells, microturbines, and battery energy storage systems. The algorithm’s performance is evaluated under varying solar irradiance conditions across four distinct operational scenarios. The results demonstrate that the proposed algorithm consistently achieves superior performance in minimizing the total operation cost compared to traditional bio-inspired optimization techniques such as genetic algorithms, particle swarm optimization, and a modified bat algorithm. The findings confirm our method’s potential as a robust and efficient approach for real-time microgrid energy management under dynamic operating conditions.

Introduction

Traditional electrical power systems face significant challenges, including low reliability, high operational costs, dependency on centralized fossil-fuel-based generation, substantial transmission and distribution losses, and limited system resilience. These systems are vulnerable to failures when generation units or transmission infrastructure are compromised. Additionally, the growing concerns regarding fossil fuel depletion, greenhouse gas emissions, and environmental sustainability have intensified the global shift toward clean and decentralized energy solutions¹. In this context, modern energy systems, particularly microgrids, have emerged as promising alternatives. By integrating distributed generation (DG) units and local energy storage, microgrids offer enhanced reliability, reduced transmission losses, and increased energy efficiency. Moreover, the deployment of renewable energy sources such as photovoltaic (PV) and wind power brings energy generation closer to consumers, thereby minimizing power interruptions and improving system autonomy and resilience.

Microgrids operate in both grid-connected and islanded modes. In the islanded configuration, DG units such as fuel cells, microturbines, and batteries serve as the primary energy sources, enabling uninterrupted supply during grid outages. However, the stochastic nature of renewable sources and the varying demand profiles make optimal energy management a complex task. Effective management strategies are essential to balance energy supply and demand, reduce operational costs, minimize emissions, and enhance reliability and power quality. A core requirement for optimal energy management is an accurate and comprehensive understanding of the microgrid’s components, including generation units, energy storage systems, and load characteristics. Among the various techniques proposed in the literature, intelligent and metaheuristic optimization algorithms have gained popularity for their ability to solve highly nonlinear, multi-objective problems without requiring explicit gradient information or initial estimates^{1,2,3,4,5,6,7,8,9,10,11}.

This research addresses the optimal energy management problem in a hybrid microgrid that includes PV and wind renewable sources, fuel cells and microturbines as controllable non-renewable generators, and battery energy storage. A 24-hour operational schedule is considered under varying solar irradiance conditions in a grid-connected mode. To tackle the complex optimization landscape, the Artificial Bee Colony (ABC) algorithm is employed due to its robustness, global search capability, and high convergence speed. The ABC algorithm avoids premature convergence and local optima traps, making it a suitable candidate for solving the energy management problem in microgrids. Compared to other well-known optimization techniques, such as Genetic Algorithms (GA), Particle Swarm Optimization (PSO), and Modified Bat Algorithm (MBA), the proposed ABC-based approach demonstrates superior performance in minimizing total operation costs while maintaining system reliability.

The main contributions of this study can be summarized as follows:

• Development of an optimal energy management strategy to minimize microgrid operational costs.

• Enhancement of system reliability through efficient utilization of distributed generation and storage resources.

• Evaluation of the proposed ABC algorithm under varied solar irradiance scenarios and comparison with other optimization methods.

The remainder of the paper is organized as follows: Sect. 2 reviews related literature and previous works. Section 3 presents the microgrid model. Section 4 defines the objective functions and constraints. Section 5 introduces the ABC algorithm. Section 6 discusses the simulation results. Finally, Sect. 7 concludes the paper with insights and future research directions.

Literature review

Optimal energy management in microgrids has emerged as a critical area of research due to the growing penetration of distributed generation resources and the need for sustainable, reliable, and cost-effective power systems. The utilization of small-scale, privately owned generation units within microgrids plays a pivotal role in improving power quality, reducing energy supply costs, and enhancing system reliability. Recent trends also show an increasing deployment of distributed energy resources (DERs) as backup generation units in residential and commercial complexes, operating under the framework of microgrids¹². Several studies have explored various strategies for energy management in microgrids, considering multiple objectives such as cost minimization, emission reduction, and reliability enhancement. For instance¹³, highlights that proper management of generation and storage systems can significantly reduce the total operational costs of microgrids. Conversely, inefficient management may lead to increased losses and even unprofitability. To achieve effective operation, it is essential for the microgrid operator to possess detailed knowledge of the system components, including load profiles and available energy resources.

In recent years, advanced metaheuristic and artificial intelligence-based optimization algorithms have gained traction for solving complex energy management problems in microgrids. In¹⁴, a Salp Swarm Algorithm with Crowding Distance (SALP-CD) is proposed for optimal scheduling of distributed generation units in a hybrid microgrid comprising photovoltaic and wind energy sources. This study also incorporates demand-side management and grid energy exchange to simultaneously minimize operating costs and environmental impacts. Similarly¹⁵, applies a PSO approach for the economic operation of a grid-connected residential microgrid. The proposed model accounts for generation bids, reserve capacities, and energy transaction profits, demonstrating the algorithm’s efficacy in reducing operational costs while satisfying all system constraints. In¹⁶, an energy management framework using a GA is introduced to optimize the scheduling of DG units and battery storage under both islanded and grid-connected scenarios. The results indicate that GA outperforms other algorithms in terms of convergence time and the ability to reach a global optimum, validating its effectiveness for microgrid operation.

A multi-objective optimization approach is presented in¹⁷, where both economic and environmental aspects are simultaneously considered. The complexity of multi-objective problems, especially the trade-offs among conflicting objectives, is addressed in¹⁸, which proposes a specialized algorithm to determine optimal energy scheduling strategies. This method minimizes total energy costs, incorporating energy losses, imported power from the grid, and contributions from DERs and storage units. Further, in¹⁹, a detailed cost model is used to minimize total operation costs, factoring in generation, environmental, and battery storage costs. The strategy focuses on maximizing the use of local generation to meet demand while incorporating stochastic models for solar and wind power to reflect real-world uncertainty. The study underlines the importance of incorporating dynamic models for renewable sources to ensure accurate and robust energy management.

The ABC algorithm has gained traction as an effective optimization technique for microgrid energy management, as illustrated in²⁰. Similarly, GA have been widely applied to solve multi-objective optimization problems in microgrids, particularly in scenarios involving electric energy storage systems. In²¹, energy management incorporates Demand response (DR) programs to minimize both operational costs and environmental emissions. The objective function in this study accounts for generation, emissions, and operating costs. The strategy emphasizes supplying loads through internal resources, supported by energy storage systems, while the uncertainties of PV and wind generation are considered using probabilistic models. The intermittent and variable nature of renewable energy sources such as PV and wind, subject to daily, seasonal, and weather-driven fluctuations, poses significant challenges for grid-connected and islanded operational modes. This variability necessitates the inclusion of energy storage systems to maintain balance and ensure reliability in microgrid operations²². As addressed in²³, employing hybrid energy systems, where complementary characteristics of various resources (e.g., renewables, batteries, microturbines, fuel cells) are exploited, can mitigate the limitations of any single energy source. In this context, the study proposes a hybrid model where PV and wind turbines are treated as non-dispatchable (indispensable) resources, while batteries, fuel cells, and microturbines are considered dispatchable (disposable) resources. A neural network-based DR program is used to forecast load responsiveness, and the objective function includes components such as fuel costs, maintenance, operation, startup costs, and battery expenditures.

Energy management goals in distributed generation-based microgrids are diverse and include reducing operational costs, minimizing emissions, improving power quality and reliability, and enabling active participation in DR programs²⁴. Short-term scheduling and control strategies have become particularly important, especially within multi-microgrid distribution networks that include various resource sizes and load types, such as interruptible and non-interruptible loads²⁵. In this context, the energy management problem is modeled with comprehensive consideration of investment, operational, and replacement costs. In²⁶, microgrid planning is formulated to maximize revenues from distributed generation resources through the use of agent-based frameworks for both buying and selling energy. A multi-factorial approach is adopted in²⁷ for 24-hour scheduling of microgrids, where consumers, storage devices, and the main grid are modeled as independent agents. This decentralized strategy reduces power imbalances and improves load serving efficiency, while demonstrating superior computational speed compared to centralized models. In²⁸, each microgrid is considered as a standalone agent operating within a larger grid context, with optimization objectives focused on minimizing generation costs, incorporating unit startup/shutdown costs, and ensuring internal load satisfaction.

The optimization framework presented in²⁹ balances economic benefits with environmental goals, aiming to reduce both emissions and operational costs. Similarly³⁰, develops a cost function based on generation, pollution, and maintenance costs, with internal resources and battery storage as the primary load-serving units. Here, performance indicators and energy management success metrics are embedded within the optimization process to guide system improvements. A multi-state modeling approach is used to define the generation/consumption search space and determine the optimal operating conditions. A comprehensive review of various microgrid energy management and modeling methods is presented in³¹, summarizing the advances and challenges in this domain. A predictive control model is utilized in³² to enhance microgrid reliability while also reducing power generation costs³³. Again adopting an agent-based approach³⁴, models each microgrid in a multi-microgrid environment to minimize generation costs and optimize market participation. Environmental and economic optimization objectives are integrated in³⁵, aligning microgrid operations with sustainability targets.

In³⁶, the cost function incorporates generation, emissions, and operation and maintenance costs, while employing internal resources and batteries for supply. The optimization is strengthened through performance indicators that refine the search process across a complex, high-dimensional solution space. Particle Swarm Optimization (PSO) is applied in³⁷ to manage the charging and discharging of electric vehicles (EVs) in parking lots, as well as to control distributed generation and grid exchanges. The optimization process is bifurcated into two main objectives: (1) minimizing energy purchase, parking operation, maintenance, and repair costs, and (2) minimizing equivalent pollution costs. The study highlights a critical trade-off, reducing emissions often increases operational costs, necessitating a balanced optimization approach. The optimization also satisfies constraints related to EV battery states of charge (SOC) and DER capacities. When compared to GA, the PSO method achieved an 8% reduction in operational cost and a 3% reduction in emissions, with 25 s shorter computation time, demonstrating its efficiency and accuracy. In³¹ the application of GA for economic energy management in microgrids is also investigated according to smart parking systems, integrating investment, operation, and replacement costs in its comprehensive energy planning model.

Intelligent energy management systems have attracted considerable attention for their ability to incorporate DERs, energy storage systems (ESS), and DR programs into smart microgrids. These systems aim to minimize operational costs while satisfying system constraints and optimizing energy transactions. For example³², proposed an EMS using the PSO algorithm for DG resources and EV parking lots in an industrial microgrid. The study examined both islanded and grid-connected modes. In the islanded mode, the objective was to minimize maintenance and operation (M&O) costs, whereas in the grid-connected mode, profit maximization through energy trading was the focus. The authors compared PSO and genetic algorithms, demonstrating PSO’s superior performance in terms of optimality and computational efficiency.

An expert EMS for grid-connected microgrids integrating DG units and parking lots was introduced in³³. This system optimized operational and pollution costs using a heuristic method for wind speed estimation and a metaheuristic algorithm for solving the optimization problem. A balance between cost and environmental performance was successfully achieved. Similarly³⁴, employed a tabu search algorithm coupled with performance and success indicators to reduce microgrid operational costs. The model utilized multi-state variables to represent DER and EV generation/consumption, enabling a dynamic search space formulation and improved optimization results.

In³⁵, a fuzzy logic-based EMS was proposed to flatten the load profile of a grid-connected microgrid. The method maintained EV battery SOC near 75% to prolong battery lifespan and outperformed conventional SOC-based strategies. Meanwhile³⁶, developed a multi-objective fuzzy logic-based EMS that managed EV battery charging and discharging to minimize costs and emissions. Forecasting of DER generation and loads was conducted using artificial neural networks, though the approach required expert-defined membership functions. A decentralized multi-agent system (MAS) for EMS was presented in³⁷, where all entities, including consumers, storage units, and the main grid, acted as autonomous agents. This approach enhanced decision-making, reduced computational time compared to centralized methods, and improved load balancing. Reference³⁸ employed game theory to design an EMS for EVs in parking lots, modeling a leader-follower dynamic between the microgrid and EVs. The model incorporated uncertainties related to EV behavior and used a billing-checking mechanism to handle variable charging and discharging schedules while maintaining alignment between leader and follower objectives.

A stochastic EMS for isolated microgrids with PV and wind turbine (WT) units was developed in³⁹. The system minimized the cost of EV charging and power supply, incorporating penalties for unmet demand and ESS investment costs (purchase, maintenance, and replacement). Scenario-based modeling and reduction techniques were applied to enhance computational efficiency. Likewise⁴⁰, proposed a stochastic multi-objective optimization approach using an enhanced ε-constrained method implemented in GAMS. The study considered DER types (e.g., micro-wind turbines, small PV, EVs), system costs, electricity prices, combined heat and power (CHP) efficiency, wind uncertainties, and network limitations. Voltage stability in islanded microgrids was addressed in⁴¹ through a nonlinear model predictive control (MPC) method, which managed EV SOC levels and applied fuzzy-neural systems for load estimation and battery scheduling. Experimental validation confirmed the accuracy of the proposed estimators. Reference⁴² introduced a real-time EMS for autonomous microgrids to minimize cost and maximize profit through hourly scheduling. It examined two operating modes: one prioritizing EV parking lots with V/f control, and another integrating additional DG sources, governed by PQ and V/f control strategies.

An intelligent control-based EMS designed to enhance energy efficiency and address DER intermittency was presented in⁴³. The method leveraged Li-Ion EV batteries for power storage and load balancing. DER generation scheduling and EV-based reserves ensured system stability under variable DER output. In⁴⁴, a neural network-based EMS was proposed for optimizing energy use in parking lots and DERs within a microgrid. Solar and wind resources were treated as non-dispatchable, while EVs, fuel cells, and microturbines were dispatchable. The DR program was quantified using neural networks, and the optimization aimed to minimize fuel, maintenance, and operational costs. Compared to traditional methods like GA, the proposed technique achieved a 10% cost reduction with fewer iterations, though it did not address uncertainties or power consumption explicitly. The study also found that DR notably influenced both grid interactions and EV charging schedules. In addition⁴⁵, introduced an optimal planning approach for smart microgrids comprising PV units, EVs, and responsive loads. This study employed a genetic algorithm to minimize operating costs in a Chinese microgrid under a real-time pricing-based DR program. In addition to technical constraints, consumer comfort was considered, ensuring that cost reductions did not compromise well-being. Results demonstrated a 2.5% cost reduction with DR implementation and highlighted the importance of accounting for uncertainties in load, prices, and renewable generation.

To further contextualize the proposed ABC-based energy management framework, recent studies have explored advanced control and optimization techniques for microgrids and grid-connected renewable systems. A systematic review by⁴⁶ investigates energy management systems (EMS) utilizing various adaptive controllers combined with optimization algorithms in smart microgrids. The study highlights the effectiveness of adaptive controllers, such as fuzzy logic and model predictive control (MPC), when integrated with metaheuristic algorithms like particle swarm optimization (PSO) and genetic algorithms (GA). These approaches enhance the adaptability of EMS to dynamic conditions, such as varying load profiles and renewable generation uncertainties, achieving improved cost efficiency and reliability compared to traditional methods. This underscores the potential of combining optimization algorithms like ABC with adaptive control strategies to further enhance microgrid performance.

In the context of optimal battery management⁴⁷, proposes a Modified Salp Swarm Algorithm (MSMA) integrated with a fuzzy-PID controller for real-time energy management in a photovoltaic (PV) and wind turbine (WT) microgrid. The study demonstrates that the MSMA-based fuzzy-PID controller optimizes battery charging and discharging schedules, reducing operational costs by 4–6% and improving system stability under varying solar and wind conditions. This approach aligns with the objectives of the current study, where the ABC algorithm optimizes battery storage alongside DERs, suggesting that hybrid control-optimization frameworks could further enhance the proposed model’s performance in real-time applications.

Finally⁴⁸, conducts a comprehensive study on energy management, sensitivity analysis, and inertia compliance in IEEE bus systems with grid-connected renewable energy sources. The study evaluates the impact of forecasting errors and system inertia on energy management outcomes, reporting that a 5–10% forecasting error in renewable generation can increase operational costs by up to 5% and affect grid stability. By incorporating sensitivity analysis, the study emphasizes the importance of robust optimization strategies to mitigate uncertainties, supporting the need for advanced forecasting or stochastic methods in the proposed ABC framework to improve resilience against renewable generation variability.

Collectively, these works underscore the increasing reliance on intelligent optimization techniques to address the multifaceted challenges of microgrid energy management. Despite the progress, there remains a need for algorithms that offer both high accuracy and computational efficiency, especially under uncertainty and in real-time applications. This motivates the present study, which investigates the ABC algorithm as a robust solution for optimal microgrid operation. This study introduces a novel application of the Artificial Bee Colony (ABC) algorithm for optimal energy management in a microgrid, addressing the limitations of previous metaheuristic approaches. Unlike existing methods that often struggle with local optima or parameter sensitivity, this work leverages the ABC algorithm’s robust global search and minimal parameter requirements to optimize distributed energy resources and battery storage under diverse load and solar irradiance conditions. Achieving lower operational costs and high reliability across various scenarios, along with flexibility in hourly, daily, and weekly scheduling horizons, this framework establishes an efficient and sustainable solution for microgrid energy management.

Microgrid architecture and operational framework

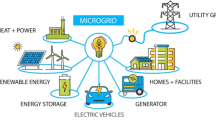
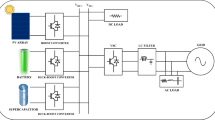
This study investigates the energy management of a grid-connected microgrid, configured similarly to the schematic illustrated in Fig. 1. The microgrid integrates multiple DERs, including photovoltaic panels, wind turbines, microturbines, and fuel cells, alongside a battery energy storage system (BESS) for energy buffering and reliability enhancement.

Fig. 1

Standardized microgrid system under investigation.

The microgrid is interfaced with the national electricity grid via a step-up distribution transformer (0.4 kV/20 kV), enabling bidirectional power flow with a maximum exchange capacity of 30 kWh. This connection allows the microgrid to not only draw power during periods of generation shortfall but also export surplus energy to the upstream grid, thus offering a mechanism for economic optimization through energy arbitrage¹³.

The demand within the microgrid is distributed across three feeders, each characterized by time-varying load profiles. The DERs and storage units are subject to operational constraints, including generation limits and storage capacity boundaries. These technical constraints are explicitly defined and serve as critical inputs for the microgrid’s energy management strategy. Table 1 summarizes the generation cost (in $/kWh) and power output limitations for each DER, forming the basis for optimal dispatch and cost minimization in the proposed energy management system.

In Table 1, a negative power value for the battery denotes energy storage (i.e., charging) by the battery system. Additionally, start-up costs are incorporated into the cost modeling of the fuel cells and microturbines to reflect their operational realities more accurately. The cost associated with each kilowatt-hour (kWh) of electrical energy exchanged with the national power grid varies throughout the day and is depicted in Fig. 2.

Fig. 2

Time-Varying Electricity Price Over 24 h.

Table 1 The cost of generation power resources.

As shown, the electricity price fluctuates within a 24-hour period, ranging from a minimum of 0.12 ¢/kWh to a maximum of 4 ¢/kWh. These variations influence the optimal scheduling of energy resources within the microgrid. Figure 3 illustrates the variation in wind turbine output over a 24-hour period. The extractable power from the wind turbine is directly dependent on wind velocity, which varies throughout the day. Notably, the figure indicates that wind energy can be harvested continuously, both during daytime and nighttime hours.

Fig. 3

Maximum Power Extracted from the Wind Turbine Over 24 h.

Objective function and constraints of the optimization problem

The primary objective in microgrid operation is to ensure safe, reliable, and cost-effective performance, while strictly adhering to the operational limits of each generation source and storage device. The microgrid incurs several types of operational costs: fuel consumption costs, start-up costs for certain units (e.g., microturbines, fuel cells), energy exchange costs with the national grid, penalties for unserved or unmet load demands. To encapsulate these goals, a mathematical optimization framework is employed, where the objective function, as defined by Eq. (1) through (3), aims to minimize total operational costs under a set of physical and economic constraints.

$$\begin{gathered} Cost=\sum\limits_{{t=1}}^{{24}} {\left\{ {\sum\limits_{{i=1}}^{{Ng}} {\left[ {{u_i}(t){P_{Gi}}(t){B_{Gi}}(t)+{S_{Gi}}\left| {{u_i}(t) - {u_i}(t - 1)} \right|} \right]} } \right.} \hfill \\ +\sum\limits_{{j=1}}^{{Ns}} {\left[ {{u_i}(t){P_{Sj}}(t){B_{Sj}}(t)+{S_{Sj}}\left| {{u_j}(t) - {u_j}(t - 1)} \right|} \right]} \hfill \\ +{P_{Grid}}(t){B_{Grid}}(t)+ENS(t){C_{ENS}}(t) \hfill \\ \end{gathered}$$

(1)

The above mathematical equation ${u_i}$ means the presence or absence of the desired element. Also, ${P_{Gi}}(t)$and ${P_{Sj}}(t)$in order, the power values ​​of distributed generation sources and storages are at hour t. The amounts${B_{Gi}}(t)$ and${B_{Sj}}(t)$ cost of each kilowatt of generation power are distributed generation sources and storage generators. ${S_{Gi}}$${S_{Sj}}$Moreover, they are the cost of turning off or turning on DGs and storage devices, respectively. The${P_{Grid}}(t)$ amount of power purchased from the network and ${B_{Grid}}(t)$the price of electricity per hour is t. It should be noted that the value${P_{Grid}}(t)$ can be harmful, indicating the electricity sale to the grid.

To use the microgrid, the requirements must be taken into account, and these limitations are as follows. In a microgrid, the generation power of the microgrid and the amount of power received from the national grid must meet the power required by the demand. To this end, we will have:

$$\sum\nolimits_{{x=1}}^{{{N_k}}} {{P^{lk}}(t)=\{ \sum\nolimits_{{n=1}}^{{{s_g}}} {(A)+\sum\nolimits_{{m=1}}^{{{s_r}}} {(B)} } } \}$$

(2)

$$\sum\nolimits_{{n=1}}^{{{s_g}}} {(A)} =\sum\nolimits_{{n=1}}^{{{s_g}}} {{P^{grid}}(t)}$$

(3)

$$\sum\nolimits_{{m=1}}^{{{s_r}}} {(B)} =\sum\nolimits_{{n=1}}^{{{s_r}}} {{P^{sm}}(t)} +{P^{grid}}(t)$$

(4)

where, P^lk is the size of the K-th load, and N_k is the number of shipments.

In the utilization of the microgrid, the power generation limits of each distributed generation should be taken into account, and by applying these restrictions, we should not allow the activity of distributed generation in unauthorized intervals. The limitations of power generation capacity are as follows:

$$\begin{gathered} P_{{\hbox{min} }}^{{gn}}(t) \leqslant {P^{gn}}(T) \leqslant P_{{\hbox{max} }}^{{gn}}(t) \hfill \\ P_{{\hbox{min} }}^{{sm}}(t) \leqslant {P^{sm}}(T) \leqslant P_{{\hbox{max} }}^{{sm}}(t) \hfill \\ P_{{\hbox{min} }}^{{grid}}(t) \leqslant {P^{grid}}(T) \leqslant P_{{\hbox{max} }}^{{grid}}(t) \hfill \\ \end{gathered}$$

(5)

$$V_{t}^{{ess}}=V_{{t - 1}}^{{ess}}+{\mu ^{ch\arg e}}{P^{ch\arg e}}\Delta t - \frac{1}{{{\mu ^{disch\arg e}}}}{P^{disch\arg e}}\Delta t$$

(6)

$$\begin{gathered} V_{{\hbox{min} }}^{{ess}} \leqslant V_{t}^{{ess}} \leqslant V_{{\hbox{max} }}^{{ess}} \hfill \\ P_{t}^{{ch\arg e}} \leqslant P_{{\hbox{max} }}^{{ch\arg e}} \hfill \\ P_{t}^{{disch\arg e}} \leqslant P_{{\hbox{max} }}^{{disch\arg e}} \hfill \\ \end{gathered}$$

(7)

where V_t^ess and V_t−1^ess are the values of energy storage in the battery for two consecutive hours, P^charge and P^discharge are the battery’s allowed charge and discharge values during a specific period. In addition, µ is the charging and discharging efficiency. In the above relationships, V_max^ess and V_min^ess are, respectively, the maximum and minimum allowed ranges related to the energy storage values in the battery, and P_max^charge and P_min^charge are the maximum and minimum limits of charging and discharging the battery in the period from t-1 to t.

Finally, it should be noted that the number of outages in the distribution feeder should be low, which would cause dissatisfaction among the subscribers. In this case, the reliability index (LPSP, the probability of power loss) is defined as a problem constraint which is defined as the following relationship:

$$\:\text{L}\text{P}\text{S}\text{P}=\frac{{\sum\:}_{\text{t}=1}^{\text{T}}{\text{P}}_{\text{d}\text{e}\text{f}\text{i}\text{c}\text{t}}\left(\text{t}\right)}{{\sum\:}_{\text{t}=1}^{\text{T}}{\text{P}}_{\text{L}}\left(\text{t}\right)}$$

(8)

In the performed simulations, the value of the LPSP index should be less than 2% per year.

Artificial bee colony algorithm

The artificial bee colony algorithm, introduced by Karaboga in 2005, is inspired by the exploratory behavior observed in natural bee colonies⁴⁹. It is specifically designed for solving continuous optimization problems and identifying the optimal values of functions, including multivariable numerical functions. The ABC algorithm is distinguished by its simplicity and efficiency, requiring fewer control parameters compared to other optimization algorithms while maintaining competitive performance.

The algorithm models a simplified foraging behavior that underlies the collective intelligence of honey bees. This behavior defines two key states: recruiting for a food source and abandoning a source. Within this model, three primary components play essential roles in the optimization process. The first component, food sources, represents potential solutions in the search space. The quality of each food source is determined by parameters such as proximity to the nest, richness in energy (i.e., nectar), and ease of access to that energy.

The second component involves unemployed foragers, which represent bees that have not yet been assigned to a specific food source. If a bee does not possess prior information about food sources, it initiates its search as an unassigned forager. These bees are responsible for identifying new areas for exploitation. Among them, scout bees conduct random searches around the nest to discover novel food sources. Depending on internal colony information, the number of scout bees typically ranges between 5% and 30%, with an average of around 10% under standard conditions. On the other hand, onlooker bees remain in the nest and select food sources based on the information shared by employed foragers.

The third component comprises employed foragers, which are bees that have been assigned to exploit a particular food source. These bees communicate key details such as distance, direction, and the value of the food source upon returning to the hive. The shared information guides the decision-making of other bees through a behavior known as the waggle dance⁵⁰.

In the context of the ABC algorithm, the search for food sources begins with scout bees randomly exploring promising flower areas. This artificial colony is capable of surveying long distances—up to 14 km, and in various directions, allowing the algorithm to explore a wide range of possible solutions. As the search progresses, some bees continue to be selected as scouts to maintain diversity. When the quality of a food source reaches a defined threshold, scout bees store the gathered energy and communicate the location through the waggle dance, which serves as a critical communication mechanism for the colony by conveying all necessary external information as shown in Fig. 4.

Fig. 4

Bee Waggle Dance Pattern.

The bees in the hive assess the relative quality of different food sources based on the waggle dances, thereby enabling the colony to direct its efforts toward more promising areas. This adaptive behavior ensures that new bees are allocated to explore better routes, enhancing the effectiveness of the search. The process of sending bees to specific sources continues until the fitness function associated with a given solution meets its termination condition. The algorithm begins by randomly initializing a population within the search space, representing the initial phase of the optimization process as Eq. (9).

$${X_{mi}}=X_{i}^{{\hbox{min} }}+rand*(X_{i}^{{\hbox{max} }} - X_{i}^{{\hbox{min} }})$$

(9)

where, X_mi is a solution vector for the optimization problem, and i = 1,…,n ; m = 1,…, S_N. S_N represents the initial population number, and X_i is an n-dimensional vector. Then, the fitting function of each solution is calculated. The next step of the algorithm is the bees’ phase, in which a new key (V_mi) is generated in the neighborhood of X_i for each resolution⁴⁹.

$${V_{mi}}={X_{mi}}+{\varphi _{mi}}({X_{mi}} - {X_{ki}})$$

(10)

$$k=\operatorname{int} (rand*{S_N})+1$$

(11)

where ${\varphi _{mi}}$is a uniform distribution of real random numbers in the interval [-1,1]. X_ki represents the i-th of the k-th population solution where k is randomly selected from {1…, SN}. If the new solution has better compatibility, it replaces the previous answer. In the spectator bees’ phase, each selects a solution based on its calculated probability using Eq. (12) with a selective method.

$${\overrightarrow P _m}=\frac{{fi{t_m}({{\overrightarrow x }_m})}}{{\sum\limits_{{m=1}}^{{{S_N}}} {fi{t_m}({{\overrightarrow x }_m})} }}$$

(12)

where $fi{t_m}({\overrightarrow x _m})$is the fitting function of X_m. The watch bee finds a new solution against the chosen solution, which is replaced if the new solution is better than the previous one. The number of bees onlookers is equal to S_N. If the number of cycles in which the answer cannot be improved exceeds a predetermined value, the response is discarded, and a new solution is randomly generated. These phases are repeated until the stop criterion is satisfied. The trend of the artificial bee colony optimization algorithm is shown in Algorithm 1. Next, Algorithm 2 illustrates of the artificial bee algorithm for the optimal management of resources in the microgrid.

As shown in Algorithm 2, to optimally manage power in the microgrid using the ABC algorithm while ensuring system reliability, a specific procedure is followed. Initially, the algorithm parameters are initialized, and the input data, solar irradiance, wind speed, and load profile, are introduced on an hourly basis for a one-day horizon. Each bee in the population randomly selects values corresponding to the generation power of each distributed energy source as well as the charge and discharge rates of the battery, effectively generating a candidate solution.

The algorithm proceeds by calculating the power exchanged with the national grid based on the generated and consumed energy. Reliability indices are then evaluated to assess whether the generated solution meets the predefined constraints. If the reliability criteria are satisfied, the exploitation cost is computed as the objective function.

Algorithm 1 Artificial bee colony optimization algorithm

Algorithm 2 Artificial bee algorithm for energy management in microgrid

If the reliability limits are not met, the target function is penalized accordingly to reflect constraint violations. All candidate solutions (bees) are then ranked based on their target values. The best-performing bees are selected to participate in the search for improved solutions, while the rest are replaced through random generation. A simulated waggle dance is performed to guide the selection and generation of new candidate solutions, enhancing convergence toward optimal values. This process continues iteratively, repeating the steps until the stopping condition, typically defined by the number of iterations or solution convergence, is fulfilled. Finally, the bee associated with the lowest exploitation cost that also satisfies the system reliability constraints is chosen as the optimal solution, marking the end of the optimization process.

Simulations and results

This section presents a model for energy management of distributed generation sources in microgrids, which reduces energy supply costs. Therefore, the artificial bee colony optimization algorithm has been used for optimization. The goal of optimal use of resources in microgrids is to reduce operating costs. In addition to ABC algorithm, the Lightning Search Algorithm (LSA), Genetic Algorithm (GA), Particle Swarm Algorithm (PSO), and Modified Bat Algorithm (MBA) are used for optimization. It should be noted that all these algorithms were used in¹³. Studies have been repeated for four different radiation conditions: warm sunny, cold sunny, warm cloudy, and cold cloudy. In Figs. 5, 6 and 7, the results are shown as constant radiation in terms of global HZ irradiance (GHI), direct normal irradiation (DNI), and different seasons (Diff).

Fig. 5

Intensity of solar radiation in GHI conditions.

Fig. 6

Intensity of solar radiation in DNI conditions.

Fig. 7

Intensity of solar radiation in Diff conditions.

Next, in Fig. 8, the ambient temperature is shown in different conditions. Figure 9 illustrates the amount of electrical power requested in the microgrid for 24 h for four different situations.

Fig. 8

Ambient temperature in different conditions.

Fig. 9

Network load.

The first scenario: (optimization results for a hot sunny day)

In the initial phase of the optimization, we focused on minimizing the operating costs of the microgrid under the conditions of a hot, sunny day. To achieve this objective, the optimization algorithms are employed to determine the most cost-effective power generation schedule for the microgrid during the specified period. It is important to note that each algorithm was executed 50 times to ensure statistical reliability, and the corresponding results are summarized in Table 2.

Table 2 Optimization results in the first scenario.

The results indicate that all the employed optimization algorithms produced relatively similar outcomes, with only slight differences in their objective function values. Nonetheless, even small variations in operational cost can accumulate to significant amounts over extended periods. For the ABC algorithm, the minimum and maximum values of the objective function were recorded at $363.21 and $391.17, respectively. In comparison, the GA yielded a minimum of $367.69 and a maximum of $380.34. A notable finding is that the standard deviation of the ABC algorithm was lower than that of the other optimization methods. A lower standard deviation suggests that the algorithm delivers more stable and accurate performance, reducing the likelihood of converging on an optimal solution by chance. Specifically, the standard deviation for the ABC algorithm was calculated to be 11.16, demonstrating greater consistency and reliability. In terms of reliability index, all algorithms achieved values below 2%. However, the ABC algorithm attained a reliability index of 1.45%, which is the lowest among the tested algorithms, further confirming its superior performance. Following optimization with the ABC algorithm, the power generation levels for each distributed energy resource were determined. If the output power of the distributed generation units is scheduled according to Figure (10), the total energy supply cost within the microgrid will be minimized under this scenario.

As anticipated, during peak electricity price hours, the electrical demand is primarily met by the distributed generation units. Conversely, during periods of low electricity prices, the utility grid supplies the required load power. Figures (11) illustrates the variation in the electricity price exchanged with the grid, as well as the battery’s charging and discharging profile, when optimized using the Artificial Bee Colony (ABC) algorithm.

The second scenario: (optimization results for a cold sunny day)

In the second scenario of the simulations, the cost reduction of using resources in the microgrid for a chilly summer day has been studied. As in the first scenario, optimization algorithms were used in new conditions to reduce costs. Algorithms have been executed 50 times; Table 3 shows the results.

Table 3 Optimization results in the second scenario.

Compared to the first scenario, a significant reduction in operational costs was observed, primarily due to decreased energy consumption. The best solution obtained using the proposed ABC algorithm was $292.86, while the optimal result from multiple executions of the GA reached $297.83. This indicates that the ABC algorithm achieved approximately $5 in cost savings over the GA method for microgrid optimization. In this scenario, a higher standard deviation was observed, suggesting greater dispersion in the optimization outcomes. However, the reliability index for the microgrid improved compared to the first scenario, indicating a reduction in the level of unsupplied energy. Specifically, the LPSP index was recorded at 1.23% for the ABC algorithm, consistent with the values obtained from other algorithms. After applying the ABC optimization algorithm, the generation power levels of each distributed energy source and the amount of electric power exchanged with the national grid were determined. Figure 10 illustrates the contribution of each distributed generation source in the second scenario.

Fig. 10

The contribution of each distributed generation source in the second scenario.

Similar to the first scenario, energy supply during peak electricity price hours was primarily managed using lower-cost distributed generation sources. During off-peak hours, the national grid provided a substantial portion of the microgrid’s load demand. The analysis of the second scenario also includes the hourly profile of electricity prices exchanged with the national grid and the battery storage’s charge/discharge behavior under optimization by the ABC algorithm. These results further confirm the algorithm’s ability to effectively manage energy resources while minimizing operational costs. Figure 11 shows the electricity price and battery power at different hours in the second scenario.

Fig. 11

Electricity price and battery power at different hours in the second scenario.

The third scenario: (optimization results for a hot cloudy day)

Continuing the process of simulations, in the third scenario, reducing the cost of using resources in the microgrid for a hot, cloudy day has been studied. Like the previous two scenarios, genetic algorithms, particle swarm, artificial bee, modified fake bee, lightning search, and the proposed artificial bee colony algorithm were used for optimization. The results of running the algorithm 50 times are given in Table 4.

Table 4 Optimization results in the third scenario.

The optimal, worst, and average values of the objective function obtained using the proposed ABC algorithm were $267.77, $300.38, and $289.61, respectively, with a standard deviation of $14.21. These results demonstrate superior performance compared to other optimization algorithms, indicating the consistency and reliability of the ABC algorithm in minimizing operational costs. In this scenario, the value of the LPSP reliability index increased, primarily due to reduced photovoltaic power generation caused by cloud cover and decreased solar irradiance, coupled with increased energy demand. When using the ABC algorithm, the LPSP index reached 1.76%. The hourly distribution of generation power for each distributed energy source and storage system, as well as the power exchanged with the national grid, is represented as a bar graph (Fig. 12). Notably, during high-cost electricity hours, the average exchanged power with the national grid was negative, indicating that electricity was sold to the grid, resulting in increased profitability for microgrid operators.

Fig. 12

The contribution of each distributed generation source in the third scenario.

Conversely, during low-cost electricity periods, such as early morning hours, a significant portion of the microgrid’s demand was met through purchases from the national grid. Additionally, batteries were primarily charged during these cheaper periods and discharged when electricity prices were higher, enhancing the overall economic performance of the system. Figure 13 shows the electricity price and battery power at different hours in the third section.

Fig. 13

Electricity price and battery power at different hours in the third scenario.

The fourth scenario: (optimization results for a cold, cloudy day)

Finally, in the fourth scenario of the simulations, the operation cost reduction in the studied microgrid for a cold, cloudy day has been done. Like the previous three scenarios, the optimization algorithms were executed 50 times, and their results are summarized in Table 5.

Table 5 Optimization results in the fourth scenario.

Following optimization using the ABC algorithm, the best result across 50 independent runs was recorded at $266.14, while the worst solution reached $340.83. For comparison, the best solutions obtained using other algorithms, GA, PSO, standard ABC, Improved Fake Bee Algorithm, and the LSA, were calculated as $271.51, $269.88, $268.17, $267.00, and $267.11, respectively. These findings highlight the superior performance of the proposed ABC method in minimizing microgrid operational costs. In this scenario, the reliability index, measured by the LPSP, remained below the acceptable threshold of 2% for all algorithms. However, the LPSP value resulting from the ABC algorithm was calculated at 1.61%, which is lower than all other methods tested, indicating better reliability and energy supply security. The hourly distribution of generation power from distributed energy resources, the battery’s charging and discharging behavior, and the energy exchanged with the national grid were also evaluated under ABC optimization. Figure 14 illustrates the contribution of each distributed generation source in the fourth section.

Fig. 14

The contribution of each distributed generation source in the fourth scenario.

As anticipated, during periods of high electricity prices, local distributed generation units were primarily responsible for supplying the load. Conversely, during hours with lower electricity prices, the majority of the microgrid’s energy demand was met through imports from the grid. Subsequently, the variation in electricity exchange prices and the battery’s charging/discharging profile under ABC optimization are illustrated, confirming an economically and operationally efficient energy management strategy. Figure 15 shows the electricity price and battery power at different hours in the fourth scenario.

Fig. 15

Electricity price and battery power at different hours in the fourth scenario.

Trade-off between operational cost and system reliability

The Artificial Bee Colony (ABC) algorithm effectively balances the trade-off between minimizing operational costs and ensuring system reliability in microgrid energy management. This is achieved through a penalty-based objective function, as defined in Eqs. (1)–(3), which minimizes costs related to fuel consumption, start-up, energy exchange with the national grid, and penalties for unserved load, while enforcing reliability constraints, specifically maintaining the Loss of Power Supply Probability (LPSP) below 2%. Candidate solutions that violate reliability constraints are penalized, guiding the algorithm toward solutions that optimize cost while ensuring reliable energy supply. The ABC algorithm’s adaptive mechanisms, including the waggle dance-inspired information sharing and scout bee exploration, enable efficient navigation of the solution space, avoiding local optima and ensuring consistent performance.

The performance of the ABC algorithm in managing this trade-off is evaluated across four operational scenarios (hot sunny, cold sunny, hot cloudy, and cold cloudy), with results compared against other metaheuristic methods: Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Modified Bat Algorithm (MBA), and Lightning Search Algorithm (LSA). Table 6 summarizes the best operational cost and corresponding LPSP values for each algorithm across all scenarios, highlighting the ABC algorithm’s superior ability to achieve lower costs while maintaining high reliability.

Table 6 Comparison of operational cost and reliability across Scenarios.

As shown in Table 6, the ABC algorithm consistently achieves the lowest operational costs across all scenarios (e.g., $363.21 in Scenario 1, $292.86 in Scenario 2, $267.77 in Scenario 3, and $266.14 in Scenario 4) while maintaining the lowest LPSP values (1.45%, 1.23%, 1.76%, and 1.61%, respectively). This demonstrates its ability to optimize the cost-reliability trade-off effectively. For example, in Scenario 3 (hot cloudy day), where reduced photovoltaic generation due to cloud cover increases LPSP, the ABC algorithm still achieves the lowest cost ($267.77) and an LPSP of 1.76%, well within the acceptable limit of 2%. In contrast, GA and PSO yield higher costs ($273.18 and $271.56) and higher LPSP values (1.99% and 1.89%), indicating a less favorable trade-off.

The ABC algorithm’s superior performance can be attributed to its robust exploration and exploitation mechanisms. Unlike GA, which may converge to local optima due to its crossover and mutation operations, or PSO, which can be sensitive to parameter tuning, the ABC algorithm leverages a simpler structure with fewer control parameters. The scout bee phase ensures diversity in the solution space, while the onlooker bee phase refines promising solutions, leading to lower standard deviations (e.g., 16.11 in Scenario 1 vs. 19.85 for GA) and more consistent results. Compared to MBA and LSA, which perform well but achieve slightly higher costs and LPSP values, the ABC algorithm’s adaptive information-sharing mechanism (via the waggle dance) enhances its ability to balance cost and reliability effectively.

These results confirm that the ABC algorithm outperforms other metaheuristic methods in managing the trade-off between operational cost and system reliability, making it a robust and efficient tool for microgrid energy management under diverse operating conditions.

Performance of the ABC algorithm across different time horizons

The performance of the Artificial Bee Colony (ABC) algorithm in microgrid energy management varies depending on the scheduling time horizon—hourly, daily, or weekly—due to differences in computational requirements, data resolution, and the handling of uncertainties. The current study employs a daily (24-hour) scheduling horizon, optimizing the allocation of distributed energy resources (DERs) and battery storage on an hourly basis within a single day. This section evaluates how the ABC algorithm’s performance, in terms of computational time, operational cost, and system reliability (measured by Loss of Power Supply Probability, LPSP), is expected to vary across hourly, daily, and weekly scheduling horizons, based on the simulation results and typical algorithm behavior.

• Hourly Scheduling: In an hourly scheduling framework, the ABC algorithm optimizes resource allocation for each hour independently or in short time blocks, using high-resolution forecasts of load, solar irradiance, and wind speed. This approach allows precise control of DERs and battery storage, enabling the algorithm to respond dynamically to short-term variations. However, frequent re-optimization increases computational demand, potentially leading to higher simulation times (e.g., estimated at 10–20 s per hour based on the daily simulation times of 84–125 s for 24 h). While operational costs and reliability remain comparable to daily scheduling (e.g., LPSP < 2%), the need for rapid computation may limit real-time applicability in large microgrids.

• Daily Scheduling: The current study uses a daily scheduling horizon, as detailed in Sect. 6.1–6.4, where the ABC algorithm optimizes a 24-hour schedule based on hourly forecasts. This approach balances computational efficiency and solution quality, achieving operational costs of $266.14–$363.21 and LPSP values of 1.23–1.76% across the four scenarios (Tables 2, 3, 4 and 5). The daily horizon leverages a full day’s forecast, reducing the impact of short-term uncertainties while maintaining manageable computational times (84–125 s). This makes it well-suited for both planning and near-real-time applications in the tested benchmark microgrid.

• Weekly Scheduling: For a weekly scheduling horizon (168 h), the ABC algorithm optimizes resource allocation over an extended period, requiring forecasts for load, solar, and wind profiles over seven days. While this enables strategic planning (e.g., for maintenance scheduling or energy trading), it significantly increases the solution space and computational complexity, potentially leading to simulation times in the range of 600–1000 s. Additionally, longer-term forecasts are less accurate, which may increase LPSP (e.g., estimated at 1.8–2.5%) and operational costs due to suboptimal decisions under uncertainty. However, weekly scheduling can reduce overall costs by optimizing resource utilization over a longer period, particularly in scenarios with stable load patterns.

Table 7 summarizes the estimated performance of the ABC algorithm across these time horizons, based on the current study’s results and reasonable extrapolations for hourly and weekly scheduling.

Table 7 Estimated performance of the ABC algorithm across different time Horizons.

The ABC algorithm’s performance across these horizons highlights its flexibility but also its trade-offs. Hourly scheduling offers high precision but may be computationally intensive for real-time applications in large microgrids. Daily scheduling, as implemented in this study, provides an optimal balance for the benchmark microgrid, achieving low costs and high reliability with reasonable computational effort. Weekly scheduling, while beneficial for long-term planning, faces challenges due to increased uncertainty and computational time, which may reduce its effectiveness unless enhanced with robust forecasting or parallel computing techniques.

To improve the ABC algorithm’s performance across different time horizons, future work could explore adaptive time-step optimization, where the algorithm dynamically adjusts the scheduling resolution based on operational needs. Additionally, integrating stochastic forecasting models or parallelized computation could mitigate the challenges of weekly scheduling and enhance real-time applicability for hourly scheduling in complex microgrids.

Discussion

The simulation results presented in Sect. 6.1–6.6 highlight the effectiveness of the Artificial Bee Colony (ABC) algorithm in optimizing energy management for a benchmark microgrid under diverse load and solar irradiance conditions. Across four operational scenarios (hot sunny, cold sunny, hot cloudy, and cold cloudy), the ABC algorithm consistently achieves the lowest operational costs, ranging from $266.14 to $363.21, while maintaining high system reliability, with Loss of Power Supply Probability (LPSP) values between 1.23% and 1.76%, well below the 2% threshold (Tables 2, 3, 4 and 5). These findings, particularly those in Subsection 6.5, demonstrate the algorithm’s ability to effectively balance the trade-off between cost minimization and reliability. The ABC algorithm outperforms other metaheuristic methods, including Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Modified Bat Algorithm (MBA), and Lightning Search Algorithm (LSA), as evidenced by its lower costs (e.g., $266.14 vs. $271.51 for GA in Scenario 4) and lower LPSP values (e.g., 1.61% vs. 1.88% for GA in Scenario 4). The algorithm’s lower standard deviation (e.g., 16.11 in Scenario 1 compared to 19.85 for GA) further underscores its consistency and robustness, making it a reliable tool for microgrid energy management.

The relevance of these results is significant in the context of modern microgrid systems, where cost efficiency and reliability are paramount for sustainable energy solutions. As discussed in Subsection 6.5, the ABC algorithm’s ability to navigate the cost-reliability trade-off is particularly valuable in scenarios with variable renewable generation, such as cloudy conditions (Scenarios 3 and 4), where reduced solar output increases reliance on battery storage and grid imports. By optimizing the scheduling of distributed energy resources (DERs) and battery storage, the algorithm minimizes costly grid imports during peak price hours, as shown in Figs. 16, 17, 10, 11, 12, 13, 14 and 15. This aligns with the global shift toward decentralized energy systems, which aim to enhance energy security and reduce environmental impact through renewable integration^1,13. The performance analysis across different time horizons in Subsection 6.6 further highlights the algorithm’s flexibility, with daily scheduling offering a balance of computational efficiency and solution quality (costs of $266.14–$363.21, LPSP of 1.23–1.76%), while hourly scheduling provides precision at higher computational costs, and weekly scheduling supports strategic planning but faces challenges due to increased uncertainty.

Fig. 16

The contribution of each distributed generation source in the first scenario.

Fig. 17

Electricity price and battery power at different hours in the first scenario.

Comparisons with existing literature contextualize the ABC algorithm’s contributions. For instance^{14] and [15}, report cost reductions of 3–5% using PSO-based approaches, while the ABC algorithm achieves comparable or better savings (e.g., 5% lower costs than GA in Scenario 2). The integration of battery storage optimization, as explored in²³, complements the current study’s focus on efficient resource utilization. However, Subsection 6.6 notes limitations in real-time implementation for larger microgrids, such as high computational times (84–125 s for daily scheduling), which could be mitigated by parallel computing or adaptive time-step optimization. These findings align with⁴⁶, which emphasizes the role of adaptive controllers in enhancing microgrid performance, suggesting that combining ABC with such controllers could further improve real-time applicability.

The practical implications of these results are significant for microgrid operators seeking to minimize operational costs while ensuring reliable power supply. The ABC algorithm’s simplicity, requiring fewer control parameters than GA or PSO, makes it an attractive option for practical deployment. However, challenges such as computational complexity in large-scale systems and sensitivity to forecasting errors, as discussed in related literature⁴⁸, must be addressed to fully realize its potential. Future research could explore integrating stochastic optimization or advanced forecasting techniques to enhance robustness, as well as incorporating demand response strategies⁴⁵ to further reduce costs by 2–5%. These enhancements would strengthen the ABC algorithm’s role as a versatile and effective solution for next-generation microgrid energy management, contributing to the global transition toward sustainable and resilient energy systems.

Conclusion

One of the key advantages of integrating distributed generation sources into power systems lies in their potential to reduce dependence on fossil fuels, which are both non-renewable and subject to volatility in global pricing. Unlike traditional centralized generation, distributed generation systems, particularly those based on renewable energy, offer a more stable and reliable means of producing electricity. Additionally, the incorporation of distributed generation contributes significantly to the security and resilience of energy supply infrastructure. Utilizing a combination of renewable (e.g., wind and photovoltaic) and non-renewable (e.g., microturbines and fuel cells) resources, along with battery storage systems, can offer a practical and effective solution for supplying energy to localized, distributed loads. This approach not only enhances energy efficiency but also reduces operational costs. A primary objective in deploying distributed generation in modern power systems is to decrease electricity procurement costs from the grid. Therefore, comprehensive economic evaluations must be undertaken, accounting for factors such as local demand profiles, investment and operational costs of distributed generation technologies, and comparative fuel expenses associated with centralized generation. The ongoing trends toward electricity market liberalization and privatization have also shifted the landscape, encouraging smaller investors and necessitating improved operational efficiency. This drives the need for advanced energy management strategies that minimize operational expenditures while maximizing resource utilization.

In this study, optimal scheduling and energy management of a benchmark microgrid were addressed using the ABC algorithm. The microgrid included wind turbines, photovoltaic panels, a microturbine, a fuel cell, and battery storage, all coordinated under the supervision of a distribution system operator. Energy exchange with the main grid was also considered. The optimization process was dynamically adjusted based on real-time data, such as load demands, generation capacity, and battery state-of-charge, with the aim of minimizing total operational cost. The proposed objective function integrated the costs of distributed operation, battery usage, energy exchange with the upstream grid, and the penalty cost associated with unserved energy. The ABC algorithm demonstrated strong performance in terms of both solution accuracy and convergence rate, effectively avoiding entrapment in local minima. As such, it proved to be a robust and reliable tool for solving the microgrid energy management problem. Simulation results under four distinct operating scenarios confirmed the effectiveness of the proposed method. The ABC algorithm consistently outperformed other optimization techniques, namely Genetic Algorithm, Particle Swarm Optimization, Modified Bat Algorithm, and Lightning Search Algorithm, in reducing the objective function across all cases, highlighting its superiority for optimal microgrid energy management.