Introduction

Hydrological modelling is an important tool in water resource planning, flood hazard mapping and infrastructure design1,2,3. It simulated the hydrological processes such as precipitation, infiltration, surface runoff, and channel flow to predict how the water will flow in a watershed4,5,6. Hydrologic Engineering Center’s Hydrologic Modelling System (HEC-HMS) is the most commonly used model among the commonly used hydrological models to analyse flood risks under different hydrological conditions7,8,9. The integration of these models with remote sensing (RS) and geographic information system (GIS) technologies has significantly increased the accuracy of these models10.

Event-based rainfall-runoff models simulate the hydrologic responses of individual peak storm events, which makes them ideal for flood forecasting and infrastructure design11,12. These models differ from continuous models in the aspect that they focus on individual storms, hence eliminating the computational needs but capturing peak discharges, which are needed for infrastructure design9. The models prove useful in areas with poor data availability, as in the Kashmir region, where flash flood occurrence and variable rainfalls necessitate efficient stormwater management strategies13. Loss (infiltration), transformation (generation of runoff), and routing processes form the essential elements, each of which is to be calibrated based according to local conditions7,14,15. HEC-HMS is broadly used for event-based modelling. Its modular structure supports various methods: SCS Curve Number for losses, Snyder’s Unit Hydrograph for transformation, and Muskingum routing16. Many studies globally have employed hydrological models to analyse flood dynamics and develop design storms. HEC-HMS was introduced by the U.S. Army Corps of Engineers (USACE) as a successor to HEC-1, with capabilities of advanced hydrological simulation16,17,18. The efficiency of HEC-HMS in the assessment of flood peaks and hydrographs at different return periods has been reported by several studies. Early studies19,20,21 showed the reliability of the HEC-HMS model in simulating rainfall runoff processes. Furthermore, some studies showed the effect of climate change22 and land-use change analysis23 on flood vulnerability, which highlights a rising susceptibility to flood risks. Recent studies have included radar-based rainfall integration for urban floods24coupled with HEC-HMS/HEC-RAS modelling for hazard mapping25and transboundary flood assessments26. These studies highlight the effectiveness of HEC-HMS for flood risk management under different geographical and hydrological conditions.

In India, HEC-HMS has been widely used for flood simulations of major river basins. Mandal and Chakrabarty27 used HEC-HMS coupled with HEC-RAS to showcase the utility of the model in mountainous basins by simulating flash floods in the Teesta Watershed and delineating flood-prone areas. Koneti et al.28 estimated the effect of land use changes on runoff processes and found the model to be reliable for long-term hydrological modelling. In urban flood studies, Rangari et al.29 applied HEC-HMS to simulate extreme storm events in Hyderabad, identifying drainage limitations with a peak discharge of 590.5 m³/s. Natarajan and Radhakrishnan17 further focused on the need for an integrated hydrologic and hydraulic modelling approach in urban flood studies. Dimri et al.30 modelled streamflows for the Tehri Dam reservoir, showing the capability of the model in capturing seasonal variability. Vegad et al.31 highlighted the role of reservoir operations in flood management by simulating the historical floods of the Ganga-Brahmputra catchments.

Numerous comparative studies have underscored the strengths of HEC-HMS over alternative models such as SWAT, MIKE NAM, HBV, and artificial neural networks (ANN), especially for event-based flood modelling. In a recent study in the sub-humid tropical Kabini Basin of Kerala, Prakash et al.32 demonstrated that HEC-HMS outperformed SWAT in simulating peak discharges, making it more suitable for flood-focused hydrological modelling in Indian conditions. Similarly, Tibangayuka et al.33 evaluated HEC-HMS, HBV, and ANN models in a high-humidity, data-scarce tropical catchment and found HEC-HMS to be superior, achieving NSE values of 0.84 during validation, compared to 0.64 for HBV and 0.55 for ANN. These results underscore the robustness of HEC-HMS in replicating observed hydrographs under variable data availability and climatic regimes. Vo et al.34 compared MIKE NAM, MIKE SHE, SWAT, and HEC-HMS in two Vietnamese stations. Their findings showed that HEC-HMS and MIKE SHE consistently achieved high correlation coefficients and lower RMSE values during both calibration and validation, outperforming both MIKE NAM and SWAT. Recent studies suggest that coupling HEC-HMS with machine learning enhances simulation accuracy in data-scarce catchments. Mugume et al.35 and Narayana Reddy and Pramada36 demonstrated the effectiveness of HEC-HMS–ANN hybrids for improved streamflow and runoff predictions, indicating a promising direction for future hydrologic modelling.

Advances in hybrid methods now couple hydrodynamic models with machinelearning techniques, improving the floodhazard susceptibility mapping in a mountainous–urban environment37. Sensitivity analysis of 2D flood inundation models, such as the Tous Dam study, has highlighted the importance of model parameters in simulating flood extent38. Riskbased design tools built on hydrodynamic simulations can visualise how floodprotection dikes redistribute expected annual damages across a floodplain39. In a similar context, Tariq et al40. emphasises on selecting measures that align with riskbased floodmanagement principles rather than fixed returnperiod practices. Hanif et al41. demonstrated that high-resolution satellite-derived land cover classifications, generated using machine learning algorithms, have a significant impact on hydrological model outputs, thereby underscoring the necessity of incorporating fine-scale inputs for accurate simulation and analysis. In this context, this study is novel in its event-based, sub-watershed-scale simulation using high-resolution rainfall inputs to derive design storms for multiple return periods across 24 sub-watersheds in the Jhelum Basin, an aspect that remains underexplored in the literature.

Lately, the urban centres such as Srinagar, Anantnag and Baramulla of Kashmir Valley have been experiencing uncontrolled urbanisation42,43. This unplanned urbanisation, along with changing land-use patterns44 and increasing climate variability, has significantly amplified the susceptibility of the Jhelum river and its tributaries to disastrous flood events45,46. The past floods, especially the 2014 flood, highlight the growing flood risk in the region47,48. Previous studies49,50,51,52,53 have employed various hydrological and hydraulic models—including MIKE 11 NAM, SWAT, HEC-RAS, and HEC-HMS to examine flood behaviour in the valley. However, most of these studies have focused on long-term hydrological trends or large-scale analyses, often overlooking short-duration, event-based flood simulations at the sub-watershed level.

Despite existing studies on flood modelling in the Kashmir Valley, there is a lack of comprehensive research on design storm development and event-based hydrological analysis for sub-watersheds. The IDF curve study by Dar and Maqbool54 was limited to data from only six rainfall gauging stations, which constrains its spatial representativeness and leaves many smaller sub-watersheds in the Kashmir Valley inadequately characterised in terms of flood risk. However, flood response is highly sensitive to spatial heterogeneity in terrain, soil types, and land use patterns, factors that vary considerably across the valley. Addressing this variability requires a high-resolution rainfall and finer modelling scale that can reveal localised flood characteristics and inform site-specific risk management.

The core objective of this study is to generate sub-watershed level design storms in the data-scarce Jhelum Basin using an event-based HEC-HMS framework. This is achieved by integrating high-resolution, gridded satellite rainfall data to construct hyetographs for varying return periods and applying them across 24 delineated sub-watersheds. By focusing on sub-watershed scale analysis, this study captures the spatial variability in flood behaviour driven by topography, land use, and soil conditions, offering a more precise understanding of flood risks and hydrologic responses.

This research fills a critical gap by demonstrating how high-resolution rainfall inputs and distributed event-based modelling can be applied effectively in data-limited mountainous basins. The findings aim to support improved flood forecasting, localised hazard mapping, and adaptive flood management strategies for the Kashmir Valley.

Materials and methods

Study area

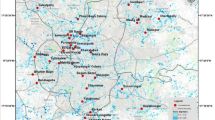
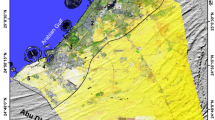
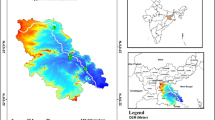
This study focuses on the Jhelum River Basin within the Kashmir Valley, extending up to its watershed outlet at Uri, a crucial hydrological unit of the larger Jhelum River system, which lies within the northwestern Himalayas. The basin is located geographically between the latitudes 33°20′30″N and 34°40′40″N and longitudes 73°42′30″E and 75°45′23″E, covering an area of 13,530.8 km2. The valley consists of alluvial plains in the low-lying areas and Himalayan peaks surrounding these plains, with elevation ranging from 1,069 m to 5,361 m above sea level, leading to different climatic and hydrological conditions. The basin encompasses 24 major watersheds (Fig. 1), each possessing unique hydro-geomorphological characteristics that control water movement in the basin55. The main soil types in the region include loamy and clay loam textures, which control the groundwater recharge and storage56 (Fig. 2) (Fig. S1 of the supplementary appendix). The valley is dominated by forest and horticulture land uses (Fig. S2 of the supplementary appendix). The annual temperature in the region varies from a low of −10 °C during winter to a high of 35 °C in summer57,58. The region receives precipitation both in the form of rainfall and snow59with a mean annual rainfall of approximately 840 mm60 and an average snowfall depth of around 30–35 cm, which has shown a declining trend over recent decades61.

Fig. 1
figure 1

(Source: SRTM DEM, https://earthexplorer.usgs.gov).

Geographic and Topographic map of study area.

Full size image

Data sets used

The study employed multiple datasets, as listed in Table 1 for model development, calibration, and validation.

Table 1 Summary of data sources and applications for hydrological Modelling.
Full size table

Methodology

The Jhelum Basin and its subwatersheds were delineated using a 30 m spatial resolution SRTM DEM in HECGeo-HMS. The land use/land cover (LULC) (Fig. 2) and the soil maps were processed in ArcMap 10.8 to derive a hydrological soil group map (HSG) and Curve Number (CN) grid (Fig. S3 and Fig. S4 of the supplementary appendix) for the study area, which was subsequently incorporated into the parameters file of the HEC-HMS model to simulate rainfall-runoff processes at the subbasin level. Spatially distributed rainfall inputs were derived from two sources: long-term Climate Hazards Group InfraRed Precipitation with Station data (CHIRPS) gridded rainfall data (1980–2022), (Fig. S5 of supplementary appendix), used to develop watershed-specific hyetographs and design storms, and IMD gridded rainfall DSS (Data Storage System) data (August 2020–August 2023), employed to calibrate the generated runoff hydrographs. Calibration of the model was performed with daily streamflow records at Sangam, Ram Munshibagh, and Asham gauging stations. Finally, design storms for varying return periods were simulated in the model to calculate peak discharges across the 24 sub-watersheds. The methodological workflow is summarised in Fig. 3.

Fig. 2
figure 2

(Source: generated from data obtained from https://earthexplorer.usgs.gov/).

LULC and Soil maps of Jhelum basin.

Full size image
Fig. 3
figure 3

Methodology Framework.

Full size image

Model development

The basic structure of the model comprises a (i) Basin model, (ii) Meteorological model, (iii) Control specification, and (iv) Time series manager. The hydrological model of the Jhelum basin, developed using the HEC-HMS program, is shown in Fig. 4.

Fig. 4
figure 4

(Source: generated in HEC-HMS 4.12 software using data obtained from https://earthexplorer.usgs.gov/).

Basin model of the Jhelum basin.

Full size image

Development of basin model

The basin model of grid resolution of 2 km x 2 km was developed using terrain pre-processing and basin processing in HEC-GeoHMS. Terrain pre-processing involves a series of steps for generating the stream network, basin boundary, and drainage outlets62,63. The outlet is defined by a batch point, and then the upstream watershed is discretised into sub-basins64. Creating a basin model of the Jhelum basin for adding various watershed characteristics and parameters into the model is the first step towards model development. To complete this step, a control point was set up at the outlet of the lower Jhelum subbasin51.

Estimation of initial losses

The Soil Conservation Service Curve Number (SCS-CN) method65 was used to calculate the initial losses (Eq. 1), due to its suitability for event-based rainfall-runoff modelling and minimal input requirements, which was helpful in the data-scarce Jhelum Basin66,67. A spatially distributed CN grid was used to estimate the infiltration losses across sub-basins.

$$Q = \frac{{\left( {P - I_{a} } \right)^{2} }}{{\left( {P - I_{a} - S} \right)}};\:I_{a} = 02\:S;\:Q = \frac{{\left( {P - 0.2S} \right)^{2} }}{{\left( {P + 0.8S} \right)}};\:S = \frac{{25400}}{{CN}} - 254$$
(1)

Where, Q = direct runoff; P = precipitation; Ia = Initial abstraction; S = potential maximum retention; CN = Curve Number.

Transformation of rainfall to runoff

The ModClark transformation method68 was utilised to convert rainfall into runoff. The ModClark method was selected over the Snyder unit hydrograph because it is explicitly designed for gridded precipitation inputs16. This method combines a gridded time-area histogram with linear reservoir routing, improving spatial representation compared to the lumped time-area approach in the original Clark method16,69. The watershed is discretised into grid cells, each assigned a travel time index (Tt, cell​) relative to the watershed’s time of concentration (Tc, watershed) and its normalised flow distance:

$$T_{{t,cell}} = T_{{c,watershed}} \left( {D_{{cell}} /D_{{\max }} } \right)$$
(2)

Where, Dcell = distance from a specific grid cell to the outlet of the basin; Dmax = Longest travel path from grid cell to outlet.

The primary input parameters include Tc and storage coefficient, both of which were derived using basin geomorphological parameters such as watershed area, longest flow path, and basin slope. The Tc was calculated using the using the Kirpich empirical formula proposed by Kirpich70as shown in Eq. (3).

$$\:{{T}}_{{c}}=0.0195\frac{{{L}}^{0.77}}{{{S}}^{0.385}}$$
(3)

Where, Tc= time of concentration; L = Basin length and S = basin slope.

Estimation of baseflow

The Linear Reservoir Method was utilised to simulate subsurface flow processes, effectively representing baseflow contributions to streamflow in event-based modelling applications71,72. This method employs one to three linear reservoirs (layers) to model baseflow recession following a storm event. In this study, two reservoirs were employed with initial conditions comprising a baseflow of 1 m³/s, a partition fraction of 0.5, and two routing steps per layer. The routing coefficient was set equal to the storage coefficient for each subbasin to ensure that the routing time interval aligned with the natural drainage rate of the storage element. This alignment preserves the physical behaviour of baseflow recession and minimises numerical damping. The trial-and-error method was used to optimise these parameters through calibration.

Channel routing setup

Flood wave propagation was modelled using the Muskingum routing method73,74, which solves the continuity equation to calculate outflow (Ot) and storage while accounting for hysteresis effects. The Muskingum method was selected due to the limited availability of channel cross-sectional data for the Jhelum River and its demonstrated reliability in previous studies of ungauged basins75. The governing equation76 (Eq. 4) is expressed as:

$$O_{t} = \left( {\frac{{\Delta t - 2KX}}{{2K\left( {1 - X} \right) + \Delta t}}} \right)I_{t} + \left( {\frac{{\Delta t - 2KX}}{{2K\left( {1 - X} \right) + \Delta t}}} \right)I_{{t - 1}} + \left( {\frac{{2K\left( {1 - X} \right) - \Delta t}}{{2K\left( {1 - X} \right) + \Delta t}}} \right)O_{{t - 1}}$$
(4)

where Ot and It are the outflow (m³/s) and inflow (m³/s) at time t, respectively; K is the travel time of the flood wave (hours); X is a dimensionless weighting factor (0 ≤ X ≤ 0.5); and Δt is the computational time step (hours). In this study, the value weighing factor (X) was assigned as 0.2, and the time of travel (K) for all 11 delineated reaches was calculated using Kirpich’s formula (Eq. 3).

A constant loss/gain method was used to simulate bidirectional interactions between streamflow and subsurface storage, capturing both losses (such as infiltration from the channel into groundwater) and gains (such as baseflow contributions from groundwater to the stream). This method was selected due to its minimal data requirements and compatibility with all routing techniques available in HEC-HMS16. It operates by applying a constant volumetric rate and a fractional adjustment to the routed flow at each reach, thus approximating stream–aquifer exchanges. In the absence of spatially distributed groundwater data, this approach offers a simplified yet effective means to represent subsurface flow processes. The loss/gain parameters were applied uniformly across all delineated reaches. The meteorological model defines the boundary conditions for the watershed throughout the simulation period and governs the spatial and temporal distribution of rainfall throughout individual sub-basins77,78. In this study, two metrological models were developed, one by using IMD gridded rainfall as a precipitation method and the other by specified hyetographs for each subbasin.

The control specification is a crucial aspect of the project that manages simulation runs, defining their start and end times. Five control specifications were set up for five identified peak events and eight additional ones for eight different return periods. The time series data manager assigns daily records of precipitation and streamflow, with computations conducted on a daily time step. In order to assign the required data, twenty-four (24) precipitation gauges for 24 subbasins and three (3) discharge gauges for three (3) computation points, namely Sangam, Ram Munshibagh and Asham, were set up. In addition to the above, a gridded data manager was set up to add IMD’s gridded rainfall DSS for the watershed.

Calibration and validation

Calibration systematically fine-tunes watershed parameters to ensure the simulated hydrograph closely aligns with the observed hydrograph79,80. In this study, the HEC-HMS model was calibrated and validated using daily discharge data from three gauging stations—Sangam, Ram Munshibagh, and Asham—spanning August 2020 to August 2023. Five significant flood peak events were identified during this period. The first three events (2020–2021) were utilised for calibration, while the last two (2022–2023) were used for validation. A manual calibration was used, where the initial parameter estimates obtained during hydrologic pre-processing were iteratively adjusted through a trial-and-error approach to assess optimal model parameters. Model performance was assessed using the coefficient of determination (R²), Nash-Sutcliffe Efficiency (NSE), RMSE-observations standard deviation ratio (RSR) and percent bias (PBIAS)81,82,83,84. The coefficient of determination (R²) quantifies the strength of the linear relationship between observed and simulated values, with values ≥ 0.70 generally reflecting good model performance. The Nash–Sutcliffe Efficiency (NSE) assesses the predictive accuracy of the model, where values > 0.5 are deemed acceptable. The RMSE–standard deviation ratio (RSR), which normalizes the root mean square error by the standard deviation of observed data, is considered indicative of good performance when values are ≤ 0.60. Percent bias (PBIAS), which measures the average tendency of the simulated values to over- or underpredict observations, is regarded as satisfactory when the absolute value falls within ± 25%16. Sensitivity analysis was carried out alongside calibration to identify the critical watershed parameters. The calibrated model was then evaluated for its predictive capability and subsequently used to generate flood hydrographs (design storms) at the sub-basin level for various return periods.

Results and discussions

Sensitivity analysis

Sensitivity analysis aids in understanding the responsiveness of model outputs to input parameters and informs calibration priorities85,86. Given the event-based modelling approach and limited availability of high-resolution input data, the analysis focused on parameters associated with the SCS-CN loss method, ModClark transformation, linear reservoir baseflow, and Muskingum channel routing. Among the tested parameters, the Curve Number (CN) exhibited the highest sensitivity, with a ± 5% variation causing up to 12% deviation in peak discharge and 9% in runoff volume, which is consistent with findings from earlier studies87. Time of concentration (Tc) and storage coefficient from the ModClark method significantly influenced hydrograph timing and attenuation. Adjustments to Tc altered the lag between rainfall and runoff response, while the storage coefficient modulated peak attenuation. This shows the importance of basin geomorphology in flood simulation and the effectiveness of Kirpich’s empirical equation70 for estimating Tc based on slope and flow length. In Muskingum routing, the travel time (K) impacted outflow peaks more than the weighting factor (X). Parameters related to baseflow (routing coefficient, partition fraction) showed moderate sensitivity, mainly affecting the hydrograph’s recession limb. This insight was instrumental in guiding the manual calibration process, emphasising CN, Tc and K as the critical parameters and supporting prioritisation of these parameters in future studies and uncertainty assessments. Table 2 summarises the relative sensitivity of the key parameters.

Table 2 Summary of the relative sensitivity of the key parameters.
Full size table

Calibration and validation

The model was calibrated at three important gauging sites along the main Jhelum River using three observed events to ensure the model’s reliability for simulating storm runoff in the Jhelum Basin (Table S1 of the supplementary appendix). During the calibration phase (Events 1–3), the model exhibited strong agreement with observed discharge (Figs. 5, 6 and 7), with R² ranging from 0.78 to 0.98, NSE values between 0.568 and 0.894 and RSR values of 0.3 to 0.6. PBIAS values largely fell within the acceptable range of ± 25% (Table 3). The slightly higher negative biases during Event 2 at RM Bagh (–20.44%) and Asham (–17.98%) suggest localised overestimation. These deviations may be attributed to spatial variability in rainfall, antecedent soil moisture conditions, or limitations in capturing urbanised flow dynamics88,89. These results confirm the model’s capability to simulate event-based runoff across spatially diverse catchments88.

In the validation phase (Events 4–5) (Table S2 of the supplementary appendix), model performance remained consistent or improved, reinforcing the robustness of the calibrated parameters (Figs. 8 and 9). R² values exceeded 0.80 across all sites, reaching as high as 0.97 at RM Bagh in Event 5. NSE values also remained strong (≥ 0.70 at all locations), with the highest efficiency (0.92) observed at Sangam. Although PBIAS values were slightly negative during validation (ranging from − 17.68% to − 10.97% in most cases), they remained well within acceptable thresholds, indicating moderate overprediction but no systematic bias (Table 4).

The model’s consistent performance in both calibration and validation phases, especially in achieving R² > 0.79, NSE > 0.56, RSR < 0.6 and |PBIAS| < 25% across varied events, underscores its suitability for flood risk assessment and design storm estimation in the study area. The inclusion of spatially distributed soil, land use, and rainfall data likely contributed to this high level of predictive accuracy89,90.

Table 3 Calibration statistics for storm events at selected Jhelum basin Stations.
Full size table
Fig. 5
figure 5

Plot of Observed vs. Simulated flow at three stations for Event 1 (19-Aug-2020 to 04-Sep-2020).

Full size image
Fig. 6
figure 6

Plot of Observed vs. simulated flow at three stations for Event 2 (19-Mar-21 to 29-Mar-21).

Full size image
Fig. 7
figure 7

Plot of Observed vs. simulated flow at three stations for Event 3 (27-Jul-2021 to 08-Aug-2021).

Full size image
Table 4 Validation statistics for storm events at selected Jhelum basin Stations.
Full size table
Fig. 8
figure 8

Plot of Observed vs. simulated flow at three stations for Event 4 (17-June-2022 to 29-June-2022).

Full size image
Fig. 9
figure 9

Plot of Observed vs. simulated flow at three stations for Event 5 (15-Apr-2023 to 25-Apr-2023).

Full size image

Design storms for different return periods

The calibrated hydrological model simulated runoff across 24 watersheds of the Jhelum Basin for eight return periods (e.g., 2, 5, 10, 25, 50, 100, 200, 500 years). Results indicate a clear upward trend in design storm intensities (peak discharge in m³/s) with increasing return period (Figs. 10, 11 and 12), reflecting the non-linear escalation of extreme rainfall and runoff responses91,92. Table 5 lists peak discharges for each watershed at different return periods, highlighting variability across sub-basins.

Among the watersheds analyzed, upstream watersheds such as Lower Jhelum, Sindh, Lidder and Pohru showed the highest peak discharges at all return periods (Fig. 13), which could be attributed to their larger drainage areas, steep slopes, higher runoff coefficients and orographic precipitation, further supporting their tendency to generate higher peak flows52,93. On the contrary, watersheds such as Gundar, Garzan, and Wular II showed lower intensities at all return periods, which could be due to their small catchment areas, larger perviousness or topographic shielding against heavy rainfall events94. Surprisingly, watersheds such as Dal, Doodhganga, and Wular I, which are situated in low-lying and comparatively flat regions, reveal moderate to high design storm intensities, particularly over high return periods. This observation is critical, as these watersheds are over the major urban and peri-urban regions of the Kashmir Valley, including Srinagar city and other surrounding settlements, which host dense populations and critical infrastructure95. The higher runoff potential witnessed in these basins can be related to larger imperviousness due to urbanisation, land-use changes, and encroachment of natural floodplains96,97,98. Although these urban low-lying areas lack steep slopes, these areas often experience compounded flood risks due to the combined effects of poor drainage, modified hydrological connectivity, and human intervention on natural water bodies5,99. The non-linear rise in peak discharge with return period implies that infrastructure designed for moderate events may be increasingly vulnerable under more extreme conditions. This risk is further exacerbated by climate change, which is expected to intensify the hydrological cycle, leading to more frequent and severe rainfall events and accelerating glacier melt100,101. The latter may shift flood seasonality in upstream basins, triggering earlier and larger flood peaks beyond the traditional monsoon period.

Due to the data-scarce nature of the Kashmir Valley, particularly in terms of long-term glacier mass balance and snow cover monitoring, the precise influence of changing meltwater regimes on flood return periods remains uncertain and merits further investigation using physically-based models and expanded observational networks102,103. These observations highlight the importance of integrated urban flood management and climate-resilient drainage planning in these watersheds.

Table 5 Peak magnitude of design storm in m3/s for different return periods for 24 Watersheds.
Full size table

Statistical spread

The statistical comparison of design storm intensities over return periods (Fig. 14) indicates extreme spatial variability and dispersion increase with growing recurrence intervals104. The mean design storms increase from 198.44 mm at the 2-year return period to 1378.25 mm at the 500-year return period, and the increasingly worsening nature of extreme precipitation events in the region is highlighted. The standard deviation also increases from 164.61 mm at the 2-year return period to 1251.01 mm at the 500-year return period, which indicates increasing variability in storm intensities among watersheds during rare and extreme events—an event often attributed to different physiographic characteristics, storm tracks, and orographic influences. The interquartile range (IQR), calculated as the difference between Q3 and Q1, also increases with the return period—from 124.26 mm at 2 years to 779.07 mm at 500 years—thus supporting the argument that the behaviour of storms becomes increasingly variable and uncertain under conditions of extreme climate105. The maximum design storm at 500-year RP (4750.3 mm in Lower Jhelum) starkly contrasts with the minimum (383.5 mm in Gundar), emphasising the importance of localised flood design and region-specific adaptation strategies, particularly for high-risk watersheds. These findings underscore the necessity of incorporating spatially resolved hydrometeorological data into regional planning to enhance resilience under changing climate regimes.

Fig. 10
figure 10

Design storms at different return periods for the lower subwatersheds of Jhelum basin.

Full size image
Fig. 11
figure 11

Design storms at different return periods for the central subwatersheds of Jhelum basin.

Full size image
Fig. 12
figure 12

Design storms at different return periods for the upper subwatersheds of Jhelum basin.

Full size image
Fig. 13
figure 13

Peak magnitude design storm for 24 watersheds.

Full size image
Fig. 14
figure 14

Design storms Statistics across Return Periods.

Full size image

Recommendations and future scope

The results of this study implies that watersheds such as Lower Jhelum, Lidder and Sindh which show peak discharge from design storms (> 4000 m3/s at 500 return period) require infrastructure designed to withstand such hydrological extremes, which implies that conventional drainage systems, culverts, and bridges often designed for lower thresholds are likely to be overwhelmed, especially in downstream or low-lying areas. Practical adaptation measures include adaptive culvert and bridge sizing based on updated return period analyses, installation of overflow or retention basins in urban areas, and implementation of threshold-based flood alert systems to enable timely evacuations. In urban areas like Doodhganga and Dal which show moderate to high peak discharge from design storms, integrating effective drainage systems with land use planning is essential to mitigate flood risks. The observed increase in variability at higher return periods indicates a growing threat from climate change, highlighting the necessity for comprehensive modelling and adaptive planning. To enhance emergency preparedness, authorities should prioritise the installation of automated rainfall gauging systems in high-risk watersheds to validate model data and improve flood forecasting accuracy. Conducting climate resilience assessments using the design storm data can inform watershed development and disaster mitigation programs. Additionally, involving local communities in participatory watershed management will strengthen flood preparedness and facilitate effective dissemination of early warning information.

Due to limited existing studies in the region, the plausibility of design storms at the sub-watershed level could not be validated directly. However, a comparative analysis with regional IDF curves (e.g., from IMD or CWC) is recommended in future work to assess their representativeness and improve reliability for engineering applications. Furthermore, the current study did not extend into flood inundation mapping or infrastructure stress testing; however, this forms a vital scope for future research. The design storms derived herein can serve as critical boundary conditions for flood modelling in HEC-RAS to simulate inundation extents at the sub-watershed level. Such applications will be instrumental in infrastructure vulnerability assessment, optimising dam and reservoir operations, and establishing early warning systems tailored to specific return period scenarios.

Conclusion

This study presents a novel application of HEC-HMS with GIS-based spatial data and gridded satellite rainfall inputs for high-resolution, event-based storm modeling at the sub-watershed scale in the Jhelum Basin, offering a valuable tool for flood risk assessment. The model’s strong performance in calibration and validation phases highlights its reliability for hydrological studies in this region. Design storm simulations revealed significant spatial variability in peak discharges across the 24 sub-watersheds. Notably, high-altitude watersheds with larger catchment areas, such as Lower Jhelum, Sindh, Lidder, and Pohru, exhibited higher peak discharges, likely due to their larger drainage areas and steeper slopes. Conversely, urbanized and low-lying areas like Dal, Doodhganga, and Wular I also showed moderate to high peak discharges, underscoring the compounded flood risks from urbanization and reduced infiltration.​ These findings underscore the necessity for targeted flood mitigation strategies that consider both natural watershed characteristics and anthropogenic influences. Integrating detailed soil, land use, and rainfall data into hydrological models enhances the accuracy of flood predictions and supports the development of effective, region-specific flood management plans. To enhance forecasting accuracy and flood preparedness, agencies are encouraged to install additional rain gauges in data-scarce sub-watersheds of the Jhelum basin, and to integrate real-time hydrometeorological monitoring systems in urban flood-prone zones like Doodhganga and Dal. Sharing basin-scale hydrologic data through open-access repositories would facilitate reproducibility, support policy decisions, and promote collaborative research. Moreover, replicating this modeling framework in other data-scarce Himalayan basins would help develop basin-wide, climate-resilient flood preparedness strategies. Strengthening data infrastructure and continuously updating land use inputs will further improve the utility of such models for early warning systems and adaptive flood management planning.