Introduction

In the context of global net-zero targets and development of new power systems1, research on energy transition, heterogeneous energy cooperation, and system optimized operations primarily focuses on three key fields2. Specifically, the first aspect relates to the optimization of multi-energy complementarity and profit distribution. For instance, Schill et al.3 establishes a mixed-integer linear programming model to analyze the impact of increasing the share of renewable energy on the combined heat and power cycle. The study finds that for every additional 1 MWh of wind and solar energy, the start-up cost of thermal power plants increases by 0.7 euros. Yang et al.4 proposes an energy sharing strategy based on an energy trading mechanism, which uses stochastic programming to describe the uncertainties of renewable energy output and load, thereby improving the economic efficiency and robustness of integrated energy systems. Zhang et al.5 proposes a unit commitment model for the coordinated operation of active distribution networks and transmission networks, which fully exploits the flexible and complementary potential of multi-level and multi-energy systems to enhance energy utilization efficiency. Cui et al.6 aims to balance the profits of all participants and optimize the overall benefits of the alliance. It constructs a collaborative operation decision-making model for multiple types of energy based on the Shapley value equilibrium method, and studies the supporting effect of auxiliary services provided by power generation entities on the optimized operation of multi-energy alliances. Cui et al.7 develops a dynamic Shapley value analysis model that links the revenues from auxiliary services and the output ratios of wind, solar, hydro, and thermal power in a multi-scale combination. This model analyzes the variation patterns between the optimal power generation proportions and revenues of each participant, providing a decision-making basis for determining optimal power output allocation and cost control during market bidding. Wei et al.8 establishes a Nash equilibrium-based optimal scheduling model for power trading among multiple microgrids, where each microgrid aims to minimize its own operating costs while trading functional electric energy with other microgrids to generate profit. The results show that the cooperation among multiple microgrids leads to improved profits for all participants. Wang et al.9 focuses on maximizing the overall benefits of integrated energy systems and adopts a profit allocation method that combines the Shapley value method with the nucleolus method. This approach achieves a relatively balanced distribution of profits and promotes the coordinated and optimized operation of the system through the active participation of different entities.

Secondly, research focuses on time-of-use electricity pricing mechanisms for both the generation side and the demand side based on supply–demand balance response. Yang et al.10 takes into account factors such as time-of-use electricity pricing and photovoltaic generation subsidies, and proposes an optimized scheduling strategy for a household integrated photovoltaic-battery energy storage system with the goal of maximizing user benefits, thereby improving battery utilization. Zhang et al.11 considers time-of-use price response and proposes a two-stage robust unit commitment model that accounts for operational risks and demand response, effectively reducing both operating costs and risks. Cui et al.12 considers demand response under time-of-use electricity pricing and aims to minimize the total operating cost of the system. It establishes a low-carbon economic dispatch model for integrated energy systems that include carbon capture power plants (CCPP). Based on a second-order cone optimization method, the model separately solves the constrained objective functions for the heating network and the gas network, ultimately obtaining a low-carbon economic dispatch strategy.

Thirdly, research focuses on the willingness of different entities to participate in alliances and the stability of their cooperation based on cooperative game theory. Liu et al.13 proposes a multi-Regional Integrated Energy System (RIES) and Virtual Power Plant (VPP) scheduling method based on a bi-level game theory approach to improve the benefits of Virtual Power Plants and regional integrated energy systems. By utilizing the differences in energy production and consumption structures of each RIES and the complementarities within regional energy system alliances, the method reduces load peak-valley differences, promotes renewable energy consumption, and achieves self-sufficient power supply and demand balance. Feng et al.14 addresses the issue of order cost allocation in a retailer alliance under complete information, and establishes a game model for order cost allocation based on cooperative game theory. The LCS method is used to analyze the stability variation process of the order decisions within multiple retailer alliances. Li et al.15 and Hu et al.16 propose corresponding system control strategies and frequency regulation methods to ensure the stability of renewable energy integration and distributed energy management, significantly improving system management efficiency and stability.

Existing research shows that: (1) Methods such as the Shapley value and nucleolus method have been widely applied in fields like integrated energy and multi-energy alliance profit or cost allocation. However, the application scenarios or allocation effects of these methods vary. For instance, the nucleolus method allocates in a completely average manner, without fully considering the differentiated contributions of different participants. The Shapley value method allocates benefits or costs based on the marginal contributions of different participants, avoiding the average distribution approach. However, it does not consider the willingness of participants to cooperate in the alliance, which could be detrimental to the long-term stability and development of the alliance. Additionally, there is a lack of in-depth research on the “multi-scale dynamic Shapley equilibrium value” cost allocation mechanism, which takes into account the interrelated constraints between the different output ratios, power generation capacities, and cost-sharing of multiple power generation entities. (2) There is insufficient research on the relationship between the time-of-use electricity price differences for different power generation entities and the optimized resource allocation within the alliance. Additionally, there is limited research on determining an alliance cooperation stability (where each power generation entity in a multi-energy alliance continues to participate in cooperative operations and does not disengage from joint operations while obtaining reasonable benefits) by considering the relationship between each entity’s dynamic cost equilibrium allocation value (hereinafter referred to as the cost value), output ratios, and preferences for participating in different alliances, with a focus on high renewable energy generation ratios.

To address these gaps, the main contributions and novelties of this study are outlined as follows: (1) In contrast to prior studies that typically assume voluntary and proactive cooperation among alliance participants, this research provides an in-depth analysis of the participation willingness (both positive and negative) of different participants in heterogeneous energy alliances for the first time. It investigates the cooperative operational stability, complementarity, and economic performance of alliances formed by various energy sources with different generation characteristics across multiple temporal and spatial scales. (2) Considering the differentiated TOU pricing of each participant, a Shapley cost allocation model is developed that maximizes the alignment of participant benefits. This model analyzes the relationship between alliance stability in multi-scale cooperation and the dynamic cost distribution of individual participants. Furthermore, the effectiveness of the combined Shapley value and LCS approach is validated for optimizing alliance operational cost control and evaluating cooperation stability. Besides, the timesharing kilowatt hour cost (TKC) is applied as a key variable to manage and optimize the dynamic relationship between individual participants’ operational costs and their willingness to participate in alliances, which can be properly regulated to facilitate the transition from unstable to stable cooperation within alliances. As a result, the evolutionary process of alliance cooperation stability is revealed, providing theoretical support for the efficient integration and stable operation of renewable and traditional energy sources. (3) Considering the consistency of maximum benefits among participants and their preferences for different alliances, this study explores the cost optimization space under various multi-scale combinations of participants. Therefore, the optimized allocation of resources within the alliance is achieved, upon which the feasibility of the proposed alliance operation optimization mechanism is validated. (4) Peak shaving and valley filling scenarios in power systems are simulated to develop power balance curves based on real time energy supply demand equilibrium, upon which alliance operation costs and individual participant costs are calculated. Based on the patterns of cost changes, system power balance, and TOU pricing on the generation side, the differentiated contributions of participants to peak shaving and valley filling operations are analyzed. These findings highlight the critical role of cooperative mechanisms within the alliance in supporting the optimized operation of new power systems.

Operation strategy modeling for heterogeneous energy alliances based on multiagent, multi-scale cooperative stability

This section develops a multi-energy alliance operation model that considers TOU electricity pricing and cooperative stability, focusing on three key aspects: First, the balance of participant benefits (In the course of economic operation, stakeholders reach a dynamic equilibrium through market mechanisms and cooperative game-based negotiations, balancing conflicts of interest and collaboration, and ultimately achieving a stable state characterized by the compatibility of multiple objectives and relatively coordinated resource allocation) and their willingness to participate in the alliance is the foundation of stable cooperative operations. It is essential to clarify how differences in power generation costs and characteristics affect each participant’s willingness to engage in different alliances. Second, the diverse alliance structures formed by integrating renewable and traditional energy sources require analysis of the dynamic relationship between cost balance and the alignment of maximum benefits among power generation participants in different alliances. Third, the investigation on the core factors supporting the optimal operation of the alliance, including costsharing balance, structural stability, the complementarity of heterogeneous energy (Different types of energy exhibit variations in terms of output characteristics, adjustment capabilities, and operational costs. Through complementary collaboration, power supply and demand can be effectively matched.), and a high proportion of renewable energy generation. Note that four assumptions are also employed in this research, as follows:

  1. (1)

    It is assumed that wind, solar, hydro, and thermal power form various cooperative alliances, with each participant expecting benefits. For alliance stability, the cooperation should satisfy three conditions: (i) individual rationality: participants receive no less benefit than from independent operation; (ii) alliance rationality: participants gain more within their current alliance than any alternative; (iii) group rationality: the distribution of benefits among all participants in the alliance achieves optimal balance;

  2. (2)

    Due to differences in electricity generation costs and time based on pricing policies across regions, each power generation entity is treated as a single participant. The Time-sharing Kilowatt Cost (TKC) of each subject is based on the time-sharing electricity price of the power generation side designed in this paper as the value of its electricity cost (this study ignores the profitable space in the time-sharing electricity price of each subject). In terms of time division and time-of-use electricity price design, this paper refers to the time-of-use electricity prices in many regions of China;

  3. (3)

    It is assumed that both the generation side and the demand side can freely engage in electricity trading to achieve power supply demand balance. The relevant power balance, frequency constraints, voltage constraints, and other equations can be referenced in literature17. Additionally, in order to facilitate qualitative analysis of the alliance’s cooperative operation performance, this study is conducted under the condition that the power system ensures safe and stable operation, with key indicators such as system voltage and frequency maintained within normal ranges;

  4. (4)

    PV generation is assumed to operate at full capacity from 9:00 to 16:00, at 50% capacity from 7:00 to 8:00 and 17:00 to 18:00, and at zero during the night (19:00 to 6:00). Wind and hydropower are assumed to be unaffected by seasonal changes and operate 24 h a day.

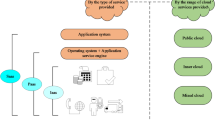
Based on Fig. 1, a heterogeneous energy alliance operation model based on multi-scale cost balance is designed. This model first measures the power generation cost characteristics of each energy subject in different periods through time-sharing electricity cost (TKC), which provides a basis for subsequent cost allocation. On this basis, the Shapley value method is used to fairly allocate the total cost of the alliance, so that each subject bears the corresponding cost according to its marginal contribution in different cooperation combinations. Then through the alliance cooperation stability index LCS (Least Core Stability), from the perspective of individual satisfaction, the degree of preference of the subject to different alliance structures is identified, so as to determine the stability and sustainability of alliance cooperation. Finally, the energy complementarity index is introduced to evaluate the synergy of the output characteristics between the subjects.

Fig. 1
figure 1

Operating framework of heterogeneous energy alliance.

Full size image

Multi-scale cost balancing and allocation for participants

Alliance operational cost objective function

The objective function for the alliance operational cost is designed as follows:

$$\min V = \mathop \sum \limits_{i = 1}^{n} \lambda_{i} u_{i} P_{{\text{B}}}$$
(1)

where \(V{ }\) represents the total cost of power generation within the alliance, \(\lambda_{i}\) is the output ratio of the ith energy source, with the sum of all n participants’ output ratios equaling 1, \(u_{i}\) denotes the TOU price corresponding to each participant, and \(P_{{\text{B}}}\) means the power deficiency. The alliance’s operation must meet both power balance and cost constraints. The active power generated by the participants must equal the active load power consumed and the active power losses, while ensuring that each participant’s cost does not exceed that of independent operation.

To simulate and analyze the impact of TOU pricing on multi-scale combinations of participants across different time periods, and to devise specific operational strategies based on the differences in multi-scale operational costs within the alliance18,19,20,21, the generation characteristics of each participant are considered.

System power balance equation considering real time load demand

To unify the calculation benchmark and achieve the goal of peak shaving and valley filling, the absolute value of the difference between the real time load values and the 24 h average load values over a 24 h period is used as the condition to satisfy the real time power demand balance in the market. This leads to the power real time balance curve (referred to as the “balance curve”), which lies between the maximum value of the actual load curve’s mid load and its base load value. With this balance condition as the target, the simulation of each party’s participation in the alliance operation is performed. The system power balance value is calculated using the equation in (2):

$$P_{{\text{B}}} = P_{{{\text{load}}}} - P_{{{\text{ave}}}}$$
(2)

where \(P_{{{\text{load}}}}\) is the realtime load value for each hour and \(P_{{{\text{ave}}}}\) denotes the average load value over the 24 h period.

Multi-scale cost allocation method for participants

The 24 h power values from the balance curve serve as the basis for calculating the distribution of power generation among alliance participants. Based on the Shapley value method22,23, the total alliance operation cost is allocated proportionally according to each participant’s marginal contribution to power generation. The Shapley cost value for a given participant is calculated as follows:

$$Y_{i} = \mathop \sum \limits_{i \in s} \left( {y\left( s \right) - y\left( {s\backslash i} \right)} \right)*\omega$$
(3)

where \(s\) represents a subset of the alliance that includes participant i. For instance, in an alliance of four participants (wind, solar, hydro, and thermal), the subsets including wind power would be {wind}, {wind, solar}, {wind, hydro}, {wind, thermal}, {wind, solar, hydro}, {wind, solar, thermal}, {wind, hydro, thermal}, and {wind, solar, hydro, thermal}. \(y\left( s \right)\) denotes the cost of subset \(s\), and \(s\backslash i\) represents the subset without participant i, \(y\left( {s\backslash i} \right)\) means the cost of subset \(s\backslash i\), and \(\omega\) denotes the cost allocation weighting factor, calculated as follows:

$$\omega \left( {\left| s \right|} \right) = \frac{{\left( {n - \left| s \right|} \right)!\left( {\left| s \right| - 1} \right)!}}{n!}$$
(4)

where n is the total number of participants in the alliance and \(\left| s \right|\) represents the number of participants in subset \(s\), \(\left| s \right| \le n\).

Multi-scale alliance operational strategy analysis

The stable cooperative operation of an alliance needs to consider the cost sharing balance of the participants and their willingness to engage in the alliance. Large fluctuations in a participant’s operating costs tend to affect their willingness to continue cooperating. Moreover, optimized resource allocation within the alliance can enhance the complementary effect of heterogeneous energy cooperation. This study primarily develops a multi-scale operational strategy for the alliance by balancing the relationships among economic performance (Measure the relationship between the total cost and total income generated by the entire multi-energy alliance in the operation process, and reflect the cost-effectiveness level of alliance operation), cooperation stability, and the effectiveness of complementary operations.

Alliance cooperation economic analysis

To facilitate the analysis of alliance operational economics, a cost area interval equation is designed based on the integral of the difference between the upper and lower limits of each participant’s multi-scale cost values. It utilizes the range of multi-scale cost variations for the alliance or each participant to analyze the fluctuation in costs across different alliances and compare the relative changes in each participant’s cost limits, as follows:

$$\left\{ {\begin{array}{*{20}l} {\mathop \smallint \limits_{{t_{1}^{{{\text{peak}}}} }}^{{{t_{2}{{\text{peak}}}} }} f_{{\text{G}}}^{{{\text{up}}}} \left( t \right) - f_{{\text{G}}}^{{{\text{low}}}} \left( t \right){\text{d}}t} \hfill \\ {\mathop \smallint \limits_{{t_{1}^{{{\text{height}}}} }}^{{{t_{2}{{\text{height}}}} }} f_{{\text{G}}}^{{{\text{up}}}} \left( t \right) - f_{{\text{G}}}^{{{\text{low}}}} \left( t \right){\text{d}}t} \hfill \\ {\mathop \smallint \limits_{{t_{1}^{{{\text{flat}}}} }}^{{{t_{2}{{\text{flat}}}} }} f_{{\text{G}}}^{{{\text{up}}}} \left( t \right) - f_{{\text{G}}}^{{{\text{low}}}} \left( t \right){\text{d}}t} \hfill \\ {\mathop \smallint \limits_{{t_{1}^{{{\text{low}}}} }}^{{{t_{2}{{\text{low}}}} }} f_{{\text{G}}}^{{{\text{up}}}} \left( t \right) - f_{{\text{G}}}^{{{\text{low}}}} \left( t \right){\text{d}}t} \hfill \\ {\mathop \smallint \limits_{{t_{1}^{{{\text{deep}}}} }}^{{{t_{2}{{\text{deep}}}} }} f_{{\text{G}}}^{{{\text{up}}}} \left( t \right) - f_{{\text{G}}}^{{{\text{low}}}} \left( t \right){\text{d}}t} \hfill \\ \end{array} } \right.$$
(5)

where A represents the area of cost variation over different time periods, which indicates the controllable range of costs. \(f_{{\text{G}}}^{{{\text{up}}}} \left( t \right)\) represents the upper cost limit, and \(f_{{\text{G}}}^{{{\text{low}}}} \left( t \right)\) represents the lower cost limit. \(t_{i}^{{{\text{peak}}}}\), \(t_{i}^{{{\text{height}}}}\), \(t_{i}^{{{\text{flat}}}}\), \(t_{i}^{{{\text{low}}}}\), and \(t_{i}^{{{\text{deep}}}}\) refer to the start (when i = 1) and end (when i = 2) periods of the peak, height, flat, low valley, and deep valley periods, respectively.

According to (1) to (5), the maximum operational cost of the alliance across multiple scales can be determined. First, the maximum operational costs of different alliances formed by various participants in different time periods are selected. Then, a comparison is undertaken between the maximum operational costs of different alliances within the same time period as well as across different time periods. If the maximum operational cost of a particular alliance is relatively small, it indicates that the alliance has a low-cost operational advantage. This comparative analysis of maximum costs in different alliances and periods provides insights into the economic performance of the alliance operations.

Alliance cooperation stability analysis

Based on the LCS method proposed in literature24, this section analyzes how participants decide to join or leave an alliance based on changes in their benefits. When each participant’s benefits are maximally aligned, the alliance operates stably. To evaluate a participant’s willingness to join or leave an alliance, the average cost across all alliances is used as a benchmark. If a participant’s cost in a specific alliance is below the average, it indicates a positive willingness to participate, and vice versa. Meanwhile, considering the relative deviations from the average cost, the degree of preference for joining different alliances can be assessed. The larger the absolute deviation between a participant’s operational cost and the average cost, the stronger their positive or negative inclination to join the alliance.

First, regarding the stability analysis based on LCS, participants tend to join alliances where their costs are lower. If the cost for all participants in Alliance L2 is lower than that in Alliance L1, they will tend to shift, resulting in a structural change from L1 to L2, denoted as L1 < L2. To determine whether a specific alliance structure is stable, the possibility of the alliance transitioning from one structure to another is considered. If certain members of the alliance do not prefer the transition from the initial structure, the shift will be obstructed. If all potential transitions are blocked, the alliance reaches a cooperative stable state. Therefore, the stability of the alliance depends on whether any participant is inclined to leave. When no member of the alliance has the tendency to leave, the structure is considered stable, and the alliance set satisfies the condition of consistency.

Then, regarding the cost deviation based on stability analysis25, suppose that \(u_{i}^{{L_{1} }}\) denotes the cost allocation value for participant i in alliance L1, and \(u_{i}^{{L_{{\text{a}}} }}\) represents the average cost for participant i across all alliances. If:

$$u_{i}^{{L_{1} }} - u_{i}^{{L_{{\text{a}}} }} < 0.$$
(6)

This indicates that the cost for participant i in alliance L1 is lower than the average, implying a positive willingness to participate in alliance L1. When all participants in an alliance demonstrate positive willingness, the alliance is considered operationally stable. Conversely, if:

$$u_{i}^{{L_{1} }} - u_{i}^{{L_{{\text{a}}} }} > 0.$$
(7)

This suggests that the cost for participant i in alliance L1 exceeds the average, resulting in a negative willingness to participate, and thus, the alliance is considered unstable. To improve the stability of the alliance, the TKC for participants with costs above the average can be adjusted. The range by which a participant’s TKC can be reduced is given by:

$$\tau_{{{\text{imp}}}} = \frac{{u_{i}^{{L_{1} }} - u_{i}^{{L_{{\text{a}}} }} }}{{P_{{\text{B}}} }}$$
(8)

where \(\tau_{{{\text{imp}}}}\) represents the extent to which the participant’s TKC can be reduced.

Analysis Method of Alliance Operation Complementarity Based on the correlation analysis of different energy output data, the degree of complementarity between different energy sources can be measured21, as shown in Eqs. (9) and (10)

$$c_{t} = {\Delta }P_{t}^{{\text{w}}} + {\Delta }P_{t}^{{\text{g}}} + \;{\Delta }P_{t}^{{\text{s}}} + {\Delta }P_{t}^{{\text{h}}} , t = 1,2, \ldots ,T - 1$$
(9)
$$\Delta P_{t} = \frac{{P_{t + 1} - P_{t} }}{{P_{{{\text{max}}}} }}$$
(10)

where \(c_{t}\) represents the complementarity coefficient, indicating the degree of complementarity between wind, solar, hydro, and thermal energy outputs at time t + 1. \({\Delta }P_{t}^{{\text{w}}}\), \({\Delta }P_{t}^{{\text{g}}}\), \({\Delta }P_{t}^{{\text{s}}}\) and \({\Delta }P_{t}^{{\text{h}}}\) represent the output fluctuation rates of wind, PV, hydro, and thermal power at time t + 1, respectively. \(P_{t + 1}\) and \(P_{t}\) denote the output values of a given participant at periods t + 1 and t, and \(P_{{{\text{max}}}}\) represents the maximum output value of the participant during the period [t, t + 1]. If \(P_{t + 1}\) > \(P_{t}\), then ΔP > 0, indicating an upward fluctuation in energy output. Conversely, if \(P_{t + 1}\) < \(P_{t}\), then ΔP < 0, indicating a downward fluctuation. If the output fluctuations of different participants move in opposite directions, this indicates potential complementarity between them.

From (10), we observe that the smaller the complementarity coefficient, the larger the output fluctuations between participants within the alliance are balanced, indicating stronger complementarity. In a given time period, if the complementarity coefficient of a particular alliance is lower than that of others, it suggests that this alliance has a stronger internal balance in output fluctuations and greater complementarity among participants. Such an alliance can be referred to as a “strong complementarity alliance”.

Based on the above analysis, this study incorporates a case-based comparison of the following variables: the cost values of each alliance member, the maximum and minimum cost variation limits of each generation entity, and the positive or negative willingness of each stakeholder to participate in the alliance, this study also considers the TKC reduction potential \(c_{t}\). of each entity and the complementarity coefficient c of the alliance as key variables for analysis.

Case studies

Datasets for validation

The daily load curve is shown in Fig. 2, with a peak-valley difference rate of 36.43%. The real time power balance curve is demonstrated in Fig. 2. According to the calculation method in (7), as shown in Fig. 3, the maximum value at 5:00 is 338.430 MW, while the minimum value at 23:00 is 14.639 MW, resulting in a range between 14.639 MW and 338.430 MW. These values lie within the range between the base load maximum and the midrange load maximum (24 h real time average load value).

Fig. 2
figure 2

Illustration of the daily load curve.

Full size image
Fig. 3
figure 3

Realtime power balance curve.

Full size image

The TOU pricing for wind, solar, hydro, and thermal power is divided into five periods: peak, height, flat, low valley, and deep valley, as shown in Table 1.

Table 1 TOU electricity price for wind, PV, hydro, and thermal power (Yuan/kWh).
Full size table

Simulation steps

Step 1: The multi-scale combination of the four energy sources forms various alliance structures. In this case, simulations involve three or more participants forming different alliances. The alliance types are as follows: Wind, PV, hydro, and thermal power form Alliance 1; wind, PV, and hydro form Alliance 2; wind, PV, and thermal form Alliance 3; wind, hydro, and thermal form Alliance 4 (according to Assumption (4), during deep valley periods, PV output is zero, making Alliance 1 and 4 structurally identical). Alliance 5 consists of PV, hydro, and thermal power. For comparison purposes, alliances consisting of four participants are referred to as “large alliances”, while those with three participants are called “small alliances”.

Step 2: Based on the 24 h load curve values (as shown in Fig. 2) and Assumption (3), the power deficits of the 24 periods of the load curve are calculated respectively. Moreover, a TOU electricity cost matrix for the four energy sources is constructed to provide the base data for the Shapley cost calculation.

Step 3: Based on Assumption 3, programming simulations for Eqs. (1) to (5) are conducted using relevant software. The iteration step size for each participant’s power generation proportion is set to 0.1, with a time scale of 1 h. Cost values for each participant in different alliances are calculated over a 24 h period, and multi time scale cost variation simulation graphs are generated as a result.

Step 4: The multi-scale trends of cost extrema for alliances and individual participants are compared to determine the upper and lower limits of multi-scale operational costs for different alliances and their corresponding output ratios. The operational processes of different alliances are analyzed, and the dynamic complementarity coefficients of the alliances are calculated based on the multi-scale output data of each participant to evaluate the strength of the complementary relationships between heterogeneous energy sources.

Alliances operational strategies under multi-scale scenarios

The stability of cooperative alliance operations can be assessed by examining changes in the cost of participants in the alliance. If a participant’s cost is significantly higher than others, there is a tendency for that participant to leave from the alliance, affecting the stability of the cooperative operations. Conversely, when participants’ costs are relatively low, their willingness to participate in the alliance increases, leading to enhanced operational stability. This section analyzes the economic performance of the alliance and explores factors that affect the operational stability of the alliance. Furthermore, cost control strategies are proposed for participants in unstable alliances.

Economic analysis of alliance operations under multi-scale scenarios

  1. (a)

    Multi-scale operational cost analysis for alliances

According to Assumption (1), each participant in the large Alliance 1 contributes with an output ratio less than 1, resulting in individual cost sharing being lower than that of independent operation during each time period. A comparative analysis of operational cost variations across different time periods in the alliance is summarized as: A comparison between Figs. 1 and 4 reveals that the trend in alliance cost variations is consistent with the trend in the system power deficit. As shown in Fig. 4, the cost of Alliance 1 fluctuates with the load curve, reaching a maximum of 200.853 kYuan at 20:00 (units omitted for brevity). The cost adjustment range is highest during peak periods at 209.075, followed by the flat, height, deep valley, and low valley periods, with respective adjustment ranges of 148.127, 139.842, 91.841, and 80.512. These data indicate that cost control is most valuable during peak load periods, and during market trading under the alliance mode, these insights can assist in setting bidding prices and determining the optimal bidding stages.

Fig. 4
figure 4

Total cost of Alliance 1 operation.

Full size image

As seen in Fig. 5, the costs of wind, hydro, and thermal power at 20:00 reach their maximum values of 113.637, 49.247, and 37.969, respectively. The peak operational costs of the three participants and the maximum cost of the alliance coincide, occurring during the nighttime peak load period, where they are primarily responsible for balancing the power supply demand. PV power reaches its maximum cost sharing at 11:00 (52.447), primarily during the daytime peak load period, where it is responsible for balancing system power supply demand.

Fig. 5
figure 5

Cost of each participant of Alliance 1.

Full size image

Among the four entities, simulations are conducted to form sub-alliances consisting of any three entities, resulting in four alliances (Alliance 2 to Alliance 5). The trend of changes for each entity in Alliance 2 is shown in Fig. 6, for Alliance 3 in Fig. 7, for Alliance 4 in Fig. 8, and for Alliance 5 in Fig. 9.

  1. (b)

    Comparative economic analysis of different alliances across multiple scenarios

Fig. 6
figure 6

Cost variations of Alliance 2 and its participants.

Full size image
Fig. 7
figure 7

Cost variations of Alliance 3 and its participants.

Full size image
Fig. 8
figure 8

Cost variations of Alliance 4 and its participants.

Full size image
Fig. 9
figure 9

Cost variations of Alliance 5 and its participants.

Full size image

This analysis aims to promote renewable energy integration and evaluate the operational cost efficiency of different alliances across various scenarios. Focusing on maximizing renewable energy output, the maximum operational costs of different alliances in various scenarios are compared to identify patterns in cost changes over time. To ensure valid comparisons, alliances consist of the same power generation participants within the same time period. However, since PV power output is zero during nighttime, the composition of participants differs across Alliances 1 to 5 during the same period. To ensure that the comparison of maximum operational costs accurately reflects the economic performance differences among the alliances, the operational scenarios are standardized, considering peak and valley periods of system operation. Based on the data tabulated in Table 4, the specific scenarios are designed as follows: 1. Nighttime scenarios: Deep valley (from 2:00 to 5:00), low valley (at 1:00, 6:00, and 24:00), height (at 19:00), and peak (from 20:00 to 21:00). 2. Daytime scenarios: Low valley (from 7:00 to 8:00), height (at 12:00, from 15:00 to 16:00, and at 18:00), and peak (at 11:00 and 17:00).

Based on the maximum cost data from Figs. 4 and 6 while referring to Table 2, we can see that the maximum cost values for Alliance 1 and Alliance 4 are equal. To promote the absorption of renewable energy while ensuring the highest proportion of renewable energy output and the lowest maximum alliance cost, Alliance 5 is excluded from the nighttime scenario economic analysis due to its lack of renewable energy output. The detailed economic performance analysis of the alliances is summarized as follows:

Table 2 Maximum alliance operational costs (Yuan).
Full size table

In the nighttime deep valley, low valley, height, and peak scenarios, Alliance 1 shows an economic advantage. A comparison of the maximum cost values of different alliances reveals that Alliance 1 has the lowest maximum cost, demonstrating higher economic efficiency. At the time of Alliance 1’s maximum cost, the output ratios of wind, hydro, and thermal power are 0.8, 0.1, and 0.1, respectively, satisfying the condition for maximizing renewable energy output (Fig. 5).

In the daytime low valley scenario, Alliance 4 demonstrates an economic advantage (Fig. 8). In daytime height or peak scenarios, Alliance 5 shows the best economic performance (Fig. 9).

Stability analysis of cooperative operations in different alliances and scenarios

Figure 10 presents a comparison of the cost values for each stakeholder participating in Alliance 1 through Alliance 5, as well as the average cost of each stakeholder across the five alliances.

Fig. 10
figure 10

The cost of different entities participating in different alliances.

Full size image

The cost deviation data for each participant (The cost deviation data for wind power is presented in Table 3, for photovoltaic power in Table 4, for hydropower in Table 5, and for thermal power in Table 6), the evolution of participant preferences in different alliances is summarized below.

  1. (a)

    Evolution of participant willingness in different alliances

Table 3 Standard deviation of wind power costs across different alliances (Yuan/kWh).
Full size table
Table 4 Standard deviation of PV power costs across different alliances (Yuan/kWh).
Full size table
Table 5 Standard deviation of hydropower costs across different alliances (Yuan/kWh).
Full size table
Table 6 Standard deviation of thermal power costs across different alliances (Yuan/kWh).
Full size table

Wind power demonstrates a positive willingness to participate in Alliance 2 or Alliance 3, with the costs in these alliances remaining below the average for the entire day. The most significant positive cost deviation is in the nighttime peak scenario (30.218), indicating a strong willingness to participate in these alliances. In contrast, wind power shows a negative preference for Alliance 4, as the costs for participating in Alliance 4 throughout the day exceed the average. The most significant negative deviation occurs at 20:00 (30.218), which mirrors the strong positive preference for Alliance 2 or 3. PV power has a positive preference for Alliance 1 during its output period, particularly during the 11:00 peak, where the positive cost deviation is significant (12.862), showing strong positive willingness. Conversely, PV has negative willingness for Alliance 2, 3, and 5, especially at 11:00, with deviations of 4.319, 3.072, and 5.471, respectively. Hydropower shows a positive willingness to participate in Alliance 2, with costs remaining below the average throughout the day, particularly at 11:00 (6.067), indicating strong positive willingness. Hydropower shows a negative preference for Alliance 4 throughout the day, particularly at 11:00 (4.683). Thermal power shows varying preferences: Alliance 3 or 5 from 1:00 to 6:00, Alliance 4 or 5 during the day, and Alliance 1 or 4 from 19:00 to 23:00, with the strongest preference for Alliance 4 at 20:00 (2.763). Thermal power shows negative willingness for different alliances depending on the time: Alliance 1 or 4 from 1:00 to 6:00, and Alliance 3 or 5 between 19:00 and 23:00, with a strong negative preference for Alliance 5 at 20:00 (2.763).

  1. (b)

    Comparison of cooperative operational stability across alliances in different scenarios

In nighttime scenarios, Alliance 2 shows stable operation with wind and hydropower having positive willingness and cost deviations of 30.218 and 4.628, respectively. In daytime low valley scenarios, Alliance 1 is stable with all participants showing positive willingness, with maximum deviations of 1.634, 2.335, 0.426, and 0.01. In the daytime height and peak scenarios, wind, PV, and hydropower have a positive willingness to join Alliance 1, while thermal power has a positive willingness to join Alliance 4 or Alliance 5. The inconsistency in participant willingness prevents the formation of a stable alliance structure.

  1. (c)

    Cost dispersion coefficient analysis

The cost coefficient of variation for Alliance 1 through Alliance 5 and the balanced cost coefficient of variation are shown in Fig. 11.

Fig. 11
figure 11

Alliance 1–5 dispersion coefficient.

Full size image

In the time period from point 1 to point 18, Alliance 3 exhibits the lowest cost coefficient of variation among all stakeholders, indicating the best cost-sharing balance within the alliance. During the time period from point 19 to point 24, Alliance 5 exhibits the lowest cost coefficient of variation among stakeholders. This is because the photovoltaic output, which has a relatively high unit electricity cost, drops to zero, and the cost-sharing is primarily undertaken by hydropower and thermal power, whose unit electricity costs differ only slightly. During the nighttime period, when photovoltaic units generate no output, the cost coefficients of variation for Alliance 1 and Alliance 4 are equal. Through the quantification of multi-temporal and spatial cost-sharing equilibrium among stakeholders within the alliance using the coefficient of variation, the effectiveness of the Shapley value method in optimizing cost allocation among alliance members is demonstrated, offering a valuable reference for the equitable distribution of operational costs in future complex energy systems.

Complementarity analysis of operations in different alliances and scenarios

The complementarity coefficients of various alliances at different periods are shown in Fig. 12. Through comparing the maximum and minimum complementarity coefficients during deep valley, low valley, height, and peak periods, the following observations can be obtained: The minimum complementarity coefficients for Alliance 1 and Alliance 4 both occur at 1:00 (low valley), with a value of 0.178; The maximum complementarity coefficient for Alliance 1 occurs at 3:00 peak), with a value of 2.700. For Alliance 4, the maximum complementarity coefficient occurs at 6:00 (low valley), with a value of 2.134; Alliances 2, 3, and 5 have their minimum complementarity coefficients at 1:00 (low valley), each with a value of 0.119. Their maximum complementarity coefficients occur at 17:00 (peak), each with a value of 2.025. The main feature across different time periods is that the complementarity during valley periods is generally higher than during peak periods. The complementarity is strongest during low valley periods and weakest during height periods.

Fig. 12
figure 12

Trend of multi-scale complementarity coefficients variations in different alliances.

Full size image

Regarding the analysis of strong complementary alliances across different scenarios: During the deep valley period at 4:00, Alliances 2, 3, and 5 exhibit the lowest complementarity coefficients, with a value of 0.175; During the low valley period at 6:00, Alliance 3 has the lowest complementarity coefficient, at 0.119; During the height period at 18:00, Alliance 3 again has the lowest complementarity coefficient, at 0.377; During the peak period at 20:00, Alliances 2, 3, and 5 have the lowest complementarity coefficients, at 0.315. Based on the complementarity coefficients of strong alliances across different time periods, Alliance 3 demonstrates relatively strong complementarity in various scenarios.

Operational strategies for different alliances across multiple scenarios

The cooperative stability alliances, economic alliances, and strong complementarity alliances across different scenarios are summarized in Table 6. During the daytime height and peak scenarios, the strongly complementary alliances vary across different periods, but all alliances experience cooperation instability. From 1:00 to 6:00 and from 19:00 to 24:00, Alliance 2 demonstrates stable operation, but Alliance 1 has better economic performance. From 7:00 to 8:00, Alliance 1 operates stably, but Alliance 4 shows more economic advantages. Based on the discussion, where strong complementarity and stability or stability and economy cannot be achieved simultaneously. To enhance alliance operational stability, the adjustable TKC of each participant within the alliance is analyzed based on (10), and the following strategies are proposed.

  1. (a)

    Cost control strategies based on cooperative stability for each participant

Taking wind power as an example (specific data shown in Table 3), the TKC control strategy is analyzed as follows: Nighttime deep valley period: At 5:00, the TKC of wind power is 0.216, and the maximum cost for participating in Alliance 1 or Alliance 4 is 26.713, higher than the average cost of 17.012. At the same time, the standard deviation of wind power costs in each alliance is the largest at 9.702, and the corresponding power vacancy is 338.430. To improve the operational stability of Alliance 1 or Alliance 4, the wind power TKC can be reduced by 0.029; Nighttime low valley period: At 6:00, the TKC of wind power is 0.27, and the maximum cost for participating in Alliance 2 or Alliance 3 is 24.219, higher than the average cost of 15.423. During this period, the standard deviation of wind power costs is the highest at 8.796, and the corresponding power vacancy is 245.464. To improve the operational stability of Alliance 1 or Alliance 4, the wind power TKC can be reduced by 0.036; Daytime low valley period: At 8:00, the TKC of wind power is 0.270, and the maximum cost for participating in Alliance 3 or Alliance 4 is 9.786 and 6.579, respectively, both higher than the average cost of 6.494. During this period, the standard deviation of wind power costs is the highest at 2.034, and the corresponding power vacancy is 99.182. To improve the operational stability of Alliance 3 or Alliance 4, the wind power TKC can be reduced by 0.001 and 0.033, respectively. The same method can be applied to analyze the TKC control strategies for solar, hydro, and thermal power during height and peak periods. The TKC control strategies for all participants across different periods are shown in Appendix Table 7.

  1. (b)

    Comprehensive strategies for cooperative alliance operations

Strategies considering synergy between strong complementarity and stability: At 8:00 or 18:00, Alliance 1 operates stably, but the strongly complementary alliance is Alliance 3. To improve the operational stability of Alliance 3 and achieve synergy between strong complementarity and stability, in the daytime off-peak scenario, the TKC of wind power and thermal power are reduced by 0.001 and 0.013. During the daytime peak period, the TKC of photovoltaic and thermal power are reduced by 0.016 and 0.010.

Strategies considering synergy between stability and economic performance: During the daytime low valley period, Alliance 1 operates stably, while Alliance 4 is the economic alliance. To improve the stability of Alliance 4 and achieve synergy between stability and economic performance, wind power, hydropower, and thermal power’s TKC can be reduced by 0.036, 0.001, and 0.005, respectively. During the nighttime scenario, Alliance 2 operates stably, while Alliance 1 is the economic alliance. Similarly, reducing wind power, hydropower, and thermal power’s TKC can enhance the synergy between economic performance and stability for Alliance 1.

Strategies considering synergy between strong complementarity, stability, and economic performance: At 11:00 and 15:00 to 17:00, Alliance 5 meets the requirements for strong complementarity and economic performance, but lacks stability. To improve the stability of Alliance 5 and achieve synergy between strong complementarity, stability, and economic performance, wind power and hydro power’s TKC can be reduced by 0.028 and 0.024 during the daytime height period, and by 0.034 and 0.029 during the peak period.

Discussions

Based on the analysis of the case studies, several insights that contribute to a deeper understanding of the operational strategies for alliances under different scenarios, along with some limitations of this work, are discussed as follows:

  1. (1)

    Results demonstrate that strong complementarity does not always align with operational stability, especially in scenarios involving renewable energy sources like wind and solar. For instance, during the low valley periods (1:00 to 6:00 and 19:00 to 24:00), Alliance 2 displays strong operational stability, but its economic efficiency is compromised due to high costs. Meanwhile, Alliance 1, although economically advantageous, struggled with stability during these same periods;

  2. (2)

    Compared with prior studies, this study discusses the willingness of individual participants to engage in energy alliances and the evolution of their intentions. Results analysis reveals that participant preferences, as reflected in their willingness to participate in alliances, are closely linked to operational costs and cost control strategies. For instance, in nighttime deep valley periods, reducing the TKC of wind power by a small margin significantly improves the operational stability of Alliance 1 and Alliance 4. This shows that even minor adjustments in operational costs can have a substantial impact on the overall stability of the alliance, particularly when participants are diverse in terms of energy generation types and costs;

  3. (3)

    The impact of the generation characteristics of each participant on alliance strategies has not been fully considered. For instance, the intermittency of wind and solar power generation can affect the stability of cooperation within the alliance. In addition, the carbon emissions from thermal power introduce carbon costs, which may influence its willingness to participate in the alliance as well as the economic performance of the alliance;

  4. (4)

    The TOU pricing for each participant is assumed to be the TKC, without considering the profit margins inherent in actual TOU pricing schemes. Furthermore, the variation between load and base load power at different periods determines the power output level of the alliance, directly affecting both the alliance’s total cost and the cost limit trends for each participant;

  5. (5)

    Each power generation participant is treated as a single entity when designing alliance operational strategies, without considering coordination between individual units within the same entity. Differences in operational costs and benefits among these units may affect the participants’ positive or negative willingness to participate in the alliance. In addition, since this study is based on assumptions that satisfy relevant physical constraints, the actual economic, stability, and complementarity outcomes in alliance operations may differ due to the influence of system physical constraints.

Conclusions

This work mainly investigates the interplay between operational stability, economic efficiency, and strong complementarity in energy alliances, revealing the operational stability mechanisms of heterogeneous energy sources under different scenarios. And the main conclusions are summarized as follows:

  1. (1)

    In the nighttime scenario, Alliance 2 demonstrates advantages in both strong complementarity and operational stability, while Alliance 1 shows economic operational advantages. It is a remarkable fact that, during the periods of 15:00 to 16:00, 11:00, and 17:00, by controlling the costs of PV and hydropower, Alliance 5 can meet the requirements for stability, economic performance, and strong complementarity;

  2. (2)

    During the daytime period from 11:00 to 17:00, proper adjustment of the TKC for wind and hydropower in Alliance 5 can achieve well synergy between strong complementarity, operational stability, and economic efficiency, thereby promoting efficient energy utilization;

  3. (3)

    This study validates the feasibility of the proposed cost control strategy, demonstrating its effectiveness in analyzing the cooperative stability of various participants. Moreover, it provides a foundation for decision making in stable energy alliance generation combinations while offering valuable insights for advancing collaborative system optimization theory;

  4. (4)

    The case study analysis demonstrates that the proposed alliance operation mechanism enables efficient internal resource allocation. Through leveraging the operational characteristics of different alliances across various time periods, alliance structures can be adjusted accordingly, which provides strong support for developing optimized strategies for the alliance’s participation in real time electricity market transactions.

In addition, the future research tends to consider the impact of the stochastic nature of renewable energy outputs and uncertainties in load demand. Studies should focus on developing alliance operation strategies that incorporate carbon reduction, providing further support for the theoretical development of new power systems aligned with dual carbon goals.