Optimizing MXene graphene based fluids for solar energy conversion and storage using a novel intelligent framework

Abstract

The thermophysical properties of novel Graphene/MXene-based fluids have great potential for enhancing the efficiency of solar energy systems. However, optimizing these properties remains challenging due to the complex interactions between nanomaterial composition and system conditions. This study presents a new hybrid framework that combines response surface methodology (RSM), heuristic and metaheuristic optimization, and advanced decision-making techniques to enhance the thermal conductivity (TC) and dynamic viscosity (DV) of these fluids. RSM-based predictive models demonstrated high accuracy (R² = 0.9997 for TC and 0.9984 for DV), validated using regression graphs, violin plots, and absolute relative deviation analysis. Optimization was conducted using enhanced hill climbing (EHC), NSGA-II, and multi-objective ant lion optimizer (MOALO), with decision-making strategies such as desirability function and VIKOR technique. Results revealed that optimal MXene ratios depend on nanomaterial mass fraction (MF) and temperature, with optimal conditions clustering around 60 °C, MF of 1.5–2 wt%, and MXene ratios of 0.47–0.5. Decision-making analysis highlighted the trade-offs between TC and DV based on varying weight distributions. This research provides a cost-effective methodology to optimize nanofluids for solar energy applications with high precision, reducing computational and laboratory costs.

Introduction

Nanofluids are colloidal suspensions comprising nanomaterials (NMs) dispersed within base fluids, such as water¹, oil², or ethylene glycol (EG)³. These NMs, mainly made from materials like metals⁴, oxides⁵, or carbon nanotubes⁶, significantly enhance the thermal attributes of the base fluids, improving heat transfer efficiency. The role of nanofluids in nanotechnology is pivotal, as they promise to transform cooling systems across multiple domains, including electrical engineering, automotive, aerospace, and renewable energy sectors, particularly in solar energy applications⁷. The thermophysical properties (TPPs) of nanofluids, including thermal conductivity (TC), convective heat transfer coefficient, and dynamic viscosity (DV), are of paramount importance^8,9. These properties drive the effectiveness and enhanced performance of heat transfer systems^10,11.

Recent nanotechnology progress highlights the crucial role of the unique properties of NMs in various applications. 2D NMs lead nanotech advancements with their exceptional physical and chemical attributes from ultra-thin, precise layers¹². Among these, MXene NMs, a family of 2D transition metal carbides and nitrides, stand out with their unique set of advantageous characteristics, including metallic conductivity, hydrophilicity, and high surface area¹³. These properties aid diverse tech applications, notably in renewable energy¹⁴. MXene NMs notably enhance solar photovoltaic/thermal (PV/T) system efficiency for sustainable energy solutions¹⁵. Their ability to absorb light and convert it into heat while optimizing the electrical conductivity for enhanced photovoltaic efficiency makes MXene an excellent candidate for such hybrid systems¹⁶. Aslfattahi et al.¹⁷ conducted a numerical study on the thermal behavior of a solar collector by adding MXene NMs to soybean oil, indicating improved thermal performance compared to the base oil. In another numerical work, Sreekumar et al.¹⁸ analyzed PV/T solar systems using an MXene-based nanofluid, demonstrating improved thermal and electrical performance. Kadirgama et al.¹⁹ investigated MXene nanofluid in solar systems, emphasizing its hydrophilic properties and capacity to boost solar efficiency in EG-water mixtures. This advancement enhances PV/T system thermal management, optimizing renewable energy conversion²⁰.

Moreover, when MXenes are incorporated into nanofluids, they alter the fluids’ TPPs, improving TC and heat transfer performance without substantially increasing DV^21,22. Jin et al.²³ performed a scientific examination to evaluate the TC and DV of water-based hybrid nanofluids enhanced with MXene and graphene NMs. The incorporation of graphene in the nanofluid exhibited a substantial enhancement, with TC increasing by 65.34% and DV experiencing a notable increase of 70.69%. Conversely, intensifying the incorporation of MXene into the graphene-based nanofluid had a negligible impact on TC while contributing to a reduction in DV. Also, Mao et al.²⁴ experienced the TC and DV of a mixture of EG and water in the presence of MXene NMs. MXene-based nanofluids showed up to 30.6% enhanced TC compared to pure water. Additionally, the TC of MXene-based EG/water nanofluid demonstrated a 27.3% improvement. They concluded that MXenes outperformed other particles like metals, oxides, and graphene without a significant growth in DV. Bao et al.²⁵ studied EG-based nanofluids containing multilayer and single-layer Ti₃C₂T_x MXene. At a 5 vol% concentration, nanofluids showed a significant increase in TC—53.1% (multilayer) and 64.9% (single layer) compared to pure EG. MXene nanofluids exhibited lower DV than graphene and carbon nanotubes, displaying self-lubricating properties. Single-layer Ti₃C₂T_x-EG nanofluids demonstrated stable behavior over 30 days without sedimentation.

In addition to MXene, graphene, another two-dimensional NM, has garnered significant attention in the scientific community. Graphene exhibits exceptional mechanical strength, high electrical and thermal conductivities, and remarkable optical characteristics as a single layer of carbon atoms arranged in a hexagonal lattice²⁶. These properties make graphene a promising candidate for various applications, particularly nanofluids²⁷. Graphene-based nanofluids have emerged as a research focus, particularly in thermal management and solar energy applications²⁸. Due to its excellent electrical conductivity and optical properties, graphene can act as a light-absorbing material, enhancing the absorption of solar radiation in solar collectors or photovoltaic devices. This feature enables improved energy conversion efficiency in solar energy systems²⁹.

The dispersion of graphene NMs can remarkably enhance the TC of the nanofluid, enabling efficient heat transfer. This characteristic is precious in thermal management systems and energy conversion applications^30,31. Additionally, the DV of Graphene-based nanofluids tends to remain relatively low, minimizing energy losses associated with fluid flow. These characteristics make graphene-based nanofluids attractive for heat transfer applications, such as heat exchangers, thermal energy storage, and cooling systems. The TC of graphene nanofluids demonstrates a positive correlation with temperature and VF³². Recent experimental analyses have demonstrated that comprising graphenes into base fluids can enhance the TC of the fluids, ranging from 1.2 to 83.4%³³. Taherialekouhi et al.³⁴ analyzed the TC of a hybrid nanofluid comprising water, graphene oxide (GO), and Al₂O₃ NMs. Their results revealed that a growth in temperature and volume fraction (VF) significantly enhanced TC, with a maximum improvement of 33.9%. Yang et al.³⁵ arranged a series of experiments to analyze the TPPs and stability of graphene oxide-based nanofluids to improve the thermal characteristics of base fluid (water). The study focused on the TC of the nanofluid, which exhibited a noteworthy increase within the studied range, with a maximum enhancement of 48.1%. The TC of a TiO₂-Graphene/Water hybrid nanofluid was examined by Bakhtiari et al.³⁶. The study observed that the increase in VF had a more considerable influence on TC than temperature. Specifically, at a VF of 0.5% and a temperature of 75 °C, the TC showed a notable increase (27.84%). Ranjbarzadeh and Chaabane³⁷ conducted laboratory work on engine oil with GO NMs. The results showed that the DV increased by 36% compared to the base fluid due to alterations in VF. Additionally, the highest growth in TC (9.73% improvement) was marked at 75 °C and a VF of 1%. Elsaid et al.³⁸ reported that graphene caused significant enhancement in the TC of nanofluids, up to 40% greater than commonly employed oxide NMs.

Recent advancements in thermal and energy system optimization have demonstrated the transformative role of artificial intelligence (AI) and machine learning (ML) algorithms in developing efficient, cost-effective, and sustainable energy solutions³⁹. Novel metaheuristics such as Enhanced Artificial Rabbit Optimization (EARO)⁴⁰, Arctic Puffin Optimization (APO)⁴¹, and Quadratic Interpolation Beluga Whale Optimization (QIBWO)⁴² have been successfully employed to optimize hybrid renewable energy systems, reducing operational costs while maximizing renewable energy fractions. Further innovations like the Quadratic Interpolation-enhanced Gorilla Troops Optimizer (QIGTO)⁴³, Hybrid Firefly-PSO (HFAPSO)⁴⁴, and Gray Wolf-Cuckoo Search (GWOCS)⁴⁵ highlight the growing importance of AI-driven techniques in managing the complexities of modern green energy systems, enabling tailored solutions for diverse applications. On the other hand, using AI and ML tools to optimize TPPs such as thermal conductivity and dynamic viscosity in nanofluids is crucial for enhancing heat transfer and improving energy efficiency⁴⁶. Balancing these factors leads to nanofluids with superior thermal and rheological performance, improving flow and heat transfer efficiency across various applications. Recently, several scholars have been actively involved in this particular area of research. Maqsood et al.⁴⁷ employed artificial neural network (ANN) and response surface methodology (RSM) to investigate the TPPs of nanofluids. They focused on modeling and optimizing the TC and DV of a nanofluid composed of MWCNTs and thermal oil. Furthermore, Ghadery-Fahliyany et al.⁴⁸ applied various ANN approaches to accurately predict the TC of hybrid nanofluids. Danish et al.⁴⁹ utilized RSM to optimize the TC and DV of TiO₂-water nanofluid simultaneously. The study analyzed the effects of temperature, VF, and NM size on the nanofluid’s TPPs. The optimized values were determined as 60 °C, 1.41 vol%, and 60 nm, respectively, using the desirability approach for multi-objective optimization. Esfe and Tilebon⁵⁰ investigated the optimization of TC and DV of Al₂O₃-MWCNT/thermal oil hybrid nanofluid using NSGA-II and RSM. The study analyzed the influence of temperature and VF on TPPs. The models developed using RSM and ANN methods demonstrated good prediction capabilities for nanofluid properties. The RSM optimization yielded an optimum condition at 49.99 °C and a VF of 1.49%, resulting in a TC of 0.1820 (W/mK), DV of 0.1174 (Pa.s), and a desirability score of 0.9725. Said et al.⁵¹ modeled and optimized water-based nano-diamond nanofluids’ experimentally determined TPPs using the ANFIS model and the marine predators’ algorithm. The multi-objective optimal values for TPPs were achieved without adding nano-diamond material, with the best results obtained at 59.48 °C, closely aligning with experimental data. Hassan et al.⁵² used precise least-squares support vector regression (LSSVR) models and genetic algorithm to predict and optimize the TC and DV of MWCNT-Fe₃O₄/water nanofluids. The optimized nanofluid design with VFs of 0.302% (Fe₃O₄) and 0.183% (MWCNT), operating at 55 °C, resulted in TC and DV values of 0.803 W/m K and 0.625 mPa·s, respectively.

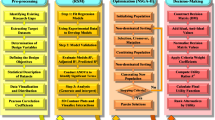
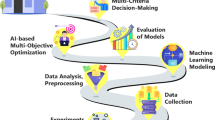
Despite extensive research on optimizing nanofluids applicable in solar-energy storage and conversion, a comprehensive methodology that integrates data-driven modeling, optimization, and decision-making for hybrid Graphene/MXene nanofluids remains absent. Addressing this gap, the present study focuses on optimizing two critical TPPs—thermal conductivity and dynamic viscosity—to enhance the applicability of these nanofluids in solar energy systems. Specifically, three key independent variables are identified: the mass fraction of nanomaterials, the MXene/Graphene ratio, and system temperature. In pursuit of this goal, the present study introduces an innovative and comprehensive framework that seamlessly combines RSM-driven modeling with cutting-edge heuristic and metaheuristic optimization strategies. The developed RSM models for TC and DV are optimized using the enhanced hill climbing (EHC) algorithm as a heuristic approach, while NSGA-II and multi-objective ant lion optimizer (MOALO) are employed as metaheuristic techniques. A distinguishing feature of this research is the incorporation of weighted decision-making strategies to refine the selection of optimal solutions. Specifically, the desirability function is applied to EHC, while VIKOR multi-criteria decision-making is utilized for NSGA-II and MOALO Pareto-optimal points, ensuring a balanced trade-off between competing objectives. This study marks the first implementation of such an integrated framework for optimizing hybrid Graphene/MXene nanofluids, providing a structured and scalable methodology for enhancing their thermal performance in solar energy applications. A summary of the research roadmap including data analysis, modeling, optimization, and decision-making is illustrated in Fig. 1.

Fig. 1

Roadmap of current research from experimental datasets to the improvement of solar PV/T systems.

Data analysis

In this study, the experimental datasets by Jin et al.²³ are utilized for validating the proposed hybrid framework. Jin et al. focused on measuring the TC and DV of a water-based hybrid nanofluid incorporating MXene and Graphene. By meticulously analyzing the effects of temperature (T), NM mass fraction (MF), and NMs ratio, the study sheds light on how these factors influence TC and DV. Their findings unlock new possibilities for introducing nanofluid formulations with superior thermal and rheological properties in specific applications. The NMs ratio is defined as follows:

$$\:\text{M}\text{X}\text{e}\text{n}\text{e}\:\text{r}\text{a}\text{t}\text{i}\text{o}=\frac{{\text{M}\text{a}\text{s}\text{s}}_{\text{M}\text{X}\text{e}\text{n}\text{e}}}{{\text{M}\text{a}\text{s}\text{s}}_{\text{M}\text{X}\text{e}\text{n}\text{e}}\:+\:{\text{M}\text{a}\text{s}\text{s}}_{\text{G}\text{r}\text{a}\text{p}\text{h}\text{e}\text{n}\text{e}}}$$

(1)

Thus, in cases where the mass of MXene in the hybrid nanofluid equals zero, the resulting nanofluid transforms into a mono nanofluid composed solely of water and graphene. Table 1 presents the statistical characteristics of experimental datasets. The table offers a comprehensive analysis of key parameters characterizing the hybrid nanofluid. It includes temperature, mass fraction, MXene ratio, TC, and DV. With a dataset of 56 values, the table provides essential statistical information such as the minimum and maximum values for each parameter, as well as the range, mean, median, average deviation (AD), standard deviation (SD), coefficient of variation (COV), skewness, and kurtosis. These statistical measures offer valuable insights into the distribution and properties of the hybrid nanofluid, enabling a deeper understanding of its behavior. The AD quantifies the average difference between each value and the mean. The SD measures the dispersion of values around the mean. The COV is obtained by dividing the SD by the mean. Skewness assesses data asymmetry: positive implies right-skewed with a long right tail; negative indicates left-skewed with a long-left tail; near zero suggests symmetry. Kurtosis gauges distribution shape: positive for peaked, negative for flat, near zero for normal-like distributions. Table 1 shows T and TC slightly right-skewed, MF and DV moderately left-skewed, and the MXene ratio moderately right-skewed. All variables have negative kurtosis, pointing to flat distributions. To better understand the data distribution for each variable, Figs. 2 and 3 depict the data frequency histogram for independent and dependent variables, respectively. Pearson’s correlation coefficient (PCC), symbolized as ‘r’, quantifies the extent and directionality of a linear interrelation between two continuous variables⁵³. This statistic’s value, which oscillates between − 1 and + 1, represents a completely positive linear correlation when approaching + 1, a completely negative linear correlation when nearing − 1, and an absence of linear correlation at 0. The coefficient is computed utilizing the formula⁵³:

$$\:r=\frac{\sum\:_{i=1}^{N}\left({X}_{i}-\stackrel{-}{X}\right)\left({Y}_{i}-\stackrel{-}{{Y}_{\:}}\right)}{\sqrt{\sum\:_{i=1}^{N}{\left({X}_{i}-\stackrel{-}{X}\right)}^{2}\sum\:_{i=1}^{N}{\left({Y}_{i}-\stackrel{-}{{Y}_{\:}}\right)}^{2}}}$$

(2)

where $\:{X}_{i}$ and $\:{Y}_{i}$ show the values for variables $\:X$ and $\:Y$ in the sample, $\:\stackrel{-}{X}$ and $\:\stackrel{-}{Y}$ denote the mean values for variables $\:X$ and $\:Y$ respectively, and $\:\sum\:_{i=1}^{N}\:$signifies summation across all data points in the sample.

Figure 4 (a) shows the linear correlation between TC and input variables. The PCCs reveal that TC has a moderate and positive linear association with temperature at 0.68 and MF at 0.67, pointing to a consistent upward trend between the pairs. However, the TC’s correlation with the MXene ratio is much weaker, at 0.13, indicating a negligible linear relationship, in which changes in the MXene ratio are less consistently associated with changes in TC. Furthermore, Fig. 4 (b) presents the PCC between DV and independent variables. According to the figure, the Pearson correlation coefficient of −0.88 between DV and T indicates a strong negative linear relationship; as temperature increases, dynamic viscosity tends to decrease significantly. In contrast, DV’s coefficient with MF is 0.36, suggesting a weak positive linear correlation; higher mass fractions might be associated with slightly increased DV. The MXene ratio has a coefficient of −0.02 with DV, implying virtually no linear relation; hence, changes in the MXene ratio do not predictably affect DV, remaining stable despite variations in the ratio. Acknowledging that the PCC is exclusively indicative of linear correlations between variables is imperative. Consequently, lower PCC values should not be underestimated as they might mask the existence of potent non-linear relationships between the variables under consideration.

Table 1 Statistical characteristics of laboratory data.

Fig. 2

Data histogram of the independent variables.

Fig. 3

Data histogram of the dependent variables.

Fig. 4

Linear correlation coefficients: (a) TC and inputs, (b) DV and inputs.

Data-Driven modeling

Response surface methodology

RSM includes mathematical and statistical techniques designed to optimize the influence of multiple variables on a process⁵⁴. This methodology is predominantly utilized to develop models by systematically designing experiments to optimize a targeted response⁵⁵. In the context of nanofluid TPPs, RSM is invaluable^56,57. It uses input variables to predict the optimal conditions of nanofluids. In RSM, various models are employed to model the relationship between input variables and the response, each escalating in complexity. The Linear model assumes direct proportionality without interactions: $\:Y={\beta\:}_{0}+\sum\:\left({\beta\:}_{i}{X}_{i}\right)$. For scenarios where the response variation is not strictly proportional to the input levels, the Two-Factor Interaction (2FI) model introduces interaction terms: $\:Y={\beta\:}_{0}+\sum\:\left({\beta\:}_{i}{X}_{i}\right)+\sum\:\left({\beta\:}_{ij}{X}_{i}{X}_{j}\right)$. The Quadratic model, used for capturing non-linear responses with curvature, includes squared factor terms: $\:Y={\beta\:}_{0}+\sum\:\left({\beta\:}_{i}{X}_{i}\right)+\sum\:\left({\beta\:}_{ii}{{X}_{i}}^{2}\right)+\sum\:\left({\beta\:}_{ij}{X}_{i}{X}_{j}\right)$. The Cubic model is less commonly utilized due to its intricacy and the potential risk of overfitting. However, it incorporates cubic terms to capture more intricate curvature variations: $\:Y={\beta\:}_{0}+\sum\:\left({\beta\:}_{i}{X}_{i}\right)+\sum\:\left({\beta\:}_{ii}{{X}_{i}}^{2}\right)+\:\sum\:\left({\beta\:}_{ij}{X}_{i}{X}_{j}\right)+\:\sum\:\left({\beta\:}_{iii}{{X}_{i}}^{3}\right)$. In the formulas, $\:Y$ represents the predicted response variable, $\:{\beta\:}_{0}$ represents the intercept (constant term), $\:{\beta\:}_{i}$, $\:{\beta\:}_{ii}$,., $\:{\beta\:}_{ijk}$ represent the coefficients for the respective terms, and $\:{X}_{i}$, $\:{X}_{j}$,., $\:{X}_{n}$ represent the input variables. The coefficients of the models are optimized using the least squares technique so that there is a minimum error between the model outputs and the observations. This comprehensive analysis not only determines the paramount factors and their interactions but also guides the enhancement of nanofluids to elevate heat transfer performance⁵⁸.

Model validation and overfitting prevention

Within the RSM framework, robust statistical validation measures are implemented to curb overfitting and enhance the model’s capacity to perform reliably on new datasets. Overfitting, in this context, occurs when a model becomes excessively tailored to the training data, thereby compromising its predictive effectiveness for previously unseen cases. The measure known as predicted R² diverges from the conventional R² by focusing on a model’s accuracy in forecasting new, unseen data. Rather than merely reflecting how well the model captures the variability within its training set, predicted R² is calculated through the use of Leave-One-Out Cross-Validation (LOOCV), which systematically validates the model’s performance on each omitted observation. LOOCV involves sequentially removing one observation from the dataset and constructing the model using the remaining data. The omitted observation is then predicted, and the corresponding prediction error is computed. This cycle is repeated for each data point, thereby generating a comprehensive assessment of the model’s predictive performance. Also, RSM employs Analysis of Variance (ANOVA) to counteract overfitting by utilizing statistical measures, such as p-values, to validate model components. Models that incorporate a high number of terms are particularly vulnerable to overfitting, as they may inadvertently capture random variations along with the genuine underlying relationships. Within the ANOVA framework, p-values serve as diagnostic tools for identifying variables that may contribute to overfitting. When a variable exhibits a high p-value, it is considered statistically insignificant, implying that it likely reflects random variability rather than a substantive relationship. By discarding these non-contributory variables, the resulting RSM model becomes more streamlined and resistant to overfitting, thereby enhancing both its predictive precision and its capacity for generalization.

Thermal conductivity modeling

According to Table 2, the reduced cubic model used to predict the TC of the hybrid nanofluid exhibits excellent accuracy and performance. With an R² (coefficient of determination) value of 0.9997, the model explains about 99.97% of the variability in the thermal conductivity. Conventional R² values may overstate a model’s performance when numerous predictors are involved. To counter this, the adjusted R² applies a penalty for complexity, thereby avoiding inflated goodness-of-fit measures. In this analysis, an adjusted R² of 0.9996 and a predicted R² of 0.9994 demonstrate both robust training fit and exceptional predictive accuracy. Additionally, an Adequacy Precision ($\:AP=({Y}_{max}-{Y}_{min})/\sqrt{{p\widehat{\sigma\:}}^{2}/n}$) score of 385.4688 vastly exceeds the minimal acceptable threshold of 4, confirming outstanding signal discrimination.

Furthermore, the standard deviation (Std. Dev.) in Table 2 measures how the predicted values are clustered around the observed values. The low standard deviation of 0.0024 suggests that the predicted TC are comparable to the actual values. The mean value of 0.8314 represents the average TC predicted by the model which is the same as the observations in Table 1. The model demonstrates low relative variability in its predictions with a coefficient of variation (C.V. %) of 0.2927. Overall, these outcomes indicate that the proposed model is highly reliable and performs well in modeling the TC of the graphene/MXene-based nanofluid, making it reliable for further analysis and practical applications. The mathematical representation of the model, along with its corresponding coefficients, is detailed in Eq. 3 and Table 3.

$$\begin{aligned} &\:TC={\alpha\:}_{0}+{\alpha\:}_{1}T+{\alpha\:}_{2}MF+{\alpha\:}_{3}{MXene}_{ratio}+{\alpha\:}_{4}TMF+{\alpha\:}_{5}T{MXene}_{ratio}\\&\qquad\qquad+{\alpha\:}_{6}{T}^{2}+{\alpha\:}_{7}{MF}^{2}+{\alpha\:}_{8}{MXene}_{ratio}^{2}+{\alpha\:}_{9}{T}^{2}MF\\&\qquad\qquad+{\alpha\:}_{10}{T}^{2}{MXene}_{ratio}+{\alpha\:}_{11}T{MF}^{2}+{\alpha\:}_{12}T{MXene}_{ratio}^{2}\\&\qquad\qquad+{\alpha\:}_{13}{T}^{3}+{\alpha\:}_{14}{MF}^{3}+{\alpha\:}_{15}{MXene}_{ratio}^{3}\end{aligned}$$

(3)

Table 2 Statistical metrics of the TC model developed by RSM.

Table 3 Coefficients of Eq. 3.

The ANOVA of the developed model for thermal conductivity is presented in Table 4. Within a modeling framework, ANOVA is employed to quantify the statistical relevance and distinct contributions of various predictors in explaining the variability exhibited by the response variable. The model is highly significant (p < 0.0001), showing that it effectively explains the variation in TC. The variables A (T), B (MF), and C (MXene ratio) also exhibit highly significant effects (p < 0.0001), demonstrating their powerful effect on TC. All terms, AB, AC, A², B², A²B, A³, B³, and C³ are all highly significant (p < 0.0001), suggesting that they contribute significantly to the variability in TC. However, the variable C² does not significantly affect TC with a p-value beyond 0.1 (p = 0.1864). The F-value is computed by dividing the average squared deviation attributable to a specific factor by the average squared deviation stemming from residual error. This ratio effectively quantifies how much the variance explained by the factor exceeds that attributable to random fluctuations. In the given ANOVA table, the F-values associated with A, B, C, AB, AC, A², B², A²B, A³, B³, and C³ are large, indicating that the respective variables and interactions significantly impact the TC. The residual term represents the unexplained variation in the model. In general, the ANOVA results demonstrate that the RSM-based model effectively captures the variation in thermal conductivity and identifies the significant factors and interactions influencing it.

Table 4 Statistical evaluation of the RSM-driven TC model through ANOVA.

Dynamic viscosity modeling

Table 5 presents the reduced cubic model’s statistical criteria for predicting the nanofluid’s DV. The RSM-based model demonstrates exceptional accuracy and reliability, supported by several key metrics: an R² value of 0.9984 indicates that 99.84% of the variance in the response variable is explained by the model, signaling a solid fit. The Adjusted R² of 0.9980 affirms the model’s predictive strength without over-fitting, despite its complexity, while the Predicted R² at 0.9975 assures robust predictive capacities. The Adequate Precision ratio at 194.0531, vastly exceeding the threshold of 4, suggests the model provides a clear and significant signal. The low Std. Dev. of 0.0122 implies that the predictions are consistent and closely clustered around the mean dynamic viscosity of 1.12. The C.V. % at a mere 1.08% further underscores the model’s precision, with very low variability relative to the mean. These indicators reflect a very precise and reliable model for forecasting the behavior of the nanofluid’s dynamic viscosity. The equation of the DV model and its coefficients are presented in Eq. 4 and Table 6.

$$\begin{aligned} &\:DV={\beta\:}_{0}+{\beta\:}_{1}T+{\beta\:}_{2}MF+{\beta\:}_{3}{MXene}_{ratio}+{\beta\:}_{4}TMF+{\beta\:}_{5}T{MXene}_{ratio}\\&\qquad\qquad+{\beta\:}_{6}{T}^{2}+{\beta\:}_{7}{MF}^{2}+{\beta\:}_{8}{MXene}_{ratio}^{2}+{\beta\:}_{9}{T}^{2}{MXene}_{ratio}\\&\qquad\qquad+{\beta\:}_{10}T{MXene}_{ratio}^{2}+{\beta\:}_{11}{MXene}_{ratio}^{3}\end{aligned}$$

(4)

Table 5 Statistical metrics of the DV model developed by RSM.

Table 6 Coefficients of Eq. 4.

The analysis of variance of the RSM-based model for predicting DV is presented in Table 7. The ANOVA showcases the statistical significance and strength of the model and its components. The model has a high F-value of 2509.67 and a p-value less than 0.0001, indicating that the model is highly significant. Individual factors such as temperature (A), MF (B), and MXene ratio (C) also present strong significance with large F-values and p-values lower than 0.0001, suggesting each factor’s substantial influence on dynamic viscosity. Interaction terms (AB, AC) and quadratic terms (A², B², C²) are all statistically significant, reflecting that both the interactions and squared effects play a crucial role in the model. The mixed terms (A²C, AC²) show considerable effects with significant F-values and small p-values, hinting at the importance of these specific interactions. The cubic term of MXene ratio (C³), while having a lower F-value of 4.69, maintains significance with a p-value of 0.0358, suggesting a minor but still meaningful contribution. A residual mean square near zero denotes a low variation unexplained by the model, complementing the earlier established model validity and robust explanatory power for the DV of the nanofluid.

Table 7 Statistical evaluation of the RSM-driven DV model through ANOVA.

In-Depth evaluation of developed models

This section evaluates the performance of the developed models. While various criteria and graphical representations can be used for model evaluation, specific methods employed in this section will be analyzed in detail. Figure 5 depicts the regression graph and violin plot for comparing TC predictions and observations. The regression graph showcasing the outputs of the RSM-based model predicting TC with an R² value of 0.9997 indicates an exceptionally precise fit to the observed data to the extent that all predicted values lie on the Y = X line, representing the perfect agreement. This alignment suggests that the RSM model can estimate TC values almost perfectly. The complementary Violin plots visualize the distribution and probability density of the observations and outputs, remarkably mirroring each other in shape, width, and spread. This congruence between the distributions further solidifies the model’s accuracy and its viability for precise TC predictions, reinforcing the model’s robustness and its potential use for effectively estimating thermal conductivity in practical applications.

Furthermore, Fig. 6 shows the regression graph and violin plot for comparing DV outputs and targets. The RSM-based model’s regression graph for predicting the nanofluid’s DV has a high R² of 0.9984. While data points closely align with the Y = X line, a slight visible deviation indicates a near-perfect but not absolute prediction. The associated Violin plots, which reveal data distribution and density, show similarity between the model outputs and actual observations, yet discernible discrepancies at specific values highlight minor inconsistencies. These differences suggest the model’s strong but not infallible capacity to capture the full complexity of the DV behavior.

Fig. 5

(a) Regression graph and (b) Violin plot for comparing TC predictions and observations.

Fig. 6

(a) Regression graph and (b) Violin plot for comparing DV predictions and observations.

The cook’s distance presented in Fig. 7 (a) for the RSM-based TC predictive model indicates that most data points have a minor influence on the model, with the cook’s distances well below 0.1. However, there are notable exceptions, with data points 17, 25, 28, 32, 33, 35, 39, 41, 42, and 53 showing significantly higher distances, suggesting these are potential outliers or have high leverage and could disproportionately impact the model’s predictions. Furthermore, according to Fig. 7 (b), analyzing the cook’s distance data for the RSM-based DV model reveals a distribution where most values are low, indicating limited effect on the model. However, peaks at data points 3, 4, 7, 10, 29, 36, and particularly 49 suggest these observations are highly influential and may be outliers, potentially skewing the predictive accuracy.

Figure 8 shows the absolute relative deviation (ARD) polar diagram for the outputs of TC and DV predictive models. The plotted polar graph for the ARD of the RSM-based TC predictive model would reveal the model’s performance across different conditions. With ARDs stretching from 0.008% to over 0.6%, a clear pattern of varied prediction accuracy emerges. Data points with ARD values greater than 0.5%, particularly 0.6047%, 0.6289%, and 0.5399%, would be flagged on the graph as pronounced spikes, indicating predictions that differ from the actual values. Conversely, ARD values below 0.1%, about 29% of outputs, correspond to points close to the graph’s center, suggesting that these predictions are pretty accurate with minor deviations from the actual values, and the model is performing well for these points. Furthermore, the ARD-based polar graph of DV model outputs would reveal the model’s performance across various data points. The graph displays a distribution of deviations at varying angles, representing different input conditions or factors affecting the predictive accuracy. The range of deviations from 0.006% to over 2.7% highlights the variability in model performance across different data points. About 30% of the outputs show an ARD value greater than 1%. Also, 37.5% of the outputs indicate an absolute relative deviation smaller than 0.5% with the observations. The presence of both high and low deviation zones within the same model suggests that while the model can predict certain conditions reliably, it struggles with others, possibly due to variability in underlying data or model limitations. Figure 9 illustrates all outputs’ relative error ($\:RE\left(\%\right)=\frac{Actual\:value-Predicted\:value}{Actual\:value}\times\:100$) for TC and DV predictive models. The relative error data provided contains both positive and negative values to analyze the tendency of the RSM-based TC predictive model’s estimations. Positive RE values represent underestimations, where the model predicts lower than actual values, and negative values indicate overestimations, with predictions higher than actual values. To determine which is more prevalent, one would count the number of positive values and compare it with those of negative values. In this data set, there appear to be 28 instances of overestimation and underestimation. This indicates the balance between overestimation and underestimation by the model. Furthermore, upon examination of the relative error percentages yielded by the RSM-based DV predictive model, the data intermittently displays patterns of both underestimation and overestimation. Similar to TC outputs, quantitative analysis reveals an equivalent frequency of 28 instances for both underestimation and overestimation. This equal distribution highlights a balance in the model’s propensity for prediction errors in either direction. The amplitude of these errors is considerable, with overestimations extending to approximately − 2.704% and underestimations ascending to roughly 2.703%. Such variability in the error margins suggests that the model’s predictive accuracy is subject to fluctuation without a discernible tendency to underestimate or overestimate.

Fig. 7

Cook’s distance for (a) TC and (b) DV outputs.

Fig. 8

ARD-based polar graph for (a) TC and (b) DV outputs.

Fig. 9

Histogram of relative error for TC and DV outputs.

The relative error of outputs for TC and DV of MXene/Graphene hybrid nanofluid across a temperature range of 5 to 60 °C and mass fractions from 0.1 to 2% are shown in Fig. 10. According to the figure, at lower temperatures (5 °C), TC relative errors are generally positive across all MFs, suggesting a consistent underestimation of TC which diminishes or turns negative as temperature increases, indicating a better match or overestimation at higher temperatures. Conversely, the DV relative errors are notably negative at T = 5 °C for lower MFs (0.1% and 0.5%), and this trend of overestimation with negative errors pervades across other temperatures like 30 °C and 60 °C. The magnitude of errors in DV, such as high positive errors at 20 °C for mass fractions of 0.1% and 0.5% and significant negative errors at 30 °C for these fractions, suggest that the model may not accurately predict DV in these areas, possibly due to complex interactions within the high mass fraction nanofluid a more sensitive to temperature changes. Mass fraction 1% shows high variability in both TC and DV relative errors, notable examples being the TC error at 20 °C (−0.60%) and DV error at 30 °C (−1.92%). Thus, the mass fractions of 0.5–1% display significant relative errors, indicating the model’s performance dips, particularly at these concentrations and the mid-temperature range (20–30 °C), potentially suggesting the influence of non-linear interactions between the MXene and Graphene particles that is not well-captured by the existing model.

Figure 11 shows the changes in TC and DV predictions under the influence of temperature and MF. Increasing the temperature enhances molecular motion and particle dispersion while increasing the MF promotes particle-particle interactions, resulting in improved heat transfer and, thus, higher TC. Also, the effect of temperature and mass fraction on the DV can vary. Increasing temperature decreases the DV due to reduced intermolecular forces. However, increasing the mass fraction of nanoparticles leads to an increase in DV. This is primarily due to the increased concentration of NMs, which can cause particle-particle interactions and hinder fluid flow. The presence of more nanoparticles creates additional resistance to flow, resulting in higher dynamic viscosity.

Figure 12 displays TC and DV predicted by the RSM models under the simultaneous influence of the temperature and MXene ratio. Increasing the ratio of MXene to Graphene at various temperatures reduces TC and DV. However, it is noteworthy that the positive influence of MXene NMs on DV is more substantial than its negative impact on TC. In other words, the increase in the MXene ratio results in a more significant decline in DV, while the decrease in TC is relatively less pronounced.

Fig. 10

Relative error of outputs in terms of T and MF for (a) TC and (b) DV.

Fig. 11

3D graph of (a) TC and (b) DV in terms of T and MF for MXene ratio = 0.25.

Fig. 12

3D graph of (a) TC and (b) DV in terms of T and MXene ratio for MF = 1%.

Heuristic optimization and desirability function

The models presented in the previous section are used as a basis for multi-objective optimization in this section. These models help to find optimal conditions under different real-world scenarios. The optimization process is performed utilizing the enhanced hill-climbing algorithm.

Enhanced hill-climbing algorithm

The hill-climbing algorithm is employed to identify the optimal solution within a given search space. This iterative process begins with an initial solution and gradually enhances it through slight changes. However, it can get stuck in local optima, where further modifications do not improve the solution. To overcome this limitation, the algorithm can be enhanced with random points. The enhanced hill-climbing (EHC) algorithm with random points introduces occasional random jumps to explore different areas of the search space. These random jumps allow the algorithm to escape from local optima and potentially find a global solution. The algorithm performs the following steps:

• 1. Start with an initial solution.

• 2. Assess the initial solution.

• 3. Generate a set of neighboring solutions by modifying the existing solution.

• 4. Assess each neighboring solution and choose the most optimal solution.

• 5. If the neighboring solution is superior to the existing solution, update the existing solution.

• 6. Random jumps are introduced by generating a random solution and evaluating it.

• 7. Compare the best solution obtained so far with the existing solution and update the best solution if necessary.

• 8. Continue iterating steps 3 to 7 until the maximum number of iterations is satisfied.

By including random jumps, the algorithm increases its chances of finding a global optimum by exploring different regions of the search space. This enhancement allows for more robust and effective optimization in complex problems.

This study focuses on concurrently optimizing two TPPs of the water-based hybrid nanofluids containing MXene and graphene: maximizing TC and minimizing DV. To optimize multiple objectives effectively, we employ the desirability technique proposed by Myers et al.⁵⁹. This technique aids in finding the optimal combination of input variables that achieve the desired values for both TC and DV simultaneously. It allows for optimizing conflicting goals by assigning weights to each objective and calculating an overall desirability score. The formula for the desirability function is:

$$\:D={\left({d}_{1}^{{w}_{1}}\cdot\:{d}_{2}^{{w}_{2}}\cdot\:\dots\:\cdot\:{d}_{n}^{{w}_{n}}\right)}^{\frac{1}{\sum\:{w}_{i}}}={\left(\prod\:_{i=1}^{n}{d}_{i}^{{w}_{i}}\right)}^{\frac{1}{\sum\:{w}_{i}}}$$

(5)

where $\:D$ represents the overall desirability score, $\:{d}_{1}$, $\:{d}_{2}$, …, $\:{d}_{n}$ are individual desirability values for each objective, and $\:{w}_{1}$, $\:{w}_{2}$, …, $\:{w}_{n}$ are corresponding weights (importance factor) assigned to each objective. The desirability function enables decision-makers to find optimal solutions that strike a balance between multiple objectives. Also, by assigning various weights to each objective (different scenarios), the optimization process can be tailored to prioritize certain objectives over others, enabling a more efficient and effective search for optimal solutions.

Optimization results

Table 8 presents three primary scenarios based on the objectives. In the first scenario, equal weight is assigned to TC and DV. Optimal conditions involve a maximum temperature of 60 °C and a mass fraction of 2%, with a limited MXene ratio of 0.077. The second scenario assigns three times more importance to thermal conductivity than dynamic viscosity, typical in practical applications. Similar to the first scenario, optimal conditions involve a maximum temperature of 60 °C and a mass fraction of 2%, but with no MXene NMs. In this case, the water-graphene mono nanofluid is preferred over the water-MXene/graphene hybrid nanofluid. The third scenario, less common in practical applications, prioritizes dynamic viscosity. Optimal conditions involve a maximum temperature of 60 °C, an MXene ratio of 0.5, and a mass fraction of 1.802%.

To provide more details of the optimal points, the optimal values of the MXene ratio at different temperatures and mass fractions were calculated and modeled. Figure 13 depicts the contours of the optimal values of the MXene ratio for different scenarios. According to Fig. 13 (a), in the first scenario (W_TC = 0.5 and W_DV = 0.5), it can be observed that at a constant mass fraction of 0.1%, the optimum MXene ratio remains constant at 0 as the temperature increases from 5 °C to 60 °C. This suggests that a mono-graphene-based nanofluid is optimal in this condition. In this scenario, the optimal nanofluid production is characterized by an augmented contribution of MXene NMs as the mass fraction increases. Concurrently, an elevated nanofluid temperature necessitates a diminished proportion of MXene NMs to attain the optimal state. Figure 13 (b) indicates that the same trend as the first scenario is observed in the second scenario (W_TC = 0.75 and W_DV = 0.25), with the difference that the optimal MXene ratio appears in lower values. In fact, with the increasing importance of thermal conductivity in different temperature and volume fraction ranges, a smaller portion of MXene is required to achieve the optimal state. According to Fig. 13 (c), the nanofluid shows a more complex behavior in the last scenario (W_TC = 0.25 and W_DV = 0.75). The mass fraction of nanofluid strongly influences the optimal ratio of MXene, and the impact of temperature is reduced in the mass fraction above 1.5%. In general, two behaviors are observed in the optimal MXene ratio with respect to temperature and mass fraction. In low mass fractions, the increase in temperature leads to an increase and then a decrease in the optimum MXene ratio. On the other hand, in high mass fractions, the increase in temperature first shows a decrease and then an increase in the optimum MXene ratio.

Table 8 The proposed optimal points based on EHC and desirability function.

Fig. 13

Optimum MXene ratio in terms of T and MF, based on EHC and desirability function for various scenarios.

Metaheuristic optimization and decision-making

In practical applications, optimizing nanofluid TPPs by maximizing thermal conductivity while minimizing dynamic viscosity is essential for improving the thermal and electrical performance of PVT panels and lowering their energy consumption. However, due to the often-opposing effects of temperature conditions and nanomaterial-related factors on these targets, identifying a unique optimal answer is unfeasible. A Pareto front technique provides an effective strategy for solving this optimization challenge by systematically exploring the feasible space and determining a set of best trade-offs. This study utilizes the multi-objective ant lion optimizer (MOALO) algorithm to obtain these Pareto-optimal solutions. MOALO, recognized for its efficiency in handling complex multi-objective problems, was chosen due to its ability to balance global exploration with local refinement, thereby enabling a thorough investigation of the Pareto front and the identification of diverse non-dominated solutions. Despite its potential, MOALO has been applied in only a limited number of studies, where it has demonstrated promising performance^60,61,62. To assess the effectiveness of MOALO, its results are benchmarked against those obtained using the widely recognized NSGA-II algorithm. The two-objective optimization problem in this study is designed as follows:

$$\:\left\{\begin{array}{c}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:Maximize\:TC={f}_{1}\left(T,MF,MXene\:ratio\right)\\\:Minimize\:DV={f}_{2}\left(T,MF,MXene\:ratio\right)\\\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:Subject\:to\:\left\{\begin{array}{c}5\le\:T(^\circ\:C)\le\:60\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:0.1\le\:MF\left(wt\%\right)\le\:2\:\:\:\:\:\\\:0\le\:MXene\:ratio\le\:0.5\end{array}\:\:\:\right.\:\:\:\:\:\:\\\:\:\end{array}\right.\:$$

(6)

Multi-objective ant Lion optimizer (MOALO)

The ant lion optimizer (ALO) is a nature-inspired metaheuristic algorithm that simulates the hunting mechanism of antlions and their interactions with ants⁶³. It is a population-based optimization method where a set of ants (solutions) explore the search space, while antlions (elite solutions) guide their movement toward optimal regions. The algorithm follows a series of steps to iteratively refine solutions and locate the global optimum. In the optimization process of the ant lion optimizer, several key mechanisms are utilized, as illustrated in Fig. 14^63,64,65:

• Ants traverse the search space through various stochastic paths.

• These stochastic paths are executed across all dimensions of the ants’ positions.

• The trajectories of ants are influenced by the traps set by antlions.

• The capacity of antlions to create traps is directly linked to their fitness; higher fitness results in more expansive traps.

• Antlions possessing more extensive traps exhibit an elevated likelihood of capturing ants.

• In every iteration, ants may be ensnared by an antlion or the elite, which is the most optimal antlion.

• The scope of the random walk is progressively reduced, simulating the ants’ gradual movement toward the antlions.

• When an ant surpasses an antlion in fitness, it signifies that the ant has been ensnared and dragged beneath the sand by the antlion.

• Following each capture, an antlion relocates itself to the latest prey’s position and reconstructs its trap to enhance its chances of future captures.

This framework underpins the dynamic interactions within the ALO algorithm, fostering efficient exploration and exploitation of the search space. For simulating this process, a population of ants is randomly generated, representing potential solutions to the optimization problem. Each ant’s fitness is evaluated using an objective function. The movement of ants is modeled as a random walk, which is influenced by the position of antlions. Unlike conventional evolutionary algorithms, the antlions are not evaluated separately; instead, they inherit the positions of ants and update based on performance. An elite antlion, representing the best solution found so far, has a global influence on all ants. If any antlion outperforms the elite, it replaces it. The algorithm iteratively refines solutions by executing these steps until a termination criterion is met. Ultimately, the elite antlion’s position and fitness serve as the best approximation of the global optimum. The MOALO is an advanced adaptation of the standard ALO, specifically designed to address optimization challenges involving multiple conflicting objectives. Instead of converging on a singular optimal solution, MOALO seeks to generate a diverse set of Pareto-optimal solutions, ensuring a well-balanced trade-off among competing performance criteria⁶⁶. Drawing inspiration from multi-objective particle swarm optimization (MOPSO), MOALO employs sophisticated leader selection and adaptive archive management techniques. To enhance solution diversity, the algorithm strategically emphasizes less populated regions within the solution space. When the archive reaches its capacity, solutions in highly populated areas are removed to maintain a well-distributed set.

MOALO retains the fundamental search behavior of ALO while incorporating mechanisms to balance exploration and exploitation across multiple objectives. By using leader selection, adaptive random walks, and elitism, it efficiently finds high-quality solutions with diverse trade-offs. This makes MOALO a powerful optimization tool for solving complex multi-objective problems in engineering, machine learning, and other domains.

Fig. 14

(a) Trap shape of ant lions; (b) Stochastic movement of an ant within the ant lion’s trap.

Non-dominated sorting genetic algorithm II (NSGA-II)

NSGA-II is a widely used multi-objective optimization algorithm designed to efficiently identify a set of optimal solutions, known as the Pareto front⁶⁷. It enhances its predecessor by incorporating key mechanisms such as fast non-dominated sorting, an elitism strategy, and a crowding distance approach to ensure a well-distributed set of solutions. NSGA-II is particularly useful for solving problems with conflicting objectives, making it a valuable tool in various engineering and scientific domains⁶⁸. The optimization process of NSGA-II consists of the following key steps^67,68:

• 1. Initialization: The algorithm begins by generating an initial population of candidate solutions, which are distributed randomly within the defined search space. Each solution represents a possible candidate for the problem and is evaluated using multiple objective functions.

• 2. Non-dominated sorting: The population is divided into different Pareto fronts based on dominance ranking. The first front consists of non-dominated solutions, while subsequent fronts are formed by progressively removing the already-ranked solutions and re-evaluating the remaining ones.

• 3. Crowding distance calculation: To maintain diversity in the population, NSGA-II calculates the crowding distance of each solution within a front. This metric measures the relative proximity of a solution to its neighbors and helps maintain a diverse spread of solutions across the Pareto front.

• 4. Selection: Tournament selection is used to choose individuals for reproduction. This process gives priority to solutions with a better Pareto ranking and, in cases where rankings are equal, favors solutions with a larger crowding distance to ensure diversity.

• 5. Crossover and mutation: Selected individuals undergo genetic operations such as crossover and mutation to generate offspring. The crossover operation combines information from two parents to create new solutions, while mutation introduces small variations to maintain genetic diversity and avoid premature convergence.

• 6. Population merging and sorting: The newly generated offspring population is combined with the parent population to form an extended population. A new non-dominated sorting process is performed on this combined set, ensuring that the best solutions are retained.

• 7. Truncation based on crowding distance: Since the combined population size exceeds the predefined limit, only the best individuals are selected for the next generation. The selection is based on Pareto dominance and crowding distance, preserving both quality and diversity.

• 8. Convergence: The process repeats for multiple generations until a stopping criterion is met, such as a maximum number of iterations. Over time, NSGA-II refines the Pareto front, ensuring an optimal balance between conflicting objectives.

Through this structured approach, NSGA-II efficiently finds high-quality solutions for multi-objective problems in various fields, ensuring convergence while maintaining a diverse solution set^69,70,71.

Optimal Pareto points

Figure 15 provides the Pareto optimal points obtained from the MOALO and NSGA-II, providing a comparative analysis of their optimization performance. Both algorithms demonstrate an acceptable trend and alignment in their Pareto fronts, indicating that they successfully capture the trade-off between TC and DV. The overlapping nature of the solutions suggests that both methods are effective in identifying high-quality solutions in the optimization space. However, a closer examination reveals that NSGA-II exhibits superior coverage of the solution space, particularly in the lower and upper bounds of the Pareto front. This suggests that NSGA-II is more effective in maintaining a diverse set of solutions, thereby exploring a broader range of optimal trade-offs. The crowding distance mechanism in NSGA-II plays a crucial role in preserving solution diversity, which contributes to a well-spread Pareto front. In contrast, while MOALO produces competitive solutions, its distribution appears slightly less extensive compared to NSGA-II. This difference highlights NSGA-II’s advantage in capturing a more comprehensive set of optimal solutions across the entire design space, making it a more potent option for multi-objective optimization in this study.

Furthermore, the results demonstrate that NSGA-II exhibits faster and more stable convergence, reaching its optimal front within fewer iterations and maintaining a consistent spread across the solution space. In contrast, MOALO also shows effective convergence, although with slightly greater fluctuations observed during the initial stages. This behavior is characteristic of MOALO’s strong global exploration capability, which allows it to probe diverse regions of the search space before gradually refining towards optimal solutions. As the iterations progress, both algorithms successfully stabilize, indicating their efficiency in balancing exploration and exploitation and their ability to reliably reach high-quality Pareto-optimal solutions.

Fig. 15

Pareto fronts obtained from the MOALO and NSGA-II algorithms.

Figure 16 illustrates the distribution of optimal input variables obtained from the multi-objective optimization of a water-based hybrid nanofluid incorporating MXene and Graphene for solar PV/T systems. In Figs. 16(a) and 16(d), the relationship between temperature and the objective functions is depicted. As temperature increases to approximately 60 °C, DV and TC reach a trade-off. The reduction in DV at higher temperatures is expected as optimal state due to the decreased intermolecular forces in the fluid, which leads to improved flow characteristics. Conversely, the increase in TC with temperature can be attributed to enhanced Brownian motion of nanoparticles, which facilitates better thermal energy transport. Figures 16(b) and 16(e) illustrate the impact of nanomaterial mass fraction on the objective functions. A higher mass fraction leads to an optimal state in both DV and TC. The wide MF range observed for the optimum points indicates a conflict of objectives in changing the mass fraction of nanomaterials, where increasing the MF leads to improved TC of the fluid and consequently improved system efficiency, but on the other hand increases DV and leads to the need for stronger pumping power and higher energy consumption. In Figs. 16(c) and 16(f), the influence of the MXene ratio on both DV and TC is analyzed. Based on the figure, optimal points with a lower MXene ratio compared to graphene exhibit higher TC, suggesting a more pronounced influence of graphene on TC at these points. Conversely, optimal points with a higher proportion of MXene tend to result in lower viscosity. Notably, the MXene-to-graphene ratio plays a crucial role in determining the interaction between TC and DV at the optimal points.

Considering Fig. 16 and its information, a quantitative analysis of the density distribution of Pareto optimal points in terms of input variables can be presented. In this regard, the highest concentration of optimal points occurs within the 59.9–60.0 °C range, encompassing nearly 90% of the data. Additionally, optimal values predominantly align with nanomaterial mass fractions between 1.5 and 2 wt%, with 58% of the points, demonstrating the significant influence of higher concentrations on both objectives. Moreover, the densest clustering of optimal values appears at MXene ratios of 0.47–0.5, accounting for 68% of the points, while 32% of optimal values are also distributed within the 0–0.2 range. This indicates that there are no optimal points between 0.2 and 0.47, suggesting that either a small percentage of MXene should be dispersed or the contributions of MXene and graphene should be considered approximately equal to achieve a trade-off between TC and DV. These findings emphasize the importance of precisely tuning MXene/Graphene nanofluid properties to achieve enhanced performance in solar PV/T systems.

Fig. 16

Distribution of DV and TC in terms of optimal input values.

VIKOR technique

Identifying the most suitable design alternative from a set of Pareto points poses a considerable challenge for decision-makers. The VIKOR technique, a well-established multi-criteria decision-making approach, effectively tackles this problem by utilizing an aggregation mechanism to determine the closeness of each alternative to an ideal solution. Extensive research has validated the effectiveness of VIKOR across various applications⁷². The methodology follows a structured four-step procedure to systematically rank the available alternatives^73,74:

• 1) Let $\:m$ denote the total number of alternatives and $\:n$ signify the number of criteria under consideration. To systematically structure the evaluation data, a decision-making matrix (DMM) is formulated and represented as $\:{{(x}_{ij})}_{m\times\:n}$, ensuring an organized framework for comparative analysis.

• 2) To identify the most and least favorable alternatives, the contributions of each criterion to the overall assessment are analyzed in terms of both positive and negative influences.

For a criterion where a higher value has a positive impact on the evaluation, the best and worst values are determined as follows:

$$\:{f}_{j}^{*}=max\left[\left.{(x}_{ij})\right|i=1,\:2,\dots\:,\:m\right],\:\:\:j=1,\:2,\dots\:,\:n$$

(7)

$$\:{f}_{j}^{-}=min\left[\left.{(x}_{ij})\right|i=1,\:2,\dots\:,\:m\right],\:\:\:j=1,\:2,\dots\:,\:n$$

(8)

Conversely, if a criterion negatively affects the overall evaluation, the best and worst values are determined as follows:

$$\:{f}_{j}^{*}=min\left[\left.{(x}_{ij})\right|i=1,\:2,\dots\:,\:m\right],\:\:\:j=1,\:2,\dots\:,\:n$$

(9)

$$\:{f}_{j}^{-}=max\left[\left.{(x}_{ij})\right|i=1,\:2,\dots\:,\:m\right],\:\:\:j=1,\:2,\dots\:,\:n$$

(10)

• 3) The significance of each criterion, represented by its weight ($\:{w}_{j}$), is incorporated into the assessment framework by utilizing both the utility measure ($\:{S}_{i}$​) and the regret measure ($\:{R}_{i}$):

$$\:{R}_{i}=max\left[{w}_{j}\cdot\:\frac{{f}_{j}^{*}-{x}_{ij}}{{f}_{j}^{*}-{f}_{j}^{-}}\right],\:\:\:j=1,\:2,\dots\:,\:n,\:\:\:i=1,\:2,\dots\:,\:m$$

(11)

$$\:{S}_{i}=\sum\:_{j=1}^{n}{w}_{j}\cdot\:\frac{{f}_{j}^{*}-{x}_{ij}}{{f}_{j}^{*}-{f}_{j}^{-}},\:\:\:j=1,\:2,\dots\:,\:n,\:\:\:i=1,\:2,\dots\:,\:m$$

(12)

• 4) The VIKOR index ($\:{Q}_{i}$​) is computed by incorporating the strategic weighting factor ($\:v$), which governs the trade-off between collective decision-making principles and overall group benefit optimization. The alternative associated with the lowest $\:{Q}_{i}$​ value is recognized as the most favorable solution, indicating its superior performance in the decision-making framework.

$$\:{Q}_{i}=v\cdot\:\frac{{S}_{i}-{S}^{*}}{{S}^{-}-{S}^{*}}+\left(1-v\right)\cdot\:\frac{{R}_{i}-{R}^{*}}{{R}^{-}-{R}^{*}},\:\:\:i=1,\:2,\dots\:,\:m$$

(13)

where

$$\:{S}^{*}=min\left[\left.{S}_{i}\right|i=1,\:2,\dots\:,\:m\right],\:\:\:{S}^{-}=max\left[\left.{S}_{i}\right|i=1,\:2,\dots\:,\:m\right]$$

(14)

$$\:{R}^{*}=min\left[\left.{S}_{i}\right|i=1,\:2,\dots\:,\:m\right],\:{\:\:R}^{-}=max\left[\left.{S}_{i}\right|i=1,\:2,\dots\:,\:m\right]$$

(15)

In VIKOR technique, $\:v$ is a fundamental component in ranking approach, ensuring a balance between utility maximization and regret minimization. Essentially, this parameter represents the decision-maker’s strategic preference. When $\:v$ is close to 1, the method emphasizes the majority rule, prioritizing the case that exhibits the most exceptional overall performance when assessed across all relevant criteria. Conversely, when $\:v$ is near 0, the focus shifts toward reducing individual regret, selecting the case that exhibits the smallest highest deviation from the ideal solution. In this study, a value of 0.5 is adopted, as it is commonly used in previous research^70,71,75.

Design points

The decision-making process for selecting optimal input parameters in MXene/Graphene hybrid nanofluids for PVT solar systems, as presented in Table 9, highlights the influence of objective function weighting on the trade-off between DV and TC. The diverse weighting scenarios ensure flexibility in decision-making based on system requirements, balancing efficiency and fluid performance. The priority of TC or DV in different application scenarios depends on the system’s requirements and the designer’s preferences.

In Scenario A, where minimizing viscosity is prioritized, the optimal nanofluid composition consists of a minimal nanomaterial mass fraction (0.1 wt%) and a high MXene ratio (0.49999). This results in the lowest DV (0.4473 mPas) but at the expense of lower TC (0.6323 W/mK), making it suitable for applications where flow efficiency and energy consumption is critical. In contrast, Scenario B maximizes TC, yielding the highest TC (1.1150 W/mK) by increasing the nanomaterial MF (1.99999 wt%) while minimizing the MXene ratio (0.00104). However, this leads to the high DV (0.9889 mPas), which may introduce higher pumping power requirements. A balanced approach is observed in Scenario C, achieving a trade-off between DV (0.7071 mPas) and TC (0.8876 W/mK) with moderate MF (1.60793 wt%) and MXene ratio (0.49832). Similar patterns are seen in Scenarios D and E, where adjusting the weighting slightly shifts the balance, favoring one objective over the other while maintaining reasonable trade-offs. Scenarios F and G further illustrate how shifting weight distribution impacts the composition. Scenario F increases TC (1.0967 W/mK) at the cost of a higher DV (0.9472 mPas), whereas Scenario G leans towards lower viscosity (0.4694 mPas) with moderate TC (0.6593 W/mK). These results emphasize the necessity of flexible weighting in decision-making, allowing designers to optimize nanofluid formulations based on specific operational requirements for PVT applications.

Figure 17 illustrates the location of decision points along the Pareto front highlights how varying objective weights influence optimal design. As weight distributions shift, different trade-offs between objectives emerge. Higher TC is achieved at the expense of increased DV, indicating that decision-makers must balance electrical and thermal efficiency and flow and energy consumption performance based on specific application needs.

Table 9 The VIKOR-based proposed design points for various design scenarios.

Fig. 17

The distribution of design points proposed by VIKOR technique along the Pareto front.

Generalization and Real-World implementation

The optimized MXene/Graphene-based nanofluids identified in this study can be directly implemented in commercial solar PV/T systems to enhance both thermal and overall energy efficiency. By tuning key parameters such as nanomaterial mass fraction and MXene-to-Graphene ratio, system designers can balance thermal conductivity and dynamic viscosity to suit specific operational needs. Higher thermal conductivity improves heat extraction from PV modules, boosting electrical efficiency and reducing thermal degradation. Meanwhile, careful control of viscosity minimizes pumping power requirements, ensuring system reliability and cost-effectiveness. These optimized formulations offer a flexible and scalable solution for next-generation PV/T systems, supporting their broader commercialization and adoption in green energy markets.

The proposed hybrid framework demonstrates strong potential for generalization beyond the specific case of MXene/Graphene nanofluids. By integrating data-driven modeling, multi-objective metaheuristic optimization, and decision-making techniques, this approach can be adapted to optimize other nanofluid formulations, including metal oxide, carbon-based, or hybrid nanofluids used in diverse thermal systems. Furthermore, the framework is scalable and can be applied to various energy applications such as heat exchangers, battery thermal management, and concentrated solar power systems. Its modular structure allows for the incorporation of different objective functions and constraints, enabling tailored optimization for specific operational and design requirements in real-world energy systems.

Conclusion

This study presents a novel, data-driven optimization framework to enhance the TPPs of hybrid Graphene/MXene nanofluids, targeting their application in solar energy systems. Unlike existing research, which often lacks an integrated approach, this work combines RSM-based predictive modeling, multi-objective heuristic and metaheuristic optimization, and advanced decision-making techniques. The primary objective was to optimize TC and DV by varying the nanomaterial mass fraction (MF), MXene ratio, and system temperature. To achieve this, RSM models were developed to predict TC and DV with high accuracy (R² = 0.9997 and 0.9984, respectively), validated through regression graphs, violin plots, and ARD analyses. Optimization was performed using the enhanced hill climbing algorithm, NSGA-II, and multi-objective ant lion optimizer, ensuring a balanced trade-off between competing objectives. The incorporation of weighted decision-making strategies, including the desirability function for EHC and VIKOR for NSGA-II and MOALO, refined the selection of optimal solutions. Key findings include:

• The TC model demonstrated minimal errors (ARD: 0.008–0.6%), while the DV model maintained reasonable accuracy (ARD: 0.006–2.7%).

• Three scenarios were explored using EHC and desirability function, with varying priorities between TC and DV. The results revealed a strong dependence of optimal MXene ratio on MF and temperature, highlighting the complex interactions governing nanofluid performance.

• A density analysis of Pareto-optimal points showed that optimal conditions clustered around 59.9–60.0 °C, with MF concentrations between 1.5 and 2 wt% and MXene ratios predominantly in the 0.47–0.5 range.

• Decision-making analysis indicated that varying weight distributions significantly influenced the trade-off between TC and DV. For instance, prioritizing viscosity led to a low MF (0.1 wt%) and high MXene ratio (0.5), while maximizing TC required high MF (1.99999 wt%) with minimal MXene content.

Despite the advancements offered by the proposed methodology, this study has certain limitations. For example, the research should be complemented by experimental validation of the results. Therefore, future work will focus on conducting practical experiments, particularly in solar PV/T applications, to validate and further refine the optimized conditions identified in this study. Additionally, it is important to note that the present models consider only mass fraction, temperature, and MXene/Graphene ratio as input variables due to the limited availability of experimental data; other influential factors, such as nanoparticle aggregation, Brownian motion, and base fluid properties, were not included, as their reliable incorporation requires further experimental investigation and a more comprehensive dataset on MXene-based nanofluids. Furthermore, with future expansion of the dataset, incorporating a wider range of experimental conditions and variables, it would be feasible to apply more advanced machine learning methods, such as ANNs, Gaussian process regression (GPR), and support vector machines (SVM), to further enhance model generalization and predictive accuracy.