Introduction

Prediction of pharmaceutical solubility in solvents is of vital importance due to its application in drug production. For instance, for pharmaceutical crystallization design and optimization, the solubility of drug in solvent must be known at the operational conditions for better operation. The driving force in crystallization is the solubility reduction which is conducted via different means such as cooling and solvent removal1,2. For cooling crystallization, analysis of solubility curve is important to find the crystal formation area as well as metastable zone. The solubility curve is constructed by measuring drug solubility at different temperatures.

In liquid-phase crystallization of pharmaceuticals, the main parameter affecting the crystallization rate and nucleation is temperature as it can change the drug solubility in the solvent. For supercritical solvents, both pressure and temperature can alter the drug solubility and therefore the crystal growth rates, and nucleation are different in supercritical solvents3,4. The solubility of drug in supercritical solvents can be estimated via thermodynamic models which is based on solid-liquid equilibrium for the solvent and solute. Development of thermodynamic models has been a first choice for estimation of drugs solubility in supercritical solvents, as there are numerous models applied for this application5,6,7. In most studies, CO2 is regarded as the green solvent in the process because it is low cost and suitable for pharmaceutical application.

Zhang et al.8 developed a thermodynamic model based on PC-SAFT equation of state (EoS) to correlate solubility of some pharmaceutical compounds in supercritical CO2. Three parameters were considered for the model, and their values were estimated via fitting the experimental data of solubility. The overall RMSE for the fitting was reported to be 0.067 for 10 drugs. There are other activity coefficient and semi-empirical correlations developed for modeling drug solubility in supercritical CO2; however, the accuracy of data-driven models has been shown to be greater than thermodynamic models. Abouzied et al.9 calculated RMSE value of 0.016 for correlation of solubility dataset using Gaussian Process Regression (GPR) which was optimized via Political Optimizer algorithm for the hyperparameters tuning. The great accuracy of GPR model was due to the learning nature of model which can capture the nonlinear relations in the solubility data. Furthermore, developing thermodynamic models for a variety of drug molecules is challenging and cannot be generalized as the model depends on the molecular structure of drugs and the functional groups in the drug and their interactions with solvent molecules. Thus, the research gap is to develop a comprehensive model with capacity for generalization to calculate solubility of various drug molecules in supercritical CO2.

Accurate prediction of drug solubility and solvent density is critically important across multiple disciplines, including pharmaceutical sciences, chemical engineering, and environmental science. Recently, machine learning (ML) techniques have shown promise in providing reliable predictions for such properties10,11,12. Regression techniques have been extensively utilized to link predictor variables (e.g., temperature and pressure) with response variables, including solubility and density. There have been different ML algorithms for prediction of drug solubility in supercritical solvent, which proved better accuracy compared to the thermodynamic models13,14. There are different steps proposed for developing ML models in pharmaceutical solubility prediction including preprocessing, outlier rejection, model selection, optimization, and testing the models. A wide range of ML models should be explored to identify the one that best fits the solubility data. Therefore, a comprehensive modeling approach is required for the accurate prediction of drug solubility in supercritical CO₂ systems.

Among the various regression algorithms, Gradient-based optimization has gained attention for effectively tuning the hyperparameters of regression models. Gradient-based optimization utilizes derivative information to progressively adjust a model’s hyperparameters, aiming to boost its overall effectiveness. This method helps the model to capture complex relationships between inputs and outputs, leading to more accurate predictions overall15.

In this study, we focus on predicting the solubility of raloxifene and the density of CO2 using temperature and pressure as input variables. To achieve this, we employ three-based regression models including Extra Trees (ET), Random Forest (RF), and Gradient Boosting (GB). These models are tuned by Gradient-based optimization methods, enabling the identification of the best hyperparameters that maximize their predictive performance. Accordingly, this study presents the first development of models that simultaneously correlate solubility data and density for CO₂, using raloxifene as the model drug.

This study mainly aims to evaluate and contrast the effectiveness of the selected models in estimating raloxifene solubility and CO₂ density. To measure their accuracy and reliability, metrics including the R² value, root mean squared error (RMSE), average absolute relative difference (AARD%), and maximum error are employed.

The results of this research will help clarify how effective gradient-based optimization is in boosting the performance of tree-based ensemble models for predicting solubility and density. This knowledge can aid researchers and practitioners in selecting the most appropriate regression models and optimization techniques for similar prediction tasks, ultimately facilitating advancements in various fields reliant on accurate solubility and density predictions. The results will be useful for design and optimization of supercritical processing in preparation of nanosized raloxifene particles using green supercritical-based process.

Dataset description

In this study we develop models on a dataset taken from16 which reported the data for solubility of raloxifene and density of supercritical CO2. Due to the importance of CO2 density and solvent compressibility, density is also correlated to pressure and temperature in this study via ML models. The dataset consists of four columns:

  • T (K): Temperature in Kelvin.

  • P (bar): Pressure in bars.

  • y: Solubility of raloxifene.

  • CO2 density: Density of CO2.

The dataset contains measurements taken at different combinations of temperature and pressure, along with the corresponding solubility of raloxifene and CO2 density11,12. Figure 1 is a pair plot that displays the interdependencies among the variables in the dataset. A pair plot arranges a series of subplots in a grid, displaying every variable in relation to all others in the dataset. The diagonal panels depict each variable’s distribution, whereas the off-diagonal panels illustrate scatter plots for each variable pair. The scatter plots provide insights into the potential correlations and patterns between variables.

Fig. 1
figure 1

Visualization of the drug dataset using Pair Plot evaluation.

Full size image

Methods

Gradient-based optimization

Gradient-based optimization is a powerful technique which is used in tuning the hyperparameters of different ML methods including regression models. It uses the concept of gradients, which provide information about the direction and magnitude of the steepest descent of an objective (fitness) function. By calculating derivatives relative to the hyperparameters, the optimization procedure can progressively refine their values, aiming to reduce the objective function and determine the most effective hyperparameter configuration17,18.

In gradient-based optimization, the process begins by specifying an objective function that measures how well the model performs given a particular set of hyperparameters. This objective function is typically a measure of error or loss, such as MSE or MAE. Indeed, the objective function’s derivatives with respect to the hyperparameters are obtained through methods like automatic differentiation or backpropagation. These gradients indicate the direction in which the hyperparameters should be updated to reduce the objective function19.

It is important to note that gradient-based optimization requires the objective function to be differentiable with respect to the hyperparameters. Additionally, care must be taken to avoid local minima and overfitting during the optimization process. Techniques like regularization and early stopping can be employed to mitigate these issues.

Gradient-based optimization of hyperparameters offers a systematic and efficient approach to finding optimal hyperparameter values for regression models. It leverages the power of gradients to guide the search in the hyperparameter space, leading to improved model performance and better generalization to unseen data. The procedure is illustrated in Fig. 219.

In this study, the Gradient-based optimization was implemented using the Adam optimization algorithm, selected for its adaptive learning rate and efficiency in non-convex optimization tasks. The objective function was defined as the mean R-squared (R²) score from 3-fold cross-validation, maximized to ensure both model accuracy and generalizability. The Adam optimizer was configured with a learning rate of 0.0012, beta1 = 0.85, beta2 = 0.98, and epsilon = 1e-8, iterating up to 130 epochs with early stopping after 10 iterations without R² improvement to mitigate overfitting.

Fig. 2
figure 2

Gradient-based optimization of hyperparameters workflow.

Full size image

Decision tree (DT)

DT regression estimates the targets by splitting the dataset into progressively smaller subsets in a hierarchical fashion, with each division based on the values of the independent variables. At each split in the tree, the algorithm chooses the predictor that produces the largest decrease in variance, reflecting the extent of heterogeneity in the target. The partitioning proceeds recursively until a termination condition is fulfilled, for example, when the leaf node contains fewer than a specified minimum number of samples20. The DT regression algorithm generates a hierarchical model presented in a tree-based format, which can be employed to predict outcomes for novel, unobserved data. The iterative process of the model involves traversing the tree structure by evaluating the independent variable values until a terminal node is reached, each time a novel data point is presented21.

The DT algorithm exhibits resilience towards outliers and missing data, and possesses the capability to effectively process both categorical and continuous variables. The risk of overfitting in this method is basically mitigated by tuning hyperparameters, e.g., Maximum Tree Depth and Minimum Leaf Sample Size20. The establishment of correlations between dependent and independent variables can be achieved through the utilization of Decision Tree regression, a valuable technique for forecasting continuous target variables. This can be accomplished through the visualization of said regression.

Random forest (RF) and extra trees (ET)

The RF model is a robust member of the ensemble learning category of models. The model in question exhibits flexibility and user-friendliness, enabling its application in a range of regression and classification tasks22,23. The present discourse will center on the Random Forest model utilized for regression assignments.

The RF model is comprised of an ensemble of DTs that collaborate to generate prognostications. The DT methodology is according to the iterative partitioning of a dataset into progressively smaller subsets, utilizing the features that exhibit the highest discriminatory power with respect to the target variable. The RF model extends this concept by generating numerous decision trees and amalgamating their results to formulate the ultimate forecast24,25.

The equation for the prediction of the RF model is26:

$$\:f\left(x\right)=\frac{1}{M}{\sum\:}_{m=1}^{M}T\left(x,{{\uptheta\:}}_{m}\right)$$

where \(\:f\left(x\right)\) signifies the predicted target value for input vector \(\:x\), \(\:M\) represents the quantity of DT in the forest, \(\:{{\uptheta\:}}_{m}\) represents the parameters of tree \(\:m\), and \(\:T\left(x,{{\uptheta\:}}_{m}\right)\) stands for the prediction of tree \(\:m\) for input vector \(\:x\) and parameters \(\:{{\uptheta\:}}_{m}\). The model’s output is determined by taking the average prediction from all the decision trees in the forest.

In this equation, the forecast of DT is determined by navigating through the tree structure from the starting node to a final node. At every internal node, a choice is formed through the value of an input parameter (\(\:{x}_{i}\)) from the input vector (\(\:x\)), leading the traversal to either the left or right child node based on the decision outcome. At each final node (leaf node), the forecast is generated by assigning the average target value of the training samples that belong to that specific leaf node. The parameters (\(\:{{\uptheta\:}}_{m}\)) of each decision tree are derived from a bootstrap sample of the training data and a random subset of the input parameters.

The ET algorithm is similar to RF but injects extra randomness into the tree-building process, often leading to an ensemble with even higher diversity among its members. This diversity contributes to the model’s robustness and can enhance its performance in regression tasks27,28.

Gradient boosting (GB)

GB is another popular ensemble learning technique that utilizes decision trees as weak models. It is known for its ability to achieve high predictive accuracy by combining multiple weak models in a sequential manner. In this discussion, we will focus on DB with DT as the weak models for regression tasks. The GB model is built by progressively expanding the ensemble with decision trees, where every subsequent tree is instructed to fix the errors. This iterative process allows the model to learn complex relationships and capture fine-grained patterns in the data29.

In GB with DTs, the weak models are typically shallow decision trees, often referred to as “stumps” or “shallow trees.” These trees have a small number of levels and are trained to make predictions based on a subset of the input features30,31. Unlike RF and ET, where each tree is constructed independently, in GB, the trees are built sequentially, with each tree learning from the mistakes of its predecessors.

The prediction equation for GB with decision trees can be represented as32:

$$\:f\left(x\right)={\sum\:}_{m=1}^{M}{\gamma\:}_{m}*T\left(x,{\theta\:}_{m}\right)$$

In this equation, f(x) denotes the predicted target value for the input vector x, M represents the total count of DTs, \(\:{\gamma\:}_{m}\)signifies the contribution (or weight) of tree m, \(\:{\theta\:}_{m}\) represents the parameters of tree m, and \(\:T\left(x,{\theta\:}_{m}\right)\) corresponds to the prediction made by tree m for input vector x using parameters \(\:{\theta\:}_{m}\). The final solution is determined by combining the predictions from all the decision trees, where each prediction is multiplied by its corresponding weight, denoted as \(\:{\gamma\:}_{m}\), and then summed.

In prediction, the input vector \(\:x\) moves through each decision tree from the root to a leaf, with the path determined by the values of particular features \(\:\left({x}_{i}\right)\). At every internal node, the chosen feature’s value dictates which branch the traversal follows. Finally, at the leaf node, the prediction is generated by assigning the output value associated with that leaf node33.

Results and discussion

The modeling and implementation of ML were carried out using Python v3.8 software accessible from the link: https://www.python.org. The present study assessed the efficacy of three regression models, namely ET, RF, and GB in calculating the CO2 density and solubility of raloxifene (y) based on the provided dataset to find out how well these models can fit the drug dataset. The assessment criteria employed encompassed the R2 score, RMSE, AARD%, and maximum error. The findings are succinctly presented in the tabular format as in Tables 1 and 2. As seen, four statistical parameters were calculated for each model to compare their precision in calculating solvent density and raloxifene solubility as the model drug.

Table 1 Results of correlations of solvent density by ML.
Full size table
Table 2 Results of models for solubility of raloxifene.
Full size table

The Gradient Boosting (GB) model is indeed the most appropriate one for predicting solvent density based on the evaluated metrics. With a remarkable R-squared score of 0.98577, the GB model exhibits a strong correlation with the CO2 density target variable. Additionally, it achieves the lowest RMSE and AARD% values, indicating its superior accuracy and precision in predicting CO2 density.

When it comes to predicting the Solubility of Raloxifene, the GB model did not outperform two other models. The ET model achieved a higher R-squared score (0.94912) and a lower RMSE and AARD% compared to the GB and RF model. The predicted and actual values for both outputs are compared in Figs. 3 and 4.

Fig. 3
figure 3

Actual and calculated Solubility of Raloxifene using three models.

Full size image
Fig. 4
figure 4

Actual and calculated CO2 Density using three models.

Full size image

Finally, based on the fitting precision and residuals, GB has been recognized as the best model for CO2 Density and ET for Solubility of drug. Individual effects of inputs on output targets are shown in Figs. 5, 6, 7 and 8 using these models. Also, 3D plots are shown in Figs. 9 and 10. The constructed design space can be utilized in analysis and evaluation of raloxifene solubility variations with temperature and pressure. Due to the compressibility of solvent, it is observed a major change of density and solubility with pressure alteration in the process which is not usually observed for liquid solvents such as organic solvents. This phenomenon was also reported by Wu et al.11 and Aldawsari et al.12 for simulation of raloxifene solubility in supercritical CO2. At higher pressure points, intermolecular interactions are increased between solvent-solvent and solute-solvent molecules which would cause enhancement of drug dissolution in the solvent phase12. Although temperature increment decreases the density of solvent (see Fig. 8), drug solubility goes up with increasing temperature as illustrated in Fig. 6.

Fig. 5
figure 5

Individual Effect of P on Solubility of Raloxifene.

Full size image
Fig. 6
figure 6

Individual Effect of T on Solubility of Raloxifene.

Full size image
Fig. 7
figure 7

Individual Effect of P on CO2 Density.

Full size image
Fig. 8
figure 8

Individual Effect of T on CO2 Density.

Full size image
Fig. 9
figure 9

3D surface for Solubility of Raloxifene. The figure is drawn by Python v3.8 which can be freely downloaded from the link: https://www.python.org.

Full size image
Fig. 10
figure 10

3D surface for CO2 Density. The figure is drawn by Python v3.8 which can be freely downloaded from the link: https://www.python.org.

Full size image

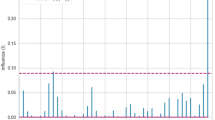
Figures 11 and 12 illustrate the feature importance scores for the GB model in predicting CO₂ density and the ET model in predicting raloxifene solubility, respectively. In Fig. 11, Pressure (P) dominates with an importance of approximately 0.63, highlighting its primary influence on density variations, while Temperature (T) contributes 0.37 that could be due to the compressibility of solvent at this condition which is highly correlated to the pressure. In Fig. 12, temperature is more influential at 0.56, compared to pressure’s 0.44, emphasizing temperature’s key role in solubility behavior under supercritical conditions.

Fig. 11
figure 11

Feature importance for Density prediction.

Full size image
Fig. 12
figure 12

Feature importance for Solubility prediction.

Full size image

To validate the generality of the proposed ML approach externally, the same model development method was applied to an independent dataset comprising solubility measurements (in g/L) for 15 different pharmaceutical compounds in supercritical CO2 under varying temperature and pressure conditions. The data have been collected from various sources and the model was implemented on the data. The ET, RF, and GB models were trained and optimized using the same Gradient-based optimization technique (Adam optimizer with mean 3-fold R² score as the fitness function). The performance metrics on this external dataset demonstrate comparable accuracy to the original raloxifene case study, confirming the method’s robustness across diverse drugs. Table 3 shows the overall performance of models on this external data with more than 400 data points.

Table 3 Results of models for solubility in the external validation dataset.
Full size table

The ET model again emerged as the best performer in predicting solubility values, achieving an R-squared score closely mirroring the main case study’s 0.949, with low RMSE and AARD% values indicating reliable predictions across the multi-compound dataset. Also, AARD is near 6.12% for ET which is greater than the thermodynamic model developed by Zhang et al.8 with AARD% of 11.45 for 10 drugs by using EoS model of PC-SAFT.

To further illustrate the model’s generality, the maximum absolute error for each compound using the ET model is presented below. These errors vary based on the solubility range of each drug but remain low relative to the measured values, demonstrating consistent performance. Table 4 shows the results for different compounds.

Table 4 Maximum errors for each drug in external validation using ET model.
Full size table

Conclusion

The objective of this investigation is to forecast the solubility of raloxifene (y) and the density of CO2 by utilizing temperature (T) and pressure (P) as independent variables. The study involved the implementation and optimization of three regression models, namely Extra Trees (ET), Random Forest (RF), and Gradient Boosting (GB), through the use of Gradient-based optimization. The GB model demonstrated a robust association between predicted and actual values, as evidenced by its R-squared score of 0.986, in the context of CO2 density prediction. The model’s root mean squared error (RMSE) was determined to be 23.20, signifying a notable level of precision. The maximum error observed was 33.06. In relation to the solubility of raloxifene, it was observed that the ET model exhibited the most optimal R-squared score of 0.949, thereby signifying a strong correspondence with the data. The model exhibited an RMSE of 0.41, with a maximum error of 0.90. Comparatively, the RF and GB models achieved slightly lower R-squared scores of 0.903 and 0.886, respectively, for the solubility of raloxifene. The Random Forest (RF) model demonstrated a Root Mean Squared Error (RMSE) of 0.55, with a maximum error of 1.17. In contrast, the Gradient Boosting (GB) model yielded an RMSE of 0.72, with a maximum error of 1.39.