Introduction

Intracranial aneurysms, particularly those occurring in the Middle Cerebral Artery (MCA), are among the most commonly diagnosed cerebral aneurysms, representing a significant subset of cases that present with subarachnoid hemorrhage (SAH) upon rupture1,2,3. MCA aneurysms, often located at bifurcation points, exhibit complex morphologies and flow patterns that challenge both diagnosis and treatment planning. While not all unruptured aneurysms necessitate immediate intervention, predicting the rupture risk remains a critical concern in clinical decision-making4,5,6.

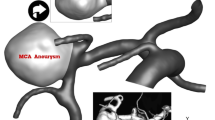
Several studies have indicated that aneurysm morphology alone is insufficient to fully characterize rupture risk7,8. Instead, hemodynamic factors—such as Wall Shear Stress (WSS), Oscillatory Shear Index (OSI), and flow patterns—have emerged as important indicators of aneurysmal instability9,10,11. These variables reflect the interaction between blood flow and vessel wall, which is thought to influence vascular remodeling, inflammation, and eventual rupture. Figure 1 displays the flow structure inside MCA aneurysm12,13.

Fig. 1
figure 1

Flow stream inside cerebral MCA aneurysm.

Full size image

Computational Fluid Dynamics (CFD) has become an invaluable tool in the non-invasive evaluation of these hemodynamic variables, enabling patient-specific simulations based on medical imaging data14,15,16. However, CFD simulations are computationally intensive and time-consuming, especially when applied to large patient cohorts or when real-time clinical support is desired.

To address this limitation, Machine Learning (ML) techniques are increasingly being integrated with CFD-based workflows17,18,19. By training ML models on CFD-derived datasets, it becomes possible to rapidly estimate key hemodynamic metrics with reasonable accuracy, significantly reducing computational cost while retaining clinically useful precision. This synergy allows for efficient hemodynamic screening of MCA aneurysms, facilitating stratified risk assessment and optimizing treatment strategies—such as surgical clipping or endovascular coiling—on a personalized basis20,21.

Moreover, ML-enhanced CFD models can help identify nonlinear patterns and latent features in the flow data that may not be apparent through conventional methods, potentially uncovering new markers of rupture-prone aneurysms22. This integrative approach supports a more data-driven, precision-medicine paradigm in cerebrovascular disease management, with the promise of improving patient outcomes while alleviating healthcare burdens.

We selected a POD– Long Short-Term Memory (LSTM) hybrid approach after reviewing several ROM strategies for unsteady fluid flow, including Galerkin-projected POD models, dynamic mode decomposition (DMD), and autoencoder-based methods23,24. Compared to Galerkin-projected ROMs, our approach avoids numerical instability issues for nonlinear, pulsatile flows in complex geometries. Compared to DMD, POD–LSTM provides greater flexibility in modeling non-periodic or nonlinear temporal dynamics. While deep autoencoders are also powerful, they typically require larger datasets than available in this pilot study. Therefore, the POD–LSTM combination provided a good balance between accuracy, stability, and feasibility for our data scale, making it an appropriate choice for investigating feasibility in aneurysm rupture risk assessment scenarios25.

In this paper, CFD results of hemodynamic factors related to the pulsatile blood flow through the saccular aneurysm has been predicted via machine learning approach. In this study, the proper orthogonal decomposition is applied for the reducing the size of the original data and then, the LSTM approach is applied for the prediction of the CFD data. Comparison of the predicted and real data is also done to evaluate the precision of the applied methodology.

Computational method for full order simulation

Modeling pulsatile blood flow within cerebral aneurysms, particularly when using a Casson non-Newtonian fluid model and excluding fluid-structure interaction (FSI), involves solving the fundamental Navier–Stokes equations under assumptions appropriate for blood dynamics26. In such simulations, blood is treated as an incompressible, laminar, and pulsatile fluid with non-Newtonian characteristics. The Casson model captures the shear-thinning behavior of blood by accounting for the yield stress—below which blood behaves as a viscoelastic solid and above which it flows as a viscous fluid. The governing equations include the continuity equation, which ensures mass conservation, and the momentum equations, modified to include the Casson model’s rheological formulation. Specifically, the apparent viscosity in the Casson model is defined as a function of shear rate, incorporating both the yield stress and a shear-rate-dependent viscosity component, which is critical in low-shear regions such as aneurysmal domes. Blood was modeled as a Casson fluid at \(\:{37}^{\circ\:}\text{C}\) with density \(\:\rho\:=1060\text{}\text{k}\text{g}{\text{}\text{m}}^{-3}\). The Casson constitutive relation, \(\:\sqrt{\tau\:}=\sqrt{{\tau\:}_{y}}+\sqrt{{\eta\:}_{PL}\stackrel{\prime }{\gamma\:}}\), was used with yield stress \(\:{\tau\:}_{y}=0.010\:\text{P}\text{a}\) and plastic viscosity \(\:{\eta\:}_{PL}=0.0040\) Pa.s. These values lie within physiological ranges reported for human blood ( \(\:{\tau\:}_{y}\approx\:\) \(\:0.002-0.03\text{}\text{P}\text{a}\); high-shear viscosity \(\:\approx\:3.5-5.5\text{m}\text{P}\text{a}\cdot\:\text{s}\) ). ANSYS-Fluent software is used for the modelling of the blood flow in three-dimensional model27.

The original patient-specific model selected for our study is demonstrated in Fig. 2. In this figure, the applied profiles at inlet and outlet of the model are also demonstrated. The selected patient is obtained from Aneurisk web project28. While mass flow rate is applied at inlet, Pressure outflow profile is used at outlets of the model. A Middle Cerebral Artery (MCA) inflow velocity waveform was taken from phase-contrast MRI measurements in healthy volunteers and used as the reference shape; peak systolic velocities of \(\:\sim\:0.6-0.9\) \(\:\text{m}{\text{s}}^{-1}\) and mean \(\:\sim\:0.4-0.5\text{}\text{m}{\text{}\text{s}}^{-1}\) are consistent with prior PC-MRI/TCD reports. The waveform was scaled to the patient-specific inlet diameter to match physiologic flow (cardiac period \(\:\text{T}=1\text{}\text{s}\) )9.

Fig. 2
figure 2

Patient-specific MCA aneurysm.

Full size image

In the absence of FSI, the vessel wall is typically modeled as rigid and no-slip, simplifying the computational domain and reducing computational cost. While this excludes the mechanical interaction between blood flow and the deformable arterial wall, it still provides reasonably accurate insights into flow-related parameters like wall shear stress (WSS), oscillatory shear index (OSI), and velocity distributions, particularly in larger vessels or aneurysms where wall compliance is less dominant29,30,31. Since the flow in our model is periodic, we used results of the 3rd cycle since the flow is fully converged in this cycle32. Peak systole was selected for most indices because it corresponds to the stage of highest flow rate and wall shear stress, making it representative of the hemodynamic loading on the vessel wall. OSI, however, is inherently a time-averaged parameter that depends on the directional changes of WSS over the entire cycle, and its value is generally more pronounced during decelerating flow (early diastole), when flow reversal occurs. For this reason, we originally chose to illustrate OSI at early diastole.

Fig. 3
figure 3

Boundary layer grid.

Full size image

The cleaned geometry is then imported into ANSYS Meshing where a high-quality computational mesh is generated, often comprising tetrahedral or polyhedral elements with boundary layer refinement near the vessel walls to capture sharp gradients in WSS33,34. Figure 3 and Figure 4 illustrates the generated grid. Four meshes (coarse/medium/fine/ very fine) with boundary-layer inflation (first-cell \(\:{y}^{+}<1\), growth \(\:\le\:1.2\) ) were tested. We monitored (i) cycle-averaged inlet-outlet pressure drop, (ii) volume-integrated TKE surrogate, (iii) area averaged TAWSS, and (iv) 95th percentile WSS on the aneurysm sac. Differences between medium and fine meshes were within \(\:\le\:3\text{\%}\) for integral metrics and \(\:\le\:5\text{\%}\) for percentile WSS, which we take as mesh converged. Finally, fine grid with 1,680,000 cells is selected and results of grid studies are presented in Table 1.

Table 1 Grid study.
Full size table
Fig. 4
figure 4

Grid generation at sac region.

Full size image

This workflow enables detailed, patient-specific hemodynamic simulations that incorporate physiologically relevant flow characteristics while balancing computational feasibility, particularly when wall compliance (FSI) is not a primary concern.

Applied POD + LSTM machine learning technique

POD modes and reconstructed POD

The Proper Orthogonal Decomposition (POD) is widely recognized in the literature as the leading method for data reduction35. In this approach, basis functions are obtained by collecting temporal snapshots of the variables from the full-order model. The snapshot matrix is built from the fluid-domain variables—velocity components (Vx, Vy, Vz) and pressure P.

Each snapshot is represented as a vector of size N, containing the solution values at the computational nodes. For example, the x-velocity component at snapshot s is stored in a vector Vsx (where the superscript indicates the spatial direction), containing N entries, with N denoting the number of nodes. The complete set of these vectors forms the snapshot matrix

$$\:{\mathcal{V}}^{x}=\left({\mathcal{V}}_{1}^{x},\dots\:,{\mathcal{V}}_{s}^{x},\dots\:,{\mathcal{V}}_{S}^{x}\right)$$
(1)

for the x-velocity component. For clarity, the procedure will be described for a general snapshot matrix \(\:\phi\:\).

POD determines an optimal set of basis functions \(\:\phi\:\) by applying Singular Value Decomposition (SVD) to the snapshot matrix:

$$\:\phi\:=U{\Sigma\:}{V}^{T}$$
(2)

where \(\:U\in\:{R}^{\mathcal{N}\times\:\mathcal{N}}\) and \(\:V\in\:{R}^{\mathcal{S}\times\:\mathcal{S}}\) are the matrices consisting orthogonal vectors for \(\:\phi\:{\phi\:}^{T}\) and \(\:{\phi\:}^{T}\phi\:\), respectively. \(\:{\Sigma\:}\) is a diagonal matrix of size \(\:\mathcal{N}\times\:S.{\Sigma\:}\) are the singular values of \(\:\phi\:\)36.

A reduced-order approximation of the field \(\:\phi\:\) can be described as follows:

$$\:\phi\:\approx\:\sum\:_{n=1}^{N}\:{\alpha\:}_{n}\left(t\right)\cdot\:{\varphi\:}_{n}$$
(3)

where \(\:\varphi\:\) are POD vectors.

Long Short-Term memory

Long Short-Term Memory (LSTM) networks are a specialized class of Recurrent Neural Networks (RNNs) developed to effectively capture temporal dependencies in time series data37. Owing to their exceptional capability to preserve long-range correlations in sequential data, LSTMs have been successfully applied across a wide range of disciplines.

The key strength of LSTMs lies in their use of gating mechanisms, which regulate the flow of information within the network. These gates selectively retain relevant information from past sequences, thereby enhancing predictive accuracy. As mentioned in the previous works38,39, the architecture of an LSTM block comprises three essential gates: the forget gate: the forget gate, \(\:{F}_{t}\), the input gate, \(\:{I}_{t}\), and the output gate, \(\:{O}_{t}\). Together, these gates control the transmission of information through the block, deciding what to retain, update, or discard. During training, the network learns to identify and preserve information most relevant to the prediction task. The mathematical formulation of the gates and the cell state is given by:

$$\:{I}_{t}=\sigma\:\left({W}_{xI}{x}_{t}+{W}_{hI}{h}_{t-1}+{W}_{cI}{c}_{t-1}+{B}_{I}\right),$$
(4)
$$\:{F}_{t}=\sigma\:\left({W}_{xF}{x}_{t}+{W}_{hF}{h}_{t-1}+{W}_{cF}{c}_{t-1}+{B}_{F}\right),$$
(5)
$$\:{c}_{t}={F}_{t}{c}_{t-1}+{I}_{t}\text{t}\text{a}\text{n}\text{h}\left({W}_{xc}{x}_{t}+{W}_{hc}{h}_{t-1}+{B}_{c}\right)$$
(6)
$$\:{O}_{t}=\sigma\:\left({W}_{xO}{x}_{t}+{W}_{ho}{h}_{t-1}+{W}_{co}{c}_{t}+{B}_{O}\right),$$
(7)
$$\:{h}_{t}={o}_{t}\text{t}\text{a}\text{n}\text{h}\left({c}_{t}\right)$$
(8)

Here, \(\:{W}_{xI},{W}_{xF},{W}_{xc}\), and \(\:{W}_{xO}\) are matrices of weights from the input gate, forget gate, long-term cell state, and output gate to input, respectively. Similarly, \(\:{W}_{hI},{W}_{hF},{W}_{hc}\), and \(\:{W}_{hO}\) are the weight matrices of the input gate, forget gate, long-term cell state, and output gate to the intermediate output, respectively. The symbol \(\:B\) denotes bias vectors, and \(\:\sigma\:(\).) stands for sigmoid function.

POD-LSTM coupling

The POD–LSTM framework, depicted in Fig. 5, is employed to predict the evolution of the fields. The procedure consists of the following steps:

  1. 1.

    Data preparation: Snapshots of selected variables (e.g., velocity components) are collected and arranged into a matrix. A POD analysis is then applied to extract spatial orthogonal modes \(\:{\varphi\:}_{n}\) and the corresponding temporal coefficients \(\:{\alpha\:}_{n}\). The number of retained modes N is chosen to capture the dominant flow features. Since N is much smaller than the full-order dimension \(\:M\) of \(\:{\varphi\:}_{n}\in\:{\mathbb{R}}^{M}\), the subspace spanned by \(\:{\varphi\:}_{n}(n=\text{1,2},\dots\:N)\) provides a low-dimensional representation of the full-order model.

  2. 2.

    Temporal coefficient segmentation: The time series of \(\:{\alpha\:}_{n}\)values is divided into multiple overlapping time windows, each of a specified length (20 in this case).

  3. 3.

    Data Splitting: The segmented dataset is split into training (80%) and testing (20%) sets.

  4. 4.

    LSTM network training: The LSTM network is trained to learn the mapping between input and output sequences of temporal coefficients.

  5. 5.

    Network validation: The trained network’s performance is assessed by comparing the predicted temporal coefficients with those from the test dataset.

  6. 6.

    Field reconstruction: Finally, the physical field is reconstructed using the dominant POD modes obtained in step 1 and the LSTM-predicted temporal coefficients40.

Fig. 5
figure 5

Overview of applied flowchart for prediction of pulsatile blood flow.

Full size image

In Table 2, sample of the used hyper-parameters chosen for WSS data in the present case is presented.

Table 2 Applied Hyper-parameters for the WSS.
Full size table

Results and discussion

Figure 6 illustrates the accumulated energy percentage as a function of the number of modes derived from the application of the Proper Orthogonal Decomposition (POD) method at the neck ostium of an aneurysm. The plot shows four distinct variables: the velocity components in the X, Y, and Z directions, and pressure. From the graph, it is evident that a small number of modes can capture the majority of the system’s dynamic energy. For all velocity components (Vel_X, Vel_Y, Vel_Z), more than 90% of the total kinetic energy is captured with fewer than 10 modes. Notably, the X and Z velocity components converge faster than the Y component, indicating more dominant coherent structures in those directions at the neck region. In contrast, the pressure variable exhibits an even steeper rise and reaches nearly full energy capture (> 99%) with just a few modes, highlighting its relatively lower dimensional complexity in this region.

Fig. 6
figure 6

required number of Mode for accumulated energy of velocity and pressure factors at plane located at ostium.

Full size image

Figure 7 presents the accumulated energy percentage versus the number of POD modes for hemodynamic quantities evaluated at the aneurysmal wall, specifically Pressure, Wall Shear Stress (WSS), and Oscillatory Shear Index (OSI). The plot reveals that pressure and WSS achieve near-total energy capture with only a few modes—both reaching over 99% of accumulated energy by approximately the 5th mode. This suggests that their spatial-temporal distributions are highly structured and can be effectively reconstructed with minimal modal content, making them well-suited for reduced-order modeling. The OSI, in contrast, displays a slower energy accumulation curve. Starting near 70%, it requires over 20 modes to exceed 99% of the total energy, reflecting its higher complexity and spatial variability across the aneurysm wall. This is consistent with OSI’s sensitivity to directional changes in wall shear over the cardiac cycle, which introduces more dynamic modes into its representation.

Fig. 7
figure 7

Required Mode number for accumulated energy of OSI, WSS and pressure factors over sac surface.

Full size image

These results underscore that POD can significantly reduce the computational load in capturing wall-related hemodynamic parameters while preserving critical information. In particular, reconstructing pressure and WSS fields with high fidelity is feasible using only a handful of modes, which is beneficial for accelerating simulation workflows and enabling real-time or near-real-time prediction in clinical applications. For more complex variables like OSI, a moderate number of modes is required, but the POD approach still offers a tractable and efficient alternative to full-resolution CFD simulations when assessing aneurysmal rupture risk based on wall dynamics.

The results suggest that POD provides an efficient dimensionality reduction technique, allowing for a compact representation of the flow dynamics at the aneurysm neck. This can be especially useful in reduced-order modeling, where retaining only the most energetic modes can significantly decrease computational costs while maintaining critical flow features—making it an attractive method when combined with machine learning or real-time simulation needs in patient-specific CFD workflows. Based on the achieved data and to preserve 95% of total energy of our model, the selected number of mode for velocity component (Vx, Vy, Vz), pressure, WSS and OSI is 8, 3, 5 and 9, respectively.

Figure 8a and b illustrate the reconstruction errors for various hemodynamic parameters, evaluated over time snapshots at two distinct regions of interest: the neck ostium (Fig. 8a) and the aneurysm wall (Fig. 8b). The vertical axis shows the L2 norm difference (%) on a logarithmic scale, indicating the relative reconstruction error between the original CFD data and the data reconstructed using a limited number of Proper Orthogonal Decomposition (POD) modes. The horizontal axis represents the number of temporal snapshots used in the dynamic simulation.

Fig. 8
figure 8

Reconstruction Errors for data at a) ostium plane b) over sac surface.

Full size image

In Fig. 8a, corresponding to the neck ostium, the reconstruction error for the pressure (black line) is the lowest among all quantities, remaining consistently below 0.1%, reflecting excellent accuracy with minimal mode inclusion. The velocity components—Vel_X, Vel_Y, and Vel_Z—show slightly higher errors, ranging approximately between 0.5% and 3%, with Vel_Y (green) showing the highest fluctuations. These small but non-negligible variations suggest that while the velocity field at the neck contains more dynamic complexity than pressure, it is still well captured by the reduced-order model.

In contrast, Fig. 8b, representing the aneurysm wall, reveals a more variable behavior. Again, pressure remains the most accurately reconstructed variable, with reconstruction error staying below 0.1% for nearly all snapshots. The Wall Shear Stress (WSS) also maintains low error, typically under 1%, confirming that the dominant features of the shear stress distribution are effectively represented with relatively few POD modes. However, the Oscillatory Shear Index (OSI) shows significantly higher reconstruction errors—especially during early snapshots—starting above 100% and gradually dropping below 10% around snapshot 100. This reflects OSI’s sensitivity to small temporal and directional variations in the shear field, which require more modes or snapshots to be reliably captured.

Together, these figures emphasize that POD-based reduced-order modeling can robustly reconstruct pressure and WSS fields in both regions with high fidelity, while OSI—due to its inherently higher temporal-spatial complexity—demands greater modal resolution. This reinforces the idea that for accurate real-time or machine learning-assisted predictions, targeted treatment of variables like OSI may be required, whereas more stable quantities like pressure can be confidently approximated using compact low-dimensional models.

Figure 9 comprises four subplots illustrating the L2 norm reconstruction error (%) over time snapshots for different hemodynamic variables at the aneurysm neck ostium, using a model trained with Proper Orthogonal Decomposition (POD) combined with a machine learning predictor. Each graph evaluates model performance across training (blue lines with diamond markers) and testing (green lines with circle markers) datasets, helping assess the model’s generalization capability.

Fig. 9
figure 9

Comparison of L2 norm for a) Vx b) Vy c) Vz and d) Pressure value in test and train dataset at neck ostium region.

Full size image

Figure 9 confirms that the POD-ML approach can accurately reconstruct flow dynamics at the aneurysm neck, especially for pressure and certain velocity components. However, test error growth—particularly in Vel_Y—emphasizes the importance of selecting appropriate training intervals and possibly enriching the model structure (e.g., using recurrent neural networks or physics-informed models) for more dynamic variables. These findings support the feasibility of using reduced-order models for real-time predictions, while highlighting the need for variable-specific modeling strategies to maintain reliability across the full cardiac cycle.

Figure 10 presents the L2 norm reconstruction error (%) over time snapshots for three critical hemodynamic variables—Oscillatory Shear Index (OSI), Wall Shear Stress (WSS), and Pressure—evaluated at the aneurysm wall. Each plot distinguishes between training data (blue line with diamond markers) and test data (green line with circle markers), allowing an assessment of the generalization ability of a machine learning-enhanced Proper Orthogonal Decomposition (POD) model.

Fig. 10
figure 10

Comparison of L2 norm for a) OSI b) WSS and c) Pressure value in test and train dataset through aneurysm wall.

Full size image

Figure 10 collectively demonstrates that pressure and WSS are well-suited for POD-based reduced-order modeling, showing high accuracy in both training and test regions. In Fig. 10b, the effects of different test-train segmentations are also presented. As expected, decreasing the test portion (equivalent to increasing train data) would result in lower errors in our proposed technique. In contrast, OSI requires greater care, potentially needing more training data or enhanced modeling techniques (e.g., hybrid physics-informed networks) to ensure accurate prediction across the entire time domain. These results have important implications for simulation acceleration and real-time assessment of aneurysm wall conditions, where WSS and pressure predictions can be trusted, but OSI must be treated with higher modeling sophistication.

Fig. 11
figure 11

Comparison of a) Vx b) Vy c) Vz and d) Pressure reconstructed (left side) and Predicted (right side) contour over near ostium section at peak systolic stage.

Full size image

Comparison of the reconstruction and prediction contours at section near ostium region is done and results are displayed in Fig. 11. The comparison of Velocity in three directions and pressure are illustrates in this figure to demonstrates the efficiency of the applied technique for the estimation of the hemodynamic factors near the ostium section where the blood flow moves along the limited passway and the hemodynamic factors such as WSS is high in this section. Comparison of the predicted and reconstructed velocity contour indicate that the velocity changes are predicted efficiently in our hybrid method although there are large velocity gradient in our results. To evaluate the methodology, comparison of OSI, WSS and pressure over sac surface of the selected model is also done and Fig. 12 displays these contours. These hemodynamic factors are also predicted reasonable via our methodology.

Fig. 12
figure 12

Comparison of a) OSI b) WSS and c) Pressure reconstructed (left side) and Predicted (right side) contour over sac surface area (it should be noted that reported data for WSS and Pressure is obtained at peak systolic stage while OSI is calculated at early diastolic stage).

Full size image

While our model achieves high accuracy on the training set, we indeed observe a 1–2 order of magnitude increase in error on the test set. This is expected in part due to the complex nature of the OSI field and the limited amount of training data available. For pressure and WSS, however, the test-set errors remain within acceptable range based on previous works17,25.

Conclusion

In this study, we presented an integrated computational framework combining Computational Fluid Dynamics (CFD), Proper Orthogonal Decomposition (POD), and machine learning techniques to efficiently evaluate and predict hemodynamic parameters associated with Middle Cerebral Artery (MCA) aneurysms. By applying this approach to patient-specific geometries derived from medical imaging, we were able to extract dominant flow features and significantly reduce the dimensional complexity of time-resolved simulations.

The POD-based modal analysis demonstrated that a small number of modes are sufficient to capture over 99% of the kinetic and hemodynamic energy for most variables, especially pressure and wall shear stress (WSS). Variables with higher temporal and spatial complexity—such as oscillatory shear index (OSI)—required a larger number of modes to achieve comparable reconstruction fidelity. Our analysis also highlighted clear differences between the neck ostium and aneurysm wall regions, with the wall exhibiting more dynamic variability in OSI, thereby posing greater challenges for reduced-order modeling.

Machine learning models trained on the reduced-order features showed high predictive accuracy for pressure and WSS, both in training and unseen testing snapshots, supporting their potential use in real-time clinical estimation or risk stratification workflows. However, OSI predictions in the test phase exhibited larger reconstruction errors, indicating that further refinement in data-driven modelling may be necessary for robust OSI prediction.

Overall, the proposed POD-ML approach provides a promising and scalable tool for non-invasive, patient-specific aneurysm assessment, enabling fast and accurate estimation of key hemodynamic indicators while substantially reducing computational cost. This methodology could support improved decision-making in aneurysm management and help identify rupture-prone cases more reliably, particularly when extended to larger patient datasets and combined with clinical outcome data. Indeed, the proposed framework is scalable in the sense that it can incorporate additional patient datasets to improve generalizability, and once trained on a sufficiently diverse cohort, it could potentially be adapted to new geometries with minimal retraining via transfer learning.