Secure and energy-efficient transmission in UAV-assisted intelligent reflecting surface networks

Abstract

With the growing demand for secure and energy-efficient wireless communication in dynamic and energy-constrained environments, integrating unmanned aerial vehicle (UAV) with intelligent reflecting surface (IRS) has emerged as a promising solution. However, air–ground communication still faces critical challenges such as eavesdropping threats and limited onboard energy of UAVs. To address these issues, this paper proposes a physical layer security (PLS) transmission framework for UAV-IRS-assisted communication systems. The proposed scheme incorporates artificial noise (AN) and simultaneous wireless information and power transfer (SWIPT) to enhance secrecy performance and ensure sustained energy harvesting (EH). The system jointly optimizes the base station (BS) beamforming, UAV positioning, and IRS phase shift to maximize the secrecy rate (SR) under EH constraints. To solve the resulting non-convex optimization problem, we design a deep reinforcement learning (DRL)-based approach using the twin delayed deep deterministic policy gradient (TD3) algorithm. Simulation results demonstrate that the proposed method significantly improves both secrecy and energy efficiency compared to existing baseline schemes.

Introduction

Recently, due to the increasing frequency of marine activities, traditional shore-based communication systems have struggled to meet the growing demands for coverage, transmission rate, and reliability. Specifically, current maritime communications mainly rely on base station (BS) deployed along the coastline. However, the coverage radius of BS is inherently limited. Moreover, complex marine environmental factors such as dynamic wave fluctuations, terrain undulations, and sea surface vapor effects create substantial challenges to the large-scale deployment of fixed BSs and relay nodes at sea. These factors not only cause severe path loss in the communication links for maritime communication but also make the system highly susceptible to interference from constantly changing sea conditions, which seriously degrades communication quality¹. Furthermore, the line-of-sight (LoS) transmission characteristics of open sea areas make maritime communication systems more vulnerable to malicious interference and eavesdropping. Therefore, developing novel maritime communication networks that offer cost-effectiveness, wide coverage, low latency, and high reliability is of great practical significance².

Unmanned aerial vehicle (UAV) have been widely recognized as an effective solution to address communication blind zones at sea, due to their flexibility, cost-effectiveness, and capability to establish LoS links³. Despite these advantages, UAVs are constrained by their limited onboard energy supply, which hampers their ability to support long-duration operations. Additionally, the maritime environment presents extra challenges, such as strong electromagnetic interference, multipath propagation, and high-frequency noise, which may significantly reduce the performance of single-UAV communication systems.

To overcome these limitations, intelligent reflective surface (IRS) has emerged as a promising solution. IRS is an artificial reconfigurable meta surface with passive reflecting units that can individually manipulating electromagnetic waves^4,5. By adjusting the phase shifts, IRS enables flexible beamforming and intelligent reconfiguration of the wireless propagation environment, thus greatly enhancing network performance⁶. Moreover, IRS offers notable advantages such as easy deployment, programmability, and high cost-efficiency. It can be flexibly integrated into building surfaces or mounted on various unmanned platforms⁷, which makes it a promising candidate for achieving full-coverage communication in dynamic scenarios and emergency situations⁸.

Despite the significant advantages of the integration of UAV and IRS (UAV-IRS), in enhancing maritime wireless communication capabilities, several critical challenges remain. Specifically, due to the broadcast property of electromagnetic waves and the openness of air-to-ground (ATG) links over the sea renders the system highly susceptible to malicious eavesdropping and jamming. While traditional cryptographic methods provide security at higher layers, they often incur significant computational overhead and are vulnerable to key distribution challenges. To complement these methods, physical layer security (PLS) has emerged as a promising paradigm. Meanwhile, the limited onboard battery capacity of UAV restricts their ability to operate continuously in remote or long-duration missions. In addition, the performance of IRS heavily depends on real-time configuration, which further increases system complexity. Therefore, it is imperative to develop an integrated optimization framework that simultaneously addresses PLS, energy harvesting (EH) requirement, and adaptability to dynamic environments.

To address these issues, we investigate an anti-eavesdropping simultaneous wireless information and power transfer (SWIPT) communication scheme for maritime networks enabled by cooperative UAV and IRS assistance. Specifically, IRS is employed to directionally improve the legitimate link signal quality, while AN is introduced to actively degrade the capacity of the eavesdropping channel. Meanwhile, SWIPT is employed to provide a sustainable energy supply for the UAV. Our objective is to jointly optimize the BS beamforming, UAV positioning, and IRS phase shift. The goal is to maximize the secrecy rate (SR) while ensuring that the UAV meets a minimum harvested energy threshold. To address the overestimation bias inherent in deep deterministic policy gradient (DDPG), we develop a twin delayed deep deterministic policy gradient (TD3) algorithm based on deep reinforcement learning (DRL) to solve the non-convexity optimization problem⁹.

Related work

Combining UAV with IRS has emerged as an effective strategy to overcome the limitations of static IRS deployment in dynamic environments. The integration of UAV and IRS can be categorized into two typical approaches. The first approach deploys the IRS on fixed ground structures, while the UAV carries the transmitter. This architecture offers high engineering feasibility and significant economic advantages, as shown in studies¹⁰ and¹¹. The other approach directly integrates the IRS onto the UAV, forming a movable aerial IRS, this configuration serves as an aerial relay node, which is capable of establishing a stable LoS communication link between ground BS and users¹². Compared with ground-fixed IRS schemes, the UAV-IRS system exhibits unique performance advantages. It enables LoS-dominated transmission for ground users, allowing for wide-area signal coverage and flexible deployment. Therefore, this paper adopts the UAV-IRS model, and the recent research progress on UAV-IRS is reviewed in the following section. In¹³, The authors evaluate outage probability, traversal capacity, power consumption, and energy efficiency (EE) under standalone UAV deployment, pure IRS implementation, and their hybrid integration. The results verify that the integrated UAV-IRS mode provides the most significant performance advantages under various configurations. Furthermore, in¹⁴, the authors studied both static UAV-IRS deployments and dynamic UAV-IRS network employing the time division multiple access (TDMA) protocol. This study revealed that the hybrid IRS architecture exhibits notable performance improvements compared to purely passive IRS systems with the same quantity of reflecting elements, particularly under constrained UAV power budgets. In¹⁵, the authors proposed a system model for the UAV-IRS-assisted ATG communications networks, which aimed to enhance the EE by jointly optimizing bandwidth allocation, IRS phase shifts, and UAV 3D positioning. These studies verify the superiority and feasibility of UAV-IRS systems from different dimensions in practical communication scenarios.

To address the communication security challenges caused by the openness of ATG propagation links, recent research has extensively explored the application of IRS-enhanced PLS in UAV-assisted networks. As demonstrated in¹⁶, the author focused on an IRS-assisted secure UAV communication scheme against both active jamming and passive eavesdropping. They aimed to maximize the average secrecy rate of uplink communication between a ground user and a UAV by jointly optimizing the ground user’s transmission power, IRS phase shift, and the UAV’s trajectory. Furthermore, in scenarios involving multiple UAVs and advanced access techniques like Non-Orthogonal Multiple Access (NOMA), PLS becomes even more critical. In¹⁷, the authors proposed a novel IRS-aided UAV-swarm NOMA system. Their primary objective was to maximize the overall security rate by jointly optimizing UAV swarm trajectories, power distribution among the UAVs, and the reflection coefficients of the IRS. In¹⁸, Wen et al. propose a secure UAV communication system leveraging IRS and artificial noise (AN) to counter multiple colluding curious users. Their work uniquely focuses on maximizing the average secrecy rate (ASR) through jointly optimizing UAV trajectory, IRS phase shifts, and AN-aware beamforming. In¹⁹, the authors examined millimeter-wave systems under active eavesdropper (Eve). In²⁰, the authors studied PLS transmission mechanisms in UAV-IRS with multiple ground-based Eves. Furthermore, in²¹, the integration of mobile edge computing (MEC) with UAV-IRS was explored. The authors proposed a secure task offloading scheme under active eavesdropping, aiming to maximize the total secure computing tasks completed by all users. In multi-user networks,²² proposed an anti-eavesdropping scheme for IRS-assisted UAV communication, the scheme achieved notable secrecy gains through joint optimization under uncertain channel state information (CSI) of both legitimate receivers and potential Eves. Similarly, in²³, the authors considered the imperfect CSI and hybrid attacks involving both jamming and eavesdropping. They proposed a UAV-mounted IRS system, which achieved substantial gains in both security and quality of service (QoS) compared to existing methods. While these IRS-assisted solutions significantly enhance the security and reliability of UAV communications, they often overlook the energy limitations of UAV platforms, whose limited onboard battery capacity continues to constrain long-term and stable operation.

Hence, radio frequency (RF)-based SWIPT offers an effective and practical solution for powering wireless devices²⁴. In²⁵, the author proposed a SWIPT system involving multiple IRSs cooperating with multi-antenna access point (AP), aiming to reducing the total power required by the AP. In²⁶, AN was introduced at the AP, and a power splitting (PS) scheme was adopted at the user side. The authors applied two algorithms to enhance user security while meeting the minimum EH threshold. Furthermore, in²⁷, the authors proposed an energy-efficient solution maintaining minimum data rate and EH requirements. Although these studies provide valuable theoretical support and technical methods to address the UAV energy bottleneck, they do not consider the use of DRL algorithms.

Although the above studies have effectively addressed the issue of limited UAV energy supply, there are still two shortcomings. Firstly, the short endurance of UAV in maritime communication scenarios has not been fully resolved. Secondly, while some works have tackled non-convex optimization problems, they do not leverage the dynamic policy learning capability of DRL. Hence, the author in⁸ proposed an innovative EH scheme that combines SWIPT and resource allocation in a UAV-IRS system. By simultaneously utilizing temporal and spatial segmentation EH models and designing a DRL-based algorithm, they significantly enhanced UAV endurance while satisfying communication QoS constraints. In²⁸, the authors developed a communication architecture based on a UAV-IRS system integrated with SWIPT, in which a DRL algorithm was applied to simultaneously address the dual challenges of limited UAV endurance and low communication efficiency. Different from previous time-domain-focused studies, the authors in²⁹ proposed a resource allocation strategy based on a harvest-transmit-store model for UAV-assisted IRS communication. They adopted the DDPG algorithm to dynamically optimize resource allocation in both time and energy domains, aiming to improve EH efficiency. However, DDPG suffers from overestimation issues during training, which can affect accurate estimation of the optimal policy. Notably, Yang et al. introduced an adaptive EH approach to extend UAV operational time and used an improved DRL algorithm for optimal EE¹. The work is highly relevant, as they successfully developed a DRL-based framework for a UAV-IRS-assisted maritime communication system with adaptive EH to combat jamming. Their work pioneers the use of advanced DRL to maximize EE in the face of active jamming attacks.

Our research builds upon these advancements by addressing a different but equally critical challenge: secure communications against a passive Eve. Our study focuses on comprehensively addressing the long-term secure and energy-sustainable operation of UAV-IRS systems under persistent eavesdropping threats. The main contributions of this work are summarized as follows:

• To address the challenges of secure and sustainable communication in maritime environments, we propose a SWIPT-assisted anti-eavesdropping and EH scheme that leverages the complementary capabilities of UAV and IRS. The proposed approach jointly optimizes BS transmit beamforming, UAV positioning, and IRS phase shift to maximize the average SR, while satisfying the UAV’s minimum harvested energy requirement.

• Considering the dynamic and high-dimensional characteristics of the maritime environment, we model the joint optimization as a DRL task and develop a TD3 algorithm, to derive the optimal policy for optimizing the SR under the EH constraint.

• The simulation results demonstrate that the proposed scheme effectively improves both the coverage range and the SR of the UAV-IRS system. It also shows significant performance gains while maintaining acceptable computational complexity.

System model

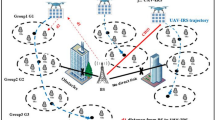
In this paper, Fig. 1 depicts a typical system model of a UAV-IRS-assisted maritime communication network. Since the LoS link between BS and maritime device (MD) is obstructed by obstacles, the BS established on shore cannot transmit signals to the MDs. Therefore, a UAV-mounted IRS is used as a wireless relay to establish a LoS link, where the BS attempts to send signals to MD and a single-antenna Eve exists to try to interfere with the information transmission. The UAV incorporates a rechargeable battery to extend duration by converting harvested energy into electrical power.

Fig. 1

UAV-IRS-assisted maritime security communication system.

We consider a Cartesian coordinate system with the BS located at the origin. The position of the $k$ th user at time slot $t$ $(0 < t \le T)$ is $q_{k} (t) = \{ x_{k} (t),y_{k} (t),z_{k} (t)\}$, where $z_{k} (t)$ and $\{ x_{k} (t),y_{k} (t)\}$ are the vertical and horizontal positions of the user, respectively. Here, both users and Eves are equipped with a single antenna, the BS is equipped with a Z-type antenna, and ${\mathcal{K}} = \{ 1,2, \cdots ,K\}$ denotes the set of all MDs. The IRS has $M \times N$ reflecting elements with uniform planar array (UPA), the IRS elements in the $i$ th $(0 < i \le I)$ row and $j$ th $(0 < j \le J)$ column are denoted by $R = \{ R_{i,j} \}_{i,j = 1}^{M,N}$. The position of the UAV-IRS at the $t$ th time slot is denoted by $q_{u} (t) = \{ x_{u} (t),y_{u} (t),z_{u} (t)\}$. In this work, the system consists of two key components: the model of the communication system and the model of SWIPT. The communication channel is modeled with two links: BS-to-UAV (B-U) link (B-U link) and UAV-to-MD (U-M) link (U-M link)¹. We assume that all channels experience quasi-static block fading and the CSI of all channels is perfectly known.

Communication model

The B-U link primarily exhibits LoS propagation characteristics, but due to path loss and shadow fading between BS and MD, we model this channel using a composite fading model that incorporates both large-scale and small-scale fading components³⁰. The distance between the BS and $R_{i,j = 1}^{M,N}$ is denoted by $d_{i,j}^{B,U} = \sqrt {\left| {x_{i,j}^{{\text{r}}} (t)} \right|^{2} + \left| {y_{i,j}^{{\text{r}}} (t)} \right|^{2} + \left| {z_{i,j}^{{\text{r}}} (t)} \right|^{2} }$.Then, the path loss can be mathematically defined as

$$PL_{i,j}^{B,U} (dB) = PL\left( {d_{0} } \right) + 10\alpha \log_{10} \left( {d_{i,j}^{B,U} /d_{0} } \right) + X_{\sigma }$$

(1)

where $PL_{i,j}^{B,U}$ represents the B-U link’s path loss, defined $PL(d_{0} )$ at distance $d_{0}$ with path loss exponent $\alpha$, and $X_{\sigma }$ accounts for random shadowing effects caused by environmental obstructions and reflections.

Given the high altitude of the UAV, the B-U link is assumed to be dominated by a strong LoS path. Therefore, we model the channel using Rician fading to accurately capture both the LoS component and scattered multipath components. The channel vector from the BS to the $R_{i,j = 1}^{M,N}$ is denoted as $h_{i,j} = [h_{i,j}^{B,U} (1), \cdots ,h_{i,j}^{B,U} (z), \cdots h_{i,j}^{B,U} (Z)]$. Thus, the channel gain of B-U link can be expressed as

$$h_{i,j}^{B,U} = \sqrt {\frac{1}{{PL_{i,j}^{B,U} }}} \cdot \mathop h\limits^{\sim } = \sqrt {\frac{1}{{PL_{i,j}^{B,U} }}} \cdot \left( {\sqrt {\frac{{K_{r} }}{{K_{r} + 1}}} g_{LoS} + \sqrt {\frac{1}{{K_{r} + 1}}} g_{NLoS} } \right)$$

(2)

where the Rician factor is denoted by $K_{r}$, $g_{LoS}$ and $g_{NLoS}$ denote the fast fading components of the LoS and non-line-of-sight (NLoS) channels, respectively.

For further presentation, the path loss is linearly transformed as follows

$$PL_{{\text{i,j}}}^{{\text{B,U}}} = 10\exp \left( {PL_{{\text{i,j}}}^{{\text{B,U}}} (dB)/10} \right)$$

(3)

The B-U link’s channel gain is given by

$$h_{i,j}^{B,U} = 10\exp \left( {\frac{{ - (PL\left( {d_{0} } \right) + 10\alpha \log_{10} \left( {\frac{{d_{{\text{i,j}}}^{B,U} }}{{d_{0} }}} \right) + X_{\sigma } )}}{20}} \right) \cdot \mathop h\limits^{\sim }$$

(4)

In the U-M link scenario, to better closely match the actual maritime communication environment, it is essential to account for the impact of air humidity, salt spray, and sea surface reflections on NLoS communication. We utilize a low-altitude UAV channel model which combines LoS and NLoS propagation characteristics. The occurrence probabilities of these propagation paths depend on the platform’s altitude and its horizontal separation from mobile devices³¹. For a typical LoS probabilistic model between the $R_{i,j = 1}^{M,N}$ and the $k$ th MD, after³², it can be represented as follows

$$PL_{{_{{{\text{LoS}}}} }}^{{\text{k}}} (dB) = \frac{1}{{1 + a\exp ( - b(\theta_{i,j} - a))}}$$

(5)

where $a$ and $b$ are channel state parameters, $H_{i,j}^{r}$ represents the height of the UAV-IRS, and the elevation angle $\theta_{i,j}$ between the U-M can be expressed as

$$\theta_{i,j} = \frac{180}{\pi }\arcsin \left( {\frac{{H_{i,j}^{r} }}{{d_{i,j}^{B,U} }}} \right)$$

(6)

The two-ray path loss model’s applicability is limited in this work due to the predominance of NLoS conditions. Therefore, the signal propagation loss in this paper is modeled as follows

$$PL_{{{\text{NLoS}}}} (dB) = PL_{{{\text{LoS}}}} (dB) + \eta_{{{\text{NLoS}}}} = 20\log_{10} \left( {\frac{4\pi fd}{c}} \right) + \eta_{{{\text{NLoS}}}}$$

(7)

where $f$ denotes the carrier frequence, $d$ is the distance from $R_{i,j = 1}^{M,N}$ to MD. Hence, the path loss between U-M is formulated as

$$PL_{i,j}^{k} (dB) = P_{LoS} \cdot PL_{LoS} + P_{NLoS} \cdot PL_{NLoS} = P_{LoS} \cdot PL_{LoS} + (1 - P_{LoS} ) \cdot PL_{NLoS}$$

(8)

For further expression, $PL_{i,j}^{k} (dB)$ is converted to the following equation

$$PL_{i,j}^{k} = 10\exp \left( {\frac{{PL_{i,j}^{k} (dB)}}{10}} \right)$$

(9)

Consequently, according to³³,the U-M link channel gain is given by

$$h_{i,j}^{k} = s_{i,j}^{k} \left( {PL_{i,j}^{k} } \right)^{ - 1/2}$$

(10)

where $s_{i,j}^{k}$ represents small-scale decay.

After²⁵, $\phi = diag[\lambda_{1} e^{{{\text{j}}\theta_{1,1} }} ,\lambda_{2} e^{{{\text{j}}\theta_{1,N} }} ,...,\lambda_{L} e^{{{\text{j}}\theta_{M,N} }} ]\,\in{\mathbb{C}}^{M \times N}$ is defined as the IRS diagonal reflection phase matrix, where ${\text{j}} = \sqrt { - 1}$ represents the imaginary unit, $\lambda_{L} \in [0,1][0,1]$ and $\theta_{M,N} \in (0,2\pi )$ represent the amplitude reflection coefficient and phase shift coefficient of the $R_{i,j = 1}^{M,N}$, respectively. For simplicity, it is assumed in this paper that $\lambda_{L} = 1,\forall l \in L$, that is, each reflecting element’s antenna features independent control capability, enabling optimal signal reflection in ideal scenarios³⁴.

Transmission model

Information security is ensured by injecting AN into transmitted signals, thereby lowering Eve’s signal-to-noise ratio (SNR). The transmitted signal generated by all MDs at the BS is mathematically represented as

$$X = \sum\nolimits_{k = 1}^{K} {w_{k} s_{k} } + w_{0} s_{0}$$

(11)

where $w_{k} \in {\mathbb{C}}^{Z \times 1}$ and $w_{0} \in {\mathbb{C}}^{Z \times 1}$ represent the beamforming vectors of the $k$ th legal MD and AN, $s_{k}$ and $s_{0}$ denote the information signals of the $k$ th MD and AN, respectively.

The signals received by the $k$ th MD and Eve can be expressed as follows

$$y_{k} = \hat{\user2{h}}_{r,k}^{H} {\Phi }{\varvec{G}}^{{\varvec{H}}} {\varvec{X}} + n_{0}$$

(12)

$$y_{e} = \hat{\user2{h}}_{r,e}^{H} {\Phi }{\varvec{G}}^{{\varvec{H}}} {\varvec{X}} + n_{0}$$

(13)

It is assumed that the channel matrix $G = [g_{1,1}^{H} , \cdots ,g_{1,N}^{H} , \cdots g_{M,N}^{H} ] \in {\mathbb{C}}^{Z \times 1}$ of the B-U link follows Rayleigh fading distribution, where $g_{i,j}$ denotes the channel vector, and $n_{0} \sim {\mathcal{C}\mathcal{N}}(0,\sigma^{2} )$ represents the additive Gaussian white noise. The channel matrices from the UAV-IRS to the $k$ th MD and Eve are denoted as $\hat{h}_{r,k}^{H}$ and $\hat{h}_{r,e}^{H}$, respectively, which can be expressed as

$$\hat{\user2{h}}_{r,k}^{H} = \left[ {\begin{array}{*{20}c} {h_{1,1} (k)} & \cdots & {h_{1,N} (k)} \\ \vdots & \ddots & \vdots \\ {h_{M,1} (k)} & \cdots & {h_{M,N} (k)} \\ \end{array} } \right]$$

(14)

$$\hat{\user2{h}}_{r,e}^{H} = \left[ {\begin{array}{*{20}c} {h_{1,1} (e)} & \cdots & {h_{1,N} (e)} \\ \vdots & \ddots & \vdots \\ {h_{M,1} (e)} & \cdots & {h_{M,N} (e)} \\ \end{array} } \right]$$

(15)

Since the PS mode is used to allocate the power of information transmission (IT) and EH, we define $\rho$ and $1 - \rho$ as the power allocation factors for IT and EH, respectively. Therefore, the received IT signals at the $k$ th MD and Eve can be expressed as $y_{k}^{ID} = \sqrt {\rho_{k} } y_{k} + n_{ID}$ and $y_{k}^{EH} = \sqrt {1 - \rho_{k} } y_{k}$, where $n_{ID} \sim {\mathcal{C}\mathcal{N}}(0,\sigma_{ID}^{2} )$ is the noise introduced in the IT phase.

SWIPT model

To extend UAV operational duration, we employ SWIPT for EH. The energy harvested from incident RF signals is given by

$$H_{t} = \sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{N} {\left\| {g_{i,j}^{H} {\varvec{X}}} \right\|^{2} } }$$

(16)

Let $\eta \in [0,1]$ denote the power conversion efficiency. Thus, the harvested energy at the UAV-IRS can be expressed as

$$E_{t} = \sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{N} {\eta \left( {1 - \rho } \right)} } \left\| {g_{i,j}^{H} {\varvec{X}}} \right\|^{2}$$

(17)

Therefore, the EH efficiency of the system can be defined as

$$\varepsilon_{t} = \frac{{E_{t} }}{{H_{t} }}$$

(18)

The SNR for the $k$ th MD can be calculated as

$$SNR_{k} = \frac{{\rho |\hat{\user2{h}}_{r,k}^{H} w_{k} |^{2} }}{{\sum\limits_{i = 0,i \ne k}^{{\mathcal{K}}} {|\hat{\user2{h}}_{r,k}^{H} w_{k} } |^{2} + \sigma^{2} + \sigma_{ID}^{2} }}$$

(19)

The SNR at the Eve during the IT phase is given by

$$SNR_{e} = \frac{{\rho |\hat{\user2{h}}_{r,e}^{H} w_{0} |^{2} }}{{\sum\limits_{i = 0,i \ne k}^{{\mathcal{K}}} {|\hat{\user2{h}}_{r,e}^{H} w_{0} } |^{2} + \sigma^{2} }}$$

(20)

Therefore, the average achievable SR for the $k$ th MD can be expressed as

$$R_{k}^{\sec } = [\log_{2} \left( {1 + SNR_{k} } \right) - \log_{2} \left( {1 + SNR_{e} } \right)]^{ + }$$

(21)

where $[z]^{ + } = \max \{ z,0\} .$

Problem formulation

Our objective is to jointly optimize the BS transmit beamforming, the UAV positioning, and the IRS phase shift under practical constraints to achieve significant improvement in the average SR. Accordingly, the optimization problem P1 is formulated as

$$\begin{gathered} P1:\mathop {\max }\limits_{{{\text{W,}}\Theta_{M,N} {\text{,q(t)}}}} \,R_{k}^{{{\text{sec}}}} \hfill \\ {\text{s}}.{\text{t}}.\quad {\text{C}}1:\,R_{k}^{{{\text{sec}}}} \ge R_{k}^{{{\text{sec}},{\text{min}}}} ,\forall k\varepsilon {\mathcal{K}} \hfill \\ {\text{ C}}2:\,R_{k} \ge R_{k}^{{{\text{min}}}} ,\forall k\varepsilon {\mathcal{K}} \hfill \\ {\text{ C}}3:\,0 \le p = \mathop \sum \limits_{{k \in {\mathcal{K}}}} \parallel W_{k} \parallel^{2} \le p_{max} \hfill \\ {\text{ C}}4:\,\theta_{M,N} \in [0,2\pi ] \hfill \\ {\text{ C}}5:\,{0} \le \rho \le {1} \hfill \\ {\text{ C}}6:\,E_{t} \ge E_{\min } \hfill \\ {\text{ C}}7:\,q_{s} = q_{u} [1],q_{e} = q_{u} [n + 1] \hfill \\ {\text{ C}}8:\,\parallel q_{u} [n + 1] - q_{u} [n]\parallel \le V_{\max } \delta_{t} \hfill \\ \end{gathered}$$

(22)

where $R_{k}^{{\text{sec,min}}}$ denotes the target SR for the $k$ th MD, $R_{k}^{\min }$ represents its required data rate, and $\theta = [\theta_{1,1} ,\theta_{1,2} , \cdots \theta_{M,N} ]$ is the phase shift vector of all IRS reflecting elements. $V_{\max }$ represents the maximum flying speed of the UAV, $n$ denotes the total number of discrete time slots into which the entire operation period $T$ is divided, $T = n\delta_{t}$, where $\delta_{t}$ is the duration of each slot. The constraints C1 and C2 ensure the worst-case SR and data rate requirements, respectively. The constraints in C3 are set to satisfy the maximum power constraints of the BS. The constraints in C4 are the constraints for the IRS reflecting element. C5 is the range constraint for the power distribution ratio. C6 guarantees minimum EH requirements while maximizing SR. C7 and C8 specify the UAV’s initial/final positions and the flight trajectory constraints. Given the time-varying characteristics of the communication environment, the UAV must adapt its strategy dynamically based on CSI. As a result, problem (22) poses significant challenges for traditional solution methods. Hence, alternative efficient approaches are required and will be introduced in the following section.

Although previous studies have provided valuable solutions, many rely on conventional optimization techniques such as alternating optimization (AO) or successive convex approximation (SCA). These methods face two main challenges when applied to our problem. First, the joint optimization problem is highly complex, non-convex, and involves tightly coupled high-dimensional variables. These iterative algorithms are prone to converging to local optima. Second, and more importantly, the maritime communication environment is highly dynamic. Traditional iterative methods need to resolve the entire optimization problem whenever the channel state changes, making them unsuitable for the real-time decision-making required and long-term optimization.

DRL offers a powerful alternative to address these challenges, particularly the TD3 algorithm. Its actor–critic architecture can directly output continuous actions and, leveraging the powerful learning capability of deep neural networks, handle high-dimensional state spaces. The TD3 algorithm introduces improvements such as dual Q-networks, delayed policy updates, and target policy smoothing over DDPG, thereby enhancing stability and performance. Hence, DRL-based methods can provide our system with a model-free, adaptive solution that is capable of learning long-term optimal strategies.

TD3-based framework

Problem transformation to RL framework

Accordingly, the optimization task can be formulated as a Markov Decision Process (MDP) characterized by the quintuple ${\mathcal{M}} = \{ {\mathcal{S}},{\mathcal{A}},{\mathcal{P}},{\mathcal{R}},\gamma \}$. Here, the state space ${\mathcal{S}}$ represents all possible states of the system, it describes the observed information of the environment. The action space ${\mathcal{A}}$ includes all possible actions that the agent can perform. The state transfer probability denoted as ${\mathcal{P}}$, which describes the probability of the system will transition from the current state $s_{t}$ to a subsequent state $s_{t + 1}$ after taking action $a_{t}$. The reward function ${\mathcal{R}}$ is used to measure the immediate benefit of an action, such as the system secrecy capacity and EH efficiency, which determines the learning effect. There is also a discount factor denoted as $\gamma \in (0,1)$ is used to balance the immediate reward with the reward obtained in the future. The detailed description is as follows:

State Space The system state represents the agent’s observable environmental information. At the $t$ th time step, the state information primarily consists of the channel of B-U link $h_{i,j}^{B,U}$, the U-M link $h_{i,j}^{k}$, the U-E link $h_{i,j}^{e}$, the current position of the UAV $q_{u} (t)$, and the current energy level of the UAV $E_{t}$. Therefore, the state $s_{t}$ is expressed as

$$s_{t} = \left\{ {h_{i,j}^{B,U} ,h_{i,j}^{k} ,h_{i,j}^{e} ,q_{u} (t),E_{t} } \right\}$$

(23)

Action space At the $t$ th time step, the UAV-IRS system selects an action $a_{t} \in {\mathbb{A}}$ based on the current state $s_{t}$. The action space includes all feasible actions the agent can execute within the environment. It comprises five main components, the BS beamforming vector $w_{t}$, the AN beamforming vector $w_{0}$, the IRS phase shift vector $\theta_{M,N}$, the UAV movement adjustment $q_{m}$ and the power allocation ratio $\rho$. Hence, the action space is given by

$$a_{t} = \left\{ {w_{t} ,w_{0} ,\theta_{M,N} ,q_{m} ,\rho } \right\}$$

(24)

Reward function The reward function assesses the effectiveness of the learned decision policy. It determines the expected feedback received by the agent upon executing a selected action. However, in practice, we observe that directly using the optimization objective function (22) as the reward function may result in unstable training or poor convergence. Therefore, we introduce appropriate penalty terms for adjustment. Without loss of generality, the reward function is reformulated as follows

$$R_{t} = \omega_{1} R_{s} + \omega_{2} R_{e}$$

(25)

where coefficients $\omega_{1}$ and $\omega_{2}$ represent the weighting factors for SR and EE, respectively, where $\omega_{1} \ge \omega_{2}$ and $\omega_{1} + \omega_{2} = 1$.

The individual reward components are defined as piecewise functions with penalties for constraint violation:

$$R_{s} = \left\{ {\begin{array}{*{20}c} { \, R_{k}^{sec} ,{\text{ if }}R_{k}^{sec} \ge R_{k}^{{{\text{sec}},{\text{min}}}} } \\ {R_{k}^{sec} - \rho_{p} (R_{k}^{{{\text{sec}},{\text{min}}}} - R_{k}^{sec} ),{\text{if }}R_{k}^{sec} < R_{k}^{{{\text{sec}},{\text{min}}}} } \\ \end{array} } \right.$$

(26)

$$R_{e} = \left\{ {\begin{array}{*{20}c} { \, E_{t} , \,{\text{ if }} E_{t} \ge E_{\min } } \\ {E_{t} - \rho_{p} (E_{\min } - E_{t} ), \,{\text{ if }} E_{t} < E_{\min } } \\ \end{array} } \right.$$

(27)

where $R_{t}$ represents the total reward calculated for the agent at a given time step, $R_{s}$ and $R_{e}$ denotes the reward component derived from the system’s actual SR and harvested energy, including any penalties for not meeting the minimum requirement, respectively, $R_{k}^{{{\text{min}}}}$ and $R_{k}^{{{\text{sec}},{\text{min}}}}$ are required to meet a minimum threshold of 1 bps/Hz and 0.1 bps/Hz, respectively. $E_{min}$ must satisfy a minimum harvested energy requirement of 0.1 W, and $\rho_{p}$ is a penalty coefficient, set to 2 in our implementation, and $\rho_{p}$ is a penalty coefficient, set to 2 in our implementation.

The MDP aims to derive an optimal control policy that maximizes the long-term expected reward for all state-action pairs under the policy’s operation. The maximum total long-term reward attainable by the agent can be defined as

$$Q^{\pi } (s,a) = {\mathbb{E}}_{\pi } \left[ {\sum\limits_{k = 0}^{\infty } {\gamma^{k} } \left. {R_{t + k + 1} } \right|\,s_{t} = s,\,a_{t} = a} \right]$$

(28)

where $R_{t + k + 1}$ denotes the immediate reward at future step $k$, and $Q^{\pi } (s,a)$ denotes the action value function.

The Bellman equation describes the recursive relationship of the state action value function. Accordingly, it can be expressed as

$$Q^{\pi } (s,a) = {\mathbb{E}}_{\pi } \left[ {R_{t + 1} + \gamma \mathop \sum \limits_{{a^{\prime}}} \pi \left( {\left. {a_{t + 1} } \right|s_{t + 1} } \right)\left. {Q^{\pi } \left( {s_{t + 1} ,a_{t + 1} } \right)} \right|\,s_{t} = s,a_{t} = a} \right]$$

(29)

where $\pi (a_{t + 1} |s_{t + 1} )$ denotes the probability of $a_{t + 1}$ in $s_{t + 1}$.

The target Q-value is defined through the Bellman equation, which combines the immediate reward $R_{t + 1}$ and the maximum future Q-value, and can be expressed as

$$y_{t} = r_{t + 1} + \gamma \mathop {\max }\limits_{{a_{t + 1} }} Q_{{{\text{target}}}} (s_{t + 1} ,a_{t + 1} ,\pi (s_{t + 1} ;\theta_{\pi } );\theta^{Q} )$$

(30)

where $Q_{{{\text{target}}}} (s_{t + 1} ,a_{t + 1} )$ represents the Q-value computed by the target network, which is used to reduce instability during the training process.

To update the Q-network, we minimize the error between $Q^{\pi } (s_{t} ,a_{t} )$ and the $y_{t}$ by optimizing the mean squared error of critic network. The loss function can be expressed as

$$L(\theta_{Q} ) = {\mathbb{E}}_{{\left( {s_{t} ,a,r,s_{t + 1} } \right)\sim {\mathcal{D}}}} \left[ {\left( {y_{t} - Q^{\pi } (s,a;\theta^{Q} )} \right)^{2} } \right]$$

(31)

where $Q^{\pi } (s,a;\theta^{Q} )$ denotes the output of the current Q-network, representing the Q-value for taking action $a_{t}$ in state $s_{t}$.

The DDPG algorithm is a DRL method designed for continuous action spaces, employing an actor-critic framework as its core architecture. It adopts an actor-critic architecture as its core framework and employs four deep neural networks: the training-actor network $\mu ( \cdot |\theta^{\mu } )$, training-critic network $\mu ( \cdot |\theta^{Q} )$, and their corresponding target-actor network $\mu^{\prime}( \cdot |\theta^{{\mu^{\prime}}} )$ and target-critic network $Q^{\prime}( \cdot |\theta^{{Q^{\prime}}} )$³⁵. During training, the actor network updates $\theta^{\mu }$ by enhancing the expected cumulative return, while the critic network updates $\theta^{Q}$ by reducing the error between the actual and target Q-value. Through this iterative process, the policy is progressively optimized.

The TD3 algorithm is an improved DRL method designed for continuous control tasks. Its core architecture is based on the DDPG framework, which incorporates the Double Q-network mechanism to optimize action-value function estimation³⁶. Specifically, TD3 adopts two critic networks and adopts a minimum value policy to mitigate the Q-value overestimation bias. This significantly improves the training stability and effectiveness in continuous action space. As illustrated in Fig. 2, the TD3 algorithm utilizes a dual-network architecture, consisting of two separate critic networks to ensure robust value function approximation.

Fig. 2

TD3 network architecture diagram.

TD3-based UAV-IRS configuration

Compared with the DDPG algorithm, the TD3 algorithm primarily addresses the problems of Q-value overestimation and unstable policy update during the training process of DDPG. The major improvements of TD3 can be summarized in the following three aspects:

Double Q-learning TD3 utilizes dual separate critic networks, denoted as $Q_{{{\text{target}},1}}$ and $Q_{{{\text{target}},2}}$, and computes the target Q-value using the smaller of the two estimates. This conservative strategy effectively mitigates overestimation bias in Q-values and enhances the stability of the training process. Accordingly, the target Q-value can be reformulated as:

$$y_{t} = r_{t + 1} + \gamma \mathop {\min }\limits_{i = 1,2} Q_{{{\text{target}},i}} \left( {s_{t + 1} ,a_{t + 1}^{\prime } } \right)$$

(32)

$a^{\prime}_{t + 1}$ is the next action generated by the policy network. To improve robustness, a small amount of noise is typically added to this action, a technique known as target policy smoothing. This approach helps reduce Q-value overestimation and improves the stability of IRS phase shift and BS transmit power optimization.

Delayed Policy Update The actor network (policy network) and critic network (value network) are updated simultaneously of the DDPG. However, if the critic network is insufficiently trained, frequent update of actor network may amplify estimation errors, leading to unstable learning. To address this issue, TD3 adopts a delayed policy update mechanism, where the critic network is updates more frequently than the actor network, which is updated with a delay of $d$ steps after each critic update to help mitigate the risk of getting stuck in local optima. During actor network updates, TD3 maximizes the Q-value estimated by the critic network through gradient ascent. The actor network’s loss function is given by

$$\nabla_{{\theta_{\mu } }} J = {\mathbb{E}}\left[ {\nabla_{a} Q_{1} (s,a;\theta_{1}^{Q} )|_{{a = \mu (s_{t} )}} \cdot \nabla_{{\theta_{\mu } }} \mu (s;\theta^{\mu } )} \right]$$

(33)

where $\nabla_{a} Q_{1} (s,a;\theta_{1}^{Q} )$ denotes the gradient of the Q-value from the critic network with respect to the action, and $\mu (s|\theta^{\mu } )$ represents the gradient of the actor network. The objective of the actor network is to update its parameters $\theta^{\mu }$ via gradient ascent.

Target Policy Smoothing TD3 introduces clipped noise to the target action in order to smooth the policy, it can prevent the policy network from overfitting to a deterministic action, thereby enhancing robustness during training. The smoothed target action is given by

$$a_{t + 1}^{\prime } = \pi_{target} \left( {s_{t + 1} } \right) + {\text{clip}}(\varepsilon , - c,c),\quad \varepsilon \sim {\mathcal{N}}(0,\sigma^{2} )$$

(34)

where $\varepsilon$ is the clipped noise sampled from a normal distribution with standard deviation $\sigma$, and $c$ is the clipping threshold.

The TD3’s loss function is computed as the mean squared error between the predicted and target Q-value $y_{t}$, it can be expressed as

$$L(\theta_{Q} ) = {\mathbb{E}}\left[ {\left( {Q_{i} \left( {s_{t} ,a_{t} ;\theta^{Q} } \right) - y_{t} } \right)^{2} } \right],\quad i \in \{ 1,2\}$$

(35)

Complexity analysis

Our computational complexity analysis focuses on two phases: offline training and online execution. During the offline training phase, the time complexity of the TD3 algorithm primarily stems from the forward and backward propagation of the two critic networks and one Actor network. Assuming a state space dimension of $d_{s}$, an action space dimension of $d_{a}$, a hidden layer size of $h$, and a batch size of $b$, the total time complexity for a single update is approximately $O(b \cdot ((d_{s} + d_{a} ) \cdot h + h^{2} ))$. The space complexity is determined by the size of the network parameters and the experience replay buffer. In contrast, the algorithm exhibits a significant advantage in the online execution phase, requiring only a single forward pass through the trained actor network. Its complexity is constant and far lower than traditional iterative optimization methods. For example, baselines such as AO method must repeatedly solve complex non-convex subproblems at each time step, involving computationally expensive operations like matrix inversions, which results in a much higher online complexity than our TD3 approach. Therefore, the low online execution complexity of our DRL-based algorithm makes it highly suitable for real-time decision-making in dynamic communication environments.

Based on the above, the complete training procedure is summarized in Table 1. Firstly, experience needs to be collected from the environment, during each interaction, the current and new state are stored in the replay buffer, followed by random sampling for network training. Next, the Double Q-network is employed to compute the target Q-value and the critic network are updated accordingly. The actor network is optimized using a delayed update strategy, while the target networks are adjusted through a soft update strategy. In addition, TD3 achieves target policy smoothing through introducing noise to the target action, which helps reduce action noise and improves training stability. Through continuous interaction with the environment, TD3 updates the critic and actor networks, softly updates the target networks, and progressively improves the learned policy. The algorithm continues this iterative process until convergence or until a predefined termination condition is met. This update process allows TD3 to achieve superior stability and performance compared to the traditional DDPG algorithm, especially in reinforcement learning tasks with continuous action spaces and increased task complexity.

Table 1 TD3-based optimization algorithm.

Simulation results analysis

This section presents the evaluation and analysis of the security performance in the UAV-IRS-assisted maritime communication system based on the proposed TD3 algorithm, with particular attention to scenarios involving eavesdropping threats. The simulation scenario is constructed within a 3D space of dimensions 1000 × 1000 × 100 meters. The environment includes a BS, a UAV-mounted IRS platform, three MDs, and an Eve. Specifically, the BS is fixed at the (0,0,25) and equipped with 4 antennas. The UAV-IRS with the IRS consisting of (M×N) = 16 reflecting elements. To simulate realistic flight constraints, the UAV-IRS is restricted to a rectangular horizontal area centered at its initial location. It is allowed to move within ±100 meters along both the x- and y-axes, with its altitude confined between 0 and 100 meters. The system is configured to operate at a carrier frequency of 2.4 GHz, and the ambient noise power is set to −110 dBm.

In our implementation, both the actor and critic networks of the TD3 agent are constructed as fully connected neural networks, also known as multilayer perceptrons (MLPs). The actor network takes the vectorized state as input and consists of two hidden layers with 400 and 300 neurons, respectively, each activated by ReLU functions. The output layer employs a Tanh activation function to generate normalized actions, which are subsequently scaled to their actual physical ranges. The actor network is optimized using the Adam optimizer. The critic networks evaluate state–action pairs. Each critic receives a concatenated state and action vector as input and, similar to the actor, is composed of two hidden layers with 400 and 300 neurons activated by ReLU functions. The output layer contains a single neuron with a linear activation function that directly predicts the Q-value. The critic networks are also trained using the Adam optimizer.

To ensure compatibility with neural network inputs, all complex-valued variables (e.g., channel gains and beamforming vectors) are decomposed into their real and imaginary parts before being fed into the actor and critic networks. Consequently, each complex variable contributes two dimensions to the input or output space. Based on this principle, with Z=4 BS antennas, three legitimate users and an IRS of M×N=16 elements, the total state space and action space dimensions are calculated to be 260 and 54, respectively.

For exploration during training, zero-mean Gaussian noise with a standard deviation of 0.2 is added to the actions output by the actor network. This exploration noise is clipped to the range of ±0.5 to prevent excessively large deviations. Similar to DDPG, TD3 employs this stochastic perturbation to encourage exploration in continuous action spaces (Table 2).

Table 2 Summarizes the simulation and training parameters in detail.

Figure 3 shows the relationship between the average SR and the number of training samples. It can be observed that the proposed TD3 algorithm consistently achieves higher reward values compared to the other two algorithms. This is due to Soft Actor-Critic (SAC) balances exploration and exploitation by maximizing an entropy-regularized reward function. However, it exhibits large performance fluctuations during the early training phase. As training progresses, SAC shows a relatively faster convergence rate in environments that require efficient exploration, and the curve gradually stabilizes at a higher level. In contrast, the DDPG suffers from overestimation bias, which results in performance oscillations, convergence difficulties, and unstable policy updates. These issues are exacerbated in dynamic and complex maritime communication environments, leading to lower reward values and significant instability. The TD3 algorithm proposed in this paper effectively alleviates these problems. By introducing mechanisms such as delayed policy updates and double Q-networks, TD3 mitigates the effects of overfitting and rapid value overestimation, leading to more stable and reliable training performance. These results verify the superiority of the TD3 approach.

Fig. 3

Performance comparison of different DRL methods.

Figure 4 shows how the SR varies with the number of IRS reflecting elements. As the element count increases, the SR also rises. This indicates that a larger IRS array significantly enhances secrecy performance, and the system can achieve finer-grained beamforming by adaptively tuning the phase responses across an expanded array of elements. As a result, the signal quality of the legitimate link is enhanced, while the equivalent channel of the eavesdropping link is effectively suppressed, leading to an overall improvement in SR performance. Moreover, the results further show that deploying more antennas at the BS leads to higher SR. This is because additional antennas provide greater beamforming gain, allowing the signal energy to be more precisely focused toward the legitimate user. At the same time, the energy directed toward potential Eves is minimized, thereby enhancing the overall communication security. In conclusion, simultaneously increasing the IRS elements and BS antennas greatly enhances the average SR.

Fig. 4

SR for different number of antennas and IRS reflecting elements.

Figure 5 compares the SR achieved by three DRL algorithms (TD3, SAC, DDPG) and the AO algorithm under different IRS reflecting element configurations. The results demonstrate that all schemes exhibit a significant improvement in SR with the expansion of the IRS element array. Under identical configurations, the proposed scheme (TD3) consistently outperforms both SAC and DDPG, as well as the traditional AO algorithm. The AO algorithm shows the poorest performance, which highlights the necessity of using DRL algorithms to optimize and improve system performance. The advantage becomes more pronounced when using larger numbers of reflecting elements. These findings validate the effectiveness of our proposed TD3 algorithm for dynamic UAV-IRS collaborative optimization.

Fig. 5

SR versus number of IRS reflecting elements under different scenarios.

Figure 6 depicts how the secrecy rate varies with the BS’s maximum transmit power for the proposed scheme and three reference schemes. As expected, all schemes show an increasing trend in SR as the BS transmit power increases, since higher transmission power improves the SNR of the legitimate user. Among the benchmarks, the "Random UAV Position" scheme achieves greater SR improvement compared to "Random Transmit Beamforming" and "Random IRS Phase Shift" under the same power levels. This highlights the sensitivity of UAV placement to overall system performance. Notably, the proposed scheme consistently outperforms all alternatives across the full power range. This confirms that joint optimization of transmit beamforming, UAV positioning, and IRS phase shifts significantly enhances the secrecy capacity and anti-eavesdropping capability of the system, thereby improving PLS.

Fig. 6

SR versus maximum transmit power for different scenarios.

Figure 7 compares the EH performance of different strategies under varying transmit power levels. The results demonstrate that the proposed joint optimization scheme achieves significant advantages, particularly in high-power regions, where its performance improvement becomes more pronounced. Furthermore, the EH efficiency of all four schemes monotonically increases with transmit power. Among them, the random UAV position strategy generally outperforms the other two baseline methods, highlighting the critical role of UAV placement in energy transfer efficiency. In contrast, the random IRS phase shift strategy exhibits the poorest performance, indicating that IRS phase control plays a crucial role in system optimization.

Fig. 7

Energy versus maximum transmit power for different scenarios.

Figure 8 illustrates the impact of the power allocation ratio between EH and IT on both SR and EE under different schemes. As shown in the figure, with an increasing EH time ratio, the SR gradually decreases, while the EE increases. Due to the longer EH duration enables the UAV to harvest more energy, whereas the reduced IT time limits data transmission, thus leading to lower SR. The proposed dynamic optimization scheme achieves an effective balance between SR and EE within the interval 0.3 and 0.5. In this range, it maintains a relatively high SR while reaching a significantly higher peak EE compared to the fixed-phase scheme. The inferior performance of the fixed-phase scheme arises from its inability to suppress the eavesdropping link and its reliance on increased transmit power to offset performance degradation. Furthermore, the no-IRS scheme yields the lowest SR and EE among all evaluated methods, due to its lack of active channel control capability. These results highlight the importance of dynamic optimization in balancing the EH and IT, and confirm its effectiveness in enhancing both security and EE.

Fig. 8

SR and EE versus power allocation factor.

As depicted in the Fig. 9, it can be seen that the UAV remains in close proximity to the user cluster, tending to hover directly above the users. When channel conditions deteriorate, the UAV dynamically maintains or increases its distance from the eavesdropper to maximize link quality and ensure secrecy rate. In addition, whenever feasible, the UAV moves as close as possible to the BS to harvest energy. This observation validates the effectiveness of the proposed DRL-based approach in solving the complex, multi-objective trajectory optimization problem.

Fig. 9

3-D UAV trajectory.

Conclusion

This paper addresses the challenges of secure communication and limited battery capacity in UAV-assisted IRS-enabled communication systems. We introduce a UAV-IRS framework into a maritime communication environment with the presence of Eves. In this setting, AN is embedded into the transmitted signals to enhance PLS, while the SWIPT mechanism ensures that the UAV meets its minimum EH requirements. Specifically, we construct an optimization problem to enhance the system’s average SR through jointly optimizing the BS transmit beamforming, IRS phase shift configuration, and UAV deployment location. To address the inherent non-convexity of this problem, we propose a TD3 algorithm within a DRL framework, which generates optimal solutions for both eavesdropping mitigation and EH. Simulation results confirm the convergence and effectiveness of the proposed algorithm. The TD3-based method significantly improves SR while satisfying the UAV’s minimum EH requirements. Compared with benchmark schemes, our approach demonstrates noticeable improvements in both SR and EH efficiency, confirming its potential for enhancing PLS and energy sustainability. Although this work focuses on a maritime communication scenario, the proposed secure and energy-efficient framework is highly generalizable. In future work, we plan to investigate robust design strategies for STAR-IRS-assisted wireless networks under imperfect CSI, based on more practical deployment scenarios.