Fixed-time leader-following speed consensus control for multi-PMSMs based on multi-agent systems consensus

Abstract

Consensus control of multi-agent systems offers scalability and robustness in group tasks. To improve the performance of multiple permanent magnet synchronous motors (multi-PMSMs) speed coordination, in this paper, we propose a fixed-time leader-following speed consensus control for multi-PMSMs based on multi-agent systems consensus. First, the concept of multi-agent systems is introduced and the multi-PMSMs speed control system is modeled as a first-order multi-agent systems subject to perturbations. Next, a fixed-time consensus protocol is designed based on an undirected graph, and construct a fixed-time extended state observer (ESO) to feedforward perturbation estimates into the protocol. The resulting consensus protocol provides the desired q-axis current for the speed control system, with the upper bound of the settling time independent of the initial conditions. Finally, the feasibility and effectiveness of the proposed scheme are validated by comparing it with relative-coupling control scheme on an experimental multi-PMSMs speed control platform.

Introduction

Permanent magnet synchronous motors (PMSM) are extensively utilized in electric vehicles, industrial robots, wind turbines, and other applications due to their high efficiency, reliability, compact size, and simple structure^1,2,3. With the rapid advancement of industrial automation, multi-PMSMs consensus control technology is extensively applied in complex scenarios requiring coordinated operation of multiple motors due to its high precision, efficiency, and dynamic response capabilities. Typical applications include industrial automation, intelligent manufacturing, robotics, new energy vehicles, aerospace, unmanned aerial vehicles, and energy and power systems. The operational performance of multi-PMSMs has raised higher demands, and the synchronous control of multi-PMSMs has become a prominent research topic. The performance of synchronous control in multi-PMSMs can be enhanced by optimizing the control structure of their drive system^4,5.

The control structure can be categorized into uncoupling and coupling types, depending on whether there is interaction between the motors’ information (e.g., torque, speed, position). The uncoupling control structure, which includes master command control and master-slave control, is proposed first. However, due to the lack of information exchange between motors, the master motor cannot respond promptly when the slave motor experiences external interference⁶. To address this issue, continuous information exchange between motors during operation is necessary. Consequently, coupling control structures have been proposed, including cross-coupling control, relative-coupled control, and virtual shaft control. Cross-coupling control compares the speed signals of two motors, generating a difference that serves as an additional feedback signal for synchronous control. However, it is not suitable for controlling more than two motors synchronously. In relative-coupling control, as the number of motors in multi-motor systems increases to three or more, the control structure evolves from simple pairwise interactions to complex multi-way interactions, which increases system complexity, reduces scalability, and makes the system prone to rotational speed deviations during load perturbations, both at startup and steady-state operation^7,8,9. Virtual shaft control simulates the physical characteristics of mechanical transmissions, exhibiting synchronization behavior similar to mechanical shaft systems, and maintains good synchronization performance in steady-state conditions. However, during dynamic processes with large load perturbations, the computation of virtual values fed back to the virtual axes introduces a time delay, which may lead to asynchrony in the system¹⁰. The increase in the number of motors in multi-PMSMs speed consensus control systems using coupling control leads to issues of limited flexibility and complex structures. Additionally, the advancement of industrialization imposes higher requirements on the operational performance of multi-PMSMs speed control systems. Developing a multi-PMSMs speed consensus control method with high flexibility and a simple structure, while ensuring control accuracy, remains a prominent research focus.

In recent years, consensus control of multi-agent systems has gained significant attention due to its advantages, including scalability and robustness in performing group tasks^11,12,13. It has been widely applied in practical systems, including robot formation, spacecraft attitude synchronization, and smart grids. Consensus control, a fundamental problem in cooperative control, involves the design of distributed controllers that allow agents to reach agreement on a specific quantity of interest through local interactions^{14,15,16,17,18}.

Fast convergence is often desired in consensus control of multi-agent systems. A key performance metric for evaluating control protocols is the convergence speed, which can be classified into asymptotic, finite-time, and fixed-time consensus based on settling time. Asymptotic consensus for multi-agent systems has been studied in^19,20,21. Finite-time consensus problem has gained significant attention. Studies in^22,23,24,25 have shown that the estimation of settling time depends on the system’s initial state. To enhance control performance in existing finite-time consensus approaches, fixed-time stability was first explored in²⁶, leading to the proposal of a fixed-time consensus strategy. A key feature of fixed-time consensus is that the stabilization time estimate is independent of the system’s initial state^27,28,29. The fixed-time consensus control problem for general linear multi-agent systems under dynamic leader guidance was studied in³⁰.

To address these challenges and inspired by the aforementioned work, this paper proposes a fixed-time disturbance observer-based fixed-time consensus control method for multi-agent systems to achieve fixed-time speed control of multi-PMSMs under disturbances. This approach offers enhanced flexibility, a simplified structure, and improved control accuracy for multi-PMSMs speed control systems. The primary contributions are summarized as follows:

• 1. The concept of multi-agent systems consensus control is applied to the speed coordination of multi-PMSMs. Under an undirected communication topology, the control problem of the multi-PMSMs consensus control system is reformulated as multi-agent systems consensus control problem. Additionally, a disturbance observer is utilized to estimate unknown lumped disturbances, which are compensated through feedforward control within the consensus protocol to achieve distributed control. Multi-agent systems offer architectural advantages, including enhanced distribution and scalability, compared to relative-coupling control.

• 2. Compared to conventional multi-agent finite-time consensus methods, this paper proposes a fixed-time consensus protocol. Notably, the upper bound of the settling time is independent of the initial conditions. Furthermore, a fixed-time disturbance observer is integrated to perform feedforward compensation for lumped disturbances. The final consensus protocol corresponds to the desired q-axis current in the speed control system.

Notation: $\:R$ represents real number set. $\:{R}_{\ge\:0}\triangleq\:\left\{x\in\:R:x\ge\:0\right\}$. $\:{R}_{+}\triangleq\:\left\{x\in\:R:x>0\right\}$. $\:\varvec{x}=\left[{x}_{1},{x}_{2},\dots\:,{x}_{N}\right]\in\:{R}^{N}$; $\:{sig}^{\sigma\:}\left({x}_{i}\right)=sign\left({x}_{i}\right){\left|{x}_{i}\right|}^{\sigma\:}$, for $\:\sigma\:\in\:R$. $\:sgn\left(.\right)$ represents a signum function. $\:{\lambda\:}_{min}\left(H\right)$ represents minimum eigenvalue of symmetric matrix $\:H$. To simplify the proof, $\:{\omega\:}_{i}\left(t\right)$,$\:{e}_{i}\left(t\right)$,$\:{u}_{i}\left(t\right)$,$\:{u}_{0}\left(t\right)$and similar terms are omitted, as are$\:{\omega\:}_{i}$,$\:{e}_{i}$,$\:{u}_{i}$,$\:{u}_{0}$ and others, in the following discussion.

Problem formulation and preliminaries

Mathematical modeling and problem formulation of a PMSM in multi-agent systems

In a multi-PMSMs system, each PMSM speed control system is considered as an independent agent. Based on the equations of motion for permanent magnet synchronous motors, the system is modeled as a first-order multi-agent system with perturbations, where adjacent PMSMs interact via network communication under a fixed communication topology. Consider a system of N PMSMs, indexed as $\:i(i=\text{1,2}\dots\:,N$). This paper examines a surface-mounted PMSM with identical $\:dq$-axis inductance, and derives the equations of motion in the $\:dq$-synchronous rotating reference frame as follows.

$${J_i}\frac{{d{\omega _i}}}{{dt}}=\frac{3}{2}{n_p}{\varphi _i}{i_{i,q}} - {T_{i,L}} - {B_i}{\omega _i}$$

(1)

Where$\:i(i=\text{1,2},\dots\:,N)$ represents the PMSM index, $\:{\omega\:}_{i}$ represents the r mechanical angular velocity; $\:{J}_{i}$ represents the rotor inert; $\:{n}_{p}$ represents the pole pairs; $\:{\phi\:}_{i}$ represents the permanent-magnet flux linkage; $\:{i}_{i,q}$ represents the $\:q$-axis currents; $\:{T}_{i,L}$ represents the load torque; $\:{L}_{i}$ represents the $\:dq$-axis inductance; $\:{B}_{i}$ represents the friction coefficient.

Based on the mathematical model of a multi-PMSMs speed control system, a virtual dynamic leader is introduced to develop a first-order leader-following multi-agent systems with perturbations, excluding the effects of load torque and other disturbances. The mathematical model is presented as follows:

$$\left\{ \begin{gathered} {{\dot {\omega }}_i}={\kappa _i}{u_i}+{f_i} \hfill \\ {{\dot {\omega }}_0}={u_0} \hfill \\ \end{gathered} \right.$$

(2)

Where $\:{\kappa\:}_{i}=(3{n}_{p}{\phi\:}_{i}/2{J}_{i})\in\:{R}^{+}$,$\:{u}_{i}\in\:R$ and$\:{f}_{i}=-({T}_{i,L}+{B}_{i}{\omega\:}_{i})/{J}_{i}\in\:R$ represent the control coefficients of the physical PMSM, the control input (for the $\:q$-axis current $\:{i}_{q,i}^{*}$​), and the load and friction torques, respectively; $\:{\omega\:}_{0}$ represents the mechanical angular velocity of the leader; $\:{u}_{0}$ represents the control input of the leader.

A PI controller is designed for the virtual leader to enable rapid tracking of the desired speed $\:{\omega\:}^{*}$. The controller is formulated as follows:

$${u_0}={k_p}({\omega _0} - {\omega ^*})+{k_i}\int {({\omega _0} - {\omega ^*})} dt$$

(3)

Where $\:{k}_{p}$ represents the proportional gain and $\:{k}_{i}$ represents the integral gain.

Preliminary knowledge

Let the undirected graph $\:G\left(A\right)=\left\{V,E\right\}$ represent the communication topology among $\:N$ agents, where $\:V=\left\{{v}_{1},{v}_{2},\dots\:,{v}_{N}\right\}$ represent the set of nodes, each node $\:{v}_{i}$ corresponding to an agent, and $\:E\subseteq\:V\times\:V$ is the set of edges. An edge $\:{e}_{ij}=({v}_{i},{v}_{j})\in\:E$ exists between nodes $\:i$ and $\:j$ implies that agents $\:i$ and $\:j$ can communicate with each other. The nodes are indexed by $\:i,j\in\:I=\left\{\text{1,2},\dots\:,N\right\}$, and the set $\:I$ is a finite set of positive integers. The adjacency matrix is denoted by $\:A=\left[{a}_{ij}\right]\in\:{R}^{N\times\:N}$, and if there is an edge $\:({v}_{i},{v}_{j})\in\:E$ between nodes $\:i$ and $\:j$, the corresponding entry in $\:{a}_{ij}$ is 1; otherwise, it is 0. Assume that the graph $\:G$ has no self-loops, i.e., $\:{a}_{ii}=0$. For undirected graphs, the adjacency matrix $\:A$ is symmetric. The Laplacian matrix of the graph is denoted by $\:L=D-A=\left[{l}_{ij}\right]\in\:{R}^{N\times\:N}$, where $\:{l}_{ii}=\sum\:_{i\ne\:j}{a}_{ij}$ and $\:{l}_{ij}=-{a}_{ij}$, with $\:D$ being the degree matrix. When a leader exists in the system, represented by the topological graph $\:{G}_{N+1}$, the leader’s index is set to 0. The adjacency matrix $\:{A}_{N+1}$ and the Laplacian matrix $\:{L}_{N+1}\in\:{R}^{(N+1)\times\:(N+1)}$ of the topological graph $\:{G}_{N+1}$ are defined accordingly. Since the leader is unaffected by the followers, we have $\:{a}_{0i}=0$. Let matrix B be defined as $\:diag({a}_{10},{a}_{20},\dots\:,{a}_{N0})$,if the followers $\:i$ can receive information from the leader, then $\:{a}_{i0}=1$; otherwise, $\:{a}_{i0}=0$. Let matrix H be defined as $\:H=L+B$.The $\:{L}_{N+1}$ is partitioned as follows:

$${L_{N+1}}=\left[ {\begin{array}{*{20}{c}} 0&{{0_{1 \times N}}} \\ {{L_1}}&H \end{array}} \right]$$

Lemma 1 establishes a key property of the matrix $\:H$. A path starting from node $\:{v}_{i}{\to\:v}_{j}$ is defined as a sequence of consecutive edges $\:\left\{\left({v}_{i},{v}_{r}\right),\left({v}_{r},{v}_{s}\right),\dots\:,\left({v}_{z}{v}_{j}\right)\right\}$. An undirected graph is considered connected if there exists at least one path between any pair of nodes.

Assumptions and relevant lemma

Definition 1

²⁷: System (2) achieves fixed-time leader-following consensus if, for any initial states $\:{x}_{i}\left(0\right)$ and $\:i\in\:V$, there exist a controller $\:{u}_{i}$ and a function $\:T\left({x}_{i}\right(0\left)\right)\triangleq\:T\ge\:0$ such that the following equation holds for $\:\forall\:i,j\in\:V$.

$$\left\{ \begin{gathered} \mathop {\lim }\limits_{{t \to T}} \left| {{x_i}(t) - {x_0}(t)} \right|=0 \hfill \\ {x_i}(t)={x_0}(t),\forall t>T \hfill \\ \end{gathered} \right.$$

where $\:T$ is bounded by a constant $\:{T}_{max}$, which is independent of the initial state, i.e., $\:T\le\:{T}_{max}$.

Assumption 1

The communication topology among the followers is undirected, and the leader has directed paths to all followers. Specifically, the communication topology between the leader and the followers forms a directed spanning tree, with the leader as the root node.

Assumption 2

For physical systems with perturbations, assume the existence of a positive constant $\:\epsilon\:\in\:{R}^{+}$ such that $\:\left|\dot{{f}_{i}}\right|<\epsilon\:$.

Assumption 3

The control input for the leader is consistently bounded, with its upper bound denoted by$\:\rho\:\in\:{R}^{+}$, such that $\:\left|{u}_{0}\right|\le\:\rho\:$,which is known a priori to all followers.

Lemma 1

³¹: The symmetry and positive definiteness of a matrix $\:H$ are guaranteed if the graph $\:G\left(A\right)$ is undirected and connected, and if the leader in graph $\:{G}_{N+1}$ has directed paths to all followers.

Lemma 2

³²: Consider the following system:

$$\dot {g}(t)=f(g(t)),g(0)={g_0}$$

(4)

where $\:g\in\:{R}^{n}$, $\:f\left(g\left(t\right)\right):{R}^{n}\to\:{R}^{n}$ is continuous on $\:{R}^{n}$ and $\:f\left(0\right)=0$. If there exists a continuous positive definite function $\:V\left(g\right(t\left)\right)$, real number $\:a$, $\:b$, $\:c>0$, and $\:\eta\:>1$ such that.

$$\dot {V}(t) \leqslant - a{V^\xi }(t) - b{V^\eta }(t) - cV(t),g \in {R^n}\backslash \{ 0\}$$

Therefore, the origin of system (4) is globally fixed-time stable, and the convergence time satisfies.

$$T<\frac{1}{{c(1 - \xi )}}\ln (1+\frac{c}{a})+\frac{1}{{b(\eta - 1)}}$$

Lemma 3

²⁸: If $\:{x}_{1},{x}_{2},\dots\:,{x}_{N}\ge\:0$, then the following inequality holds:

$$\begin{gathered} {\sum\limits_{{i=1}}^{N} {x_{i}^{\delta } \geqslant \left( {\sum\limits_{{i=1}}^{N} {{x_i}} } \right)} ^\delta },0 \leqslant \delta \leqslant 1 \hfill \\ {\sum\limits_{{i=1}}^{N} {x_{i}^{\delta } \geqslant {N^{1 - \delta }}\left( {\sum\limits_{{i=1}}^{N} {{x_i}} } \right)} ^\delta },\delta >1 \hfill \\ \end{gathered}$$

Fig. 1

Block diagram of the multi-PMSMs speed control system.

Design of fixed-time ESO

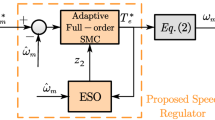
The equations of motion of the PMSM, along with its actual operating conditions, indicate that the motor is subject to load perturbations and other unknown disturbances during operation. To achieve fast transient response and improve robustness against load perturbations and other unknown disturbances, a fixed-time ESO is designed, the obtained perturbation estimates are feedforward into the consensus protocol for compensation to further enhance system robustness. The control block diagram of the multi-PMSMs speed control system is presented in Fig. 1.

The equations of motion for the $\:i$-th PMSM are rewritten as follows:

$${\dot {\omega }_i}={\kappa _i}{u_i}+{f_i}$$

(5)

Let $\:{z}_{i,1}$ denote the estimate of $\:{\omega\:}_{i}$, and $\:{z}_{i,2}$ the estimate of $\:{f}_{i}$. The fixed-time ESO is designed as follows:

$$\left\{ \begin{gathered} {{\dot {z}}_{i,1}}={z_{i,2}} - {k_1}si{g^{{p_1}}}({z_{i,1}} - {\omega _i}) \hfill \\ - {k_2}si{g^{{q_1}}}({z_{i,1}} - {\omega _i})+{\kappa _i}{u_i} \hfill \\ {{\dot {z}}_{i,2}}= - {k_3}si{g^{{p_2}}}({z_{i,1}} - {\omega _i}) \hfill \\ - {k_4}si{g^{{q_2}}}({z_{i,1}} - {\omega _i}) - \varepsilon sign({z_{i,1}} - {\omega _i}) \hfill \\ \end{gathered} \right.$$

(6)

Where $\:{p}_{m}=m\stackrel{-}{p}-(m-1)\in\:\left(\text{0,1}\right)$; $\:{q}_{m}=m\stackrel{-}{q}-(m-1)\in\:(1,+\infty\:)$, $\:m=\text{1,2}$;$\:\stackrel{-}{p}\in\:(1-{\tau\:}_{1},1)$, $\:\stackrel{-}{q}\in\:\left(\text{1,1}{+\tau\:}_{2}\right)$, Let $\:{\tau\:}_{1}$ and $\:{\tau\:}_{2}$ be sufficiently small positive constants. The observer gain is designed such that the following matrices are Hurwitz matrices.

$${B_1}=\left[ {\begin{array}{*{20}{c}} { - {k_1}}&1 \\ { - {k_3}}&0 \end{array}} \right],{B_2}=\left[ {\begin{array}{*{20}{c}} { - {k_2}}&1 \\ { - {k_4}}&0 \end{array}} \right]$$

Theorem 1

Under Assumption 2, the fixed-time ESO can estimate both the total perturbation $\:{f}_{i}$ and the mechanical angular velocity $\:{\omega\:}_{i}$, with the estimation error converging within a fixed time. The convergence time is given by:

$${T_1} \leqslant \frac{{\lambda _{{\hbox{max} }}^{{{\Xi _1}}}({Q_1})}}{{{\mu _1}{\Xi _1}}}+\frac{1}{{{\mu _2}{\Xi _2}{\vartheta ^{{\Xi _2}}}}}$$

Where $\:{{\Xi\:}}_{1}=1-\stackrel{-}{p}$, $\:{{\Xi\:}}_{2}=\stackrel{-}{q}-1$, $\:{\mu\:}_{1}={\lambda\:}_{min}\left({P}_{1}\right)/{\lambda\:}_{max}\left({P}_{1}\right)$, $\:{\mu\:}_{2}={\lambda\:}_{min}\left({P}_{2}\right)/{\lambda\:}_{max}\left({P}_{2}\right)$,$\:\vartheta\:\in\:{R}^{+}\le\:{\lambda\:}_{min}\left({P}_{2}\right)\:$. Let $\:{P}_{1},\, {P}_{2}, \, {Q}_{1}$and $\:{Q}_{2}$ be non-singular, symmetric, positive definite matrices. Additionally, the above parameter matrices satisfy conditions $\:{B}_{1}^{T}{Q}_{1}+{Q}_{1}{B}_{1}={-P}_{1}$ and $\:{B}_{2}^{T}{Q}_{2}+{Q}_{2}{B}_{2}={-P}_{2}$.

Proof

Let the estimation error be defined as

$$\left\{ \begin{gathered} {{\tilde {e}}_{i,1}}={\omega _i} - {z_{i,1}} \hfill \\ {{\tilde {e}}_{i,2}}={f_i} - {z_{i,2}} \hfill \\ \end{gathered} \right.$$

(7)

The derivation of Eq. (7) yields

$$\left\{ \begin{aligned} & {{\dot {\tilde {e}}}_{i,1}}={{\tilde {e}}_{i,2}} - {k_1}si{g^{{p_1}}}({{\tilde {e}}_{i,1}}) - {k_2}si{g^{{q_1}}}({{\tilde {e}}_{i,1}}) \hfill \\ & {{\dot {\tilde {e}}}_{i,2}}={{\dot {f}}_i} - {k_3}si{g^{{p_2}}}({{\tilde {e}}_{i,1}}) - {k_4}si{g^{{q_2}}}({{\tilde {e}}_{i,1}}) \hfill \\ & - \varepsilon sign({{\tilde {e}}_{i,1}}) \hfill \\ \end{aligned} \right.$$

(8)

According to³³, to demonstrate that the estimation error converges to zero in fixed time, the proof is divided into two steps:

• 1. Show that the following error system converges to zero in fixed time, i.e.,

  $$\left\{ \begin{aligned} & {{\dot {\tilde {e}}}_{i,1}}={{\tilde {e}}_{i,2}} - {k_1}si{g^{{p_1}}}({{\tilde {e}}_{i,1}}) - {k_2}si{g^{{q_1}}}({{\tilde {e}}_{i,1}}) \hfill \\ & {{\dot {\tilde {e}}}_{i,2}}= - {k_3}si{g^{{p_2}}}({{\tilde {e}}_{i,1}}) - {k_4}si{g^{{q_2}}}({{\tilde {e}}_{i,1}}) \hfill \\ \end{aligned} \right.$$

  (9)

  According to Theorem 2 in³⁴, A can converge to zero in fixed time.

• 2. According to³⁵, the following equation holds:

  $${\dot {\tilde {e}}_{i,2}}={\dot {f}_i} - \varepsilon sign({\tilde {e}_{i,1}})=0,t \geqslant {T_1}$$

  (10)
  $$\:\text{T}\text{h}\text{a}\text{t}\:\text{i}\text{s},\:\text{w}\text{h}\text{e}\text{n}\:t\ge\:{T}_{1},{z}_{i,1}={\omega\:}_{i},{z}_{i,2}={f}_{i}.$$

  .

Design of the fixed-time consensus protocol

In conjunction with the fixed-time ESO described above, a fixed-time consensus protocol $\:{u}_{i}$ is designed to replace the speed loop controller in the multi-PMSMs speed control system. The proposed protocol ensures that the system’s rotational speeds (Eq. 2) achieve consensus within a fixed time.

The following factors must be considered when selecting a suitable Lyapunov function: (1) As the consensus protocol includes an adaptive parameter $\:{c}_{i}$, it is crucial to determine the boundedness of $\:{c}_{i}$ within the time interval $\:\left[0,\right.\left.+\infty\:\right)$. (2) Since the convergence of $\:{c}_{i}$ is unknown, the boundedness of $\:{c}_{i}$ and fixed-time convergence of $\:{e}_{i}$ are analyzed separately. Therefore, two Lyapunov functions are constructed in this paper, with the proof divided into two steps: one to verify the boundedness of.

$\:{c}_{i}$, and the other to prove the fixed-time convergence of $\:{e}_{i}$.

The proposed fixed-time protocol for the $\:i$-th follower is expressed as follows:

$$\begin{aligned} {u_i} & =\frac{1}{{{\kappa _i}}}[ - \alpha si{g^a}(\sum\limits_{{j=0}}^{N} {{a_{ij}}({\omega _i} - {\omega _j})} ) \hfill \\ & \quad - \beta si{g^b}(\sum\limits_{{j=0}}^{N} {{a_{ij}}({\omega _i} - {\omega _j})} ) \hfill \\ & \quad - {c_i}(\sum\limits_{{j=0}}^{N} {{a_{ij}}({\omega _i} - {\omega _j})} ) \hfill \\ & \quad - \rho \operatorname{sgn} (\sum\limits_{{j=0}}^{N} {{a_{ij}}({\omega _i} - {\omega _j})} ) - {z_{i,2}}] \hfill \\ \end{aligned}$$

(11)

Where $\:{\kappa\:}_{i}=(3{n}_{p}{\phi\:}_{i}/2{J}_{i})\in\:{R}^{+}$ represents the control coefficients of the physical PMSM.$\:a\in\:\left(\text{0,1}\right)$, $\:b\in\:(1,+\infty\:)$, $\:{c}_{i}$, is an adaptive parameter that satisfies $\:\dot{{c}_{i}}={\left(\sum\:_{i=1}^{N}{a}_{ij}({\omega\:}_{i}-{\omega\:}_{j})\right)}^{2}$. $\:{z}_{i,2}$ represents the perturbation estimate of the observer.

The tracking error of the $\:i$-th follower is defined as $\:{e}_{i}={\omega\:}_{i}-{\omega\:}_{0}$,$\:e={\left[{e}_{1},{e}_{2},\dots\:,{e}_{N}\right]}^{T}$, $\:\omega\:={\left[{\omega\:}_{1},{\omega\:}_{2},\dots\:,{\omega\:}_{N}\right]}^{T}$, $\:f={\left[{f}_{1},{f}_{2},\dots\:,{f}_{N}\right]}^{T}$, $\:z={\left[{z}_{1},{z}_{2},\dots\:,{z}_{N}\right]}^{T}$.

The error system is then expressed as follows:

$$\begin{gathered} \dot {e}=\dot {\omega } - {1_N}{{\dot {\omega }}_0}= - \alpha si{g^a}(He) \hfill \\ - \beta si{g^b}(He) - \Lambda He - \hfill \\ \rho \operatorname{sgn} (He)+f - {1_N}{u_0} \hfill \\ \end{gathered}$$

(12)

Where $\:{\Lambda\:}=diag\left\{{c}_{1},{c}_{2},\dots\:,{c}_{N}\right\}$.

Theorem 2

Suppose the communication topology satisfies Assumption 1, and Assumptions 2and 3are also satisfied. If $\:{c}_{0}=\delta\:$, the control protocol (11) achieves fixed-time consistency of the multi-agent system (2). Furthermore, the convergence time satisfies:

$$T \leqslant \hbox{max} \left\{ {{T_1},\frac{1}{{{l_l}(1 - a)}}\ln (1+\frac{{2\delta }}{{{l_2}}})+\frac{1}{{{l_3}(b - 1)}}} \right\}$$

Where${l}_{1}=\delta\:{\lambda\:}_{min}\left(H\right),\:{l}_{2}=\alpha\:{\left({\lambda\:}_{min}\right(H\left)\right)}^{\frac{a-1}{2}},\:{l}_{3}=\beta\:{N}^{\frac{1-b}{2}}{{(\lambda\:}_{min}\left(H\right))}^{\frac{b+1}{2}}.$

Proof

Step 1: Construct the Lyapunov function as $\:{V}_{1}{=V}_{2}+{V}_{3}$.

Where $\:{V}_{2}={e}^{T}He$, $\:{V}_{3}=\sum\:_{i=1}^{N}{({c}_{0}-{c}_{i})}^{2}$ and $\:{\xi\:}_{i}=\sum\:_{i=0}^{N}{a}_{ij}({\omega\:}_{i}-{\omega\:}_{j})$ are defined.

Taking the derivative of both sides of the above equation and substituting it into Eq. (12) yields

$$\begin{gathered} {{\dot {V}}_2}=2{e^T}H( - \alpha si{g^a}(He) - \beta si{g^b}(He) \hfill \\ - \Lambda He - \rho \operatorname{sgn} (He)+f - {z_2} - {1_N}{u_0}) \hfill \\ \end{gathered}$$

(13)

$$\begin{gathered} \leqslant - 2\alpha {({e^T}HHe)^{\frac{{a+1}}{2}}} - 2\beta {({e^T}HHe)^{\frac{{b+1}}{2}}} \hfill \\ - 2{e^T}H\Lambda He+2{e^T}H(\rho \operatorname{sgn} (He) \hfill \\ +f - {z_2} - {1_N}{u_0}) \hfill \\ \end{gathered}$$

(14)

From Lemma 3, it follows that $\:-2{e}^{T}H{1}_{N}{u}_{0}\le\:2\rho\:\sum\:_{i=1}^{N}\left|{\xi\:}_{i}\right|$holds. Additionally, from Lemma 3, $\:{\left({e}^{T}HHe\right)}^{\frac{a+1}{2}}\ge\:{\left({\lambda\:}_{min}\right(H\left)\right)}^{\frac{a+1}{2}}{{V}_{2}}^{\frac{a+1}{2}}$ and $\:{N}^{\frac{1-b}{2}}{\left({e}^{T}HHe\right)}^{\frac{b+1}{2}}\ge\:{N}^{\frac{1-b}{2}}{\left({\lambda\:}_{min}\right(H\left)\right)}^{\frac{b+1}{2}}{{V}_{2}}^{\frac{b+1}{2}}$ holds, and when δ > 0, $\:-2{e}^{T}H{\Lambda\:}He=-{e}^{T}H\left(2{\Lambda\:}-2\delta\:I\right)He-2\delta\:{e}^{T}HHe\le\:-{e}^{T}H\left(2{\Lambda\:}-2\delta\:I\right)He-2\delta\:{\lambda\:}_{min}\left(H\right){V}_{2}$ is established .

From the previous discussion, $\:f={z}_{2}$ holds when $\:t\ge\:{T}_{1}$. Substituting these conditions yields

$$\begin{gathered} {{\dot {V}}_2} \leqslant - 2\delta {\lambda _{\hbox{min} }}(H){V_2} - 2\alpha {({\lambda _{\hbox{min} }}(H))^{a+1/2}}V_{2}^{{\frac{{a+1}}{2}}} \hfill \\ - 2\beta {N^{\frac{{1 - b}}{2}}}{({\lambda _{\hbox{min} }}(H))^{\frac{{b+1}}{2}}}V_{2}^{{\frac{{b+1}}{2}}} - 2\sum\limits_{{i=1}}^{N} {({c_i} - \delta )} \xi _{i}^{2} \hfill \\ \end{gathered}$$

(15)

Since $\:{\dot{V}}_{3}=2\sum\:_{i=1}^{N}\left({c}_{i}{-c}_{0}\right){\xi\:}_{i}^{2}$ holds, it follows that

$$\begin{gathered} {{\dot {V}}_1} \leqslant - 2\delta {\lambda _{\hbox{min} }}(H){V_2} - 2\alpha {({\lambda _{\hbox{min} }}(H))^{\frac{{a+1}}{2}}}V_{2}^{{\frac{{a+1}}{2}}} \hfill \\ - 2\beta {N^{\frac{{1 - b}}{2}}}{({\lambda _{\hbox{min} }}(H))^{\frac{{b+1}}{2}}}V_{2}^{{\frac{{b+1}}{2}}} \hfill \\ \end{gathered}$$

(16)

The previous analysis confirms that $\:{\dot{V}}_{1}$ is semi-negative definite, ensuring that $\:{V}_{1}$、$\:{c}_{i}$ and $\:e$ do not diverge to infinity, thereby guaranteeing the boundedness of $\:{c}_{i}$ and $\:e$.

In the second step, the Lyapunov function is chosen as $\:{V}_{2}={e}^{T}He$.

$$\begin{gathered} {{\dot {V}}_2}=2{e^T}H\dot {e}={{\dot {V}}_1} - {{\dot {V}}_3} \hfill \\ \leqslant 2\sum\limits_{{i=1}}^{N} {({c_0} - {c_i})} \xi _{i}^{2} - 2\delta {\lambda _{\hbox{min} }}(H){V_2} \hfill \\ - 2\alpha {({\lambda _{\hbox{min} }}(H))^{\frac{{a+1}}{2}}}V_{2}^{{\frac{{a+1}}{2}}} \hfill \\ - 2\beta {N^{\frac{{1 - b}}{2}}}{({\lambda _{\hbox{min} }}(H))^{\frac{{b+1}}{2}}}V_{2}^{{\frac{{b+1}}{2}}} \hfill \\ \end{gathered}$$

(17)

$\:2{\sum\:}_{i=1}^{N}({c}_{0}-{c}_{i}){\xi\:}_{i}^{2}\le\:0$ holds due to the monotonicity of $\:{c}_{i}$. Therefore

$$\begin{gathered} {{\dot {V}}_2} \leqslant - 2\delta {\lambda _{\hbox{min} }}(H){V_2} - 2\alpha {({\lambda _{\hbox{min} }}(H))^{\frac{{a+1}}{2}}}V_{2}^{{\frac{{a+1}}{2}}} \hfill \\ - 2\beta {N^{\frac{{1 - b}}{2}}}{({\lambda _{\hbox{min} }}(H))^{\frac{{b+1}}{2}}}V_{2}^{{\frac{{b+1}}{2}}} \hfill \\ \end{gathered}$$

(18)

Based on Lemma 2, it can be demonstrated that the system is globally fixed-time stable at the origin. Specifically, system (2) achieves fixed-time consensus, and the convergence time satisfies:

$$T \leqslant \hbox{max} \left\{ {{T_1},\frac{1}{{{l_l}(1 - a)}}\ln (1+\frac{{2\delta }}{{{l_2}}})+\frac{1}{{{l_3}(b - 1)}}} \right\}$$

Where${l}_{1}=\delta\:{\lambda\:}_{min}\left(H\right),\:{l}_{2}=\alpha\:{\left({\lambda\:}_{min}\right(H\left)\right)}^{\frac{a+1}{2}},\:{l}_{3}=\beta\:{N}^{\frac{1-b}{2}}{{(\lambda\:}_{min}\left(H\right))}^{\frac{b+1}{2}}.$

Experimental investigations

Experimental setup

The physical experimental platform is shown in Fig. 2 and consists of a host computer, controller group, driver group, drive PMSM group, and load PMSM group. Each PMSM is configured with the parameters listed in Table 1. The multi-PMSMs speed control system model is implemented on the host computer, which sends control signals to the drive and load PMSM groups to apply the proposed control scheme and drive PMSM rotation. The controller group connects to the host computer via a switch to form a local area network (LAN), using IP as the underlying protocol and transmitting data over UDP.

Fig. 2

Description of the experimental setup.

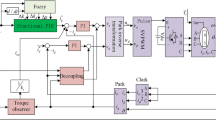
Considering the practical applications in engineering, the comparison experiments in this paper include operations such as speed variation, forward and reverse rotation, and loading and unloading tests. The control scheme proposed in this paper is referred to as Scheme 1 and the parameters for Scheme 1 are listed in Table 2, while the relative-coupling control is designated as Scheme 2 and the parameters for Scheme 2 are listed in Table 3. Additionally, in the relative-coupling control structure, each motor requires an algorithm for individual tracking control. Since PID control is widely used, PID algorithms are employed in this paper‘s relative-coupling control. Both schemes use PID control in their current loops with identical parameters. The block diagram of the relative-coupling control is shown in Fig. 3.

Fig. 3

Block diagram of the relative-coupling control structure.

Table 1 PMSM parameters.

Table 2 Parameters for scheme 1.

Table 3 Parameters for scheme 2.

The matrix H is specified as follows:

$$H=\left[ {\begin{array}{*{20}{c}} 3&{ - 1}&{ - 1} \\ { - 1}&2&{ - 1} \\ { - 1}&{ - 1}&2 \end{array}} \right]$$

The minimum eigenvalue of the matrix H is given by $\:{\lambda\:}_{min}\left(H\right)$=0.267, Substituting $\:a=0.9,b=1.1,\alpha\:=\:\beta\:=30$,$\:\delta\:=0.8$ and $\:{\lambda\:}_{min}\left(H\right)$=0.267 into $\:1/{l}_{1}\left(1-a\right)ln\left(1+2\delta\:/{l}_{2}\right)+1/{l}_{3}(b-1)$,the theoretical upper bound of the settling time is calculated as T ≤ 9.95s, the actual settling time of the system is approximately 9 s. The expected outcome is that, after approximately 9 s, the speeds of the three PMSMs track the speed of the virtual leader, indicating that the multi-PMSMs speed control system achieves fixed-time leader-following consensus.

Speed up and down experiment

The initial speed is set to 400 r/min. After 30 s, it increases to 600 r/min, and after 60 s, it decreases back to 400 r/min, with a total duration of 90 s. The results of the comparison test are presented in Figs. 4 and 5.

Fig. 4

(a) Velocity response curve for Scheme 1. (b) Velocity tracking error curve for Scheme 1. (c) Velocity synchronization error curve for Scheme 1.

Fig. 5

(a) Velocity response curve for Scheme 2. (b) Velocity tracking error curve for Scheme 2. (c) Velocity synchronization error curve for Scheme 2.

From Fig. 4, it can be observed that the control scheme 1 proposed in this paper accurately tracks the given trajectory of each motor under lifting and lowering conditions. There is no overshoot during the startup and operation phases, and the speed chattering is approximately 0.8 r/min at 400 r/min steady-state operation and 1.5 r/min at 600 r/min steady-state operation.

From Fig. 5, it is evident that the control scheme 2 exhibits an overshoot of approximately 17 r/min. The speed chattering is around 1.4 r/min at 400 r/min steady-state operation and about 2 r/min at 600 r/min steady-state operation.

A comparison shows that the control scheme proposed in this paper exhibits superior tracking and synchronization performance under lifting and lowering conditions. Compared to Scheme 2, it results in smaller chattering and no overshoot.

Forward and reverse experiment

The initial speed was set to 400 r/min, reversed to -400 r/min after 30 s, and then increased back to 400 r/min after 60 s. The total duration was 90 s. The results of the comparison test are presented in Figs. 6 and 7.

Fig. 6

(a) Velocity response curve for Scheme 1. (b) Velocity tracking error curve for Scheme 1. (c) Velocity synchronization error curve for Scheme 1.

Fig. 7

(a) Velocity response curve for Scheme 2. (b) Velocity tracking error curve for Scheme 2. (c) Velocity synchronization error curve for Scheme 2.

Figure 6 demonstrates that the proposed control scheme accurately tracks the given trajectory for each motor under both forward and reverse conditions. Notably, there is no overshooting during the startup phase or at the forward/reverse transition points. Additionally, the speed chattering is approximately 0.8 r/min during steady-state operation at both 400 r/min and − 400 r/min.

Figure 7 illustrates that the scheme 2 exhibits an overshoot of approximately 17 r/min. This overshoot increases to around 220 r/min during the forward and reverse stages. The speed chattering is about 1.3 r/min at 400 r/min steady-state operation and rises to 2 r/min at 600 r/min.

A comparison shows that the proposed control scheme exhibits superior tracking and synchronization performance under lifting and lowering conditions. Compared to Scheme 2, the proposed approach achieves smaller speed chattering and eliminates overshooting.

Loading and unloading experiment

The initial rotational speed is set to 400 r/min. The load experiments are categorized into two types: (1) applying different loads simultaneously (operation 1), and (2) applying different loads at distinct moments (operation 2).

In operation 1, loads of 0.6 N, 0.5 N, and 0.2 N are applied to motors 1, 2, and 3, respectively, at 30 s. The loads are then removed at 40 s, resulting in a total running time of 50 s. The comparison test results are presented in Figs. 8 and 9.

In operation 2, a load of 0.8 N is applied to motor 1 at 30 s and removed at 40 s. Subsequently, a load of 0.6 N is applied to motor 2 at 50 s and removed at 60 s, with a total running time of 70 s. The comparison test results are shown in Figs. 10 and 11.

Fig. 8

(a) Velocity response curve for Scheme 1. (b) Velocity tracking error curve for Scheme 1. (c) Velocity synchronization error curve for Scheme 1.

Fig. 9

(a) Velocity response curve for Scheme 2. (b) Velocity tracking error curve for Scheme 2. (c) Velocity synchronization error curve for Scheme 2.

Fig. 10

(a) Velocity response curve for Scheme 1. (b) Velocity tracking error curve for Scheme 1. (c) Velocity synchronization error curve for Scheme 1.

Fig. 11

(a) Velocity response curve for Scheme 2. (b) Velocity tracking error curve for Scheme 2. (c) Velocity synchronization error curve for Scheme 2.

As shown in Fig. 8, under operation 1, the proposed control scheme exhibits a speed variation of approximately 13 r/min during loading and unloading. In contrast, Fig. 9 indicates that Scheme 2 has a speed variation of about 15.8 r/min.

According to Fig. 10, under operation 2, the proposed control scheme shows speed changes of approximately 7.3 r/min and 6.8 r/min during loading and unloading, respectively. Figure 11 shows that Scheme 2 exhibits speed changes of about 9 r/min and 7.5 r/min, respectively. Specifically, the speed variations during loading and unloading are reduced by approximately 15–20%, highlighting the effectiveness of the proposed approach in minimizing system perturbations.

The proposed control scheme demonstrates smaller speed variations compared to Scheme 2, ensuring improved system robustness.

The proposed algorithm is based on multi-agent systems consensus, inherits both the advantages and disadvantages of such systems, including distribution, flexibility, and scalability. However, consensus control presents challenges, as it relies heavily on real-time communication. Delays or packet loss can result in decision conflicts or task failures, and the design and implementation thresholds remain high. Finally, achieving consensus under communication delays or data loss remains an important direction for our future research.

Conclusion

Considering the integration of multi-PMSMs speed control system and consensus control in multi-agent systems for achieving unified control outcomes. This paper adopts the framework of multi-agent systems theory, modeling the multi-PMSMs speed control system as a perturbed first-order multi-agent system. A fixed-time distributed cooperative control strategy is proposed to replace the speed loop controller in traditional vector control systems. This strategy integrates a fixed-time ESO to achieve fixed-time speed consensus across the multi-PMSMs speed control system. Experimental results confirm that the proposed control scheme achieves fixed-time speed consensus for the multi-PMSMs control system, with excellent tracking performance and no overshooting. Under varying speeds and loads, the proposed scheme demonstrates smaller synchronization errors compared to scheme 2. Additionally, the scheme offers strong robustness and scalability, making it suitable for broader applications.

In addition, the proposed algorithm, based on multi-agent system consensus, offers enhanced flexibility in adjusting the number of motors in a multi-PMSMs speed consensus control system. This flexibility arises because changes in communication topology do not influence the mathematical formulation of the consensus protocol.