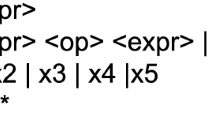Introduction

The World Health Organization (WHO) global action plan highlights the urgent need to address the rising burden of diabetes, including type 1 diabetes in adolescents and young adults, which has significantly increased across 195 countries over 28 years. In 2017, diabetes led to 476 million cases and 1.37 million deaths, with projections for 20251,2. Diabetes mellitus is a metabolic disorder resulting from inadequate insulin secretion by pancreatic β-cells or impaired glucagon secretion by pancreatic α-cells. T1D is an autoimmune system in which the pancreaticβ-cells are destroyed, resulting in insulin secretion. This deficiency leads to significant fluctuations in blood glucose levels and increases the risk of complications such as cardiac vascular diseases (CVD), myocardial infarction (MI) or stroke, kidney issues, and vision loss. As a result, external insulin administration is essential for individuals with T1D. However, patients often face challenges with traditional glucose monitoring and insulin infusion methods. Developments in healthcare due to advancements in engineering and substantial progress in the sensing of blood glucose levels, developing physics-based/ data-driven models for metabolic systems, and designing control schemes for delivering insulin. Advancements in Artificial Intelligence (AI) led to the design of a device called Artificial Pancreas (AP) for continuous glucose monitoring (CGM) and closed-loop control systems.

Considerable research and standard of care have been conducted in monitoring and controlling blood glucose levels3,4,5,6,7,8,9 and recent advancements also explores IoMT innovations in diabetes management using predictive models and wearable data10. In11 a comprehensive survey on the key components of AP systems, covering insulin delivery, glucose measurement, and control strategies or algorithms used in treating T1DM. Single hormone APs, which deliver only insulin are designed to manage hyperglycemia, and recent advancements continue to mode closer to ultimate goal of a fully autonomous artificial pancreas, significantly transforming care for individuals with Type 1 diabetes12. However, as reported in13, postprandial glucose spikes and exercise-induced hypoglycemia pose significant challenges in improving glucose control and reducing glucose variability for many T1D patients with single hormone APs. In14 the effectiveness of dual-hormone artificial pancreas systems (using both insulin and glucagon), single-hormone artificial pancreas systems (insulin alone), and conventional insulin pump therapy for overnight glucose control in patients with T1D. From their findings, they confirmed that single hormone APs are sufficient for overnight glycemic control. However, exercise-related hypoglycemia remains a challenge for T1DM. In15 introduced a novel dual-hormone switching model predictive control and compared its performance to single-hormone systems, both with and without an integrated exercise model. Their findings showed that the dual hormone AP outperformed single hormone APs in managing hypoglycemia, particularly when considering a comprehensive T1D patient model that includes exercise. AI has been applied to many aspects of medical health like diagnosis, precision medicine, drug delivery control, personalized decision support system development, etc. The application of AI has received more attention, especially in diabetes research to detect glucose variability and insulin delivery systems16,17,18,19.

The artificial pancreas continuously monitors the blood glucose and preserves the blood glucose within the healthy range by taking proper control action. Hence, the control system plays a major role in APs. The control system in AP has three generations (i) open-loop therapy, (ii) closed-loop therapy with single hormone closed-loop control, and (iii) closed-loop therapy with multi-hormone closed-loop control. Commonly used feedback control systems in APs are Proportional- Integral and Derivative (PID) and Model Predictive Control (MPC) algorithms20,21. Similarly, feedback feed-forward control schemes are developed to control blood glucose against meal disturbance. Nowadays, self-regulated drug delivery control systems to deliver insulin and glucagon to control hyperglycemia and hypoglycemia have been proposed22,23. However, continuous monitoring and control of blood glucose levels is computationally expensive. Hence, event-triggered control is recommended for glycemic regulation in patients with T1D.

The two major challenges in AP systems are the slow response of glucose sensors and delayed insulin absorption, both of which contribute to elevated blood glucose levels24. To address the issue of glucose sensing, a predictive model utilizing machine learning algorithms has been proposed. In most literature, glucose variability has been detected using various machine-learning approaches. Similarly, delayed insulin absorption is addressed by APs with model predictive control schemes and event-triggered control schemes25,26. A lot of research works have been reported in event-triggered control for blood glucose variability27,28.

The primary goal of an event-triggered control is to minimize the energy consumption of the AP by reducing the frequency of controller while maintaining patient safety. Additionally, the event-triggered mechanism helps to prevent simultaneous infusion of insulin and glucagon. However, there has been no prior report of an integrated Smart Dual Hormone Artificial Pancreas (SDHAP) system that combines glucose level detection, prediction, and event-triggered control to regulate blood glucose by adjusting insulin and glucagon levels, along with a feedforward control scheme for disturbance rejection. To the best of our knowledge, this is the first work that comprehensively addresses recent advancements in AP components while laying robust groundwork for future research in the management of T1DM making a significant contribution to the field.

This paper is structured as follows: “Methodology” describes the proposed methodology, focusing on the detection and prediction models for hypoglycemia and hyperglycemia models. Section “Results and discussion” introduces the mathematical framework of the glucose-insulin metabolic system. Section “Hardware implementation” discusses the design of an event-triggered controller aimed at minimizing blood glucose variability. Section 5 presents the results and discussion, while “Conclusion and challenges” concludes the paper by outlining the key challenges in this field.

Methodology

This paper presents SDHAP, an advanced technology designed to help individuals with T1DM manage glucose levels more effectively by automating insulin and glucagon delivery based on real-time glucose monitoring. The innovation of SDHAP lies in its event-triggered algorithm, which dynamically calculates and administers only the necessary hormone doses, enabling precise, responsive glucose regulation through automated dual-hormone infusion. Figure 1 shows the proposed methodology for event– triggered SDHAP. The main components of SDHAP are:

  • Patient Data Analysis: Preprocess and clean the T1DiabetesGranada dataset, extracting relevant features and managing missing values for effective glucose trend analysis.

  • Classification of Glycemic Events: Define threshold-based criteria to classify hypoglycemia and hyperglycemia events using SVM and KNN classifiers for targeted analysis.

  • Blood Glucose Prediction: ARIMA and GRU models are used to predict the future blood glucose levels evaluating accuracy with RMSE and MAE to manage outliers and ensure reliability.

  • Event-Triggered Controller Design: Develop an event-triggered control mechanism for SDHAP delivery using BMM to model glucose-insulin dynamics, followed by PI and MPC-based FB - FF controller implementation for guiding insulin and glucagon infusions based on deviations from predicted glucose levels.

  • Hardware Implementation: The SDHAP system is prototyped using low-cost components including an Arduino UNO, NEMA 17 stepper motor with TB6560 driver, and 10 ml syringes for dual-hormone delivery. MATLAB and Arduino IDE coordinate control logic and actuation, enabling real-time response to glycemic events.

Fig. 1
figure 1

Proposed methodology for event-triggered SDHAP.

Full size image

Patient data analysis

Data description

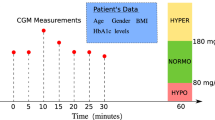
The T1DiabetesGranada dataset is openly accessible through the Zenodo repository29 and offers a highly detailed, four-year longitudinal dataset for 736 patients with Type 1 diabetes, captured in Granada, Spain. The glucose monitoring data was collected every 15 min using devices like the Freestyle Libre. This frequency provides over 2,57,000 patient days of data, allowing for fine-grained analyses of glucose trends and fluctuations across different timescales. It also includes a comprehensive demographic as well as relevant clinical and biochemical data. Table 1 provides detailed information related to the dataset. Figure 2. shows the changes in CGM measurement over time for a particular period.

Table 1 Description of the dataset.
Full size table
Fig. 2
figure 2

CGM measurement and glycemic variability over time.

Full size image

Data pre-processing and feature selection

Continuous glucose data were collected as a time series input, consisting of 124 values per day, recorded at five-minute intervals. A range of time series features was extracted across temporal, statistical, and spectral domains utilizing the feature engineering machine learning framework outlined by30. In addition, diabetes-related metrics were included, such as Time in Range (TIR), Time Below Range (TBR), and Time Above Range (TAR), which represent the percentage of time that glucose levels remain within, below, or above the target range of 70 to 180 mg/dL. High and low glucose indexes were also incorporated. To tackle the issue of imbalanced data, which can negatively impact classifier performance, feature rescaling was applied during the training process.

Additionally, the Synthetic Minority Over-Sampling TechniquE (SMOTE) was used to generate synthetic samples for the minority class. Before applying SMOTE, the dataset was imbalanced, with hyperglycemic events significantly outnumbering hypoglycemic events. The distribution showed a higher frequency of hyperglycemic cases. After applying SMOTE, synthetic samples were generated for the hypoglycemic class by interpolating closely related positive instances, balancing the dataset. This improved model performance by increasing sensitivity to hypoglycemia, reducing classification errors, and enhancing overall accuracy, particularly for the minority class.

Classification using machine learning algorithms

In this section, BG levels detected from the time series and diabetes-related metrics were used for further analysis. Various machine learning models were discussed in the literature relating the importance of AI and machine learning in classification and multi-step ahead prediction of glucose by31,32 The following two machine learning algorithms SVM and KNN were used.

Support vector machine (SVM)

Support Vector Machine (SVM) is a powerful supervised learning algorithm that constructs an optimal decision boundary to separate different classes in the feature space. In this study, SVM was employed to classify blood glucose levels into hypoglycemic, normoglycemic, and hyperglycemic states using features derived from the T1DiabetesGranada dataset. Its effectiveness in handling high-dimensional and non-linear physiological data makes it well-suited for glucose classification tasks. SVM provides high accuracy in classifying glucose levels and identifying early signs of glycemic events, which supports its integration into the SDHAP system for timely hormone administration.

Multi-class SVM, the One-vs-One or One-vs-All which divides the multi-class problem into multiple binary class problems. In multi-class SVM, the One-vs-All multi-class methods, box limitations, and the kernel function are all important. The hyperplane’s\(\:{Y}_{i}=\:{w}^{T}{X}_{i}\:+\:b\:\ge\:\:1-{\epsilon\:}_{i},\:i=\:\text{1,2},...m\:,\) where \(\:w\) is weight vector, \(\:{X}_{i}\) are input vectors and \(\:{Y}_{i}\) represent the class label and \(\:{\epsilon\:}_{i}\) is a slack variable. For separable data, the optimal margin length is \(\:\frac{2}{\left|\right|\:w\left|\right|}\) and ‘b’ is the bias term. The objective of SVM is to minimize the \(\:{0.5\left|\right|w\left|\right|}^{2}+E{\sum\:}_{i=0}^{m}{\epsilon\:}_{i}\)subject to \(\:{Y}_{i}({w}^{T}{X}_{i}+\:b)+{\epsilon\:}_{i}\ge\:\:1\), \(\:{\epsilon\:}_{i}\ge\:\:0,i=\:\text{1,2},...m\) and ‘E’ represents the box constraint. Figure 3 shows the classification output using a multi-class SVM classifier.

Fig. 3
figure 3

Multi-class glycemic classification using SVM classifier.

Full size image

K-nearest neighbor

K-Nearest Neighbor (KNN) is a simple yet effective non-parametric algorithm that classifies new data points based on the majority label of their nearest neighbors. In our framework, KNN was used to classify blood glucose readings by comparing them to past observations with similar feature patterns. Its ability to capture local data structures makes it particularly useful in detecting transitions into hypo- or hyperglycemia.

The Euclidean distance\(\:D{(\:x}_{i},\:{x}_{j})\) between the two data points indicates how comparable the two data points are. The Euclidean distance is calculated using closeness.\(\:D{(\:x}_{i},\:{x}_{j})=\sqrt{{\sum\:}_{k=1}^{n}{{(x}_{ik}-{x}_{jk})\left({(x}_{ik}-{x}_{jk}\right)}^{{\prime\:}}}\)where\(\:{x}_{ik}={(\:x}_{i1},\:{x}_{i2}{,\:x}_{i3},{x}_{i4},\:{x}_{i5}\dots\:\dots\:..{x}_{i\left(n-1\right)},\:\:{x}_{in}\:)\), ‘\(\:k\)’ indicates the dimension of the dataset and \(\:{X}_{jk}=(\:{x}_{j1}\),\(\:{x}_{j2}\), \(\:{x}_{j3},{x}_{j4}\)……….\(\:{x}_{j\left(n-1\right)}\), \(\:{x}_{jn})\). Figure 4 shows glycemic classification using KNN.

Fig. 4
figure 4

Glycemic classification using KNN classifier.

Full size image

BG time-series prediction model

Time-series forecasting techniques are widely used to predict BG levels, which leverage historical glucose data to forecast future BG trends, aiding in the prevention of glycemic events like hypoglycemia and hyperglycemia. Common approaches include autoregressive models, machine-learning methods, and advanced neural networks. In our study, we apply ARIMA and GRU models to forecast BG levels, leveraging both linear and non-linear patterns to support proactive glycemic management and minimize risks of hypoglycemia and hyperglycemia.

ARIMA

The Auto-Regressive Integrated Moving Average (ARIMA) model, introduced by Box and Jenkins, is a time series analysis technique widely used for predicting trends in BG data. The ARIMA model’s structure includes three parameters: p - autoregressive order, d – differencing order, and q – moving average order. The following equation describes the model:

$$\:{y}_{t}=c+\:{\upphi }_{1}{{y}_{t}}_{-1}+{\upphi }_{1}{{y}_{t}}_{-2}+\dots\:{\upphi }_{p}{{y}_{t}}_{-p}+{\theta\:}_{1}\:{{\varepsilon}_{t}}_{-1}+\:{\theta\:}_{1}\:{{\varepsilon}_{t}}_{-2}+\dots\:{\theta\:}_{q}\:{{\varepsilon}_{t}}_{-q}+{\varepsilon}_{t}$$

where: \(\:{y}_{t\:}\)—current value of the time series; c—constant term; \(\:\:\upphi\)—parameters for the AR part; \(\:\:\theta\:\)—parameters for the MA part; \(\:\:{\varepsilon}_{t}\)—errorterm.

The adaptability of this model helps to maintain predictive accuracy, and stability, accommodating daily variations in glucose patterns due to meals, exercise, or insulin use. This refined approach enhances the reliability of CGM-based BG forecasting, helping to predict and mitigate hypoglycemic and hyperglycemic events.

The ARIMA model was chosen for its effectiveness in modeling stationary and autocorrelated glucose trends. Prior studies, such as Yang et al. (2019), have demonstrated ARIMA’s utility in forecasting short-term glucose levels and hypoglycemia events in Type 1 Diabetes patients [Yang et al., Journal of Healthcare Engineering, 2019]. ARIMA, as a traditional time series model, can be employed for forecasting short-term glucose dynamics in a structured and interpretable manner. Its strength lies in handling linear and stationary blood glucose trends, which can support basic predictive control mechanisms in artificial pancreas systems. For instance, in a dual-hormone closed-loop system, ARIMA can be used to anticipate slight deviations in glucose levels and guide minor insulin or glucagon dosing decisions. However, its univariate structure and reliance on manual preprocessing steps such as differencing limit its application in modeling complex patient-specific glycemic responses. Furthermore, ARIMA lacks adaptability for real-time, multivariate, and nonlinear interactions among physiological variables—such as hormone kinetics, meal intake, and circadian variation—which are crucial in an event-triggered drug delivery system. Thus, ARIMA may be better suited as a baseline comparator rather than a core component of adaptive pancreas control.

In contrast, the GRU model, a type of Recurrent Neural Network, was selected for its proven ability to handle non-linear dependencies and learn long-term patterns in physiological time-series data. Mohebbi et al. (2020) showed that GRU outperformed ARIMA in predicting BG levels over longer horizons, especially under noisy and variable conditions [Mohebbi et al.,2002]. GRU networks offer a powerful alternative by learning nonlinear, long-term dependencies in blood glucose dynamics from multivariate data, making them well-suited for real-time, personalized dual-hormone delivery. Unlike ARIMA, GRUs automatically learn temporal patterns from historical glucose, insulin, glucagon, physical activity, and meal-related inputs, enabling robust forecasting even in non-stationary and highly individualized glycemic conditions. In the context of event-triggered control, GRUs can dynamically adapt to sharp glucose excursions and guide timely dosing interventions by predicting upcoming hypo- or hyperglycemic events. Their ability to process large datasets and handle multivariate physiological signals in real-time makes them ideal for building intelligent, adaptive pancreas systems tailored to individual patient responses.

GRU

The Gated Recurrent Unit (GRU), introduced by Kyunghyun Cho and colleagues in 2014, is widely used for time-series due to its ability to capture temporal dependencies effectively. For blood glucose prediction, a GRU model captures complex patterns over time, including hypoglycemic and hyperglycemic events. GRUs use two gates: the reset gate (rt = σ(Wr.[ht−1,xt] + br)) to decide how much past information of glucose to keep, and the update gate (zt = σ(Wz.[ht−1,xt] + bz)) to balance past and current glucose information. These gates combine to calculate the candidate hidden state (h҇t = tanh(Wh.[rt*ht−1,xt]+bh)) and final hidden stage (ht = zt * ht−1 + (1-zt * h҇t ), which represents the predicted glucose levels. This design supports accurate blood glucose forecasting, enhancing diabetes management and reducing adverse glycemic events. Figure 5 shows the GRU architecture that efficiently captures temporal dependencies using update and reset gate. It is particularly well-suited for modeling time-series data like blood glucose levels due to its effectiveness in handling sequential information. Table 2 shows the GRU parameters used for blood glucose prediction model.

Fig. 5
figure 5

GRU architecture for BG prediction model.

Full size image
Table 2 GRU parameter setting for BG prediction model.
Full size table

Testing and evaluation

The predicted accuracy of blood glucose levels using the dataset is evaluated through the following performance metrics:

$$\:\text{R}\text{o}\text{o}\text{t}\:\text{M}\text{e}\text{a}\text{n}\:\text{S}\text{q}\text{u}\text{a}\text{r}\text{e}\text{d}\:\text{E}\text{r}\text{r}\text{o}\text{r}\:\left(\text{R}\text{M}\text{S}\text{E}\right):\sqrt{\frac{1}{\text{n}}(}{\sum\:}_{\text{i}=1}^{\text{n}}(\widehat{\text{y}\text{i}}-\text{y}\text{i})^{2}$$
$$\:\text{M}\text{e}\text{a}\text{n}\:\text{A}\text{b}\text{s}\text{o}\text{l}\text{u}\text{t}\text{e}\:\text{E}\text{r}\text{r}\text{o}\text{r}\:\left(\text{M}\text{A}\text{E}\right):\frac{1}{n}{\sum\:}_{i=1}^{n}|\widehat{\text{y}\text{i}}-yi|^{2}$$

where \(\:\widehat{\text{y}\text{i}}-\text{y}\text{i}\) represent the predicted and actual glucose values at time index i, respectively, and n denotes the total number of data points evaluated.

Mathematical model for Bg parameter Estimation

The BMM parameters were derived from the insulin-glucose model, and the parameters related to hypoglycemia and hyperglycemia are discussed in the following section.

BMM model

The Bergman Minimal Model (BMM) is a mathematical framework that simplifies the analysis of glucose and insulin dynamics within the human body. The core parameters of the BMM include glucose effectiveness, insulin sensitivity, insulin action, and glucose appearance rate. This paper aims to develop a mathematical model derived from the differential equations of BMM, as outlined by33. The parameters of the BMM model are described in Table 3.

$$\:\text{G}\text{l}\text{u}\text{c}\text{o}\text{s}\text{e}\:\text{D}\text{y}\text{n}\text{a}\text{m}\text{i}\text{c}\text{s}:\:\frac{dG\left(t\right)}{dt}={\:G}_{inn}-{p}_{1}(G\left(t\right)-{G}_{b})-X\left(t\right)G\left(t\right)$$
(1)
$$\:\text{I}\text{n}\text{s}\text{u}\text{l}\text{i}\text{n}\:\text{A}\text{c}\text{t}\text{i}\text{o}\text{n}\:\text{D}\text{y}\text{n}\text{a}\text{m}\text{i}\text{c}\text{s}:\:\frac{dX\left(t\right)}{dt}=\:-{p}_{2}X\left(t\right)+{p}_{3}(\:I\left(t\right)-{I}_{b})$$
(2)
$$\:\mathbf{I}\text{n}\text{s}\text{u}\text{l}\text{i}\text{n}\:\text{D}\text{y}\text{n}\text{a}\text{m}\text{i}\text{c}\text{s}:\:\frac{dI\left(t\right)}{dt}=\:-n\left(\:I\left(t\right)-{I}_{b}\right)+\:\gamma\:\:\left(\:G\left(t\right)-h\right)+U\left(t\right)$$
(3)
Table 3 BMM model parameters for insulin-glucose model.
Full size table

\(\:where\:{p}_{1}\), \(\:{p}_{2}\),\(\:{\:p}_{3}\), h, n, γ parameter values of the BMM model are crucial in modeling hypoglycemic and hyperglycemic condition.

Hypoglycemic model using BMM

For patients experiencing hypoglycemia, the BMM model has been adjusted to account for the absence of insulin infusion. In this modification, the term representing exogenous insulin infusion U(t), has been removed from the original BMM equations.

figure a

Parameters

\(\:n\)

\(\:h\)

\(\:\gamma\:\)

\(\:{p}_{1}\)

\(\:{p}_{2}\)

\(\:{p}_{3}\)

\(\:{G}_{b}\)

\(\:{I}_{b}\)

\(\:{G}_{inn}\)

\(\:U\left(t\right)\)

BMM values for Hypoglycemia model

17

18.04

19.134

1.7

0.5

3.5*10^-8

70

700

16

–

  1. Transfer function of hypoglycemia model from the simulated BMM model: \(\:G\left(s\right)=\frac{13.3}{s+3.905}\)

Hyperglycemia model using BMM

For patients experiencing hyperglycemia, the BMM model has been adapted by eliminating the glucose infusion term Ginn. This modification reflects scenarios where glucagon infusion is focused on managing elevated blood glucose levels.

figure b

Parameters

\(\:n\)

\(\:h\)

\(\:\gamma\:\)

\(\:{p}_{1}\)

\(\:{p}_{2}\)

\(\:{p}_{3}\)

\(\:{G}_{b}\)

\(\:{I}_{b}\)

\(\:{G}_{inn}\)

\(\:U\left(t\right)\)

BMM values for hyperglycemia model

16.5

77

1801

0

2.5

191.6*10^-6

70

700

–

306.5

  1. Transfer function of the hyperglycemia model from the simulated BMM model: \(\:G\left(s\right)=\frac{-10}{30s+13.85}\)

Event-triggered control for dual hormone regulation

Blood glucose regulation in insulin-dependent diabetic patients can be managed either through open-loop control, which involves multiple daily insulin injections, or through closed-loop control using APs. Insulin and glucagon are the primary hormones regulating blood glucose levels. This physiological process has been mathematically modeled, with several control-oriented models providing valuable insights and visualization of this complex system, as demonstrated by34. The SDHAP system leveraged the event-triggered responses to dynamically adjust both insulin and glucagon infusion. By combining the event-triggered response mechanism with the dual-hormone model, the system effectively mimicked the physiological processes of glucose regulation, offering a more refined and adaptive treatment option for T1DM patients.

PI-based event-triggered control

In the context of glucose regulation, a PI (Proportional - Integral) controller could be used to maintain glucose levels within a desired range. The PI controller would adjust the insulin dosing/glucagon dosing based on the difference between the measured glucose level (the output) and the target glucose levels (the reference point).

$$u(t) = {k_p}e(t) + {k_i}\int\limits_0^t {e(t)dt}$$

where u (t) represents the overall control action (insulin/glucose infusion rate) of the PI controller, Kp and Ki represent proportional, integral gain respectively.

MPC-based event-triggered control scheme

A comprehensive overview of the control strategy used in improving glucose regulation was addressed by35. In an AP system, MPC treats glucose levels as the dependent variable and adjusts independent factors such as body mass index, carbohydrate intake, and insulin. This real-time modeling, updating every few minutes, allows the MPC algorithm to address external disturbances like meals and physical activity while compensating for the inherent delay in BG monitoring. The versatility of MPC enables an event-triggered model to handle challenges like inter-patient variability, unannounced disturbances, and safety constraints. By linearizing the glucose-insulin relationship into a state-space form, MPC ensures precise glucose regulation, making it a crucial tool for enhancing the safety and efficacy of SDHAP.

Event-triggered response mechanism

For this study, a detailed explanation of event–triggered response protocol fully discussed by36 was used to manage blood glucose levels and associated vital parameters in the patients. Figure 6 shows the block diagram of the same.

  • Hypoglycemic event (BG < 70 mg/dL): Upon detecting a BG value below 70 mg/dL, a hypoglycemic event is identified, triggering the activation of the glucagon infusion model to rapidly increase the blood glucose levels and prevent the risk associated with severe hypoglycemia.

  • Hyperglycemic event (BG > 180 mg/dL): Upon detecting a BG value exceeding 180 mg/dL, a hyperglycemic event is identified. The system responds by activating the insulin infusion model to lower BG levels.

  • Euglycemic range (BG 70–180 mg/dL): If the BG value remained within the normal range of 70-180 mg/dL, the SDHAP system maintained a monitoring state without initiating any control actions.

Fig. 6
figure 6

Block diagram of event-triggered control SDHAP.

Full size image

Performance metrics

The effectiveness of the proposed controller was evaluated using the following performance metrics:

$$\:\text{I}\text{n}\text{t}\text{e}\text{g}\text{r}\text{a}\text{l}\:\text{S}\text{q}\text{u}\text{a}\text{r}\text{e}\:\text{E}\text{r}\text{r}\text{o}\text{r}\:\left(\text{I}\text{S}\text{E}\right)\:={\int\:}_{0}^{t}{\left|e\left(t\right)\right|}^{2}\:dt$$
$$\:\text{C}\text{o}\text{n}\text{t}\text{r}\text{o}\text{l}\:\text{e}\text{f}\text{f}\text{o}\text{r}\text{t}\:\left(\text{C}\text{E}\right)\:={\int\:}_{0}^{t}{\left|u\left(t\right)\right|}^{2}\:dt$$

PI-based feedforward controller

The block diagram of the FB-FF controller is shown on Fig. 7. The FF controller was designed to reject known disturbances in glucose due to food intake/exercise in hyperglycemia and hypoglycemia conditions. The transfer function of FF controller is given below: -

$$\:{G}_{ff}\left(s\right)=-\frac{{G}_{d}\left(s\right)}{{G}_{p}\left(s\right)}$$

In this work, a static feedback controller with a gain of − 1 was designed to reject the disturbance by predicting the effect of disturbances variables on blood glucose.

Fig. 7
figure 7

Block diagram of FB-FF controller with disturbance.

Full size image

MPC-based feedback/feed-forward controller

Figure 8 depicts an MPC system tailored for blood glucose regulation. The system represents the mathematical model for human glucose-insulin dynamics in the human body, where blood glucose levels are the output signal. The MPC aims to maintain blood glucose at a target level (set point) by calculating an optimal control signal (e.g., insulin or glucagon administration). It considers measured disturbances such as food intake, exercise, and insulin dosing, directly fed into the controller, and unmeasured disturbances managed indirectly through a feedback mechanism. The MPC operates using two main strategies: feedforward control, which proactively adjusts the control signal based on measured disturbances, and feedback control, which continuously corrects deviations by comparing the actual blood glucose levels (output) to the target.

Fig. 8
figure 8

Block diagram for MPC-based FB-FF controller.

Full size image

Results and discussion

Performance of classifier

The T1DiabetesGranada dataset provides extensive data on BG levels, biochemical parameters, and demographic and clinical characteristics of patients. A multi-class SVM model with a “One-vs-Rest” strategy is employed to perform the classification. The glucose levels were labeled into three classes: Hypoglycemia, Normal, and Hyperglycemia. The data is split into 70% for training and 30% for testing, and feature scaling is applied to standardize the input features for SVM. The KNN algorithm is implemented with k = 10, which is determined based on cross-validation to optimize performance. The model works by classifying each test instance based on the majority of its nearest neighbors in the training set. The Euclidean distance metric is used to compute the distances between the glucose levels. Table 4; Fig. 9 show the results of the performance of the classifier model.

Table 4 Performance metrics of the classifier model.
Full size table
Fig. 9
figure 9

Performance metrics using SVM and KNN algorithm.

Full size image

Performance analysis of the predicted model

Table 5 presents the results of the model’s performance in predicting BG levels 15 min, 30 min, and 60 min ahead, both overall and for specific glycemic states. Overall, the model achieved an RMSE of 21.75 ± 3.13 and an MAE of 17.20 ± 4.23. For hypoglycemia, the model accuracy of RMSE value of 21.45 ± 5.98 and MAE of 18.01 ± 2.29. For hyperglycemia, the model accuracy of RMSE was 17.45 ± 3.87 and MAE of 16.15 ± 3.87. Figure 10 shows the BG Forecast for PH – 30 min.

Table 5 Performance analysis of the prediction model.
Full size table
Fig. 10
figure 10

Forecast of BG Prediction when PH = 30 min. (a) ARIMA model. (b) GRU model.

Full size image

Closed loop response of event-triggered SDHAP

The controller parameters of PI and MPC are considered for this under hypoglycemia and hyperglycemia Tables 6 and 7.

Table 6 Parameter values of PI controller under hypoglycemia and hyperglycemia.
Full size table
Table 7 Parameter values of MPC controller under hypoglycemia and hyperglycemia.
Full size table

The simulation was run for 20 h with a blood glucose setpoint of 78 mg/dl. Figure 11a, b show the closed-loop response of SDHAP under hyperglycemia conditions. MPC anticipated the impact of insulin on glucose levels, aiming to avoid exacerbating hyperglycemia. It predicts future glucose levels and adjusts infusion rates to minimize overshoot and stabilize glucose. Hence the control effort taken by MPC was less than PI controller. Meanwhile, the PI Controller provides better performance with a minimum ISE of 5642 by making a larger control effort to bring back the blood glucose level from 300 mg/dl to a normal level.

Fig. 11
figure 11

(a) Closed loop response of SDHAP with PI and MPC controller under hyperglycemia condition and (b) associated variations in insulin.

Full size image

To analyze the performance of SDHAP with PI and MPC, the performance measures such as ISE and CE were calculated and tabulated in Table 8. From Table 8, it was found that MPC outperforms PI with a minimum CE of 2.699e+ 06.

Table 8 Comparison of performance measures of SDHAP under hyperglycemia condition.
Full size table

For hypoglycemia management, dextrose/glucagon was used to raise the glucose levels. Figure 12a, b shows the closed-loop response of SDHAP under hypoglycemia conditions. From the figure, it was found that MPC provides a more optimized response to changes in glucose levels and manages glucagon infusion more effectively. The PI controller adjusts glucagon infusion based on the error between the actual and desired glucose levels.

Fig. 12
figure 12

(a) Closed loop response of SDHAP with PI and MPC controller under hypoglycemia condition and (b) associated variations in glucagon infusion.

Full size image
Table 9 Comparison of performance measures of SDHAP under hypoglycemia condition.
Full size table

Table 9 shows the performance measures of PI and MPC under hypoglycemia conditions. It was observed that MPC outperforms PI with a minimum control of 2648 by compromising ISE.

Response of PI-based FB-FF controller with external disturbances

Hyperglycemia condition

Figure 13a, b show the output response and associated manipulated variables of the PI-based FB-FF controller when exercise was introduced as a disturbance variable at the 10th hr under hyperglycemia conditions. Also, the feedforward controller’s responses to hyperglycemia concerning setpoint were shown. From Fig. 13a, it was found that the blood glucose level started decreasing due to exercise at 10th hr. Consequently, the controller took corrective action to reduce the level of insulin infusion to reject the disturbance as shown in Fig. 13b.

Fig. 13
figure 13

(a) PI Controller response with respect to disturbance under hyperglycemia condition and (b) associated variations in insulin infusion.

Full size image

Hypoglycemia condition

Figure 14a, b show the response of the PI-based FB-FF controller when food intake was introduced as a disturbance variable at 10th hr under hypoglycemia condition. Also, the feedforward controller’s responses of hypoglycemia with respect to setpoint were shown. From Fig. 14a, it was found that the blood glucose level started increasing due to food intake at 10th hr. Consequently, the controller took corrective action to reduce the level of glucagon infusion to reject the disturbance as shown on Fig. 14b.

Fig. 14
figure 14

(a) PI Controller response with respect to disturbance under hypoglycemia conditions and (b) associated variations in glucagon infusion.

Full size image

The performance measures of PI-based FB-FF controller under Hypoglycemia& Hyperglycemia were presented in Table 10. From Table 10, it was noted that the ISE increased due to external disturbance and the controller took corrective action with more control effort to bring back the responses to normal conditions.

Table 10 Performance measures of PI-based FB-FF controller under hypoglycemia and hyperglycemia.
Full size table

Response of MPC-based FB-FF controller with external disturbances

Hyperglycemia condition

The closed-loop responses of the MPC-based FB-FF controller are shown on Fig. 15 and b. It was found that disturbance affects blood glucose slightly as compared to PI controllers under hyperglycemia conditions for the same disturbance magnitude.

Fig. 15
figure 15

(a) MPC controller response with respect to disturbance under hyperglycemia condition and (b) associated variations in insulin infusion.

Full size image

Hypoglycemia condition

Figure 16a,b show the response of the MPC-based FB-FF controller when food intake was introduced as a disturbance variable at 10th hr under hypoglycemia conditions. From Fig. 16a, it was found that the blood glucose level started increasing due to food intake at 10th hr. From Fig. 16a, it was observed that MPC does not perform satisfactory output under regulatory operation with unknown disturbance conditions and provides a large overshoot at 10th hr. Consequently, the controller took corrective action to reduce the level of glucagon infusion to reject the disturbance as shown in Fig. 16b. In addition, as compared to PI-based FB-FF, MPC-based FB-FF took less control effort by compromising ISE and was presented in Table 11.

Fig. 16
figure 16

(a) MPC Controller response with respect to disturbance under hypoglycemia condition and (b) associated variations in Glucagon infusion.

Full size image
Table 11 Performance measures of MPC-based FB-FF under hypoglycemia & hyperglycemia.
Full size table

Hardware implementation

Figure 17a illustrates the schematic diagram of the SDHAP hardware. The hardware implementation of the dual-hormone delivery system shown in Fig. 17b involves a combination of low-cost, portable components integrated to precisely administer insulin/glucagon as needed to maintain blood glucose levels within the 60 mg/dL range. The core components include a NEMA 17 Stepper motor, which allows precise control over syringe actuation, the TB6560 Motor Driver, which provides current amplification and ensures efficient motor control with protection features, and Arduino UNO microcontroller, which governs the control logic and communication between sensors and actuators, a 12 V DC power supply for stable power delivery and a 10 ml syringe for hormone administration. The system is programmed using MATLAB and Arduino IDE, enabling seamless coordination between prediction algorithms and mechanical actuation.

Fig. 17
figure 17

(a) Schematic implementation of the SDHAP hardware. (b) Hardware implementation of the SDHAP delivery system.

Full size image

Table 12 below highlights the precision of the syringe ejection mechanism based on the step resolution of the stepper motor. The stepping angle of the motor controls how much the syringe plunger is pushed, which in turn determines the volume of insulin or glucagon delivered. For example, a full 360° rotation injects 1.5 ml, and finer step resolutions like 1/8 or 1/6 allow for very small, precise doses based on patient needs.

Table 12 Calibration of syringe ejection of liquid with respect to stepping of motor.
Full size table

Conclusion and challenges

In this paper, SDHAP has been designed to automatically detect, predict and control blood glucose by infusing insulin/glucagon using event-triggered control mechanisms to more effectively regulate blood glucose levels in personalized treatment for diabetic patients. To address the major issues in the current existing technique, which is the slow dynamics in glucose sensing, we have proposed a machine learning model-based prediction and delayed insulin absorption with MPC. The combination offers enhanced control and responsiveness in both hypoglycemic and hyperglycemic conditions. From the event- triggered SDHAP closed-loop performances, the following conclusions were made: -.

  • From the classification results, it was found that SVM provides higher accuracy for hyperglycemia and hypoglycemia detection with an accuracy of 90.23% and 88.58% respectively.

  • From the prediction results, GRU model provides better RMSE and MAE compared with for PH-15 min, 30 min and 60 min compared with ARIMA model.

  • Closed loop performance comparison results of PI and MPC controller for hypoglycemia and hyperglycemia show that MPC provides better performance as compared to PI.

  • Event-triggered mechanism results show that the computation of the proposed algorithm is less than that of the controller with continuous control action (include about computational load and battery).

Challenges: While SDHAP shows promising results, several practical and technical challenges remain.

  1. 1.

    Dosing Complexity: Incorporating two hormones requires the design of more sophisticated and individualized dosing algorithms. These algorithms must dynamically adjust to varying physiological conditions, which increases both the algorithmic complexity and the need for frequent calibration or retraining.

  2. 2.

    Clinical Validation: Though promising in simulation, the proposed system requires extensive validation in pre-clinical and clinical settings to account for inter-individual variability, sensor noise and environmental factors.

  3. 3.

    Cost and Integration: The inclusion of multiple hormones and advanced controllers raises concerns regarding cost, device miniaturization, and battery life. Integration into compact and user-friendly hardware remains a significant barrier to clinical translation.

Future directions: Building on the findings of this study, future research will focus on several key directions.

  1. 1.

    Non-linear Control Algorithms: To better manage the complex and nonlinear dynamics of glucose-insulin-glucagon interactions, future implementation will explore advanced non-linear control techniques. These controllers are expected to enhance system robustness against disturbances and parameter uncertainties.

  2. 2.

    Hardware Implementation: Real-time development of the SDHAP will be pursued through implementation on embedded platforms such as FPGAs. Emphasis will be placed on minimizing energy consumption, latency, and system size for wearable integration.

  3. 3.

    Pre-clinical Studies: The algorithms will be tested on validated in silico platforms like the UVA/Padova T1D Simulator a potentially extended toward human clinical trials.

  4. 4.

    User Personalization: Future versions of the SDHAP will integrate real-time physiological feedback and user-specific learning mechanisms to enable continuous personalization of hormone delivery, making the system adaptive to lifestyle changes, meal patterns, and stress levels.