Introduction

Rising concerns about global warming, driven by harmful greenhouse gas emissions, have increased the focus on clean energy research. Natural gas, primarily consisting of methane, is an affordable and environmentally friendly fossil fuel. Methane (CH4), the primary component of natural gas, is viewed as a significant alternative to petroleum1. Nonetheless, separating methane (CH4) from nitrogen (N2) is the most challenging and crucial step in enriching low-concentration coal bed methane (CBM), as both components exhibit similar kinetic diameters (0.381 nm for methane and 0.364 nm for nitrogen) and their critical temperatures are quite low. Nevertheless, numerous natural gas reserves hold high levels of nitrogen, necessitating upgrading to meet pipeline standards, which require a nitrogen concentration below 4%2. The upgrading of natural gas is closely related to the separation of olefins and paraffins, which stands out as one of the most urgent industrial challenges that could have significant economic implications3. The process of separating methane from nitrogen is also important in enhanced oil recovery, where N2 is introduced into the reservoir and subsequently extracted as part of the gas stream together with other petroleum gases. In addition, separating methane from nitrogen is essential for upgrading landfill gas (LFG), coal bed gas, and natural gas to attain a profitable energy content for methane.

As a result, there is a need for advancing technologies for gas separation and purification. The recovery of nitrogen is currently a crucial challenge across multiple fields, including energy, environmental, and medical applications. Examples include its role in oil extraction, air separation processes, and the generation of hydrogen from industrial gases produced in the steel manufacturing sector4.

Various technologies have been investigated for the separation and purification of coal-based methane. Nitrogen can be extracted from methane using cryogenic distillation, which is an expensive and energy-demanding process. The application of adsorption processes and membrane technologies presents a viable alternative for selectively capturing N2 in a cost-effective and energy-efficient manner2,5.

Adsorbents are crucial for the effective separation of CH4 and N2 in PSA (Pressure Swing Adsorption) technology6. The process of separation happens as a result of differences in molecular weight, dipole, shape, polarity, and quadrupole moments, which lead to some molecules being more tightly bound to the adsorbent surface, or due to the pores being excessively small to accommodate larger molecules. Materials with porous structures that operate on the principle of physisorption may be suitable for separating and purifying these gases. Currently, the most commonly used adsorbents for the separation of CH4 and N2 gases include activated carbon, carbon molecular sieves, and zeolite molecular sieves. For instance, titanium silicate ETS-47 stands out as one of the few porous materials capable of efficiently separating nitrogen from methane through kinetic mechanisms, thanks to the slight size difference between the two molecules (3.8 Å for CH4 compared to 3.64 Å for N2)2. Creating a porous material that effectively balances high equilibrium preference for N2 compared to CH4, substantial N2 adsorption capacity, and ease of regeneration poses a significant challenge for separation technologies. According to studies on the adsorption characteristics of CH4–N2 binary gas mixtures8,9, the ideal adsorbent must exhibit both high structural selectivity and excellent thermal stability.

Among various porous materials, metal-organic frameworks (MOFs) have garnered substantial focus due to their extensive design flexibility and high porosity9,10,11. These frameworks are a relatively recent category of multifunctional crystalline materials, created by the self-assembly of metal ions or clusters with organic ligands. Designing porous MOFs with unsaturated transition metal sites that strongly bind N2 provides a promising route to achieving N2-selective capture at equilibrium due to the easy control of both the reactivity and the concentration of these sites. Due to their remarkable modular design, wide-ranging and captivating topologies, and tunable pore properties, MOFs have been extensively researched across numerous fields, including gas storage12, separation13, catalysis14, photochemistry15, chemical sensing16, and others.

Furthermore, novel MOF materials featuring high methane capacity and exceptional CH4/N2 adsorption selectivity have been developed in recent years. For instance, Zhou et al.17 developed an innovative molecular sieve known as MAMS-1, which is characterized by its flexible mesh design that utilizes the molecular door effect. This unique structure enables the molecular door to adjust its position in response to varying temperatures. At a low temperature of 113 K, this sieve displayed a kinetic selectivity ratio for N2 over CH4 greater than 3. In addition, Sumer et al.18 conducted molecular simulations to study the adsorption and diffusion of CH4/N2 mixtures across 102 different MOFs, assessing their performance for both adsorption-based and membrane-based separations. Among these, three MOFs-BERGAI01, PEQHOK, and GUSLUC- demonstrated the highest selectivity for adsorption.

Conversely, laboratory experiments tend to be costly, labor-intensive, and time- intensive.

Alternatively, it is strongly advised to create more comprehensive and robust models. One could posit that soft computing techniques may yield reliable solutions in comparison to traditional methods19. Machine learning (ML) methods are highly effective for modeling the mathematical connections between variables and objectives within extremely intricate datasets20,21,22,23,24,25,26. Numerous advanced models can be utilized to derive useful solutions for various issues without the need for experimental investigations. Several studies have investigated the application of artificial intelligence (AI) techniques in modeling gas adsorption and uptake. For instance, Khosrowshahi examined the role of natural product-derived porous carbons in CO2 capture as a strategy for climate change mitigation27. Rahimi employed support vector machines and genetic algorithms to predict and optimize hydrogen and CO2 concentrations during biomass steam gasification using a calcium oxide adsorbent28. Similarly, Wang et al. utilized GRNN and XGBoost models to accurately predict hydrogen adsorption in coal, highlighting the potential of machine learning to enhance hydrogen storage methods29. Recently, there has been a surge in research on gas storage within MOFs, reflecting the increasing interest in advanced materials for energy applications. Machine learning models, particularly XGBoost, have been used effectively to forecast hydrogen wettability in geological storage reservoirs, showing high accuracy (R2 = 0.941) and strong correlation with real data30.

In the context of CO2 adsorption in MOFs, Dashti et al.31 introduced several ML models, identifying the radial basis function (RBF) as the most effective approach. Their study utilized a dataset comprising 506 data points collected from the literature, covering information on 13 different MOFs. Subsequently, Li et al.32 employed a dataset with 348 data points, achieving a correlation coefficient of 0.9 using their Random Forest (RF) model for CO₂ adsorption prediction. In addition, Larestani et al.33 applied white-box ML algorithms, namely group method of data handling (GMDH), gene expression programming (GEP), and genetic programming (GP), to develop accurate models for assessing the CO2 adsorption capacity of MOFs. Their models achieved a root mean square error (RMSE) of 2.77 and a coefficient of determination (R2) of 0.8496. Furthermore, Naghizadeh et al.34 employed various ML techniques, such as convolutional neural network (CNN), deep neural network (DNN), and Gaussian process regression with Rational Quadratic Kernel (GPR-RQ), to model the hydrogen storage capacity in MOFs. Notably, their results highlighted the outstanding performance of the GPR-RQ model, yielding an impressive R2 value of 0.99. Table 1 summarizes recent studies in gas adsorption modeling using numerous machine learning techniques. This table outlines the key contributions, input parameters, R2 values, applied machine learning models, targeted gases, and material types used in each study.

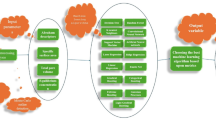
Based on the available evidence, previous studies have not employed innovative models to predict the efficiency of MOFs in storing N2 gas. The primary contribution and novelty of this study lie in the utilization of innovative methods to predict the N2 uptake under varying operational circumstances. Another notable aspect of this study is the collection of a comprehensive dataset consisting of 3246 data points, offering detailed information on N2 adsorption in various MOFs (65 types) under diverse conditions. This approach represents a significant step forward in integrating machine learning with MOF research, opening new avenues for optimizing MOF properties and enhancing their application in N2 storage technologies. The dataset encompasses essential factors such as pore volume, surface area, pressure, and temperature. Subsequently, advanced and robust techniques such as Categorical Boosting (CatBoost), Extreme gradient boosting (XGBoost), DNN, and GPR-RQ are utilized to forecast the efficiency of N2 uptake by the MOFs. Subsequently, the effectiveness of the models is assessed using a range of statistical and visual evaluations. Moreover, additional trend examinations are carried out to validate the most well-established model. Evaluating feature importance is essential for comprehending how input variables affect the prediction of the target variable in ML applications. Thus, the SHAP (Shapley Additive explanations) method is applied to investigate the intricate relationships between features and their importance. Ultimately, the Leverage method is applied to appraise the reliability and applicability of the most accurate predictive model. A comprehensive illustration of the technical procedure is presented in Fig. 1.

Table 1 Overview of key literature on ML applications in gas adsorption.
Full size table
Fig. 1
figure 1

A diagrammatic representation of this research.

Full size image

Dataset collecting

As mentioned previously, this study aims to predict N2 storage in MOFs using numerous ML algorithms. For this project, a comprehensive dataset was compiled, comprising 3246 real data points with pressures reaching up to 1054.7 bar and temperatures up to 473 K, sourced from previous studies46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68. Before producing the final target, an impeccable dataset, crucial corrective steps were undertaken during the data pre-processing phase, including data cleaning and integration, to facilitate the creation of more accurate predictive models. The dataset was then grouped into two separate sets: one for training, encompassing 2596 data points, and one for testing, with 650 data points for all algorithms. All models were evaluated on the same independent test set, separate from training and validation data. Performance metrics (R2, RMSE, MAE) reported are based exclusively on this test set to ensure unbiased comparison.

The models used input parameters such as pore volume and surface area of the various MOFs, as well as temperature and pressure. Comprehensive explanations of the dataset are provided in Tables 2 and 3. In addition, Fig. 2 demonstrates the Box plots representing input and output variables.

Table 2 Comprehensive details about the assembled database.
Full size table
Table 3 The statistical methods used to analyze the data set.
Full size table
Fig. 2
figure 2

Box plots representing input and output variables.

Full size image

Modeling techniques

Categorical boosting (CatBoost)

The CatBoost algorithm, a recent development in gradient boosting decision trees (GBDT), relies heavily on the integration of categorical columns, which is a key aspect of its modeling process. This algorithm is specially optimized for structured data and performs exceptionally well in handling categorical features69. In addition, it utilizes oblivious decision trees, a type characterized by level-wise growth. This change involves using a vectorized representation of the tree, allowing it to be tested in a brief period. Various processing techniques are commonly employed in the CatBoost model. Two key techniques include target-based statistics and one_hot_max_size (OHMS). In a dynamically expanding tree, a grid search is necessary for each branch to identify the most significant changes applied to each feature of the CatBoost method69. Understanding CatBoost implementation fundamentally relies on distinguishing between testing and training datasets70. An essential benefit of the CatBoost model is its use of random permutations to predict leaf values when determining the tree structure, effectively mitigating overfitting. When analyzing categorical features, the CatBoost algorithm leverages the entire training dataset for its learning process. For each sample, numerical transformations of features are executed, with the target value calculated initially. Next, the sample’s weight and priority are factored into the process69,71. The network’s predicted output is derived using Eq. (1)69:

$$T=H({x_i})=\sum\nolimits_{{n=1}}^{N} {{c_n}{1_{\left\{ {x \in {R_n}} \right\}}}}$$
(1)

where Rn represents the disjoint region associated with the tree leaves, xi serves as the explanatory variable, and H denotes the decision tree function. As mentioned above, CatBoost mitigates overfitting by utilizing ordered boosting, regularization, and early termination. This ensures the efficient management of categorical features and enhances model performance. The algorithm’s flowchart representation is shown in Fig. 3.

Fig. 3
figure 3

A graphical depiction of the flowchart for the CatBoost algorithm.

Full size image

Extreme gradient boosting (XGBoost)

XGBoost, an open-source framework, is a prominent tool in ML that delivers an efficient, versatile, and portable approach to implementing gradient-boosted decision trees. XGBoost is highly regarded for its outstanding performance, scalability, and ability to handle diverse data types and tasks, including regression, classification, ranking, and predictive modeling challenges. In other words, in tree-based ensemble methods, a group of classification and regression trees (CARTs) is used to align with the training data by minimizing a regularized objective function. To elaborate on the structure of a Classification and Regression Tree (CART), it is composed of (I) a root node, (II) internal nodes, and (III) leaf nodes, as shown in Fig. 4. Based on the binary splitting approach, the initial node node, which contains the total dataset, is split into internal nodes, with the leaf nodes representing the concluding classes72.

Fig. 4
figure 4

A flowchart of the XGBoost algorithm.

Full size image

Deep neural network (DNN)

DNNs represent a crucial subset of artificial intelligence technology that leverages a multi-layer architecture to learn and represent complex features. The complexity of interconnected neurons somewhat mirrors the intricacy of biological neurons in the brain73. The presence of multiple hidden layers allows for the combination of components from earlier layers, enabling the creation of networks that can handle complex data while utilizing fewer neurons74. Over the past decade, DNN frameworks have enabled significant achievements across various fields. Unlike traditional neural networks, DNNs feature non-linear hidden layers that are capable of learning intricate non-linear connections between input data and target variables. Figure 5 illustrates the structure of a DNN algorithm. The input variable is processed through multiple layers to generate the output. The output from each layer acts as the input for the subsequent layer, where an activation function, incorporating weights and biases, adjusts the input in each connected neuron to calculate the result for the current layer. These activation functions empower neurons to model non-linear relationships, enabling neural networks to capture intricate interactions between variables.

Fig. 5
figure 5

A flowchart of the DNN algorithm.

Full size image

Gaussian process regression (GPR)

The GP model has emerged as a popular choice for tackling challenges in non-linear classification and regression due to its widespread application75. The Gaussian process refers to a set of random variables, such that any finite group adheres to a Gaussian distribution, serving as a natural generalization76. In the last ten years, neural networks have rapidly advanced in addressing complex issues in petroleum geology and reservoir engineering. However, their flexibility makes them prone to overfitting, which can be mitigated by weight regularization, though tuning its parameters remains challenging. An increasingly popular mathematical technique, the Bayesian Network (BN), also known as Bayes Net, is a probabilistic framework that has garnered significant attention for addressing the complexity as mentioned above 77. GPR is a powerful kernel-based framework designed to learn hidden relationships among numerous variables in the training dataset, ensuring it is particularly effective for addressing complex, non-linear prediction problems78. In every GPR framework, the GP employs a non-linear multivariate Gaussian function to model the data, as shown in Eq. (2)79:

$${f_x}({x_1},{x_2},...{x_k})=\frac{{\exp \left( {\frac{{ - 1}}{2}(x - \mu ){\Sigma ^{ - 1}}(x - \mu )} \right)}}{{\sqrt {{{(2\pi )}^k}\left| \Sigma \right|} }}$$
(2)

The vector \(x=({x_1},{x_2},...,{x_k})\) represents the input variables, \(\Sigma\)signifies convergence, and \(\mu\)represents the mean of the dataset. Given randomly chosen training and testing data, the GPR process yields an output value as described below79:

$$y=f(x) \approx GP(m(x),k(x,x^{\prime})$$
(3)
$$m(x)=E(f(x))$$
(4)
$$k(x,x^{\prime})=\operatorname{cov} (f(x),f(x^{\prime}))=E\left\{ {(f(x) - m(x)),(f(x^{\prime}) - m(x^{\prime}))} \right\}$$
(5)

In the given equations, y represents the desired output, while \(k(x,x^{\prime})\)functions as the convergence operator, and m(x) serves as the mean function. GPR is easy to implement, automatically adapts for improved variable prediction, and offers flexibility by accommodating non-parametric inferences. An essential characteristic of any GPR method is its ability to mitigate overfitting80. Additionally, GPR techniques can interpret the predictive distribution associated with the test dataset81.

Results and discussion

Intelligent schemes

Based on the provided information, the models were designed with four input parameters and structured to generate the N2 uptake in MOFs as the target output. These methods were formulated utilizing a comprehensive dataset comprising 3246 experimental observations. Consequently, the intelligent models were trained using 2596 data points and later evaluated against the remaining 650 data points. Subsequently, the errors in the developed models are examined through various approaches, including statistical and visual analyses. Notably, K-fold cross-validation was implemented to mitigate overfitting and ensure model validation. It is crucial to highlight that determining the ideal features and values for the necessary hyperparameters of the previously mentioned models is a key aspect of the model development process. To guarantee strong performance and reduce the risk of overfitting, all machine learning models developed in this work underwent methodical hyperparameter tuning. Each method employed a grid search approach combined with five-fold cross-validation. The mean squared error (MSE) on the validation data was minimized. Early stopping was incorporated into the DNNs to halt training upon reaching a performance plateau on the validation set. Early stopping rounds, as well as subsample and depth constraints, were used to regularize the XGBoost and CatBoost models. For the GPR-RQ, kernel parameters were optimized using the fmin_l_bfgs_b algorithm. The optimal hyperparameters identified in this study are available in Table 4.

Table 4 The optimal hyperparameters of ML algorithms.
Full size table

Statistical model assessment

After constructing the models, the effectiveness and exactness of each algorithm can be assessed through various standard statistical measures. In the present work, root mean square error (RMSE), standard deviation (SD), mean absolute error (MAE), correlation coefficient (R2), and mean bias error (MBE) were applied to measure each algorithm’s effectiveness in predicting N2 uptake and to benchmark its performance against other models. The aforementioned parameters are outlined below22:

$$MAE = \frac{1}{N}\sum\limits_{{i = 1}}^{N} {\left| {Z_{i}^{{\exp }} - Z_{i}^{{cal}} } \right|}$$
(6)
$$RMSE = \sqrt {\frac{{\sum\nolimits_{{i = 1}}^{N} {(Z_{i}^{{\exp }} - Z_{i}^{{cal}} )^{2} } }}{N}}$$
(7)
$$SD = \sqrt {\frac{1}{{N - 1}}\sum\limits_{{i = 1}}^{N} {(\frac{{Z_{i}^{{\exp }} - Z_{i}^{{cal}} }}{{Z_{i}^{{\exp }} }}} } )^{2}$$
(8)
$$MBE = \frac{1}{N}\sum\limits_{{i = 1}}^{N} {(Z_{i}^{{exp}} - Z_{i}^{{cal }} )}$$
(9)
$$R^{2} = 1 - \frac{{\sum\nolimits_{{i = 1}}^{N} {(Z_{i}^{{\exp }} - Z_{i}^{{cal}} )^{2} } }}{{\sum\nolimits_{{i = 1}}^{N} {(Z_{i}^{{\exp }} - \overline{{Z_{i} }} )^{2} } }}$$
(10)

Here, \(Z_{i}^{{exp}}\) and \(Z_{i}^{{cal}}\) denote the ith actual and forecasted N2 storage values, respectively. \({\bar {Z}_i}\)signifies the mean of the observed data, with N indicating the dataset’s size. The labels ‘cal’ and ‘exp’ as superscripts indicate the calculated and experimental data points, respectively. Table 5 provides a detailed overview of the statistical error values for the models developed in this study, broken down into three sets: training, testing, and overall. As indicated by this table, all constructed models demonstrated predictions that were closely aligned with the observed values. This table clearly shows that the XGBoost model exhibits the highest R2 and the lowest RMSE (R2 = 0.9984, RMSE = 0.6941) compared to all other advanced models established in this study. To evaluate whether there was a meaningful statistical difference between the forecasted and real values, a paired t-test was performed for the XGBoost model. The analysis revealed no significant difference (t(3245) = 0.146, p = 0.884), exhibiting strong alignment with empirical observations. Moreover, the Pearson correlation coefficient between the anticipated and real values was calculated to be 0.999, demonstrating a robust linear association.

The GPR-RQ and CatBoost models followed, achieving (R2 = 0.9984, RMSE = 0.6941) and (R2 = 0.9968,RMSE = 0.8607), respectively. In comparison to the other three models, the DNN model demonstrates a lower level of prediction accuracy. The DNN model, despite being ranked fourth in accuracy, demonstrates a satisfactory level of precision.

Table 5 The evaluation of the presented models through statistical analysis.
Full size table

Graphical model assessment

In the cross plot, the model’s forecasted data points are plotted against the experimental data along a 45-degree line (unit-slope line) that intersects the origin of the diagram. The reliability and validity of the developed models are assessed by the extent to which the data points cluster along the unit-slope line. Figure 6 displays the cross plots for all four smart models created in this study. According to Fig. 6a–d, all four models designed to predict N2 uptake are deemed acceptable and valid, as they show a satisfactory alignment between the predicted and observed values. Besides, it is evident that the estimations from XGBoost and GPR-RQ models, closely match the actual target values.

Fig. 6
figure 6

The cross-plots of the proposed models for forecasting N2 uptake.

Full size image

As an additional validation approach, Fig. 7 presents the error distribution plots for the established algorithms, depicting the residual errors between each predicted value and its corresponding actual value. In this plot, the smaller the deviation of points from the zero-error line, the more reliable the model is considered to be. The results suggest that all advanced approaches discussed in this study are reliable and credible, as the calculated error values are predominantly clustered around the zero-error line. This figure illustrates that XGBoost and GPR-RQ models demonstrate promising results, featuring minimal errors and an absence of a discernible error trend. However, the XGBoost model exhibits a more concentrated grouping of points near the zero-error line, indicating reduced residual errors and greater accuracy. Depending on the predictions from the XGBoost model (Fig. 7a), it is clear that the data points fall within a narrow error range (between − 7.63 and 9.86).

Fig. 7
figure 7

The error distribution compared to experimental N2 uptake for the suggested models.

Full size image

Another graphical method to assess the models’ predictive performance is to plot a cumulative frequency curve. This involves plotting the cumulative frequency of data points against the absolute error values obtained from the models, as shown in Fig. 8. According to this diagram, over 90% of the data points can be forecasted by the XGBoost and GPR-RQ models with an absolute error of around 0.30. Consequently, this graph demonstrates that these models accurately predict N2 storage in MOFs.

Fig. 8
figure 8

The cumulative frequency plot of all established models.

Full size image

After that, Fig. 9 illustrates the Taylor plots for the models analyzed in this research. This plot demonstrates the correlation between the predicted and observed behaviors by integrating three statistical metrics: SD, RMSE, and Pearson’s correlation coefficient (r). The SD is associated with the distance from the origin, while RMSE indicates the distance to the observed data points, and r represents the azimuthal angle, respectively.

Based on Fig. 9, the point associated with the suggested XGBoost model is closest to the observed point. This indicates the superior performance of this model across all models analyzed in this research, despite the fact that the accuracy of other models is comparable and satisfactory.

Fig. 9
figure 9

Taylor’s diagram illustrates the comparison among four intelligent models.

Full size image

Group error analysis

This procedure starts by categorizing independent variables into distinct categories based on the extent of their changes. The RMSE values for the target variable are later calculated for each range and illustrated in a chart. Figure 10 illustrates group-error plots for predicting N2 uptake in MOFs using four proposed models. These plots are based on four independent variables: temperature (K), pressure(bar), pore volume (cm3/g), and surface area (m2/g).

As shown in Fig. 10a, all models exhibit the highest error within the surface area range of 4704–6240 m2/g. In addition, XGBoost outperforms with lower RMSE in the range of 3171–4704 as a superior model. Additionally, the group error diagram based on pressure indicates that the systems have the highest deviation in the range of 0.00084–100 bar, while the lowest error is observed between 100 and 1054.7 bar. Furthermore, the XGBoost model consistently demonstrates lower error values across all pore volume ranges.

As illustrated in Fig. 10a, for all models, the highest error occurs in the surface area range of 4704–6240 m2/g. In addition, the group error diagram based on pressure in Fig. 10b indicates that the systems exhibit the least deviation within the range of 0.00084–100 bar, while the highest error occurs in the range of 100–1054.7 bar. For Fig. 10c, the constrained XGBoost model demonstrated lower error values across all pore volume ranges in comparison to other models. Additionally, as shown in Fig. 10d, the suggested XGBoost model showcases high accuracy for temperatures within the range of 209 to 473 K, compared to temperatures below 209 K.

Fig. 10
figure 10figure 10

Error graph comparison for multiple models over varying intervals of independent variables, including (a) surface area, (b) pressure, (c) pore volume, and (d) temperature.

Full size image

Shapely explanation plot (SHAP)

SHAP Analysis, developed by Lundberg and Lee82, is an extensive strategy for interpreting ML models that introduces the idea of Shapley additive explanations. Rooted in game theory, SHAP enables detailed insight into model behavior by quantifying the influence of each variable on the forecasting results. In simple terms, the Shapley value is a procedure for illustrating the comparative influence and impact of individual input features in generating the final output. It’s worth noting that the XGBoost model demonstrates superior accuracy in the current context when compared to the other models. As a result, XGBoost has been utilized for performing SHAP analysis. Figure 11 provides a comprehensive visualization of the SHAP analysis results. First, Fig. 11a illustrates the significance of input variables in understanding how the attributed features affect the predictions of the target variable. The results presented here are derived by averaging the Shapley values across the entire dataset. This figure indicates the mean absolute influence of each variable, emphasizing temperature as the most impactful parameter in predicting N2 uptake in MOFs. In addition, Fig. 11b shows summary plots that illustrate the relationship of the respective variable and the arrangement of SHAP values for a specific feature. In this plot, the y-axis displays the input variables used in the analysis, arranged by their significance, while the x-axis represents the corresponding SHAP values. The color of the dots reflects their size, ranging from small to large, with each dot representing a sample from the database. The x-axis shows the level of model output attributed to SHAP values for each feature, corresponding to changes in feature magnitude. Additionally, it should be noted that the lower section of the plot represents the variables with the least effect, while the upper section highlights the variables with the greatest impact. Based on this figure, temperature exerts a considerable influence, whereas pore volume has a minimal effect on the output. It can be concluded that summary plots play a crucial role in SHAP analysis, as they not only display the prioritization of input variables based on their significance but also illustrate their correlation with the target variable. In fact, in this figure, the gradient of colors spans from red to blue, where deeper red hues signify larger eigenvalues and deeper blue hues signify smaller eigenvalues. A wider range of colors corresponds to a more prominent impact of the characteristic, signaling its heightened significance in shaping the model’s forecasts.

Fig. 11
figure 11

Global insights into the LightGBM algorithm using SHAP values: (a) SHAP feature significance; and (b) SHAP summary plot.

Full size image

Furthermore, to deepen the analysis of how each variable influences the target, Shapley values were evaluated. Figure 12 presents the Shapley values associated with the model’s input factors considered in this research, namely surface area, pressure, temperature, and pore volume. As depicted in Fig. 12, the Shapley values for the surface area and pore volume rise as the corresponding feature values increase, implying that higher feature values are associated with elevated N2 uptake in MOFs. However, for temperature, the impact is negative, and its trend declines as the feature value increases.

Fig. 12
figure 12

Shapley value dependency plot for the selected input parameters; (a) Surface area, (b) pressure, (c) temperature, and (d) pore volume.

Full size image

Model trend analysis

To verify the forecasting ability of the created model in aligning with the anticipated physical trends of N2 uptake with changes in pressure, the N2 uptake forecasts produced by the XGBoost model are presented relative to pressure. Fig. 13 depicts how the N2 adsorption varies as pressure increases. The results are shown for three MOFs— Bio-MOF1 (surface area = 1680, pore volume = 0.75), Bio-MOF1@TEA (surface area = 1220, pore volume = 0.55), and Bio-MOF1@TMA (surface area = 1460, pore volume = 0.65)— both experimentally and via modeling. As shown in this figure, increasing pressure raises gas density, enhancing molecular collisions with MOF surfaces and increasing adsorption. This observed behavior closely matches the predictions made by the XGBoost model. This strong alignment showcases the model’s capability to precisely depict how pressure the N2 uptake.

Fig. 13
figure 13

The impact of pressure on the N2 uptake: empirical data and predictions from the XGBoost model.

Full size image

Outlier identification of the XGBoost model

Detecting outliers using the leverage approach is an important method for identifying anomalous data points that might differ notably from the rest of the dataset. A further goal of the previously discussed approach is to assess the validity and reliability of the database being modeled83,84. Within this framework, the method utilizes the values R, indicating standardized residuals, along with H, denoting the hat matrix. These values are derived from the observed and forecasted outputs of the XGBoost framework. All Hat indexes are determined using the Hat matrix (H) as follows85.

$$H=X{({X^T}X)^{ - 1}}{X^T}$$
(11)

Here, X denotes a matrix of size (p × q), where p corresponds to the number of data samples and q refers to the model’s input parameters. The matrix T signifies the transpose of X. Besides, the warning leverage value (H*) and standardized residuals are computed as below86:

$${H^*}=\frac{{3 \times (q+1)}}{p}$$
(12)
$$S{R_i}=\frac{{{z_i}}}{{{{(MSE(1 - {H_{ii}}))}^{0.5}}}}$$
(13)

Data points with a hat value between 0 and H*, and a standardized residual SR ranging from − 3 to 3, are considered valid. Conversely, data with SR values exceeding 3 or falling below − 3 are regarded as suspected data. As displayed in Fig. 14, most data points are located within the range of 0 ≤ H ≤ H* and − 3 ≤ R ≤ 3. As a result, only 2.1% of the data points were detected as falling beyond the model’s designed range, which is negligible given the large volume of data points utilized in constructing the model. Therefore, the findings of this method show that the XGBoost approach developed exhibits strong reliability and accuracy in predicting N2 uptake.

Fig. 14
figure 14

Detection of outliers in the executed XGBoost model.

Full size image

Conclusions

In this study, four advanced machine learning models— CatBoost, XGBoost, Deep Neural Network (DNN), and Gaussian Process Regression (GPR)— were developed to predict nitrogen (N2) uptake in a range of Metal-Organic Frameworks (MOFs). A curated dataset comprising over 3246 experimental entries from 65 distinct MOFs was used, incorporating four key input features: pore volume, surface area, pressure, and temperature.

The findings indicate that XGBoost consistently Surpasses the other models in terms of predictive accuracy, achieving the highest (R2 = 0.9984) and the lowest (RMSE = 0.6085). The comparative analysis ranks model performance as follows: XGBoost > GPR-RQ > CatBoost > DNN. SHAP analysis revealed temperature as the most influential factor in predicting N₂ adsorption, whereas pore volume had the least impact. Moreover, trend analysis confirmed that the XGBoost model accurately captures the physical relationship between pressure and nitrogen uptake, where increased pressure leads to greater adsorption due to enhanced gas density and intermolecular interactions. Finally, leverage analysis using the William plot indicated that approximately 94% of the dataset is located within the model’s applicability domain, confirming the reliability and robustness of the established models.

These findings highlight the potential of machine learning approaches particularly XGBoost, for accurately modeling gas adsorption behavior in porous materials and supporting the design of next-generation MOFs for efficient gas purification processes.