Numerical modeling and simulation of stochastic fractional order model for COVID-19 infection in Mittag–Leffler kernel

Abstract

In this work, we develop and analyze a fractional-order stochastic model for COVID-19 transmission, incorporating the effects of vaccination. The model is formulated using the Atangana–Baleanu fractional derivative in the Caputo sense, which captures memory and hereditary properties of disease transmission more accurately than classical derivatives. We first examine the positivity and boundedness of the deterministic fractional model and determine its equilibrium points. The model is then extended to a fractional stochastic differential equation (FSDE) to account for random fluctuations and uncertainties in disease dynamics. We establish the existence and uniqueness of solutions for the FSDE model using stochastic analysis techniques. To numerically solve the FSDE, we develop a novel numerical scheme that accommodates the non-local nature of the Atangana–Baleanu derivative. The real data of COVID-19 in Pakistan have been used to estimate the model parameters. Numerical simulations are presented for both the deterministic fractional model and its stochastic counterpart. These simulations illustrate the impact of the fractional-order parameter on disease dynamics, showing how different orders influence the rate of infection and convergence to equilibrium. Additionally, we analyze scenarios under varying parameter values to explore conditions for disease elimination, highlighting the role of vaccination and stochasticity. Our findings demonstrate that fractional stochastic modeling provides deeper understanding of COVID-19 transmission dynamics and can be a valuable tool in assessing control strategies under uncertainty. The originality of this work stems from the integration of Atangana–Baleanu fractional derivatives with stochastic modeling, supported by a new numerical solution method providing a more realistic and flexible approach to modeling COVID-19 transmission under uncertainty.

Introduction

The COVID-19 infection shook the world economy and human health. A lot of infected cases have been reported around the globe, and at the same time, a high number of deaths have been reported throughout the world. As the infection continues to spread within the human population, different variants of COVID-19 have been reported in many parts of the world, where one variant is found to be more severe than the other. Researchers and scientists are always exploring vaccine development to combat coronavirus disease. Different types of COVID-19 vaccines have been developed with different names for the disease curtail. After the vaccination of the people in each country, the number of infected people dropped day by day, and after some time, the cases have almost reached to minimum.

The COVID-19 infection has been identified in nearly all parts of the world, resulting in a significant number of cases and fatalities. Various mathematical models or other theoretical approaches are presented to highlight the COVID-19 issue^1,2,3,4,5. For example, the authors in¹ considered the COVID-19 model in fractional derivative using the impact of public health awareness. In², the authors considered the COVID-19 model in fractional derivatives by considering the Atangana-Baleanu derivative concept. The impact of public sentiments on the modeling of COVID-19 infection dynamics is described in³. The COVID-19 model employed to investigate the early reported cases using a fractional-order approach is presented in⁴, while the COVID-19 model with optimal control interventions based on real data is given in⁵. The literature regarding the mathematical models that were developed to find out the disease propagation, the early control of the disease, and to determine their basic reproduction number. Some simple mathematical models were also presented to determine the basic reproduction and some statistical approaches were used to show the possible details of the infected cases and the future trend of the disease. One important thing that we saw in the COVID-19 cases was the peak of the infected cases, where one can determine the peak of the cases using statistical or mathematical modeling approaches to determine/predict the possible peak and the days required for the disease elimination based on the specific data used.

Various mathematical models utilizing fractional derivatives have been reported to investigate disease dynamics; see, for example,^6,7,8,9. The concept of stochastic differential equations has been applied to analyze the coronavirus disease, as presented in¹⁰. The real cases of the coronavirus in the UAE have been used to obtain parameters with realistic values, and further to obtain results for curtailing the infection in the UAE. A mathematical model that incorporates the assumptions of treatment of the infected individuals of COVID-19 has been explored in¹¹. A mathematical model that focuses on vaccination strategies for coronavirus infection is discussed in¹². In¹³, the authors analyzed COVID-19 infection data from India using a Caputo–Fabrizio derivative model. A cholera infection model in terms of fractional derivative is discussed in¹⁴. A monkeypox disease model considering the fractional derivative has been used in¹⁵. A coronavirus infection under the environmental contamination has been considered in¹⁶. Some more work on fractional order models, we can refer the readers to see^17,18,19,20.

Mathematical models that are designed in terms of stochastic environments are considered useful for the prediction of disease and spread, as they account for uncertainty and randomness in biological mathematical models. The deterministic mathematical systems usually have some constraints²¹. Disease extinction probability cannot be taken into consideration by a deterministic model²². In order to depict random fluctuations in physiological parameters and natural processes like cell development and death, this model incorporates stochastic components. Particularly in human viral infections, random variations in environmental factors like temperature, humidity, and precipitation can greatly influence the transmission of the disease. These stochastic effects capture the impact of shifting environmental variables in biological models. A fractional stochastic mathematical model that is designed to study the media awareness in disease spread has been explored in²³. An SIR fractional model in a stochastic environment has been analyzed in²⁴. A fractal-fractional stochastic coronavirus model incorporating the vaccination effects has been explored in²⁵. The dynamics of Ebola infection in terms of stochastic fractional environments have been analyzed by the authors in²⁶. The combined effects model with stochastic and fractional calculus to understand the coronavirus infection has been explored in²⁷.

In this investigation, the COVID-19 infection model with vaccination in stochastic fractional differential equations is considered. The model is first presented with integer-order derivatives, subsequently reformulated in terms of the ABC derivative, and later generalized to fractional stochastic differential equations. We provide the EU of the system, their positivity and boundedness, and a non-negative solution. The sensitivity analysis has been performed by using the PRCC method and provided comprehensive details about the sensitive parameters that have an effect on the disease model. A numerical solution for the model with an effective scheme has been shown. Numerical simulations are performed and analyzed to evaluate the influence of different parameter values on disease control.

Mathematical model

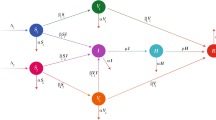
This section presents the mathematical modeling of the COVID-19 infection model in integer order derivative. We partition the total population into six distinct compartments: susceptible individuals S(t), representing unvaccinated persons at risk of infection; vaccinated individuals V(t); exposed individuals E(t), who are infected but not yet infectious; asymptomatic infectious individuals A(t); symptomatic infectious individuals I(t); and recovered individuals R(t). The overall population at time t is therefore expressed as

$$\begin{aligned} N(t) = S(t) + V(t) + E(t) + A(t) + I(t) + R(t). \end{aligned}$$

Vaccinated individuals are initially protected from infection due to the immunological response induced by the vaccine. However, as vaccine efficacy wanes over time, some vaccinated individuals may become susceptible to the virus again. On the basis of these assumptions, we formulate a system of nonlinear ordinary differential equations to characterize the transmission dynamics of the virus across the defined compartments²⁸.

$$\begin{aligned} \left\{ \begin{aligned}&\frac{dS}{dt}=-\frac{(a_1 I+a_2 A)S}{N}-S(\mu +\omega ) +\kappa R+\theta V+\Pi ,\\ &\frac{dV}{dt}= \omega S- (1-\psi ) \frac{(a_1 I+a_2 A)V}{N}-(\theta +\mu ) V,\\ &\frac{dE}{dt}= -(\delta +\mu ) E+\frac{(a_1 I+a_2 A)S}{N}+ (1-\psi ) \frac{(a_1 I+a_2 A)V}{N},\\ &\frac{dA}{dt}=\delta q E-(\mu +\rho _1) A,\\ &\frac{dI}{dt}=-(\mu +d+\rho ) I+(1-q) \delta E,\\ &\frac{dR}{dt}=-(\kappa +\mu ) R+\rho I+\rho _1 A. \end{aligned}\right. \end{aligned}$$

(1)

According to the initial assumption

$$\begin{aligned} \begin{aligned}&S(0)=S_0> 0, ~V(0)=V_0\ge 0,~ E(0)=E_0\ge 0,~ A(0)=A_0\ge 0,~ I(0)=I_0\ge 0,~ R(0)=R_0\ge 0. \end{aligned} \end{aligned}$$

(2)

The system is characterized by several key parameters that govern its dynamics. The recruitment rate of the healthy people is given by $\Pi$, while $\mu$ denotes the natural death rate. Disease propagates when susceptible persons are exposed to infectious contacts through either symptomatic or asymptomatic transmission routes, characterized by the rates $a_1$ and $a_2$, respectively. Vaccination of susceptible individuals is administered at a rate $\omega$, while waning vaccine immunity occurs at a rate $\theta$. Recovered individuals may experience natural loss of immunity, represented by the rate $\kappa$.

Given the absence of a perfect coronavirus vaccine, the parameter $\psi$ accounts for vaccine efficacy. The incubation period following exposure is denoted by $\delta$. The movement of exposed individuals into the asymptomatic compartment A(t) occurs with rate $q\delta$. Individuals who develop symptoms move to the symptomatic infectious compartment I(t) at a rate $(1 - q)\delta$. The recovery rate for asymptomatic infections is denoted by $\rho _1$, while that for symptomatic infections is represented by $\rho$. Disease-induced mortality at the symptomatic stage is represented by the parameter d. Coronavirus has been responsible for significant mortality worldwide.

Formulation of fractional model and related definitions

The following basic definitions will be utilized in developing the fractional-order model.

Definition 1

The Atangana-Baleanu derivative in Caputo sense $\mathbb {(ABC)}$ and their respective fractional integral is hereby presented:

$$\begin{aligned} ^{\mathbb {ABC}}\mathcal {D}_{t}^{\zeta }(\phi (t))=\frac{\mathbb {ABC}(\zeta )}{(1-\zeta )}\int _0^t \phi '(\theta )E_{\zeta }\bigg [\frac{\zeta (t-\theta )^{\zeta }}{\zeta -1}\bigg ]d\theta , \end{aligned}$$

$\mathbb {ABC}(\zeta )$ is the normalization function which satisfies $\mathbb {ABC}(1)=\mathbb {ABC}(0)=1$. The AB arbitrary integral of order $\zeta$ for a function $\phi$ is given by

$$\begin{aligned} ^{\mathbb {ABC}}\mathcal {I}_{t}^{\zeta }(\phi (t))-\frac{1-\zeta }{\mathbb {ABC}(\zeta )}\phi (t) =\zeta (\mathbb {ABC}(\zeta )\Gamma (\zeta ))^{-1} \int _0^t(t-\theta )^{\zeta -1}\phi (\theta )d\theta , \end{aligned}$$

where $0<\zeta \le 1$$, $t\in [0, \infty )$, and $\phi (t)$ defines a differentiable function over the interval $[0,\infty )$ such that $\phi ' \in L^1(0,\infty )$, $E_{\zeta }$ is the Mittag-Leffler function (MLF).

Converting an integer-order epidemiological model to a fractional-order model offers several key advantages. Fractional models incorporate memory and hereditary properties, making them more suitable for capturing the long-term dynamics and history-dependent behavior of infectious diseases. Unlike integer-order models, which assume that the future state depends only on the present, fractional models account for the influence of past states, leading to more accurate and realistic descriptions of disease spread. This enhanced modeling capability often results in better fitting of real-world data and improved predictions, especially in complex systems like COVID-19, where disease transmission is influenced by delayed responses and long-term immunity effects. Therefore, the classical differential operator given in (1) is replaced by the Atangana–Baleanu (AB) fractional derivative.

$$\begin{aligned} \left\{ \begin{aligned}&^{\mathbb {ABC}}_{0}D_{t}^{\zeta }S(t)=\Pi -\frac{(a_1 I+a_2 A)S}{N}-(\mu +\omega ) S+\kappa R+\theta V,\\ &^{\mathbb {ABC}}_{0}D_{t}^{\zeta }V(t)= \omega S- (1-\psi ) \frac{(a_1 I+a_2 A)V}{N}-(\theta +\mu ) V,\\ &^{\mathbb {ABC}}_{0}D_{t}^{\zeta }E(t)= \frac{(a_1 I+a_2 A)S}{N}+ (1-\psi ) \frac{(a_1 I+a_2 A)V}{N}-(\delta +\mu ) E,\\ &^{\mathbb {ABC}}_{0}D_{t}^{\zeta }A(t)=\delta q E-(\mu +\rho _1) A,\\ &^{\mathbb {ABC}}_{0}D_{t}^{\zeta }I(t)=-(d+\mu +\rho ) I+\delta (1-q) E,\\ &^{\mathbb {ABC}}_{0}D_{t}^{\zeta }R(t)=\rho _1 A+\rho I-(\mu +\kappa ) R, \end{aligned}\right. \end{aligned}$$

(3)

with the associated non-negative initial conditions,

$$\begin{aligned}\begin{aligned}&S(0)=S_0>0, ~V(0)=V_0\ge 0,~ E(0)=E_0\ge 0,~ A(0)=A_0\ge 0,~ I(0)=I_0\ge 0,~ R(0)=R_0\ge 0. \end{aligned} \end{aligned}$$

Before analyzing model (3), we first verify its biological feasibility by examining the existence, uniqueness, and positivity of solutions, as well as the invariance of the feasible region in $\mathbb {R}_+^6$. The feasible region is defined as

$$\begin{aligned} \mathbb {R}_+^6 = \Big \{ (S,V,E,A,I,R) \in \mathbb {R}^6 \;\big |\; S,V,E,A,I,R \ge 0 \Big \}. \end{aligned}$$

In the next subsection, this condition will be elaborated.

Existence and Uniqueness (EU)

Here, we establish the EU results for the model (3) in non-integer order derivative in ABC sense. For this purpose, we present the following result:

Theorem 1

²⁹There exists a unique solution to the fractional differential equation

$$\begin{aligned} {}^{\mathbb {ABC}}_{0}D_{t}^{\zeta }x(t) = f(t), \end{aligned}$$

(4)

which can be obtained through the inverse Laplace transform and the convolution theorem, and is given by

$$\begin{aligned} x(t) - \mathcal {A}f(t) = \mathcal {B}\int _{0}^{t} f(s)\,(t-s)^{\zeta -1}\, ds. \end{aligned}$$

(5)

Now, we use Theorem 1 to transform the system (3) into a Volterra-type integral equation, given by:

$$\begin{aligned} \left\{ \begin{aligned}&S(t)-S(0)-\mathcal {A} H_{11}(S,t)= \mathcal {B}\int _{0}^{t} H_{11}(S,s)(t-s)^{\zeta -1} ds,\\ &V(t)-V(0)-\mathcal {A} H_{12}(V,t)= \mathcal {B}\int _{0}^{t} H_{12}(V,s)(t-s)^{\zeta -1} ds,\\ &E(t)-E(0)-\mathcal {A} H_{13}(E,t)= \mathcal {B}\int _{0}^{t} H_{13}(E,s)(t-s)^{\zeta -1} ds,\\ &A(t)-A(0)-\mathcal {A} H_{14}(A,t)= \mathcal {B}\int _{0}^{t} H_{14}(A,s)(t-s)^{\zeta -1} ds,\\ &I(t)-I(0)-\mathcal {A} H_{15}(I,t)= \mathcal {B}\int _{0}^{t} H_{15}(I,s)(t-s)^{\zeta -1} ds,\\ &R(t)-R(0)-\mathcal {A} H_{16}(R,t)= \mathcal {B}\int _{0}^{t} H_{16}(R,s)(t-s)^{\zeta -1} ds. \end{aligned}\right. \end{aligned}$$

(6)

where $\mathcal {A}=\frac{1-\zeta }{{\mathbb {ABC}}(\zeta )}$ and $\mathcal {B}=\frac{\zeta }{\Gamma (\zeta ) {\mathbb {ABC}}(\zeta )}$. Also,

$$\begin{aligned} \left\{ \begin{aligned}&H_{11}(S,t)= \Pi -\frac{(a_1 I+a_2 A)S}{N}-(\mu +\omega ) S+\kappa R+\theta V,\\ &H_{12}(V,t)= \omega S- \frac{(1-\psi ) (a_1 I+a_2 A)V}{N}-(\theta +\mu ) V,\\ &H_{13}(E,t)= \frac{(a_1 I+a_2 A)S}{N}+ \frac{(1-\psi )(a_1 I+a_2 A)V}{N}-(\delta +\mu ) E,\\ &H_{14}(A,t)= -(\mu +\rho _1) A+\delta q E,\\ &H_{15}(I,t)= -(\mu +d+\rho ) I+(1-q) \delta E,\\ &H_{16}(R,t)=-(\kappa +\mu ) R+\rho I+\rho _1 A. \end{aligned}\right. \end{aligned}$$

(7)

To prove that the kernels $H_{1i}$, for i, 1 to 6 satisfy the Lipschitz condition, we have to show that these kernels are Lipschitz continuous with respect to the given functions. Consider that S, $\bar{S}$, V, $\bar{V}$, A, $\bar{A}$, E, $\bar{E}$, I, $\bar{I}$, R, and $\bar{R}$ representing bounded functions, such that

$$\begin{aligned} max \bigg \{S, \bar{S}, V, \bar{V}, A, \bar{A}, E, \bar{E}, I, \bar{I}, R, \bar{R} \bigg \} <\beta . \end{aligned}$$

For $H_{11}(S,t)$ and $H_{11}(\bar{S},t)$, the following inequality holds,

$$\begin{aligned} ||H_{11}(t, S)-H_{11}(t, \bar{S})||= & \bigg |\bigg |-\frac{(a_1 I+a_2 A)(S-\bar{S})}{N}-(\mu +\omega ) (S-\bar{S})\bigg |\bigg |,\\\\\le & \frac{(a_1+a_2)\beta }{N}||S-\bar{S}||+(\mu +\omega ) ||S-\bar{S}||,\\\\\le & \bigg (\frac{(a_1+a_2)\beta }{N}+(\mu +\omega )\bigg ) ||S-\bar{S}||, \le \gamma _{1} ||S-\bar{S}||. \end{aligned}$$

(8)

where $\gamma _1= \bigg (\frac{(a_1+a_2)\beta }{N}+(\mu +\omega )\bigg )$. Follow the results given in³⁰ (see Theorem 1), the kernel $H_{11}(t, S)$ satisfies the Lipschitz condition. In a similar way, the following inequalities can be obtained:

$$\begin{aligned} \begin{aligned}&||H_{12}(t,V)-H_{12}(t,\bar{V})|| \le \gamma _{2} ||-\bar{V}+V||,\\ &||H_{13}(t, E)-H_{13}(t, \bar{E})|| \le \gamma _{3} ||-\bar{E}+E||,\\ &||H_{14}(t, A)-H_{14}(t, \bar{A})|| \le \gamma _{4} ||-\bar{A}+A||,\\ &||H_{15}(t, I)-H_{15}(t, \bar{I})|| \le \gamma _{5} ||-\bar{I}+I||,\\ &||H_{16}(t, R)-H_{16}(t, \bar{R})|| \le \gamma _{6} ||-\bar{R}+R||,\\ &\end{aligned} \end{aligned}$$

(9)

where $\gamma _2= \frac{(1-\psi )(a_1+a_2)\beta }{N}+(\mu +\theta )$, $\gamma _3= \mu +\delta$, $\gamma _4= \mu +\rho _1$, $\gamma _5= \mu +\rho +d$ and $\gamma _6= \kappa +\mu$. Thus, for all kernels $H_{1i}$, $i=1,2,3,...,6$, the Lipschitz condition holds. Furthermore, we use the fixed point theory to obtain the existence of the solution of the system (3). The recursive formulation of the Eq. (6) is shown by the following expressions,

$$\begin{aligned} \left\{ \begin{aligned}&S_{n}(t)-\mathcal {A} H_{11}(S_{n-1},t)= \mathcal {B}\int _{0}^{t} (t-s)^{\zeta -1} H_{11}(S_{n-1},s) ds,\\ &V_{n}(t)-\mathcal {A} H_{12}(V_{n-1},t)= \mathcal {B}\int _{0}^{t} (t-s)^{\zeta -1} H_{12}(V_{n-1},s) ds,\\ &E_{n}(t)-\mathcal {A} H_{13}(E_{n-1},t)= \mathcal {B}\int _{0}^{t} (t-s)^{\zeta -1} H_{13}(E_{n-1},s) ds,\\ &A_{n}(t)-\mathcal {A} H_{14}(A_{n-1},t)= \mathcal {B}\int _{0}^{t} (t-s)^{\zeta -1} H_{14}(A_{n-1},s) ds,\\ &I_{n}(t)-\mathcal {A} H_{15}(I_{n-1},t)= \mathcal {B}\int _{0}^{t} (t-s)^{\zeta -1} H_{15}(I_{n-1},s) ds,\\ &R_{n}(t)-\mathcal {A} H_{16}(R_{n-1},t)= \mathcal {B}\int _{0}^{t} (t-s)^{\zeta -1} H_{16}(R_{n-1},s) ds. \end{aligned}\right. \end{aligned}$$

(10)

The appropriate initial conditions for (10) are $S_{0}=S(0)$, $V_{0}=V(0)$, $E_{0}=E(0)$, $A_{0}=A(0)$, , $I_{0}=I(0)$ and $R_{0}=R(0)$. From (10), the various expressions for the successive terms are provided as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\Phi _{1,n}=S_{n}(t)-S_{n-1}(t)=\mathcal {A} (H_{11}(S_{n-1},t)-H_{11}(S_{n-2},t))+ \mathcal {B}\int _{0}^{t} (H_{11}(S_{n-1},s)-H_{11}(S_{n-2},s))(t-s)^{\zeta -1} ds,\\ &\Phi _{2,n}=V_{n}(t)-V_{n-1}(t)=\mathcal {A} (H_{12}(V_{n-1},t)-H_{12}(V_{n-2},t))+ \mathcal {B}\int _{0}^{t} (H_{12}(V_{n-1},s)-H_{12}(V_{n-2},s))(t-s)^{\zeta -1} ds,\\ &\Phi _{3,n}=E_{n}(t)-E_{n-1}(t)=\mathcal {A} (H_{13}(E_{n-1},t)-H_{13}(E_{n-2},t))+ \mathcal {B}\int _{0}^{t} (H_{13}(E_{n-1},s)-H_{13}(E_{n-1},s))(t-s)^{\zeta -1} ds,\\ &\Phi _{4,n}=A_{n}(t)-A_{n-1}(t)=\mathcal {A} (H_{14}(A_{n-1},t)-H_{14}(A_{n-2},t))+ \mathcal {B}\int _{0}^{t} (H_{14}(A_{n-1},s)-H_{14}(A_{n-2},s))(t-s)^{\zeta -1} ds,\\ &\Phi _{5,n}=I_{n}(t)-I_{n-1}(t)=\mathcal {A} (H_{15}(I_{n-1},t)-H_{15}(I_{n-2},t))+ \mathcal {B}\int _{0}^{t} (H_{15}(I_{n-1},s)-H_{15}(I_{n-2},s))(t-s)^{\zeta -1} ds,\\ &\Phi _{6,n}=R_{n}(t)-R_{n-1}(t)=\mathcal {A} (H_{16}(R_{n-1},t)-H_{16}(R_{n-2},t))+ \mathcal {B}\int _{0}^{t} (H_{16}(R_{n-1},s)-H_{16}(R_{n-2},s))(t-s)^{\zeta -1} ds. \end{aligned}\right. , \end{aligned}$$

(11)

and hence we have

$$\begin{aligned} \begin{aligned} S_{n}-\sum _{i=1}^{n} \Phi _{1,i}(t)=0, V_{n}-\sum _{i=1}^{n} \Phi _{2,i}(t)=0, E_{n}-\sum _{i=1}^{n} \Phi _{3,i}(t)=0,\\ A_{n}-\sum _{i=1}^{n} \Phi _{4,i}(t)=0, I_{n}-\sum _{i=1}^{n} \Phi _{5,i}(t)=0, R_{n}-\sum _{i=1}^{n} \Phi _{6,i}(t)=0. \end{aligned} \end{aligned}$$

(12)

By using Eqs. (8) and (9), the norms of both sides of Eq. (11) can be solved. We obtain

$$\begin{aligned} \left\{ \begin{aligned}&||\Phi _{1,n}|| \le \mathcal {A} \gamma _1 ||\Phi _{1,n-1}||+ \mathcal {B} \gamma _1 \int _{0}^{t} ||\Phi _{1,n-1}(s)||(t-s)^{\zeta -1} ds,\\ &||\Phi _{2,n}|| \le \mathcal {A} \gamma _2 ||\Phi _{2,n-1}||+\mathcal {B} \gamma _2 \int _{0}^{t} ||\Phi _{2,n-1}(s)||(t-s)^{\zeta -1} ds,\\ &||\Phi _{3,n}|| \le \mathcal {A} \gamma _3 ||\Phi _{3,n-1}||+ \mathcal {B} \gamma _3 \int _{0}^{t} ||\Phi _{3,n-1}(s)||(t-s)^{\zeta -1} ds,\\ &||\Phi _{4,n}|| \le \mathcal {A} \gamma _4 ||\Phi _{4,n-1}||+ \mathcal {B} \gamma _4 \int _{0}^{t} ||\Phi _{4,n-1}(s)||(t-s)^{\zeta -1} ds,\\ &||\Phi _{5,n}|| \le \mathcal {A} \gamma _5 ||\Phi _{5,n-1}||+ \mathcal {B} \gamma _5 \int _{0}^{t} ||\Phi _{5,n_1}(s)||(t-s)^{\zeta -1} ds,\\ &||\Phi _{6,n}||\le \mathcal {A} \gamma _6 ||\Phi _{6,n-1}||+ \mathcal {B} \gamma _6 \int _{0}^{t} ||\Phi _{6,n-1}(s)||(t-s)^{\zeta -1} ds. \end{aligned}\right. \end{aligned}$$

(13)

We now state the following Theorem.

Theorem 2

Model (3) contains a specific solution if and only if we can find $t_{max}$ such that

$$\begin{aligned} \gamma _{i} \mathcal {A}+\frac{t_{max}^{\zeta } \gamma _{i}}{\Gamma (\zeta )\mathbb {ABC}(\zeta )}<1,~~ i=1,2,...,6. \end{aligned}$$

(14)

Proof

It is assumed that S, V, E, A, I and R representing bounded functions, and also it has been proven previously that these functions also holds the Lipschitz condition. As we can see from the Eq. (13) and applying the recursive principle, the below inequalities hold:

$$\begin{aligned} \left\{ \begin{aligned}&||\Phi _{1,n}|| \le \bigg (\mathcal {A} \gamma _1+ \frac{t^{\zeta }\gamma _1}{\mathbb {ABC}(\zeta ) \Gamma (\zeta )}\bigg )^{n} ||S_0||,~ ||\Phi _{2,n}|| \le \bigg (\mathcal {A} \gamma _2+ \frac{t^{\zeta }\gamma _2}{\mathbb {ABC}(\zeta ) \Gamma (\zeta )}\bigg )^{n} ||V_0||,\\ &||\Phi _{3,n}|| \le \bigg (\mathcal {A} \gamma _3+ \frac{t^{\zeta }\gamma _3}{\mathbb {ABC}(\zeta ) \Gamma (\zeta )}\bigg )^{n} ||E_0||,~~ ||\Phi _{4,n}|| \le \bigg (\mathcal {A} \gamma _4+ \frac{t^{\zeta }\gamma _4}{\mathbb {ABC}(\zeta ) \Gamma (\zeta )}\bigg )^{n} ||A_0||,\\ &||\Phi _{5,n}|| \le \bigg (\mathcal {A} \gamma _5+ \frac{t^{\zeta }\gamma _5}{\mathbb {ABC}(\zeta ) \Gamma (\zeta )}\bigg )^{n} ||I_0||,~ ||\Phi _{6,n}|| \le \bigg ( \frac{t^{\zeta }\gamma _6}{\mathbb {ABC}(\zeta ) \Gamma (\zeta )}+\mathcal {A} \gamma _6\bigg )^{n} ||R_0||. \end{aligned}\right. \end{aligned}$$

(15)

We establish the existence and uniqueness of the solution to (12) by analyzing the behavior of $||\Phi _{i,n}(t)||\rightarrow 0$, as $n\rightarrow \infty$ and $t=t_{max}$ with $i=1, ,...,6$. To demonstrate that Eq. (6) is the solution of Eq. (3), we consider the following:

$$\begin{aligned} \left\{ \begin{aligned}&S(t)-S(0)=S_n-\Psi _{1,n},~ V(t)-V(0)=V_n-\Psi _{2,n},\\ &E(t)-E(0)=E_n-\Psi _{3,n},~ A(t)-A(0)=A_n-\Psi _{4,n},\\ &I(t)-I(0)=I_n-\Psi _{5,n},~ R(t)-R(0)=R_n-\Psi _{6,n}. \end{aligned}\right. \end{aligned}$$

(16)

where $\Psi _{i,n}(t)$, for $i=1,...,6$ refers to the remainder terms in the series expansions. The norm of the term $\Psi _{1,n}(t)$ is given by,

$$\begin{aligned} ||\Psi _{1,n}(t)||\le & \mathcal {A}||H_{11}(S,t)-H_{11}(S_{n-1},t)||+ \frac{\zeta }{\mathbb {ABC}(\zeta ) \Gamma (\zeta )} \int _{0}^{t} ||H_{11}(S,s)-H_{11}(S_{n-1},s)|| (t-s)^{\zeta -1} ds,\\\\\le & ||S-S_{n-1}|| \bigg (\mathcal {A} +\frac{t^{\zeta }}{\mathbb {ABC}(\zeta ) \Gamma (\zeta )}\bigg )\gamma _1. \end{aligned}$$

(17)

As one can now apply an iteration method to inequality (17) at $t=t_{max}$, we obtain

$$\begin{aligned} \begin{aligned}&||\Psi _{1,n}(t)|| \le \bigg (\mathcal {A} +\frac{t_{max}^{\zeta }}{\mathbb {ABC}(\zeta ) \Gamma (\zeta )}\bigg )^{n+1} \gamma _1^{n+1} N. \end{aligned} \end{aligned}$$

(18)

We achieve $||\Psi _{1,n}(t)||\rightarrow 0$ as $n\rightarrow \infty$. According to laid down procedure we have $||\Psi _{i,n}(t)|| \rightarrow 0$, $i=2,3,...,6$. Thus, the function that meets the requirement of Eq. (6) is the solution of Eq. (3). The fact that the solution to model Eq. (3) is now established. Consider $S^*$, $V^*$, $E^*$, $A^*$, $I^*$ and $R^*$ represent another set of solution for the system (3). Thus, the below relationship is satisfied:

$$\begin{aligned} \begin{aligned}&S(t)-S^*(t)=\mathcal {A} \bigg (H_{11}(S, t)-H_{11}(S^*, t)\bigg ) +\mathcal {B} \int _{0}^{t} \bigg (H_{11}(S, t)-H_{11}(S^*,t)\bigg ) (t-s)^{\zeta -1} ds. \end{aligned} \end{aligned}$$

(19)

By applying the same procedure as in Eq. (13) and (15) to take the norm of both sides on Eq. (19), we obtain:

$$\begin{aligned} \begin{aligned}&\bigg (1-\mathcal {A}\gamma _1 -\frac{ \gamma _1 t^{\zeta }}{\mathbb {ABC}(\zeta ) \Gamma (\zeta )}\bigg ) ||S(t)-S^*(t)|| \le 0 . \end{aligned} \end{aligned}$$

(20)

We confirm that for $t=t_{max}$ we have

$$\begin{aligned} \begin{aligned}&\bigg (1-\mathcal {A}\gamma _1 -\frac{ \gamma _1 t^{\zeta }}{\mathbb {ABC}(\zeta ) \Gamma (\zeta )}\bigg ) \ge 0 . \end{aligned} \end{aligned}$$

(21)

which clearly state that $||S-S^*||=0$. As the result, we conclude $S=S^*$. By using a similar approach, it can be obtained $V=V^*$, $E=E^*$, $A=A^*$, $I=I^*$ and $R=R^*$. $\square$

Positivity and boundedness

Here, we determine the solution space (S, V, E, A, I, R) associated with the model (3) under non-negative initial conditions. Specifically, we focus on identifying a feasible region, denoted as $\mathbb {R}_{+}^{6}$, which remains positively invariant under the dynamics of the system (3). We present the following theorem:

Theorem 3

Let $N=S+V+E+A+I+R$ and

$$\begin{aligned} \begin{aligned} \Gamma =\bigg \{(S,V,E,A,I,R)\in \mathbb R_{+}^{6}| 0\le S+V+E+A+I+R=N\le \frac{\Pi }{\mu }\bigg \}. \end{aligned} \end{aligned}$$

It can be demonstrated that the closed set $\Gamma$ is positively invariant under the dynamics of the system (3).

Proof

We can confirm that N is the total population of the model under consideration. By computing fractional derivative at $\zeta \in (0, 1]$, we get

$$\begin{aligned} \begin{aligned}&^{\mathbb {ABC}}D_{t}^{\zeta }N(t)=^{\mathbb {ABC}}D_{t}^{\zeta }S(t)+^{\mathbb {ABC}}D_{t}^{\zeta }V(t)+^{\mathbb {ABC}}D_{t}^{\zeta }E(t)+^{\mathbb {ABC}}D_{t}^{\zeta }A(t)+^{\mathbb {ABC}}D_{t}^{\zeta }I(t)+^{\mathbb {ABC}}D_{t}^{\zeta }R(t)\\ &=\Pi -\mu (S+V+E+A+I+R)-d I. \end{aligned} \end{aligned}$$

(22)

We obtain the following by using the Laplace transform on Eq. (22) both sides:

$$\begin{aligned} & \mathcal {L}[\ {}^\mathbb {ABC}{}D^{\zeta }_t (N(t))]=\mathcal {L}[\Pi -\mu N-d I]\le \mathcal {L}[\ \Pi -\mu N],\nonumber \\ & \frac{\mathbb {ABC}(\zeta ) s^{\zeta } N(s)}{s^{\zeta }(1-{\zeta })+{\zeta }}+\mu N(s)\le \frac{\Pi }{s}+\frac{\mathbb {ABC}(\zeta )s^{\zeta -1}N(0)}{s^{\zeta }(1-{\zeta })+{\zeta }}, \end{aligned}$$

(23)

where N(s) will represent the Laplace transform of [N(t)](s) and N(0) is the initial condition. Write (23) in term of N(s), we have

$$\begin{aligned} N(s)\le \frac{\Pi s^{\zeta -(\zeta +1)}[s^\zeta (1-\zeta )+\zeta ]+\mathbb {ABC}(\zeta )s^{\zeta -1}N(0)}{\mathbb {ABC}(\zeta )s^\zeta +\mu [s^\zeta (1-\zeta )+\zeta ]}, \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} N(s)\le&\frac{\Pi s^{\zeta -(\zeta +1)}[s^\zeta (1-\zeta )+\zeta ]}{[\mathbb {ABC}(\zeta )+(1-\zeta )\mu ]s^\zeta +\mu \zeta }+\frac{\mathbb {ABC} (\zeta )s^{\zeta -1}N(0)}{[\mathbb {ABC}(\zeta )+(1-\zeta )\mu ]s^\zeta +\mu \zeta },\\&=\left( \frac{\Pi (1-\zeta )}{[\mathbb {ABC}(\zeta )+(1-\zeta )\mu ]}\right) \frac{s^{\zeta -1}}{s^\zeta +\frac{\mu \zeta }{\mathbb {ABC}(\zeta )+(1-\zeta )\mu }}\\&+\left( \frac{\Pi \zeta }{\mathbb {ABC}(\zeta )+(1-\zeta )\mu }\right) \frac{s^{\zeta -(\zeta +1)}}{s^\zeta +\frac{\mu \zeta }{\mathbb {ABC}(\zeta )+(1-\zeta )\mu }}\\&+\left( \frac{\mathbb {ABC}(\zeta )N(0)}{\mathbb {ABC}(\zeta )+\mu (1-\zeta )}\right) \frac{s^{\zeta -1}}{s^\zeta +\frac{\mu \zeta }{\mathbb {ABC}(\zeta )+\mu (1-\zeta )}}, \end{aligned} \end{aligned}$$

Exerting inverse Laplace transform on both sides, we obtained the following inequalities

$$\begin{aligned} \begin{aligned} N(s)\le&\left( \frac{\Pi (1-\zeta )}{\mathbb {ABC}(\zeta )+(1-\zeta )\mu }+\frac{\mathbb {ABC}(\zeta )N(0)}{\mathbb {ABC}(\zeta )+(1-\zeta )\mu }\right) E_{\zeta ,1}\left( \frac{-\zeta \mu t^\zeta }{\mathbb {ABC}(\zeta )+(1-\zeta )\mu }\right) \\&+\left( \frac{\Pi \zeta t^\zeta }{\mathbb {ABC}(\zeta )+(1-\zeta )\mu }\right) E_{\zeta ,\zeta +1}\left( \frac{-\zeta \mu t^\zeta }{\mathbb {ABC}(\zeta )+(1-\zeta )\mu }\right) , \end{aligned} \end{aligned}$$

(24)

MLF with two parameter $p>0, ~q>0$ is interpreted as

$$\begin{aligned} E_{p,q}(Y)=\sum _{j=0}^{\infty }\frac{Y^j}{p j+q} \end{aligned}$$

Laplace transform of this function is,

$$\begin{aligned} \mathcal {L}[t^{q-1}E_{p,q}(\pm \nu t^p)]=\frac{s^{p-q}}{s^p\mp \nu } \end{aligned}$$

Given that $s>|\nu |^\frac{1}{p}$. MLF gratify²

$$\begin{aligned} E_{p,q}(Y)=\frac{1}{Y}\left[ E_{p,q-p}(Y)-\frac{1}{\Gamma (q-p)}\right] \end{aligned}$$

(25)

The MLF has asymptotic behavior, which is given as follows by³¹,

$$\begin{aligned} E_{q,q+1}(Y)\approx \sum _{j=1}^{i}\frac{Y^{-j}}{q+(q+1)j}+\mathcal {O}(|Y|^{-1-i}), |Y|\rightarrow \infty ,\frac{q\pi }{2}<|arg Y|\le \pi . \end{aligned}$$

(26)

Follows from Eqs. (24) to (25) and (26), one can see the result, $N(t)\le \frac{\Pi }{\mu }$ as $t\rightarrow \infty$. Consequently, $\Gamma$ is interpreted as positively invariant in the region concerning (3). $\square$

Solution non-negativity

We now demonstrate that the solution to model (3) remains non-negative for all variables, provided that the ICs are non-negative. We provide the following result:

Theorem 4

The solution of associated with the system (3) will always remain non-negative, provided that the ICs are non-negative.

Proof

Let’s begin with the first equation of the system (3), given by:

$$\begin{aligned} \begin{aligned} ^{\mathbb {ABC}}_{0}D_{t}^{\zeta }S(t)&=\Pi -\frac{(a_1 I+a_2 A)S}{N}-(\mu +\omega ) S+\kappa R+\theta V\\&\ge -\bigg ( \frac{(a_1 I+a_2 A)}{N}+(\mu +\omega ) \bigg )S \end{aligned} \end{aligned}$$

According to Theorem 3, all populations are confined within bounds, and therefore, we have:

$$\begin{aligned} \begin{aligned}&max \bigg \{S, V, E, A, I, R \bigg \} \le M,~~~ M>0. \end{aligned} \end{aligned}$$

(27)

So, we get

$$\begin{aligned} \begin{aligned} ^{\mathbb {ABC}}_{0}D_{t}^{\zeta }S(t)&\ge - c_1 S \end{aligned} \end{aligned}$$

where $c_1=\frac{(a_1 I+a_2 A)}{N}+(\mu +\omega )$. The application of Laplace transform and its inverse, as described previously, we get the below result:

$$\begin{aligned} \begin{aligned}&S(t)= \frac{\mathbb {ABC}(\zeta )S(0) s^{\zeta -1} }{\mathbb {ABC}(\zeta )+c_1 (1-\zeta )} E_{\zeta ,1}\bigg (\frac{- \zeta t^\zeta c_1 }{\mathbb {ABC}(\zeta )+c_1 (1-\zeta )}\bigg ). \end{aligned} \end{aligned}$$

(28)

Utilizing the characteristics of MLF, the terms on the right-hand side of the bounding Eq. (28) guarantee that $S \ge 0$ for all $t \ge 0$. In the same way, we are able to confirm that $V\ge 0$, $E\ge 0$, $A\ge 0$, $I\ge 0$, and $R\ge 0$. This completes the proof. $\square$

The potential equilibrium points of model (3) will be examined in the following subsection:

Disease Free Equilibrium (DFE)

We represent the DFE of the system (3) by $E_0$ which is given by,

$$\begin{aligned}\begin{aligned}&E_0=(S_0,V_0,E_0,A_0,I_0,R_0)=\bigg ( \frac{\Pi (\theta +\mu )}{\mu (\theta +\mu +\omega )}, \frac{\Pi \omega }{\mu (\theta +\mu +\omega )}, 0, 0, 0, 0 \bigg ) . \end{aligned} \end{aligned}$$

Basic reproduction number ($\mathcal {R}_0$)

The basic reproduction number with the vaccine $\mathcal {R}_v$ is provided in²⁸, specifically,

$$\begin{aligned} \mathcal {R}_v=\frac{(\theta +\mu +\omega (1-\psi ))}{(\mu +\delta )(\theta +\mu +\omega )} \bigg ( \frac{a_1 \delta (1-q)}{(d+\mu +\rho )}+\frac{a_2 \delta q}{(\mu +\rho _1)}\bigg ). \end{aligned}$$

The value of $\mathcal {R}_0$ stands for the mean number of person to person transmission in a community. When $\psi = 1$ and $\omega = \theta = 0$, $\mathcal {R}_v$ simplifies to the number of generations in a population at which the transmission of the social infection is maintained ($\mathcal {R}_0$):

$$\begin{aligned} \mathcal {R}_0=\frac{1}{(\mu +\delta )} \bigg ( \frac{a_1 \delta (1-q)}{(d+\mu +\rho )}+\frac{a_2 \delta q}{(\mu +\rho _1)}\bigg ). \end{aligned}$$

Endemic steady state point

We have the expression for the endemic equilibrium (EE) for the system (3) is shown by $E_1$ and obtained as follows:

$$\begin{aligned}\begin{aligned}&E_1=(S_*,V_*,E_*,A_*,I_*,R_*) . \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \left\{ \begin{aligned} S_*&= \frac{\theta V_* + \Pi + \kappa R_*}{\beta _* + \mu + \omega }, ~~ V_* = \frac{\omega S_*}{\mu + \theta + (1 - \psi ) \beta _*}, \\ E_*&= \frac{\beta _* (S_* + (1 - \psi ) V_*)}{\mu + \delta }, ~~ A_* = \frac{q \delta E_*}{\rho _1 + \mu }, \\ I_*&= \frac{\delta (1 - q) E_*}{d + \mu + \rho }, ~~ R_* = \frac{\rho I_* + \rho _1 A_*}{\kappa + \mu }. \end{aligned} \right. \end{aligned}$$

(29)

When the expression given in (29) are substituted in $\beta _*=\frac{\beta _1 I_* + \beta _2 A_*}{S_*+V_*+E_*+A_*+I_*+R_*}$, we obtain a quadratic equation in $\beta _*$ and it is given below:

$$\begin{aligned} b_1 \beta _*^2+b_2 \beta _*+b_3 =0. \end{aligned}$$

(30)

where

$$\begin{aligned}\left\{ \begin{aligned}&b_1=(1-\psi )(\mu +\rho _1)((\kappa +\mu )(\mu +d+\delta (1-q)+\rho )+\delta (1-q) \rho )+\\ &\delta q(1-\psi )(d+\mu +\rho )(\rho _1+\kappa +\mu ),\\ &b_2= (1-\psi )(d+\mu +\rho ){(\kappa +\mu )[(\rho _1+\mu )(\delta +\mu +\omega )+\delta q (\omega -a_2)]+\delta \rho _1 q \omega }+\\ &\delta (1-q)(1-\psi )(\rho _1+\mu )[(\omega -a_1)(\kappa +\mu )+\rho \omega ]+(\theta +\mu )(d+\mu +\rho )\\ &\times ((\kappa +\mu )(\rho _1+\mu +\delta q)+\delta \rho _1 q)+\delta (1-q) (\rho _1+\mu )(\theta +\mu )(\kappa +\mu +\rho ), \\ &b_3= (\kappa +\mu )(\mu +d+\rho )(\mu +\rho _1)(\delta +\mu )(\mu +\omega +\theta )(\theta +\mu +(1-\psi )\omega )(1-\mathcal {R}_v). \end{aligned}\right. \end{aligned}$$

For more details about this, we refer the reader to see²⁸. Further, the work in²⁸, has explained in details the stability of DFE and EE, so we omit it here, see²⁸.

Table 1 Description of the parameters obtained from the fitting process (3).

Parameter estimation

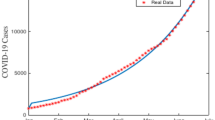
This section outlines the estimation process for the model parameters based on real COVID-19 data in Pakistan. The cumulative confirmed cases from 13 May 2022 to 30 September 2022 were obtained from a reliable online source ^33,34. All simulations were conducted using a daily time scale.

A nonlinear least-squares curve fitting technique was applied to estimate the model parameters by fitting the model to the observed cumulative data. The model considered for parameter fitting excluded vaccination, focusing on the natural transmission dynamics of the disease. Some of the parameters involved in the model such as the natural birth rate $\Pi = 9330$ and the natural death rate $\mu = \frac{1}{67.7 \times 365}$ were computed directly from demographic data. The remaining parameters were estimated by fitting the model output to the reported case data.

The total population of Pakistan in 2022 was considered as $N(0) = 230,557,367$ ³⁵. The initial values for the model compartments were given by: $S(0) = 230,255, 033$, $E(0) = 3\times 10^{5}$, $A(0) = 2\times 10^3$ , $I(0) = 334$ (the reported symptomatic cases on 13 May 2022), and $R(0) = 0$. There is no specific information regarding the exposed and asymptomatic are assumed as a best fit in model fitting.

After fitting, the estimated parameter values were obtained and is given in Table 1. Using these fitted parameters, the basic reproduction number was computed to be approximately $\mathcal {R}_0 \approx 1.2591$, indicating the potential for sustained transmission in the absence of interventions.

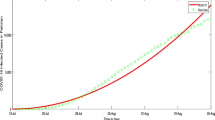
The data fitting results are shown in Fig. 1(a), which demonstrates a strong agreement between the model and observed case data, validating the estimated parameters. Figure 1 (b) represents the corresponding residual of the data fitting.

In the next phase of the study, we introduce vaccination into the model to assess its impact on controlling the outbreak. In this context, the parameter $\omega$ represents the vaccination rate of susceptible individuals and is set to $\omega = 0.001$. The vaccine efficacy is modeled by $\psi = 0.6$, and waning immunity following vaccination is captured by the parameter $\theta = 0.01$. These values account for imperfect vaccine protection and the gradual loss of immunity over time, which are critical factors in the evaluation of long-term disease control strategies.

Fig. 1

The graph represents the data fitting of the model (3) for $\zeta =1$, and their corresponding residuals. Sub-figures (a) and (b) respectively represents the model versus data fitting and their corresponding residuals.

Sensitivity analysis

In order to analyze the interactions of the different parameters of our model, we use Latin Hypercube Sampling (LHS), a method for generating sets of parameter sets, such that each dimension is sampled across the entire domain with probability density proportional to the given density for each variable^3,36,37. Meanwhile, to assess the degree of variability in the model parameters, LHS is combined PRCCs.

We use the discretization approximation and assume that there are uncertain parameters that have a chance variable distributed uniformly within ±30% of a baseline value. Latin Hypercube Sampling was performed for these distributions with 1000 samples being randomly created. Partial Rank Correlation Coefficients (PRCCs) were calculated for each of the following parameters: $(\mu , a_1, a_2, \omega , \theta , \psi , \delta , q, \rho _1, \rho , d)$ in relation to the outcome variable, the basic reproduction number $\mathcal {R}_v$. The sign of the PRCC indicates whether variations in the input parameters have a positive or negative impact on the output variable^38,39.

Parameters with PRCC values greater than 0.4 (in absolute value) are considered to have a strong influence, with a negative PRCC indicating an inverse relationship^38,39. A moderate correlation is defined for parameters with $0.2< |PRCC| < 0.4$, while weaker correlations are observed when $|PRCC| \le 0.2$⁴⁰.

Fig. 2

Sensitivity analysis showing PRCC results that demonstrate the dependence of $\mathcal {R}_v$ on the model parameters.

Figure 2 highlight that the parameters $(a_2, \theta , q, \omega , \psi , \rho _1)$ exhibits the most significant impact on the outcome function, specifically the reproduction number $\mathcal {R}_v$. Conversely, the parameters $(\mu , a_1, \delta , \rho , d)$ demonstrate a moderate impact on the basic reproduction number. We see in Fig. 3 (a) to (b) that decreasing $a_2$ reducing the basic reproduction number from 1.2591 to 1.0296 which shows a strong impact in absence of vaccination, and so the number of cases in asymptomatic and symptomatic classes are decreased well. Similarly, in Fig. 3 (c) to (d), when reducing q, the asymptomatic cases decreases while in (d) the symptomatic cases increases which shows an impact for the basic reproduction number reduce it to 1.1285. The key parameters that contribute to increasing the reproduction number $\mathcal {R}_v$ are the transmission rate $a_2$. On the contrary, the parameters that lead to a decrease in $\mathcal {R}_v$ include the proportion of natural death rate $\mu$.

Epidemiology often faces challenges in predicting the daily infection rate, as it tends to fluctuate based on the prevailing circumstances. This variability can be incorporated by applying a stochastic process. By accounting for environmental white noise, the model in (3) is transferred into a stochastic system, incorporating the derivative of Brownian motion, through the introduction of nonlinear perturbations in each of the model⁴⁰. A detailed explanation for such derivation and of how the model is transformed into its stochastic version can be found in^41,42.

Fig. 3

The impact of $a_2=0.3827, 0.3127$ and $q= 0.9931, 0.7931$ on the asymptomatic and symptomatic individuals, see Sub-Fig. 3 (a) and (c), and symptomatic compartments, see Sub-Fig. 3(b), and (d).

Stochastic fractional model using ABC derivative

In real-world disease dynamics, not everything follows a fixed pattern random events, unpredictable behavior, and inconsistencies in data reporting often play a major role. A purely deterministic model assumes perfect knowledge and uniform behavior, which isn’t always realistic. That’s why incorporating randomness, or stochasticity, becomes essential. By transitioning to a stochastic fractional model, especially one based on the Atangana–Baleanu–Caputo (ABC) derivative, we can better reflect the unpredictable nature of disease transmission. This approach adds a layer of realism, accounting for the chance-driven variations that a deterministic model might miss. The stochastic fractional model in ABC sense is given below:

$$\begin{aligned} \left\{ \begin{aligned}&^{\mathbb {ABC}}_{0}D_{t}^{\zeta }S(t)=\Pi -\frac{(a_1 I+a_2 A)S}{N}-(\mu +\omega ) S+\kappa R+\theta V+\nu _1 H_1(t,S) \dot{W}_0 (t),\\ &^{\mathbb {ABC}}_{0}D_{t}^{\zeta }V(t)= \omega S- (1-\psi ) \frac{(a_1 I+a_2 A)V}{N}-(\theta +\mu ) V+\nu _2 H_2(t,V) \dot{W}_1(t),\\ &^{\mathbb {ABC}}_{0}D_{t}^{\zeta }E(t)= \frac{(a_1 I+a_2 A)S}{N}+ (1-\psi ) \frac{(a_1 I+a_2 A)V}{N}-(\delta +\mu ) E+\nu _3 H_3(t,E) \dot{W}_2(t),\\ &^{\mathbb {ABC}}_{0}D_{t}^{\zeta }A(t)=\delta q E-(\mu +\rho _1) A+\nu _4 H_4(t,A) \dot{W}_3(t),\\ &^{\mathbb {ABC}}_{0}D_{t}^{\zeta }I(t)=(1-q) \delta E-(\mu +d+\rho ) I+\nu _5 H_5(t,I) \dot{W}_4(t),\\ &^{\mathbb {ABC}}_{0}D_{t}^{\zeta }R(t)=\rho I+\rho _1 A-(\kappa +\mu ) R+\nu _6 H_6(t,R) \dot{W}_5(t). \end{aligned}\right. \end{aligned}$$

(31)

$$\begin{aligned}\begin{aligned}&S(0)=S_0> 0, ~V(0)=V_0\ge 0,~ E(0)=E_0\ge 0,~ A(0)=A_0\ge 0, ~I(0)=I_0\ge 0,~ R(0)=R_0\ge 0. \end{aligned} \end{aligned}$$

where ${W}_0 (\cdot )$, ${W}_1 (\cdot )$, ${W}_2 (\cdot )$, ${W}_3 (\cdot )$, ${W}_4 (\cdot )$, ${W}_5 (\cdot )$ depicts the standard Brownian motion and $H_1$, $H_2$, $H_3$, $H_4$, $H_5$, $H_6$ represents the stochastic constants, and $\nu _i$, for $i=1,..., 6$ are noise intensity parameters.

Existence and Uniqueness (EU)

Here we examine the EU of the solution to system (31) in the presence of stochastic components.

$$\begin{aligned} {\left\{ \begin{array}{ll} ^{\mathbb {ABC}}_{0}D_{t}^{\zeta }S(t) - H_{11}(S,t) = \nu _1 H_1(t,S) \dot{W}_0(t), \\ ^{\mathbb {ABC}}_{0}D_{t}^{\zeta }V(t) - H_{12}(V,t) = \nu _2 H_2(t,V) \dot{W}_1(t), \\ ^{\mathbb {ABC}}_{0}D_{t}^{\zeta }E(t) - H_{13}(A,t) = \nu _3 H_3(t,E) \dot{W}_2(t), \\ ^{\mathbb {ABC}}_{0}D_{t}^{\zeta }A(t) - H_{14}(E,t) = \nu _4 H_4(t,A) \dot{W}_3(t), \\ ^{\mathbb {ABC}}_{0}D_{t}^{\zeta }I(t) - H_{15}(I,t) = \nu _5 H_5(t,I) \dot{W}_4(t), \\ ^{\mathbb {ABC}}_{0}D_{t}^{\zeta }R(t) - H_{16}(R,t) = \nu _6 H_6(t,R) \dot{W}_5(t). \end{array}\right. } \end{aligned}$$

(32)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} H_{11}(S,t)= \Pi -\frac{(a_1 I+a_2 A)S}{N}-(\mu +\omega ) S+\kappa R+\theta V, \\ H_{12}(V,t)= \omega S- (1-\psi ) \frac{(a_1 I+a_2 A)V}{N}-(\theta +\mu ) V,\\ H_{13}(A,t)= \frac{(a_1 I+a_2 A)S}{N}+ (1-\psi ) \frac{(a_1 I+a_2 A)V}{N}-(\delta +\mu ) E,\\ H_{14}(E,t)= \delta q E-(\mu +\rho _1) A,\\ H_{15}(I,t)= (1-q) \delta E-(\mu +d+\rho ) I,\\ H_{16}(R,t)=\rho I+\rho _1 A-(\kappa +\mu ) R. \end{array}\right. } \end{aligned}$$

(33)

The following conditions are proved, $|H_{1i}(t,Y_i)|^2$,  

$$|H_{i}(t,Y_i)|^2< K_i (1+|Y_i|^2), ~\forall ~t \in [0,T],$$

and $|H_{1i}(t,Y^1_i)-H_{1i}(t, Y^2_i)|^2$,  

$$|H_{i}(t,Y^1_i)-H_{i}(t,Y^2_i)|^2< \bar{K}_i (|Y^1_i-Y^2_i|^2),~ \forall t\in [0,T], ~~ ~for~ i=1,2,..,6.$$

, and $Y_i=S, V, A, E, I, R.$

$$\begin{aligned} |H_{11}(S,t)|^2= & \bigg |\Pi -\frac{(a_1 I+a_2 A)S}{N}-(\mu +\omega ) S+\kappa R+\theta V\bigg |^2,\\\\\le & 3 \bigg (\pi ^2 +\frac{|S|^2}{N^2}({a_1^{2} |I|^2+a_2^{2} |A|^2}) + (\mu +\omega )^2 |S|^2 + \theta ^2 |V|^2 +\kappa ^2 |R|^2\bigg ),\\\\\le & 3 \bigg (\pi ^2 +\frac{|S|^2}{N^2}\bigg ({a_1^{2} \sup _{0 \le t\le T}|I|^2+a_2^{2} \sup _{0 \le t\le T}|A|^2}\bigg ) + (\mu +\omega )^2 |S|^2 + \theta ^2 \sup _{0 \le t\le T} |V|^2 +\kappa ^2 \sup _{0 \le t\le T}|R|^2\bigg ),\\\\\le & 3 \bigg (\pi ^2 +\frac{|S|^2}{N^2}\bigg ({a_1^{2} ||I^2||_\infty +a_2^{2} ||A^2||_\infty }\bigg ) + (\mu +\omega )^2 |S|^2 + \theta ^2 ||V^2||_\infty +\kappa ^2 ||R^2||_\infty \bigg ),\\\\\le & 3 \bigg (\bigg (\pi ^2 + \theta ^2 ||V^2||_\infty +\kappa ^2 ||R^2||_\infty \bigg )+\bigg ( \frac{1}{N^2}\bigg ({a_1^{2} ||I^2||_\infty +a_2^{2} ||A^2||_\infty }\bigg )+ (\mu +\omega )^2\bigg ) |S|^2 \bigg ),\\\\\le & 3 \bigg (\pi ^2 + \theta ^2 ||V^2||_\infty +\kappa ^2 ||R^2||_\infty \bigg ) \bigg (1+\frac{ \frac{1}{N^2}\bigg ({a_1^{2} ||I^2||_\infty +a_2^{2} ||A^2||_\infty }\bigg )+ (\mu +\omega )^2}{K_1/3} |S|^2 \bigg ) ,\\\\\le & K_{1} (1+|S|^2). \end{aligned}$$

(34)

where $K_{1}=3 \bigg (\pi ^2 + \theta ^2 ||V^2||_\infty +\kappa ^2 ||R^2||_\infty \bigg )$ and $\frac{ \frac{1}{N^2}\bigg ({a_1^{2} ||I^2||_\infty +a_2^{2} ||A^2||_\infty }\bigg )+ (\mu +\omega )^2}{K_1/3}<1$.

$$\begin{aligned} |H_{12}(V,t)|^2= & \bigg |\omega S- (1-\psi ) \frac{(a_1 I+a_2 A)V}{N}-(\theta +\mu ) V\bigg |^2,\\\\\le & 3 \bigg (\omega ^2 |S|^2+ (1-\psi )^2 \frac{1}{N^2}\bigg (a_1^2 |I|^2+a_2^2 |A|^2 \bigg )|V|^2+(\theta +\mu )^2 |V|^2\bigg ),\\\\\le & 3 \bigg (\omega ^2 \sup _{0 \le t\le T}|S|^2+ \frac{(1+\psi )^2}{N^2}\bigg (a_1^2 \sup _{0 \le t\le T}|I|^2+a_2^2 \sup _{0 \le t\le T}|A|^2 \bigg )|V|^2+(\theta +\mu )^2 |V|^2\bigg ),\\\\\le & 3 \bigg (\omega ^2 ||S^2||_\infty + \frac{(1+\psi )^2}{N^2}\bigg (a_1^2 ||I^2||_\infty +a_2^2 ||A^2||_\infty \bigg )|V|^2+(\theta +\mu )^2 |V|^2\bigg ),\\\\\le & 3 \omega ^2 ||S^2||_\infty \bigg (1+ \frac{\frac{(1+\psi )^2}{N^2}\bigg (a_1^2 ||I^2||_\infty +a_2^2 ||A^2||_\infty \bigg )+(\theta +\mu )^2}{K_2/3} |V|^2\bigg ),\\\\\le & K_{2} (1+|V|^2). \end{aligned}$$

(35)

where $K_{2}=3 \omega ^2 ||S^2||_\infty$ and $\frac{\frac{(1+\psi )^2}{N^2}\bigg (a_1^2 ||I^2||_\infty +a_2^2 ||A^2||_\infty \bigg )+(\theta +\mu )^2}{K_2/3}<1$.

$$\begin{aligned} |H_{13}(E,t)|^2= & \bigg |\frac{(a_1 I+a_2 A)S}{N}+ (1-\psi ) \frac{(a_1 I+a_2 A)V}{N}-(\delta +\mu ) E\bigg |^2,\\\\\le & \frac{3}{N^2}\bigg (|S|^2+(1-\psi )^2 |V|^2 \bigg )\bigg (a_1^2|I|^2+a_2^2|A|^2\bigg )+(\delta +\mu )^2 |E|^2,\\\\\le & \frac{3}{N^2}\bigg (\sup _{0 \le t\le T}|S|^2+(1+\psi )^2 \sup _{0 \le t\le T}|V|^2 \bigg )\bigg (a_1^2 \sup _{0 \le t\le T}|I|^2+a_2^2 \sup _{0 \le t\le T}|A|^2\bigg )+(\delta +\mu )^2 |E|^2,\\\\\le & \frac{3}{N^2}\bigg (||S^2||_{\infty }+(1+\psi )^2 ||V^2||_{\infty } \bigg )\bigg (a_1^2 ||I^2||_\infty +a_2^2 ||A^2||_\infty \bigg )+(\delta +\mu )^2 |E|^2,\\\\\le & 3 \frac{1}{N^2}\bigg (||S^2||_{\infty }+(1+\psi )^2 ||V^2||_{\infty } \bigg )\bigg (a_1^2 ||I^2||_\infty +a_2^2 ||A^2||_\infty \bigg )\times \\\\ & \bigg (1+\frac{(\delta +\mu )^2}{\frac{1}{N^2}\bigg (||S^2||_{\infty }+(1+\psi )^2 ||V^2||_{\infty } \bigg )\bigg (a_1^2 ||I^2||_\infty +a_2^2 ||A^2||_\infty \bigg )} |E|^2\bigg ),\\\\\le & K_3 \bigg (1+\frac{(\delta +\mu )^2}{K_3/3} |E|^2\bigg ),\\\\\le & K_{3} (1+|E|^2). \end{aligned}$$

(36)

where $K_{3}=3 \frac{1}{N^2}\bigg (||S^2||_{\infty }+(1+\psi )^2 ||V^2||_{\infty } \bigg )\bigg (a_1^2 ||I^2||_\infty +a_2^2 ||A^2||_\infty \bigg )$ and $\frac{(\delta +\mu )^2}{K_3/3}<1$.

$$\begin{aligned} |H_{14}(A,t)|^2= & \bigg |\delta q E-(\mu +\rho _1) A\bigg |^2,\\\\\le & 3 \bigg (\delta ^2 q^2 \sup _{0 \le t\le T} |E|^2+(\rho _1+\mu )^2 |A|^2 \bigg ),\\\\\le & 3 \bigg (\delta ^2 q^2 ||E^2||_\infty +(\rho _1+\mu )^2 |A|^2 \bigg ),\\\\\le & 3 \delta ^2 q^2 ||E^2||_\infty \bigg (1+\frac{(\rho _1+\mu )^2}{K_4/3} |A|^2\bigg ),\\\\\le & K_{4} (1+|A|^2), \end{aligned}$$

(37)

where $K_{4}=3 \delta ^2 q^2 ||E^2||_\infty$ and $\frac{(\rho _1+\mu )^2}{K_4/3}<1$.

$$\begin{aligned} |H_{15}(I,t)|^2= & \bigg |(1-q) \delta E-(\mu +d+\rho ) I \bigg |^2,\\\\\le & 3 \bigg (\delta ^2 (1+q)^2 |E|^2+(\mu +d+\rho )^2 |I|^2 \bigg ),\\\\\le & 3 \bigg (\delta ^2 (1+q)^2 \sup _{0 \le t\le T} |E|^2+(\mu +d+\rho )^2 |I|^2 \bigg ),\\\\\le & 3 \bigg (\delta ^2 (1+q)^2 ||E^2||_\infty +(\mu +d+\rho )^2 |I|^2 \bigg ),\\\\\le & 3 \delta ^2 (1+q)^2 ||E^2||_\infty \bigg (1+\frac{(\rho +\mu +d)^2}{K_5/3} |I|^2\bigg ),\\\\\le & K_{5} (1+|I|^2), \end{aligned}$$

(38)

where $K_{5}=3 \delta ^2 (1+q)^2 ||E^2||_\infty$ and $\frac{(\rho +\mu +d)^2}{K_5/3}<1$.

$$\begin{aligned} |H_{15}(R,t)|^2= & \bigg | \rho I+\rho _1 A-(\kappa +\mu ) R \bigg |^2,\\\\\le & 3 \bigg (\rho ^2 |I|^2+(\kappa +\mu )^2 |R|^2 \bigg ),\\\\\le & 3 \bigg (\rho ^2 \sup _{0 \le t\le T} |I|^2+(\kappa +\mu )^2 |R|^2 \bigg ),\\\\\le & 3 \bigg (\rho ^2||I^2||_\infty +(\kappa +\mu )^2 |R|^2 \bigg ),\\\\\le & 3 \rho ^2||I^2||_\infty \bigg (1+\frac{(\kappa +\mu )^2}{K_6/3} |R|^2\bigg ),\\\\\le & K_{6} (1+|R|^2). \end{aligned}$$

(39)

where $K_{6}=3 \rho ^2||I^2||_\infty$ and $\frac{(\kappa +\mu )^2}{K_6/3}<1$. We get the following, for every $t \in [0, T]$:

$$\begin{aligned} {\left\{ \begin{array}{ll} |H_1(t,S)|^2 = \nu _1^2 |S|^2 \le \nu _1^2( 1+|S|^2),~~ |H_2(t,V)|^2 = \nu _2^2 |V|^2 \le \nu _2^2( 1+|V|^2),\\ |H_3(t,E)|^2 = \nu _3^2 |E|^2 \le \nu _3^2( 1+|E|^2),~~ |H_4(t,A)|^2 = \nu _4^2 |A|^2 \le \nu _4^2( 1+|A|^2),\\ |H_5(t,I)|^2 = \nu _5^2 |I|^2 \le \nu _5^2( 1+|I|^2),~~ |H_6(t,R)|^2 = \nu _6^2 |R|^2 \le \nu _6^2( 1+|R|^2). \end{array}\right. } \end{aligned}$$

(40)

We verifying the other condition given by,

$$\begin{aligned} & {\left\{ \begin{array}{ll} |H_{11}(t, S)-H_{11}(t, S_1)|^2 = |\Pi -\frac{(a_1 I+a_2 A)S}{N}-(\mu +\omega ) S+\kappa R+\theta V-\\ \Pi +\frac{(a_1 I+a_2 A)S_1}{N}+(\mu +\omega ) S_1-\kappa R-\theta V|^2,\\ =|-\frac{(a_1 I+a_2 A)(S-S_1)}{N}-(\mu +\omega ) (S-S_1)|^2,\\ \le 4 \bigg (\frac{(a^2_1 |I|^2+a^2_2 |A|^2)|S-S_1|^2}{N^2}+(\mu +\omega )^2 |S-S_1|^2 \bigg )\\ \le 4 \bigg (\frac{(a^2_1 ||I^2||_\infty +a^2_2 ||A^2||_\infty )}{N^2}+(\mu +\omega )^2 \bigg ) |S-S_1|^2 \\ \le \overline{K}_1 |S-S_1|^2 . \end{array}\right. } \end{aligned}$$

(41)

$$\begin{aligned} & {\left\{ \begin{array}{ll} |H_{12}(t, V)-H_{12}(t, V_1)|^2 = |\omega S- (1-\psi ) \frac{(a_1 I+a_2 A)V}{N}-(\theta +\mu ) V-\\ \omega S+ (1-\psi ) \frac{(a_1 I+a_2 A)V_1}{N}+(\theta +\mu ) V_1|^2,\\ =|- (1-\psi ) \frac{(a_1 I+a_2 A)(V-V_1)}{N}- (\theta +\mu ) (V-V_1) |^2,\\ \le 4 \bigg ( (1+\psi )^2 \frac{(a^2_1 |I|^2+a^2_2 |A|^2)|V-V_1|^2}{N^2}+(\theta +\mu )^2 |V-V_1|^2 \bigg )\\ \le 4 \bigg ((1+\psi )^2 \frac{(a^2_1 ||I^2||_\infty +a^2_2 ||A^2||_\infty )}{N^2}+(\mu +\theta )^2 \bigg ) |V-V_1|^2 \\ \le \overline{K}_2 |V-V_1|^2 . \end{array}\right. } \end{aligned}$$

(42)

$$\begin{aligned} & {\left\{ \begin{array}{ll} |H_{13}(t, E)-H_{13}(t, E_1)|^2 = |\frac{(a_1 I+a_2 A)S}{N}+ (1-\psi ) \frac{(a_1 I+a_2 A)V}{N}-(\delta +\mu ) E-\\ \frac{(a_1 I+a_2 A)S}{N}- (1-\psi ) \frac{(a_1 I+a_2 A)V}{N}+(\delta +\mu ) E_1|^2,\\ =|-(\delta +\mu )(E-E_1)|^2,\\ \le 4 (\delta +\mu )^2 |E-E_1|^2 \\ \le \overline{K}_3 |E-E_1|^2. \end{array}\right. } \end{aligned}$$

(43)

$$\begin{aligned} & {\left\{ \begin{array}{ll} |H_{14}(t, A)-H_{14}(t, A_1)|^2 = |\delta q E-(\mu +\rho _1) A-\delta q E+(\mu +\rho _1) A_1|^2,\\ =|-(\mu +\rho _1)(A-A_1)|^2,\\ \le 4 (\mu +\rho _1)^2 |A-A_1|^2 \\ \le \overline{K}_4 |A-A_1|^2 . \end{array}\right. } \end{aligned}$$

(44)

$$\begin{aligned} & {\left\{ \begin{array}{ll} |H_{15}(t, I)-H_{15}(t, I_1)|^2 = |(1-q) \delta E-(\mu +d+\rho ) I-(1-q) \delta E+(\mu +d+\rho ) I_1|^2,\\ =|-(\mu +d+\rho )(I-I_1)|^2,\\ \le 4 (\mu +d+\rho )^2 |I-I_1|^2 \\ \le \overline{K}_5 |S-S_1|^2 . \end{array}\right. } \end{aligned}$$

(45)

$$\begin{aligned} & {\left\{ \begin{array}{ll} |H_{16}(t, R)-H_{16}(t, R_1)|^2 = |\rho I+\rho _1 A-(\kappa +\mu ) R-\rho I+\rho _1 A+(\kappa +\mu ) R_1|^2,\\ =|-(\kappa +\mu ) (R-R_1)|^2,\\ \le 4 (\kappa +\mu )^2 |R-R_1|^2 \\ \le \overline{K}_6 |R-R_1|^2. \end{array}\right. } \end{aligned}$$

(46)

$$\begin{aligned} & {\left\{ \begin{array}{ll} |H_{11}(t, S)-H_{11}(t, S_1)|^2 = \frac{3}{2} \nu _1^2 |S-S_1|^2 \le \overline{K_1}|S-S_1|^2,\\ |H_{12}(t, V)-H_{12}(t, V_1)|^2 = \frac{3}{2} \nu _2^2 |V-V_1|^2 \le \overline{K_2}|V-V_1|^2,\\ |H_{13}(t, E)-H_{13}(t, E_1)|^2 = \frac{3}{2} \nu _3^2 |E-E_1|^2 \le \overline{K_3}|E-E_1|^2,\\ |H_{14}(t, A)-H_{14}(t, A_1)|^2 = \frac{3}{2} \nu _4^2 |A-A_1|^2 \le \overline{K_4}|A-A_1|^2,\\ |H_{15}(t, I)-H_{15}(t, I_1)|^2 = \frac{3}{2} \nu _5^2 |I-I_1|^2 \le \overline{K_5}|I-I_1|^2,\\ |H_{16}(t, R)-H_{16}(t, R_1)|^2 = \frac{3}{2} \nu _6^2 |R-R_1|^2 \le \overline{K_6}|R-R_1|^2. \end{array}\right. } \end{aligned}$$

(47)

We get the result if the condition given below is satisfied

$\max \bigg \{ \frac{ \frac{1}{N^2}\bigg ({a_1^{2} ||I^2||_\infty +a_2^{2} ||A^2||_\infty }\bigg )+ (\mu +\omega )^2}{K_1/3},\frac{\frac{(1+\psi )^2}{N^2}\bigg (a_1^2 ||I(t)^2||_\infty +a_2^2 ||A(t)^2||_\infty \bigg )+(\theta +\mu )^2}{K_2/3} , \frac{(\delta +\mu )^2}{K_3/3}, \frac{(\rho _1+\mu )^2}{K_4/3}, \frac{(\rho +\mu +d)^2}{K_5/3},\frac{(\kappa +\mu )^2}{K_6/3}\bigg \}<1.$

Numerical scheme for the model using Atangana-Baleanu derivative

Now consider the case where the differential operator is Atangana-Baleanu. The following results are presented:

$$\begin{aligned} S(t)&= \mathcal {A} H_{11}(S,\tau )+ \mathcal {A} \nu _1 H_{1}(S,\tau )\dot{W}_0(\tau )+ \mathcal {B} \int _0^{t}\mathcal {C} H_{11}(S,\tau )d\tau +&\mathcal {B} \int _{0}^{t} \mathcal {C} H_1(S, \tau ) \nu _1 \dot{W}_0(\tau ) d\tau +S(0), \end{aligned}$$

(48)

$$\begin{aligned} V(t)&= \mathcal {A} H_{12}(V,\tau )+ \mathcal {A} \nu _2 H_{2}(V,\tau )\dot{W}_1(\tau )+ \mathcal {B} \int _0^{t}\mathcal {C} H_{12}(V,\tau )d\tau +&\mathcal {B} \int _{0}^{t} \mathcal {C} H_2(V, \tau ) \nu _2 \dot{W}_1(\tau ) d\tau +V(0), \end{aligned}$$

(49)

$$\begin{aligned} E(t)&= \mathcal {A} H_{13}(E,\tau )+ \mathcal {A} \nu _3 H_{3}(E,\tau )\dot{W}_2(\tau )+ \mathcal {B}\int _0^{t}\mathcal {C} H_{13}(E,\tau )d\tau +&\mathcal {B} \int _{0}^{t} \mathcal {C} H_3(E, \tau ) \nu _3 \dot{W}_2(\tau ) d\tau +E(0), \end{aligned}$$

(50)

$$\begin{aligned} A(t)&= \mathcal {A} H_{14}(A,\tau )+ \mathcal {A} \nu _4 H_{4}(A,\tau )\dot{W}_3(\tau )+ \mathcal {B} \int _0^{t}\mathcal {C} H_{14}(A,\tau )d\tau +&\mathcal {B} \int _{0}^{t} \mathcal {C} H_4(A, \tau ) \nu _4 \dot{W}_3(\tau ) d\tau +A(0), \end{aligned}$$

(51)

$$\begin{aligned} I(t)&= \mathcal {A} H_{15}(I,\tau )+ \mathcal {A} \nu _5 H_{5}(I,\tau )\dot{W}_4(\tau )+ \mathcal {B} \int _0^{t}\mathcal {C} H_{15}(I,\tau )d\tau +&\mathcal {B} \int _{0}^{t} \mathcal {C} H_5(I, \tau ) \nu _5 \dot{W}_4(\tau ) d\tau +I(0), \end{aligned}$$

(52)

$$\begin{aligned} R(t)&= \mathcal {A} H_{16}(R,\tau )+ \mathcal {A} \nu _6 H_{6}(R,\tau )\dot{W}_5(\tau )+ \mathcal {B} \int _0^{t}\mathcal {C} H_{16}(R,\tau )d\tau +&\mathcal {B} \int _{0}^{t} \mathcal {C} H_6(R, \tau ) \nu _6 \dot{W}_5(\tau ) d\tau +R(0), \end{aligned}$$

(53)

where $\mathcal {C}=(t-\tau )^{\zeta -1}$. Here the function $H_{11}$ and $H_1$ are approximately using the Lagrange Polynomials taken from⁴³. This yields to:

$$\begin{aligned} \begin{aligned} S(t_{n+1})&= \mathcal {A} H_{11}(S_{n}, t_n)+ \mathcal {A} \nu _1 H_{1}(S_n,t_n)[W_0(t_{n+1})-W_0(t_{n})]+ \mathcal {B}_1 \sum _{g=2}^{n} H_{11}(S_{g-2}, t_{g-2}) M_{01} \\&\quad +\mathcal {B}_2 \sum _{g=2}^{n} \bigg \{H_{11}(S_{g-1}, t_{g-1}) -H_{11}(S_{g-2}, t_{g-2})\bigg \} M_{02}+\mathcal {B}_3 \sum _{g=2}^{n} \bigg \{H_{11}(S_{g}, t_g)-2 H_{11}(S_{g-1}, t_{g-1}) \\&\quad +H_{11}(S_{g-2}, t_{g-2})\bigg \} \times M_{03}+ \mathcal {B}_1 \nu _1 \sum _{g=2}^{n} H_{1}(S_{g-2},t_{g-2}) M_{01}[W_0(t_{g-1})-W_0(t_{g-2})] +\mathcal {B}_2 \nu _1 \\&\quad \sum _{g=2}^{n} \bigg \{H_{1}(S_{g-1},t_{g-1}) [W_0(t_{g})-W_0(t_{g-1})] -H_{1}(S_{g-2},t_{g-2}) [W_0(t_{g-1})-W_0(t_{g-2})]\bigg \} M_{02} \\&\quad + \mathcal {B}_3 \nu _1 \sum _{g=2}^{n} \bigg \{ H_{1}(S_{g},t_{g})[W_0(t_{g+1})-W_0(t_{g})]-2 H_{1}(S_{g-1},t_{g-1})[W_0(t_{g})-W_0(t_{g-1})] \\ &\quad + H_{1}(S_{g-2},t_{g-2})[W_0(t_{g-1})-W_0(t_{g-2})]\bigg \} M_{03}, \end{aligned}\end{aligned}$$

(54)

where $\mathcal {B}_1= \frac{\zeta (\Delta t)^{\zeta -1}}{AB(\zeta ) \Gamma {(\zeta +1)}}$, $\mathcal {B}_2= \frac{\zeta (\Delta t)^{\zeta -1}}{AB(\zeta ) \Gamma {(\zeta +2)}}$ and $\mathcal {B}_3= \frac{\zeta (\Delta t)^{\zeta -1}}{AB(\zeta ) \Gamma {(\zeta +3)}}$,

$$\begin{aligned} V(t_{n+1})&= \mathcal {A} H_{12}(V_{n}, t_n)+ \mathcal {A} \nu _2 H_{2}(V_n,t_n)[W_1(t_{n+1})-W_1(t_{n})]+ \mathcal {B}_1 \sum _{g=2}^{n} H_{12}(V_{g-2}, t_{g-2}) M_{01} \nonumber \\&\quad +\mathcal {B}_2 \sum _{g=2}^{n} \bigg \{H_{12}(V_{g-1}, t_{g-1}) -H_{12}(V_{g-2}, t_{g-2})\bigg \} M_{02}+\mathcal {B}_3 \sum _{g=2}^{n} \bigg \{H_{12}(V_{g}, t_g)-2 H_{12}(V_{g-1}, t_{g-1}) \nonumber \\&\quad +H_{12}(V_{g-2}, t_{g-2})\bigg \} \times M_{03}+ \mathcal {B}_1 \nu _2 \sum _{g=2}^{n} H_{2}(V_{g-2},t_{g-2}) M_{01}[W_1(t_{g-1})-W_1(t_{g-2})] +\mathcal {B}_2 \nu _2 \nonumber \\&\quad \sum _{g=2}^{n} \bigg \{H_{2}(V_{g-1},t_{g-1}) [W_1(t_{g})-W_1(t_{g-1})] -H_{2}(V_{g-2},t_{g-2}) [W_1(t_{g-1})-W_1(t_{g-2})]\bigg \} M_{02}\nonumber \\&\quad + \mathcal {B}_3 \nu _2 \sum _{g=2}^{n} \bigg \{ H_{2}(V_{g},t_{g})[W_1(t_{g+1})-W_1(t_{g})]-2 H_{2}(V_{g-1},t_{g-1})[W_1(t_{g})-W_1(t_{g-1})] \nonumber \\&\quad + H_{2}(V_{g-2},t_{g-2})[W_1(t_{g-1})-W_1(t_{g-2})]\bigg \} M_{03}, \end{aligned}$$

(55)

$$\begin{aligned} E(t_{n+1})&= \mathcal {A} H_{13}(E_{n}, t_n)+ \mathcal {A} \nu _3 H_{3}(E_n,t_n)[W_2(t_{n+1})-W_2(t_{n})]+ \mathcal {B}_1 \sum _{g=2}^{n} H_{13}(E_{g-2}, t_{g-2}) M_{01} \nonumber \\&\quad +\mathcal {B}_2 \sum _{g=2}^{n} \bigg \{H_{13}(E_{g-1}, t_{g-1}) -H_{13}(E_{g-2}, t_{g-2})\bigg \} M_{02}+\mathcal {B}_3 \sum _{g=2}^{n} \bigg \{H_{13}(E_{g}, t_g)-2 H_{13}(E_{g-1}, t_{g-1}) \nonumber \\&\quad +H_{13}(E_{g-2}, t_{g-2})\bigg \} \times M_{03}+ \mathcal {B}_1 \nu _3 \sum _{g=2}^{n} H_{3}(E_{g-2},t_{g-2}) M_{01}[W_2(t_{g-1})-W_2(t_{g-2})] +\mathcal {B}_2 \nu _3 \nonumber \\&\quad \sum _{g=2}^{n} \bigg \{H_{3}(E_{g-1},t_{g-1}) [W_2(t_{g})-W_2(t_{g-1})] -H_{3}(E_{g-2},t_{g-2}) [W_2(t_{g-1})-W_2(t_{g-2})]\bigg \} M_{02}\nonumber \\&\quad + \mathcal {B}_3 \nu _3 \sum _{g=2}^{n} \bigg \{ H_{3}(E_{g},t_{g})[W_2(t_{g+1})-W_2(t_{g})]- 2 H_{3}(E_{g-1},t_{g-1})[W_2(t_{g})-W_2(t_{g-1})] \nonumber \\&\quad + H_{3}(E_{g-2},t_{g-2})[W_2(t_{g-1})-W_2(t_{g-2})]\bigg \} M_{03}, \end{aligned}$$

(56)

$$\begin{aligned} A(t_{n+1})&= \mathcal {A} H_{14}(A_{n}, t_n)+ \mathcal {A} \nu _4 H_{4}(A_n,t_n)[W_3(t_{n+1})-W_3(t_{n})]+ \mathcal {B}_1 \sum _{g=2}^{n} H_{14}(A_{g-2}, t_{g-2}) M_{01} \nonumber \\&\quad +\mathcal {B}_2 \sum _{g=2}^{n} \bigg \{H_{14}(A_{g-1}, t_{g-1}) -H_{14}(A_{g-2}, t_{g-2})\bigg \} M_{02}+\mathcal {B}_3 \sum _{g=2}^{n} \bigg \{H_{14}(A_{g}, t_g)-2 H_{14}(A_{g-1}, t_{g-1}) \nonumber \\&\quad +H_{14}(A_{g-2}, t_{g-2})\bigg \} \times M_{03}+ \mathcal {B}_1 \nu _4 \sum _{g=2}^{n} H_{4}(A_{g-2},t_{g-2}) M_{01}[W_3(t_{g-1})-W_3(t_{g-2})] +\mathcal {B}_2 \nu _4 \nonumber \\&\quad \sum _{g=2}^{n} \bigg \{H_{4}(A_{g-1},t_{g-1}) [W_3(t_{g})-W_3(t_{g-1})] -H_{4}(A_{g-2},t_{g-2}) [W_3(t_{g-1})-W_3(t_{g-2})]\bigg \} M_{02}\nonumber \\&\quad + \mathcal {B}_3 \nu _4 \sum _{g=2}^{n} \bigg \{ H_{4}(A_{g},t_{g})[W_3(t_{g+1})-W_3(t_{g})]- 2 H_{4}(A_{g-1},t_{g-1})[W_3(t_{g})-W_3(t_{g-1})] \nonumber \\&\quad + H_{4}(A_{g-2},t_{g-2})[W_3(t_{g-1})-W_3(t_{g-2})]\bigg \} M_{03}, \end{aligned}$$

(57)

$$\begin{aligned} I(t_{n+1})&= \mathcal {A} H_{15}(I_{n}, t_n)+ \mathcal {A} \nu _5 H_{5}(I_n,t_n)[W_4(t_{n+1})-W_4(t_{n})]+ \mathcal {B}_1 \sum _{g=2}^{n} H_{15}(I_{g-2}, t_{g-2}) M_{01} \nonumber \\&\quad +\mathcal {B}_2 \sum _{g=2}^{n} \bigg \{H_{15}(I_{g-1}, t_{g-1}) -H_{15}(I_{g-2}, t_{g-2})\bigg \} M_{02}+\mathcal {B}_3 \sum _{g=2}^{n} \bigg \{H_{15}(I_{g}, t_g)-2 H_{15}(I_{g-1}, t_{g-1}) \nonumber \\&\quad +H_{15}(I_{g-2}, t_{g-2})\bigg \} \times M_{03}+ \mathcal {B}_1 \nu _5 \sum _{g=2}^{n} H_{5}(I_{g-2},t_{g-2}) M_{01}[W_4(t_{g-1})-W_4(t_{g-2})] +\mathcal {B}_2 \nu _5 \nonumber \\&\quad \sum _{g=2}^{n} \bigg \{H_{5}(I_{g-1},t_{g-1}) [W_4(t_{g})-W_4(t_{g-1})] -H_{5}(I_{g-2},t_{g-2}) [W_4(t_{g-1})-W_4(t_{g-2})]\bigg \} M_{02} \nonumber \\&\quad + \mathcal {B}_3 \nu _5 \sum _{g=2}^{n} \bigg \{ H_{5}(I_{g},t_{g})[W_4(t_{g+1})-W_4(t_{g})]- 2 H_{5}(I_{g-1},t_{g-1})[W_4(t_{g})-W_4(t_{g-1})] \nonumber \\&\quad + H_{5}(I_{g-2},t_{g-2})[W_4(t_{g-1})-W_4(t_{g-2})]\bigg \} M_{03}, \end{aligned}$$

(58)

$$\begin{aligned} R(t_{n+1})&= \mathcal {A} H_{16}(R_{n}, t_n)+ \mathcal {A} \nu _6 H_{6}(R_n,t_n)[W_5(t_{n+1})-W_5(t_{n})]+ \mathcal {B}_1 \sum _{g=2}^{n} H_{16}(R_{g-2}, t_{g-2}) M_{01} \nonumber \\&\quad +\mathcal {B}_2 \sum _{g=2}^{n} \bigg \{H_{16}(R_{g-1}, t_{g-1}) -H_{16}(R_{g-2}, t_{g-2})\bigg \} M_{02}+\mathcal {B}_3 \sum _{g=2}^{n} \bigg \{H_{16}(R_{g}, t_g)-2 H_{16}(R_{g-1}, t_{g-1}) \nonumber \\&\quad +H_{16}(R_{g-2}, t_{g-2})\bigg \} \times M_{03}+ \mathcal {B}_1 \nu _6 \sum _{g=2}^{n} H_{6}(R_{g-2},t_{g-2}) M_{01}[W_5(t_{g-1})-W_5(t_{g-2})] +\mathcal {B}_2 \nu _6 \nonumber \\&\quad \sum _{g=2}^{n} \bigg \{H_{6}(R_{g-1},t_{g-1}) [W_5(t_{g})-W_5(t_{g-1})] -H_{6}(R_{g-2},t_{g-2}) [W_5(t_{g-1})-W_5(t_{g-2})]\bigg \} M_{02}\nonumber \\&\quad + \mathcal {B}_3 \nu _6 \sum _{g=2}^{n} \bigg \{ H_{6}(R_{g},t_{g})[W_5(t_{g+1})-W_5(t_{g})]- 2 H_{6}(R_{g-1},t_{g-1})[W_5(t_{g})-W_5(t_{g-1})] \nonumber \\&\quad + H_{6}(R_{g-2},t_{g-2})[W_5(t_{g-1})-W_5(t_{g-2})]\bigg \} M_{03}, \end{aligned}$$

(59)

where $M_{01}=[(n-g+1)^\zeta -(n-g)^\zeta ]$

$M_{02}=\bigg [(n-g+1)^\zeta (n-g+3+2 \zeta )-(n-g)^\zeta (n-g+3+3\zeta ) \bigg ]$

$M_{03}=\bigg [(n-g+1)^\zeta \bigg [2(n-g)^2+(3 \zeta +10)(n-g)+2 \zeta ^2 +9 \zeta +12\bigg ]-(n-g)^\zeta \bigg [2(n-g)^2+(5 \zeta +10)(n-g)+6 \zeta ^2 +18 \zeta +12\bigg ] \bigg ]$.

Numerical simulations

Using the numerical scheme described earlier, we present numerical simulations for different values of the fractional-order $\zeta$. For all simulations, a fixed temporal step size of $h = 0.01$ was used to ensure numerical stability and to accurately capture the system’s dynamics. Both the deterministic and stochastic schemes were confirmed to converge robustly to the true steady-state solutions.

The baseline numerical values for the model parameters are taken from Table 1. The constants for the stochastic noise terms are set to $\nu _1=2 \times 10^{-4}$ and $\nu _i=2 \times 10^{-2}$ for $i=2, \ldots , 6$.

Specifically, the results shown in Figs. 4 to 9 correspond to the Disease-Free Equilibrium (DFE) case, simulated with the following parameter values: $\mu =1/(67.7 \times 365)$, $\Pi =\mu \times 230557367$, $a_1=0.8983$, $a_2=0.3827$, $\omega =0.01$, $\kappa =0.3129$, $\delta =0.9982$, $q=0.9931$, $\rho _1=0.3028$, $\rho =0.7926$, $d=0.6784$, $\theta =0.01$, $\psi =0.6$, and the aforementioned noise constants $\nu _1$–$\nu _6$, using a step size of $h=0.01$.

We provide simulation results in Figs. 4 to 16. Figure 4 compares the susceptible compartment S(t) for the fractional-order and stochastic fractional-order systems across various values of $\zeta$. Figure 5 presents a similar comparison for the vaccinated compartment V(t). Likewise, Figs. 6 to 9 show the comparison for the exposed (E), asymptomatic (A), infected (I), and recovered (R) compartments, respectively. These results demonstrate that the solution converges to the disease-free equilibrium (DFE).

Fig. 4

Comparison of the susceptible compartment S(t) for different values of the fractional-order $\zeta$. Parameters for the Disease-Free Equilibrium (DFE) case: $\mu =1/(67.7 \times 365)$, $\Pi = \mu \times 230557367$, $a_1=0.8983$, $a_2=0.3827$, $\omega =0.01$, $\kappa =0.3129$, $\delta =0.9982$, $q=0.9931$, $\rho _1=0.3028$, $\rho =0.7926$, $d=0.6784$, $\theta =0.01$, $\psi =0.6$, $\nu _1=2\times 10^{-4}$, $\nu _i=0.02$ (for $i=2,...,6$).

Fig. 5

Comparison of the vaccinated compartment V(t) for different values of $\zeta$. Parameters are the same as in Fig. 4 for the DFE case.

Fig. 6

Comparison of the exposed compartment E(t) for different values of $\zeta$. Parameters are the same as in Fig. 4 for the DFE case.

Fig. 7

Comparison of the asymptomatic infected compartment A(t) for different values of $\zeta$. Parameters are the same as in Fig. 4 for the DFE case.

Fig. 8

Comparison of the symptomatic infected compartment I(t) for different values of $\zeta$. Parameters are the same as in Fig. 4 for the DFE case.

Fig. 9

Comparison of the recovered compartment R(t) for different values of $\zeta$. Parameters are the same as in Fig. 4 for the DFE case.

Figures 10 to 15 represent the model solutions for the fractional and stochastic fractional differential equations. The results show that the solutions approach the endemic equilibrium (EE) point. The parameter values used in these simulations (Figures 10–15) are:

$$\begin{aligned}&\mu = 1/(67.7 \times 365), \quad \Pi = \mu \times 230557367, \quad a_1 = 0.8983, \quad a_2 = 0.3827, \\&\omega = 0.001, \quad \kappa = 0.3129, \quad \delta = 0.9982, \quad q = 0.9931, \\&\rho _1 = 0.3028, \quad \rho = 0.7926, \quad d = 0.6784, \quad \theta = 0.01, \quad \psi = 0.6, \\&\nu _1 = 2 \times 10^{-4}, \quad \nu _2 = 2 \times 10^{-2}, \quad \nu _3 = 2 \times 10^{-2}, \\&\nu _4 = 2 \times 10^{-2}, \quad \nu _5 = 2 \times 10^{-2}, \quad \nu _6 = 2 \times 10^{-2}, \end{aligned}$$

with a step size of $h = 0.01$.

The variation in the fractional-order $\zeta$ correctly captures both the disease-free equilibrium (DFE) and endemic equilibrium (EE) solution behaviors, which is characteristic of fractional model simulations.

Fig. 10

Comparison of the susceptible compartment S(t) for different values of the fractional-order $\zeta$. Parameters for the Endemic Equilibrium (EE) case: $\mu =1/(67.7 \times 365)$, $\Pi = \mu \times 230557367$, $a_1=0.8983$, $a_2=0.3827$, $\omega =0.001$, $\kappa =0.3129$, $\delta =0.9982$, $q=0.9931$, $\rho _1=0.3028$, $\rho =0.7926$, $d=0.6784$, $\theta =0.01$, $\psi =0.6$, $\nu _1=2\times 10^{-4}$, $\nu _i=0.02$ (for $i=2,...,6$).

Fig. 11

Comparison of the vaccinated compartment V(t) for different values of $\zeta$. Parameters are the same as in Fig. 10 for the EE case.

Fig. 12

Comparison of the exposed compartment E(t) for different values of $\zeta$. Parameters are the same as in Fig. 10 for the EE case.

Fig. 13

Comparison of the asymptomatic infected compartment A(t) for different values of $\zeta$. Parameters are the same as in Fig. 10 for the EE case.

Fig. 14

Comparison of the symptomatic infected compartment I(t) for different values of $\zeta$. Parameters are the same as in Fig. 10 for the EE case.

Fig. 15

Comparison of the recovered compartment R(t) for different values of $\zeta$. Parameters are the same as in Fig. 10 for the EE case.

Figure 16 shows the impact of the vaccine efficacy rate $\psi$ for a fixed fractional-order $\zeta = 0.95$. As the vaccine efficacy $\psi$ decreases, the population sizes of the model compartments change accordingly.

Fig. 16

Impact of the vaccine efficacy rate ($\psi$) on the system compartments for a fixed fractional-order $\zeta =0.95$. Parameters: $\mu =1/(67.7 \times 365)$, $\Pi = \mu \times 230557367$, $a_1=0.8983$, $a_2=0.3827$, $\omega =0.01$, $\kappa =0.3129$, $\delta =0.9982$, $q=0.9931$, $\rho _1=0.3028$, $\rho =0.7926$, $d=0.6784$, $\theta =0.01$.

Conclusion

In the present work, we formulated a mathematical model for COVID-19 infection using fractional differential equations with the Mittage-Leffler kernel, which effectively captures the memory effects in disease dynamics. The model was further extended into a fractional stochastic differential equation framework to account for random fluctuations and uncertainty inherent in real world epidemic spread.

We established the positivity and boundedness of the model and derived its equilibrium points in the fractional deterministic case. The existence and uniqueness of solutions to the FSDE were rigorously proven, and a new numerical scheme tailored to the Atangana–Baleanu-type fractional stochastic model was proposed and implemented. The real COVID-19 data from Pakistan for the specified period were used to estimate realistic parameter values. Simulations were carried out to examine the influence of the fractional-order parameter and other key parameters on disease dynamics, particularly their role in disease elimination scenarios.

The novelty of this study lies in the integration of fractional calculus in the Mittag-Leffler sense with stochastic modeling, offering a more realistic and flexible framework for capturing both memory effects and randomness in COVID-19 dynamics. This approach enhances the ability to simulate and understand the impact of fractional dynamics on control strategies, including vaccination.

This research provides a foundation for several important extensions. Future work will focus on incorporating spatial heterogeneity to analyze geographic variation in transmission and intervention efficacy. Furthermore, the model will be extended to include additional compartments, particularly a vaccinated-but-susceptible class, to more accurately represent waning immunity and breakthrough infections.