Introduction

Global warming has emerged as one of the most pressing challenges. Carbon dioxide (CO₂), a primary greenhouse gas, is a major contributor to climate change1. Cement production alone contributes 7–8% of global CO₂ output2. The environmental toll of cement manufacturing is overwhelming: for every ton of cement Manufactured, an estimated 0.9 tons of CO₂ are released into the atmosphere3. The construction industry has become a critical focus area for reducing carbon emissions and advancing sustainability goals. To combat climate change, the sector has increasingly adopted eco-friendly building technologies and materials4,5,6,7,8 as part of carbon neutrality initiatives. Among these innovations, geopolymer concrete (GC) has gained significant attention for demonstrating mechanical strengths surpassing those of conventional Portland cement (PC) concrete, alongside enhanced durability against chemical reactions9, corrosion10, and high-temperature exposure11. Unlike PC-based materials, GC is synthesized through alkaline activation solutions (such as silicates, alkali hydroxides, and carbonates) and industrial byproduct precursors, including blast furnace slag, fly ash, metakaolin, rice husk ash, and red mud. This substitution eliminates the energy-intensive clinker production required for PC, thereby enabling substantial reductions in lifecycle carbon emissions.

It should be noted that GC may suffer from low compressive strength and poor durability performance. Therefore, the development of high-performance geopolymer concrete (HPGC)—an advanced variant of GC with enhanced mechanical and durability properties—has attracted wide attention in infrastructure applications, including high-rise buildings and long-span bridges. However, HPGC optimization requires balancing competing objectives: compressive strength, cost, and carbon emissions. While compressive strength continues to dominate mix design criteria, cost and carbon emissions have emerged as equally critical constraints. Traditional laboratory trial-and-error approaches12 and non-destructive methods13,14,15,16 to optimize these multi-variable systems are excessively resource-intensive and inefficient. Consequently, there is an urgent need for computational frameworks capable of simultaneously maximizing compressive strength, minimizing costs, and reducing carbon emissions in HPGC production.

Machine learning (ML) becomes a powerful and alternative way to solve complicated nonlinear and high-dimensional problems17,18. It has demonstrated significant potential across diverse civil engineering applications, including structural health monitoring19, damage detection20, structural response prediction21,22,23, and strength prediction24,25,26,27,28,29,30,31,32,33,34. Notably, ML has been successfully employed to forecast compressive strength in GC35,36,37 and ultra-high-performance geopolymer concrete (UHPGC)38,39,40. Parallel advancements in multi-objective optimization (MOO) have explored trade-offs between strength, cost, and CO₂ emissions in GC41 and UHPGC42. However, to the authors’ knowledge, no prior study has integrated ML-based predictive modeling with MOO frameworks for HPGC—a gap this work seeks to bridge as its principal contribution.

Traditional ML workflows are highly complex, typically comprising five key stages: (1) Data Collection: Collecting relevant datasets refer to the research objective. (2) Data Preprocessing: Cleansing anomalies such as outliers and missing values, followed by partitioning the dataset into training, testing, and validation subsets. (3) Model Selection: Identifying suitable ML algorithms based on problem type (regression/classification), data characteristics, and performance criteria. (4) Hyperparameter Tuning: Optimizing model configurations via grid search or randomized methods to enhance predictive accuracy. (5) Model Evaluation: Quantifying performance on test data using metrics like the coefficient of determination (R²), root mean squared error (RMSE), and mean absolute error (MAE). This labor-intensive workflow presents significant barriers for non-specialists.

Motivated by advancing data science and the growing demand for democratized ML tools, Automated Machine Learning (AutoML)43,44 has emerged as a robust alternative. AutoML achieves predictive accuracy comparable to state-of-the-art ensemble models like XGBoost45 and LightGBM46, while automating iterative tasks. AutoML eliminates resource-intensive tasks such as hyperparameter optimization, thereby lowering technical entry barriers and enhancing accessibility for non-experts in using ML models. In this study, AutoML is deployed to predict the compressive strength of HPGC, benchmarked against conventional ensemble methods. However, while AutoML surpasses in performance, its “black-box” nature obscures interpretability.

To address this limitation, Shapley Additive Explanations (SHAP) methodology47,48 is integrated into the framework. SHAP quantifies the contribution of individual input variables to model predictions and ranks their relative importance, enabling actionable insights into HPGC strength determinants. Thus, the study’s secondary contribution lies in establishing an AutoML-SHAP framework that harmonizes predictive accuracy with interpretability, streamlining sustainable concrete design.

ML algorithms have proven effective for assessing the compressive strength of concrete; however, optimizing mix design requires the integration of advanced optimization techniques. Meta-heuristic optimization methods, inspired by natural phenomena such as predator-prey dynamics, are widely applied across disciplines, including mining49, materials science50, and civil engineering51. Common meta-heuristic algorithms include the genetic algorithm (GA)52, particle swarm optimization (PSO)53, simulated annealing (SA)54, and ant colony optimization (ACO)55. Recent applications demonstrate their effectiveness in concrete mix design. For instance, Zhang et al.56,57 utilized PSO and beetle antennae search (BAS) algorithms to optimize ML parameters and conduct multi-objective optimization (MOO) of concrete. Similarly, Huang et al.58 employed the firefly algorithm to optimize steel fiber-reinforced concrete (SFRC) mix ratios, achieving dual-objective minimization of cost while maximizing compressive strength.

However, prior research predominantly converted MOO into single-objective problems through weighted summation of competing objective. While this approach simplifies the optimization process, it may induce incorrect results by disproportionately emphasizing specific objectives, thereby constraining the solution space and neglecting critical trade-offs. To address these limitations, this study employs Pareto dominance criteria by integrating the non-dominated sorting algorithm59. This methodology enables a systematic exploration of the solution space, avoiding biases imposed by subjective weight assignments. The introduction of Pareto non-dominated sorting into MOO for HPGC constitutes the study’s third contribution, advancing the development of equitable, sustainable mix designs.

This study develops an explainable AutoML framework for predicting HPGC compressive strength, augmented by SHAP to elucidate model behavior. Subsequently, Pareto non-dominated sorting principles are applied to conduct MOO. The article structure is briefly summarized as follows: The research significance is articulated in the opening sections. This is followed by a detailed description of the integrated framework for interpretable AutoML prediction and MOO. Subsequent passages outline the development of the HPGC database and present key predictive and optimization results. The study concludes by summarizing the main findings and their implications.

Research significance

First, there is no existing studies integrated ML-based predictive models with MOO frameworks for HPGC. Therefore, our study develops AutoML-based predictive modelling with MOO for HPGC. This paper demonstrates that the AutoML model can achieve comparable prediction performance as other powerful ensemble learning models, but it is more user-friendly and does not require complicated processes such as hyperparameter tuning.

In addition, most conventional ML approaches are black-box models and cannot provide perceptions as mechanics-based or empirical regression-based models. Feature importance is a traditional way to explain ML models. However, feature importance is difficult to determine how a feature correlates to the outputs and cannot provide a quantitative influence of each feature on the predicted result of each sample. To overcome the issue, SHAP is adopted in this study to enhance the interpretability of the AutoML model. SHAP cannot only provide a global interpretation for whole sets like feature importance, but also provide a local interpretation for each sample.

Finally, most studies convert MOO into single-objective optimization problems. This simplified method restrains the solution space and omit critical trade-offs. To overcome this problem, the Pareto non-dominated sorting is introduced into MOO to avoid possible biases induced by subjective weight assignments. This approach improves the MOO results compared with the conventional MOO strategies.

Explainable automl and MOO framework

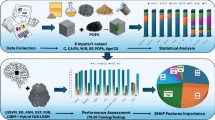
Figure 1 shows the research development flowchart, beginning with data collection and followed by evaluating the prediction performance of various ML models. The best ML model is subsequently integrated with a selected MOO algorithm to accomplish the optimization process.

Fig. 1
figure 1

Research development flowchart.

Full size image

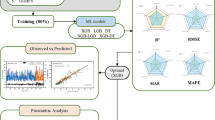
Figure 2 illustrates the workflow of the explainable AutoML prediction and MOO framework for HPGC. The framework comprises three phases: (1) AutoML Prediction: An AutoML model predicts the compressive strength of HPGC. Genetic programming optimizes hyperparameters through crossover and mutation operations. (2) Interpretability Analysis: SHAP interprets feature importance and predictions generated by the AutoML model. (3) Pareto-Optimized MOO: Leveraging the trained AutoML model, a Pareto dominance criterion guides MOO to balance compressive strength, cost, and carbon emissions. Traditional weighted-sum methods, while computationally simpler, fail to satisfy true Pareto optimality. Instead, solutions x1 and x2 are compared using dominance relationships defined in Eq. (1): x1 dominates x2 if if it outperforms x2 across all objectives without compromise. Non-dominated solutions, i.e., those not inferior to any other in all objectives, collectively form the Pareto front, enabling unbiased trade-off analysis.

$$\begin{gathered} \exists i,{f_i}({x_1}) \leqslant {f_i}({x_2}) \hfill \\ \forall j,{f_j}({x_1})<{f_j}({x_2}),j \ne i \hfill \\ \end{gathered}$$
(1)

where fi(x) and fj(x) denote the i-th and j-th objective function values for a candidate solution x.

Fig. 2
figure 2

Explainable AutoML and MOO framework for sustainable HPGC design.

Full size image

Database construction

The HPGC database comprises 295 experimental datasets sourced from 19 peer-reviewed international journals60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78. In alignment with the CEB-FIP specification79, all mixes conform to a minimum compressive strength threshold of 50 MPa at 28 days. As recommended by previous studies38,41, ten input variables were selected, representing material constituents and curing conditions: fly ash (F), blast furnace slag (S), sodium hydroxide (SH), sodium silicate (SS), water (W), fine aggregate (FA), coarse aggregate (CA), curing temperature (T), relative humidity (RH), and curing age (Age). Compressive strength (CS), the primary performance metric, serves as the sole output variable. Detailed information for all variables is provided in Table 1.

Table 2 outlines six design constraints for HPGC, where Pi corresponds to the percentage composition of constituent i, and Wi indicates the unit weight of component i, as indicated in Table 1. The total concrete cost is derived from Eq. (2).

$${\text{Cost}}={P_F}{U_F}+{P_S}{U_S}+{P_{SH}}{U_{SH}}+{P_{SS}}{U_{SS}}+{P_W}{U_W}+{P_{FA}}{U_{FA}}+{P_{CA}}{U_{CA}}$$
(2)

where Ui denotes the unit price of each constituent, as indicated in Table 1.

Table 1 Detailed information of variables.
Full size table
Table 2 Relevant constraints of HPGC.
Full size table

Figures 3 and 4 depict the frequency distributions and fitted curves for the input variables and output variable, respectively. These empirical results demonstrate comprehensive coverage of the designated parameter ranges, ensuring robust representation for model training. This range of data facilitates the ML algorithm in capturing complex, nonlinear relationships among input features and the target variable, thereby enhancing predictive accuracy. Furthermore, the ML model exhibits significant scalability, enabling seamless integration of novel data points as they become available. Such adaptability supports its application in optimizing HPGC mix designs, which necessitates identifying optimal combinations of input parameters under predefined constraints (Table 2) and cost objectives (Eq. 2).

Fig. 3
figure 3

Frequency distribution and fitting curve of input variables.

Full size image
Fig. 4
figure 4

Frequency distribution and fitting curve of output variable.

Full size image

Figure 5 presents a heatmap illustrating correlations between input variables and the output variable. This visualization enables researchers to quantify linear dependencies, identify redundant features (e.g., variables with correlation coefficients |r| ≥ 0.7), and iteratively refine feature selection to mitigate multicollinearity, thereby enhancing model interpretability and generalizability. Each cell in the heatmap displays the Spearman correlation coefficient (r) between two variables: positive values signify direct proportionality, while negative values indicate inverse relationships. Coefficients below |0.7| across all input pairs (Fig. 5) confirm the absence of multicollinearity, reducing overfitting risks during model training. Additionally, the heatmap reveals input-output linkages; for instance, fly ash (F) and coarse aggregate (CA) exhibit negative correlations with CS (r = − 0.1257 and r = − 0.2021, respectively), suggesting that optimizing aggregate proportions could improve compressive strength.

Fig. 5
figure 5

Heat map of input and output variables.

Full size image

Prediction and optimization results

Prediction performance of ML models

Three ensemble learning algorithms—Random Forest (RF), XGBoost, and LightGBM—were implemented for comparison. Hyperparameters significantly influence the predictive accuracy of conventional ML algorithms. Systematic hyperparameter tuning enhances model performance by optimizing these variables. Grid search, a traditional hyperparameter tuning technique, follows three steps: (1) defining candidate parameter ranges, (2) exhaustively evaluating all combinations via cross-validation, and (3) selecting the configuration yielding the highest accuracy. However, grid search suffers from two critical limitations: (1) discretizing continuous hyperparameters may exclude optimal values, and (2) computational inefficiency in high-dimensional spaces due to exponentially increasing combinatorial complexity. In contrast, Bayesian optimization leverages probabilistic surrogate models to approximate the relationship between hyperparameters and performance, enabling efficient navigation of high-dimensional search spaces. Consequently, Bayesian optimization was employed for tuning three ensemble models. Conversely, AutoML eliminates manual hyperparameter adjustment through built-in optimization pipelines. It employs genetic algorithms to automatically optimize ML hyperparameters in candidate pipelines by simulating the biological evolutionary process of “selection-crossover-mutation,” ultimately retaining the best-performing solution.

No preprocessing like normalization80,81 or encoding was applied to input features or target variables during the training of ML models for predicting concrete compressive strength. This decision was driven by two primary considerations: (1) Compressive strength, as a critical engineering parameter, carries inherent physical significance and industry standards in its original units (MPa). Maintaining raw scale ensures model predictions are directly applicable to subsequent MOO algorithms; (2) It eliminates potential numerical precision loss and computational redundancy from inverse transformation steps, particularly when handling high-dimensional constrained optimization problems.

The dataset was partitioned into training, testing, and validation subsets with a 7:2:1 ratio. The predictive performance of the four ML models is plotted in Fig. 6. It can be seen from Fig. 6 that all ML models achieved excellent prediction performance.

Fig. 6
figure 6

Predicted data versus real data (experimental data) of different ML models.

Full size image

To evaluate model performance, five widely recognized metrics—R2, RMSE, MAE, mean absolute percentage error (MAPE), a20 index82,83—were analyzed across all ML algorithms (Table 3). Validation results revealed R2 values exceeding 0.84 for all models, indicating their robust capacity to model nonlinear input-output relationships and deliver reliable predictions. Notably, the AutoML framework demonstrated comparable accuracy to the XGBoost and LightGBM models, achieving a R² of 0.9280 on the validation set. In contrast, the RF algorithm exhibited the lowest predictive accuracy among the evaluated models. The dataset comprises 295 samples, it substantially exceeds the fundamental requirement in ML for input parameter coverage (i.e., sample size ≥ 10× feature count)84,85. Models on validation datasets demonstrate R²>0.84 without error amplification at parameter boundaries, proving the dataset’s adequacy for reliable engineering decision-making.

Table 3 Prediction error indicators for ML models.
Full size table

The predictive accuracy of the four ML models is also compared via a Taylor diagram in Fig. 7. The diagram has two indices: correlation coefficient and standard deviation. It can be seen from Fig. 7 that the AutoML, LightGBM, and XGBoost exhibited very close predictive performance.

Fig. 7
figure 7

Taylor diagram for ML models.

Full size image

Figure 8 displays the frequency distribution of the predicted-to-actual compressive strength (CS) ratios for HPGC. Compared to LightGBM, the XGBoost model exhibits a higher concentration of ratios near 1 on the testing dataset. The RF model demonstrates greater dispersion in its ratios, with a Markedly low frequency of values close to 1, indicating Limited generalization capability. In contrast, the AutoML framework achieved the most tightly clustered ratios around 1 among the four ML models on the validation set, signifying superior prediction stability.

Fig. 8
figure 8

Frequency distribution of ML predicted-to-actual compressive strength ratios for HPGC.

Full size image

The 10-fold cross-validation was also conducted for the AutoML model to demonstrate the model’s robustness and avoid overfitting86,87. Figure 9 plots the 10-fold cross-validation results.

Fig. 9
figure 9

10-fold cross-validation results of the AutoML model.

Full size image

It should be highlighted that the AutoML model does not require hyperparameter tuning. The key hyperparameters of three ensemble learning models are listed in Table 4.

Table 4 Key hyperparameters for ML models.
Full size table

Explainability of automl model

SHAP is an explanation method grounded in game theory. It quantifies the contribution of each feature to model predictions by computing Shapley values. This approach enables the visualization of both positive and negative feature impacts and additively decomposes prediction outcomes. Consequently, it assists researchers in identifying potential biases and enhances model interpretability. The SHAP method was applied to interpret the trained AutoML model. SHAP enables both local and global interpretation, including feature importance analysis. By calculating SHAP values, the method identifies each feature’s impact on model predictions and detects potential biases, thereby enhancing interpretability for researchers.

Figure 10 presents the SHAP values for the AutoML model, depicting feature importance in descending order. Age, Sodium Silicate, and Fine Aggregate are identified as the three most influential features, whereas Relative Humidity demonstrates the least impact on CS. A color gradient in Fig. 10 illustrates the directional influence of SHAP values on CS. For example, increased Age correlates positively with CS enhancement, while elevated Water and Coarse Aggregate levels exhibit negative correlations.

Fig. 10
figure 10

SHAP values of the AutoML model.

Full size image

Figure 11 illustrates the SHAP diagrams for two representative prediction cases. In Fig. 11, the base value represents the mean model output across the entire training dataset, while f(x) denotes the model’s predicted output. Features marked in red drive the prediction above this baseline, while those in blue suppress the output below it. For example, in Fig. 11(a), the predicted value (f(x) = 74.98 MPa) exceeds the base value (60 MPa), indicating that contributions from red-region features outweigh those of the blue region. Notably, SH and W are the primary contributors to the blue-region effects. Similarly, in Fig. 11(b), elevated levels of FA, SS, S, and CA result in a reduced f(x) due to dominant blue-region influences.

Fig. 11
figure 11

SHAP diagram for two prediction cases.

Full size image

Figure 12 presents the SHAP dependency plot for input parameters. Among these, SH demonstrates the strongest overall relevance and exhibits significant interactions with FA, W, and FA. Both low and high concrete age Levels yield elevated SHAP values, highlighting age as a critical determinant of CS. However, after 50 days, the compressive strength demonstrates only minimal enhancement as the concrete approaches its ultimate hardening state. The associated SHAP values consequently remain stable without obvious increase compared to earlier stages. Relative humidity (RH) exhibits SHAP values oscillating between 1 and − 4, reflecting its limited yet measurable impact on compressive strength development.

Fig. 12
figure 12

Dependency diagram for input variables.

Full size image

Optimization results

Three objectives (CS, unit cost, and CO₂ emissions) were considered in the MOO. The Multi-Objective PSO (MOPSO) algorithm was employed for triple-objective optimization. MOPSO algorithm leverages particle memory and swarm collaboration (personal best + global best) to achieve superior computational efficiency over other algorithms, particularly for high-dimensional non-convex parameter spaces in concrete mix design. Its adaptive inertia weight dynamically balances exploration-exploitation, avoiding premature convergence. The emissions per cubic meter (m³) of HPGC were calculated via Eq. (3)41.

$$C{O_2}={a_F}{P_F}+{a_S}{P_S}+{a_{SH}}{P_{SH}}+{a_{SS}}{P_{SS}}+{a_W}{P_W}+{a_{FA}}{P_{FA}}+{a_{CA}}{P_{CA}}$$
(3)

where Pi is the quantity of the variable i in 1 m3, ai is the emission factor of variable i:

$${a_F}=0.00151,{a_S}=0.143,{a_{SH}}=1.915,{a_{SS}}=1.514,{a_W}=0.000347,{a_{FA}}=0.0139,{a_{CA}}=0.0459$$

The total computational time for AutoML prediction and optimization was approximately 563 s, achieved under the following configuration: PSO (200 particles × 300 iterations) executed on an engineering workstation with i7-12700 H CPU and 16GB RAM.

Figure 13 presents the non-dominated solutions and their fitted surface for the triple-objective optimization. The solutions exhibit a diagonal distribution from the lower left to upper right, reflecting the trade-off between increasing CS, unit cost, and CO₂ emissions. Specifically, higher CS correlates with elevated sodium silicate content, driving cost and emissions upward. A plateau in CO₂ emissions (~ 100 kg/m³) is observed for CS between 50 and 85 MPa, indicating minimal emission sensitivity to CS variations within this range. Beyond 85 MPa, emissions rise sharply, peaking at approximately 240 kg/m³ when CS is maximized.

Fig. 13
figure 13

Pareto front and its fitting surface of triple-objective optimization.

Full size image

The cost-gain ratio (Eq. 4) was introduced to identify optimization points with high cost-effectiveness.

$${\text{Cost-gain ratio=}}\frac{{{\text{CS}}}}{{{\text{Unit cost}}}}$$
(4)

where CS, unit cost, and cost-gain ratio are expressed in MPa, $/m3, and MPa·m3/$, respectively.

Figure 14 presents the CS-cost projection and the cost-gain trend Line. Costs exhibit a positive correlation with CS. The triple-objective optimization lacks distinct cost-benefit Pareto optimal solutions. Instead, the cost-benefit ratio oscillates near 1.6. This may arise because the optimization algorithm prioritizes CS, unit cost, and CO2 emissions simultaneously, thereby diminishing the clarity of cost-benefit trade-offs.

Fig. 14
figure 14

CS-Cost projection diagram and cost-gain fitting curve.

Full size image

Figure 15 illustrates the relationships between CS, CO2 emissions, and unit cost. As shown in Fig. 15(a), CO2 emissions exhibit a gradual nonlinear increase with CS, particularly within specific compressive strength ranges. For instance, growth rates remain stable between 50 and 85 MPa but accelerate significantly at 85–100 MPa. Emissions show minimal variation in low-to-medium CS ranges; however, beyond this threshold, higher CS necessitates increased sodium silicate content, leading to a substantial rise in CO2 emissions. Figure 15(b) reveals that when CO2 emissions approximate 100 kg/m³, the unit cost fluctuates between 40 and 50 $/m³. Beyond 120 kg/m³ of CO2 emissions, costs surge sharply.

Fig. 15
figure 15

CO2-CS projection diagram and CO2-Cost projection diagram.

Full size image

Since the triple-objective functions exhibit inherent trade-offs, the target CS must be determined based on the project’s specific requirements. Table 5 presents two optimal mix proportions derived via triple-objective optimization. For comparison, Table 6 summarizes the CS, unit cost, and CO₂ emissions of database specimens with comparable CS to the optimized mixes. Based on Tables 5 and 6, the optimization framework reduces CO₂ emissions by 23–60% and unit costs by 16–36%, confirming the method’s efficacy in balancing competing objectives. These results underscore the viability of the proposed approach in achieving multi-objective sustainability goals.

Table 5 Two recommended mix proportions based on tripe-objective optimization.
Full size table
Table 6 Relevant parameters of the specimens in the database.
Full size table

Conclusion

This study leverages AutoML and MOO to identify optimal HPGC mix designs, ensuring a balanced compromise between CS, unit cost, and CO₂ emissions. Key findings include:

  1. 1)

    The AutoML framework outperforms conventional ensemble learning models tuned via Bayesian optimization, yielding comparable predictive accuracy. Validation metrics confirm this advantage, with R², RMSE, MAE, MPAE, and a20 index of 0.9280, 5.2954 MPa, 4.2307 MPa, 0.0724, and 0.9677, respectively.

  2. 2)

    SHAP analysis elucidates feature impacts on CS, enhancing model transparency. Curing age, sodium silicate, and fly ash are the three most influential factors, with curing age and sodium silicate content exerting positive effects, whereas water and coarse aggregate ratios demonstrate negative correlations.

  3. 3)

    Triple-objective optimization (CS, cost, and CO₂) reduces emissions by 23–60% and unit costs by 16–36% relative to conventional mixes. This approach aligns material properties, economic viability, and sustainability objectives.

We must acknowledge the current study has certain limitations, especially on the ML model. The most important limitation lies in its sensitivity to data distribution and model generalizability. To resolve the issue, more experimental data will be collected from other resources to construct a more powerful and comprehensive database. After that, the well-trained ML tool will be more reasonable and accurate.