A disaggregated system dynamics and agent-based modeling of the water-energy-food nexus for optimizing water allocation

Abstract

Asymmetric water distribution in agriculture is a significant threat to water, energy, and food security in water-limited areas. This work presents an integrated model framework based on System Dynamics and Agent-Based (SD-AB) modeling applying multi-objective evolutionary optimization with the non-dominated sorted genetic algorithm (NSGA)-II, and post-optimization analysis through Analytic Hierarchy Process (AHP) that facilitates sustainable water supply. The SD-AB model simulates the intricate interactions among energy consumption, water supply, agricultural yield, and economic outcomes. The NSGA-II resolves the trade-offs between energy, groundwater utilization, and agriculture net benefit, wherein water allocation to every crop represents decision variables and the groundwater level is treated as a state variable. The solutions are ranked by implementing the AHP technique considering environmental sustainability, water availability, and cost-effectiveness. Local hydrology, agriculture, and socio-economic data are used as model inputs. This work’s framework was applied to the Zayandehrud Basin, Iran. The model outputs show that optimal allocation schemes cut water use by 13.1%, increase the average groundwater level by 1 m, decrease energy demand by 23.96%, and enhance environmental water allocation by 355% compared to the business-as-usual (BAU) baseline scenario, which is the current water allocation without optimization. Net agricultural benefit decreases by 22.4%, revealing a trade-off between returns and sustainability. This paper’s methodology provides strong policy implications while it is constrained by uncertainty in data and behavioral assumptions. Overall, this paper’s methodology represents a useful decision-support tool for sustainable water resource planning in water-scarce basins with possible extension to other socio-environmental situations worldwide.

Introduction

The demand for water, energy, and food resources is expected to escalate dramatically as global populations grow^1,2,3. This trend poses acute challenges in arid and semi-arid regions, where water scarcity intensifies competition between the agriculture, industry, and domestic sectors^4,5. Agriculture alone accounts for nearly 70% of global freshwater withdrawals, often triggering groundwater depletion, environmental degradation, and increased energy consumption⁶. These dynamics highlight the tightly coupled nature of the water-energy-food (WEF) nexus, in which interventions in one sector invariably ripple across the others².

Conventional modeling frameworks have struggled to represent the complexity of the WEF nexus despite growing recognition of these interdependencies. SD models excel at capturing macro-level feedbacks but tend to oversimplify the diverse behaviors of individual actors^7,8,9. Conversely, AB models effectively simulate heterogeneity and adaptive decision-making but often lack the systemic integration needed to evaluate long-term trade-offs. Integrating these two approaches offers a promising path forward: SD provides insights into the structural feedback mechanisms that govern resource flows, while AB introduces bottom-up behavioral dynamics that shape local responses to policy and environmental change^10,11.

The compounded effects of increasing agricultural water demand, falling groundwater levels, and higher energy requirements for extraction create a feedback loop that undermines long-term sustainability¹². Addressing such challenges requires modeling frameworks capable of quantifying trade-offs and supporting decisions across interconnected domains. Previous applications of SD have explored a range of resource management challenges—from agricultural economic evaluation¹³ to environmental change impacts¹⁴, WEF interactions^2,15, and regional wetland degradation¹⁶—but many fail to incorporate behavioral heterogeneity or spatial dynamics. Furthermore¹⁷, applied an SD model to evaluate the complexity and uncertainty associated with water transfers, impacting factors like crop yield and distribution efficiency.

This study presents the following innovations in the modeling of the WEF nexus:

Develops a hybrid SD–AB model designed to simulate both systemic interconnections and agent-level behavior within the agricultural WEF nexus.

• The model is integrated with the Non-dominated Sorting Genetic Algorithm II (NSGA-II) to identify optimal water allocation strategies across conflicting objectives, including reduced water and energy use and increased agricultural profitability.

• The resulting Pareto-optimal solutions are further evaluated using the AHP, considering multiple sustainability criteria such as water availability, environmental impact, and cost-effectiveness.

This study provides a robust tool to deal with trade-offs in complex socio-environmental systems that incorporate multi-objective optimization in a spatially disaggregated SD–AB model. The SD–AB model simulates the WEF system through 14 spatial units that constitute important agricultural management regions in the Zayandehrud Basin, and employs an annual simulation time step, capturing long-term dynamics and regional heterogeneity in water and energy demand. Elements of this integrated methodology have been employed in previous studies^10,11; none, however, have integrated SD–AB modeling, NSGA-II optimization, and AHP-based evaluation in a single decision-support system for WEF governance.

Methodology and data

This study introduces an integrated modeling framework rooted in the WEF nexus to assess and optimize agricultural resource allocation in the Zayandehrud River Basin. The methodology consists of three primary components: (1) simulation of the WEF system using a hybrid SD-AB approach, (2) multi-objective optimization using NSGA-II, and (3) prioritization of Pareto-optimal strategies through the AHP as shown in Fig. 1.

Fig. 1

Flowchart of the simulation–optimization model.

SD-AB simulation model

The SD–AB hybrid model captures both the macroscopic feedback across water, energy, food, and economic subsystems and the behavioral diversity of decentralized agents (e.g., farmers, water users, subregions). SD modeling is applied to represent dynamic feedback and flows between WEF components over time, incorporating causal loop diagrams to structure reinforcing and balancing mechanisms^7,18.

Each of the 14 agricultural subregions within the AB part of the SD–AB modeling framework is characterized as an autonomous agent. The agents are heterogeneous in terms of groundwater availability, crop type, irrigation efficiency, and economic conditions. The behavior of each agent—expressed by their water use, field area decisions, and the associated costs and benefits—is modeled separately for each subregion. The results produced by each of the agents are synthesized within the system dynamics model in order to determine their collective effect on basin-scale variables, including the surface water flux and the groundwater balance. There are no direct interactions among the agents, but their activities are coupled via shared resource dynamics and system-level feedback mechanisms.

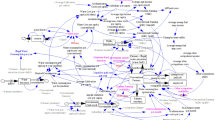
The schematic representation of the interactions among the internal components of the WEF nexus system is shown in Fig. 2. This diagram is the basis for SD modeling, serving a crucial role in visualizing and capturing the dynamic behavior of the WEF nexus. The functionality of the WEF nexus is thoroughly investigated using the SD model, which allows for an in-depth exploration of the interrelated factors within the system.

Fig. 2

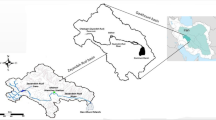
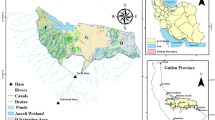
The Zayandehrud River basin. This map was created by the authors using ArcMap version 10.7.1 (Esri, https://www.esri.com/en-us/arcgis/products/arcgis-desktop/overview)”.

The CLD shown in Fig. 3 delineates the behavior of the modeled WEF system, identifies potential feedback mechanisms, and provides insights into the long-term impacts of various policies and interventions. The model subsystems are interconnected through nexus variables, which represent the interactions and interdependencies among the water, energy, food and economics subsystems. These nexus variables are essential for analyzing how changes in one subsystem can influence the others and for understanding the overall system dynamics¹⁹.

Fig. 3

Schematic of the interactions that exist in the water-energy-food-economic system elements (SW: surface water, GW: groundwater).

Water availability -shaped by agricultural water demand and groundwater abstraction- is identified as a nexus variable impacting the food subsystem, particularly through irrigation practices, and the energy subsystem, notably through hydropower generation. Fluctuations in water availability include cascading effects throughout the energy and food subsystems, creating significant feedbacks and interconnections²⁰.

The food subsystem is intricately linked to the water subsystem through multiple key pathways, as illustrated in Fig. 3. It relies on the water subsystem to fulfill crop water requirements. The total water supply is connected to agricultural water demand, which subsequently affects crop yield. As crop yields increase, the demand for irrigation water may rise correspondingly, highlighting the dependence of food production on adequate water resources²¹. Furthermore, the relationship between population growth and food demand illustrates how increasing food requirements exacerbate reliance on the system’s water resources. In this context, “Cultivated land” emerges as another significant nexus variable that connects the water and food subsystems, reflecting relationships among these components.

The water subsystem

The water subsystem includes surface water (SW), groundwater (GW), water demands (WD), and return water to water resources (InfSWD and InfGWD).

The surface water balance is presented in Eq. (1). All dimensions are expressed in million cubic meters (MCM) and time is expressed in years.

$$\sum_{t=1}^{T}{\left({SW}_{net}\right)}_{t}=\sum_{t=1}^{T}\left({SW}_{t}+{P}_{t}+{Q}_{t}+{TW}_{t}-{E}_{t}-{InfSW}_{t}-{\left({SWD}_{Total}\right)}_{t}\right)$$

(1)

$${InfSW}_{t}={SW}_{t}\times SWInfCo$$

(2)

in which, ${SW}_{net}$, SW, P, Q, TW, E, InfSW, and ${SWD}_{Total}$ denote respectively the surface water balance, available surface water, rainfall, inflow (runoff), transferred water, evaporation, surface water infiltration into groundwater (i.e., recharge), and total surface water demand at time t. SWInfCo is the coefficient of surface water infiltration into groundwater.

The groundwater balance is presented in Eq. (3) and infiltration from rainfall is calculated using Eq. (4).

$$\sum_{t=1}^{T}{\left({GW}_{net}\right)}_{t}=\sum_{t=1}^{T}\left({GW}_{t}+{InfP}_{t}+{InfSWD}_{t}+{InfGWD}_{t}{ + InfRunoffPlain}_{t}+{InfRunoffHeight}_{t}-{\left({GWD}_{Total}\right)}_{t}\right)$$

(3)

$${InfP}_{t}=PrecipInfCo\times {Precipitation}_{t}$$

(4)

in which ${GW}_{net}$, GW, InfP, InfSWD, InfGWD, and ${GWD}_{Total}$ represent the groundwater balance, available groundwater, infiltration from rainfall, return flow from surface water usage, the return flow from groundwater usage, and the total groundwater demand at time t, respectively. PrecipInfCo and Precipitation_t denote, the precipitation infiltration coefficient and the amount of precipitation, respectively.

InfSW denotes surface water infiltration into groundwater, as presented in Eq. (5).

$$\begin{array}{l}{InfSWD}_{t}={\left({SWD}_{Agr}\right)}_{t}\times {InfCoSWD}_{Agr}+{\left({SWD}_{Ind}\right)}_{t}\\ \qquad \qquad \qquad \times {InfCoSWD}_{Ind}+{\left({SWD}_{Dom}\right)}_{t}\times {InfCoSWD}_{Dom}\end{array}$$

(5)

in which SWD_Agr, SWD_Ind, and SWD_Dom, denote agricultural, industrial, and domestic surface water demand, respectively, and InfCoSWD_Agr, InfCoSWD_Ind, and InfCoSWD_Dom denote the coefficients for agricultural, industrial, and domestic surface water demand, respectively.

Return flow from groundwater usage is calculated as Eq. (6).

$$\begin{array}{*{20}{c}} {nfGW{D_t} = {{\left( {GW{D_{AgrC}}} \right)}_t} \times InfCoGW{D_{AgrC}} + {{\left( {GW{D_{AgrH}}} \right)}_t}{\text{ }}} \\ {\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\times InfCoGW{D_{AgrH}} + {{\left( {GW{D_{Ind}}} \right)}_t} \times InfCoGW{D_{Ind}} + {{\left( G \right)}_t} \times InfCoGW{D_{Dom}}} \end{array}$$

(6)

in which GWD_AgrC, GWD_AgrH,, GWD_Ind, and GWD_Dom denote, respectively, the groundwater demand for agricultural crops, agricultural horticulture, industrial use, and domestic use, and InfCoGWD_AgrC, InfCoGWD_Ind, and InfCoGWD_Dom denote, respectively, the coefficients for groundwater demand for agricultural crops, agricultural horticulture, industrial use, and residential use.

The infiltration values from runoff in plains and heights were obtained using Eqs. (7) and (8).

$${InfRunoffPlain}_{t}=RunoffPlainCo\times {Precipitation}_{t}\times InfCoRunoffPlain$$

(7)

$${InfRunoffHeight}_{t}=RunoffHeightCo\times {Precipitation}_{t}\times InfCoRunoffHeight$$

(8)

in which RunoffPlainCo and RunoffHeightCo denote, respectively, the conversion coefficients of precipitation to runoff in plains and heights (elevated areas), and InfCoRunoffPlain and InfCoRunoffHeightCo denote, respectively, the runoff infiltration coefficients.

Initial parameter values were determined based on historical hydrological records (2001–2021), supplemented by values reported in the literature and adjusted through calibration using observed surface water and groundwater levels. Table 1 lists the model parameters of fundamental significance, both their preliminary estimates and final values, thereby illustrating the adjustments achieved through the process of model calibration.

Table 1 Calibrated coefficients related to surface and groundwater balance.

The sum of the inputs to and outputs from the aquifer expresses the changes in the storage volume [Eq. (9)].

$$\pm \Delta V=S\cdot A\cdot \Delta H$$

(9)

in which $\Delta$ V, S, A, and ΔH represent the storage change in the aquifer, the storage coefficient of the aquifer, the area of aquifer (square kilometers), the fluctuation of groundwater level (meter), respectively. If there is a balance between inputs and outputs the storage change would equal zero.

The storage coefficient is a hydrodynamic characteristic, which varies with the specific storage factor and the thickness of the aquifer, varies between 5 × 10^–5 and 5 × 10^–3. The storage coefficient of aquifers in the areas is listed in Table 1.

The surface water demands and groundwater demands are presented in Eq. (10) and Eq. (11), respectively

$$\sum_{t=1}^{T}{\left({SWD}_{Total}\right)}_{t}=\sum_{t=1}^{T}\left({\left({SWD}_{Agr}\right)}_{t}+{\left({SWD}_{Ind}\right)}_{t}+{\left({SWD}_{Dom}\right)}_{t}+{\left({SWD}_{Env}\right)}_{t}\right)$$

(10)

$$\sum_{t=1}^{T}{\left({GWD}_{Total}\right)}_{t}=\sum_{t=1}^{T}\left({\left({GWD}_{Agr}\right)}_{t}+{\left({GWD}_{Ind}\right)}_{t}+{\left({GWD}_{Dom}\right)}_{t}\right)$$

(11)

in which ${SWD}_{Agr}$ ${SWD}_{Ind}$, ${SWD}_{Dom}$, ${SWD}_{Env}$, denote respectively surface water demand ((MCM) in the agricultural, industrial, domestic, and environmental sector, and ${GWD}_{Agr}$, ${GWD}_{Dom}$, ${GWD}_{Ind}$, denote respectively groundwater demands (MCM) in the agricultural, industrial, and domestic sectors.

Domestic water demand and total agricultural water demand is calculated using Eqs. (12) and (13), respectively.

$$\sum_{t=1}^{T}{\left({WD}_{Dom}\right)}_{t}=\sum_{t=1}^{T}{\left({Q}_{Dom}\times N\right)}_{t}$$

(12)

in which ${Q}_{Dom}$ and N denote respectively domestic water consumption per person and population size.

$${({WD}_{Agr})}_{t}=\sum_{t=1}^{T}{({SWD}_{Agr})}_{t}+\sum_{t=1}^{T}\sum_{m=1}^{M}{({GWD}_{Agr})}_{t,m}$$

(13)

in which $m$ is an index denoting a crop type (there are $M$ crops considered as decision variables in this work).

The Food Subsystem

The food subsystem estimates crop water requirements using FAO Penman–Monteith²² evapotranspiration models, integrating cultivation pattern, yield, irrigation efficiency, and cropping patterns (Eqs. (14) to (18)).

$${ET}_{c}={ET}_{0}\times {K}_{c}$$

(14)

$${I}_{n}={ET}_{c}-({P}_{e}+{G}_{e})$$

(15)

$${I}_{n}={ET}_{0}\times {K}_{c}-{P}_{e}$$

(16)

$${ET}_{0}=\frac{0.408\Delta \left({R}_{n}-G\right)+\gamma [\frac{900}{T}+273]{U}_{2}({e}_{a}-{e}_{d})}{\Delta +\gamma (1+0.34{U}_{2})}$$

(17)

$${I}_{g}=\frac{In}{E}$$

(18)

in which I_n, ET_o, P_e, G_e, K_c, I_g and E denote, respectively, the crop net water requirement, actual crop evapotranspiration, effective rain, groundwater absorbed by crops, crop coefficient, gross water requirement, irrigation efficiency. R_n, G, e_a, e_d, T,$\gamma$, Δ, U₂ denote, respectively, the net radiation flux (MJ/m²day), soil heat flux (MJ/m²day), mean saturation vapor pressure (kPa), mean ambient vapor pressure (kPa), air temperature at 2 m height, psychrometric constant (kPa/°C), slope of the saturation vapor pressure vs air temperature function at the air temperature at a height of 2 m, the wind speed at a height of 2 m (m s⁻¹).

The energy subsystem

The energy subsystem calculates energy consumption primarily for groundwater extraction based on hydraulic head (${lift}_{t}$) and water mass (${mass}_{t}$), establishing water–energy coupling^23,24 in Eq. (19).

$$\sum_{t=1}^{T}{E}_{t}(KWh)=\sum_{t=1}^{T}(\frac{9.8\left(m.{s}^{-1}\right)\times {lift}_{t}\left(m\right)\times mass \left(Kg\right)}{3.6\times {10}^{6}\times \in \left(\%\right)})$$

(19)

In which, ${E}_{t}$ and $\varepsilon$ denote, respectively, the energy requirement in period t and the efficiency of the energy generating system (typically between 0.7 and 0.9).

The economic subsystem

The economic subsystem computes agricultural net benefits using crop-specific costs, prices, and yields, connecting profitability to WEF performance indicators through Eqs. (20) and (21), respectively:

$$\sum_{j=1}^{J}\sum_{t=1}^{T}{CY}_{j}^{t} \left(Kg{ha}^{-1}\right)=\sum_{j=1}^{J}\sum_{t=1}^{T}\left(\frac{{Production}_{j}^{t} (Kg)}{{Area}_{j }^{t}(ha)}\right)$$

(20)

$$\sum_{j=1}^{J}\sum_{t=1}^{T}{NetBen}_{j}^{t} \left(Rial\right)=\sum_{j=1}^{J}\sum_{t=1}^{T}\left({Area}_{j}^{t}\cdot \left({CY}_{j}^{t}\times {Price}_{j}^{t}\left(Rial{Kg}^{-1}\right)-{Cost}_{j}^{t}(Rial{ha}^{-1}\right)\right)$$

(21)

in which ${CY}_{j}^{t}$, ${Production}_{j}^{t}$, ${Area}_{j}^{t}$, ${NetBen}_{j}^{t}$, ${Price}_{j}^{t}$, and ${Cost}_{j}^{t}$ respectively denote the yield of crop $j$ in period t (Kg ha⁻¹), production of crop $j$ in period t (Kg), cultivation area of crop $j$ in period t (ha), net benefit from crop $j$ in period t (Rial), price and cost of crop $j$ in period t (Rial).

The AB component models the agricultural subregions as autonomous agents with the AnyLogic simulation software²⁵. Each agent responds dynamically to simulated groundwater levels, profitability, and water access, influencing spatial allocation decisions. A detailed description of decision variables is found in Sect. “Multi-objective Optimization”.

Data sources

This study’s WEF simulation uses 20 years (2001–2021) based on the datasets listed below, with policy relevance and historical calibration listed in Table 2. The model operates with a yearly time step, which is consistent with the temporal resolution of available meteorological, hydrological, and agricultural, energy, and socio-economic data and enables the analysis of long-term trends in water, energy, and food system dynamics.

Table 2 Types of data used in this study.

The model uses the following datasets:

• Hydrological data: Precipitation, evapotranspiration, infiltration, surface/groundwater flows and returns;

• Agricultural data: Crop-specific land use, yield, irrigation need;

• Energy data: Electricity use for irrigation, with 85% allocated to agriculture;

• Economic data: Crop prices, production costs, per capita food demand, population.

The last column of Table 2 offers a comprehensive view of the principal sources of primary data and their corresponding agencies in charge of each kind of dataset. The agencies are the Iran Water Resource Management Company (IWRMC), Agricultural Jihad Organization of Isfahan Province, Ministry of Energy of Iran, Ministry of Agriculture (Jihad), and the Statistical Center of Iran.

Missing data in hydrological and meteorological data sets were filled in by linear regression using data from nearby stations. Missing data in agricultural and energy-related data sets were completed with national reports and planning documents. These actions assured completeness and consistency of input data for the 2001–2021 modeling horizon.

Model calibration and validation

The water subsystem calibration was performed using 70% of the historical data (13 years), while 30% (6 years) was used for validation.

A combination of graphical techniques, dimensionless statistics, and error indices was employed to evaluate model performance²⁸. Specifically, the correlation coefficient (R), Normalized Relative Root Mean Square Error (NRMSE) and, Nash–Sutcliffe efficiency (NSE). Performance ratings for the NRMSE and the NSE values are listed in Table 3.

Table 3 Performance rating for the NSE and NRMSE (Moriasi et al., 2007).

The SD-AB model demonstrated excellent performance with respect to surface water simulation with a calibration NSE of 0.988, R = 0.996, and NRMSE = 0.034. During the validation period, NSE remained high at 0.933, with R = 0.966 and NRMSE = 0.106, as listed in Table 4. The SD-AB model accuracy with respect to groundwater simulation varied across subregions and generally indicated reliable performance. For instance, in sub-basin 4205, the validation NSE reached 0.91 with R = 0.98, while sub-basin 4201 exhibited lower performance during validation (NSE = 0.67, R = 0.93). In the subregions where there are the lower calculated values for the NSE in the validation period the lower performance is due to input data of poorer quality or to local hydrologic heterogeneity not completely represented by the aggregated model structure. In addition, the accuracy of the model is diminished in situations of uncontrolled human intervention—such as over-abstraction of groundwater—or discrepancies in the observational records.

Table 4 Calibration and validation results for the surface water predictions.

The full range of calibration and validation results across subregions is listed in Table 5. The model’s predictions aligned closely with the observed trends and values, demonstrating a strong agreement between the simulated and actual data. It is important to note that groundwater levels for regions 4210, 4215, and 4216 are not recorded.

Table 5 Calibration and validation results for the groundwater level predictions.

Multi-objective optimization

Sustainable strategies under competing objectives were identified by coupling the model with the NSGA-II evolutionary algorithm²⁹. The optimization sought to:

• Minimize water consumption (Z₁) (defined by Eq. (13)),

• Minimize energy consumption (Z₂) (defined by Eq. (19),

• Maximize net agricultural benefit (Z₃) (defined by Eq. (21)).

The model incorporates nine decision variables, which are the agricultural surface water uses (X₁), and groundwater allocation for wheat (X₂), barley (X₃), maize (X₄), alfalfa (X₅), rice (X₆), potato (X₈), other crops (X₉), and orchards (X₉).

The NSGA-II algorithm is configured with a population size of 20, crossover rate of 0.2, and 50 generations, balancing computational efficiency with solution diversity³⁰. These values were determined through trial-and-error testing, balancing the model’s computational demands with the need for adequate solution diversity. Larger population sizes or more generations only slightly improved the quality of the solutions while greatly increasing the computational load.

Several constraints were imposed in the optimization model. Limitation of surface water (Eq. (22)) and groundwater (Eq. (23)): The water allocated for different uses cannot exceed the available water resources (SW and GW).

$$\sum_{t=1}^{T}\left({\left({SWD}_{Agr}\right)}_{t}+{\left({SWD}_{Ind}\right)}_{t}+{\left({SWD}_{Dom}\right)}_{t}+{({SWD}_{Env})}_{t}\right)\le \sum_{t=1}^{T}{SW}_{t}$$

(22)

$$\sum_{t=1}^{T}\left({\left({GWD}_{Agr}\right)}_{t}+{\left({GWD}_{Hor}\right)}_{t}+{\left({GWD}_{Ind}\right)}_{t}+{\left({GWD}_{Dom}\right)}_{t}\right)\le \sum_{t=1}^{T}{GW}_{t}$$

(23)

Limitation of the water balance (Eq. (24)): Establishing the balance equation is one of the conditions that must be met in the study region, and it is calculated based on evapotranspiration and precipitation.

$$\sum_{t=1}^{T}{\left({SWD}_{Total}\right)}_{t}+{\left({GWD}_{Total}\right)}_{t}=\sum_{t=1}^{T}{(ET}_{t}-{P}_{t})$$

(24)

Limitation of the area under cultivation (Eq. (25)): The cultivated land (${Area}_{t}^{j}$) for crop j in period t (ha) cannot exceed the total arable land (${Area}_{Total}^{t}$).

$$\sum_{j=1}^{J}\sum_{t=1}^{T}{Area}_{t}^{j}\le \sum_{t=1}^{T}{Area}_{Total}^{t}$$

(25)

Limitation of food security³¹ (Eq. (26)): Food security means the access of all people at any time to sufficient, healthy and nutritious food that is necessary to meet nutritional needs and lead an active and healthy life³². The food demand (FD) for each person is the same as the per capita consumption of each person per year, which is determined by the total of drink production and imports per population.

$${\sum }_{t=1}^{T}({CY}_{t}.{Area}_{t})\ge {\sum }_{t=1}^{T}({FD}_{t}.{Population}_{t})$$

(26)

The WEF nexus multi-objective optimization model was solved with the NSGA-II optimization algorithm^{29,33,34,35,36,37,38,39}.

solution evaluation viaAHP

The AHP method is used to rank alternatives based on criteria defined by stakeholders given the trade-offs among Pareto solutions: water availability, environmental impact, and cost-effectiveness^40,41. The most appropriate strategy is selected through pairwise comparisons and weighted scoring and aligning technical performance with policy priorities.

Case study

The Zayandehrud Basin (Fig. 4) in central Iran covers ~ 27,000 km² and is an important critical region for agriculture, industry, and urban supply. Persistent water conflicts, high agricultural demand, and ecological degradation in the Gavkhuni wetland make this basin an ideal setting for WEF-integrated modeling^42,43.

Fig. 4

The developed conceptual loop diagram (CLD) model’s graphical representation.

Discussion and results

Machine learning and explainable AI (XAI) have proven to be very promising for water prediction and assessment based on data-driven methodologies even though they cannot replicate the dynamic interactions that occur over a period of time. For instance⁴⁴, applied a SHAP-based explanation to machine learning algorithms like XGBoost to determine the major drivers affecting water quality. This maintained to a very high standard of predictive validity and model transparency, but these models suffer from limited capacity to represent systemic feedback loops, policy dynamics, or stakeholder interactions. This study, conversely, combines SD with AB modeling and multi-objective optimization with the provision of an integrated framework to simulate short-term and long-term trade-offs across the WEF nexus. This combined strategy facilitates optimal allocation decisions and yields a better comprehension of their socio-environmental effects subjected to different constraints and goals.

The NSGA-II algorithm generated a Pareto front with trade-offs among water use (Z₁), energy use (Z₂), and agricultural revenue (Z₃). Figure 5 presents the Pareto front.

Fig. 5

Pareto front resulting from the NSGA-II multi-objective optimization algorithm.

The optimal solution was ultimately chosen with the AHP, which weighed the stakeholders’ preferences over critical factors such as water availability, environmental effects, and cost-savings (Table 6). The relative weights of these factors, according to their relative significance in meeting sustainable water allocation objectives, were determined through pairwise comparisons⁴⁵. For these comparisons to remain valid, AHP validation encompassed the derivation of the Consistency Ratio (CR), this result being 0.06—well beneath the general benchmark threshold value of 0.10—and yielding high consistency and good methodology.

Table 6 Weight of the selected criteria.

It is seen in Table 6 that water availability carries the largest weight, indicating its critical role in the decision-making process. This prioritization reflects the necessity of ensuring sufficient access to water resources for stakeholders across various sectors, as inadequate water access can have serious repercussions for agriculture, industry, and other essential uses⁴⁶. The environmental impact criterion is weighted lower than water availability, yet, its importance in minimizing pollution and conserving ecosystems remains significant⁴⁷. The moderate weight assigned to cost-effectiveness suggests that financial savings and efficiency must also be considered in the decision-making processes. Striking a balance between economic benefits and other critical dimensions, such as water availability and environmental sustainability, is essential for effective resource management.

The weighted criteria and performance of objective functions listed in Table 7 produced a sustainable and optimal solution. This solution represents the best trade-offs among environmental sustainability, resource availability, and economic feasibility, with water availability being the most significant criterion because it influences the agricultural, industrial, and residential sectors. The last column in Table 7 results from multiplying the weights of the objective functions by their corresponding criteria weights from Table 6, followed by summation, providing a comprehensive assessment of the optimal solution.

Table 7 Weights of selected criteria for each of the objective functions.

Water subsystem optimization

The allocation of resources prioritizes drinking water uses in the water subsystem, which reflects its fundamental importance for public health^48,49. Ensuring access to adequate and safe drinking water is paramount when distributing water resources among domestic, industrial, agricultural, and environmental sectors. Industrial water use is also crucial for economic productivity even though meeting the population’s basic drinking needs remains the top priority. Therefore, industrial water use is ranked second, with agricultural water consumption placed third in the hierarchy.

Table 8 lists the optimal solution derived from the AHP method, alongside boundary solutions 1 and 2, and the current baseline scenario. These are evaluated based on the objectives (Z₁, Z₂, and Z₃) and decision variables (X₁ to X₉). The optimal solution (Z₁ = 3,820 MCM) resulted in a 13.1% reduction in total water use compared to the baseline (Z₁ = 4,398 MCM). This reduction increased groundwater levels by one meter on average. Such recovery is essential for long-term aquifer sustainability and cost savings that arise from reduced pumping.

Table 8 Optimal values of the objectives (Z) and decision variables (X).

Excessive exploitation of water resources can lead to significant ecological repercussions^{49,50,51,52,53}. The optimization of agricultural water use has altered environmental water allocation from its normal state. Maintaining ecological flows in the Gavkhuni wetland is critical for supporting aquatic ecosystems, as illustrated in Fig. 6. A comparison of environmental water allocation across various solutions-baseline, optimal, solution 1, and solution 2-demonstrates that optimizing agricultural water significantly impacts the volume of water available for environmental needs, thereby influencing ecosystem health and sustainability. The wetland requires 60 (MCM) of water to support bird population and 142 (MCM) during dry years to maintain ecosystems viability⁵⁴.

Fig. 6

The Gavkhuni wetland environmental inflow.

Furthermore, as shown in Fig. 6, the optimal solution significantly improves environmental water allocation. The baseline scenario allocated an average of approximately 14 MCM of surface water annually to environmental needs. The optimal solution, on the other hand, increases this to near 65 MCM, indicating a 355% improvement. The range of environmental inflows observed across all four scenarios (min = –2.4 MCM; max = 147.6 MCM) is summarized in Table 9, which also reports a mean value of 55.9 ± 67.4 MCM and confirms that the 355% rise lies well within the overall variability. This underscores the environmental benefits of integrating energy and water considerations within the WEF nexus and supports sustainable resource management strategies.

Table 9 Descriptive statistics of key indicators corresponding to the the four scenarios (2001–2021).

The agricultural sector’s heavy dependence on groundwater, due to limited surface water availability, has led to declining groundwater levels during the simulation period. However, reducing total water consumption—especially in areas relying primarily on groundwater—can reverse this trend. It is illustrated in Fig. 7 that the optimal solution leads to an average groundwater level increase of one meter.

Fig. 7

The groundwater level (m) in the Zayandehrud basin.

Figure 8 presents a radar chart comparing groundwater sustainability indices across different allocation strategies, with several criteria represented on radial axes. The optimal solution outperforms others across most criteria, indicating a well-balanced allocation strategy. In contrast, the baseline scenario shows more variability, reflecting inefficiencies in current practices. Solutions 1 and 2 demonstrate fluctuating performance and highlight distinct trade-offs and strengths across evaluation criteria.

Fig. 8

Groundwater sustainability index.

Energy subsystem optimization

The results listed in Table 8 indicate that the optimal energy use (Z₂) associated with the agricultural water demand (Z₁) is 82,984 KWh, which represents a 24% reduction compared to the baseline scenario. It is shown in Table 9 that the energy use corresponding to different scenarios ranges from 82,984 to 109,119 KWh, with a mean of 94,313 ± 12,641 KWh, which allows a 24% reduction in energy use. The energy required for agricultural water pumping, along with water needs for industrial and urban uses, contributes significantly to electricity consumption and subsequent greenhouse gas emissions⁴⁷. Therefore, optimizing agricultural water use leads to a reduction in electricity demand within the study basin.

Figure 9 indicates that decreasing both water and energy consumption correlates with a reduction in CO₂ emissions, which is of significance given the deleterious effect of greenhouse gases resulting from fossil fuel use. This reduction is particularly significant in the context of climate change and environmental sustainability.

Fig. 9

CO₂ emissions from pumping groundwater for agricultural use.

Figure 10 depicts average CO₂ emissions across selected solutions, with each axis representing subregions identified by their respective codes (e.g., 4201, 4202, etc.). The baseline solution reflects current emissions practices, while the shape and position of the graph indicate variations in emissions across the subregions. The optimal solution represents the best-case configuration, leading to emissions that are lower than other solutions in most subregions. This highlights the co-benefits of integrated water-energy optimization.

Fig. 10

Comparison of average CO2 emissions in subregions under selected solutions.

Solutions 1 and 2 illustrate alternative strategies for managing CO₂ emissions, with varying effectiveness across different subregions. Policymakers and water managers can identify opportunities for enhancing sustainable energy use by analyzing these results. This would improve energy efficiency in water systems, and optimize the water-energy trade-offs. Incorporating energy considerations into the WEF nexus, as demonstrated in this study, can lead to more effective and sustainable management practices.

The ideal option provides a basin-scale emission reduction of approximately 15.7 metric tons of CO₂ emissions compared to the baseline using an intermediate emission factor of 0.6 kg CO₂ per KWh. This reduction is small on a national account but nevertheless contributes to Iran’s greenhouse gas mitigation objectives as part of the Paris Agreement, while highlighting the climate mitigation potential of integrated WEF strategies on a sub-basin scale level.

Food subsystem optimization

Effective water allocation for agriculture must strike a balance between conserving water resources and sustaining agricultural production to meet food demands^55,56.

It is seen in Fig. 11 (compares the Food Security Index (FSI) across various crops) that each axis represents a different crop, with values on the radial axes indicate the FSI, likely on a scale from 0 to 2.5. The FSI improved by 21% on average across crops under the optimal solution. This improvement is attributed to better alignment of irrigation allocations with crop water requirements, especially for wheat and orchards, which experienced notable gains. Crops such as maize and rice exhibit relatively low FSI values, which indicates areas where further improvements are needed and highlights the challenges faced in achieving food security for these crops⁵⁷.

Fig. 11

Food security index (FSI).

Economic subsystem optimization

Increasing the volume of water supply for agriculture leads to an expansion of cultivated areas. However, this may also result in a decreased net benefit from crop production⁵⁸. In the current allocation framework, Agricultural water use is prioritized third, after domestic and industrial uses, yet its consumption is significantly higher than that of the other sectors. Consequently, optimizing water allocation may necessitate a reduction in water supply to agriculture, potentially affecting farmers’ revenues from crop production.

Balancing the trade-off between minimizing water consumption and maximizing net agricultural benefits are essential for achieving efficient resource use while maintaining agricultural productivity. Reducing water use can improve crop yields, ultimately leading to increased net benefits^55,56. However, this optimization must also consider the intricate relationship between energy consumption and agricultural profitability.

Table 8 shows that the net agricultural benefit (Z₃) derived from optimized water demand, quantified at 3,820 MCM, is 1,242 billion Rials.

Figure 12 compares the net benefits of different agricultural management strategies, measured in billion Rials. The second solution, with the highest bar, yields a net benefit of 1,800 billion Rials, reflecting a 12.5% improvement over the baseline (1,600 billion Rials). The optimal solution results in a net benefit of 1,242 billion Rials, which represents a 22.4% reduction compared to the baseline. Descriptive statistics in Table 9 show that net agricultural benefit ranges from 897 to 1,847 billion Rials, with a mean of 1,409 plus or minus 424 billion Rials. The 22% decline falls within one standard deviation of the long-term average.

Fig. 12

Net agricultural benefit corresponding to selected solutions.

This reduction is primarily due to a 13.1% decrease in agricultural water consumption under the optimal solution, which leads to lower cultivation levels and, consequently, reduced agricultural output and net benefit. The model does not specify which crops were reduced, yet, the trade-off reflects a shift toward more sustainable resource use and is consistent with the primary objective of minimizing water use. Meanwhile, the first solution shows the lowest net benefit of 900 billion Rials, indicating a 43.75% reduction.

The optimal solution, despite yielding lower economic returns than solution 2, features a smaller overall negative impact compared with the impacts that occur in the baseline across different regions. It was therefore selected as the as the sustainable solution.

Modeling assumptions

This study relies on several modeling assumptions that define the scope and applicability of the results.

• The SD-AB framework assumes fixed climatic conditions during the simulation period from 2001 to 2021, and it does not include inter-annual climate variability.

• Urban and industrial water demands are considered fully met and not open to optimization, while agricultural water use is optimized with the NSGA-II.

• Multiple energy sources such as electricity, gas, and diesel are included, but only the electric consumption from groundwater pumping is specifically optimized, and its environmental impact is measured through carbon emissions.

• Food production refers only to agricultural crop output and does not cover livestock or processing sectors.

• Surface water and groundwater flows between subregions are included, which allows for a representation of hydrological connectivity across the basin.

• While direct interactions between agents are not modeled their behaviors are linked indirectly through shared resources and system-level feedback.

These assumptions allow for a manageable and scalable model. At the same time they limit how well the results could be extended to areas with similar water, farming, and organizational systems. Nevertheless, the model’s modular and spatially disaggregated structure allows its application to other basins as long as suitable local data and specific policy conditions are used.

Sensitivity analysis

A sensitivity analysis was conducted by reducing the irrigated area of rice, a water-intensive crop, by 20% relative to the business‑as‑usual (BAU) baseline to assess model robustness and examine system behavior under an ‘actual’ management intervention. Table 10 summarizes the average performance over 2001–2021 for both scenarios. A pairwise comparison of the three objectives (Z₁: water use, Z₂: energy use, Z₃: net benefit) reveals the following insights.

• (i) Water–energy nexus (Z₁ vs. Z₂). A 1.8% reduction in irrigation water use (–78 MCM/year) leads to a disproportionately large 19.3% drop in agricultural electricity consumption (–426 MWh/year). This tenfold difference highlights the high sensitivity of energy use to the cultivation of water-thirsty crops such as rice, underscoring how modest water savings at basin scale can produce substantial energy co-benefits.

• (ii) Water–profit trade-off (Z₁ vs. Z₃). The same 1.8% reduction in water use results in only a 0.6% decrease in net agricultural benefit (–0.02 trillion Rials/year), indicating that farmer income is far less sensitive to moderate reductions in irrigation. This suggests that it is possible to maintain economic returns while reallocating water toward other or environmental uses through modest crop-mix adjustments.

• (iii) Energy–profit trade-off (Z₂ vs. Z₃). A nearly 20% reduction in energy use is achieved with virtually no impact on profit. Electricity costs account for a small share of total production costs in the basin, therefore, reducing energy demand does not erode farmers’ revenue. This supports the adoption of demand-side electricity measures (e.g., more efficient pumps, incentive-based tariffs) to improve the water-energy-food-economic system.

Table 10. 20% reduction in rice cultivation area vs. baseline (2001–2021).

Collectively, these comparisons demonstrate that a targeted 20% reduction in rice cultivation delivers double-digit energy savings and meaningful water conservation at minimal economic cost. These findings reinforce the importance of multi-objective optimization for identifying leverage points—such as strategic crop-mix changes—that advance water and energy goals without undermining rural livelihoods.

In addition, Fig. 13 generalizes the analysis to six rice‑area multipliers (0.25, 0.50, 1.0, 1.5, 2.0, 4.0), indicating a smooth but non-linear increase in water and energy demand as rice area increases. The non-linearities are due to head‑dependent pumping power, efficiency losses, and hydraulic friction.

Fig. 13

Water-to-energy change ratio associated with rice cultivation reduction.

Summary and conclusion

This study presented an integrated approach for optimizing agricultural water allocation within the WEF nexus using a combined SD-AB modeling framework, enhanced by the NSGA-II multi-objective optimization algorithm and the AHP. This model’s framework was applied to the Zayandehrud Basin in Iran. The model addressed complex interdependencies among water, energy, food production, and economic outcomes under conditions of water scarcity and competing sectoral demands. The model comprised four interlinked subsystems—water, energy, food, and economics—allowing for a comprehensive assessment of policy scenarios. Results revealed significant trade-offs between minimizing water and energy consumption and maximizing net agricultural benefits. The application of AHP enabled the prioritization of optimal solutions based on multiple stakeholder-driven criteria, with water availability emerging as the most influential factor, followed by environmental impact and cost-effectiveness.

The optimal solution reduced total water consumption by 13.1% compared to the baseline, leading to a measurable improvement in groundwater sustainability (an average increase of one meter in groundwater levels) and a 355% increase in environmental water allocation, thereby supporting ecosystem health. Simultaneously, energy use dropped by 24%, contributing to significant reductions in CO₂ emissions, demonstrating the environmental co-benefits of integrated resource management. The net agricultural benefit under the optimal scenario was smaller than that of one of the alternative solutions, yet, it represents a more balanced trade-off, with smaller regional disparities and better performance across the sustainability indicators. Food security also improved by 21% across most crops, particularly for wheat and orchards, although some crops like rice and maize require targeted strategies for improvement.

Overall, this research emphasizes the importance of integrated modeling frameworks in managing the intricate dynamics of the WEF nexus. The proposed approach facilitates sustainable resource allocation and environmental conservation, and equips policymakers with actionable insights for prioritizing water allocations across sectors, setting groundwater extraction limits, and designing incentive mechanisms for cultivating low-water-use crops. Policymakers can use these outcomes to develop balanced water-energy-food policies that consider long-term environmental sustainability and regional socio-economic constraints.

This work showcases the applicability of this model in a water-stressed region, and highlights its potential for adaptation in similar contexts globally. Future work can build upon this foundation by incorporating climate change projections, advanced renewable energy integration, and socio-political dynamics to further refine decision-making processes. The developed framework contributes to long-term sustainability, resilience, and informed governance in resource-constrained settings.