Introduction

The nonlinear Shrödinger (NLS) equation has drawn a lot of attention from researchers in recent decades due to its numerous applications in optical fibers, plasma, neural networks and other scientific and engineering fields1,2,3,4,5. The Shrödinger equations explain many key ideas, including processing, control acoustics, electro-magnetic, and electro-chemistry6,7,8. Mainly, In nonlinear optics, solitons in optics are pulses or waveforms that form the fundamental basis for soliton transmission technology in optical fibers9. These solitons maintain their shape over long distances due to a balance between nonlinear and dispersive effects, making them highly suitable for long-haul data transmission. They are crucial in the telecommunications industry for reliable data transmission across transcontinental and transoceanic distances10,11,12.

The technology relies on various sophisticated mathematical models to describe and predict soliton behavior. Complex Ginzburg–Landau model, this model describes the evolution of wave packets in nonlinear media and is essential for understanding dissipative structures and soliton stability13. Fokas-Lenells equation generalizes the nonlinear Schrödinger equation to account for certain physical phenomena like higher-order dispersion and nonlinearity14. Kaup–Newell Equation integrable system that provides insights into the dynamics of solitons with specific properties15. Lakshmanan–Porsezian–Daniel model that addresses the effects of higher-order dispersion and nonlinearity in optical fibers16. Kundu–Eckhaus model that extends the nonlinear Schrödinger equation to include higher-order nonlinearity and perturbation terms, making it suitable for modeling complex wave interactions17. Gerdjikov–Ivanov equation a variant of the nonlinear Schrödinger equation that includes specific nonlinear terms to model pulse propagation in certain types of fibers18. These models help researchers and engineers design and optimize optical fiber systems for efficient, high-capacity data transmission, addressing challenges such as dispersion management, nonlinear effects, and soliton interactions.

The development of soliton solutions for the nonlinear partial differential equations is growing field of research and many researchers are working on it. Duran et al.19,20 investigated the Zoomeron and Kudryashov-Sinelshchikov equations by using the analytical techniques and derived various types of soliton solution. Numerous analytical aspects of coupled Higgs system and Bogoyavlensky-Konopelchenko equation have discussed by the efficient apparoaches by Yokus et al.21,22. Iqbal et al.23,24 examined the shock waves and analyzed the dispersive solitons and their deep insights. Murad et al.25,26 contributed in this area by use of fractional derivative and visualized deep dynamics of solitons. Hu et al.27,28 developed structure-preserving method to investigate the vibration of moving cracked cantilevered beam and proposed multi-symplectic method for the vibration of the thick plate. Xu et al.29 presented dynamic analysis on the asymmetrical structures. Huai et al.30 displayed dynamic equations of the flexible magnetic hub-beam model subjected to the external magnetic field force. Many reserachers have worked in different field31,32,33,34,35.

Triki-Biswas equation is also one of these critical governing models and has been utilized in optical networks. The description of ultrashort and femtosecond pulse propagation in extremely nonlinear optical fibers can be based on this model36,37.

$$\begin{aligned} \iota \varphi _{t}+{\mathbb {A}} \varphi _{xx}+\iota {\mathbb {B}}(|\varphi |^{2j} \varphi )=0, \end{aligned}$$
(1)

when, \(j=1\), the variable \(\varphi\) represents the wave profile, \(\varphi _{xx}\) denotes the group velocity dispersion (GVD) with dispersion parameter \({\mathbb {A}}\). The term \((|\varphi |^{2j} \varphi )\) represents non-Kerr dispersion (NKD), where \({\mathbb {B}}\) is nonlinear perturbation (self-steepening term). It has been resolved by numerous authors via various techniques, and the outcomes have been documented in38,39,40,41

In the present investigation, we applied the \(\phi ^6\)-model expansion method to derive the solitary wave solutions of the Triki-Biswas equation. The results are in the from of periodic solitary wave solution, dark solitary wave solution, bright solitary wave solution, multi-smooth kink solitary wave solution, periodic anti-peaked solitary wave solution, and smooth solitary wave solution. Soliton solutions in optical fibers have numerous important applications, significantly enhancing various aspects of telecommunications and data transmission. The article is arranged as section (2) describes the construction of analytical solutions as well as traveling wave structures and graphical representation. Section (3) describes the graphical discussion and applications. Then finally conclusion.

Novelty statement

While the Triki–Biswas model has been investigated using several analytical approaches such as the tanh expansion, sine–cosine method, and the Riccati approach, these techniques often restrict the obtained solutions to a narrow class (mostly solitonic or periodic forms). In contrast, applying the more general \(\phi ^{6}-\)expansion method provides a unified and systematic framework that not only recovers existing solutions as special cases but also yields new families of exact waveforms, including breathers, rational solutions, and singular excitations. This broader solution space significantly enriches the physical interpretation of the TB model, offering deeper insights into nonlinear wave propagation, energy localization, and oscillatory phenomena relevant to optics, plasma physics, fluid dynamics, and biomolecular systems.

Formulation of analytical exact solutions

The \(\Phi ^{6}-\)model expansion scheme42,43

Take into account a general differential equation:

$$\begin{aligned} {\mathbb {W}}(\varphi ,\varphi _{t},\varphi _{x},\varphi _{tt},\varphi _{xx},\ldots ) = 0. \end{aligned}$$
(2)

This can be turned to an ODE:

$$\begin{aligned} {\mathfrak {Y}}({\mathfrak {B}},{\mathfrak {B}}',{\mathfrak {B}}'',\ldots ) = 0. \end{aligned}$$
(3)

Employed the transformation:

$$\begin{aligned} \varphi (x,t)={\mathfrak {B}}(\eta ), \end{aligned}$$
(4)

where, \(\eta =\phi _{1}x+\phi _{2}t\). Assuming the solution of Eq. (3) can be written as follows:

$$\begin{aligned} {\mathfrak {B}}(\eta )=\sum _{N=0}^{2M} \bigg [{\mathfrak {b}}_{N}{\mathbb {W}}^{N}(\eta )\bigg ], \end{aligned}$$
(5)

where M is a balancing constant. The function \({\mathbb {W}}(\eta )\) fulfill ,

$$\begin{aligned} \begin{aligned} {\mathbb {W}}'^{2}(\eta )={\mathfrak {h}}_{0}+{\mathfrak {h}}_{2}{\mathbb {W}}^{2}(\eta )+{\mathfrak {h}}_{4}{\mathbb {W}}^{4}(\eta )+{\mathfrak {h}}_{6}{\mathbb {W}}^{6}(\eta ),\\ {\mathbb {W}}''(\eta )={\mathfrak {h}}_{2}{\mathbb {W}}(\eta )+2{\mathfrak {h}}_{4}{\mathbb {W}}^{3}(\eta )+3{\mathfrak {h}}_{6}{\mathbb {W}}^{5}(\eta ). \end{aligned} \end{aligned}$$
(6)

The Eq. (6) satisfies,

$$\begin{aligned} {\mathbb {W}}(\eta )=\frac{\Pi (\eta )}{\sqrt{{\mathfrak {f}}\Pi ^{2}(\eta )+{\mathfrak {g}}}}, \end{aligned}$$
(7)

where \({\mathfrak {f}}\Pi ^{2}(\eta )+{\mathfrak {g}}>0\) and \(\Pi (\eta )\) is the result of the Jacobi elliptic equation,

$$\begin{aligned} \Pi '^{2}(\eta )=\textrm{l}_{0}+\textrm{l}_{2}\Pi ^{2}(\eta )+\textrm{l}_{4}\Pi ^{4}(\eta ), \end{aligned}$$
(8)

where \(\textrm{l}_{0},~\textrm{l}_{2},\) and \(\textrm{l}_{4}\) are constants yet to be find out, whereas \({\mathfrak {f}}\) and \({\mathfrak {g}}\) are defined as,

$$\begin{aligned} {\mathfrak {f}}=\frac{{\mathfrak {h}}_{4}(\textrm{l}_{2}-{\mathfrak {h}}_{2})}{3\textrm{l}_{0}\textrm{l}_{4}+({\mathfrak {h}}^{2}_{2}-\textrm{l}^{2}_{2})},~~ {\mathfrak {g}}=\frac{3{\mathfrak {h}}_{4}\textrm{l}_{0}}{3\textrm{l}_{0}\textrm{l}_{4}+({\mathfrak {h}}^{2}_{2}-\textrm{l}^{2}_{2})}, \end{aligned}$$
(9)

under the constraint,

$$\begin{aligned} {\mathfrak {h}}^{2}_{4}(\textrm{l}_{2}-{\mathfrak {h}}_{2})[9\textrm{l}_{0}\textrm{l}_{4}-(\textrm{l}_{2}-{\mathfrak {h}}_{2})(2\textrm{l}_{2}+{\mathfrak {h}}_{2})]+3{\mathfrak {h}}_{6}[-\textrm{l}^{2}_{2}+{\mathfrak {h}}^{2}_{2}+3\textrm{l}_{0}\textrm{l}_{4}]^{2}=0. \end{aligned}$$

The given Table 1 represents the Jacobi elliptic functions.

Table 1 Extreme behaviour of functions
Full size table

Propagating solitary wave structures of Eq. (1)

We use a traveling wave transformation to determine results to Eq. (1):

$$\begin{aligned} \varphi (x,t)={\mathcal {G}}(\eta )e^{\iota ({\mathfrak {n}}x-{\mathfrak {m}}t)},\ \eta =x-{\textbf{k}} t \end{aligned}$$
(10)

The variables \({\mathfrak {m}}\) and \({\textbf{k}}\) represent frequency and velocity, respectively. Chirp is indicated by

$$\begin{aligned} \tau f(x,t-\frac{\partial }{\partial x}[{\mathfrak {n}}(\eta )-{\mathfrak {m}} t]={\mathfrak {n}}^{'}(\eta ). \end{aligned}$$
(11)

We can get the following equations by putting Eq. (11) inside Eq. (10) and splitting the results into real and imaginary parts:

$$\begin{aligned} f {\mathcal {G}}+k_{0} \varphi ' {\mathcal {G}}+{\mathbb {A}} {\mathcal {G}}''-{\mathbb {A}} {\mathcal {G}}(\varphi ')^{2}-{\mathbb {B}} \varphi ' {\mathcal {G}}^{2j+1}=0, \end{aligned}$$
(12)

and

$$\begin{aligned} {\mathbb {A}} {\mathcal {G}} \varphi '' +2{\mathbb {A}} {\mathcal {G}}' \varphi ' -k_{0} {\mathcal {G}}'+{\mathbb {B}}(2j+1){\mathcal {G}}^{2j}{\mathcal {G}}'=0. \end{aligned}$$
(13)

We use the following presumptive solution to solve the previously mentioned equations:

$$\begin{aligned} {\mathcal {G}}'=l_{0}{\mathcal {G}}^{2j}+l_{2}, \end{aligned}$$
(14)

where, \(l_{1}, l_{2}\) are constants that is the nonlinear chirp parameters. Therefore, we derive

$$\begin{aligned} \ \tau g(x,t)=-(l_{1} {\mathcal {G}}^{2j}+l_{2}). \end{aligned}$$
(15)

By putting the Eq. (14) within Eq. (13), to derive the chirped parameters that is given as:

$$\begin{aligned} l_{1}=-\frac{{\mathbb {B}}(2j+1)}{2{\mathbb {A}}(j+1)},\ l_{2}=\frac{k_{0}}{2{\mathbb {A}}}. \end{aligned}$$
(16)

Putting the Eq. (14) into Eq. (12), to obtained

$$\begin{aligned} \ {\mathcal {G}}^{''}+r_{0} {\mathcal {G}}^{4j+1}+r_{2} {\mathcal {G}}^{2j+1}+r_{3} {\mathcal {G}}=0, \end{aligned}$$
(17)

where, \(r_{1}=\frac{{\mathbb {B}}(2j+1)}{4{\mathbb {A}}^{2}(j+1)},\ r_{2}=\frac{k_{0} {\mathbb {B}}}{2 {\mathbb {A}}^{2}}, r_{3}=\frac{4f{\mathbb {A}}+k^{2}}{4 {\mathbb {A}}^{2}}.\)

An elliptic equation that explains how a field’s strength varies in nonlinear media is Eq. (17). There are additional ways to express this equation.

$$\begin{aligned} ({\mathcal {G}}')^{2}+\frac{l_{1}}{2j+1} {\mathcal {G}}^{4j+1}+\frac{l_{2}}{j+1} {\mathcal {G}}^{2j+1}+l_{3}{\mathcal {G}}^{2}. \end{aligned}$$
(18)

The following transformation can be used to rewrite Eq. (18) in a different way:

$$\begin{aligned} {\mathcal {G}}(\eta )={\mathcal {P}}(\eta )^{\frac{1}{2}}. \end{aligned}$$
(19)

Eq. (18) reduced as:

$$\begin{aligned} {\mathcal {P}}''+\tau {\mathcal {P}}+\omega {\mathcal {P}}^{j+1}+\pi {\mathcal {P}}^{2j+1}=0, \end{aligned}$$
(20)

where, \(\tau =4 r_{3},\ \omega =\frac{2 r_{2}(j+2)}{j+1},\ \pi =\frac{4 r_{1}(j+1)}{2j+1}.\) We apply the following change of variable to obtain the solutions of Eq. (20).

$$\begin{aligned} {\mathcal {P}}(\eta )={\mathfrak {P}}(\eta )^{\frac{1}{j}}. \end{aligned}$$
(21)

Eq. (20) reduced:

$$\begin{aligned} j^{2} \tau {\mathfrak {P}}^{2}+j^{2} \omega {\mathfrak {P}}^{3}+j^{2} \pi {\mathfrak {P}}^{4}+(1-j){\mathfrak {P}}'^{2}+j {\mathfrak {P}} {\mathfrak {P}}''=0. \end{aligned}$$
(22)

The homogeneous balancing constant \(M=1\) to Eq. (22), then,

$$\begin{aligned} {\mathfrak {P}}(\eta )={\mathfrak {b}}_{0}+{\mathfrak {b}}_{1}{\mathbb {W}}(\eta )+{\mathfrak {b}}_{2}{\mathbb {W}}^{2}(\eta ), \end{aligned}$$
(23)

where,

$$\begin{aligned} \begin{aligned} {\mathbb {W}}'^{2}(\eta )={\mathfrak {h}}_{0}+{\mathfrak {h}}_{2}{\mathbb {W}}^{2}(\eta )+{\mathfrak {h}}_{4}{\mathbb {W}}^{4}(\eta )+{\mathfrak {h}}_{6}{\mathbb {W}}^{6}(\eta ),\\ {\mathbb {W}}''(\eta )={\mathfrak {h}}_{2}{\mathbb {W}}(\eta )+2{\mathfrak {h}}_{4}{\mathbb {W}}^{3}(\eta )+3{\mathfrak {h}}_{6}{\mathbb {W}}^{5}(\eta ). \end{aligned} \end{aligned}$$
(24)

Here, \({\mathfrak {b}}_{0}, {\mathfrak {b}}_{1}, {\mathfrak {b}}_{2}\) are unknown parameters. Once Eq. (24) and Eq. (22) have been substituted, compare the coefficients of the polynomial to zero. After that, we solved the problem with Maple Software and got the following set.

Set 1:

$$\begin{aligned} \bigg [{\mathfrak {b}}_{0}=0,~{\mathfrak {b}}_{1}=0,~{\mathfrak {b}}_{2}={\mathfrak {b}}_{2},{\mathfrak {h}}_{2}=\frac{-1}{4}j^{2} \tau ,\ {\mathfrak {h}}_{4}=\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4},\ {\mathfrak {h}}_{6}=\frac{-{\mathfrak {b}}_{2}j^{2}\pi }{4j+4} \bigg ]. \end{aligned}$$
(25)

We will formulate the solution using only Set 1 for the sake of conciseness. The precise answers to Equation (1) .

if \(\textrm{l}_{0}=1,~\textrm{l}_{2}=-1-s^{2},~\textrm{l}_{4}=s^{2}, ~0<s<1,\) then \(\Pi (\eta )=sn(\eta ,s)\) or \(\Pi (\eta )=cd(\eta ,s)\), we have,

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sn^{2}(\eta ,s)}{{{\mathfrak {f}} sn^{2}(\eta ,s)+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(26)

where functions f and \({\mathfrak {g}}\) are,

$$\begin{aligned} & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( -1-s^{2}+\frac{1}{4}j^{2}\tau \right) }{\left( -1-s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}+3s^{2}-2\left( -1-s^{2}\right) \left( -1-s^{2}+\frac{1}{4}j^{2}\tau \right) },\\ & {\mathfrak {g}}=\frac{3 \left( \frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\right) }{\left( -1-s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}+3s^{2}-2\left( -1-s^{2}\right) \left( -1-s^{2}+\frac{1}{4}j^{2}\tau \right) }, \end{aligned}$$

when \(s\rightarrow 1\), \(\Pi (\eta )=sn(\eta )=tanh(\eta )\)

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{1,1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ tanh^{2}(\eta )}{{{\mathfrak {f}} tanh^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(27)
Fig. 1
figure 1

The appearance as 3-D, 2-D, along with Contour for solution \({\mathfrak {P}}_{1,1}(x, t)\).

Full size image

or \(\Pi (\eta )=cd(\eta )=1\),

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{1,2}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ \Pi ^{2}(\eta )}{{{\mathfrak {f}} \Pi ^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(28)

when \(s\rightarrow 0\), \(\Pi (\eta )=sn(\eta )=sin(\eta )\)

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{1,3}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sin^{2}(\eta )}{{{\mathfrak {f}} sin^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(29)

or \(\Pi (\eta )=sn(\eta )=cos(\eta )\)

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{1,4}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ cos^{2}(\eta )}{{{\mathfrak {f}} cos^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(30)

under the constraint condition,

$$\begin{aligned} \begin{aligned}&\left( -\frac{{\mathfrak {b}}_{2}^{2} \omega j^{2}}{2j+4} \right) ^{2} \left( -1-s^{2}+\frac{1}{4}j^{2}\tau \right) \left[ 9 s^{2}-\left( -1-s^{2}+\frac{1}{4}j^{2}\tau \right) \left( -2-2s^{2}-\frac{1}{4}j^{2} \tau \right) \right] \\&+3\left( -\frac{{\mathfrak {b}}_{2}^{2} \pi j^{2}}{4j+4} \right) \left[ 3 s^{2}-\left( (-1-s^{2})^{2}-(-\frac{1}{4} j^{2} \tau )^{2} \right) \right] ^{2}=0. \end{aligned} \end{aligned}$$
Fig. 2
figure 2

The appearance as 3-D, 2-D, along with Contour for solution \({\mathfrak {P}}_{1,3}(x, t)\).

Full size image

if \(\textrm{l}_{0}=1-s^{2},~\textrm{l}_{2}=2s^{2}-1,~\textrm{l}_{4}=-s^{2}, ~0<s<1,\) thus \(\Phi (\eta )=cn(\eta ,s)\),

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{2}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ cn^{2}(\eta )}{{{\mathfrak {f}} cn^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(31)

where functions f as well as \({\mathfrak {g}}\) are,

$$\begin{aligned} & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( -1+2s^{2}+\frac{1}{4}j^{2}\tau \right) }{\left( -1+2s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}+3(1-s^{2})(s^{2})-2\left( -1+2s^{2}\right) \left( -1+2s^{2}+\frac{1}{4}j^{2}\tau \right) },\\ & {\mathfrak {f}}=\frac{3(1-s^{2})\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}}{\left( -1+2s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}+3(1-s^{2})(s^{2})-2\left( -1+2s^{2}\right) \left( -1+2s^{2}+\frac{1}{4}j^{2}\tau \right) }, \end{aligned}$$

when \(s\rightarrow 1\), \(\Pi (\eta )=cn(\eta )=sech(\eta )\)

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{2,1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sech^{2}(\eta )}{{{\mathfrak {f}} sech^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(32)

when \(s\rightarrow 0\), \(\Pi (\eta )=sn(\eta )=cos(\eta )\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{2,2}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ cos^{2}(\eta )}{{{\mathfrak {f}} cos^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(33)

under the constraint condition,

$$\begin{aligned} \begin{aligned}&\left( -\frac{{\mathfrak {b}}_{2}^{2} \omega j^{2}}{2j+4} \right) ^{2} \left( -1+2s^{2}+\frac{1}{4}j^{2}\tau \right) \left[ 9 (1-s^{2})(-s^{2})-\left( 1-s^{2}+\frac{1}{4}j^{2}\tau \right) \left( 2(-1+2s^{2})-\frac{1}{4}j^{2} \tau \right) \right] \\&+3\left( -\frac{{\mathfrak {b}}_{2}^{2} \pi j^{2}}{4j+4} \right) \left[ 3 (-s^{2})(1-s^{2})-\left( (-1+2s^{2})^{2}-(-\frac{1}{4} j^{2} \tau )^{2} \right) \right] ^{2}=0. \end{aligned} \end{aligned}$$
Fig. 3
figure 3

The appearance as 3-D, 2-D, along with Contour for solution \({\mathfrak {P}}_{2,2}(x, t)\).

Full size image

if \(\textrm{l}_{0}=s^{2}-1,~\textrm{l}_{2}=2-s^{2},~\textrm{l}_{4}=-1, ~0<s<1,\) thus \(\Pi (\eta )=dn(\eta ,s)\),

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{3}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ dn^{2}(\eta )}{{{\mathfrak {f}} dn^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(34)

where functions f as well as \({\mathfrak {g}}\),

$$\begin{aligned} & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) }{\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}-3(s^{2}-1)-2\left( 2+s^{2}\right) \left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) }\end{aligned}$$
$$\begin{aligned} & {\mathfrak {g}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( 3(s^{2}-1) \right) }{\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}-3(s^{2}-1)-2\left( 2+s^{2}\right) \left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) } \end{aligned}$$

when \(s\rightarrow 1\), \(\Pi (\eta )=dn(\eta )=sech(\eta )\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{3,1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sech^{2}(\eta )}{{{\mathfrak {f}} sech^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(35)

when \(s\rightarrow 1\), \(\Pi (\eta )=dn(\eta )=1\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{3,2}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ \Pi ^{2}(\eta )}{{{\mathfrak {f}} \Pi ^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(36)

under the constraint condition,

$$\begin{aligned} \begin{aligned}&\left( -\frac{{\mathfrak {b}}_{2}^{2} \omega j^{2}}{2j+4} \right) ^{2} \left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) \left[ 9 (1-s^{2})-\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) \left( 2(2-s^{2})-\frac{1}{4}j^{2} \tau \right) \right] \\&+3\left( -\frac{{\mathfrak {b}}_{2}^{2} \pi j^{2}}{4j+4} \right) \left[ 3 (1-s^{2})-\left( (2-s^{2})^{2}-(-\frac{1}{4} j^{2} \tau )^{2} \right) \right] ^{2}=0. \end{aligned} \end{aligned}$$

if \(l_{0}=s^{2},~l_{2}=-1-s^{2},~l_{4}=1, ~0<s<1,\) thus,

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{4}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ \Pi ^{2}(\eta )}{{{\mathfrak {f}} \Pi ^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(37)

where functions f as well as \({\mathfrak {g}}\),

$$\begin{aligned} & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( -1-s^{2}+\frac{1}{4}j^{2}\tau \right) }{\left( -1-s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}+3s^{2}-2\left( -1-s^{2}\right) \left( -1-s^{2}+\frac{1}{4}j^{2}\tau \right) }\\ & {\mathfrak {g}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( 3s^{2} \right) }{\left( -1-s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}+3s^{2}-2\left( -1-s^{2}\right) \left( -1-s^{2}+\frac{1}{4}j^{2}\tau \right) } \end{aligned}$$

when \(s\rightarrow 1\), \(\Pi (\eta )=ns(\eta )=coth\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{4,1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ coth^{2}(\eta )}{{{\mathfrak {f}} coth^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(38)

or \(\Pi (\eta )=ds(\eta )=1\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{4,2}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ \Pi ^{2}(\eta )}{{{\mathfrak {f}} \Pi ^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(39)

when \(s\rightarrow 0\), \(\Pi (\eta )=ns(\eta )=csc(\eta )\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{4,3}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ csc^{2}(\eta )}{{{\mathfrak {f}} csc^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(40)

or \(\Pi (\eta )=dc(\eta )=sec(\eta )\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{4,4}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sec^{2}(\eta )}{{{\mathfrak {f}} sec^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(41)

under the constraint condition,

$$\begin{aligned} \begin{aligned}&\left( -\frac{{\mathfrak {b}}_{2}^{2} \omega j^{2}}{2j+4} \right) ^{2} \left( s^{2}+\frac{1}{4}j^{2}\tau \right) \left[ 9s^{2}-\left( -1-s^{2}+\frac{1}{4}j^{2}\tau \right) \left( 2(1-s^{2})-\frac{1}{4}j^{2} \tau \right) \right] \\&+3\left( -\frac{{\mathfrak {b}}_{2}^{2} \pi j^{2}}{4j+4} \right) \left[ 3s^{2}-\left( (-1-s^{2})^{2}-(-\frac{1}{4} j^{2} \tau )^{2} \right) \right] ^{2}=0. \end{aligned} \end{aligned}$$
Fig. 4
figure 4

The appearance as 3-D, 2-D, along with Contour for solution \({\mathfrak {P}}_{4,4}(x, t)\).

Full size image

if \(\textrm{l}_{0}=-s^{2},~\textrm{l}_{2}=-1+2s^{2},~\textrm{l}_{4}=1-s^{2}, ~0<s<1,\) thus \(\Pi (\eta )=nc(\eta ,s)\),

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{5}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ nc^{2}(\eta )}{{{\mathfrak {f}} nc^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(42)

where functions f as well as \({\mathfrak {g}}\),

$$\begin{aligned} & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( -1+2s^{2}+\frac{1}{4}j^{2}\tau \right) }{\left( -1+2s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}+3(-s^{2})(1-q^{2})-2\left( -1+2s^{2}\right) \left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) }\\ & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( -3s^{2} \right) }{\left( -1+2s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}+3(-s^{2})(1-q^{2})-2\left( -1+2s^{2}\right) \left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) } \end{aligned}$$

when \(s\rightarrow 1\), \(\Pi (\eta )=nc(\eta )=cosh\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{5,1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ cosh^{2}(\eta )}{{{\mathfrak {f}} cosh^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(43)

when \(s\rightarrow 0\), \(\Pi (\eta )=nc(\eta )=sec\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{5,2}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sec^{2}(\eta )}{{{\mathfrak {f}} sec^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(44)

under the constraint condition,

$$\begin{aligned} \begin{aligned}&\left( -\frac{{\mathfrak {b}}_{2}^{2} \omega j^{2}}{2j+4} \right) ^{2} \left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) \left[ 9(-s^{2})(1-q^{2})-\left( -1+2s^{2}+\frac{1}{4}j^{2}\tau \right) \left( 2(-1+2s^{2})-\frac{1}{4}j^{2} \tau \right) \right] \\&+3\left( -\frac{{\mathfrak {b}}_{2}^{2} \pi j^{2}}{4j+4} \right) \left[ 3(-s^{2})(1-q^{2})-\left( (-1+2s^{2})^{2}-(-\frac{1}{4} j^{2} \tau )^{2} \right) \right] ^{2}=0. \end{aligned} \end{aligned}$$

if \(\textrm{l}_{0}=-1,~\textrm{l}_{2}=2-s^{2},~\textrm{l}_{4}=-1+s^{2}, ~0<s<1,\) thus \(\Pi (\eta )=nd(\eta ,s)\),

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{6}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ nd^{2}(\eta )}{{{\mathfrak {f}} nd^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(45)

where functions f as well as \({\mathfrak {g}}\),

$$\begin{aligned} & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) }{\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}+3(1-q^{2})-2\left( 2-s^{2}\right) \left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) }\\ & {\mathfrak {f}}=\frac{(-3)\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}}{\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}+3(1-q^{2})-2\left( 2-s^{2}\right) \left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) } \end{aligned}$$

when \(s\rightarrow 1\), \(\Pi (\eta )=nd(\eta )=cosh\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{6,1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ cosh^{2}(\eta )}{{{\mathfrak {f}} cosh^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(46)

when \(s\rightarrow 0\), \(\Pi (\eta )=nd(\eta )=1\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{6,2}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ \Pi ^{2}(\eta )}{{{\mathfrak {f}} \Pi ^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(47)

under the constraint condition,

$$\begin{aligned} \begin{aligned}&\left( -\frac{{\mathfrak {b}}_{2}^{2} \omega j^{2}}{2j+4} \right) ^{2} \left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) \left[ 9(1-q^{2})-\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) \left( 2(2-s^{2})-\frac{1}{4}j^{2} \tau \right) \right] \\&+3\left( -\frac{{\mathfrak {b}}_{2}^{2} \pi j^{2}}{4j+4} \right) \left[ 3(1-q^{2})-\left( (2-s^{2})^{2}-(-\frac{1}{4} j^{2} \tau )^{2} \right) \right] ^{2}=0. \end{aligned} \end{aligned}$$

if \(\textrm{l}_{0}=1,~\textrm{l}_{2}=2-s^{2},~\textrm{l}_{4}=1-s^{2}, ~0<s<1,\) thus \(\Pi (\eta )=sc(\eta ,s)\),

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{7}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sc^{2}(\eta )}{{{\mathfrak {f}} sc^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(48)

where functions f as well as \({\mathfrak {g}}\),

$$\begin{aligned} & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) }{\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}+3(1-q^{2})-2\left( 2-s^{2}\right) \left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) }\\ & {\mathfrak {f}}=\frac{(-3)\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}}{\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}+3(1-q^{2})-2\left( 2-s^{2}\right) \left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) } \end{aligned}$$

when \(s\rightarrow 1\), \(\Pi (\eta )=sc(\eta )=sinh\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{7,1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sinh^{2}(\eta )}{{{\mathfrak {f}} sinh^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(49)

when \(s\rightarrow 0\), \(\Pi (\eta )=sc(\eta )=tan(\eta )\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{7,2}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ tan^{2}(\eta )}{{{\mathfrak {f}} tan^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(50)

under the constraint condition,

$$\begin{aligned} \begin{aligned}&\left( -\frac{{\mathfrak {b}}_{2}^{2} \omega j^{2}}{2j+4} \right) ^{2} \left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) \left[ 9(1-s^{2})-\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) \left( 2(2-s^{2})-\frac{1}{4}j^{2} \tau \right) \right] \\&+3\left( -\frac{{\mathfrak {b}}_{2}^{2} \pi j^{2}}{4j+4} \right) \left[ 3(1-s^{2})-\left( (2-s^{2})^{2}-(-\frac{1}{4} j^{2} \tau )^{2} \right) \right] ^{2}=0. \end{aligned} \end{aligned}$$

if \(\textrm{l}_{0}=1,~\textrm{l}_{2}=2s^{2}-1,~\textrm{l}_{4}=-s^{2}(1-s^{2}), ~0<s<1,\) thus \(\Pi (\eta )=sd(\eta ,s)\),

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{8}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sd^{2}(\eta )}{{{\mathfrak {f}} sd^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(51)

where functions f as well as \({\mathfrak {g}}\),

$$\begin{aligned} & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) }{\left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) ^{2}+3(-s^{2}(1-s^{2}))-2\left( 2s^{2}-1\right) \left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) }\\ & {\mathfrak {f}}=\frac{3\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}}{\left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) ^{2}+3(-s^{2}(1-s^{2}))-2\left( 2s^{2}-1\right) \left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) } \end{aligned}$$

when \(s\rightarrow 1\), \(\Pi (\eta )=sd(\eta )=sinh\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{8,1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sinh^{2}(\eta )}{{{\mathfrak {f}} sinh^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(52)

when \(s\rightarrow 0\), \(\Pi (\eta )=sd(\eta )=sin\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{8,1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sin^{2}(\eta )}{{{\mathfrak {f}} sin^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(53)

under the constraint condition,

$$\begin{aligned} \begin{aligned}&\left( -\frac{{\mathfrak {b}}_{2}^{2} \omega j^{2}}{2j+4} \right) ^{2} \left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) \left[ 9(-s^{2}(1-s^{2}))-\left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) \left( 2(s^{2}-1)-\frac{1}{4}j^{2} \tau \right) \right] \\&+3\left( -\frac{{\mathfrak {b}}_{2}^{2} \pi j^{2}}{4j+4} \right) \left[ 3(-s^{2}(1-s^{2}))-\left( (2s^{2}-1)^{2}-(-\frac{1}{4} j^{2} \tau )^{2} \right) \right] ^{2}=0. \end{aligned} \end{aligned}$$

if \(\textrm{l}_{0}=1-s^{2},~\textrm{l}_{2}=2-s^{2},~\textrm{l}_{4}=1, ~0<s<1,\) thus \(\Pi (\eta )=cs(\eta ,s)\),

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{9}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ cs^{2}(\eta )}{{{\mathfrak {f}} cs^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(54)

where functions f as well as \({\mathfrak {g}}\),

$$\begin{aligned} & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) }{\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}+3(1-s^{2})-2\left( 2-s^{2}\right) \left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) }\\ & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( 3(1-s^{2})\right) }{\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) ^{2}+3(1-s^{2})-2\left( 2-s^{2}\right) \left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) } \end{aligned}$$

when \(s\rightarrow 1\), \(\Pi (\eta )=cs(\eta )=csch\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{9,1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ csch^{2}(\eta )}{{{\mathfrak {f}} csch^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(55)

when \(s\rightarrow 0\), \(\Pi (\eta )=sd(\eta )=cot\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{9,2}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ cot^{2}(\eta )}{{{\mathfrak {f}} cot^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(56)

under the constraint condition,

$$\begin{aligned} \begin{aligned}&\left( -\frac{{\mathfrak {b}}_{2}^{2} \omega j^{2}}{2j+4} \right) ^{2} \left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) \left[ 9(1-s^{2})-\left( 2-s^{2}+\frac{1}{4}j^{2}\tau \right) \left( 2(2-s^{2})-\frac{1}{4}j^{2} \tau \right) \right] \\&\quad +3\left( -\frac{{\mathfrak {b}}_{2}^{2} \pi j^{2}}{4j+4} \right) \left[ 3(1-s^{2})-\left( (2-s^{2})^{2}-(-\frac{1}{4} j^{2} \tau )^{2} \right) \right] ^{2}=0. \end{aligned} \end{aligned}$$

if \(\textrm{l}_{0}=-s^{2}(1-s^{2}),~\ \textrm{l}_{2}=2s^{2}-1,~\textrm{l}_{4}=1, ~0<s<1,\) then \(\Pi (\eta )=ds(\eta ,s)\) , we have,

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{10}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ ds^{2}(\eta )}{{{\mathfrak {f}} ds^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(57)

where functions f as well \({\mathfrak {g}}\),

$$\begin{aligned} & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) }{\left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) ^{2}+3(-s^{2}(1-s^{2}))-2\left( 2s^{2}-1\right) \left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) }\\ & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( 3(-s^{2}(2s^{2})) \right) }{\left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) ^{2}+3(-s^{2}(1-s^{2}))-2\left( 2s^{2}-1\right) \left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) } \end{aligned}$$

when \(s\rightarrow 1\), \(\Pi (\eta )=ds(\eta )=csch\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{10,1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ csch^{2}(\eta )}{{{\mathfrak {f}} csch^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(58)

when \(s\rightarrow 0\), \(\Pi (\eta )=ds(\eta )=csc\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{10,2}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ csc^{2}(\eta )}{{{\mathfrak {f}} csc^{2}(\eta )+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(59)

under the constraint condition,

$$\begin{aligned} \begin{aligned}&\left( -\frac{{\mathfrak {b}}_{2}^{2} \omega j^{2}}{2j+4} \right) ^{2} \left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) \left[ 9(-s^{2}(1-s^{2}))-\left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) \left( 2(2s^{2}-1)-\frac{1}{4}j^{2} \tau \right) \right] \\&+3\left( -\frac{{\mathfrak {b}}_{2}^{2} \pi j^{2}}{4j+4} \right) \left[ 3(-s^{2}(1-s^{2}))-\left( (2-s^{2})^{2}-(-\frac{1}{4} j^{2} \tau )^{2} \right) \right] ^{2}=0. \end{aligned} \end{aligned}$$

if \(\textrm{l}_{0}=\frac{1-s^{2}}{4},~\textrm{l}_{2}=\frac{1+s^{2}}{2},~\textrm{l}_{4}=\frac{1-s^{2}}{4}, ~0<s<1,\) then \(\Phi (\eta )=nc(\eta )\pm sc(\eta )\) or \(\Phi (\eta )=\frac{cn(\eta ,s)}{1\pm sn(\eta ,s)}\) , we have,

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{11}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ (nc(\eta )\pm sc(\eta ))^{2}}{{{\mathfrak {f}} (nc(\eta )\pm sc(\eta ))^{2}+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(60)

where functions f as well as \({\mathfrak {g}}\),

$$\begin{aligned} & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( \frac{1}{2}(s^{2}+1)+\frac{1}{4}j^{2}\tau \right) }{\left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) ^{2}+\frac{3}{4}(1-s^{2})^ {2}-\left( s^{2}+1\right) \left( (s^{2}+1)+\frac{1}{2}j^{2}\tau \right) }\\ & {\mathfrak {g}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( \frac{3}{4}(1-s^{2}) \right) }{\left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) ^{2}+\frac{3}{4}(1-s^{2})^ {2}-\left( s^{2}+1\right) \left( (s^{2}+1)+\frac{1}{2}j^{2}\tau \right) } \end{aligned}$$

when \(s\rightarrow 1\), \(\Pi (\eta )=nc(\eta ) \pm sc(\eta ) =csch(\eta ) \pm sinh(\eta )\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{11,1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ (csch(\eta ) \pm sinh(\eta ))^{2}}{{{\mathfrak {f}} (csch(\eta ) \pm sinh(\eta ))^{2}+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(61)

or \(\Pi (\eta )=\frac{cn(\eta )}{1 \pm sn(\eta )} =\frac{sech(eta)}{1 \pm tanh(\eta )}\), we derive that

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{11,2}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sech^{2}(\eta )}{{{\mathfrak {f}} sech^{2}(\eta )+{\mathfrak {g}}(1 \pm tanh(\eta ))^{2}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(62)

when \(s\rightarrow 0\), \(\Pi (\eta )=nc(\eta ) \pm sc(\eta ) =sec(\eta ) \pm tan (\eta )\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{11,3}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ (sec(\eta ) \pm tan(\eta ))^{2}}{{{\mathfrak {f}} (sec(\eta ) \pm tan(\eta ))^{2}+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(63)

or \(\Pi (\eta )=\frac{cn(\eta )}{1 \pm sn(\eta )} =\frac{cos(eta)}{1 \pm sin(\eta )}\), we derive that

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{11,4}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ cos^{2}(\eta )}{{{\mathfrak {f}} cos^{2}(\eta )+{\mathfrak {g}}(1 \pm sin(\eta ))^{2}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(64)

under the constraint condition,

$$\begin{aligned} \begin{aligned}&\left( -\frac{{\mathfrak {b}}_{2}^{2} \omega j^{2}}{2j+4} \right) ^{2} \left( \frac{1}{2}(s^{2}+1)+\frac{1}{4}j^{2}\tau \right) \left[ \frac{9}{4}(1-s^{2})-\left( \frac{1}{2}(s^{2}+1)+\frac{1}{4}j^{2}\tau \right) \left( s^{2}+1)-\frac{1}{2}j^{2} \tau \right) \right] \\&+3\left( -\frac{{\mathfrak {b}}_{2}^{2} \pi j^{2}}{4j+4} \right) \left[ \frac{3}{4}(1-s^{2})^{2}-\left( (\frac{1}{2}(s^{2})+1)^{2}-(-\frac{1}{4} j^{2} \tau )^{2} \right) \right] ^{2}=0. \end{aligned} \end{aligned}$$

if \(\textrm{l}_{0}=-\frac{(1-s^{2})^{2}}{4},~\textrm{l}_{2}=\frac{1+s^{2}}{2},~\textrm{l}_{4}=-\frac{1}{4}, ~0<s<1,\) then \(\Pi (\eta )=ncn(\eta ,s)\pm dn(\eta ,s)\) , we have,

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{12}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ (ncn(\eta )\pm dn(\eta ))^{2}}{{{\mathfrak {f}} (ncn(\eta )\pm dn(\eta ))^{2}+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(65)

where the functions f and \({\mathfrak {g}}\) are,

$$\begin{aligned} & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( \frac{1}{2}(s^{2}+1)+\frac{1}{4}j^{2}\tau \right) }{\left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) ^{2}+\frac{3}{4}(1-s^{2})^ {2}-\left( s^{2}+1\right) \left( (s^{2}+1)+\frac{1}{2}j^{2}\tau \right) }\\ & {\mathfrak {g}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( \frac{-3}{4}(1-s^{2})^{2} \right) }{\left( 2s^{2}-1+\frac{1}{4}j^{2}\tau \right) ^{2}+\frac{3}{4}(1-s^{2})^ {2}-\left( s^{2}+1\right) \left( (s^{2}+1)+\frac{1}{2}j^{2}\tau \right) } \end{aligned}$$

when \(s\rightarrow 1\), \(\Pi (\eta )=ncn(\eta ) \pm dn(\eta ) =q sech(\eta ) \pm sech(\eta )\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{12,1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ (q sech(\eta ) \pm sech(\eta ))^{2}}{{{\mathfrak {f}} ( q sech(\eta ) \pm sech(\eta ))^{2}+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(66)
Fig. 5
figure 5

The appearance as 3-D, 2-D, along with Contour for solution \({\mathfrak {P}}_{12,1}(x, t)\).

Full size image

when \(s\rightarrow 0\), \(\Pi (\eta )=ncn(\eta ) \pm dn(\eta ) =q cos(\eta ) \pm 1\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{12,2}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ (q cos(\eta ) \pm 1)^{2}}{{{\mathfrak {f}} ( q cos(\eta ) \pm 1)^{2}+{\mathfrak {g}}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(67)

under the constraint condition,

$$\begin{aligned} \begin{aligned}&\left( -\frac{{\mathfrak {b}}_{2}^{2} \omega j^{2}}{2j+4} \right) ^{2} \left( \frac{1}{2}(s^{2}+1)+\frac{1}{4}j^{2}\tau \right) \left[ \frac{-9}{4}(1-s^{2})-\left( \frac{1}{2}(s^{2}+1)+\frac{1}{4}j^{2}\tau \right) \left( s^{2}+1)-\frac{1}{2}j^{2} \tau \right) \right] \\&+3\left( -\frac{{\mathfrak {b}}_{2}^{2} \pi j^{2}}{4j+4} \right) \left[ \frac{3}{4}(1-s^{2})^{2}-\left( (\frac{1}{2}(s^{2})+1)^{2}-(-\frac{1}{4} j^{2} \tau )^{2} \right) \right] ^{2}=0. \end{aligned} \end{aligned}$$

if \(\textrm{l}_{0}=\frac{1}{4},~\textrm{l}_{2}=\frac{1-2s^{2}}{2},~\textrm{l}_{4}=\frac{1}{4}, ~0<s<1,\) then \(\Pi (\eta )=\frac{sn(\eta ,s)}{1\pm cn(\eta ,s)}\) , we have,

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{13}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sn^{2}(\eta )}{{{\mathfrak {f}} (sn^{2}(\eta )+ {\mathfrak {g}}(1\pm cn(\eta ))^{2} }}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(68)

where the functions f and \({\mathfrak {g}}\) are,

$$\begin{aligned} & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( \frac{1}{2}(1-s^{2})+\frac{1}{4}j^{2}\tau \right) }{\left( \frac{1}{2}(1-2s^{2})+\frac{1}{4}j^{2}\tau \right) ^{2}+\frac{3}{4}-\left( 1-2s^{2}\right) \left( (1-2s^{2})+\frac{1}{2}j^{2}\tau \right) }\\ & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( \frac{3}{4} \right) }{\left( \frac{1}{2}(1-2s^{2})+\frac{1}{4}j^{2}\tau \right) ^{2}+\frac{3}{4}-\left( 1-2s^{2}\right) \left( (1-2s^{2})+\frac{1}{2}j^{2}\tau \right) } \end{aligned}$$

when \(s\rightarrow 1\), \(\Pi (\eta )=\frac{sn(\eta )}{1 \pm 1+cn(\eta )} =\frac{tanh(\eta )}{1\pm sech(\eta )}\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{13,1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ tanh^{2}(\eta )}{{{\mathfrak {f}} tanh^{2}(\eta )+{\mathfrak {g}} (1 \pm sech(\eta ))^{2}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(69)

when \(s\rightarrow 0\), \(\Pi (\eta )=\frac{sn(\eta )}{1 \pm 1+cn(\eta )} =\frac{sin(\eta )}{1\pm cos(\eta )}\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{13,2}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sin^{2}(\eta )}{{{\mathfrak {f}} sin^{2}(\eta )+{\mathfrak {g}} (1 \pm cos(\eta ))^{2}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(70)

under the constraint condition,

$$\begin{aligned} \begin{aligned}&\left( -\frac{{\mathfrak {b}}_{2}^{2} \omega j^{2}}{2j+4} \right) ^{2} \left( \frac{1}{2}(1-2s^{2})+\frac{1}{4}j^{2}\tau \right) \left[ \frac{9}{4}(1-s^{2})-\left( \frac{1}{2}(1-2s^{2})+\frac{1}{4}j^{2}\tau \right) \left( 1-2s^{2})-\frac{1}{2}j^{2} \tau \right) \right] \\&+3\left( -\frac{{\mathfrak {b}}_{2}^{2} \pi j^{2}}{4j+4} \right) \left[ \frac{3}{4}(1-s^{2})^{2}-\left( (\frac{1}{2}(s^{2})+1)^{2}-(-\frac{1}{4} j^{2} \tau )^{2} \right) \right] ^{2}=0. \end{aligned} \end{aligned}$$

if \(\textrm{l}_{0}=\frac{1}{4},~\textrm{l}_{2}=\frac{1+s^{2}}{2},~\textrm{l}_{4}=\frac{(1-s^{2})^{2}}{4}, ~0<s<1,\) then \(\Pi (\eta )=\frac{sn(\eta )}{cn(\eta )\pm dn(\eta ,s)}\) , we have,

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{14}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sn^{2}(\eta )}{{{\mathfrak {f}} sn^{2}(\eta )+ {\mathfrak {g}}(cn(\eta ) \pm dn(\eta ))^{2} }}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(71)

where the functions f and \({\mathfrak {g}}\) are,

$$\begin{aligned} & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( \frac{1}{2}(s^{2}+1)+\frac{1}{4}j^{2}\tau \right) }{\left( \frac{1}{2}(s^{2}+1)+\frac{1}{4}j^{2}\tau \right) ^{2}+\frac{3}{4}(1-s^{2})^{2}-\left( s^{2}+1\right) \left( (s^{2}+1)+\frac{1}{2}j^{2}\tau \right) }\\ & {\mathfrak {f}}=\frac{\frac{-{\mathfrak {b}}_{2}j^{2}\omega }{2j+4}\left( \frac{3}{4} \right) }{\left( \frac{1}{2}(s^{2}+1)+\frac{1}{4}j^{2}\tau \right) ^{2}+\frac{3}{4}(1-s^{2})^{2}-\left( s^{2}+1\right) \left( (s^{2}+1)+\frac{1}{2}j^{2}\tau \right) } \end{aligned}$$

when \(s\rightarrow 1\), \(\Pi (\eta )=\frac{sn(\eta )}{1 \pm cn(\eta )+dn(\eta )} =\frac{tanh(\eta )}{sech(\eta ) \pm sech(\eta )}\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{14,1}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ tanh^{2}(\eta )}{{{\mathfrak {f}}\ tanh^{2}(\eta )+{\mathfrak {g}} (sech(\eta ) \pm sech(\eta ))^{2}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(72)
Fig. 6
figure 6

The appearance as 3-D, 2-D, along with Contour for solution \({\mathfrak {P}}_{14,1}(x, t)\).

Full size image

when \(s\rightarrow 0\), \(\Pi (\eta )=\frac{sn(\eta )}{cn(\eta )+dn(\eta )} =\frac{sin(\eta )}{cos(\eta ) \pm 1}\), we have

$$\begin{aligned} \begin{aligned} {\mathfrak {P}}_{14,2}(x,t)={\mathfrak {b}}_{2}{\bigg (\frac{ sin^{2}(\eta )}{{{\mathfrak {f}}\ sin^{2}(eta)+{\mathfrak {g}} (cos(\eta ) \pm 1)^{2}}}\bigg )}\times e^{({\mathfrak {n}}(x-k_{0}t)-{\mathfrak {m}}t)}, \end{aligned} \end{aligned}$$
(73)
Fig. 7
figure 7

The appearance as 3-D, 2-D, along with Contour for solution \({\mathfrak {P}}_{14,1}(x, t)\).

Full size image

under the constraint condition,

$$\begin{aligned} \begin{aligned}&\left( -\frac{{\mathfrak {b}}_{2}^{2} \omega j^{2}}{2j+4} \right) ^{2} \left( \frac{1}{2}(s^{2}+1)+\frac{1}{4}j^{2}\tau \right) \left[ \frac{9}{4}(1-s^{2})^{2}-\left( \frac{1}{2}(s^{2}+1)+\frac{1}{4}j^{2}\tau \right) \left( s^{2}+1)-\frac{1}{2}j^{2} \tau \right) \right] \\&+3\left( -\frac{{\mathfrak {b}}_{2}^{2} \pi j^{2}}{4j+4} \right) \left[ \frac{3}{4}(1-s^{2})^{2}-\left( (\frac{1}{2}(s^{2}+1)^{2}-(-\frac{1}{4} j^{2} \tau )^{2} \right) \right] ^{2}=0. \end{aligned} \end{aligned}$$

Graphical discussion

The Triki-Biswas equation is a generalized form of the derivative nonlinear Schrödinger (DNLS) equation, developed by Triki and Biswas to simulate the propagation of ultrashort pulses in optical fiber networks. Applying the \(\phi ^6\)-model expansion method to derive the soliton solutions of the Triki-Biswas equation.

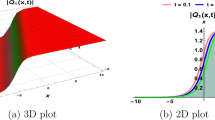
In Fig. 1 we illustrate the pictorial results of the solution \({\mathfrak {B}}_{1,3}\) and derive the periodic behavior by taking the different values of the \({\mathfrak {b}}_{2}=0.2\), \({\mathfrak {n}}=1\), \(\omega =1.1\), \(\tau =0.09\), \(j=\)0.1, \(s=0.001\) \({\mathfrak {m}}\) represent frequency and \({\textbf{k}}\) velocity. The variation in \({\textbf{k}}=0.02, 0.2, 2\) to derive the different amplitude. Periodic, non-decaying waveforms are described by periodic solitons, commonly referred to as cnoidal waves, which are solutions to nonlinear wave equations. These solutions are especially important for optical fibre networks because they provide special benefits for processing and transmitting signals.

In Fig. 2 we illustrate the pictorial results of the solution \({\mathfrak {B}}_{1,1}\) and derive the dark soliton by taking the different values of the \({\mathfrak {m}}\) represent frequency and \({\textbf{k}}\) velocity. The variation in \({\textbf{k}}=0.02, 0.2, 2\) to derive the different amplitude. Dark solitons are used in high-speed data transmission systems because of their stability and ability to maintain their shape over long distances. Dark solitons can effectively manage dispersion in optical fibers.

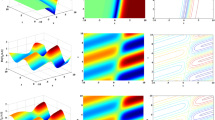
In Fig. 3 we illustrate the pictorial results of the solution \({\mathfrak {B}}_{2,2}\) and derive the bright soliton and lump solutions with different amplitudes by taking the different values of the \({\mathfrak {m}}\) represent frequency and \({\textbf{k}}\) velocity. The variation in \({\textbf{k}}=0.01, 0.1,\) to derive the different amplitude.

In Fig. 4 we illustrate the pictorial results of the solution \({\mathfrak {B}}_{4,4}\) and derive the multi smooth kink solitary wave solution by taking the different values of the \({\mathfrak {m}}\) represent frequency and \({\textbf{k}}\) velocity. The variation in \({\textbf{k}}=0.01, 0.1,\) to derive the different amplitude.

In Fig. 5 we illustrate the pictorial results of the solution \({\mathfrak {B}}_{4,4}\) and derive the bright solitary wave solution by taking the different values of the \({\mathfrak {m}}\) represent frequency and \({\textbf{k}}\) velocity. The variation in \({\textbf{k}}\) to derive the different amplitude.

The application of soliton solutions in optical fiber networks offers significant benefits, including improved signal integrity, enhanced capacity, and advanced processing capabilities. These advantages make periodic solitons a valuable tool in the development and optimization of modern optical communication systems, enabling high-speed, reliable data transmission across long distances and complex network configurations. In WDM systems, bright solitons can be used to carry data over multiple channels simultaneously. Their stability ensures minimal crosstalk and signal degradation. The \(\phi ^{6}-\)expansion method is applied to the Triki–Biswas equation, it yields a rich spectrum of soliton solutions—including bright, dark, kink-type, periodic, anti-peaked, and smooth solitary waves—that carry significant physical meaning and practical relevance. Each type of soliton corresponds to a distinct nonlinear wave phenomenon: bright solitons represent localized energy pulses that can travel long distances in optical fibers without dispersion, making them highly valuable in high-capacity data transmission; dark solitons model localized intensity dips on a continuous wave background, important in plasma wave dynamics and signal processing; kink and anti-kink solutions describe sharp transitions between stable states, useful for modeling switching phenomena in nonlinear optical devices; and periodic or anti-peaked structures capture oscillatory patterns relevant to fluid surface waves and plasma oscillations. The diversity of soliton solutions obtained through the \(\phi ^{6}-\)approach provides deeper insight into the balance between nonlinearity and dispersion in the Triki–Biswas framework, offering potential applications in optical communication networks, plasma confinement systems, energy transport in biomolecular chains, and shallow water wave prediction. This broader solution space enriches solitary wave theory while supporting technological advancements in nonlinear wave-based systems (Figs. 6 and 7).

Conclusion

This work presents the examination of the Triki-Biswas equation, which describes the propagation in the optical fiber network. The \(\phi ^6-\)model expansion method is applied because it provides a more general, flexible, and powerful framework than other expansion techniques, enabling the construction of a wider spectrum of exact solutions, including solitons, periodic waves, and singular structures. Its strength lies in handling higher-order nonlinearities and unifying various existing expansion methods under a single systematic approach, which makes it particularly valuable for modeling realistic nonlinear physical systems. By applying the more general \(\phi ^6-\)expansion method provides a unified and systematic framework that not only recovers existing solutions as special cases but also yields new families of exact waveforms, including breathers, rational solutions, and singular excitations. This broader solution space significantly enriches the physical interpretation of the TB model, offering deeper insights into nonlinear wave propagation, energy localization, and oscillatory phenomena relevant to optics, plasma physics, fluid dynamics, and biomolecular systems. Derive the soliton solutions in the form of dark solitons, bright soliton, periodic soliton, multi-smooth kink solitary wave solution, and smooth soliton solutions. Giving the arbitrary constants many values illustrates the physical behavior of the solutions, which may be important for understanding. Numerous applications in the disciplines of physics and other physical sciences might benefit from the given results. The findings of this study will aid in the comprehension of a few events that occur in optical fibres.