Introduction

The escalation of data rates and the expansion of coverage in modern mobile wireless communications systems pose significant challenges. Microstrip patch antennas stand out as prominent innovations in this domain because of their low cost, compact size, lightweight nature, ease of fabrication, and compatibility with printed circuit boards (PCBs)1. They find extensive applications in the wireless industry, including but not limited to airborne radar, radio telemetry, and satellite communications1. The conventional approach to antenna design typically involves the following steps:

  • The selection of a dielectric material, often flame retardant 4 (FR-4), is characterized by a dielectric constant (\(\epsilon _{r}\)) and a thickness (h).

  • The physical parameters, including the antenna’s feeding point, are calculated via mathematical equations.

  • Electromagnetic (EM) simulations are performed to obtain antenna parameters such as gain, bandwidth, radiation pattern, beamwidth, polarization, and impedance. It is common for the final antenna design to require optimization through iterative adjustments of physical parameters to obtain the desired response. The geometry optimization process is time-consuming as it is a multiobjective optimization with several variables to account for. In addition, the method relies on the designer’s experience and requires extensive simulations following a trial-and-error methodology2. Consequently, this manual approach consumes considerable computational resources and time3.

This paper proposes an artificial intelligence-based solution to improve design efficiency and alleviate the burden on human efforts. By leveraging artificial intelligence (AI), this approach aims to streamline the antenna design process, reducing reliance on manual optimization and accelerating the attainment of desired performance metrics. Some studies in the literature have shown the application of AI to antenna design.

First, a k-nearest neighbors’ algorithm was applied in4 to predict the response of the antenna in terms of return loss (\(S_{11}\)). Three antennas were considered: a circular patch antenna, a fractal antenna and a pyramidal horn antenna. Each antenna is characterized by different geometrical parameters, some of which are varied to obtain training data via an EM solver. Then, a machine learning (ML) model was trained and validated on the test data. Finally, the predicted output was compared with the EM solver response. However, the study does not specify the dielectric material used, making it difficult to assess the practical feasibility of the proposed designs.

Another approach is shown in3. This paper presents a method that begins by classifying the type of antenna to be designed via a support vector machine (SVM) model. The classification is based on performance requirements such as gain, bandwidth, resonant frequency, and \(S_{11}\). A second model subsequently provides detailed geometric specifications to meet the identified requirements. To accomplish this, the significant variables were selected and varied in EM simulations to obtain the dataset. Then, the classification model is trained. Finally, the second model is trained by experimenting with various ML algorithms ultimately selecting the stacking ensemble learning approach. The same method was applied in5, but the k-nearest neighbors’ algorithm was used to select between a square patch antenna, a pyramidal horn antenna and a helical antenna. Then, another algorithm obtains the geometrical parameters. In this study, dielectric parameters are swept arbitrarily during simulations without ensuring that the resulting configurations correspond to physically realizable substrate materials. Building on this approach,6 introduces a four-layer feedforward ANN trained using the Levenberg–Marquardt algorithm to design microstrip patch antennas with square, triangular, and trapezoidal geometries. Unlike earlier models that focus solely on predicting physical dimensions, this network is capable of estimating both the patch dimensions and the optimal feed point, directly from performance parameters such as resonance frequency, gain, and return loss. The main problem with this work is the limited size of the datasets employed: none of them exceeds 200 samples. In addition, the study employs a single commercial substrate (Polytetrafluoroethylene (PTFE)) without assessing whether it is the most suitable choice for the antenna configurations explored. Finally, in7 the authors propose a ML methodology to predict the equivalent resonant circuit (LRC) of a meandered slot patch antenna. The authors generate a dataset through CST simulations, extract resonance frequencies and return losses, and compute equivalent inductance and capacitance values. A random forest regression model is then trained to predict \(S_{11}\), L, and C from the antenna’s slot dimensions. However, it is limited to a single commercial substrate (RT/Duroid 5880), which restricts the generalization of the method across different dielectric materials.

In8, a technique employing regression-based ML approaches was introduced for designing a square patch antenna with a slot. The dataset is generated through EM simulations, wherein the design parameters such as frequency, slot size, dielectric material, patch thickness, and length are varied. Three models were developed, each adjusting the inputs to produce a distinct output. One model yields the resonance frequency, another provides the length, and the third determines the slot size. Additionally, various ML regression algorithms have been tested, such ANN, SVM, and decision tree-based regression methods, to evaluate their performance in predicting antenna parameters. Ultimately, a physical antenna designed via their method was presented, along with its \(S_{11}\) measurement, which was compared with the results obtained from EM simulations. In addition, in9 a comparative analysis of four machine learning models: ANN, random forest (RandForest), decision trees (DTs), and support vector regression (SVR) for predicting the physical dimensions of rectangular patch antennas is presented. Using a dataset of 3111 samples generated through HFSS simulations, their results showed that the random forest model outperformed the others in terms of mean squared error. This paper highlights the growing role of diverse ML strategies in reducing design time and enhancing geometric prediction accuracy. While the study in8 considers four distinct substrate materials with relative permittivities of 2.1, 2.2, 2.94, and 4, no systematic analysis is conducted to determine the most appropriate substrate for each design scenario. In contrast,9 restricts the entire dataset to a single material (FR4), which may limit the performance of the antennas. Another contribution is found in1, where ML algorithms were employed to predict the resonance frequency of a rectangular patch antenna. This study selects a dielectric material and frequency range, generating the antenna dataset through EM simulations. After that, various algorithms are tested to determine the optimal performance in predicting the resonance frequency. Additionally, a prototype is shown in this study. The main limitation of this work lies in the use of one substrate (FR4), with no consideration of its effectiveness in terms of electrical performance for the intended dual-band application.

This paper presents an AI-driven toolbox for designing rectangular patch antennas using machine learning. Its key innovation is the use of two independent models: one predicts antenna dimensions from the target frequency, and the other estimates performance (\(S_{11}\), gain) from those dimensions. This modular strategy, aligned with the conventional design workflow, outperforms a single deep model by improving generalization and simplifying training. Most state-of-the-art studies do not prioritize selecting the optimal dielectric material. For example, in4, the dielectric is not specified. In Refs.3,5 the parameters of the dielectric are swept, regardless of whether the material exists. In Refs.1,6,7,8,9, a specific material was employed without ensuring its suitability as the optimal choice. The main idea of this paper is to work with commercial materials, compare the results obtained in terms of \(S_{11}\) and gain to choose the best option. This toolbox incorporates multiple commercial dielectric substrates and evaluates their suitability across different frequencies. Histograms are employed to analyze the real operability range of each material, enabling the system to recommend the most appropriate substrate for a given frequency. By combining predictive modeling with material screening, the toolbox facilitates a practical, fast, and accurate antenna design process.

This paper is structured as follows: “Antenna design” describes the antenna design theory, including the physical parameters and the feeding. Additionally, a study of dielectric theory is included. Section “Machine learning” outlines the most important considerations to the ML design. Section “Toolbox description” provides a comprehensive description of the entire methodology, from frequency selection to complete antenna design. Experiments to verify the methodology are presented in “Experiments”, while “Conclusion” summarizes the conclusions drawn from the study.

Antenna design

This section describes the common analytical design process for rectangular patch antennas10,11. The most important parameter is the working frequency (f), followed by the substrate parameters, namely the dielectric constant (\(\epsilon _r\)) and thickness (h).

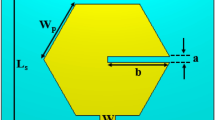
Equations (1)–(5) outline the dimensions of a rectangular patch antenna10. To better illustrate the patch antenna geometry, Fig. 1 provides a physical representation of the antenna.

The rectangular patch antenna width (W) can be computed as described in Eq. (1)

$$\begin{aligned} {W=\frac{c}{2f}\sqrt{\frac{2}{ {\varepsilon _{r}+1}}}} \end{aligned}$$
(1)

where f is the working frequency and \(\epsilon _r\) is the dielectric constant of the material. To calculate the effective dielectric constant (\({\varepsilon _{eff}}\)), Eq. (2) can be used:

$$\begin{aligned} \epsilon _{eff}=(\epsilon _r+1)/2+(\epsilon _r-1)/2\ \sqrt{(}1+12\ h/W\ \ ) \end{aligned}$$
(2)

where W denotes the width and where h and \(\epsilon _r\) are the thickness and the dielectric constant of the substrate respectively. Using Eq. 3, the length of the patch (L) is calculated:

$$\begin{aligned} { L = L_{eff} - 2\Delta L} \end{aligned}$$
(3)

where \({L_{eff}}\) represents the effective length, which is determined via Eq. (4), and \(\Delta L\) denotes the length extension, which is computed via Eq. (5):

$$\begin{aligned} {L_{eff} = \frac{c}{2f\sqrt{ {\varepsilon _{eff}}}}} \end{aligned}$$
(4)
$$\begin{aligned} {\Delta L = 0.412h\frac{(\varepsilon _{eff}+0.3)(\frac{W}{h}+0.264)}{(\varepsilon _{eff}-0.258)(\frac{W}{h}+0.8)}} \end{aligned}$$
(5)

where \({\varepsilon _{eff}}\) is the effective dielectric constant, f is the working frequency, W is the width of the patch and h is the thickness of the substrate.

A key consideration in antenna design is the feeding point, as it determines the reflection coefficient (\(S_{11}\)) of the antenna, and affects the matching bandwidth directly. As illustrated in Fig. 1, there are two methods for feeding patch antennas.

Figure 1
figure 1

Patch antenna feeding methodologies: (a) microstrip line and (b) feeding Point.

Full size image

  • A microstrip line was used (Fig. 1a). This method is optimal when the feeding circuit and the antenna are on the same layer.

  • A point inside the patch antenna is used (Fig. 1b). This method is used if the circuit feeding the antenna and the patch antenna are in different layers12.

In this case, the chosen method uses a microstrip line. The dimensions of the microstrip line that feeds the antenna can be determined using Eqs. (6)–(12)11:

  • \(x_0\) is the space between the antenna and the feeding microstrip line. It can be calculated with the Eq. (6)

    $$\begin{aligned} x_0=\lambda _0/100 \end{aligned}$$
    (6)

    where \(\lambda _0\) is the wavelength of the system.

  • \(w_0\) is the width of the microstrip. This is an important value because it determines the input impedance matching. It is calculated with Eq. (7)

    $$\begin{aligned} Z_c = \frac{120\pi }{\sqrt{\epsilon _eff}[\frac{W}{h}+1.393 +0.337ln(\frac{W_0}{h}+1.444)]} \end{aligned}$$
    (7)

    where \(Z_c\) is the resonant input resistance without the impedance matching.

  • \(y_0\) is the insertion of the microstrip in the antenna. It can be calculated as shown in Eqs. (8)–(11).

    $$\begin{aligned} & R_{in}(y=y_0)=R_{in}(y=0)cos^2\left( \frac{\pi }{L}y_0 \right) \end{aligned}$$
    (8)
    $$\begin{aligned} & R_{in}(y= 0) = \frac{1}{2(G_1 \pm G_{12})} \end{aligned}$$
    (9)
    $$\begin{aligned} & G_1 = \frac{1}{120}\frac{W}{\lambda _0} \end{aligned}$$
    (10)
    $$\begin{aligned} & G_{12} = \frac{1}{120\pi ^2} \int _{0}^{\pi } \left[ \frac{sin(\frac{k_0 W}{2})cos\theta }{cos\theta }\right] ^2 J_0(k_0Lsin\theta )sin^3\theta \,d\theta \end{aligned}$$
    (11)

    where \(R_{in}\) is the input resistance, \(G_1\) is the conductance of a single slot, \(G_{12}\) is the mutual conductance, \(k_0\) is the wavenumber and \(J_0\) is the Bessel function of the first kind of order zero. The ± sign depends on the field distribution, where + represents odd distributions and – represents even distributions. In the case of the patch antenna, + is the selected sign.

  • \(L_0\) is the length of the feeding microstrip. Equation (12) was empirically defined in this study, since the length of the feeding line is phase-dependent and does not affect the antenna performance in this case.

    $$\begin{aligned} L_0 = 2y_0 \end{aligned}$$
    (12)

The design expressions described above depend on the electrical properties of the dielectric materials used. Not all dielectric materials exhibit the same behavior across different frequency ranges, making the choice of dielectric crucial for achieving optimal antenna performance.

Dielectrics are materials with a low capacity to conduct electricity but support dielectric polarization when placed in an electric field. Positive charges align with the field direction, whereas negative charges align in the opposite directions. In antenna design, not all dielectric materials are suitable for all frequency designs because of several factors.

First, dielectric materials are characterized by their permittivity or dielectric constant, which is frequency-dependent. At lower frequencies, the material charges have more time to align and polarize. This alignment does not occur at higher frequencies13. Consequently, the dielectric constant is inversely proportional to the frequency14. Additionally, the thickness of the dielectric affects the frequency in the same manner. As the thickness increases, the operational frequency decreases because of the fringing effect14. This effect arises from the air gap in the magnetic field and is influenced by frequency15, as the waves travel through both the dielectric and the air because of the finite antenna dimensions14.

Another factor to consider is the dielectric loss tangent, which indicates the dissipation of electrical energy caused by various physical processes, such as electrical conduction or dielectric resonance16. Materials with higher loss tangents dissipate more energy, making them less suitable for higher frequencies.

After reviewing the necessary antenna theory for this paper, we delve into machine learning and the techniques that will be employed in this study.

Machine learning

The term ML is one of the fundamental topics of AI. It uses existing information, following the strategy of supervised learning, to learn and generate a model, so that new data can be predicted17. The main goal involves the development of mathematical models capable of being trained with relevant data from an environment to determine the future without knowing all the external influence information17.

There are different algorithms available, such as linear regression, logistic regression, SVM and Naïve Bayes. In this case, three regression algorithms have been tested: ANN, RandForest, and SVR. This section provides an overview of the algorithms tried.

Artificial neural network

An ANN is a structured network that links an input layer to an output layer17,18. It is composed of layers, which can be expressed as18,19:

  • Input layer. It obtains the features of the system to analyse. Typically these data are normalized to improve the numerical precision of the network.

  • Hidden layers. They extracted the pattern of the analysed system by using neurons.

  • Output layer. It is also formed by neurons, and provides the final network outputs, which are products of the previous layers.

ANNs can be implemented via different types of architectures, defining the organization of different neurons and their connections. Some of the architectures available are18,19:

  • Single-layer feedforward architecture. This architecture has one input layer and a single output layer which also works as a hidden layer. These networks are used in pattern classification and linear filtering problems.

  • Multiple-layer feedforward architecture. It is similar to the previous method but has multiple hidden layers. This is the solution for function approximation, pattern classification, system identification, process control, optimization, robotics, etc.

  • Feedback architecture. This architecture has a particular output layer, as it feedbacks inputs for other neurons. These are employed in dynamic information processing.

  • Mesh architecture. In this architecture, the spatial position of neurons is considered with the goal of pattern extraction.

Support vector regression

SVR is a ML technique derived from SVM, specifically adapted for regression problems. It is widely used in areas such as classification, regression, and signal processing. SVR is particularly effective in dealing with nonlinear and high-dimensional problems by applying the principle of local optimization20,21.

The core idea behind SVR is to find a function \(f(x)\) that has at most \(\epsilon\) deviation from the actual target values for all training data, while maintaining the model as flat as possible. The flatness is enforced by minimizing the norm of the weights, \(\Vert w\Vert ^2\), thus leading to better generalization capability21,22.

Key components of SVR include:

  • Kernel function. SVR uses kernel tricks to transform input data into higher-dimensional spaces where linear separation is more feasible. Common kernels include linear, polynomial, and radial basis function (RBF).

  • \(\epsilon\)-insensitive loss. The model ignores errors smaller than \(\epsilon\), focusing only on predictions that lie outside the margin.

  • Regularization parameter \(C\). This controls the trade-off between the flatness of the function and the tolerance for deviations larger than \(\epsilon\). A smaller \(C\) allows more violations, while a larger \(C\) penalizes them heavily.

SVR is widely used in applications where accurate continuous prediction is required and the dataset may contain noise or nonlinear relationships22.

Random forest

RandForest is a powerful ensemble learning method used for both classification and regression tasks17. It often delivers performance comparable to advanced methods such as boosting and adaptive bagging. By incorporating random feature selection during training, RandForest enhances model robustness and accuracy, especially when working with large and complex datasets. Nevertheless, in certain scenarios, the method is susceptible to to overfitting, which may lead to noisy predictions or reduced generalization in both classification and regression tasks23,24.

RandForest is composed of several key components24,25:

  • DT. Each tree is trained on a different subset of the original dataset, created through a process called bootstrap sampling. This means that some samples may be repeated, while others are left out.

  • Random feature selection. At each split within a tree, a random subset of features is selected, rather than evaluating all of them. This increases diversity among trees and reduces overfitting.

  • Aggregation mechanism. The final output is obtained by averaging the predictions of all trees (for regression) or taking the majority vote (for classification).

The main advantage of RandForest lies in its robustness and accuracy, especially when dealing with complex, high-dimensional datasets. It is less susceptible to overfitting than a single decision tree due to the averaging of multiple diverse models25. However, in some cases, if the number of trees or the depth is too large, the model may still become overfitted or computationally expensive.

Toolbox description

This section provides a comprehensive description of the development of the proposed antenna design toolbox. Figure 2 graphically illustrates the workflow for better understanding. The process begins with the creation of the dataset, followed by the design of the ANNs and the analysis of histograms, concluding with the AI-driven antenna design toolbox.

Figure 2
figure 2

Methodology to create the AI-driven antenna design toolbox.

Full size image

Dataset generation

The dataset is created by combining MATLAB scripts with PathWave Advanced Design System (ADS) EM simulations. The automation of antenna layout generation is achieved via application extension language (AEL), the internal language of ADS. The patch antenna model used is shown in Fig. 1a. First, the physical parameters of the antennas (W, L, W0, L0, X0, Y0) are calculated following the procedure explained in “Antenna design”. For a given substrate, i.e. for a given \(\epsilon _{r}\) and h pair, an antenna is generated for each frequency between 0.5 and 10.5 GHz in increments of 0.1 GHz, resulting in an initial dataset of 1000 antennas. Then, through AEL scripting, all the antenna layouts and EM simulation setups are created. Once all the EM simulations are executed, a dataset is compiled in a comma-separated values (CSV) file, and the frequency, gain, \(S_{11}\), and physical parameters of each patch antenna are recorded. All EM simulations were performed using the ADS Momentum solver with default mesh settings, which offer a good trade-off between accuracy and computation time for this type of structure and frequency range.

Before the training process, the data need to be analysed, and nonoperational antennas, identified by \(S_{11}\) values exceeding -10 dB and gains below 0 dB, are removed from the dataset. For specific substrates, there are frequency ranges without valid antennas. This can be seen in the histogram which shows the number of functional antennas as a function of frequency. For example, Fig. 3 displays the histogram of functional antennas for a substrate with \(\epsilon _{r}\) = 3.48 and h = 2mm. It is evident that from 8 GHz to 10.5 GHz there are no data. This is because the dielectric material is not suitable for operation within that bandwidth or because the analytical equations lack precision in that range. Therefore, this information is saved in a database that records the frequency ranges in which each studied dielectric material does not produce valid antennas.

Once the data have been analysed, they are normalized by scaling the values in the range from 0 to 1. This ensures that the values are not excessively large, preventing neuron saturation during training. Finally, the dataset is divided into two subsets: training data and test data, at a ratio of 80:20.

Figure 3
figure 3

Histogram of valid antennas for a substrate with \(\epsilon _{r}\) = 3.48 and h = 2mm.

Full size image

ML design

This study addresses the problem by dividing it into two parts. The first aims to derive the geometrical parameters (W, L) from the desired frequency, while the second focuses on estimating the performance parameters (\(S_{11}\) and gain). The geometrical parameters of the microstrip line that feeds the antenna are determined analytically via the procedure explained in “Antenna design”, based on the antenna’s W and L, and the substrate properties \(\epsilon _{r}\) and h. For this task, three machine learning (ML) algorithms were evaluated.

Artificial neural networks (ANN)

The ANNs applied in this work use a two-layer feedforward network architecture. Each network consists of an input layer, a hidden layer with a sigmoid transfer function, and an output layer with a linear transfer function. The optimal configuration was found to include 10 hidden neurons, selected manually by testing different values ranging from 5 to 15. This setup achieved the best trade-off between accuracy and generalization.

More complex deep neural networks (DNNs) were deliberately avoided. For instance, in9, the authors address a significantly more complex problem using a four-layer feedforward network with three hidden layers to manage a broader set of inputs. In contrast, such depth was not necessary in our case. Given the structured and low-dimensional nature of our input parameters, a simpler and more efficient approach was adopted.

This work implemented two independent feedforward neural networks: the first one predicts the antenna’s physical dimensions (W, L), and the second estimates its performance metrics (gain, \(S_{11}\)) based on those dimensions. The proposed architectures are illustrated in Fig. 4.

Figure 4
figure 4

ANN architectures for deriving (a) geometrical parameters (W, L) and (b) performance parameters (\(S_{11}\), gain).

Full size image

Support vector regression (SVR)

In this study, an SVR model was implemented using MATLAB’s fitrsvm function with a radial basis function (RBF) kernel. The input data was the normalized frequency, and the outputs (W, L, gain, \(S_{11}\)) were predicted independently using a one-output-per-model strategy. Hyperparameters such as KernelScale and BoxConstraint were optimized to minimize the validation error.

Random forest (RandForest)

In this work, the RandForest model was built using MATLAB’s fitrensemble function with the Bag method. The algorithm was trained using normalized input frequency to predict the output vector composed of either antenna dimensions (W, L) or performance metrics (gain, \(S_{11}\)). Hyperparameter optimization via Bayesian search was applied to identify the optimal values for NumLearningCycles (number of learners), MaxNumSplits (maximum tree depth), and MinLeafSize (leaf size).

Results

For each commercial substrate material under evaluation, a set of independent neural networks or regression models was trained. The performance metrics reported – the mean squared error (MSE) and coefficient of determination (\(R^2\)) – correspond to the average values obtained from all trained models for each material.

This approach reduces the impact of model initialization variability and ensures that the reported results reflect a consistent and representative estimate of each model’s predictive capacity across the entire dataset. Results are summarized in Table 1.

Table 1 Regression performance comparison of three machine learning models (ANN, SVR, and RandForest) for predicting antenna size parameters (W, L) and performance metrics (gain, \(S_{11}\)).
Full size table

To evaluate the generalization capacity of the trained models, a 5-fold cross-validation procedure was applied. This method involves dividing the dataset into five equally sized subsets (folds). In each iteration, one fold is used as the test set while the remaining four folds serve as the training data. This process is repeated five times so that each fold is used once as test data. The final MSE obtained for the three algorithms is compared in Table 2.

Table 2 Average MSE obtained through 5-fold cross-validation for each machine learning model: Artificial Neural Network (ANN), Support Vector Regression (SVR), and Random Forest (RandForest).
Full size table

For the design of patch antennas, the selected architecture is the ANN, which demonstrated the best overall performance among the evaluated models. This architecture is particularly well-suited for capturing complex nonlinear relationships between frequency and antenna characteristics. As shown in Tables 1 and 2, the ANN achieved the best values of MSE and \(R^2\) in size prediction. Additionally, regularization techniques have been applied to improve generalization and prevent overfitting, thereby enhancing the model’s performance on unseen data.

Although training time remained approximately constant across different configurations, hyperparameter tuning contributed to improved model stability. In particular, selecting appropriate values (e.g., the number of hidden neurons in the ANN or the tree depth in the RandForest) reduced fluctuations during training and improved generalization, as reflected in the validation metrics.

AI-driven antenna design toolbox

The proposed toolbox includes two key functionalities:

  • Material Listing: For each material, the geometrical and performance parameters are provided to help the user select the optimal antenna for a specific application. The commercially available materials implemented in this study include Shengyi Technology S1150G FR-4, Rogers RT Duroid 6006 and Rogers RO3206, each offered in various thicknesses. Table 3 summarizes the most important properties of these materials. These materials have been selected for their accessibility and proven reliability in antenna fabrication. They provide valid antenna designs either across the entire frequency range studied or within specific portions of it, depending on their dielectric properties and thicknesses.

  • AEL Antenna Generation for ADS: Generates the layout, including the feeding point, ready to be simulated in ADS.

Table 3 Properties of materials used.
Full size table

It is important to note that, in the proposed methodology, the substrate is not selected in advance by the user. Instead, the user simply provides a target operating frequency, and the toolbox internally evaluates all available substrates (with their respective \(\epsilon _{r}\) and h values) and ranks them based on predicted performance. Substrate parameters were considered as additional input features during model development. However, it significantly degraded the predictive accuracy of the model, likely due to the increased dimensionality and nonlinear dependencies. Therefore, the final implementation keeps substrate selection implicit and data-driven. In practice, the toolbox evaluates all available trained substrates for the given frequency and provides the user with predicted performance parameters (W, L, \(S_{11}\), and gain) for each material. The final choice is left to the user, who can take into account not only electrical performance but also practical aspects such as cost, availability, or fabrication preferences.

Experiments

To measure the quality of the models, two metrics are used: the \(R^2\) and the MSE.

The MSE measures the average squared difference between the predicted and actual values. As shown in Equation (13)29, the MSE is calculated using the number of predictions (n) and the observed (E(\(\theta\))) and predicted (\(\theta\)) values.

$$\begin{aligned} MSE = \frac{1}{n} \sum _{i=1}^{n} (E(\theta )-\theta )^2 \end{aligned}$$
(13)

The \(R^2\) measures how well a regression model fits the data. It is calculated as the ratio of the explained variance to the total variance30. As shown in Eq. (14), \(R^2\) ranges from 0 to 1, with higher values indicating a better fit.

$$\begin{aligned} R^2 = \frac{\sum _{i=1}^{n} (E(\theta )-\bar{\theta })^2}{\sum _{i=1}^{n} (\theta - \bar{\theta })^2} \end{aligned}$$
(14)

As previously mentioned, for each dielectric material, an antenna was generated for each frequency between 0.5 GHz and 10.5 GHz in steps of 0.1 GHz, starting with an initial dataset of 1000 antennas. Figure 5 presents the histogram of functional antennas obtained for the first substrate analyzed, Shengyi Technology S1150G FR-4, with an \(\epsilon _r\) of 4.6 and an h of 1.6 mm. As shown, this material exhibited 609 working antennas within a frequency range of 1 GHz to 10.5 GHz. However, the sample density begins to stabilize at approximately 5.5 GHz. The regression plots for the first ANN designed to predict geometric parameters are illustrated in Fig. 6. The MSEs for training and testing were \(9.92 \times 10^{-5}\) and \(2.12 \times 10^{-4}\), respectively. Notably, the \(R^{2}\) values were 0.998 for training and 0.997 for testing, indicating a perfect fit. Figure 7 depicts the regression plots for the second ANN designed to predict the performance parameters. The MSE for training was 0.0009, and for testing, it was 0.029. The \(R^{2}\) values were 0.9788 for training and 0.6604 for testing, suggesting a strong correlation between predicted and actual values.

Figure 5
figure 5

Histogram for valid antennas for a substrate with \(\epsilon _r\) = 4.6 and t = 1.6 mm.

Full size image
Figure 6
figure 6

Regression plot for (a) training (b) test (c) all for \(\epsilon _r\) = 4.6 and t = 1.6 mm obtaining geometrical parameters W and L.

Full size image
Figure 7
figure 7

Regression plot for (a) training (b) test (c) all for \(\epsilon _r\) = 4.6 and t = 1.6 mm obtaining performance parameters \(S_{11}\) and gain.

Full size image

To validate the generated models, three antennas were designed for frequencies of 3 GHz, 6 GHz, and 9 GHz for this substrate. Figure 8 compares the simulated and predicted \(S_{11}\) parameters for these antennas, revealing a larger error for the 3 GHz antenna. This is due to the substrate’s limitations, which, as shown in Fig. 5, were not suitable for frequencies below 3.5 GHz. Figure 9 shows the excellent agreement between the predicted and simulated gain values for the 6 GHz and 9 GHz antennas.

Figure 8
figure 8

EM simulated \(S_{11}\) parameters for the (a) 3 GHz (b), 6 GHz (c) and 9 GHz antennas compared with those of the predicted model (red dots).

Full size image
Figure 9
figure 9

2D cut far field simulated gain for the (a) 6 GHz and (b) 9 GHz antennas compared with those of the predicted model (blue dots).

Full size image

The same analysis was performed for different substrates. Table 4 summarizes the obtained results, where the ’pred’ column corresponds to the predicted values and the ’sim’ column corresponds to the simulated values. Additionally, the errors committed are summarized, with their absolute error (AE) and relative error (RE).Both error represents a consistent outcome. This validates the approach and suggests potential for other applications in related areas of study.

Table 4 Predicted (Pred) and simulated (Sim) \(S_{11}\) and gain for different substrates at 6 GHz and 9 GHz with their absolute errors (AEs) and relative errors (REs).
Full size table

To verify the predictions and simulations, two antennas were manufactured using the same material as in the simulation: one designed for 6 GHz and the other for 9 GHz, as shown in Fig. 10. The 6 GHz antenna has physical dimensions of 15.2 mm \(\times\) 14.9 mm, while the 9 GHz antenna measures 9.7 mm \(\times\) 10.0 mm. These dimensions were directly obtained from the neural network model, ensuring that the fabricated prototypes match the layouts predicted during the design stage.

Figure 10
figure 10

From left to right: 6 GHz antenna and 9 GHz antenna.

Full size image

A Keysight Technologies N5225B PNA Microwave Network Analyser model was used to obtain the S-parameter results. The results obtained are presented in Fig. 11. The simulation and measurement results for the 6 GHz antenna (Fig. 11a) are highly consistent, with the \(S_{11}\) peak value being identical at -10.8 dB. For the 9 GHz antenna (Fig. 11b), the peak frequency of \(S_{11}\) was shifted by 250 MHz, with a peak value of -11.08 dB. At 9 GHz, the measured \(S_{11}\) value is -9.6 dB, while the peak value in the simulation is -10.5 dB.

Figure 11
figure 11

\(S_{11}\) simulated and measured results for the (a) 6 GHz and (b) 9 GHz antennas.

Full size image

Table 5 provides a comprehensive comparison of ML-based antenna design methodologies reported in the literature. The table summarizes the antenna types, ML techniques used, design objectives, substrate considerations, and whether the results were experimentally validated.

The analyzed studies cover a variety of antenna geometries, such as rectangular patches, circular horns, fractal and slot structures. In terms of ML techniques, there is a diverse range including traditional models like decision trees (DT) and regression, RandForest, SVR, and ANN, including convolutional neural networks (CNNs). Notably, hybrid or combined approaches are also explored, such as ensemble learning or models integrating both classification and regression.

The design objectives vary widely–from predicting resonant frequency or \(S_{11}\) parameters to selecting antenna geometry or directly determining physical dimensions like W and L. This diversity reflects the flexibility of ML techniques in addressing different stages of the antenna design pipeline.

Regarding substrates, only a few works specify whether commercial or theoretical materials were used. Several studies sweep the dielectric constant \(\epsilon _{r}\) without focusing on physically realizable materials, which may compromise real-world applicability. This highlights the need for greater attention to material feasibility in ML-driven antenna design.

In terms of measured validation, some studies support their findings through physical prototyping and empirical measurements, whereas others depend exclusively on simulation results, which–despite their usefulness–may fall short in confirming real-world performance.

Compared to the existing literature, the present work offers several key advancements. First, unlike other studies that either focus on predicting a single electromagnetic parameter (such as \(S_{11}\) or resonant frequency) or treat geometry generation and performance prediction as isolated tasks, this work simultaneously predicts both physical dimensions (W and L) of the antenna and its performance (\(S_{11}\) and gain) from the desired frequency.

Moreover, while many prior works either do not specify the substrate or sweep the dielectric constant \(\varepsilon _r\) across non-commercial values, this work operates strictly with commercially available dielectric materials. This ensures that all predicted designs are practically feasible.

Unlike several references that rely exclusively on simulated data, this study includes a physical prototype fabricated using the predicted parameters. The experimental results are compared with simulation outcomes, providing strong evidence of the model’s accuracy.

Finally, the methodology adopted in this work simplifies the modeling process. By focusing on a limited but well-chosen set of input parameters, the need for deep or overly complex neural network architectures is eliminated. Instead, simple but effective models are enough to make accurate predictions. This contrasts with other studies that rely on deeper networks or complex models to handle more extensive or unstructured inputs.

Table 5 Comparison of ML-based antenna design methodologies.
Full size table

Conclusion

The integration of ML into rectangular patch antenna design offers a promising approach to streamline the design process and enhance efficiency. This study introduces a new methodology that not only automates iterative design steps but also generates an AEL file, allowing easy layout generation within ADS software. By automating the iterative design process, ML algorithms significantly reduce human intervention and computational resources compared with traditional trial-and-error methods.

Furthermore, the proposed approach takes into account commercially available substrates, ensuring more practical and applicable results. This study underscores the critical importance of selecting appropriate dielectric materials for optimal antenna performance. It is evident that not all materials are suitable for all frequency ranges, leading to substantial inaccuracies in antenna behavior within certain frequency bands.

The proposed ML-based methodology demonstrates remarkable accuracy in calculating antenna geometrical parameters (W and L) and predicting performance metrics (return loss “\(S_{11}\)” and gain). The results obtained are comparable to those achieved through electromagnetic simulations.

This approach outlines significant opportunities for future advancements in the field of electromagnetic device optimization. This methodology could be extended to more complex antenna geometries, such as fractal, horn, or array configurations, which would further expand its applicability across a broader range of wireless communication systems. In addition to antenna design, this machine learning-driven approach may also be applied for the optimization of other radiofrequency (RF) and microwave components, such as filters, amplifiers, and phased arrays, where high precision and reduced design time are critical.

Regarding computational efficiency, the proposed ML-based approach offers significant advantages. For example, on a PC with an Intel Core i7-12700K @ 3.60 GHz and 32 GB RAM, the complete prediction process takes around 5 seconds. In contrast, the traditional workflow often requires hours of manual work, especially for non-experts, due to iterative EM simulations, substrate selection, feeding optimization, and validation. Even for skilled designers, reaching a well-matched antenna design can take more than 45 minutes. The ML toolbox not only accelerates the design process, but also removes the dependency on specialized knowledge.