AgriFact framework for modelling the impact of farmers’ information demand on nationwide wheat productivity in India

Abstract

Understanding the link between farmers’ information needs and crop yield is vital for crafting effective, sustainable agricultural policies. However, existing research has yet to comprehensively investigate the impact of farmers’ information demand on crop yield using advanced analytical tools. In this direction, the presented study introduces the AgriFact framework to explore the relationship between Indian farmers’ information inquiries and crop yield using Deep Learning (DL)-based modelling and numerical methods-based variables’ relationship analysis. The study examines 1.8 million farmer query calls collected over a decade from Kisan Call Centers, alongside district-wise wheat yield data across India. In the first phase, six DL models are developed and compared to estimate crop productivity based on topic-wise query calls per hectare. From the experiments, it is noted that the 1-D CNN model delivered the highest predictive accuracy, achieving the lowest RMSE (0.759 t/ha) and MAE (0.585 t/ha) among all evaluated models. Later, the study integrates ceteris paribus analysis and factor-wise partial derivatives, demonstrated through a nationwide wheat yield case study. The presented research offers deeper insights into the association between farmers’ information demand and wheat crop productivity, potentially informing the formulation of evidence-based agricultural interventions.

Introduction

Agriculture faces growing challenges from rising food demand, climate change, and resource constraints, making it essential to adopt innovative strategies like ICTs to improve farmers’ access to vital information¹. A growing body of research highlights the transformative role of ICTs in enhancing agricultural productivity in India. Studies such as² show that mobile-based information services significantly improve decision-making among smallholder farmers³. demonstrated that providing timely price and agronomic information via mobile phones led to better market engagement and farm management⁴. emphasized the positive impact of call center-based advisory services on yield outcomes. More recently⁵, analyzed large-scale ICT deployments and confirmed their role in bridging information gaps and improving yield, especially in marginalized regions. While past studies have explored the impact of agricultural extension programs, key gaps remain–including limited focus on long-term effects, inadequate representation of marginalized groups, and insufficient analysis of how information access influences productivity⁶. Notably, no existing research has examined the role of farmers’ information demand in predicting crop yield or the relationship between different types of agricultural information and productivity⁷.

While several existing studies have explored Deep Learning (DL) techniques for crop yield estimation modeling⁸, there remains limited investigation into how DL models can be used to analyze the relationship between independent variables, such as farmers’ information demand, and the dependent variable, crop yield⁹. Methodologically, the use of Ceteris Paribus (CP) and Partial Derivative (PD) analyses in conjunction with DL models has not yet been widely adopted, likely due to the inherent challenges involved in integrating these interpretability techniques with complex DL architectures.

Deep Learning (DL) models are inherently complex and high-dimensional, which poses challenges in interpreting the influence of individual input variables. These models often achieve high predictive performance, but this comes at the cost of reduced interpretability compared to traditional, more transparent models. In this scenario, Ceteris Paribus (CP) analysis–an interpretability technique that examines the effect of changing one variable while holding others constant–becomes computationally demanding in such settings. Similarly, calculating Partial Derivatives (PD), which measure the sensitivity of the model’s output with respect to small changes in input features, is complicated by non-linear activations and deep architectures. The proposed AgriFact framework overcomes these limitations by introducing customized algorithms for CP and PD analysis, enabling a more transparent understanding of how various types of agricultural information affect crop yield.

The presented study addresses the gaps in the current literature on using DL-based models for estimating crop yields based on farmers’ information demand. Moreover, the demonstrated case study is conducted in the context of the wheat crop, which is a critical staple crop and a major source of nutrition for billions of people worldwide. Besides, the target region of the presented case study includes the wheat-growing territories of India, which is one of the leading producers of the Wheat crop, contributing to $\approx 12.5$% of global wheat production¹⁰.

The proposed AgriFact framework analyzes $\approx$1.8 million farmer query calls (2011–2021) alongside district-wise wheat yield data, focusing on 14 key wheat-related topics. Data preprocessing involved merging district names using a Levenshtein-distance approach and transforming query logs into seasonal topic-wise call counts, normalized as query calls per hectare (q/ha). Big Data tools handled the large dataset efficiently, and Box-Cox transformation addressed skewed variable distributions. Six DL models were evaluated for yield prediction, with 1-D CNN performing best and used for further CP and PD analysis. The framework also explored variable effects and topic interactions using polynomial modeling. Based on the provided text, following are the research questions that this study addresses:

• 1. How does farmers’ information demand influence crop yield, particularly in the context of wheat production in India?

• 2. Can DL models effectively predict crop yield based on topic-wise farmer information queries collected via ICT platforms?

• 3. What is the relative predictive performance of different DL models (e.g., CNN, RNN, LSTM, GRU, Transformer and MLP) in estimating wheat yield from large-scale ICT-based datasets?

• 4. How can interpretability techniques like CP and PD be integrated into DL models to understand the impact of individual information topics on crop yield?

The proposed framework offers valuable insights for shaping targeted agricultural policies and interventions, with potential applications across crops and regions. By emphasizing the role of ICTs in enhancing productivity and sustainability, it supports better decision-making and resource optimization. The study also benefits various stakeholders-such as agro-input firms, market intermediaries, and financial institutions-by identifying key productivity factors, ultimately contributing to more sustainable and productive agriculture.

The remainder of the article is arranged as follows: Section 2 explains the internal parts and methods employed within the AgriFact framework. In Section 3, we delve into the case study, providing insights into the basic statistics of the input data and the outcomes achieved at each phase of the framework. Section 4 explores the potential explanations behind the results obtained from the case study, citing studies that share similar observations. This section also discusses the study’s limitations and outlines future avenues for research. Finally, Section 5 summarises the study with an overview of the research findings.

Methodology

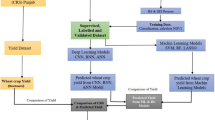
The AgriFact framework’s methodology consists of four key modules: Data Collection and Preparation, DL-based Modelling, Variables’ Relationship Analysis, and Results Interpretation (Fig. 1). Initially, farmer query call data from Kisan Call Centres was merged with district-wise crop yield data and normalized using the Box-Cox transformation. Six DL models were trained and the best-performing one was selected for further analysis. The third module employed CP and PD analyses to examine the impact of the top 14 query topics–measured as calls per hectare–on crop yield, including interaction effects, especially with weather-related queries. Finally, polynomial equations were fitted using the least squares method to interpret variable effects, offering a comprehensive understanding of yield-influencing factors. The remainder of this section gives a detailed explanation of each step of the methodology.

Fig. 1

Internal modules of the AgriFact framework for exploring the association between nationwide farmers’ information demand and crop yield.

Data preparation

The first module of the methodology focuses on data collection and preprocessing. Farmer query call data was sourced from the Kisan Knowledge Management System (KKMS)¹¹, and district-wise crop yield and cultivation area data from the Ministry of Agriculture and Farmers Welfare portal¹². Kisan Call Centers (KCC), accessible via the toll-free number 1800-180-1551, provide agricultural advice to farmers, with call-log data publicly available at https://kcc-chakshu.icar.gov.in/¹³.. A customized web crawler was developed to collect $\approx$10 years (2011–21) of district-wise monthly call-log files, which were merged into a unified dataset and combined with yield and cultivation area data. The number of query calls per hectare was then computed for the top 14 wheat-related topics. To accurately merge records from both datasets, district names were matched using a modified Levenshtein Distance Index (LDI)¹⁴.

$$\begin{aligned} \begin{aligned} ldi(n_1, n_2)&= \left( 1 - \frac{ld(n_1,n_2)}{max(|n_1|,|n_2|)} \right) \times 100\\ where,\ ld(x,y)&= {\left\{ \begin{array}{ll} |x| & \text {if } |x|= 0,\\ |y| & \text {if } |y|= 0,\\ ld(tail(x),tail(y)) & \text {if } if |x| = |y|,\\ 1 + min {\left\{ \begin{array}{ll} ld(tail(x),y) & \\ ld(x,tail(y)) & \\ ld(tail(x),tail(y)) & \\ \end{array}\right. } & \text {otherwise}\\ \end{array}\right. } \end{aligned} \end{aligned}$$

(1)

Here, $n_1,n_2$ are the input character strings between whom the LDI is to be calculated, $|n_1|$ represents the length of string $n_1$, and tail(x) is the string x without the first character. The next step included transforming the data into a normal distribution using the Box-Cox transformation¹⁵. This transformation helps stabilize the variance of the data and makes it more symmetrical. Besides, the Box-Cox transformation method is utilized to normalize skewed data distributions by raising each observation to a power, lambda, calculated based on the data. The formula for Box-Cox transformation is represented as Eq. 2.

$$\begin{aligned} y(\lambda ) = {\left\{ \begin{array}{ll} \frac{(y^\lambda - 1)}{\lambda } & \text {if } \lambda \ne 0 \\ \log (y) & \text {if } \lambda = 0 \end{array}\right. } \end{aligned}$$

(2)

Deep learning-based modeling

DL-based modeling is a powerful tool for analyzing complex datasets with multiple variables. The use of DL-based models in this study allows for a more comprehensive data analysis, considering multiple variables and their interactions. In this module, the dataset prepared in the previous stage is evaluated using 5-fold cross-validation to ensure robust and unbiased model performance assessment. The data is partitioned into five equal subsets, where in each iteration, four subsets are used for training and one for testing, rotating across all folds. This approach mitigates the risk of overfitting and provides a more reliable estimate of model generalization. Six different DL-based models–MLP, RNN, LSTM, GRU, 1-D CNN, and Transformer–are trained and validated within this framework. This comprehensive evaluation helps identify the most effective architecture for yield prediction based on farmers’ information demand.

The models selected for analysis represent a mix of sequential, convolutional, and fully connected architectures, allowing for the capture of both spatial and temporal patterns in the input data. The inclusion of RNN-based models (RNN, LSTM, GRU) facilitates effective modeling of sequential dependencies within seasonal information demand. CNN and Transformer models were chosen for their strength in extracting hierarchical features and capturing long-range dependencies, respectively. The MLP model serves as a baseline to assess the added value of advanced architectures in handling high-dimensional agricultural data. A brief explanation of each of the undertaken models is as follows.

Deep learning models for sequential and structured data

Several deep learning architectures are used to model temporal and structured input data. This section summarizes the core principles and mathematical operations of commonly used models in this study.

• 1. Multi-Layer Perceptron (MLP): An MLP is a feedforward neural network with one or more hidden layers, where each neuron computes a weighted sum of inputs followed by a nonlinear activation function¹⁶. It is used here to predict crop yield from transformed inputs. The operation of a perceptron is defined as:

  $$\begin{aligned} y_j = \psi \bigg ( \sum _{i=1}^{u} w_{ji} x_i \bigg ) \end{aligned}$$

  (3)

• 2. Recurrent Neural Network (RNN): RNNs are designed to process sequences by retaining information from past inputs through hidden states¹⁷. The hidden state at each time step is updated as:

  $$\begin{aligned} h^{(t)} = tanh(b + Wh^{(t-1)} + Ux^{(t)}) \end{aligned}$$

  (4)

• 3. Long Short-Term Memory (LSTM): LSTM is a specialized RNN variant that uses gates to regulate memory retention and update over time¹⁸. The forget gate, which discards irrelevant information, is defined as:

  $$\begin{aligned} f_t = \sigma (W_f [h_{t-1}, X_t] + b_f) \end{aligned}$$

  (5)

• 4. Gated Recurrent Unit (GRU): GRU simplifies the LSTM by combining the forget and input gates into an update gate, and it uses a reset gate to control past information influence¹⁹. The update gate is given by:

  $$\begin{aligned} z_t = \sigma (W_z [h_{t-1}, X_t] + b_z) \end{aligned}$$

  (6)

• 5. 1-D Convolutional Neural Network (1-D CNN): 1-D CNNs apply convolutional filters over temporal sequences to extract local features²⁰. The dilated causal convolution for sequence modeling is:

  $$\begin{aligned} F(s) = \sum _{i=0}^{k-1} f(i)\cdot q_{s-d\cdot i} \end{aligned}$$

  (7)

• 6. Transformer: Transformers use self-attention to capture dependencies across entire sequences without recurrence, allowing parallel processing²¹. The attention mechanism is formulated as:

  $$\begin{aligned} Attention(Q, K, V) = softmax\bigg (\frac{QK^T}{\sqrt{d_k}}\bigg )V \end{aligned}$$

  (8)

Hyperparameter tuning

Hyperparameters (HP) are important factors that significantly affect the performance of any DL-based model, and finding the best set of HP is a challenging task. In the context of DL, HP include the learning rate, batch size, number of layers, number of neurons in each layer, activation functions, and regularization techniques. In the presented study, the Random search technique is used for HP tuning, it is an efficient and effective method as it explores the HP space more efficiently than other HP-tuning techniques, which can be computationally expensive and time-consuming²². In this method, the HP are randomly selected from a given range or distribution, and the corresponding model is trained and evaluated. The process is repeated multiple times with different random combinations of HP to find the best set of HP that optimize the performance of the model. Furthermore, each model in the study is trained using the early stopping technique to prevent overfitting and enhance generalization performance.

Models’ testing and comparison

After the training of each model, the accuracy of the models is evaluated using two metrics, i.e. Root Mean Square Error (RMSE) and Mean Absolute Error (MAE), expressed by Eqs. 9 and 10.

$$\begin{aligned} RMSE = \sqrt{\frac{1}{n} \sum _{i=1}^{n} (Y_i - \hat{Y_i})^2} \end{aligned}$$

(9)

$$\begin{aligned} MAE = \frac{1}{n} \sum _{i=1}^{n} |Y_i - \hat{Y_i}| \end{aligned}$$

(10)

here, n is the number of output data point, $\hat{Y}$ is the output of the DL-based model, and Y is the desired output.

Variables’ relationship analysis

The third section of the methodology involves the CP analysis, the variable-wise PD calculation, and visualizing the second-order interaction effect of the selected variables, using the trained model.

The CP analysis is a powerful tool for understanding the relationship between a dependent variable and a set of independent variables²³. The study uses the best-performing DL model to estimate crop yield based on the variables to conduct the CP analysis. Then, the variables are modified one at a time, while the other variables are held constant to observe the changes in the predicted crop yield. Algorithm 1 gives the CP algorithm utilised by the AgriFact framework.

Algorithm 1

Ceteris Paribus Analysis with DL Model

Initially, the algorithm requires inputs including the best-performing DL model ($M$), a set of independent variables ($X$) likely to impact crop yield, and the dependent variable ($y$), which represents crop yield itself. The desired output consists of non-linear models and plots illustrating how predicted crop yield changes with variations in independent variables. The algorithm begins by generating a vector $v$ of length $n$ to hold the values of the independent variables. Subsequently, it initializes the vector with the mean values of the variables to establish a baseline. Then, for each independent variable $x_i$ in $X$, the algorithm iterates through each level of $x_i$ to explore different values or categories of the variable. At each level, it modifies the vector $v$ to reflect the current level of $x_i$, uses the DL model $M$ to predict crop yield based on the modified vector $v$, and stores these predicted values. Additionally, it performs non-linear regression to understand the relationship between the independent variable $x_i$ and the dependent variable $y$. Finally, it plots the relationship between $x_i$ and $y$ using the results of the non-linear regression and the stored predicted crop yield values. After completing the analysis for each independent variable, the algorithm resets the vector $v$ to its original mean values in preparation for the next iteration.

The PD gives the rate of change of the dependent variable (wheat yield) concerning a particular independent variable (number of query calls related to a target topic) while keeping all other variables constant. By calculating the PD for each variable, we can understand the direction and magnitude of the effect of that variable on crop yield. Furthermore, the presented study calculates the PD corresponding to each variable using the Symmetric Difference Quotient (SDQ) technique²⁴. In this technique, first, the centroid point corresponding to the dataset is calculated using Eq. 11.

$$\begin{aligned} \begin{aligned} C&= \langle c_1, c_2, ...,c_k\rangle \\ where,\ c_j&= \frac{1}{n} \sum _{m=1}^{n} x_{jm} \end{aligned} \end{aligned}$$

(11)

Here, C represents the centroid vector, n represents the total number of rows in the dataset, and $x_{jm}$ represents the $m^{th}$ row element (data point) of the $j^{th}$ column (variable). In the second step, the PD is calculated using Eq. 12:

$$\begin{aligned} \begin{aligned} \frac{\partial f(C)}{\partial v_j}&= \frac{f(C^{j+})-f(C^{j-})}{2 \times h^j} \\ where,\ C^{j+}&= \langle c_1, c_2,..., (c_j+h^j),..., c_k \rangle ,\\ \ C^{j-}&= \langle c_1, c_2,..., (c_j-h^j),..., c_k \rangle \\ and,\ h^j&= c_j \times 0.001 \end{aligned} \end{aligned}$$

(12)

Here, $v_j$ is the variable corresponding to which the PD is to be calculated. In the study, PDs corresponding to each variable are calculated by varying the $c_j$ in the range of the target variable.

The study also captured the interaction effects between weather-related query calls and the four most-inquired topics (plant protection, varieties, fertilizer usage, and weed management) by performing a second-order interaction analysis. This was done by simultaneously varying two variables while keeping all other variables constant at their mean values. The obtained results were then visualized using a heatmap, where the color gradient indicated the yield values at different levels of the two interacting variables.

Results interpretations

In the fourth section of the methodology, the output corresponding to the CP and PD analysis is expressed into first, third and fifth-order polynomial equations for easy interpretation. A polynomial equation helps in visualizing the relationship between the variables and yield. This study uses the least squares method to fit the equations to the data, minimizing the sum of the squared differences between the predicted and actual values²⁵. Mathematically, it can be represented as given in Eq. 13.

$$\begin{aligned} minimize \sum _{i=1}^{n} (y_i - (mx_i + b))^2 \end{aligned}$$

(13)

where $(x_i, y_i)$ are the data points, $m$ is the slope, and $b$ is the intercept of the line or curve. After fitting the polynomial equations, the coefficients of the equations are analyzed to determine the significance of each variable on yield. The coefficients indicate the strength and direction of the relationship between the variables and yield.

Experiments and results

This section presents the outcomes of the applied methodology in analyzing a decade (2011-21) of query call and yield data. The analysis was executed using a Python 3.0 script on the Google Colab platform, which was equipped with a dual Intel(R) Xeon(R) CPU @ 2.20GHz microprocessor, 13GB RAM, and 108GB disk space. The analysis utilizes libraries including NumPy, Pandas, Matplotlib, Scikit-learn, Keras, and SciPy for data preprocessing, modeling, evaluation, and visualization. The following sub-sections present the results obtained from each module of the proposed methodology.

Data preparation

Table 1 Number and percentage of query calls in the dataset corresponding to each topic along with the lambda values, mean and standard deviation of the distribution obtained after the Box-Cox transformation.

Fig. 2

District-wise (a) Wheat yield, (b) Wheather-related number of query calls/ha, and (c) Plant protection-related number of query calls/ha (variables in log scale). The figure was created using Python 3.10 with the matplotlib (v3.8.0) and geopandas (v0.14.1) libraries.

Table 1 gives the undertaken query types in the study along with their corresponding count and percentage in the preprocessed dataset. The preprocessed dataset comprises the query call logs related to wheat cultivation during the specified timeframe. The most frequent query type in the dataset is “Weather” with a count of 6,73,399, which accounts for 29.54% of the total dataset. This query type corresponds to the “weather”-related questions asked by the Indian farmers to the KCC helpline. The second most frequent query type is “Plant Protection” with a count of 3,12,363, accounting for 13.70% of the dataset. Moreover, the least frequent query type considered in the study is “Sowing Time and Weather” with a count of 19,091, which accounts for only 0.84% of the total dataset.

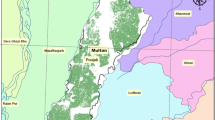
Overall, the analyzed dataset contained information from 18,98,564 queries, which is 83.28% of the complete KCC dataset (total of 22,79,709 call-log records). Here, the discarded call logs belong to either an unknown query type, or the count is too low (<0.5%) to extract any insights from them. Besides, the top five query types are “Weather,"“Plant Protection,"“Varieties,"“Fertilizer Use and Availability,"and “Weed Management,"which together accounted for more than 60% of the total queries. To understand the wheat yield distribution across India, the district-wise yield (log-scaled) was plotted on the country’s physical map (Fig. 2 (a)). The figure revealed that the highest wheat yield is concentrated in the Indo-Gangetic region, while the yield is lower in the regions that are farther away from central India.

To further investigate the patterns between wheat yield and the types of questions asked by farmers, the geo-coordinates of district-wise “weather"and “plant protection"-related queries were plotted (in log scale, Fig. 2 (b), (c)). The plots revealed an interesting trend, i.e., it seems that the areas with higher wheat yield had more “weather"and “plant protection"queries per hectare of cultivated land. The final dataset obtained after merging the two datasets (KCC and wheat yield) consisted of 4,465 rows ($\approx$450 districts $\times$ 10 seasons).

Fig. 3

(a) Raw data distribution of the weather-related calls variable, (b) Box-Cox transformed data distribution of the weather-related calls variable, (c) Raw data distribution of the Plant protection-related calls variable, and (d) Box-Cox transformed data distribution of the Plant protection-related calls variable.

The variable-wise distribution plots (Fig. 3) show the spread of the “weather"and “plant protection"variables’ data points in the dataset. From the plots, it is observed that most of the raw data points for both variables are concentrated within the range of 0.0 and 0.1. This suggests that the original data may have been skewed towards lower values. To address this, the Box-Cox transformation was applied to each variable separately. After applying the transformation, the distribution of the data changed, and the scale of the data points increased, i.e., the range of the dataset expanded. Table 1 contains the lambda values corresponding to each transformed variable along with their mean and standard deviation values. Moreover, the before-and-after distribution plots for each variable are given in the supplementary sheet, Figs. 1,2,3,4,5.

DL-based modeling

In the presented study, six DL-based models (MLP, RNN, LSTM, GRU, CNN, and Transformer) were trained and tested on the dataset to predict wheat yield based on input variables. Each developed model is designed to take 14 values (number of query calls per hectare, corresponding to each considered topic, Box-Cox transformed) and estimate wheat yield (scaled from 0.0 to 1.0). The architectural details (including the number of layers, type of layers, number of nodes, and other relevant information) of the DL-based models developed in the study are given in the supplementary sheet (Section 1).

Fig. 4

Actual and Predicted sample data points from the (a) CNN-based model, (b) RNN-based model, (c) transformer-based model, and (d) GRU-based model.

Fig. 5

Actual and Predicted trendline comparison for (a) CNN-based model, (b) RNN-based model, (c) transformer-based model, (d) GRU-based model, (e) LSTM-based model, and (f) MLP-based model.

Figure 4 shows the actual and their corresponding predicted yield values obtained from the best four models (1-D CNN, RNN, Transformers, and GRU) on the sample of unseen/testing dataset. From the figure, it is observed that the trained models are able to capture the variation in the data points, as the predicted values closely follow the actual values. This indicates that the DL-based models have learned the underlying patterns in the data and are able to make accurate predictions for wheat yield based on the given input features.

In this study, the R$^2$ values of the trained models were also computed (on the testing dataset) to evaluate their performance in predicting wheat yield (Fig. 5). The highest R$^2$ value was achieved by the 1-D CNN-based model, with a value of 0.615, followed by the RNN-based model with a value of 0.602. The Transformer-based model had a value of 0.556, while the GRU and LSTM-based models had lower values of 0.496 and 0.367, respectively. The MLP model had the lowest R$^2$ value of 0.265.

These results suggest that the 1-D CNN and RNN-based models are better suited for predicting wheat yield than the other models. The higher R$^2$ values for these models indicate that they are able to capture more of the variation in the dataset and provide more accurate predictions. However, it is important to note that the performance of these models can vary depending on the specific dataset and the HP used in their training.

The acceptability of an R$^2$ value in a research work depends on several factors such as the nature of the data, the complexity of the model, and the research question being addressed²⁶. The range of R$^2$ values for models predicting crop yield can vary widely depending on factors such as the crop type, the model’s complexity, and the quality and quantity of data used to train the model. Generally, an R$^2$ value between 0.5 to 0.9 is considered suitable for predictive models in social science and agriculture research²⁶. In the case of our research work on the correlation between farmers’ information demand and crop yield in India, an R$^2$ value of 0.6 can be considered acceptable due to the nationwide extensive study region, which has a diverse range of geographic and climatic conditions affecting crop yield. Moreover, the relationship between farmers’ information demand and crop yield is influenced by several complex factors, including weather conditions, soil quality, availability of resources, and access to technology. Therefore, a 0.6 R$^2$ value indicates a moderately strong relationship between the variables and can provide valuable insights for policymakers and stakeholders in the agriculture sector. However, it is important to note that R$^2$ should not be used as the sole metric for evaluating model performance. Other metrics, such as RMSE and MAE, should also be considered to provide a more comprehensive assessment of the model’s performance.

Fig. 6

Models’ comparison based on RMSE and MAE values.

Figure 6 presents a comparative analysis of the models based on their RMSE and MAE values obtained through 5-fold cross-validation on the dataset. Among the models, the 1-D CNN model achieved the best performance with the lowest RMSE value of 0.759 t/ha, indicating the highest accuracy in wheat yield prediction. It is closely followed by the RNN model, which recorded an RMSE of 0.788 t/ha. The Transformer-based model also demonstrated competitive performance with an RMSE of 0.815 t/ha. On the other hand, the LSTM and GRU models exhibited moderately higher RMSE values of 0.876 t/ha and 0.905 t/ha, respectively, reflecting relatively lower predictive accuracy. The MLP-based model showed the poorest performance with the highest RMSE of 1.025 t/ha.

In terms of MAE, the CNN-based model again outperformed others with the lowest MAE of 0.585 t/ha, followed by the RNN model with 0.607 t/ha. The Transformer-based model recorded a MAE of 0.636 t/ha, whereas the LSTM and GRU models had MAE values of 0.681 t/ha and 0.711 t/ha, respectively. The MLP-based model showed the highest MAE of 0.829 t/ha, indicating the least reliable predictions. Overall, Fig. 6 clearly suggests that the 1-D CNN and RNN-based models provide superior performance in predicting wheat yield compared to the other deep learning models evaluated.

Variables’ importance analysis

Fig. 7

Variables’ Importance Graph.

To assess the contribution of various input features towards wheat yield prediction, a feature importance analysis was conducted using a Random Forest Regressor model. The model was trained on the complete dataset, and permutation importance was applied to evaluate the impact of each feature on prediction accuracy. The analysis revealed that Nutrient Management had the highest importance score (0.3285), making it the most influential factor (Fig. 7). It was followed by Water Management (0.2768) and Fertilizer Use and Availability (0.2604), highlighting the critical role of resource management in crop yield. Other significant contributors included Weather, Plant Protection, and Cultural Practices. Features like Seeds, Varieties, and Government Schemes showed lower importance scores, indicating a comparatively lesser direct impact on yield in the current dataset.

Variables’ relationship analysis

Fig. 8

Effect on Wheat yield of the (a) weather-related queries variable, (b) Plant protection-related queries variable, (c) Fertilizer usage-related queries variable, and (d) Weed management-related queries variable.

Figure 8 illustrates the fitted polynomial equations on the output of the CP analysis. The first-order equation corresponding to the “weather"variable suggests that the linear relationship between weather and wheat yield is positive (Fig. 8 (a)). It implies that with an increase in the weather variable by 1 unit (Box-Cox transformed), the wheat yield increases by 0.0152 units (scaled in range 0.0 to 1.0), keeping all other variables constant. The coefficients of the equation indicate that the cubic term has the highest impact on the wheat yield, followed by the quadratic term and the linear term. The fifth-order polynomial equation suggests a more complex relationship between weather and wheat yield than the previous equations. The coefficients of the equation show that the quintic term has the highest impact on the wheat yield, followed by the quartic term. In addition to this analysis, we transformed the variable’s values back to their original scale using the inverse Box-Cox transformation with the corresponding lambda value²⁷. This allowed us to determine that the highest crop yield is observed when the farmers make 0.40 calls related to weather-topic per hectare (per season) of wheat-cultivated land.

From the first-order polynomial equation corresponding to the “plant protection"variable, it is noted that the coefficient of the variable is 0.0675, which indicates that a unit increase in the “plant protection"-related queries corresponds to an increase in yield by 0.0675 units (Fig. 8 (b)). The third and fifth-order polynomial equations indicate that the relationship between “plant protection"-related queries and yield is complex and can be modeled as a higher degree polynomial function with a coefficient of 0.195 and 0.1147, respectively. The negative coefficients of the higher-order terms indicate that the effect of plant protection on yield diminishes as the level of “plant protection"-related queries increases beyond a certain threshold. The inversely transformed values of the variable indicate that the best yield value for crop production was observed at a rate of 0.37 calls per hectare (per season) related to the “plant protection"topic.

Similarly, Fig. 8 (c) and (d) illustrates the fitted polynomial equations corresponding to the “varieties"and “fertilizer use"related variables, respectively. Overall, the relationship between the “varieties"variable and wheat yield seems to be non-linear, with the variable having a positive impact until the peak is achieved, after which it seems to negatively correlate with the wheat yield. Based on the further analysis, the optimal amount of farmers’ query calls related to “varieties"topic seems to be 0.00023 calls per hectare. Additionally, if the number of calls made by farmers exceeds this threshold, it is anticipated that the wheat yield would decline.

The first-order polynomial representing the “fertilizer use"variable shows a linear equation with a positive slope. This means that as the query calls related to “fertilizer use"increase, so does the yield. However, the relationship is relatively weak with a low coefficient value of 0.0006. Whereas, the third and fifth-order polynomial indicates that the relationship between “fertilizer use"and yield is non-linear, with a decreasing trend as the level of “fertilizer use"increases beyond a certain point. The optimal number of calls farmers made regarding “fertilizer use"was calculated to be 0.026 calls per hectare, corresponding to the highest yield value.

The fitted equations (Figures and tables) depicting the relationship between all other considered variables and wheat yield are given in the supplementary material (Tables 1,2, Figs. 6,7,8,9,10,11). These plots can offer a more detailed understanding of the relationships between the variables and their impact on crop yield. The supplementary sheet can serve as a valuable resource for further analysis and aid in replicating this study.

Partial derivative analysis

Fig. 9

Partial derivatives plots of the (a) weather-related queries variable, (b) Plant protection-related queries variable, (c) Fertilizer usage-related queries variable, and (d) Weed management-related queries variable.

PDs are used to analyse how the change in the target variable affects the rate of change in response variable when all the other variables are held constant. Observing the coefficients of the “weather"variable, we noted that as the order of polynomials increases, the effect of weather on the response variable becomes more pronounced (Fig. 9). In the case of a first-order polynomial equation, the coefficient of the linear term is negative but small (−0.0077), indicating that although the direct relationship between the two variables is positive (PD > 0) the rate of change in yield decreases as we move to a higher range of the variable. On the other hand, the fifth-order term’s coefficient is substantially negative (−0.1059), which implies a much more pronounced negative PD of the “weather"variable concerning the response variable when it is in the upper range.

The PD equations representing the relationship between “Plant Protection"variable and the crop yield shows a negative non-linear relationship that varies across the different polynomial orders (Fig. 9 (b)). However, in the range that we have considered, the relationship between the PD seems to be positive with all three equations.

Figure 9 (c) and (d) plots the fitted polynomial equations on the PDs corresponding to the “varieties"and “fertilizer use"related variables, respectively. The first-order polynomial shows that PDs, if expressed in a linear equation, follow a negative trend for both variables. The higher-order equations show that the PDs are non-linear and show positive and negative trends depending on the variables’ values.

Second-order Interaction effect visualisation

Fig. 10

Interaction effect of Weather-related query calls variable with (a) plant protection-related queries variable, (b) Varieties protection-related queries variable, (c) Fertilizer usage-related queries variable, and (d) Weed management-related queries variable.

To gain further insights, we conducted an analysis that involved varying two variables simultaneously to observe the impact of their interaction on wheat yield. This approach allowed us to capture the second-order interaction effect of the variables on the response variable. However, to ensure a fair comparison, we kept all other variables constant at their average values, which provided us with a baseline or “normal"situation. The presented research focuses on the interplay between “weather"-related query calls and four other frequently asked topics, i.e., “plant protection", “varieties", “fertilizer usage", and “weed management"(Fig. 10). The analysis revealed that the interaction between “weather"and “plant protection"-related variables positively affect crop yield. This indicates that the cases when farmers ask more questions on both topics seem to achieve the highest yield.

The heatmap from Fig. 10 (b) illustrates the interaction effect between “weather"-related query calls and “varieties". The findings suggest that the relationship between these two variables is not linear, and the highest yield is achieved only at certain levels of “varieties"-variable in combination with the “weather"variable. The yellow region in the heatmap represents the optimal combination of these variables to achieve the highest yield. Interestingly, it was observed that the yield tends to be low when farmers ask no questions regarding varieties, even if they ask a high number of questions about “weather". This indicates the importance of considering multiple factors in agricultural decision-making rather than focusing on a single variable.

Figure 10 (c) shows that the interaction of “weather"-related queries are positive when observed with the “fertilizer use"variable. In other words, the wheat yield is observed to be at the peak in cases when “fertilizer use"and “weather"-related queries are both low or high. Conversely, the yield decreases when the value corresponding to one variable is high, and the other is low.

The heatmap from Fig. 9 (d) shows the interaction effect between “weather"and “weed management"-related queries. Interestingly, the figure indicates that there is no significant interaction between the two variables. It is observed that variations in the wheat yield are only due to the changes in the “weed management"-related queries, which seems to have a negative impact on the yield. This suggests that, unlike other variables, “weather"-related queries do not play a significant role in determining wheat yield in conjunction with “weed management"-related queries. Moreover, the Box-Cox inverse transformation method can be used to determine the values of the two variables corresponding to the highest possible yield.

Discussion

The analysis reveals a positive correlation between “weather”-related queries and wheat yield, suggesting that increased demand for weather information is associated with higher productivity. This finding is consistent with previous studies; for instance²⁸, reported that weather forecast information improved wheat yield in China, while²⁹ found that access to timely weather updates enhanced maize yield in India.

Similarly, the positive association between “plant protection”-related information demand and wheat yield implies that farmers who actively seek guidance on crop protection are better equipped to manage pests and diseases, leading to higher yields. However, the polynomial model indicates diminishing returns beyond an optimal level of information usage. Supporting this³⁰, highlighted that plant protection is especially effective under high pest pressure, though excessive measures offer limited additional benefits. Likewise³¹, showed that integrated pest management significantly boosts yield but also exhibits an optimal threshold for maximum effectiveness.

Similar trends are observed for “varieties”-related information, where a negative relationship between its partial dependence (PD) and yield suggests diminishing yield returns as the dissemination of varietal information increases. A direct relationship is also noted between “fertilizer use”-related queries and wheat yield, indicating that farmers seeking fertilizer information tend to achieve higher productivity. However, the polynomial model shows diminishing returns, and excessive fertilizer information or use may negatively impact soil health, as overuse can lead to chemical buildup and reduced fertility³².

Prior research supports these findings³³. demonstrated that balanced fertilization significantly boosts wheat yield, while³⁴ also confirmed the positive effect of fertilizer application on crop yield. Moreover, the negative effects of excessive fertilizer use are well documented in literature^35,36,37.

The experimental results of the presented study indicate that the 1-D CNN model achieved the highest predictive accuracy, recording the lowest RMSE of 0.759 t/ha and MAE of 0.585 t/ha among all the models evaluated. Moreover, from the existing studies, it is noted that the yield prediction models with RMSE under 1 t/ha–especially those achieving around 0.6–0.7 t/ha–are generally regarded as acceptable and reliable in wheat yield forecasting contexts^38,39,40,41.

Therefore, the insights presented in this study have practical implications. The positive link between “weather”-related queries and yield emphasizes the role of agricultural extension services in providing timely weather information via mobile platforms. Similarly, encouraging farmers to adopt integrated pest management (IPM) practices, backed by proper training and government incentives, can enhance yield through effective crop protection. Furthermore, promoting optimal fertilizer use can maximize crop growth, while caution is needed regarding the overuse of crop variety information, as excess may not lead to proportional yield benefits.

The analysis of interaction effects highlights an upward trend between weather"-related queries and plant protection"in achieving optimal wheat yield. This may be attributed to the interdependence between weather patterns and pest dynamics, where weather awareness enables farmers to anticipate and manage pest outbreaks more effectively. Farmers who seek information on both aspects are also likely to adopt integrated and sustainable farming practices, contributing to improved yields.

A non-linear interaction is observed between weather"-related and varieties"-related queries. Farmers seeking variety-related information might be better informed about crop selection and management practices, enhancing yield. Conversely, those lacking such information may not employ optimal techniques. Additionally, certain varieties may respond differently to specific weather conditions, and informed farmers can better tailor their practices accordingly.

Furthermore, the interaction between weather"-related queries and fertilizer use"shows a positive yield correlation. This suggests that knowledge of weather conditions supports more effective nutrient management, improving plant resilience to stress. Low engagement in both factors typically leads to reduced yield, while a balanced, high-level engagement in both indicates a more holistic and productive approach to crop management. These findings underscore the importance of integrating multiple sources of agricultural information to optimize wheat yield.

The absence of a significant interaction between weather"- and weed management"-related queries suggests that weather information alone may not substantially influence yield outcomes when farmers focus on weed management. Additionally, the negative association of weed management queries with yield could stem from the intensive labor and resource demands required for effective weed control. Improper or excessive use of herbicides may further reduce yield, as supported by⁴².

The supplementary materials accompanying this study offer detailed insights into the relationship between all considered variables and wheat yield. The fitted response curves provide a visual and analytical resource for future research replication and agricultural policy design. Future research directions include evaluating the influence of additional variables such as credit access, irrigation infrastructure, and the adoption of modern agricultural technologies. Potential confounding variables such as farmers’ educational background, and regional agro-climatic differences may also influence both information demand and crop yield, potentially biasing model interpretations. These factors were not explicitly accounted for in the current analysis and should be integrated into future research to enhance the robustness and generalizability of findings. Moreover, expanding the analysis to other regions could also enhance the robustness and generalizability of the model. Moreover, these findings lay the groundwork for developing a decision support system to guide farmers using personalized data on weather, fertilizer, and crop protection.

However, the study has certain limitations. It focuses on a specific crop and geographic area (India), which may restrict broader applicability. The reliance on self-reported farmer data introduces potential biases such as recall errors. Additionally, the static nature of the analysis does not fully capture the evolving dynamics of farming practices in response to environmental changes.

Conclusion

In conclusion, the AgriFact framework effectively analyzed the link between farmers’ information demand and wheat yield using deep learning models. Among six DL models, the 1-D CNN achieved the highest prediction accuracy (RMSE 0.76 t/ha, MAE 0.56 t/ha). The CP analysis further revealed topic-wise insights into how query variations relate to yield outcomes. The study used the symmetric difference quotient to analyze how each variable influences wheat yield, offering detailed insights into their impact. Second-order interactions were examined by jointly varying two variables, and polynomial models were fitted using the least squares method. Results highlight that weather, plant protection, and fertilizer-related information positively affect wheat yield. The study reveals that beyond a certain point, more information does not lead to significant yield improvements. This emphasizes the importance of targeted, efficient agricultural information dissemination. Besides, integrating the proposed system with existing agricultural extension platforms and mobile apps to enable real-time, personalized advisory services for farmers is also recommended. In this direction, future research could examine how access to technology and financial resources further influence yield outcomes.