Introduction

Bogie, as a key bearing component of rail vehicles, bears important functions such as load transfer, traction braking, etc., and the safety and reliability of its structure will directly affect the operation safety of vehicles1. Fatigue damage, as the main failure form of bogie frame, has the characteristics of hidden and sudden, which seriously threatens the safety of train operation2. Therefore, it is of great engineering significance to seek accurate and effective fatigue life analysis methods to predict the fatigue life of the frames and strengthen the service safety of the vehicles.

Fatigue damage is a form of failure in which damage accumulates and performance deteriorates until a fracture occurs in a structure under cyclic loading. The proposed cumulative damage theory explains the fatigue damage mechanism and realizes the calculation of fatigue life. Fatigue cumulative damage models are mainly divided into two categories: linear cumulative damage3,4 and nonlinear cumulative damage5,6. The linear cumulative damage theory is represented by Miner’s rule, which assumes that the fatigue damage is independent of the loading history and is linearly related to the cycle ratio. Due to its simple formula and easy calculation, it is still widely used in engineering calculations. Many scholars have found that under variable amplitude loading, Miner’s rule ignores the influence of loading sequence and interactions between loads on the accumulation of fatigue damage, which leads to lower prediction accuracy. A large amount of experimental data and engineering practice also show that the loading sequence and interactions between loads are factors that cannot be ignored in fatigue damage calculations.

Compared with normal amplitude loading, the biggest difference in fatigue damage evolution under variable amplitude loading is to consider the influence of loading sequence and load interactions on cumulative damage. A large number of tests have shown that different loading sequences change the damage effects of loads. The mutual effect between loads refers to the correlation between fatigue damage and loading history, i.e., the damage produced under the current load is not only related to the current state but also closely related to the size and order of the loads in the previous sequence. Bogies of rail vehicles are subjected to complex variable-amplitude loads in the course of operation, and the influence of the interactions between loads should not be neglected when fatigue life prediction is carried out for them.

To make up for the insufficiency of the linear cumulative damage model, many scholars have proposed to use the nonlinear cumulative damage model to effectively track the nonlinear accumulation process of fatigue damage. Marco et al.7 were the first to combine the damage mechanics with the fatigue cumulative damage theory and proposed the Marco-Starkey nonlinear cumulative damage model. Manson S S and Halford G R8 considered the nonlinear relationship between cumulative damage and cycle ratio, and used the damage curve method to establish the Manson-Halford model (M-H model). The M-H model was established by using the damage curve method to consider the nonlinear relationship between the cumulative damage and the cycle ratio. The model can better consider the effect of load order on the cumulative damage, but does not take into account the interaction effect between the loads, which is still insufficient for the fatigue life prediction under complex loads. Yuan9 and Gao10 proposed an improved nonlinear cumulative damage model based on the M-H theory, introduced the minimum value of the load ratio before and after, and verified that the improved model had higher prediction accuracy compared with the traditional model by comparing the two-stage loading test data. Yue et al.11 proposed an improved cumulative damage model based on the damage curve method. By introducing the equivalent force range ratio to consider the loading sequence and load interaction effects, and comparing with the test data, the prediction model is verified to have a high degree of agreement. Gao12 introduced the load interaction effect into the traditional M-H model in the form of an exponential function, proposed an improved cumulative damage model, and verified the prediction accuracy of the improved model through the fatigue test of standard 45-gauge steel and 16Mn steel. Xue et al.13 constructed a fatigue design pattern based on the M-H model that effectively considers multi-level load sequences and interactions, ensuring the accuracy and reliability of fatigue life analysis of welded joints. Jiang et al.14 proposed a cumulative damage model considering material degradation based on the residual strength degradation law of metal materials, and verified the accuracy of the model in predicting the fatigue life under multilevel loading. Gao et al.15 modified the characteristic index of the M-H model by introducing load interaction coefficients, and verified the accuracy of the modified model through two-stage and multi-stage load tests on five materials. Zhao et al.16 introduced stress ratio and strength degradation coefficient to modify the M-H model, and verified the engineering applicability of the improved model through multi-stage load test data of materials such as carbon steel, alloy steel, and aluminum alloy.

In summary, extensive research on fatigue cumulative damage and fatigue life prediction has confirmed the influence of loading sequence and load interaction on cumulative damage and material degradation on the remaining life of structures. Most existing studies reflect the influence of loading sequence and interaction on damage by introducing stress ratio and characterizing the strength degradation law of materials through a mathematical model of tensile strength after a certain number of cycles of loading and the number of cycles. However, this approach ignores the coupling effect between the front and rear stage loads during the fatigue process and the action law of the number of cycles on the remaining fatigue strength, which may lead to errors in the prediction results. This article constructs a residual fatigue strength degradation function model that can effectively characterize the effect of multi-level loadings based on fatigue test data and uses this model to modify the M-H model, proposing an improved M-H model. The fatigue test data are employed to verify the prediction accuracy of the improved model for fatigue damage under two-level and multi-level loadings. Finally, the improved model is applied to predict the remaining life of the bogie of rail vehicles.

Cumulative damage modeling

Linear cumulative damage model

Fatigue is the process of damage accumulation in structures subjected to alternating loads, and each load cycle produces a certain amount of damage. Miner theory is a linear cumulative damage theory widely used in engineering17,18, which suggests that the damage produced by a structure subjected to cyclic loading is linearly cumulative, i.e.

$$\:D=\sum\:\frac{{n}_{i}}{{N}_{i}}$$
(1)

where D is the cumulative fatigue damage, \(\:{n}_{i}\) is the number of loading cycles for the stress \(\:{\sigma\:}_{i}\), Ni is the fatigue life that the structure can withstand under stress \(\:{\sigma\:}_{i}\).

The Miner criterion states that fatigue failure occurs when the cumulative damage D = 1. The combination of the Miner rule and material S-N curve yields.

$$\:D=\sum\:\frac{{n}_{i}}{{N}_{i}}=\sum\:\frac{{n}_{i}{\left({\sigma\:}_{i}\right)}^{m}}{C}$$
(2)

where m and C are both material constants.

M–H model

The M-H model19 suggests that there is a relationship between the crack length of materials and the cycle ratio as follows

$$\:a={a}_{0}+({a}_{f}-{a}_{0}){\left(\frac{{n}_{a}}{{N}_{f}}\right)}^{\frac{2}{3}{{N}_{f}}^{0.4}}$$
(3)

where a is the crack length of the material after na loading cycles, a0 is the defect length of the material when \(\:{n}_{a}/{N}_{f}=0\), indicating the initial state of cumulative damage, \(\:{N}_{f}\) is the total number of cycles until material failure, af is the crack length when the final structure is damaged, and \(\:{a}_{f}=0.18\) is given as a recommendation through a large number of experimental verifications.

Manson defines the fatigue damage value D as the ratio of the crack length to the final crack length, which can be interpreted as the ratio of the existing crack length to the crack length at final damage.

$$\:D=\frac{a}{{a}_{f}}=\frac{1}{0.18}\left[{a}_{0}+(0.18-{a}_{0}){\left(\frac{{n}_{a}}{{N}_{f}}\right)}^{\frac{2}{3}{{N}_{f}}^{0.4}}\right]$$
(4)

According to Eq. (4), when the specimen is subjected to a stress with an amplitude of \(\:{{\upsigma\:}}_{1}\) after cyclic loading \(\:{n}_{1}\) times, the cumulative damage to the specimen is caused as shown in the OA segment in Fig. 1, and the damage value is

$$\:{D}_{A}=\frac{1}{0.18}\left[{a}_{0}+(0.18-{a}_{0}){\left(\frac{{n}_{1}}{{N}_{f1}}\right)}^{\frac{2}{3}{{N}_{f1}}^{0.4}}\right]$$
(5)
Fig. 1
figure 1

Complex load fatigue cumulative damage curve.

Full size image

Before the second level loading, since the first level loading has already caused cumulative damage to the specimen, according to the principle of material damage consistency, the first level loading damage can be equated to the damage caused by the stress cycle \(\:{n}_{2}^{{\prime\:}}\) times with the magnitude of \(\:{{\upsigma\:}}_{2}\), as shown in the Fig. 1 in the OB paragraph.

$$\:{D}_{B}=\frac{1}{0.18}\left[{a}_{0}+(0.18-{a}_{0}){\left(\frac{{n}_{2}^{{\prime\:}}}{{N}_{f2}}\right)}^{\frac{2}{3}{{N}_{f2}}^{0.4}}\right]$$
(6)
$$\:{D}_{A}={D}_{B}$$
(7)

By substituting Eqs. (5) and (6) into Eq. (7), the expression for the cyclic ratio \(\:{n}_{2}^{{\prime\:}}/{N}_{f2}\) can be obtained as

$$\:\frac{{n}_{2}^{{\prime\:}}}{{N}_{f2}}={\left(\frac{{n}_{1}}{{N}_{f1}}\right)}^{{\left(\frac{{N}_{f1}}{{N}_{f2}}\right)}^{0.4}}$$
(8)

where \(\:{n}_{2}^{{\prime\:}}\) is the number of cycles required to increase the damage from O to B along the damage curve 2 under the stress \(\:{{\upsigma\:}}_{2}\), i.e., the number of stress cycles corresponding to the OB section.

Then, When the stress with amplitude \(\:{{\upsigma\:}}_{2}\) is loaded cyclically for \(\:{n}_{2}\) times, i.e., the cumulative damage of the OABC segment in Fig. 1 can be expressed as

$$\:{D}_{C}=\frac{{n}_{2}^{{\prime\:}}}{{N}_{f2}}+\frac{{n}_{2}}{{N}_{f2}}={\left(\frac{{n}_{1}}{{N}_{f1}}\right)}^{{\left(\frac{{N}_{f1}}{{N}_{f2}}\right)}^{0.4}}+\frac{{n}_{2}}{{N}_{f2}}$$
(9)

Before proceeding to the third level loading, the damage caused by the first two levels of loading can be equated to the damage caused by loading \(\:{n}_{3}^{{\prime\:}}\) times with a stress of amplitude \(\:{{\upsigma\:}}_{3}\), as shown in the OD section of Fig. 1.

$$\:{D}_{D}=\frac{1}{0.18}\left[{a}_{0}+(0.18-{a}_{0}){\left(\frac{{n}_{3}^{{\prime\:}}}{{N}_{f3}}\right)}^{\frac{2}{3}{{N}_{f3}}^{0.4}}\right]$$
(10)
$$\:{D}_{C}={D}_{D}$$
(11)

By substituting Eqs. (9) and (10) into Eq. (11), the expression for the cyclic ratio \(\:{n}_{3}^{{\prime\:}}/{N}_{f3}\) can be obtained as

$$\:\frac{{n}_{3}^{{\prime\:}}}{{N}_{f3}}={\left[{\left(\frac{{n}_{1}}{{N}_{f1}}\right)}^{{\left(\frac{{N}_{f1}}{{N}_{f2}}\right)}^{0.4}}+\frac{{n}_{2}}{{N}_{f2}}\right]}^{{\left(\frac{{N}_{f2}}{{N}_{f3}}\right)}^{0.4}}$$
(12)

where \(\:{n}_{3}^{{\prime\:}}\) is the number of cycles required to increase the damage from O to D along the damage curve 3 under the stress \(\:{{\upsigma\:}}_{3}\), i.e., the number of stress cycles corresponding to the OD section.

Then, When the stress with amplitude \(\:{{\upsigma\:}}_{3}\) is loaded cyclically for \(\:{n}_{3}\) times, i.e., the cumulative damage of the OABCDE segment in Fig. 1 can be expressed as

$$\:{D}_{E}=\frac{{n}_{3}^{{\prime\:}}}{{N}_{f3}}+\frac{{n}_{3}}{{N}_{f3}}={\left[{\left(\frac{{n}_{1}}{{N}_{f1}}\right)}^{{\left(\frac{{N}_{f1}}{{N}_{f2}}\right)}^{0.4}}+\frac{{n}_{2}}{{N}_{f2}}\right]}^{{\left(\frac{{N}_{f2}}{{N}_{f3}}\right)}^{0.4}}+\frac{{n}_{3}}{{N}_{f3}}$$
(13)

By analogy, the cumulative damage under multistage loading is

$$\:{D=\left\{{\left[{\left(\frac{{n}_{1}}{{N}_{f1}}\right)}^{{\alpha\:}_{\text{1,2}}}+\frac{{n}_{2}}{{N}_{f2}}\right]}^{{\alpha\:}_{\text{2,3}}}+\dots\:+\frac{{n}_{i-1}}{{N}_{f(i-1)}}\right\}}^{{\alpha\:}_{i-1,i}}+\frac{{n}_{i}}{{N}_{fi}}$$
(14)
$$\:{\alpha\:}_{i-1,i}={\left(\frac{{N}_{f(i-1)}}{{N}_{fi}}\right)}^{0.4}$$
(15)

The M-H model suggests that a material reaches a critical value for fatigue failure when the cumulative damage D = 1.

Improved cumulative damage modeling

Compared with the Miner rule, the M-H model considers the effect of loading sequence on damage accumulation, but in practice, not only the effect of the size and sequence of the preceding loads on the subsequent loads should be considered, but also the degradation of structural performance caused by the size and sequence of the preceding loads should not be ignored. Therefore, this section improves and optimizes the M-H model based on existing research to better consider the effects of load interactions and the degradation effects caused by the preceding loads on cumulative damage.

Gao12 carried out fatigue tests based on two commonly used materials for welded joints, i.e., standard 45 steel and 16Mn steel, and obtained the fatigue test data for both samples as shown in Table 1.

Table 1 Fatigue data of samples under two-level load.
Full size table

For the seven standard samples of 45# steel, the stress amplitudes used were 331.46 MPa and 284.4 MPa for the two-level load test. When the cyclic ratio of the first level load reached n1/Nf1, the second level load was applied until the specimens failed. According to the standard fatigue test data of 45# steel, it can be obtained that at a stress amplitude of 331.46 MPa and 284.4 MPa, the fatigue life of standard 45# steel corresponds to 5 × 104 and 5 × 105 cycles, respectively.

For the 8 standard samples of 16Mn steel, the stress amplitudes used were 562.9 MPa and 392.3 MPa for the two-level load test. When the cyclic ratio of the first level load reached n1/Nf1, the second level load was applied until the specimens failed. According to the standard fatigue test data, it can be obtained that at a stress amplitude of 562.9 MPa and 392.3 MPa, the fatigue lives corresponding to standard 16Mn steel are 3.9680 × 103 cycles and 7.8723 × 104 cycles, respectively.

Both Miner’s rule and the M-H model assume that fatigue damage occurs in the structure when the cumulative damage is equal to 1. Based on Eq. (2) and Eq. (14), the cumulative damage due to the precession load cycle can be calculated, then the predicted cycle ratio is equal to 1 minus the precession load cycle ratio.

According to the data in Table 1, it can be found that the M-H model has a smaller prediction error compared to the Miner model, indicating that the M-H model has higher prediction accuracy of the cyclic ratio of the second level load. However, there is still a certain prediction error, especially for 16Mn steel. And, 16Mn is the main material for the bogie frame of rail vehicles. To more accurately predict the fatigue life of the bogie, the experimental data in reference12 is further supplemented by adding three sets of test samples to enrich the test samples. The fatigue test data of the samples are shown in Table 2.

Table 2 Fatigue test data of 16Mn under two-level load.
Full size table

In theory, the critical value for material fatigue failure is D = 1. Therefore, in the case where the sample fails during the two-level load fatigue test, the cumulative damage value of the secondary load should theoretically be 1. However, based on the analysis of the fatigue test data of 16Mn steel in Table 2, it can find that as the first level load cycle ratio increases, the second level load cycle ratio of the sample is smaller than the theoretical value. Moreover, as the first-level load cycle ratio increases, the difference between the second-level load cycle ratio and the theoretical value gradually increases, which means that the degradation of the second cycle ratio of the material intensifies.

In the two-level load fatigue test, the first level load cycle ratio can be equivalently considered as the pre-existing damage caused by the material bearing the preceding load, and the second level load cycle ratio can be equivalently considered as the remaining life. Then, the difference between the secondary load cycle ratio and the theoretical cycle ratio can be considered to be the degradation of the fatigue performance of the material caused by the pre-existing load that the material is subjected to. The test data confirms that the load interaction effect, especially the structural performance degradation caused by the preceding load, should not be neglected in the fatigue life prediction.

Define the material performance degradation rate as T, and its function expression is shown in Eq. (16). The degradation rate can be used to determine the degree of degradation between the actual residual strength and the theoretical residual strength of the material.

$$\:T=\left[{\left(\frac{{n}_{2}}{{N}_{f2}}\right)}_{E}-{\left(\frac{{n}_{2}}{{N}_{f2}}\right)}_{S}\right]/{\left(\frac{{n}_{2}}{{N}_{f2}}\right)}_{S}$$
(16)

where \(\:{\left(\frac{{n}_{2}}{{N}_{f2}}\right)}_{E}\) is the secondary load cycle ratio test data, \(\:\:{\left(\frac{{n}_{2}}{{N}_{f2}}\right)}_{S}\) is the secondary load cycle ratio theoretical data, which is numerically equal to \(\:1-\frac{{n}_{1}}{{N}_{f1}}\).

In the service process, the damage will be accumulated with the load cycle, while the residual strength of the material will also be reduced. Previously in the sample 16Mn fatigue load test, T can be equated to the degree of degradation of the residual strength of the material, \(\:{n}_{1}/{N}_{f1}\) can be equated to the material to withstand the previous sequence of load cycle ratio, then for an accurate description of the degree of degradation of the residual strength of the material with the change of the relationship of the load cycle. Based on the fatigue test data of multiple sets of samples in Table 2, the correlation between T and \(\:{n}_{1}/{N}_{f1}\) can be analyzed.

Numerical fitting of the fatigue test data for 8 sets of samples yields linear, quadratic polynomial, cubic polynomial, and exponential fitting curves and functional relationships between the degradation rate and the load-cycle ratio, as shown in Fig. 2.

Fig. 2
figure 2

Comparison of different fitting curves for degradation rate vs. load cycle ratio.

Full size image

By numerically fitting the fatigue test data of 8 sets of samples, linear, quadratic polynomial, cubic polynomial, exponential fitting curves and functional relationships between T and \(\:{n}_{1}/{N}_{f1}\) can be obtained, as shown in Fig. 2.

R-squared measures the degree of explanation of the variability of the dependent variable by the fitted model, which is derived by comparing the ratio of the sum of squares of the residuals of the fitted model to the sum of squares of the total variability, and is used to assess the degree of explanation of the variability of the dependent variable by the fitted model. R-squared can be taken as a range of values from 0 to 1. The closer the R-squared is to 1, the higher the accuracy of the fitted model in explaining the variability of the original data. From the fitting data of the four fitting models in Fig. 2, it can be found that the exponential model has the highest fitting accuracy, therefore, the exponential model was chosen to represent the relationship between T and \(\:{n}_{1}/{N}_{f1}\) as shown in Eq. (17).

$$\:T=0.00134\text{*}\text{exp}\left(\frac{{n}_{1}/{N}_{f1}}{0.15225}\right)+0.09927$$
(17)

From Eq. (16), it can be seen that T is calculated based on \(\:{n}_{2}/{N}_{f2}\) obtained from a large number of fatigue tests, and at the same time, the fitting model of T about \(\:{n}_{1}/{N}_{f1}\) can be obtained according to Eq. (17). So, the degradation rate fitting expression includes the influence of load interaction and performance degradation on the remaining fatigue life.

When the structure is subjected to H-L level loads, the amplitude of the first level load is greater than that of the second level load, and the fatigue life \(\:{N}_{f1}\) corresponding to the amplitude of the first level load is less than \(\:{N}_{f2}\) of the second level load. I.e. \(\:{N}_{f1}<{N}_{f2}\), \(\:\frac{{N}_{f1}}{{N}_{f2}}<1\).Combining Eq. (14), introducing the degradation rate T into the denominator position of the exponential term can effectively amplify the weight of the original empirical constant 0.4. Then,\(\:\:{\alpha\:}_{\text{1,2}}\) decreases, \(\:{\left(\frac{{n}_{1}}{{N}_{f1}}\right)}^{{\alpha\:}_{\text{1,2}}}\)increases. This indicates an increase in cumulative damage to the material.

By analogy, when the structure is subjected to L- H level loads, the cumulative damage of the material will be reduced by introducing the degradation rate into the denominator term of the parameter. This is consistent with the fatigue test data of the sample, namely the coaxing effect of the material, which has also been confirmed in many studies20,21.

Therefore, Integrate the degradation rate fitting model into \(\:{\alpha\:}_{i-1,i}\) of the conventional M-H model to obtain the cumulative damage model considering the load interaction effect and material degradation as shown in Eq. (18).

$$\:\left\{\begin{array}{c}{D=\left\{{\left[{\left(\frac{{n}_{1}}{{N}_{f1}}\right)}^{{\alpha\:}_{\text{1,2}}}+\frac{{n}_{2}}{{N}_{f2}}\right]}^{{\alpha\:}_{\text{2,3}}}+\cdots\:+\frac{{n}_{i-1}}{{N}_{f(i-1)}}\right\}}^{{\alpha\:}_{i-1,i}}+\frac{{n}_{i}}{{N}_{fi}}\\\:{\alpha\:}_{i-1,i}={\left(\frac{{N}_{f(i-1)}}{{N}_{fi}}\right)}^{0.4\bigg/\left[1-\left(0.00134\text{*}\text{exp}\left(\frac{\sum\:{n}_{(i-1)}/{N}_{f(i-1)}}{0.15225}\right)+0.09927\right)\right]}\end{array}\right.$$
(18)

Model validation

To verify the effectiveness and accuracy of the improved cumulative damage model, two sets of experimental data were analyzed and compared with the Miner model and traditional M-H model to verify the accuracy of the improved model in predicting remaining life under two-level and multi-level cyclic loading.

Two-level load condition

When the first-level load cycle ratio is loaded to 0.100, 0.250, 0.500, and 0.750 for H-L loading, the second-level load is applied until the specimen fails. When the L-H loading ratio is increased to 0.100, 0.250, and 0.500, the first-level load cycle is transformed into a second-level load failure.

This article uses an improved M-H model to predict the two-level load cycle ratio and compares the predicted results with Miner’s rule and traditional M-H model prediction calculations. The specific results are shown in Table 3 and plotted in Fig. 3.

Table 3 Experimental and model prediction data under two-level load.
Full size table
Fig. 3
figure 3

Two-level load experimental data and model predictions.

Full size image

The experimental results show that the model proposed in this paper has a more accurate prediction performance than the miner rule, conventional m-h model under different two-level loading sequences of H-L and L-H.

Multi-level load condition

To further verify the accuracy of the proposed model for multi-level loading damage prediction, literature22,23 conducted multi-level loading fatigue tests on C45 steel as an example and investigated three different loading sequences: H-L, L-H, and random loading sequences. In this paper, the fatigue damage under multi-level loading is predicted based on the improved model, and the last-level cycle ratios calculated by Miner linear, traditional M-H model, and the improved model is compared and analyzed with the test cycle ratios. The loaded stress amplitudes are 326.9 MPa, 334.1 MPa, 341.3 MPa, and 348.5 MPa, and the corresponding fatigue lives are 711,900, 369,400, 231,500 and 161,400 cycles, respectively. The predicted and tested cycle ratios at the last stress are shown in Table 4. At the same time, the improved M-H model (referred to as G’s M-H model) proposed in reference12 was used to predict the cycle ratios under three different loading orders, and compared with the Miner criterion, M-H model, the proposed improved model, and experimental data. The results are shown in Fig. 4.

Table 4 Experimental and model prediction data multi-level load.
Full size table
Fig. 4
figure 4

Multi-level load experimental data and model predictions.

Full size image

The above results show that the prediction results of the improved model proposed in this article are closer to the experimental values compared to the other three models, whether it is an H-L, L-H, or random loading sequence. Meanwhile, the prediction and experimental results also verify the Coaxing effect24,25,26,27, i.e., the lower amplitude of the precession loading cycle improves the fatigue performance of the material, whereas the Miner, M-H model does not accurately explain and predict this effect.

Application of fatigue analysis in rail vehicles

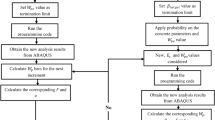
Mastering the measured dynamic stress data of measuring points is the basis for fatigue life calculation and analysis of rail vehicle bogie frame20,28. Therefore, in this section, the dynamic stress data of the measurement point positions obtained from the bogie frame line test are compiled, and a stress spectrum21,29 is developed to analyze the fatigue life of the bogie frame measurement point using the improved nonlinear cumulative damage model.

Line test

In this paper, 6 measurement points in different locations are selected on the bogie frame, and the strain data of the measurement points are collected through the line test, and the locations of the measurement points are shown in Fig. 5. The strain data are collected through the dynamic data acquisition equipment of HBM Company, and the sampling rate is set at 500 Hz, to ensure the completeness and validity of all the dynamic stress data. The train travels from Yuanping West Station to Xinzhou West Station, which includes turnouts, tunnels, curves of different radii, straight lines, and other conditions during the entire operation.

Fig. 5
figure 5

Diagram of measuring points location.

Full size image

Data processing

The dynamic data obtained from the experiment were processed using nCode software for filtering, deburring, strain stress conversion, etc., to obtain the measured stress time-domain data of the measurement point position, as shown in Fig. 6. Among them, measuring point C-3 (brake seat measuring point) showed very obvious stress fluctuations at the end of the test, which was caused by the reaction of the braking force generated by the brake caliper and the brake seat when the train slowed down and stopped. Measurement point H-2 (gearbox seat measurement point) shows significant stress data fluctuations at the beginning and end of the test, due to changes in gearbox speed during train start-up and braking force during train deceleration and stopping, resulting in stress changes in the gearbox seat.

Fig. 6
figure 6

Measurement point dynamic stress and velocity curve: (a) C-1 point (b) C-2 point (c) C-3 point (d) H-1 point (e) H-2 point (f) H-3 point.

Full size image

The measured stress data can be processed by the rainflow technique method to obtain the amplitude and mean values of each stress cycle period throughout the entire time history, with a large amount of data and random variables. To facilitate subsequent fatigue life analysis, a one-dimensional 8-level stress spectrum was developed using the fluctuation center method30, as shown in Table 5.

Table 5 One-dimensional stress spectrum of measuring points.
Full size table

Fatigue analysis

According to the stress amplitude and cycle frequency in Table 5, the fatigue life N under different stress amplitudes is calculated based on BS7608. The BS7608 standard classifies welded joints into 10 grades (B, C, D, E, F, F2, G, W, S, T) based on factors such as geometric shape of the joint, loading direction, potential failure locations, and welding type. Through extensive fatigue tests, S-N curves for different joint grades have been obtained, as depicted in Fig. 7. These subdivided grades account for influences from local stress concentration, dimensions and geometry of the welded structure, stress direction, metallographic structure effects, residual stress, fatigue crack morphology, welding processes, and post-welding improvement methods.

$$\:\text{log}N=\text{log}{C}_{0}-d\sigma\:-m\text{log}{S}_{r}$$
(19)

where C0 is a constant. Considering the complexity of engineering problems, the S-N curve usually takes two standard deviations downwards, i.e., d = -2, at which time the confidence level is 97.5%. The slope m of the S-N curve is 3.

Fig. 7
figure 7

BS7608 standard mean S-N curve.

Full size image

According to the actual situation of the weld where the measuring point is located, the joint grade is determined as F or F2. By substituting the S-N curve data in Fig. 7 into Eq. (19), the fatigue life Ni corresponding to each load amplitude level in Table 5 can be obtained. By substituting the frequency ni and the fatigue life Ni under each level of load amplitude calculated according to BS standards into Eqs. (2), (14), and (18), the fatigue damage of the frame measurement points under Miner rule, M-H model, and improved M-H model can be calculated and compared, as shown in Fig. 7.

From Fig. 8, the cumulative damage trend of each measurement point calculated by the three cumulative damage models is generally consistent, in which the damage value of the measurement point C-2 at the positioning of the arm is the largest, which is 3.023E-5, and the damage value of the measurement point C-1 at the position of the transverse and longitudinal beam connection is the smallest, which is 1.480E-6. Based on the dynamic stress and stress spectrum data in Fig. 6; Table 5, it can be observed that both the stress amplitude and frequency at measuring point C-2 are greater than those at other measuring points. This indicates that the area near this position bears larger stress amplitudes and higher vibration frequencies during vehicle operation, making the location of measuring point C-2 relatively dangerous. Meanwhile, the stress concentration caused by the sudden changes in geometric structure and stiffness near this position is also a factor contributing to the greater fatigue damage at this location. The nonlinear cumulative damage values of all measurement points are significantly greater than the linear cumulative damage values, indicating that the improved nonlinear cumulative damage model can fully consider the influence of load interaction on cumulative damage. At the same time, the cumulative damage value of the improved model is larger than that of the traditional M-H model, which has higher prediction accuracy and can better characterize the impact of performance degradation on fatigue damage.

Fig. 8
figure 8

Comparison of cumulative damage at each measuring point.

Full size image

Conclusion

In this paper, an improved nonlinear cumulative damage model is proposed, and the accuracy and validity of the proposed model are verified by combining two-level load and multi-level load fatigue tests, finally, the fatigue damage of rail vehicle bogie frames is predicted based on the improved model. Through theoretical derivation, experimental verification, and engineering application, the following conclusions are obtained.

  1. 1.

    Based on the material strength fatigue test, the functional relationship between fatigue strength degradation and preceding loading is established, and the degradation function is introduced to modify the M-H model, which effectively takes into account the load interaction effect and material degradation on the cumulative damage.

  2. 2.

    A new improved cumulative damage model is proposed, which is combined with two-level load and multi-level load fatigue tests to verify that the improved model has higher prediction accuracy, and at the same time, the improved model can better explain and predict the Coaxing effect.

  3. 3.

    Based on the stress spectrum data of measurement points obtained from rail vehicle line test, the improved cumulative damage model was used to evaluate and compare the fatigue damage of the frame. The results indicate that the improved damage model can consider the effects of load interaction and performance degradation on fatigue damage.

  4. 4.

    The engineering application of improved predictive models in damage assessment of bogie frames provides theoretical support and engineering value for the fatigue life assessment and prediction of rail vehicle bogies and related components. However, the experimental verification conducted in this paper is limited to smooth standard specimens. Further fatigue testing on welded structures to validate and optimize the applicability of the model remains an important direction for future research.