Introduction

Full-field Digital Mammography (FFDM) today represents the most common imaging technique for screening programs for the detection of any breast malignancy, having been shown to reduce mortality related to breast cancer1,2, allowing rapid diagnosis thanks to high diagnostic accuracy. Despite this, the sensitivity of digital mammography tests is around 80–90%, still producing a high number of false negatives3,4.

The analysis of digital images is, therefore, a fundamental tool for improving the sensitivity of diagnostic examination, playing a crucial role in the detection of pathologies and lesions. The analysis of digital medical images has proven useful in many fields of application, such as the automatic detection of suspicious masses and calcifications5, and the automatic identification of possible risk factors for the development of pathologies6,7.

A key preprocessing step in medical image analysis is denoising, for which several techniques have been developed over the years. It is important to note, however, that denoising is one of several tools within a broader image processing framework that contributes to the final diagnostic quality of the image but cannot recover information that has been entirely lost due to noise. Rather, it can only enhance the visibility of the signal already present in the image, improving perceptual quality and potentially aiding interpretation. Radiological images require special attention to the dose delivered to the patient, which is essential to minimize patient exposure to ionizing radiation, increasing the safety of the diagnostic examination. However, low doses result in increased quantum noise, which combined with information losses due to hardware limitations and external effects during acquisition, can degrade image quality and hinder early diagnosis. In particular, in a mammogram, we can mainly identify components of quantum noise and electronic noise (accentuated for small currents)8, which take the form of Poisson noise, salt and pepper noise and Gaussian noise. Although noise affects image quality, one of the main issues that hinders the interpretation and detection of lesions in mammography is tissue overlapping. However, denser and overlapping tissues can generate more noise due to a strong noise component that derives from the interaction between the X-rays and the biological tissue (Compton effect, photoelectric effect) which translates into a scatter component that reaches the detector despite the presence of the anti-scatter grid9,10. This component appears to be more significant for denser and thicker tissues11.

The presence of noise on the image negatively influences all well-established image processing techniques, such as segmentation, automatic detection, but also visual evaluation, and classical diagnosis12,13,14,15,16. Traditionally, especially in the medical field where denoising becomes a fundamental need to make accurate diagnoses, many techniques have been developed based mainly on filters (Wiener, Gaussian, Median, etc.) and transformations (Wavelet, Contourlet, Curvelet, etc.). More recently, considering the complexity of noise on the radiological image, Deep Learning (DL) approaches are becoming increasingly used for image denoising. In general, this approach can be difficult to implement, since DL-based methodologies would require a noisy and clean image pair for training the network and, in the medical field, clean images are not available with the current medical equipment.

Thus, unsupervised or self-supervised approaches have been developed. In particular, Lehtinen et al.17 introduced the concept that it is possible to restore clean images by training the model with only images corrupted by noise, developing a network architecture known as Noise2Noise (N2N). N2N is based on the concept that the training of regressors does not actually imply a 1:1 mapping between input and target, but the mapping is on multiple values, i.e. the network returns as output the average of all possible explanations. This can be exploited in the case of unsupervised denoising as we know that long and noise-free exposure in images is given by the average of the individual short and noisy exposures. So, mapping can be done between the noisy input and the average of all possible noisy explanations, without clean images. However, this implies that the images have the same content, but different inputs and targets independent noises are present. Therefore, the N2N requires noisy pairs of the same image that are not easy to find in the medical field.

To overcome this limitation, Krull et al.18 introduced a new architecture called Noise2Void (N2V). This architecture uses a blind spot masking scheme during training and allows the use of different noisy images as input and target, creating a self-supervised approach.

A blind spot network is necessary because, in a conventional network the prediction for a single pixel depends on a square portion of input pixels, and, by training such a network using the same noise image as input and as the target, the network will simply learn the identity. Instead, by using a network of blind spots, the square portion around the pixel excludes the central pixel itself, preventing it from learning its identity. So, a blind-spot network applies a mask to each patch of the input, excluding the central pixel. Therefore, while a network with the noisy image as input and training target would generate a replica of the noisy input, the use of the mask that excludes the central pixel encourages a blind-spot network to seek information from the surrounding pixels and use it to learn to remove noise.

Subsequently, several applications and evolutions of N2V have been applied in literature. In 2021, Song et al.19 adapted N2V to PET neuroimaging data, using simulations and clinical data, demonstrating that pre-training and/or anatomical guidance leads to superior performance compared to conventional approaches. On the other hand, Papkov et al.20 presented an extension of the N2N method to image stacks, leveraging the fact that there is a shared signal between spatially adjacent planes. In their experiments, they utilized brain MRI scans and multiplane microscopy data, demonstrating that in multiplane imaging learning only from neighboring images in a stack is sufficient to obtain very good results. In the same year, Huang et al. used MRI images from the public Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset to train a new network inspired by the N2V blind spot network. This network employs two distinct blind spot strategies for different branches: one branch fills blind spots with neighboring pixel values, while the other fills them with zeros. On the one hand, neighboring pixel features are used to predict the corresponding blind spots, while on the other hand, the results of the two branches converge to the final clean image21.

The next year Kojima et al.‘s study involved scanning a kiwi (used as a phantom for prostate MRI in a previous report) through the MRI system22. The authors then tested the effectiveness of N2V in improving image quality using a small data set (only 8 images). The results of signal-to-noise ratio (SNR) measurement and visual noise assessment indicated that noise reduction with N2V significantly improves SNR (p-value < 0.05). Although this result is similar to previous studies, N2V effectively removed noise for images obtained from the low-field MRI system. Zhang et al.23 instead focused on denoising the PET CHO image of patients with pathologically confirmed primary diffuse glioma. They applied two conventional denoising methods (BM3D and NLM) and two deep learning-based approaches (N2N and N2V). All algorithms improved image quality. In particular, both conventional algorithms improved image quality to a similar extent, while the deep learning methods presented higher N2N and N2V improvement indices than NLM and BM3D.

Ashwini et al. published a paper in 2023 whose aim was to develop denoising models capable of effectively removing different types of noise from chest X-rays and CT images using N2V and N2N. The quality of the images was assessed by comparing them with the original images using evaluation metrics such as PSNR and SSIM. The study showed that N2V outperforms N2N in the presence of Gaussian noise, speckle, and salt-and-pepper in chest X-rays and CT images24.

These studies have demonstrated that N2V performs well when applied to several imaging modalities, however, to our knowledge, it has never been applied to digital mammography.

Therefore, taking into account the importance of denoising in digital mammography and the potential of N2V in medical image denoising, this study aims to present and evaluate the performance of the N2V approach applied and adapted to the denoising of digital mammograms. The performance of the approach is assessed considering multiple parameters (including contrast to noise, signal to noise, similarity indexes, etc.) and from both technical and clinical perspectives (i.e., including qualitative assessment from expert radiologists) and is compared with state-of-the-art denoising algorithms and filters.

In summary, our main contributions are: (i) the first application of N2V, a novel self-supervised approach that does not require ground truth images to be trained, to digital mammography; (ii) multiparametric comparison of N2V-based denoising with conventional algorithms commonly adopted in digital mammography.

Materials and methods

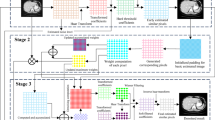
Figure 1 represents the methodological workflow followed in this study, described in detail below.

Fig. 1
figure 1

Flowchart of the methodologies used in this study.

Full size image

Clinical data

The dataset comprises digital mammograms from 100 female patients (age of the subjects (mean ± SD) is 55.5 ± 9.0), acquired using the “Giotto Class” system (IMS Giotto S.r.l., Bologna, Italy). This imaging system employs an amorphous selenium (a-Se) flat-panel detector, an X-ray tube with tungsten (W) anode, and a silver filter. The retrospective study was approved by the Ethics Committee of the University of “Luigi Vanvitelli” in Naples, Italy (deliberation no. 469, dated 23/07/2019), and the requirement for informed consent was waived. All procedures were conducted in accordance with relevant guidelines and regulations.

For each patient, mammograms were acquired in two standard projections: cranio-caudal (CC) and medio-lateral-oblique (MLO), resulting in four images per patient (right and left CC, right and left MLO), for a total of 400 images. Patients were randomly selected from the available clinical database to ensure diversity in the dataset, which includes a representative range of breast thicknesses and glandular densities (breast density based on the BI-RADS classification: 12.5% A, 51.5% B, 28.8% C, 7.2% D) Only “FOR PROCESSING” images were used in this study. These are raw images that have not undergone post-acquisition processing and thus retain the original X-ray attenuation information, which is essential for accurate and consistent image analysis. The original images are 16-bit DICOM files with dimensions of 2812 × 3580 pixels and a pixel size of 0.083 mm × 0.083 mm. To standardize input dimensions and reduce computational requirements, each image was cropped to a square format of 2048 × 2048 pixels. From each of these cropped images, 64 non-overlapping patches of size 256 × 256 pixels were extracted by uniformly dividing the entire image area, without selecting specific regions. This grid-based extraction ensures complete image coverage, including both breast tissue and background areas, and avoids random selections or biases towards specific anatomical zones. This patch-based approach allows for more efficient training and enables localized analysis of different regions of the breast tissue.

In total, the training dataset consisted of 25,600 patches derived from the full set of mammograms.

Simulated data

To better evaluate the performance of the network, it was decided to add further noise to the images, obtaining images that we will call simulated images. It is carried out a second training with simulated images to analyze the results obtained with the algorithm in this case. To realistically simulate FFDM image noise, we adopted a hybrid noise model that reflects the two main sources of noise typically encountered in X-ray imaging: signal-dependent quantum (Poisson) noise and signal-independent electronic (Gaussian) noise. This modeling approach is consistent with previous work25,26.

We first characterized the noise properties of the original mammographic images by analyzing sampled regions across the entire breast area, ensuring the inclusion of both high- and low-intensity signal regions. For this analysis, we used fixed-size square patches of 72 × 72 pixels, approximately corresponding to the 6 × 6 cm² region of interest (ROI) recommended by Bouwman et al.26.

For each patch, we calculated the mean pixel intensity and the corresponding noise variance (estimated as the squared standard deviation). The relationship between mean intensity and noise variance was then modeled using both linear and quadratic regression, showed in Figure S1 of Supplementary Materials, allowing us to distinguish and estimate the respective contributions of the Gaussian and Poisson noise components: the constant term (intercept) captures the signal-independent electronic noise; the signal-proportional term models the behavior of quantum noise, which increases with signal intensity.

Based on the estimated parameters, Poisson noise was simulated by applying a random sampling process in which each pixel value was treated as the expected value (λ) of a Poisson distribution. This model’s quantum noise introduces fluctuations proportional to the local signal intensity.

Gaussian noise was added independently, drawn from a zero-mean normal distribution with a fixed standard deviation equal to the root of the estimated intercept, which reflects the electronic background noise observed in the original images.

The resulting noisy image showed an increase in noise variance from ~ 10 to ~ 30, consistent with a dose reduction by a factor of 3, as expected from the inverse relationship between dose and variance.

Network architecture

As already mentioned, the N2V approach owes its success to the fact that it is possible to use a single noisy image both as input and as target, without ground truth, using a blind-spot network avoiding the network to learn the identity, as represented graphically in Figure S2 of Supplementary Materials.

To apply the N2V algorithm, the well-known U-Net architecture was implemented as a blind-spot network.

The effectiveness of the N2V algorithm depends on the quality of the training data and the correct configuration of the network parameters. The implemented U-Net architecture has a depth of 2 layers, i.e. there are 2 encoder blocks and 2 decoder blocks. It features 96 Kernel filters of size 3 × 3 in the first convolutional layer, with the number of filters doubling after each downsampling step. It has a ReLu activation function in all layers except the last one where the activation function is linear. A batch normalization layer follows each of the layers, to make the network more stable and speed up the convergence time27.

In Fig. 2 you can see the topology of the network described above.

Fig. 2
figure 2

Network architecture. Each blue box represents a multi-channel feature map. The colored arrows indicate the different operations performed, as detailed in the legend on the right. The number of channels is shown above each box, while the spatial dimensions are indicated on the left side. The white boxes in the upsampling path represent the feature maps copied and concatenated from the downsampling path.

Full size image

Data preparation and network implementation

The dataset patches, both from clinical data and simulated data, were divided into training, validation, and test in the proportions of 65%, 15%, and 20%, respectively (16640 patches for training, 3840 patches for validation, and 5120 patches for test). It is important to note that the patches were divided into training, validation, and test sets, separating them based on the source mammograms. In fact, they were organized in sequential blocks of 64, this organization allows for easy reconstruction of the complete mammograms from the network output during the evaluation, since each consecutive group of 64 patches corresponds to one image.

The network parameters configuration was defined based on what was described by Krull et al.18. Our approach used a learning rate of 0.0004 by adopting the default learning rate schedule of CSBDeep18,28. This schedule involves halving the learning rate when a plateau on the validation loss is detected. The epochs and batch size were set to 200 and 128, respectively.

The loss function is based on calculating the Mean Squared Error (MSE), a metric used to evaluate the loss (error) between the values predicted by the model and the actual values.

Finally, the parameters relating to the N2V algorithm were chosen.

As mentioned, to prevent the network from learning the identity, some input pixels are manipulated. To do this you need to set the n2v_manipulator parameter with the type of manipulator you want to use. There are several pixel manipulators, the one chosen in this case is uniform_withCP, thanks to which the values of the manipulated pixels are replaced with a value based on neighboring pixels. In particular, the neighborhood is sampled with a normal Gaussian distribution but without the central pixel. With the parameter n2v_neighborhood_radius, we control the width of the pixel window to be considered, this parameter was chosen equal to 2.

For training on N2V, it is possible to pass arbitrarily large patches to the network (in our case, they have size 256 × 256), from these patches, during training, random sub-patches of size given by the n2v_patch_shape parameter are extracted. In this case, the sub-patch size is set to 64 × 64. In conclusion, for faster training, you can manipulate more pixels per patch. We chose to manipulate approximately 0.198% of the input pixels per patch, which for a patch size of 64 × 64 pixels corresponds to approximately 8 pixels. This fraction is adjusted via the n2v_perc_pix parameter.

Traditional techniques

Many conventional denoising approaches based on spatial filtering techniques, which operate on the image based on its spatial properties, replacing the current pixel with a combination of nearby pixels, have been developed over the years and applied to digital mammography.

Among these, we find the Gaussian filter, which is a linear filter that replaces the current pixel with a weighted average of nearby pixels24. This type of filter is particularly efficient when applied to reduce Gaussian noise, but it causes a blurring effect. Therefore, it is necessary to pay attention not to lose details present within the image, finding a balance between the aggressiveness of the filtering and preserving edges and anatomical structures present in the image. In particular, for the Gaussian filter, a standard deviation of 1 was adopted, offering a good compromise between noise reduction and detail preservation.

To preserve edges, the bilateral filter is used, which operates on a principle similar to the Gaussian filter24. It relies on a weighted average of pixel values that are close to the current pixel. Unlike the Gaussian filter, however, the bilateral filter considers not only the position occupied by the pixels but also their values for filtering purposes. A pixel, to influence another, must not only be close in space but must also have a similar value. This way, edges are preserved because pixels that straddle discontinuities are not replaced by their average, even if they are close in space, as is the case with the Gaussian filter.

Another linear filter commonly used for Gaussian noise is the Wiener filter27. The goal of this filter is to minimize the mean squared error between the estimated image and the desired one. It follows a statistical approach, as the weights are calculated based on the estimation of covariance and cross-correlation matrices. Unlike the Gaussian filter, not all pixels are filtered in the same way; rather, the aggressiveness of the filtering depends on the noise variance within a given set of pixels. For the Wiener filter, the default 3 × 3 local neighborhood was used.

To reduce impulse noise, such as salt and pepper noise, a non-linear filter is commonly used the median filter28. A window of defined size moves along the image, finding the median value of the pixels within the window and replacing this value with the current pixel. If the window contains an odd number of pixels, the median value is obtained by numerically ordering the pixels and selecting the one in the middle; if the window contains an even number of pixels, there may be more than one median value. This way, the output values produced by the filter tend to be more similar to their neighbors. This filter preserves the edges of the image and was applied using a 5 × 5 kernel.

The non-local mean (NLM) filter, instead, operates on a statistical assumption: if you replace the grayscale value of a pixel with the average of the grayscale values of a set of pixels that are similar to the starting pixel, then the standard deviation of the noise affecting the image decreases29,30. These similar pixels do not necessarily have to be close in space, hence this filter is called a non-local mean filter. However, these similar pixels are still searched within a searching window, whose size depends on the standard deviation of the noise.

Finally, we have the BM3D filtering technique, which consists of three stages: grouping, filtering, and aggregation. The grouping and filtering steps are collectively referred to as ‘Collaborative Filtering’31. Given a patch within the input image, similar patches are searched for and grouped into a 3D block, which then undergoes a linear transformation. All 2D patches grouped into 3D blocks are filtered simultaneously. Finally, the inverse transform is computed. The operating principle of this filtering technique resembles that of the NLM filter, where similar patches were filtered simultaneously, with the difference that the filtering involved only the patch mean using a 1D technique.

Performance evaluation

Evaluation metrics

To quantify the effectiveness of denoising on mammograms, several image quality evaluation metrics have been used. Selected metrics include Mean Square Error (MSE), Peak Signal-to-Noise Ratio (PSNR), and Structural Similarity Index metric (SSIM). A comparison was also made between the contrast-to-noise ratio (CNR) on the image before and after denoising. Specifically, CNR was computed for both fibroglandular and adipose tissues, using mean pixel intensities within manually selected regions of interest, guided by intensity profiles, and estimating noise statistics (mean and standard deviation) from background patches free of anatomical structures. PSNR was calculated using the maximum pixel value (255) and the mean squared error between predicted and reference images. The formulas are given below:

$$CN{R_{tissue}}=\frac{{{\mu _{ROI\_tissue}} - ~{\mu _{ROI\_noise}}}}{{{\sigma _{noise}}}}$$
(1)
$$PSNR=20~x~{\log _{10}}\frac{{ma{x^2}}}{{MSE}}$$
(2)

The Wilcoxon signed-rank test was performed to compare image quality before and after denoising, with a significance level of α = 0.05. All statistical analyses were performed using R (version 4.4.1, The R Foundation for Statistical Computing). Also a Noise Power Spectrum (NPS) analysis, following the approach described by Dobbins et al.32, to provide a more detailed characterization of noise, particularly with respect to spatial frequency, was done. The NPS was computed for patches from both fibroglandular and adipose tissues, and the corresponding maps are calculated.

Qualitative evaluation

The comparison between the mammographic images, before and after denoising, was presented to two expert radiologists, who were asked to qualitatively evaluate the image appearance and perceived diagnostic utility. The radiologists were presented with full mammographic images reconstructed by assembling the 64 denoised output patches produced by the network. This ensured that the assessment was conducted on complete, clinically realistic images and not on isolated patches, maintaining the practical relevance of the evaluation process. To evaluate the images, the radiologists, after having observed and visually analyzed them, answered 10 statements in a questionnaire on the quality of the images in the Likert table33. The response options of the Likert table provided to the radiologists were Strongly disagree, Disagree, Neutral, Agree, and Strongly agree.

Each radiologist looking at all pairs of images responded with one of the scores given in the table to the statements below:

  1. 1.

    The image appears less noisy than the original image

  2. 2.

    I would choose this image for breast density evaluation

  3. 3.

    I would choose this image for lesion detection

  4. 4.

    I notice a better distinction between fibroglandular and adipose tissues

  5. 5.

    The image quality is sufficient for mass analysis

  6. 6.

    I notice a better definition of contours

  7. 7.

    I would choose this image for identifying areas of asymmetry

  8. 8.

    I notice less presence of artifacts in mammographic structures

  9. 9.

    The sharpness of the image allows better evaluation of microstructures

  10. 10.

    I would choose this image to detect the presence of microcalcifications

Subsequently, Cohen’s Kappa34 was calculated to measure the agreement between the two radiologists. The formula used is as follows:

$$K=\frac{{{P_o} - {P_e}}}{{1~ - ~{P_e}}}$$
(3)

where: K represents Cohen’s Kappa value; P0 is the observed proportion of agreement between the radiologists. It is calculated as the ratio of the number of cases where the observers agree to the total number of cases; Pe is the expected proportion of agreement between the observers based on the assumption that their responses are independent. It is calculated as the sum of the products of the marginal proportions for each response category, derived from the confusion matrix of the two radiologists’ responses.

A Cohen’s Kappa value close to 1 indicates a high level of agreement between the radiologists, while a value close to 0 indicates a lack of agreement, and a negative value suggests agreement less than that expected by chance.

Results

N2V approach

We will now present the results acquired for the metrics illustrated above when applying N2V.

The results for the CNR indicate that it is consistently higher for the predicted patches than the original patches. In the boxplots in Fig. 3a and b, we observe an increase in the median line after training, both for the fibroglandular tissue and the adipose tissue.

MSE, PSNR, and SSIM metrics were calculated only on simulated data since their implementation required comparison with the clean ground-truth image. These metrics were calculated on all patches where only tissue was present (excluding only background patches) that formed the dataset, but, for a higher readability of the graphs, we manually selected 200 patches related to 20 different patients, with 10 patches per patient.

From the graphs in Fig. 4a, we notice a significant decrease in the MSE, which suggests that the algorithm, when working with images with added Gaussian noise, is getting closer to the original data, demonstrating greater prediction accuracy.

Furthermore, in Fig. 4b, we observe an increase in the PSNR evaluated on the images predicted by the network during training on simulated data, compared to the PSNR calculated on the images with added Gaussian noise.

The results related to SSIM indicate that the addition of Gaussian noise did not cause a deformation of the anatomical structures, SSIM being already very high in the pre-denoising phase. After denoising with N2V, SSIM does not improve significantly (p-value < 0.05) compared to the previous case, demonstrating, however, that N2V maintains structural similarity without altering the anatomical structures of the image. We highlight that neither the simulated noise nor the denoising technique alters the structure, as demonstrated by the SSIM mean values (0.99979 vs. 0.99995), which are all close to unity.

Subsequently, a statistical analysis was carried out to compare the results obtained. First, a paired Wilcoxon test was performed to statistically compare the metrics calculated on the images before and after denoising with N2V, both on original data and on simulated data.

Fig. 3
figure 3

Boxplot for CNR of a fibroglandular on original data, b adipose tissue on original data, c fibroglandular on simulated data, d adipose tissue on simulated data.

Full size image

Table S1 of Supplementary Materials reported the results from the statistical Wilcoxon test for training with original data and simulated data. In all cases, the p-value is lower than the predetermined significance level of 0.05, indicating a statistically significant difference between the measured parameters before and after training, both with real and simulated data.

The NPS was computed for patches from both fibroglandular and adipose tissues. Thecorresponding maps and 1D representations are shown in Figs. S3 and S4, respectively, of the Supplementary materials.

These maps show that after applying the N2V network, there is a reduction in noise power at higher spatial frequencies, evidenced by a decrease in peripheral intensity in the NPS plots. However, the central region remains relatively bright, suggesting that structured noise at lower frequencies is less affected, likely due to the nature of the N2V method, which is more effective against uncorrelated noise. This trend is confirmed by the 1D graph, where a decrease in NPS is seen only at high spatial frequencies.

In addition to the quantitative results presented so far, a qualitative evaluation was also made to evaluate the quality of the mammography image for diagnosis in the eyes of expert radiologists.

Based on the responses to the statements in the questionnaire presented to the radiologists for a qualitative evaluation of the study results (in Table S2 of Supplementary Materials), the degree of agreement between the two observers was calculated, resulting in a Cohen’s Kappa of 0.5, indicating moderate agreement in positively evaluating the improvement in image quality and the better diagnostic power of the images after denoising. A visual representation of a few sample patch images, showing side-by-side comparisons between the original and simulated patches, as well as the corresponding denoising results using N2V, is shown in Fig. S5 of the Supplementary Materials.

Fig. 4
figure 4

Pairwise plot for a MSE and b PSNR, calculated on simulated data. Each circle represents the PSNR or MSE calculated for a single patch in the simulated dataset (with added Gaussian noise), before and after the denoising process. The lines connecting the pairs of circles indicate the improvement in PSNR (or MSE) for each simulated patch after denoising.

Full size image

Comparison with conventional denoising approaches

In this section, the results of the comparison with traditional denoising techniques will be presented. In Fig. 5, the boxplots for the comparison of the CNR, for both fibroglandular and adipose tissues, are shown. They are calculated on images on which different traditional denoising techniques were applied, compared with the N2V approach and the original image without denoising.

It is readily seen that all denoising techniques lead to a higher CNR, compared to the scenario without denoising. Specifically, the NLM technique shows the most promising results, while the BM3D technique exhibits less favorable outcomes in both tissues. It is worth noting that, despite this fact, improvements in CNR are observed, compared to the scenario where no denoising technique is applied. Subsequently, we shall present the results acquired by calculating the metrics on the patches after denoising is implemented on simulated data to compare the various algorithms. Also in this case, in the various plots, we included the median calculated before applying denoising and the first boxplot displays the metric calculated before denoising was implemented.

Figure 5 shows the boxplots for the comparison of CNR, both for fibroglandular and adipose tissues, calculated on both real and simulated images with added noise. They are calculated on images on which different traditional denoising techniques have been applied, compared with the N2V approach and the original image without denoising. It is immediately evident that all the denoising techniques lead to a higher CNR, compared to the scenario without denoising, excluding the median filter. In Fig. 6a, we notice that all the considered denoising techniques allow for obtaining a lower MSE value compared to the scenario where no denoising technique is applied. The values obtained from the other techniques considered are very similar. In this case, the technique using the BM3D filter and NLM show the best result, followed by N2V approach.

Furthermore, in Fig. 6b we observe that the boxplots related to the PSNR values calculated on the images where various denoising techniques have been implemented are higher than the scenario where no denoising is applied.Among all the techniques considered, the one using BM3D presents the highest PSNR values, followed by NLM and N2V.

Fig. 5
figure 5

Boxplots the CNR calculated on a fibroglandular and b adipose tissue on real images and c fibroglandular and d adipose tissue on simulated images, using the denoising techniques.

Full size image

SSIM varies significantly (p-value < 0.005) between the different techniques, both traditional and N2V, remaining at values very close to 1, highlighting also in this case that neither the simulated noise nor the denoising techniques, both traditional and DL-based, alter the structure, as demonstrated by the SSIM values (not reported in the figure for simplicity) which are all close to unity.

The results of the p-value from the paired Wilcoxon test, conducted on each metric to determine if there was a statistically significant difference between the metrics calculated before and after denoising, showed that there was a significant difference between the metrics calculated before and after denoising for all denoising techniques considered.

Subsequently, we conducted repeated measures to perform statistical tests. So, a Kruskal–Wallis test was conducted.

The null hypothesis for this test is that the metrics calculated with different denoising techniques all have the same median. Table S3 of Supplementary Materials shows the results of the p-value from the Kruskal–Wallis test calculated for all the metrics.

We can observe that the p-values are all much lower than the significance level. This indicates that there is a statistically significant difference in the variances of the metrics calculated for the different denoising techniques considered.

Discussion

The need for reducing noise in medical images is a crucial point and still attracts great research interest nowadays, also due to the significant advancements in the field of artificial intelligence, with particular regard to the development of DL techniques35, which have been extensively explored in the field of positron emission tomography16,20,35 as well as of computed tomography and magnetic resonance imaging36,37. However, the potential of unsupervised approaches, which are the most interesting approaches to date as they do not require clean images for the neural network training phase, has not been fully explored in the medical field and especially in the field of FFDM. In this work, given the importance of denoising in the field of mammography38,39,40, we adapted a N2V-based framework to digital mammography and compared it to conventional denoising algorithms. The results obtained from the application of N2V to digital mammography images highlight a clear improvement in mammographic image quality. Both a qualitative and quantitative evaluation were carried out, which underlines the potential of this approach. From the quantitative results of the comparison between the patch predicted by the network (denoised) and the original patch (noisy), it emerged that the N2V network manages to reduce the noise in the image andimprove the contrast of the image, making all the structures of the breast tissues more visible, significantly increasing the CNR (p-value < 0.05). Further application was made on simulated data, adding Gaussian noise to the images considered and thus also having a corresponding ground truth reference image to calculate and evaluate other evaluation metrics such as MSE, PSNR, and SSIM.

Fig. 6
figure 6

Boxplots representing the a MSE and b PSNR, calculated on simulated data before and after applying denoising with the described techniques.

Full size image

Also in this case, significant improvements emerged, confirmed by the statistical tests carried out, which highlight how both the mean square error and the noise power decrease significantly, leading to an increase of the PSNR; SSIM does not improve significantly (p-value > 0.05) compared to original images, demonstrating however that N2V maintains structural similarity without altering the anatomical structures of the image. This last point is confirmed by a qualitative evaluation made by two expert radiologists to link technical improvements to clinical perception. Based on a questionnaire on the perceived quality of the clean images predicted by the network for diagnostic purposes, the radiologists showed a good agreement in stating that the processed images show better than the original images. Specifically, the two expert radiologists highlighted a perceived improvement in key aspects of clinical interpretation, including visibility of microstructures and tissue assessment.

It is interesting to notice how the performances are equally good on both fibroglandular and adipose tissue, highlighting how the noise reduction and the resulting improvement in CNR are consistent across different tissue types.

It is also worth noting that, despite proving to improve the overall image quality both quantitatively and qualitatively, N2V does not perform better than traditional methods. However, the results show that NLM seems to be the best technique for all the metrics considered, surpassed by BM3D and bilateral filter as regards simulated patches. The N2V approach presents good performances, maintaining a good balance between the performances measured with all the evaluation metrics, also confirmed by the qualitative evaluations of the radiologists. On original data, while improving the quality of mammographic images, it fails with structural noise, as confirmed by the NPS reported in Figs. S3 and S4 of the Supplementary Materials.

In addition to the data-driven perspective adopted in this work, alternative strategies such as total variation (TV) minimization offer a consolidated framework for denoising. TV minimization is a well-established approach for reducing noise in medical images, particularly in X-ray breast imaging and digital breast tomosynthesis (DBT), due to its ability to reduce noise while preserving important structural details such as edges and microcalcifications41,42,43,44. Several studies have demonstrated the effectiveness of TV-based techniques in this area, reporting significant improvements in CNR, SNR, and even a potential radiation dose reduction of 20–30% without compromising diagnostic image quality41.

By comparison, N2V represents a data-driven, self-supervised learning framework that does not require access to clean or high-dose reference images, a significant practical advantage in clinical settings where such data are rarely available. Compared to traditional TV approaches, N2V leverages image statistics learned from noisy data to predict clean pixel values, making it particularly attractive for use in retrospective analyses or on datasets acquired under varying conditions.

However, this flexibility has proven to come at a cost. Our results indicate that, although N2V performs well in improving image quality, compared to standard methods such as NLM in terms of global image quality metrics (e.g., SNR, CNR, NPS), it does not significantly outperform them. Furthermore, N2V lacks the theoretical rigor of TV-based methods, which rely on variational principles and offer strong guarantees in terms of edge preservation and convergence. In contrast, N2V’s performance is data-dependent and is influenced by factors such as network architecture, patch selection, and training stability.

In summary, while N2V offers a compelling unsupervised alternative, proven to be effective in many medical imaging contexts such as PET, MRI, chest X-ray, and CT, for denoising in the absence of clean training targets, it should be considered complementary rather than superior to other mammography denoising methods. Future work could explore hybrid strategies that combine the theoretical advantages of variational models with the adaptability of data-driven learning.

It would therefore be interesting to do further analysis with new state-of-the-art strategies, which represent the evolution of the simple N2V (i.e. Probabilistic Noise2Void (PN2V)45, Sparsity Constrained Network (SC-Net)46, StructN2V47, Noise2Score48, etc.), which will be the subject of future work in the field of digital mammography. Furthermore, comparative analyses on larger and more heterogeneous samples would therefore be useful to generalize the findings of this study. Ours is in fact a monocentric study, therefore the images considered do not present a great variability regarding the acquisition parameters or the characteristics of the population under examination. Furthermore, since they come from screening programs, they are mostly healthy subjects. However, a certain variability can be considered regarding the composition of the breast. Comparative analyses with other unsupervised approaches would be helpful in the identification of the most promising unsupervised denoising approaches over conventional noise-reduction techniques in the field of digital mammography.

Conclusions

Denoising techniques based on unsupervised deep learning represent a new perspective in medical image denoising. In this work, we applied for the first time N2V architecture to digital mammography images. Despite the encouraging results obtained in terms of improved image quality, in the systematic and multiparametric comparison of the proposed N2V approach for FFDM with several state-of-the-art algorithms already employed to treat mammographic images, N2V does not perform better than the traditional approaches. Although N2V has not shown a clear quantitative advantage over traditional methods such as NLM, its clinical applicability remains relevant, as it offers a solution that can be used even in retrospective datasets and in the context of ionizing radiation, where supervised or variational methods require unavailable background information or meticulous parametric optimization. In this context, N2V offers a number of practical advantages that make it highly suitable for real-world clinical environments. One of the most promising areas for N2V application is low-dose imaging, as demonstrated by its application on simulated low-dose images. N2V, which does not require clean training targets, can be applied directly to these noisy, low-dose datasets, offering a means to restore image quality without altering acquisition protocols or relying on unavailable high-dose images.

Furthermore, N2V is particularly well-suited for retrospective analysis of heterogeneous image archives, improving image quality and enabling the reuse of previously unusable or suboptimal scans for research or secondary reading purposes.

Furthermore, N2V’s modularity allows for its integration into more complex processing pipelines. Acting as a front-end denoising step, N2V can improve the performance of downstream tasks without introducing structural distortions, as supported by both our SSIM analysis and radiologists’ assessments.

Even with comparable performance with simpler techniques, which do not justify the increased computational burden, these application scenarios warrant further research and potential clinical translation.