Introduction

Holography is an optical technique that reconstructs the three-dimensional wavefront of an object by recording both amplitude and phase components of light waves1,2. At the time of Gabor’s invention, the practical implementation of holography was limited due to the absence of coherent light sources. The evolution of holography began with the invention of lasers, leading to advanced imaging and display applications3. Alternatively, computer-generated holography (CGH)4,5 synthesizes holograms using computational methods, enabling the creation of both real and virtual objects for dynamic holographic 3D displays6,7,8. Due to this computational flexibility, CGH is a promising technology for applications in education, entertainment, and medical treatment, where interactive and high-resolution visualization is essential9,10.

Spatial light modulators (SLMs) are key optical display devices used in holography for wavefront modulation. However, commercially available SLMs cannot perform complex field modulation, as they can only modulate amplitude or phase individually11. Therefore, a complex hologram needs to be converted into an amplitude-only or phase-only hologram using encoding techniques12. Compared to amplitude-only holograms, phase-only holograms offer higher diffraction efficiency and effectively suppress the conjugate image during reconstruction. However, amplitude control of the reconstructed image is challenging in phase-only holograms13.

Over the years, a variety of encoding methods have been proposed for phase-only holograms. Iterative methods, including the Gerchberg-Saxton (GS) algorithm14,15 and stochastic gradient descent (SGD)16,17,18 have demonstrated the capability to achieve high-quality reconstructed images. On the other hand, non-iterative methods, such as error diffusion and down-sampling techniques, were developed but often result in reduced image quality19,20,21. Moreover, a hybrid technique22 based on the optimized random phase method was introduced, enabling rapid synthesis of phase-only holograms. Shi et al.23,24 introduced a deep learning approach that enables real-time phase-only hologram generation, significantly reducing computational complexity while improving reconstruction quality for holographic display applications.

The double phase encoding method (DPM) is an efficient and computationally fast technique for phase-only holograms. In DPM, both amplitude and phase are encoded into two-phase components25 often arranged in a checkerboard pattern26. Despite its advantages, the encoded holograms are affected by spatial artifacts due to the conversion of complex amplitude into a phase-only representation. To address these issues, the band-limited double phase method was developed, incorporating optical filtering27 in the frequency domain to suppress high-frequency artifacts. Kim et al.28 proposed a weight factor method to improve diffraction efficiency and suppress noise. In 2020, Sui et al.29 introduced a spatiotemporal double phase hologram approach that reduces speckle noise. In 2023, Zhong et al.30 proposed a real-time 4 K CGH generation based on encoding conventional neural network with learned layers, demonstrating effective 3D hologram generation at a single wavelength. In 2024, Yan et al.31 demonstrated a deep learning approach using full convolution neural networks for recoding double phase holograms, effectively suppressing fringe artifacts at the edges of the diffraction field.

However, due to the spatial artifacts and the filtering structure that blocks part of the light, the reconstruction image quality and optical efficiency of the conventional DPM remain limited. In this work, we enhance the light efficiency of phase-only holograms by using a neural network-based encoding method. The proposed model, ShuffleResnet, achieves a 59% improvement in light efficiency, maintains high reconstruction quality, and significantly reduces artifacts compared to the conventional DPM. To achieve this, we employ a combination of supervised and unsupervised loss functions, along with an efficiency term. Moreover, the proposed model encodes RGB 2 K CGHs within 4.74 milliseconds, offering both speed and efficiency suitable for real-time applications.

Conventional DPM

DPM is a widely used non-iterative method for encoding complex amplitude fields into phase-only holograms, using two phase values per pixel, enabling high image quality hologram reconstruction. To represent the complex field, \(\:U\left(x,y\right)\), using only phase values, DPM decomposes the field into two phase terms26.

$$\:U\left(x,y\right)={e}^{{i\theta\:}_{1}}+{e}^{i{\theta\:}_{2}}$$
(1)

where the two-phase values of \(\:{\theta\:}_{1}\) and \(\:{\theta\:}_{2}\) are defined as:

$$\:{\theta\:}_{1}=\phi\:+\text{a}\text{r}\text{c}\text{c}\text{o}\text{s}\left(\frac{A}{{A}_{max}}\right),$$
(2)
$$\:{\theta\:}_{2}=\phi\:-\text{a}\text{r}\text{c}\text{c}\text{o}\text{s}\left(\frac{A}{{A}_{max}}\right).$$
(3)

To implement the encoding, the two phase values \(\:{\theta\:}_{1}\) and \(\:{\theta\:}_{2}\) are alternately arranged across the pixel array, creating a checkerboard pattern of the phase-only values32.

Figure 1 illustrates the conventional DPM of the complex field \(\:U\left(x,y\right)\). The original complex field, represented in the left block, consists of individual cells, in which each cell of \(\:U\left(x,y\right)\) has a complex number with both amplitude and phase components. The middle block shows the core of DPM, where the complex field is split into two phase components \(\:{\theta\:}_{1}\), \(\:{\theta\:}_{2}\).

Fig. 1
figure 1

Schematic of the conventional DPM. The first panel shows the original complex field, the middle panel illustrates the calculated phase components from the complex field, and the final panel shows the encoded complex field.

Full size image

Training of neural network

Figure 2 presents the detailed training process of the neural network model. The proposed model consists of pixel shuffle and unshuffle operations combined with residual blocks, as explained in detail in the methods section. The model takes complex holograms as input, and its output corresponds to the phase encoded value. The training process employs a hybrid loss function, which combines both supervised (\(\:{L}_{DPM}\)) and unsupervised loss (\(\:{L}_{r}\)) along with an efficiency term, \(\:{L}_{e}\). The supervised loss accelerates training, and the unsupervised loss is used to minimize the reconstruction error to enhance the reconstruction quality. The scaling ratios \(\:\alpha\:,\beta\:,\gamma\:\) balance the contribution of each term during training, as further discussed in the hyperparameter tuning result section. As a result, the total loss function can be written as:

$$\:L={r}_{s}\left(n\right)\alpha\:{L}_{DPM}+\left(1-{r}_{s}\left(n\right)\right)\left(\beta\:\right(-{L}_{e})+{\gamma\:L}_{r}).$$
(4)

\(\:{L}_{DPM}\)​ is calculated as:

$$\:{L}_{DPM}=\frac{1}{N}\sum\:_{x,y}\frac{1}{M}\sum\:_{i=1}^{M}\left[\right(Re({z}_{i}\left)\right(x,y)-Re\left({t}_{i}\right)(x,y){)}^{2}+(Im\left({z}_{i}\right)(x,y)-Im\left({t}_{i}\right)(x,y){)}^{2}]$$
(5)

\(\:{L}_{DPM}\) is the mean squared error loss between the network output \(\:{z}_{i}(x,y)\) and conventional DPM output \(\:{t}_{i}(x,y)\) ​ as target, calculated for both real and imaginary components. \(\:N\) is the number of holograms in one training batch. \(\:M\) is the number of pixels in each hologram.

\(\:{L}_{r}\) is computed as:

$$\:{L}_{r}=\frac{1}{N}\sum\:_{x,y}\frac{1}{M}\sum\:_{i=1}^{M}\left[\right(Re({c}_{i}\left)\right(x,y)-Re\left({r}_{i}\right)(x,y){)}^{2}+(Im\left({c}_{i}\right)(x,y)-Im\left({r}_{i}\right){(x,y))}^{2}]$$
(6)

\(\:{L}_{r}\) computes the mean squared error loss between the original complex field \(\:{c}_{i}(x,y)\) and reconstructed complex field \(\:{r}_{i}\:(x,y)\) for both real and imaginary components.

The light efficiency \(\:{L}_{e}\) is computed as:

$$\:{L}_{e}=\frac{1}{N}\sum\:_{x,y}|{U}_{recon}\left(x,y\right){|}^{2}$$
(7)

where \(\:{U}_{recon}\left(x,y\right)\) is the reconstructed complex field, and \(\:N\) is the total number of pixels.

where \(\:{r}_{s}\left(n\right)\) is the supervised ratio at epoch \(\:n\), which determines the relative weight between supervised and unsupervised loss components. To ensure a smooth transition from supervised encoding to unsupervised encoding, we define \(\:{r}_{s}\left(n\right)\) using exponential decay as, \(\:{r}_{s}(n+1)=d{r}_{s}\left(n\right)\), where \(\:d\) is a decay constant. In other words, \(\:{r}_{s}\left(n\right)\) can be expressed as:

$$\:{r}_{s}\left(n\right)={r}_{s}\left(0\right){e}^{dn}$$
(8)

where \(\:{r}_{s}\left(0\right)\) is the initial supervised ratio set to 1. The exponential decay allows the model to initially learn from supervised double phase encoding targets and gradually rely more on unsupervised reconstruction and efficiency objectives as training progresses.

Fig. 2
figure 2

Overview of the training scheme using a neural network for hologram encoding. The model takes a complex amplitude on the hologram plane as input and produces an encoded hologram as output. The hologram synthesized by the conventional DPM is used as the supervised target. The model output is numerically reconstructed and compared with the original input to compute the unsupervised reconstruction loss. Additionally, an efficiency term is used to evaluate the reconstruction quality. Finally, the total loss, which integrates all three loss terms, is backpropagated to optimize the network.

Full size image

Figure 3 illustrates the training performance of ShuffleResnet and U-Net in terms of peak-signal-to-noise ratio (PSNR) and light efficiency across training epochs. In Fig. 3a, the reconstruction PSNR of ShuffleResnet increases steadily and reaches a peak value of approximately 32 dB. The stable PSNR indicates that the network learns a consistent and effective encoding strategy to improve reconstruction quality. In Fig. 3b, the reconstruction efficiency of ShuffleResnet shows a gradual increase after 10 epochs, eventually reaching a maximum value of approximately 0.42. The improved efficiency after ten epochs is due to the exponential decay of \(\:{r}_{s}\left(n\right)\), which shifts the training focus from supervised encoding to optimizing reconstruction and efficiency. The enhanced efficiency reflects how effectively the input light is utilized in the reconstruction process.

Fig. 3
figure 3

Comparison of training performance between ShuffleResnet and U-Net. (a) Reconstruction PSNR. (b) Reconstruction efficiency as a function of training epochs.

Full size image

For comparison, a U-Net model was trained under the same conditions, and its performance was evaluated along with ShuffleResnet in Fig. 3. Compared to ShuffleResnet, the U-Net model exhibits significantly lower PSNR and reduced light efficiency. During initial epochs, U-Net’s light efficiency increases rapidly because the model initially learns the conventional DPM patterns using the supervised target. However, after epoch 10 when the supervised weight begins exponential decay, the model gradually shifts its focus toward the more challenging unsupervised reconstruction objective. After the transition, the model is no longer trained by DPM, but by a complex objective that optimizes both reconstruction quality and light efficiency. As a result, the measured light efficiency gradually declines to approximately 0.25 by the end of training, as shown in Fig. 3b. The comparison results confirm that ShuffleResnet performs better than U-Net.

Evaluation results

To evaluate the reconstruction performance of the proposed model, we compared the complex field reconstruction results of ShuffleResnet and conventional DPM. We used conventional DPM as our baseline because its output was used to generate the targets for our initial supervised training phase. The CGHs used in the validation assumed that the 2D floating hologram is 10 mm away from the SLM, where the 2D floating images are the DIV2K validation dataset. To synthesize the CGHs, the images were numerically propagated using the angular spectrum method (ASM). During the complex field reconstruction using the encoded output, a band-limiting optical filter was applied to suppress high-frequency diffraction noise. Although random propagation depths were used during training to improve generalization, a fixed depth was adopted to ensure consistent metric calculation.

Fig. 4
figure 4

Numerical reconstruction results of the complex field, compared with the original CGH as the target. Target CGHs (a–d), numerically reconstructed holograms from ShuffleResnet (e–h), and numerically reconstructed holograms from conventional DPM (i–l) are presented with their PSNR and optical efficiency values.

Full size image

Figure 4 presents the numerical complex field reconstruction results obtained using ShuffleResnet and the conventional DPM, compared against the target complex holograms. The figure displays the magnitude of the reconstructed complex fields for visual comparison, while the quantitative evaluation (PSNR and efficiency) is performed on the complete complex data including both real and imaginary components. In the numerical reconstructions, the ringing patterns and diffractions are visible, serving as indicators of depth. While the reconstructed output from ShuffleResnet is nearly identical to the target, the conventional method presents noticeable spatial artifacts. For instance, in Fig. 4j, there are speckles in the eye of the animal, whereas the corresponding output in Fig. 4f shows a clear view of the eye that closely matches the target. As a result, the reconstructed complex field outputs from ShuffleResnet achieve higher PSNR and improved light efficiency values compared to the conventional method.

Encoding results comparison

Fig. 5
figure 5

Comparison of encoded output and reconstructed intensity between ShuffleResnet and conventional DPM. (a) Phase of ShuffleResnet output with yellow box indicating region of interest and corresponding zoomed-in view. (b) Corresponding reconstructed intensity with PSNR and SSIM metrics. (c) Phase of conventional DPM output with red box indicating region of interest and corresponding zoomed-in view. (d) Corresponding reconstructed intensity demonstrating the high frequency noise.

Full size image

Figure 5 provides a visual and quantitative comparison of the encoded holograms and corresponding intensity reconstruction results from the proposed ShuffleResnet and conventional DPM. In Fig. 5a, the encoded output produced by ShuffleResnet achieves a well-structured checkerboard pattern, clearly preserved in the magnified region in the yellow box. This consistent pattern indicates stable and accurate encoding of phase information. The corresponding reconstruction in Fig. 5b achieves a high PSNR of 32.1dB and SSIM of 0.948. In contrast, Fig. 5c shows the encoded output generated by the conventional DPM, where the checkerboard structure appears irregular and disrupted in the zoomed region of the red box, is present, it appears disrupted in the zoomed region of the red box, especially near textured or low-contrast regions of the image. As a result, the reconstruction in Fig. 5d exhibits high frequency artifacts, particularly in the background and low-contrast areas. These limitations are quantitatively reflected in the significantly lower PSNR of 9.01 dB and SSIM of 0.561.

Hyper-parameter tuning results

Light efficiency plays a crucial role in hologram reconstruction. By analyzing different efficiency ratios \(\:\beta\:\), we observed a trade-off between light efficiency and reconstruction quality. Although a higher efficiency ratio increases light efficiency up to 0.9994, it also leads to a reduction in PSNR, which negatively impacts reconstruction quality.

Fig. 6
figure 6

Trade-off analysis between reconstruction quality (PSNR) and light efficiency at varying efficiency ratios \(\:\varvec{\beta\:}\). Increasing \(\:\varvec{\beta\:}\) enhances the light efficiency but reduces reconstruction quality.

Full size image

Figure 6 illustrates the variation of light efficiency and PSNR as a function of efficiency ratios \(\:\beta\:\). At lower efficiency ratios, the model achieves optimal reconstruction performance, with maximum PSNR and high light efficiency. As the efficiency ratio increases, light efficiency improves, but reconstruction quality decreases. For instance, at the highest ratio, efficiency reaches 0.9994, but the PSNR drops significantly to 12.66 dB. These results highlight a clear inverse relationship between PSNR and light efficiency.

Intensity-field comparison results

Fig. 7
figure 7

Numerical reconstruction results after propagation for intensity-field representation. (a–d) Target ground-truth images from DIV2K validation dataset. (e–h) Numerically reconstructed holograms from ShuffleResnet. (i–l) corresponding reconstructions from the conventional DPM. Each output is annotated with PSNR and SSIM.

Full size image

While Fig. 4 evaluated the complex field reconstruction quality at the SLM plane, Fig. 7 presents the simulated optical reconstruction results after propagation to a fixed observation plane for intensity-field comparison. The encoded holograms were numerically propagated using the ASM at a distance of 5 mm. Each image is annotated with its corresponding image quality metrics, such as PSNR and SSIM values. Compared to the conventional DPM, the ShuffleResnet reconstructions appear closer to the targets, with high PSNR and SSIM. The reconstructed output from ShuffleResnet demonstrates enhanced light efficiency and reconstruction quality.

Table 1 Evaluation metrics of ShuffleResnet and conventional method based on the 100 images in the validation dataset for intensity field calculation.
Full size table

Table 1 summarizes the average PSNR, SSIM, and light efficiency values for both ShuffleResnet and the conventional DPM using 100 images from the DIV2K validation dataset. Overall, the proposed model ShuffleResnet yields a 0.75 dB increase in PSNR, indicating improved reconstruction fidelity. The SSIM improves by 4.2% reflecting better structural similarity to the target intensity field. Most notably, light efficiency increases by 59%, showing that a significantly larger portion of light contributes to the final image. These improvements collectively demonstrate the enhanced reconstruction quality and improved light efficiency, making it more suitable for real-world holographic display applications.

Experiment results

Fig. 8
figure 8

Comparison of experimental results between ShuffleResnet (a,c) and conventional DPM (b,d). The relative optical efficiency of ShuffleResnet result, compared to the conventional DPM result, is indicated in the figure.

Full size image

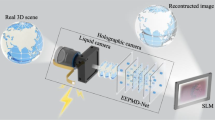
To validate the simulation results, we conducted experimental reconstructions. In our experiment, we first generated a 2D floating hologram, as in the simulation. Then we performed encoding using both the conventional DPM and our ShuffleResNet model, and experimentally reconstructed the hologram. We reconstructed the hologram using only the red channel and a red laser to simplify the experiment. To evaluate the light efficiency of the methods, we defined the relative efficiency as the ratio of the total intensity, defined as the sum of all pixel values of the reconstructed image produced by ShuffleResnet, to that of the DPM output under identical conditions. This metric quantifies how much brighter the reconstruction is when using our encoding approach.

As shown in Fig. 8, although the image quality remains visually similar between both methods, the ShuffleResnet significantly improves light throughput efficieny. In Fig. 8a, ShuffleResnet achieves a relative efficiency of 1.608, while in Fig. 8c, the ShuffleResnet achieves 2.909 compared to conventional DPM. These results clearly confirm that the ShuffleResnet model achieves a substantial increase in light efficiency over the conventional approach.

Discussion and conclusion

While an end-to-end model that directly generates a phase-only hologram from a target image offers advantages in terms of application simplicity, our approach of decoupling the generation of the complex field from its encoding provides significant advantages in flexibility and modularity. Many computational holography algorithms first compute a complex field to address specific challenges before encoding it for display. For instance, sophisticated methods have been developed to enhance depth representation33 or to expand the display eyebox34. By implementing only the encoding stage, our method provides compatibility with such high-performance algorithms.

In this study, we introduced a model, ShuffleResnet, designed to enhance the reconstruction quality and light efficiency of double phase encoded holograms. Numerical simulation results demonstrate that the proposed model achieves higher quality of reconstructed holograms compared to conventional methods. The model significantly reduces the artifacts and increases the light efficiency of reconstructed holograms. Compared to conventional DPM, ShuffleResnet achieves a 59% increase in light efficiency without compromising reconstruction quality, making it well-suited for real-time holographic applications.

Methods

Network training and architecture

The overall framework consists of hologram generation, conventional double phase encoding for supervision, model training and evaluation. In our training pipeline, the ShuffleResnet model is trained on complex-valued holograms generated at random propagation depths to promote generalization in learning wavefront propagation. The actual propagation depth for each image is randomly selected as:

$$\:z=\frac{{z}_{base}\times\:\text{r}\text{a}\text{n}\text{d}(1,N)}{N}$$
(9)

Where \(\:{z}_{base}\:\)is the base propagation depth, \(\:\text{r}\text{a}\text{n}\text{d}(1,N)\) selects a random integer from \(\:1\:to\:N\), and \(\:N\) is number of depth levels considered. Once the propagation depth is determined, the complex wavefield is generated using the ASM, which simulates wave propagation in free space.

The initial wave field \(\:U\left(x,y\right)\) is first transformed into the spatial frequency domain:

$$\:U\left({f}_{x},{f}_{y}\right)=\mathcal{\:}\mathcal{F}\left\{U\left(x,y\right)\right\}$$
(10)

Where \(\:\mathcal{F}\) denotes the Fourier transform, \(\:U\left(x,y\right)\) is the input complex field at the initial plane, \(\:U\left({f}_{x},{f}_{y}\right)\:\)is the Fourier domain representation, which describes the spatial frequency components of the wavefront. The wavefield is propagated at depth \(\:Z\) by multiplying it with a phase term in the frequency domain as:

$$\:U\left({f}_{x},{f}_{y},z\right)=U\left({f}_{x},{f}_{y}\right).{e}^{j{k}_{z}z}$$
(11)

Where \(\:{k}_{z}\) is the propagation term, defined by:

$$\:{k}_{z}=\sqrt{{k}^{2}-{\left(2\pi\:{f}_{x}\right)}^{2}-{\left(2\pi\:{f}_{y}\right)}^{2}}$$
(12)

With \(\:k=\frac{2\pi\:}{\lambda\:}\) as the wave number. \(\:\left({f}_{x},{f}_{y}\right)\:\)denoting the spatial frequency coordinates. The propagated wavefield is transformed back into the spatial domain using the inverse Fourier transform given by:

$$\:U\left(x,y,z\right)=\:{\mathcal{F}}^{-1}\left\{U\left({f}_{x},{f}_{y},z\right)\right\}$$
(13)

Where \(\:{\mathcal{F}}^{-1}\) is inverse Fourier Transform, \(\:U\left(x,y,z\right)\) is the propagated complex field at depth z.

The generated CGH is encoded using conventional DPM which serves as the supervised training target. The real and imaginary components of the complex-valued holograms are separated and concatenated as input channels for the model. These holograms undergo pixel unshuffling operations as followed by residual blocks35 and pixel shuffling36 operations as shown in Fig. 9. The double-phase encoding method arranges two phase components (\(\:{\theta\:}_{1}\) and \(\:{\theta\:}_{2}\)) in alternating pixels forming a checkerboard pattern. Standard convolutional neural networks apply uniform operations across all pixels, which is inefficient for this alternating structure where adjacent pixels represent different phase types. Pixel shuffling operations address this limitation by reorganizing the checkerboard pattern into separate channels, enabling independent processing of \(\:{\theta\:}_{1}\) and \(\:{\theta\:}_{2}\)components before reconstructing the spatial arrangement required for SLM display.

The Pixel Unshuffling operation increases the number of channels while reducing the spatial resolution by a Pixel shuffle factor \(\:\left(r\right)\). This transformation rearranges spatial information into separate feature channels, making it easier for convolutional layers to extract meaningful representations.

$$\:\left(B,C,\:H,W\right)\to\:\left(B,C\times\:{r}^{2},\frac{H}{r},\frac{W}{r}\right)$$
(14)
Fig. 9
figure 9

The schematic model architecture of ShuffleResnet. The model ShuffleResnet contains pixel unshuffling operation as the first followed by Resnet blocks in the middle, and pixel shuffling operation as the final stage.

Full size image

The Resnet Blocks consist of multiple stacked residual layers, each containing two \(\:(3\times\:3)\) convolutional layers, followed by Batch Normalization and ReLU activation. This skip connection ensures stable gradient flow and prevents vanishing gradient issues. The residual unit can be represented by:

$$\:H\left(X\right)=F\left(X\right)+X$$
(15)

Where \(\:F\left(X\right)\:\)represents the convolutional transformation applied to the input \(\:X\). The final activation function used in ShuffleResnet is Hardtanh, which constrains the output values within a fixed range. The Pixel Shuffling operation restores the spatial resolution while reducing the number of channels, effectively reconstructing the output. The transformation is:

$$\:\left(B,C\times\:{r}^{2},\frac{H}{r},\frac{W}{r}\right)\to\:\left(B,C,\:H,W\right)$$
(16)

The training dataset contains 800 images in DIV2K dataset, which consists of high-resolution natural images. Each image is resized to 1080 × 1920 pixels and converted into a complex-valued hologram. To enhance generalization, a random propagation depth is assigned for each sample. The base propagation \(\:{z}_{base}\) is taken as 40 mm and \(\:N=8\) represents the number of discrete propagation depths. The complex hologram is separated into real and imaginary components, which are concatenated along the channel dimension to form the input to the model. These holograms undergo pixel unshuffling to rearrange spatial information before being processed by Resnet blocks, after which pixel shuffling restores the spatial arrangement while preserving phase structure. The model is trained for 400 epochs using Adam optimizer with a learning rate of 0.0001, and a batch size of 1. The training time for the model is 25 h. For validation, we use DIV2K validation dataset, which contains 100 images. In this case, the fixed depth of -10 mm was used to generate the hologram input. The reconstruction was performed in the SLM plane using ASM. A band-limiting optical filter was applied during the simulation to reduce diffraction noise. Finally, the reconstructed output was propagated to 5 mm to get the final intensity-field representations, simulating the output seen on a real optical display.

Validation results across various distances

Table 2 shows the validation performance of proposed model across various distances for complex field in terms of PSNR and light efficiency using 100 images from the DIV2K validation dataset. The results demonstrate that reconstruction quality shows minimal dependency on propagation distance, with PSNR values remaining within a narrow range of ± 0.8 dB and efficiency values stable around 0.44–0.47, confirming the model’s robust generalization across different depths.

Table 2 Validation results performance of ShuffleResnet across various distances for complex field in terms of PSNR and light efficiency.
Full size table

Ablation study results

To validate the contribution of each proposed component in ShuffleResnet, we conducted systematic ablation experiments by removing key architectural elements and training objectives. Table 3 summarizes the ablation study results, demonstrating the impact of individual components on reconstruction quality and light efficiency for complex field.

Table 3 Ablation study results for individual components on reconstruction quality and light efficiency.
Full size table

The removal of pixel shuffle and unshuffle operations yielded a PSNR decrease of 7.39 dB, illustrating their critical role in managing the complex spatial structure of double phase encoding. While the efficiency slightly increased to 0.4954 in this configuration, this improvement came at the severe cost of reconstruction quality. Elimination of the unsupervised reconstruction loss produced an even more substantial performance degradation, with PSNR decreasing by 7.94 dB and efficiency declining to 0.2764, performing lower than conventional DPM. These results indicate that the reconstruction loss constitutes the primary mechanism driving both quality enhancement and efficiency improvement, as it optimizes the network to generate clean, artifact-free holograms from the original complex field rather than replicating conventional DPM patterns.

Experimental setup

Our experimental setup consists of a 638 nm red laser, a phase-only SLM, a 4-f imaging system, and a camera to capture the reconstructed hologram. The phase-only hologram, generated by either the ShuffleResnet model or the conventional DPM method, is uploaded onto the SLM. The collimated laser beam illuminates the SLM, modulating the wavefront based on the encoded phase. The modulated light is then relayed through a 4-f system to remove the undesired patterns, and the resulting reconstructed field is recorded by a CMOS camera placed at a propagation distance of − 60 mm from the SLM plane. The captured intensity data is used to assess light efficiency by computing the sum of pixel intensities in the red channel.