Introduction

Environmental pollution has become a major worldwide concern due to rapid urbanization, industrialization, and unsustainable farming methods. Pollutants such as organic chemicals, microbiological contaminants, and heavy metals are frequently present in water bodies like lakes1,2,3, rivers4,5, ponds6 and seas. The existence of these pollutants can lead to major ecological imbalances that can have an adverse effect on aquatic life, human health, and water quality. There has been a lot of research on mathematical modeling approaches which can explain and predict how pollutants will behave in complex ecosystems due to the need for effective ways to degrade pollutants7,8,9.

Mathematical models play a crucial role in understanding propagation, degradation, and interactions of pollutants with chemical or biological agents. Traditional models based on integer-order differential equations, which have been widely used to represent these processes, often fail to capture the inherent memory effects and long-range dependencies observed in real-world environmental conditions. Recent advances in fractional calculus (FC) have enabled new modeling tools that provide a more accurate and comprehensive framework for understanding pollutant dynamics10.

The concept of differentiation and integration is extended to non-integer orders by FC, which makes it possible to represent systems with memory and hereditary properties11. Fractional-order models (FOM) are especially beneficial for modeling systems whose past activity influences future dynamics because they consider past states, unlike classical models that assume a pollutant’s rate of change depends only on its current state. The application of fractional differential equations (FDEs) in the creation of model simulation techniques is growing in significance. The solutions to these FDEs in any order are essential for illustrating the characteristics of complex problems related to applied mathematics and technology. Solutions to these DEs are quite challenging to find. Integral transformations are one of the most practical and effective approaches in applied mathematics to address this problem, and they have been used in a variety of fields, including biology12,13, biotechnology14, fluid dynamics15,16,17, hydrodynamics18, population control19, chaos20, financial models21, human diseases22,23,24,25, control vectors26, viscoelasticity27,28 and many more29,30,31,32,33.

FC has several benefits when it comes to modeling pollutant degradation. The model is more realistic for systems with residual impacts because fractional derivatives (FDs) take historical pollutant concentrations into consideration. FOM present an effective mathematical tool for simulating memory and hereditary effects retained in environmental systems that cannot be explained by classical integer-order models. In the case of water pollution, pollutants generally exists in the status of delayed diffusion, adsorption, and desorption over sediments and the water body. Such procedures can indicate that the current concentration of a pollutant depends not only on the inputs at that time but also on the past condition. Non-locality of FDs is ideal for modelling such memory effects, corresponding to pollutant retention, slow release and anomalous transport phenomena. Thus, they offer a more realistic framework for describing pollutant persistence and spread in water bodies. Complex degradation behaviours and anomalous diffusion seen in polluted environments can be explained by the influence of previous states. A better match to experimental data can be achieved by tuning fractional models by varying the fractional order parameter. These models provide better recommendations for environmental management by improving the prediction of pollutant dissipation and equilibrium states by adding memory effects. Integer-order differential equation modeling of pollutant degradation has been the subject of numerous investigations. The models usually assume first-order or second-order reaction kinetics, in which the rate at which pollutants break down is proportional to the concentration of the pollutant and the activity of the degrading agent. However, there are a number of limitations to classical models, such as their inability to describe anomalous diffusion, simplified interaction assumptions and lack of memory effects. FOM overcomes these problems by accounting for past pollutant concentrations and for more complex interaction dynamics. FD have been shown in recent studies to better fit experimental data on microbial growth, pollutant degradation and biochemical oxygen requirement processes.

The results of this study have important implications for pollution control and environmental management plans. The integration of FC into pollutant degradation models provides:

  • Comprehension of microbial and chemical interactions.

  • Yields greater precision in pollutant dissipation predictions.

  • Improving the modeling of memory-dependent degradation processes.

  • Enhanced methods for creating efficient biological remediation procedures.

Through the application of the Predictor-Corrector (PC) approach and the FD of Caputo-type, our study aspires to comprehend the fractional-order water pollution model (FOWPM). The PC technique that has been specified has not yet been used to address the suggested framework. Several methods can be used to solve FOM, but each has limitations, such as over simplification, assumptions, and discretization. The proposed numerical method overcomes the limitations. Recent studies34,35,36 illustrate the efficiency and flexibility of this technique, which has been successfully applied to numerous models. Because this methods can handle nonlinear systems and capture the complex dynamics of pollution dispersion, it is a perfect fit for the present study. Its iterative approach assures precise results while remaining computationally simple, which is critical when studying complex environmental models. This study is novel in that it formulates a FOWPM with Caputo derivatives that capture memory effects, rigorously establishes stability and existence results, and employs the PC approach to ensure accurate simulations. Unlike existing studies, we rigorously establish stability, existence results, and validate numerical simulations for diverse fractional-orders. Consequently, our model illustrates the efficacy of the PC method in this situation and offers new insights on the long-term persistence of pollutants.

The study is organized as follows: “Preliminaries” includes essential terms and preliminary information about FC. The proposed model formulation and broad derivation of the FOWPM are given in “Model formulation”. “Existence and uniqueness analysis” delves into the uniqueness and existence of the model, providing a solid foundation for subsequent analysis. To ensure the accuracy and reliability of the model, “Stability analysis” expands on this by looking into its stability. “Model solution using PC scheme” presents the solution of the model, which is a thorough numerical solution obtained by applying the PC approach. Interpretation of the results and insights into practical applications is offered in “Results and discussion”, where the results are examined and their relevance is emphasized using graphical representations. Finally, the paper concludes with a summary of key findings and potential directions for further study in “Conclusion”.

Preliminaries

To set the stage for future discussion, we give a summary of the key concepts and properties related to FD in this section.

Definition 2.1

According to Riemann–Liouville11, the fractional integral of order \(\beta \geqslant 0\) for a function \(v(t) \in C_{ - 1}^s\) is given as

$$\begin{aligned} I^\beta v(t) = \frac{1}{{\Gamma (\beta )}}\int _0^t {(t - \xi )^{\beta - 1} } v^{(s)} (\xi )d\xi ,\,\,\,\, t>0, \,\,\,\,\beta >0, \end{aligned}$$
(1)
$$\begin{aligned} I^0 v(t) = v(t). \end{aligned}$$

Definition 2.2

A function \(v \in C_{ - 1}^s\) has the following FD described in terms of Caputo11:

$$\begin{aligned} D_t^\beta v(t) = \left\{ \begin{array}{ll} \frac{{d^s v(t)}}{{dt^s }},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\beta = s \in \mathbb {N}, \\ \,\frac{1}{{\Gamma (s - \beta )}}\int _0^t {(t - \xi )^{s - \beta - 1} v^{(s)} (\xi )d\xi },\,\,\,\,s - 1< \beta < s,\,\,s \in \mathbb {N}. \\ \end{array} \right. \end{aligned}$$
(2)

Linear property of Caputo fractional derivative (CFD) is

$$\begin{aligned} D_c^\beta (\gamma f(t) + \mu g(t)) = \gamma D_c^\beta f(t) + \mu D_c^\beta g(t), \end{aligned}$$

where \(\gamma\) and \(\mu\) are some constants.

Definition 2.3

The Mittag–Leffler function using a single operator11 can be described as:

$$\begin{aligned} E_\beta (v) = \sum \limits _{\delta = 0}^\infty {\frac{{v^\delta }}{{\Gamma (\beta \delta + 1)}}}, \,\,\,\, v \in \mathbb {C}, \,\,\,\, \beta >0. \end{aligned}$$
(3)

Definition 2.4

 Fractional-order stability criteria:

Let us consider the form of linear fractional-order system

$$\begin{aligned} {}^{C}D_{t}^{\beta } u(t) = A u(t), \qquad 0 < \beta \le 1. \end{aligned}$$

If all of the eigenvalues \(\lambda _i\) of the matrix A have a negative real part or meet the condition that \(|\arg (\lambda _i)| > \frac{\beta \pi }{2},\, i=1,2,\dots ,n.\), then the equilibrium point of the fractional-order system is asymptotically stable. The theoretical foundation for the stability analysis conducted in this study is provided by this criteria, which offers the necessary and sufficient condition for assuring the stability of fractional-order systems.

Model formulation

Three important variables interact as described by the set of differential equations provided:

  • x(t): represents the concentration of a pollutant in a water body.

  • y(t): indicates the concentration of a microorganism or chemical agent involved in pollutant degradation.

  • z(t): denotes an additional interacting aspect like dissolved oxygen, a secondary contaminant, or another biological component.

$$\begin{aligned} \left\{ \begin{array}{ll} {x^{\prime } (t)} = k_3 z(t) + k_1 x(t) (a - x(t)) - k_2 y(t), \\ {y^{\prime } (t)} = k_4 x(t) (a - x(t)) + k_6 z(t) + k_5 y(t) (b - y(t)), \\ {z^{\prime } (t)} = k_7 x(t) - k_8 y(t). \\ \end{array} \right. \end{aligned}$$
(4)

The initial conditions for the proposed model are given below

$$\begin{aligned} x (0) = x_0,\,\,y (0) = y_0,\,\,z (0) = z_0. \end{aligned}$$
(5)

Where \(k_1\), \(k_2\), \(k_3\), \(k_4\), \(k_5\), \(k_6\), \(k_7\) and \(k_8\) are rate constants that govern different processes in the system. a and b are parameters that regulate the nonlinear interaction terms.

x(t) simulates the pollutant’s movement through the water, degradation brought on by chemical or biological reactions and interactions with other environmental elements. \(k_3 z(t)\) term suggests that the secondary factor z(t) contributes to the accumulation of the pollutant. The logistic growth term \(k_1 x(t) (a - x(t))\) indicates that the pollutant self-regulates as a result of limiting pollutant generation or natural dilution. \(k_2 y(t)\) denotes the pollutant’s elimination as a result of chemical reactions, microbiological breakdown, or sediment adsorption.

y(t) captures how microbial or chemical agents responsible for pollutant degradation evolve over time, influenced by pollutant levels and additional environmental factors. \(k_4 x(t) (a - x(t))\) denotes a logistic-type interaction where microbial growth is dependent on pollutant availability. \(k_6 z(t)\) implies that microbiological or chemical activity is also influenced by the secondary component z(t). \(k_5 y(t) (b - y(t))\) is another logistic term ensuring that microbial growth is limited by environmental constraints such as nutrient availability.

An external environmental component that depends on microbial activity and the presence of pollutants is simulated by z(t). \(k_7 x(t)\) suggests that the pollutant concentration either produces or influences the secondary factor. Microbial activity causes the secondary component to be consumed or diminished, as indicated by \(k_8 y(t)\).

The application of CFD to water pollution models is a significant advancement in environmental modeling, particularly for understanding and predicting pollutant behavior in aquatic ecosystems. In contrast to integer-order derivatives, the CFD captures the memory-dependent and non-local properties of systems, which are critical for accurately modeling complex environmental phenomena including persistence, degradation, and pollution transport. Since initial conditions may be described in terms of integer-order derivatives, which are frequently more understandable and simpler to test experimentally, the Caputo derivative is favored in real-world applications. This attribute is particularly significant in environmental modeling since initial contaminant concentrations and change rates are typically determined from actual data.

Table 1 A description of the parameters symbolized in the proposed system Eq. 4 and their values10.
Full size table

Now consider the FOWPM, which is nonlinear having parameter values (Table 1) and initial conditions10

$$\begin{aligned} \left\{ \begin{array}{ll} {}^CD_t^\beta \left[ {x (t)} \right] = 0.4 z(t) + 0.2 x(t) (10 - x(t)) - 0.3 y(t), \\ {}^CD_t^\beta \left[ {y (t)} \right] = 0.2 x(t) (10 - x(t)) + 0.3 z(t) + 0.3 y(t) (5 - y(t)), \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, 0 < \beta \leqslant 1 \\ {}^CD_t^\beta \left[ {z (t)} \right] = 0.4 x(t) - 0.3 y(t), \\ \end{array} \right. \end{aligned}$$
(6)

with initial settings

$$\begin{aligned} x (0) = 2,\,\,y (0) = 4,\,\,z (0) = 3. \end{aligned}$$
(7)

Where \({}^CD_t^\beta\) denotes the FD of order \(\beta\), typically defined in the Caputo sense.

Existence and uniqueness analysis

The theorem employs fixed-point theorem and FDEs based on Caputo derivatives to verify that the model’s solutions are well-defined and mathematically valid under certain conditions.

In order to prove this, we rephrase model Eq. 4 as follows in a simple way for easy understanding

$$\begin{aligned} \left\{ \begin{array}{ll} {}^CD_\ell ^\beta \left[ {x (\ell )} \right] = \textrm{X}_1 (\ell ,x ), \\ {}^CD_\ell ^\beta \left[ {y (\ell )} \right] = \textrm{X}_2 (\ell ,y ), \\ {}^CD_\ell ^\beta \left[ {z (\ell )} \right] = \textrm{X}_3 (\ell ,z ), \\ \end{array} \right. \end{aligned}$$
(8)

with the initial conditions Eq. 5. The CFD of order \(\beta\) is represented here by \({}^CD_\ell ^\beta\). Based on the findings of fixed point theory, we demonstrate that there is a unique solution to the FOWPM. We demonstrate the analysis for \(x(\ell )\); the other equations in the system Eq. 8 will follow suit. Consider

$$\begin{aligned} {}^CD_\ell ^\beta \left[ {x (\ell )} \right] = \textrm{X}_1 (\ell ,x ), \,\,\, \ell \in \left[ {0,\mathrm T} \right] , \,\,\, 0 < \beta \leqslant 1, \end{aligned}$$
(9)

with the initial setting

$$\begin{aligned} x (0) = x_0, \end{aligned}$$
(10)

where \(x \in {\Re }^n,\,\,T > 0\) and \(\textrm{X}_1:\left[ {0,\mathrm T} \right] \times {\Re }^n \times {\Re }^n \rightarrow {\Re }^n\) is continuous.

Using the norm \(\left\| . \right\|\), the Euclidean space with n dimensions is denoted as \({\Re }^n\).

Lemma 4.1

37 Let \(x \in C(\left[ {0,\mathrm T} \right] ;{\Re })\), the space of continuous functions \(x:\left[ {0,\mathrm T} \right] \rightarrow {\Re }\) equipped with the sub norm \(\left\| . \right\| _\infty\). Then, x is a solution to the initial value problems (IVPs) given by Eqs. 9and 10on the interval \(\left[ {0,\mathrm T} \right]\) if and only if it satisfies the corresponding Volterra integral equation (VIE).

$$\begin{aligned} x (\ell ) = x (0) + \frac{1}{{\Gamma (\beta )}}\int \limits _0^\ell {(\ell - \vartheta )^{\beta - 1} \textrm{X}_1 (\vartheta ,x )d\vartheta ,\,\,\,\,\forall \, \ell \in } \left[ {0,T} \right] . \end{aligned}$$
(11)

Theorem 4.2

(Existence theorem)35 Let \(\mathrm T^ * > 0\), \(P>0\), \(x_0 \in {\Re }\), and \(0 < \beta \leqslant 1\). Assuming that the mapping \(\textrm{X}_1: X \rightarrow \Re\) is continuous, we derive \(X: = \left\{ {\left( {\ell , x } \right) :\ell \in \left[ {0,\mathrm T^ * } \right] ,\,\,\left| {x - x_0 } \right| \leqslant P} \right\}\). \(Q: = \sup _{(\ell ,x,y,z) \in G} \left| \mathrm{X_1 (\ell ,x )} \right|\) is also defined and

$$\begin{aligned} \mathrm T = \left\{ \begin{array}{ll} \mathrm T^ *,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,\,Q = 0, \\ \min \left\{ \mathrm{T^ *,\left( {\frac{{P\Gamma (\beta + 1)}}{Q}} \right) ^{\frac{1}{\beta }} } \right\} ,\,\,\,\,\,\,\,otherwise. \\ \end{array} \right. \end{aligned}$$
(12)

The function \(x \in C\left[ {0,T} \right]\) may then be used to solve the IVP Eqs. 9and 10.

Proof

If \(Q = 0\) then \(\textrm{X}_1 (\ell ,x) = 0\,\,\,\forall \,(\ell ,x)\, \in \,\textrm{X}\). In this scenario, it is straightforward to verify through direct substitution that the constant function \(x:[0,T] \rightarrow \Re\), defined by \(x(\ell ) = x_0\), satisfies the problem under consideration. Hence, a solution exists in this case.

The set \(S: = \left\{ {x \in C[0,T]:\left\| {x - x_0 } \right\| \leqslant P} \right\}\) is defined accordingly. It is evident that S is a closed and convex subset of the space of continuous functions on [0, T], which constitutes a Banach space, given the Chebyshev norm. We show that Eqs. 9 and 10 map to Eq. 11, a VIE, for \(Q \ne 0\). As a result, S is a Banach space subset. This means that the set S is not empty because \(x_0 \in S\). We define the operator E on this set S.

$$\begin{aligned} (Ex)(\ell ): = x(0) + \frac{1}{{\Gamma (\beta )}}\int \limits _0^\ell {(\ell - \vartheta )^{\beta - 1} \textrm{X}_1 (\vartheta ,x)d\vartheta ,\,\,\,\,\forall \ell \in } \left[ {0,T} \right] . \end{aligned}$$
(13)

Thus, the Eq. 11 may be written using \(x=Ex\) and as a result, we need to proof that the operator E contains a fixed point. This can be achieved using Schauders Second Fixed Point Theorem (SSFPT). We begin by demonstrating that S has closure, which implies that \(Ex \in S\) is equivalent to \(x \in S\). In the case of \(0 \leqslant \ell _1 \leqslant \ell _2 \leqslant T\), we notice this

$$\begin{aligned} |(Ex)(\ell _1 ) - (Ex)(\ell _2 )| = \frac{1}{{\Gamma (\beta )}}|\int \limits _0^{\ell _1 } {(\ell _1 - \vartheta )^{\beta - 1} \textrm{X}_1 (\vartheta ,x)d\vartheta - \int \limits _0^{\ell _2 } {(\ell _2 - \vartheta )^{\beta - 1} \textrm{X}_1 (\vartheta ,x)d\vartheta } } | \end{aligned}$$
$$\begin{aligned} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,= \frac{1}{{\Gamma (\beta )}}|\int \limits _0^{\ell _1 } {[(\ell _1 - \vartheta )^{\beta - 1} - (\ell _2 - \vartheta )^{\beta - 1} ]\textrm{X}_1 (\vartheta ,x)d\vartheta + \int \limits _{\ell _1 }^{\ell _2 } {(\ell _2 - \vartheta )^{\beta - 1} \textrm{X}_1 (\vartheta ,x)d\vartheta } } | \end{aligned}$$
$$\begin{aligned} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\leqslant \frac{Q}{{\Gamma (\beta )}}\left( {\int \limits _0^{\ell _1 } {|(\ell _1 - \vartheta )^{\beta - 1} - (\ell _2 - \vartheta )^{\beta - 1} |d\vartheta + \int \limits _{\ell _1 }^{\ell _2 } {(\ell _2 - \vartheta )^{\beta - 1} d\vartheta } } } \right) . \end{aligned}$$

On the right side of the previous inequality, the value of the second integral portion is \((\ell _2 - \vartheta )^\beta\). For the part of first integral, we have to consider the two cases \(\beta < 1\), \(\beta =1\), separately. When \(\beta =1\), the integral equals zero. For \(\beta < 1\), implies \((\ell _1 - \vartheta )^{\beta - 1} \geqslant (\ell _2 - \vartheta )^{\beta - 1}\).

Thus,

$$\begin{aligned} \begin{array}{ll} \int \limits _0^{\ell _1 } {|(\ell _1 - \vartheta )^{\beta - 1} - (\ell _2 - \vartheta )^{\beta - 1} |d\vartheta = \int \limits _0^{\tau _1 } {[(\ell _1 - \vartheta )^{\beta - 1} - (\ell _2 - \vartheta )^{\beta - 1} ]d\vartheta } } \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = (\ell _1 \beta - \ell _2 \beta ) + (\ell _2 - \ell _1 )^\beta \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \leqslant (\ell _2 - \ell _1 )^\beta . \\ \end{array} \end{aligned}$$

When these results are combined, we get

$$\begin{aligned} |(Ex)(\ell _1 ) - (Ex)(\ell _2 )| \leqslant \frac{{2Q}}{{\Gamma (\beta + 1)}}(\ell _2 - \ell _1 )^\beta . \end{aligned}$$
(14)

The expression at the right side of Eq. 14 convergence occurs to zero in either case when \(\ell _2 \rightarrow \ell _1\). Consequently, Ex is a continuous function since x(0) is continuous. It is equally valid for \(x \in S\) and \(\,\ell \in [0,T]\).

$$\begin{aligned} |(Ex)(\ell _1 ) - x(0)| = \frac{1}{{\Gamma (\beta )}}|\int \limits ^\ell {(\ell - \vartheta )^{\beta - 1} \textrm{X}_1 (\vartheta ,x)d\vartheta |} \end{aligned}$$
$$\begin{aligned} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \leqslant \frac{Q}{{\Gamma (\beta + 1)}}\ell ^\beta \leqslant \frac{Q}{{\Gamma (\beta + 1)}}T^\beta \end{aligned}$$
$$\begin{aligned} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \leqslant \frac{Q}{{\Gamma (\beta + 1)}} \cdot \frac{{P\Gamma (\beta + 1)}}{Q}\, = \,P. \end{aligned}$$
(15)

Thus, we have \(Ex \in S\) if \(x \in S\). In particular, the set S is mapped onto itself. Next, we must demonstrate the relative compactness of \(E(S): = \left\{ {Es:s \in S} \right\}\). In order to accomplish this, the Arzel’a-Ascoli Theorem (AAT) is used. To establish that E(S) is a uniformly bounded set, let’s look at \(f \in E(S)\). This is evident for each \(\ell \in [0,T]\).

$$\begin{aligned} \begin{array}{ll} |f(\ell )| = |(Ex)(\ell )| \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, \leqslant \left\| {x(0)} \right\| _\infty + \frac{1}{{\Gamma (\beta )}}\int \limits _0^\ell {(\ell - \vartheta )^{\beta - 1} |\textrm{X}_1 (\vartheta ,x)|d\vartheta } \\ \,\,\,\,\,\,\,\,\,\,\,\,\, \leqslant \left\| {x(0)} \right\| _\infty + \frac{1}{{\Gamma (\beta + 1)}}QT^\beta \, \leqslant \,\left\| {x(0)} \right\| _\infty + P. \\ \end{array} \end{aligned}$$

This is the boundedness attribute that is required. The property of equicontinuity can be easily derived from Eq. 14. In the situation \(\beta \leqslant 1\), we demonstrated \(0 \leqslant \ell _1 \leqslant \ell _2 \leqslant T\) that

$$\begin{aligned} |(Ex)(\ell _1 - \ell _2 )| \leqslant \frac{{2Q}}{{\Gamma (\beta + 1)}}(\ell _2 - \ell _1 )^\beta . \end{aligned}$$

When the Triangular Inequality and Mean Value Theorem are applied, we get

$$\begin{aligned} \begin{array}{ll} |(Ex)(\ell _1 ) - (Ex)(\ell _2 )| \leqslant \frac{{2Q}}{{\Gamma (\beta + 1)}}(\ell _2 - \ell _1 )^\beta \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{2Q}}{{\Gamma (\beta + 1)}}(\ell _2 - \ell _1 )^\beta \,. \\ \end{array} \end{aligned}$$

Therefore, if \(\,|\ell _1 - \ell _2 |\, < \,\zeta\), we get

$$\begin{aligned} |(Ex)(\ell _1 ) - (Ex)(\ell _2 )| \leqslant Q^{\prime}&\zeta + \frac{{2Q}}{{\Gamma (\beta + 1)}}\zeta ^\beta T^\beta . \end{aligned}$$

x(0) is consistently continuous in the interval [0, T]. The equicountinous set E(S) can be observed since the right-hand assertion is independent of \(\ell _1\), \(\ell _2\), and x. Since the preceding theorem, known as the AAT, indicates that E(S) is compact relatively, the SSFPT asserts that there is a fixed point that occurs in E in either case. The necessary solution for Eqs. 9 and 10 is the fixed point.

We now discuss the uniqueness findings. We start by noting that operator E possesses the following property. Consequently, let \(x_1,x_2 \in C[0,T] \subset [0,\ell ]\) while there is a constant \(\lambda > 0\) that is independent of \(\ell\), \(x_1\), and \(x_2\) such that \(|\textrm{X}_1 (\ell ,x_1 ) - \textrm{X}_1 (\ell ,x_2 )| \leqslant \lambda |x_1 - x_2 |\) for all \(|\textrm{X}_1 (\ell ,x_1 ) - \textrm{X}_1 (\ell ,x_2 )| \leqslant \lambda |x_1 - x_2 |\). Then, we get

$$\begin{aligned} \begin{array}{ll} \left\| {Ex_1 - Ex_2 } \right\| _{L_\infty [0,\ell ]} = \frac{1}{{\Gamma (\beta )}}\mathop {\sup }\limits _{0 \leqslant \alpha \leqslant \ell } |\int \limits _0^\alpha {(\alpha - \vartheta )^{\beta - 1} \left[ {\textrm{X}_1 (\vartheta ,x_1 ) - \textrm{X}_1 (\vartheta ,x_2 )} \right] d\vartheta } | \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \leqslant \frac{\lambda }{{\Gamma (\beta )}}\mathop {\sup }\limits _{0 \leqslant \alpha \leqslant \ell } |\int \limits _0^\alpha {(\alpha - \vartheta )^{\beta - 1} |x_1 (\vartheta ) - x_2 (\vartheta )|d\vartheta } | \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \leqslant \frac{\lambda }{{\Gamma (\beta )}}\left\| {x_1 - x_2 } \right\| _{L_\infty [0,\ell ]} \mathop {\sup }\limits _{0 \leqslant \alpha \leqslant t} |\int \limits _0^\alpha {(\alpha - \vartheta )^{\beta - 1} d\vartheta } | \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \leqslant \frac{\lambda }{{\Gamma (\beta )}}\left\| {x_1 - x_2 } \right\| _{L_\infty [0,\ell ]} \mathop {\sup }\limits _{0 \leqslant \alpha \leqslant \ell } |(\alpha - \vartheta )^\beta \mathop |\nolimits _0^\alpha | \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{\lambda }{{\Gamma (\beta + 1)}}\left\| {x_1 - x_2 } \right\| _{L_\infty [0,\ell ]}. \\ \end{array} \end{aligned}$$

\(\square\)

Theorem 4.3

(Uniqueness theorem)35 Assume that \(x (0) \in {\Re }\), \(P>0\), and \(\mathrm T^*> 0\). Additionally, consider \(q = \lceil \beta \rceil\) and \(0 < \beta \leqslant 1\). For the second variable, let \(\textrm{X}_1:X \rightarrow {\Re }\) be a continuous mapping that meets the Lipschitz conditions, which are as follows:

$$\begin{aligned} \left| {\textrm{X}_1 (\ell ,x_1 ) - \textrm{X}_1 (\ell ,x_2 )} \right| \leqslant \lambda \left| {x_1 - x_2 } \right| , \end{aligned}$$
(16)

for certain constants \(\lambda >0\), \(x_1\) and \(x_2\) are independent of \(\ell\). Then, there is a unique solution \(x \in C\left[ {0,\mathrm T} \right]\) for the IVPs.

Proof

According to above theorem, the IVPs under consideration admit a solution. Now, we proceed to establish uniqueness. To do so, We utilize the operator E as defined in Eq. 13 and note that it binds the nonempty, convex and closed set \(S = \left\{ {x \in C[0,T]:\left\| {x - x_0 } \right\| _\infty \leqslant P} \right\}\) to itself.

To demonstrate that E has a unique fixed point, we apply Weissingers Fixed Point Theorem. Let \(j \in N_{0\,},\,\,t \in [0,\,T]\) and \(x_1,\,x_2 \in S\). Using the Chebyshev norms on the closed interval [0, T], we find that

$$\begin{aligned} {\left\| { {E}^j {x} - {E}^j {x}^{\prime }}\right\| }_\infty \leqslant {\left\| {x - {x}^{\prime } } \right\| }_\infty \left[ {\frac{{\lambda ^j }}{{\Gamma (\beta j + 1)}}} \right] . \end{aligned}$$

Put \(\alpha _j = \lambda ^j /\Gamma (\beta j + 1)\) in the definition. The convergence of the series \(\sum \limits _{j = 0}^\infty {\alpha _j }\) is sufficient to apply the theorem. It is clear that a power series is used to define the Mittag-Leffler function \(E_\beta ^*\), and that the series convergence ensures the outcome.

To possess global convergence of order \(O\!\left( h^{\min \{2,\,1+\beta \}}\right)\), where \(h\) is the time step size and \(\beta\) is the fractional order. Specifically, for \(\beta \in (0,1)\), the error bound satisfies

$$\Vert u(t_n) - u_n\Vert \le C h^{1+\beta }, \quad t_n = n h,$$

with \(C\) being a constant depending on the Lipschitz constant of the governing system. Thus, the proof is complete. \(\square\)

The proof of existence and uniqueness theorems for the FOWPM are crucial to the proposed framework’s mathematical reliability and constancy. According to the uniqueness characteristic, the system generates a single, deterministic solution for a specific set of initial conditions. The model is reliable for environmental planning and decision-making because of this feature, which enables constant estimations of pollution transmission and degradation. The existence of the solution verifies that the model may be applied to real-world problems by demonstrating that it can be resolved in practical situations. This suggests that the fractional-order formulation is capable of accurately representing and assessing complex pollution processes in aquatic environments in addition to being theoretical.

Stability analysis

In order to understand the long-term behavior of dynamic systems, stability analysis is essential. In contrast to integer-order systems, FDs lead to distinct stability conditions in fractional-order systems. A three-variable fractional-order system with nonlinear interactions between the state variables is examined for stability in this paper.

We can get the equilibrium points of water pollution model by setting the right-hand side of Eq. 4 to zero.

$$\begin{aligned} x^{\prime } (t) = y{\prime } (t) = z{\prime } (t) = 0. \end{aligned}$$

The obtained equilibrium points are \(\left\{ x\rightarrow 0,y\rightarrow 0,z\rightarrow 0\right\}\) and

$$\begin{aligned} x\rightarrow \frac{k_8 (a k_8 (k_3 k_4-k_1 k_6)+b k_3 k_5 k_7+k_2 k_6 k_7)}{-k_1 k_6 k_8{^2}+k_3 k_4 k_8{^2}+k_3 k_5 k_7{^2}},y\rightarrow \frac{k_7 (a k_8 (k_3 k_4-k_1 k_6)+b k_3 k_5 k_7+k_2 k_6 k_7)}{-k_1 k_6 k_8{^2}+k_3 k_4 k_8{^2}+k_3 k_5 k_7{^2}},\\ z\rightarrow \frac{k_7 \left( k_1 k_5 k_8 (b k_8 -a k_7)+k_2 \left( k_4 k_8{^2}+k_5 k_7{^2}\right) \right) (a k_8 (k_3 k_4-k_1 k_6)+b k_3 k_5 k_7+k_2 k_6 k_7)}{\left( -k_1 k_6 k_8{^2}+k_3 k_4 k_8{^2}+k_3 k_5 k_7{^2}\right) ^2}. \end{aligned}$$

The Jacobian matrix \(J^{\prime }\) for the model Eq. 4 can be found as

$$\begin{aligned} J = \left[ {\begin{array}{*{20}c} k_{1}a-2k_{1}x(t) & -k_{2} & k_{3} \\ k_{4}a-2k_{4}x(t) & k_{5}b-2k_{5}y(t) & k_{6} \\ k_{7} & -k_{8} & 0 \\ \end{array} } \right] . \end{aligned}$$

Now, we can get the equilibrium points of FOWPM by setting the right-hand side of Eq. 6 to zero.

$$\begin{aligned} {}^CD_t^\beta x (t) = {}^CD_t^\beta y (t) = {}^CD_t^\beta z (t) = 0. \end{aligned}$$
(17)

To determine the equilibrium points for the system of Eq. 6, we set \(x^*\), \(y^*\), \(z^*\) such that:

$$\begin{aligned} \begin{array}{ll} 0 = 0.4 z^*(t) + 0.2 x^*(t) (10 - x^*(t)) - 0.3 y^*(t), \\ 0 = 0.2 x^*(t) (10 - x^*(t)) + 0.3 z^*(t) + 0.3 y^*(t) (5 - y^*(t)), \\ 0 = 0.4 x^*(t) - 0.3 y^*(t). \\ \end{array} \end{aligned}$$

The equilibrium points are obtained by solving these equations. There is always a solution to the trivial equilibrium at (0, 0, 0). Another equilibrium point is \((x^*=4.8, y^*=6.4, z^*=-7.68)\).

The Jacobian matrix J is computed for the model in consideration as

$$\begin{aligned} J = \left[ {\begin{array}{*{20}c} 2-0.4x(t) & -0.3 & 0.4 \\ 2-0.4x(t) & 1.5-0.6y(t) & 0.3 \\ 0.4 & -0.3 & 0 \\ \end{array} } \right] . \end{aligned}$$

Evaluating at (0, 0, 0):

$$\begin{aligned} J = \left[ {\begin{array}{*{20}c} 2 & -0.3 & 0.4 \\ 2 & 1.5 & 0.3 \\ 0.4 & -0.3 & 0 \\ \end{array} } \right] \end{aligned}$$

The Jacobian matrix at (0, 0, 0) has the following eigenvalues:

\(\omega _1=1.79371 + 0.791336i, \,\, \omega _2=1.79371 - 0.791336i, \,\, \omega _3=-0.0874179\).

Evaluating at \((x^*=4.8, y^*=6.4, z^*=-7.68)\):

$$\begin{aligned} J^* = \left[ {\begin{array}{*{20}c} 0.08 & -0.3 & 0.4 \\ 0.08 & -2.34 & 0.3 \\ 0.4 & -0.3 & 0 \\ \end{array} } \right] \end{aligned}$$

The following are the eigenvalues that correspond to the matrix \(J^{*}\):

\(\gamma _1=-2.29785, \,\, \gamma _2=-0.401786, \,\, \gamma _3=-0.363934\).

At the equilibrium point, the system in discussion is locally asymptotically stable since all of the eigenvalues are negative. This suggests that through minimal perturbations associated with the equilibrium, the system will ultimately return to its steady state. Therefore, in these circumstances, the provided fractional-order model shows local stability..

At the conclusion of the stability study, the FOWPM’s resistance is confirmed, and its potential as an effective tool for environmental research is highlighted. Further advances in modeling, monitoring, and controlling pollution in aquatic ecosystems will be facilitated by this study’s improved comprehension of the conditions necessary for system stability.

Model solution using PC scheme

We now discuss the PC approach, which is a generalization of the classical trapezoidal rule. The PC technique operates using a two-step iterative process. The predictor phase creates a computationally efficient estimate by applying an explicit formula to obtain an initial approximation of the solution. This approximation is subsequently improved by the corrector phase using an implicit formula, increasing the solution’s accuracy. For handling nonlinear and memory-dependent systems, like those seen in the model of water pollution, this iterative combination implies that the approach is precise and computationally realistic. This approach is very versatile and suitable for complicated and dynamic environmental settings since it can handle different orders of FDs and system nonlinearities. Here, we employ the PC approach to determine the predicted model’s solution34.

Let us examine the FDE of preferred model

$$\begin{aligned} {}^CD_t^\beta \left[ {x (t)} \right] = \textrm{X}_1 (t,x ),\,\,\,t \in [0,\mathrm T],\,\,\,0 < \beta \leqslant 1, \end{aligned}$$
(18)
$$\begin{aligned} x (t) = x_0. \end{aligned}$$
(19)

Let us consider a uniform grid \(\left\{ {t_s = sh:\,s = \, - r,\,\, - r + 1,\, - r + 2,...,\, - 1,\,0,\,1,...\,\,\mathbb {N}} \right\}\) and \(\mathbb {N}h = T\), where m are integers and \(\mathbb {N}\) is the set of natural number.

$$\begin{aligned} x_h (t_m ) = x_0,\,\,m = - r,\, - r + 1,\, - r + 2...,\, - 1,\,0. \end{aligned}$$
(20)

Let us assume that the approximations have already been computed,

\(x_h (t_m ) \approx x (t_m ),\,(m = - r,\, - r + 1,\, - r + 2...,\, - 1,\,0,\,1,...,\,s)\) and we wish to compute \(x_h (t_{s + 1} )\) using the VIE, which is equal to Eq. 18 and Eq. 19.

$$\begin{aligned} x (t_{s + 1} )\, = x (0) + \frac{1}{{\Gamma (\beta )}}\int _0^{t_{s + 1} } {(t_{s + 1} - \vartheta )^{\beta - 1} \textrm{X}_1 (\vartheta ,x (\vartheta ))d\vartheta }. \end{aligned}$$
(21)

For \(x (t_s )\) in Eq. 21, we make use of approximations \(x_h (t_s )\). Moreover, Eq. 21 uses the product trapezoidal quadrature formula to evaluate the integral. Therefore, the corrector formula is

$$\begin{aligned} x_h (t_{s + 1} )\,\, = \,\,x (0)\,\, + \,\,\frac{{h^\beta }}{{\Gamma (\beta + 2)}}\,\,\textrm{X}_1 (t_{s + 1},x_h (t_{s + 1} ))\, + \,\,\frac{{h^\beta }}{{\Gamma (\beta + 2)}}\,\,\sum \limits _{m = 0}^s {u_{m,s + 1} } \,\,\textrm{X}_1 (t_m,x_h (t_m )), \end{aligned}$$
(22)

where

$$\begin{aligned} u_{m,s + 1} = \left\{ \begin{array}{ll} s^{ 1 + \beta } - (s + 1)^\beta (r - \beta ),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,m = 0 \\ (s - m)^{1 + \beta } + (s + 2 - m )^{1 + \beta } - 2\,s +1 - m)^{1 + \beta },\,\,\,\,\,1 \leqslant m \leqslant s \\ 1,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,m = s + 1.\, \\ \end{array} \right. \end{aligned}$$
(23)

The term \(x_h (t_{s + 1} )\) which is unknown appears on both sides of Eq. 22. Because of the nonlinearity of \(\textrm{X}_1\), it is not possible to solve Eq. 22 explicitly for \(x_h (t_{s + 1} )\). Therefore, we substitute an estimate \(x_h ^p (t_{s + 1} )\), known as the predictor, for the term \(x_h (t_{s + 1} )\) on the right-hand side. Eq. 22 evaluates the predictor term using the product rectangle rule.

$$\begin{aligned} x_h ^p (t_{s + 1} )\, = x (0) + \frac{1}{{\Gamma (\beta )}}\sum \limits _{m = 0}^s {v_{m,r + 1} } \textrm{X}_1 (t_m,x_h (t_m )), \end{aligned}$$
(24)

where

$$\begin{aligned} v_{m,s + 1} = \frac{{h^\beta }}{\beta }((s + 1 - m)^\beta - (s - m)^\beta ). \end{aligned}$$
(25)

Accordingly, the corrector formulas for every system of equations Eq. 6 derived from the computations above are

$$\begin{aligned} \begin{array}{ll} x_h (t_{s + 1} )\,\, = \,\,x (0)\,\, + \,\,\frac{{h^\beta }}{{\Gamma (\beta + 2)}}\,\,\textrm{X}_1 (t_{s + 1},x_h (t_{s + 1} )) + \,\,\frac{{h^\beta }}{{\Gamma (\beta + 2)}}\,\,\sum \limits _{m = 0}^s {u_{m,s + 1} } \,\,\textrm{X}_1 (t_m,x_h (t_m )), \\ y_h (t_{s + 1} )\,\, = \,\,y (0)\,\, + \,\,\frac{{h^\beta }}{{\Gamma (\beta + 2)}}\,\,\textrm{X}_2 (t_{s + 1},y_h (t_{s + 1} ))\,\, + \,\,\frac{{h^\beta }}{{\Gamma (\beta + 2)}}\,\,\sum \limits _{m = 0}^s {u_{m,s + 1} } \,\,\textrm{X}_2 (t_m,y_h (t_m )), \\ z_h (t_{s + 1} )\,\, = \,\,z(0)\,\, + \,\,\frac{{h^\beta }}{{\Gamma (\beta + 2)}}\,\,\textrm{X}_3 (t_{s + 1},z_h (t_{s + 1} ))\,\, + \,\,\frac{{h^\beta }}{{\Gamma (\beta + 2)}}\,\,\sum \limits _{m = 0}^s {u_{m,s + 1} } \,\,\textrm{X}_3 (t_m,z_h (t_m )). \\ \end{array} \end{aligned}$$
(26)

Likewise, the predictor terms are

$$\begin{aligned} \begin{array}{ll} x_h ^p (t_{s + 1} )\, = x (0) + \frac{1}{{\Gamma (\beta )}}\sum \limits _{m = 0}^s {v_{m,s + 1} } \textrm{X}_1 (t_m,x_h (t_m )), \\ y_h ^p (t_{s + 1} )\, = y (0) + \frac{1}{{\Gamma (\beta )}}\sum \limits _{m = 0}^s {v_{m,s + 1} } \textrm{X}_2 (t_m,y_h (t_m )), \\ z_h ^p (t_{s + 1} )\, = z(0) + \frac{1}{{\Gamma (\beta )}}\sum \limits _{m = 0}^s {v_{m,s + 1} } \textrm{X}_3 (t_m,z_h (t_m )). \\ \end{array} \end{aligned}$$
(27)
Fig. 1
figure 1

PC solution of x(t) for different fractional-order \(\beta\).

Full size image
Fig. 2
figure 2

y(t) PC solution for a different fractional-order \(\beta\).

Full size image
Fig. 3
figure 3

PC solution of z(t) with a distinct fractional-order \(\beta\).

Full size image

Results and discussion

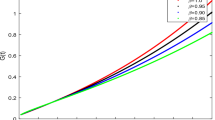
We used the PC approach to solve fractional-order DEs in order analyse the behaviour of the system. The fractional-order derivatives in the range \(0 < \beta \leqslant 1\) to observe the impact of memory effects on pollutant concentration were used in the system parameters, which were selected based on standard environmental degradation models. We got the solutions Eqs. 26 and 27 of the considered model using mathematica code and having the stepsize value h=0.01. Figures 1, 2 and 3 show the time evolution of pollutant concentration x(t), degrading agent y(t) and the interaction factor z(t) under various fractional-orders \(\beta\). As shown in Fig. 1, x(t) is gradually increases as a result of chemical or microbial degradation, which is impacted by \(k_2y(t)\) and nonlinear interactions with available capacity \(a-x(t)\). As it reacts to pollutant levels, Fig. 2 shows an initial growth phase of y(t), after which it either stabilizes or oscillates based on system characteristics. z(t) exhibits memory-dependent behaviour in fractional situations, as shown in Fig. 3, and varies according to the equilibrium between pollutant availability and degrading effects. The system exhibits standard degradation dynamics and rapidly approaches equilibrium for \(\beta =1\) (classical case). The system shows prolonged memory effects for \(\beta <1\), which might lead to slower convergence and possibly oscillatory behaviour before stabilization. Pollutant dissipation is strongly influenced by past conditions, as evidenced by the more apparent nonlocal effects for lower levels of \(\beta\). The slower convergence shown at lower fractional-order \(\beta\) suggests that contaminants are more persistent in the environment, which is indicative of aquatic systems memory and inherited impacts. This suggests that in actual pollution situations, pollutants would not leave water bodies as rapidly but instead stay there because of intricate relationships like slow diffusion, delayed biodegradation, or sediment absorption. Accordingly, fractional-order modeling, as opposed to classical models, offers a more accurate depiction of pollutant persistence. This emphasizes how crucial it is to take fractional dynamics into account when evaluating pollution control plans and long-term environmental hazards.

By including memory-dependent effects, the fractional model expands on traditional integer-order solutions, improving the predictive power for slow-reacting pollutants, non-exponential decay behaviours that are consistent with experimental observations, and a more accurate depiction of real-world pollutant degradation processes. The ability of the fractional-order model to properly represent the complex linkages in pollutant degradation shows that FDs offer a more realistic and extended framework than integer-order models. The simulation results highlight the need for enhanced supervision and prompt responses by demonstrating how fractional dynamics capture long-term pollution persistence. In order to effectively reduce pollution risks and protect ecosystems and public health, these insights assist policymakers in developing sustainable water management measures, such as enhanced wastewater treatment, more stringent industrial rules, and early-warning systems. Fractional-order has an important role in transient reactions, equilibrium behavior, and system stability. In order to improve environmental management methodologies, future studies can include experimental validation and degradation parameter adjustment.

Conclusion

In aquatic ecosystems, this FOWPM provides a more realistic framework for understanding the dynamic interactions of pollutants, microbial degradation, and environmental factors. Since integer-order models fail to account for memory effects, anomalous diffusion, and long-term persistence of pollutants, FDs are introduced to the model to assist in it do so. This problem was solved using the PC Method, a numerical technique designed specifically for FDEs. The approach is a helpful tool for researching environmental models since it can effectively handle fractional-order nonlinear systems. It offers a method for solving FDEs that is computationally effective without being excessively complex. Applications for this concept are numerous, and it offers insightful information for pollution control, policymaking, and environmental monitoring. It offers researchers and decision-makers with a potent tool to more accurately anticipate pollutant behavior and formulate efficient remediation strategies. Future research could expand the model to incorporate stochastic implications, multi-pollutant systems, or the effects of climate change to gain a deeper understanding of aquatic ecosystems under human activity.

This is particularly important in actual pollution instances where contaminants build up in sediments, degrade gradually, or decline non-exponentially:

  • Predicting the permanence of contaminants and creating more effective treatment methods are two aspects of managing water quality.

  • Implementing chemical or microbiological techniques to enhance the breakdown of pollutants is part of optimizing wastewater treatment.

  • The objective of climatic and environmental impact studies is to comprehend the behavior of pollutants over the long term under changing environmental conditions.

The proposed model offers significant advancement in the modeling of aquatic pollution and there are a number of encouraging directions for further research. A more thorough grasp of real-world situations will result from expanding the model to include multi-pollutant systems, especially those affected by seasonal and temperature variations. To verify the model’s applicability and dependability in real-world scenarios, experimental validation utilizing actual water quality data is crucial. Additionally, examining the best control methods for pollution reduction will assist in converting these discoveries into workable plans, allowing for improved aquatic ecosystem management.