Real time SOC estimation for Li-ion batteries in Electric vehicles using UKBF with online parameter identification

Abstract

In the recent era, Lithium ion batteries plays a significant role in EV industry due to their high specific energy density, power density, low self-discharge rate, and prolonged lifespan. Modeling the battery precisely and estimating its State of Charge with great precision is essential to improve the performance of the lithium-ion batteries. Though numerous methods has been proposed for estimating the SOC, accurate estimation approach is not proposed yet since all these approaches consider the discrete-time dynamics of the battery. Hence in this proposed approach, the implementation of Thevenin 2RC battery model in conjunction with the Unscented Kalman Bucy Filter (UKBF) for SOC estimation is suggested. Thevenin 2RC battery model is used to captures the nonlinear relationship between the battery’s voltage, current, and SOC. The UKBF is then used to estimate the SOC by fusing the battery model with noisy measurements of the battery’s voltage and current. The UKBF is able to handle the nonlinearity of the battery model and the noise in the measurements, resulting in a more accurate estimate of the SOC by capturing the continuous-time dynamics of the battery. The model is simulated in Matlab Simulink. With similar covariance noise and measurement noise taken into consideration, the battery’s SOC is estimated using the EKF, UKF, and UKBF. The performance comparison indicate that the UKBF approach provides an accurate estimation of the SOC, with a significantly lower RMSE of 0.003276.

Introduction

The automotive industry is increasingly recognizing the importance of electrification and low-carbon technology as a response to the growing energy consumption and adverse environmental impacts¹. The issues with the restricted driving range in contemporary electric vehicles and the variable power generation of renewable energy sources can be adequately resolved by the progress of sophisticated and dependable electrochemical energy storage technologies. The electric vehicle sector extensively utilises LIB because of its exceptional attributes, including high power and energy density, low self-discharge rate, and environmental durability². Additionally, they do not include environmentally harmful substances such as mercury, cadmium, and lead in their internal components¹.

The main challenges that persistently afflict electric vehicles are excessive charging and discharging. These issues not only lead to substantial battery overheating but also have adverse impacts on battery longevity and the potential to trigger thermal runaway². Moreover, the economic viability of the energy storage facility is greatly influenced by the deterioration of the batteries, leading to extra costs for battery energy storage systems (BESS). Battery management systems, often known as BMS, are control circuits responsible for overseeing and controlling the charging and discharging processes of batteries. The primary purpose of the BMS is to oversee the battery’s current, temperature, and voltage, as well as the environmental conditions. Additionally, it is responsible for forecasting the battery’s state of charge, health, energy, and power. The calculation of the Remaining Useful Life (RUL) of a battery and the management of its temperature conditions are crucial functions of a battery³. Figure 1 illustrates the schematic representation of the BMS. The estimation of SOC is of utmost importance among all the functions⁴. The SOC is determined by the US Advanced Battery Consortium (USABC) as the ratio of the battery’s remaining capacity to its rated capacity under particular conditions⁵.

Fig. 1

Various functions of battery management system.

Numerous methods have been proposed by the researchers with the objective of estimating the SOC with higher accuracy, namely the Coulomb counting method, lookup table method, model-based approaches, filler-based, data, and hybrid methods¹. The conventional SOC estimation approach is the CC method and look up table method. In the CC method, SOC is determined by integrating discharge current over time. The major limitation of this method is that it requires accurate initial SOC for the precise estimation of LIBs SOC. Look up the table method estimates SOC using reference voltage. Furthermore, this approach is not strongly favored in EV applications as it is limited to laboratory testing purpose⁶.

An innovative model-based methodology was developed to overcome the constraints of conventional techniques, which require a comprehensive knowledge of battery properties including electrolytic reaction, solid-phase diffusion, polarization, and cathode-anode behaviors. Previously suggested model-based approaches include Empirical, Equivalent Circuit (ECM), and Electrochemical Models. Empirical model includes Shepherd, Unnewehr and Nerst models. ECM model includes R_int, Partnership for a New Generation of Vehicles (PNGV) model, Thevenin model and General Non-Linear (GNL) model. Among all model based approaches ECM and Electrochemical models are mostly preferred. By employing only the most basic electrical components—such as resistances, which stand in for both inner and diffusion resistance, and capacitors, which illustrate the effects of capacitive diffusion in a cell—the ECM seeks to replicate the characteristics of a cell. The electrochemical model employs chemical equations to simulate the diffusion, intercalation, and kinetics of a cell^7,8,9,10. The comparison of various model based approaches with their merits and demerits proposed are listed in Table 1.

Table 1 Comparison of various model based approaches to estimate SOC of LIB.

Lately, researchers have been primarily concerned with Kalman filter-based SOC estimation and black box model-based estimation¹¹. In¹², the author proposed SOC estimation using various machine learning algorithms, including SVM, GPR, and ANN. The SOC estimation using deep learning approaches, namely, LSTM, GRU, and BiLSTM, is proposed in¹³. Though data based approaches have higher benefits, they also possess drawbacks. The generalization of a data-based approach in real-time scenarios is highly complex. The data-based approaches are highly affected by the outliers present in the data. Improper selection of hyper parameters for ML and DL algorithms and selection of non-correlated input parameters with the output SOC can also affect the estimation accuracy¹⁴.

Unlike traditional and data-based methods, state space equation-based models for SOC estimation that do not depend on starting SOC or large amounts of training data are proposed. Therefore, they possess a high level of responsibility and adaptability¹⁵. Kalman, H infinity and particle filters are popular within filter-based techniques^16,17. In¹⁸, particle filter-based SOC estimation is proposed as it can handle Gaussian noise and system nonlinearity. The demerit of this approach is the occurrence of particle diversity during pre-sampling that reduces the estimation accuracy. The different categories of Kalman filter-based approaches, namely, Extended KF (EKF), Adaptive EKF, Unscented KF, Dual EKF, and Sigma point KF, have been proposed for SOC estimation of LIBs¹. The EKF improves SOC estimation but ignores higher-order elements and requires trial-and-error noise covariance selection. Its linearization and convergence stability could be better¹⁹. The Cubature KF solves high-dimensional nonlinear system filtering efficiently. This approach uses cubature point and state vector linearity. A disadvantage of CKF over EKF is its higher cost. CKF cannot simultaneously identify parameters and estimate state²⁰. A Sigma point KF was suggested to accurately estimate SOC in third-order nonlinear systems. Square-Root KF avoids the Jacobian matrix. This alternative uses more sigma points generated by Sterling interpolation which leads to rounding issues^21,22. The UKF employs a deterministic selection of sigma points and applies nonlinear transformations to them. The transformed points have mean and covariance matrix values that are precise up to the second order of the Taylor series expansion²³. In²⁴, Adaptive Strong Tracking Square-Root Extended Kalman Filter (ASTSEKF) for recursive correction, denoising, and optimizing the state of charge (SOC) estimation of lithium-ion batteries in electric vehicles has been proposed to deal with high battery nonlinearity. Hybrid approach such as variational epoch selector for a multi-layered long short-term memory network with an adaptive weighted extended Kalman filter (LSTM-AWEKF), long-short-term memory-squared gain EKF (SGEKF) and long-short-term memory-weighted fading extended Kalman filtering (LSTM-WFEKF) for estimating SOC with minimized fluctuation and error is proposed in^25,26,27,28.

By analyzing the literatures proposed earlier it is clear that, EKF and AEKF requires linearinsation of non-linear model and fails to handle non – guassian distribution. Sigma point Kalman filter generates discretization errors during estimation and Square root Kalman filter requires square root matrix operations. Hybrid approaches has better performance but they increases the computational complexity. In addition, all the proposed filters are designed for discrete-time systems, requiring discretization of continuous-time models for EV application. Hence, in this proposed work, Unscented Kalman Bucy Filter (UKBF) based SOC estimation technique is proposed. Unlike other filters, UKBF is specially designed for continuous-time systems and hence avoids discretization error. It has the ability to handle nonlinearities without linearization and its flexibility in handling non-Gaussian distributions without high computational complexity making the system suitable for real world application.

The article has five sections, including an introduction. The second section explains 2RC battery modeling. Section three analyses the UKBF in depth. Analysis of the simulation and findings is conducted in part 4, while the conclusion is presented in Sect. 5.

Methodology

Thevenin 2RC-ECM battery modeling

Battery modeling is crucial in estimating the SOC. Battery modeling refers to the process of creating a mathematical representation of a battery, taking into account its internal structure and the way it charges and discharges²⁹. Figure 2 depicts ECM-Kalman filter SOC estimation.

Fig. 2

Pictorial representation of ECM battery modeling and Kalman filter-based SOC estimation.

Fig. 3

Classification of Battery modelling²⁹.

Equivalent circuit modeling offers a pragmatic approach by portraying the battery as an electrical network consisting of passive components. The components mentioned, such as resistors, capacitors, and ideal voltage sources, accurately represent the fundamental traits of the battery’s behavior. Equivalent circuit modeling allows engineers and researchers to optimize battery designs, increase performance, and extend battery life by correctly mimicking the battery’s behavior in various operating circumstances. Recent proposals for ECM based on fractional order models do away with the need for additional RC elements^30,31,32. IOECMs continue to be a viable and dependable option for numerous applications because of their more straightforward mathematical representation, reduced computational cost, established methodology, and demonstrated performance, even though FOECM may have advantages in capturing complex battery dynamics. Their status as a useful tool for battery modeling and control further strengthened by their robustness to noise, compatibility with current tools, and the easy physical interpretation of their properties. Although FOECMs might be more accurate, their practical utility may be limited by their greater complexity and computing requirements. Their practical applicability may be limited by their computing needs and complexity. Hence in this work IOECM is preferred. Various ECM models are compared and tabulated in Table 2. The Thevenin model is the most favored among all ECM models for representing lithium-ion batteries in electric vehicle applications. This is because it offers reduced computation complexity and superior dynamic performance. Figure 3 shows classification of battery modelling. Since it provides a straightforward yet accurate description of Li-ion batteries, equivalent circuit modeling has proven to be a very useful method for addressing this need. Despite their small size, Li-ion batteries are complicated electrochemical systems that encompass intricate processes, including ion diffusion, intercalation, and side reactions.

Fig. 4

Two RC Thevenin model.

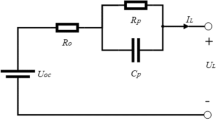
In this proposed work, the 2RC Thevenin model is used. In this model, the 2RC network is used to illustrate the effect of diffusion in the battery along with a SOC-dependent voltage source (V_OC), which represents the battery model’s OCV and an internal Ohmic resistance (R₀). Figure 4 displays the circuit diagram of a 2 RC Thevenin model. Mathematically, the model is represented as follows using Kirchhoff’s law:

$$\:SOC=\frac{\eta\:I}{Q}$$

(1)

$$\:{{V}^{*}}_{1}=-\frac{{V}_{1}}{{R}_{1}{C}_{1}}+\frac{{I}_{1}}{{C}_{1}}$$

(2)

$$\:{{V}^{*}}_{2}=-\frac{{V}_{1}}{{R}_{2}{C}_{2}}+\frac{{I}_{2}}{{C}_{2}}$$

(3)

The terminal voltage can be stated as

$$\:{V}_{t}\:=\:{V}_{OC}\:-{{V}^{*}}_{1}-\:{{V}^{*}}_{2}-I{R}_{0}+e$$

(4)

Where,

• V1 Voltage in the first RC branch.

• V2 Voltage in the second RC branch.

• Q Battery Capacity.

• $\:\eta\:$ Columbic efficiency

• I Battery current.

• $\:{V}_{t}$ Terminal resistance

• E Measurement noise.

• $\:{{V}^{*}}_{1}\:\text{a}\text{n}\text{d}\:{{V}^{*}}_{2}$ Polarization voltages

• R₁ and C₁ Polarization resistance & capacitance.

• R₂ and C₂ Diffusion resistance & capacitance.

Table 2 Comparison of ECM models^1,29.

Unscented Kalman Bucy filter

An approach to estimate SOC in linear dynamic systems was introduced by using a KF. Nonlinear properties are observed in the battery system used in EV. Therefore, in order to analyze the dynamic features of a battery, the EKF was proposed as a method that employed a state space model to quantify the nonlinear features of a battery. An inherent limitation of the EKF when used in real-world situations is the presence of linearization error throughout the estimate procedure. This error arises when employing the Taylor series approximation in settings with strong nonlinearity. Moreover, the inclusion of the Jacobian matrix in the EKF algorithm introduces intricacy.

Fig. 5

Block diagram of SOC estimation using UKBF.

The UKF was developed as a solution to the constraints of the EKF for estimating the SOC as shown in Fig. 5. The UKF technique obviates the necessity of employing Taylor approximation. The UKF approach produces additional sigma points around the present condition by utilizing the covariance values. Accurate estimated values of the mean and covariance of SOC are obtained by propagating the generated sigma points through a nonlinear mapping. Therefore, it obviates the need as to use the Jacobian matrix in computations. The unscented transformation is used to accurately represent the numerical average and variability of a nonlinear system. Sigma points serve to enhance the accuracy of the unscented transformation approach in estimating the state by precisely storing the mean and variance. UKF, although a very efficient derivative-free filtering technique for estimating solutions to nonlinear optimal filtering problems, was specifically developed for discrete-time processing. Therefore, it cannot be directly applied to continuous-time filtering problems where the measurement and state processes are represented as stochastic processes that occur over continuous time. The UKBF is the product of the differential equations that lead to the continuous-time limit of the UKF^{32,33,34,35,36}.

Consider a nonlinear continuous-time filtering system and represent it as

$$\:dx\left(t\right)=f\left(x\left(t\right),t\right)dt+A\left(t\right)d\gamma\:\left(t\right)$$

(5)

$$\:dy\left(t\right)=f\left(x\left(t\right),t\right)dt+B\left(t\right)d\delta\:\left(t\right)$$

(6)

Where,

• $\:x\left(t\right)\in\:{R}^{n}$ State process

• $\:y\left(t\right)\in\:{R}^{n}$ Measurement process

• F Drift function.

• h Measurement model function.

• $\:A\left(t\right),\:B\left(t\right)$ Arbitrary time-varying matrix, which does not depend on state and measurement process

• $\:\gamma\:\left(t\right),\:\delta\:\left(t\right)$ Independent Brownian motion

The equation can be rewritten in the presence of white noise and differential measurement as

$$\:dx\left(t\right)=f\left(x\left(t\right),t\right)dt+A\left(t\right){e}_{\gamma\:}\left(t\right)$$

(7)

$$\:Z\left(t\right)=f\left(x\left(t\right),t\right)dt+B\left(t\right){e}_{\delta\:}\left(t\right)$$

(8)

Where,

• $\:{e}_{\gamma\:}\left(t\right)$= $\:\frac{d\gamma\:\left(t\right)}{dt}$

• $\:{e}_{\delta\:}\left(t\right)$= $\:\frac{d\delta\:\left(t\right)}{dt}$

• $\:Z\left(t\right)$= $\:\frac{dy\left(t\right)}{dt}$

The subsequent section provides a discussion on the procedures entailed in formulating the UKBF for a nonlinear stochastic continuous-time system:

$$\:\{ X_{0} (t) = \mathop x\limits_{\_} (t)\:X_{i} \left( t \right) = \mathop x\limits_{\_} \left( t \right) + \left( {\sqrt {cM_{X} } } \right),\:i = {\text{1,2}},3 \ldots \: \ldots \:A,\:X_{i} = \mathop x\limits_{\_} - \left( {\sqrt {cM_{X} } } \right),\:i = A + 1, \ldots \: \ldots \:2{\text{~}}A$$

(9)

$$\:{\omega\:}_{m}={[{W}_{m}^{\left(0\right)}\dots\:\dots\:.{W}_{m}^{\left(2n\right)}]}^{T}$$

(10)

$$\:W=\left(I-\left[\:{\omega\:}_{m}\dots\:\dots\:{\omega\:}_{m}\right]\:\right)\:\:х\:diag\:\left[{W}_{c}^{\left(0\right)}\dots\:\dots\:.{W}_{c}^{\left(2n\right)}\right]\:\:\:\:х{\:\left(I-\:\:\:\left[{\omega\:}_{m}\dots\:\dots\:{\omega\:}_{m}\right]\right)\:}^{T}$$

(11)

$$\:C={\alpha\:}^{2}(n+k)$$

(12)

The scaling parameter is defined as:$\:\:=\:{\alpha\:}^{2}\left(n+k\right)-n$ (13)

Where,

• C Tuning parameter.

• $\:X$ Sigma point matrix

• $\:{\omega\:}_{m}$ Opposite Vector

• W Opposite Matrix.

• $\:{W}_{m}^{\left(0\right)}$ $\:\frac{}{n+}\:for\:i=0$

• $\:{W}_{m}^{\left(i\right)}$ $\:\frac{}{\left[2\left(n+\right)\right]}\:for\:i=\text{1,2}\dots\:.2n$

• $\:{W}_{c}^{\left(0\right)}$$\:\frac{}{(n+)+(1-{\alpha\:}^{2}+\beta\:)}\:for\:i=0$

• $\:{W}_{c}^{\left(2n\right)}$$\:\frac{}{\left[2\left(n+\right)\right]}\:for\:i=\text{1,2}\dots\:.2n$

• $\:{R}_{c},{\:Q}_{c}$ Spectral densities

  • Scaling parameter.

• $\:\alpha\:,\:\beta\:,\:k$ Positive constants

The UKBF can be obtained as follows, which correspond to the stochastic differential equations of the UKF in continuous time:

$$\:d\stackrel{-}{x}\left(t\right)=f\left(X\left(t\right),t\right){\omega\:}_{m}+K\left(t\right)[Z\left(t\right)-h\left(X\left(t\right),t\right){\omega\:}_{m}]$$

(14)

$$\:K\left(t\right)=X\left(t\right)W{h}^{T}\left(X\left(t\right),t\right){\left[B\left(t\right){R}_{c}\left(t\right){B}^{T}\left(t\right)\right]}^{-1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(15)

$$\:\frac{d{M}_{X}\left(t\right)}{dt}=X\left(t\right)W{f}^{T}\left(X\left(t\right),t\right)+\:\:f\left(X\left(t\right),t\right)\:W\left({X}^{T}\left(t\right)\right)+A\left(t\right){Q}_{c}\left(t\right){A}^{T}\left(t\right)-\:K\left(t\right)B\left(t\right){R}_{c}\left(t\right){B}^{T}\left(t\right){K}^{T}\left(t\right)$$

(16)

The following matrix form can be used to express the predicted covariance$\:\widehat{{\:M}_{X}}\left(t\right)$), measurement covariance S (t), and cross-covariance of the state and measurement C (t).

$$\:\frac{d\widehat{{M}_{X}}\left(t\right)}{dt}=\:X\left(t\right)W{f}^{T}\left(X\left(t\right),t\right)+f\left(X\left(t\right),t\right)\:W\left({X}^{T}\left(t\right)\right)+A\left(t\right){Q}_{c}\left(t\right){A}^{T}\left(t\right)$$

(17)

$$\:\frac{dS\left(t\right)}{dt}=h\left(X\left(t\right),t\right)W{h}^{T}\left(X\left(t\right),t\right)+\left[B\left(t\right){R}_{c}\left(t\right){B}^{T}\left(t\right)\right]$$

(18)

$$\:\frac{dC\left(t\right)}{dt}=X\left(t\right)W{h}^{T}\left(X\left(t\right),t\right)+\left[B\left(t\right){R}_{c}\left(t\right){B}^{T}\left(t\right)\right]$$

(19)

The procedure for estimating the SOC of LIB using UKBF is explained below:

Step 1: Battery modeling and parameter estimation.

Step 2: Measurement of battery parameters (current and voltage) using respective sensors.

Step 3: Addition of noise to the input parameters.

Step 4: initialization of state process and state error covariance matrix.

Step 5: Estimation of Kalman gain $\:K\left(t\right)$

Step 6: Estimation of system state $\:d\stackrel{-}{x}\left(t\right)$

Step 7: Estimation of error covariance $\:\frac{d{M}_{X}\left(t\right)}{dt}$

Step 8: observe the SOC of the battery.

Using performance indicators like RMSE, MSE, MAE, and R squared, the effectiveness of UKBF is calculated. The evaluation metric in this article is RMSE.

$$\:RMSE=\sqrt{\frac{1}{n}}\sum\:_{k=1}^{n}{(\stackrel{-}{x}\left(t\right)-\stackrel{-}{y}\left(t\right))}^{2}$$

(20)

$$\:\text{E}\text{R}\text{R}\left(\text{t}\right)=(\stackrel{-}{x}\left(t\right)-\stackrel{-}{y}\left(t\right))$$

(21)

Results and discussion

Parameter estimation of proposed battery modeling

The simulation of the 2RC Thevenin physical model is carried out in Matlab Simulink by making use of Simulink Simscape. The most significant advantage comes from Simscape’ s capacity to generate text files for all of the battery modeling components. In the text file that is associated with Simscape, all of the battery modeling parameters, mathematical expressions, and physical connections are included. Through the employment of the Lookup table, the Simscape programming language assigns the appropriately relevant values to the various battery components. In the process of modeling a 2RC battery, the six relevant parameters that need to be taken into consideration are R₁, R₀, R₂, C₁, C₂, and V_OC. Each of these variables has a different effect on the output SOC. A significant number of charging and discharging cycles have been performed in order to arrive at an approximation of these parameters. For each of the seven different SOC points, which range from 0 to 1, as well as each of the six different temperature points (-20 °C, -15 °C, -10 °C, 0 °C, 20 °C, and 40 °C), the parameters of the battery have been determined. In the process of parameter estimation, the simscape equivalent circuit is connected to the simple charging circuit. The measured Voc is compared with the actual Voc value. The parameters are confirmed once the measured Voc is equal to the actual Voc. Otherwise, the parameters are changed, and the Voc is measured. The process gets repeated until both Voc gets equal.

Fig. 6

Variation of R₀ for the vector of SOC and temperature points.

Fig. 7

Variation of R₁ for the vector of SOC and temperature points.

Fig. 8

Variation of R₂ for the vector of SOC and temperature points.

Fig. 9

Variation of C₁ for the vector of SOC and temperature points.

Figure 6 illustrates the variation of Ohmic or internal resistance in response to variations in SOC and temperature. Upon examination of the figure, it is evident that the R₀ value decreases as the temperature increases. Furthermore, there are significant differences between the R₀ values at low and high temperatures.

The parameters of the 2RC model identified using simscape language are shown in the Figs. 7, 8, 9 and 10.

Fig. 10

Variation of C₂ for the vector of SOC and temperature points.

Fig. 11

VOC curve for varied SOC and temperature points.

The OCV is utilized to adjust the estimated SOC. The link between SOC-OCV is crucial not just in open-circuit voltage-based estimation but also in model-based estimations. The battery SOC to OCV relationship at various temperatures is shown in Fig. 11. The OCV-SOC function exhibits significant variations, particularly in response to drastic fluctuations in environmental temperature.

Performance evaluation of modeled LIB

Once the battery parameters have been estimated, the battery model is simulated using a MATLAB Simulink environment. The simulation lasts for a period of 6 h, encompassing three separate cycles of charging and discharging. The simulation model comprises a 2RC lithium battery block, characterized by a circuit model of a 25 A-hour capacity battery operating at a nominal voltage of 3.6 volts. The monitoring module will assess the current electrical current, terminal voltage, SOC, and temperature of the stored battery. The management of state initialization and prediction correction is carried out in distinct subsystems, while the filter design forms the UKBF. The display block presents the estimated SOC, the real SOC, and the associated margin of error. Figures 12, 13 and 14 shows the graphical representation of the current, voltage, and temperature of the simulated battery.

Fig. 12

(a) Battery current profile without Gaussian noise. (b) Battery current profile without Gaussian noise.

Fig. 13

(a) Battery Voltage profile without Gaussian noise. (b) Battery Voltage profile without Gaussian noise.

Figure 12 (a) displays the progression of battery current over time in the absence of Gaussian noise, while Fig. 12 (b) displays battery current with Gaussian noise. Analysis of the data reveals that the current stays consistent at 15 A throughout the charging process. Upon discharge, the battery current decreases to -45 A.

Similarly to the current profile, Fig. 13(a) illustrates the change of battery voltage with respect to time without the addition of Gaussian noise, and Fig. 13(b) illustrates battery voltage with Gaussian noise included. During the process of charging, the voltage of the battery rises to 4.2 V from 3.8 V, and during the process of discharging, it falls to 3.2 V at its lowest point. In each and every cycle of charging and draining, the fluctuation remains the same. The graph in Fig. 14 illustrates the rate of change in temperature of the battery in relation to the passage of time.

Fig. 14

Battery Temperature variation.

Performance comparison of SOC estimation of the modeled LIB using EKF, UKF, and UKBF

Table 3 EKF Simulation parameter.

The EKF approach is employed to provide the first SOC estimate for the simulated battery. The parameters of the EKF simulation are shown in Table 3. The outcomes of the EKF are graphically represented in Fig. 15. The Figure illustrates a comparison between the estimated SOC by the EKF and the actual SOC waveform. It is evident from the figure that the measured and actual SOC differ slightly with the RMSE of 0.018754.

Fig. 15

SOC estimation using EKF.

Followed by EKF, the model is simulated using UKF by considering the parameters tabulated in Table 4. Figure 16 displays the estimated SOC through UKF. The UKF method efficiently minimizes the initial SOC inaccuracy and accurately tracks the SOC. The disparity between the real SOC and the SOC calculated using the UKF method is 0.009803 which is minimal in comparison to the EKF approach.

Table 4 UKF and UKBF Simulation parameter.

.

Fig. 16

SOC estimation using UKF.

Finally, the SOC is estimated using UKBF for continuous time series by considering the same parameters as of UKF. The UKBF algorithm has clear capability in accurately tracking the SOC once the early inaccuracies have been resolved. The estimated SOC using UKBF and the actual SOC is plotted in Fig. 17. The UKBF method, when combined with the dynamic battery model, exhibits robust performance with reduced RMSE of 0.003276.

Fig. 17

SOC estimation using UKBF.

Figures 15, 16 and 17 clearly demonstrate that all three EKF, UKF, and UKBF methods can effectively address the initial estimation inaccuracy and accurately track the true SOC value. The data illustrate that UKBF exhibits a rapid convergence rate with a lower estimation error RMSE of 0.0032 compared to EKF (0.018) and UKF (0.0098). Insufficient knowledge of higher order systems is the primary cause of the greatest estimation inaccuracy in EKF. Although UKF achieves greater accuracy by include the Jacobian matrix, its performance is inferior to UKBF since it treats the system as discrete time systems.

Table 5 Performance comparison of EKF, UKF, and UKBF.

To establish the efficacy of the proposed work, the outcome of the suggested UKBF is compared with the existing literature. The finding of the comparison is presented in Table 6. An analysis of the table clearly indicates that the proposed work exhibits superior performance.

Table 6 Comparison of proposed UKBF based SOC estimation with existing literature.

Conclusion

The economy, power, and reliability of an electric vehicle are directly influenced by the performance of its power battery, which serves as its primary power source. For electric vehicles to operate safely in challenging driving conditions, power battery management and battery longevity must be optimized. In a complex and dynamic environment, the battery management system must precisely model and estimate power battery conditions to perform safely and reliably. To reliably estimate SOC, this article employs an optimized Unscented Kalman-Bucy filter. A 2RC Thevenin network battery equivalent circuit model was built, and MATLAB’s least squares curve fitting approach estimated battery parameters. The parameters were calculated for various SOC and temperature values. Several simulations verified the projected UKBF’s performance. Results show RMSE values of 0.003276 for the suggested strategy. In order to assess the efficacy of the suggested method, the SOC of the battery model is estimated using both the EKF and the UKF. The RMSE for the EKF approach is 0.018754, while the UKF method has an RMSE of 0.009803. Upon examining the performance of the three techniques, it is evident that UKBF exhibits a reduced error rate in comparison to both EKF and UKF. In future, UKBF will be combined with data driven approaches to leverage their complementary strength and state of heath (SOH) of battery can be estimated in conjunction with SOC estimation.