Introduction

Over the past few years, there has been a concerning increase in the contamination of liquid substances across various industries, including food, beverages, and pharmaceuticals1,2. Adulteration is a method used to increase profitability by altering the original composition of substances, resulting in a loss of nutritional value3. Regular consumption of even small amounts of contaminated food can lead to serious health complications, such as nutritional deficiencies, allergies, kidney problems, cardiac diseases, and organ dysfunction4,5. In developing nations, the rate of adulteration in liquid foods and other products is higher than in developed countries due to the lack of efficient and cost-effective detection devices4. Various methods have been used to detect adulteration, such as chemical analysis6, spectroscopy7, fingerprinting and chromatography8. While these methods can be effective, they often require complex procedures, expensive equipment, and are time-consuming. As a result, there is a growing demand for the development of reliable and cost-effective detection methods for adulteration in edible oils9.

In recent years, radio frequency (RF) and microwave sensors have emerged as promising tools for detecting adulteration in various substances, particularly when advanced materials are used. Microwave sensors, constructed using metamaterials (MTMs)10 have been shown to enhance the performance of sensors by improving sensitivity and the quality factor (Q-factor)11. MTMs significantly enhance sensor performance by manipulating electromagnetic waves in innovative ways, thereby improving efficiency and reducing interference. Furthermore, they facilitate the development of compact, lightweight, and cost-effective sensors for various applications. Microwave sensor structures based on MTM have been successfully utilized in various fields12,13, including diagnostic and imaging14,15, medical applications16, invisibility cloak technology17,18, super lens development19,20, cancer cell detection21,22,23, antenna design22,24,25, fuel uncertainty detection26,27,28 and sensor technology29,30.

Over the past 3 to 4 years, researchers have increasingly focused on developing MTM-based sensors to detect adulteration in both liquid and solid substances31,32,33,34,35,36,37,38. For instance36, demonstrated a cost-effective radio frequency planar sensor capable of accurately identifying adulteration in vegetable oils. The sensor’s resonance characteristics vary based on the electrical properties of the sample. For the detection of adulteration in dairy products, a MTM-based sensor operating within the 8–9 GHz frequency range was proposed in37. The structure consists of a copper SRR on a dielectric substrate (Arlon Diclad-527), designed to detect changes in the dielectric constant. However, both sensors were quite large, and no calculations were provided for sensitivity and the Q-factor. A tri-circle SRR was implemented by Islam et al. to detect adulteration in various types of fuel and cooking oils39. However, the SRR structure was quite large, and the maximum resonance frequency shifted by around 210 MHz. A highly sensitive terahertz (THz) MTM-based sensor, operating in dual-band, was presented in40, using a split metal stacking ring resonator design. Detection reliability was improved by aligning resonance frequencies with analyte characteristics, though this has not yet been experimentally verified. A microwave sensor employed dielectric spectroscopy to detect and analyze impurities in edible oil was presented in41. A triple hexagonal split ring resonator was presented by Abdulkarim et al. to detect fuel adulteration by measuring resonance frequency shifts due to changes in concentration and humidity42. An FR-4 substrate was used to design this sensor, which, at 1.66 mm thickness, can detect adulteration in olive oil between 10 and 30%. However, this sensor had a large geometric size of \(35 \times 35\;{\text{mm}}^{2}\). An AI-assisted microwave sensor was developed with ultra-high sensitivity and selectivity for material characterization, leveraging coupled complementary split-ring resonators (CSRRs) to enhance performance in analyzing complex liquid mixtures43. Two planar resonant sensors were designed to measure oil permittivity and detect adulteration in vegetable oils44, operating in the 2.4 GHz ISM band. However, the quality factor was only 46.51, and the sensor’s overall dimensions were \(30 \times 20 \times 1.6\;{\text{mm}}^{3}\). A highly efficient metamaterial absorber with multiple peak absorptions and high Q factors across S, X, and Ku bands for sensing application was presented by Rabbani et al., showing robust performance independent of incident and polarization angles45. For soil moisture detection applications, Amir et al. designed a compact MTM absorber with a high absorption rate and sensitivity46.

An MTM structure was employed to analyze and classify reused oil samples within the X-band spectrum47. This structure consists of a split plus-shape enclosed within a square SRR. While the quality factor and sensitivity of this sensor were not measured, the dimensions of the structure were \(22.86 \times 10.16\;{\text{mm}}^{2}\). A cost-effective, highly sensitive, non-invasive microwave sensor for analyzing liquid dielectrics was presented48. Notably, the sensor, constructed using the cost-effective FR-4 material, demonstrated exceptional sensitivity despite its relatively large size. Another cost-effective DS-CSRR microwave sensor, capable of accurately measuring the complex permittivity of liquid samples, was presented in49. This sensor can detect the permittivity of unknown samples with decimal-level precision. However, it is unable to detect adulteration in liquids, and its size is relatively large at \(30 \times 20\;{\text{mm}}^{2}\).

The existing literature highlights several critical limitations in mass production, such as the need for expensive substrates, large product size, low sensitivity, and poor quality factor values. This study introduces an SRR based on the MTM approach to address these challenges by improving the detection of cooking oil adulteration using an MTM-based SRR microwave sensor. The MTM SRR structure is used to analyze the changes in the scattering parameters of the tested samples. The proposed structure offers various industrial applications, including real-time quality monitoring and dielectric characterization. Additionally, it is compact, cost-effective, and suitable for commercial use. This paper comprehensively analyzes the design, fabrication, and performance of the MTM-based SRR for detecting liquid adulteration, particularly in edible oils. We demonstrate the superior capabilities of the proposed sensor system through experimental validation and comparative studies, highlighting its ability to enhance the accuracy and reliability of liquid quality evaluation.

Materials and resources for experimentation

Sample and resources

To conduct the experiment, we purchased two different types of oil: coconut oil and sunflower oil, along with one locally sourced oil for adulteration purposes. The coconut oil and sunflower oil were acquired from a reputable department store, while the local oil was obtained from a nearby shop. The required amounts of sunflower and coconut oil were mixed with the local oil to create concentrations ranging from 0 to 100%, in 20% increments. A PNA Network Analyzer, connected to the SMA (SubMiniature version A) waveguide interface, was used to collect the transmission curve (S11) of the oil solutions at various concentrations. To ensure accuracy, five repetitions were performed for each concentration. A total of 20 parameter sets were obtained for each oil mixture by sampling four times. After averaging the parameters for each concentration, we derived the reflection curve for oil solutions ranging from 0 to 100%. All measurements were conducted at an approximate temperature of 26 ± 1 °C.

Fundamental operating principle

The optimal size of the proposed structure is achieved by incorporating waveguide measurements into the modeling approach and applying multiple boundary conditions, such as perfect electrical conditions (PEC) and perfect magnetic conditions (PMC), as shown in Fig. 2b. Considering these boundary conditions is critical due to the metallic nature of the side-wall waveguide. Factors such as space availability, uniform distribution, and the application of PEC and PMC all contribute to these requirements. It is often assumed that additional space along the z-axis during propagation is unrestricted, while the PEC and PMC boundary conditions are applied to the x and y-axes. A perpendicularly incident electromagnetic wave enters the air waveguide through the coaxial port. Upon reaching the unit cell, the electromagnetic energy splits into two parts: one part is reflected as a wave, and the other continues through the unit cell as a transmitted wave. The transmitted wave interacts with the unit cell, generating a strong electromagnetic resonance. Figure 1 illustrates the proposed working principle of the unit cell.

Fig. 1
figure 1

The fundamental operational principle of the sensor.

Full size image

The sample holder solution causes the reflection and transmission of partially transmitted electromagnetic energy, similar to the behavior observed in the unit cell. Changes in liquid concentration can alter the dielectric environment of the unit cell structure, resulting in a shift in the resonant frequency. The sensing process is conducted by analyzing the frequency shift of the resonant peak. In the theory of vertical incidence of uniform plane waves, the analysis is simplified by equating the transmission and reflection coefficients with the resonant frequencies of the liquid solution at various concentrations. If the incident wave is considered as an electric field in the xy-plane, the electric and magnetic fields of the incident wave can be expressed as50.

$$\nabla \times {\text{E}} = - \upmu_{0} \upmu_{{\text{r}}} \frac{{\partial {\text{H}}}}{{\partial {\text{t}}}}$$
(1)
$$\nabla \times {\text{H}} = - \epsilon_{0} \epsilon_{{\text{r}}} \frac{{\partial {\text{E}}}}{{\partial {\text{t}}}}$$
(2)

Configuration of SRR sensor

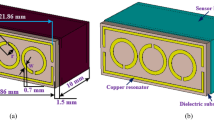
Figure 2b depicts the schematic diagram of the sensor, which consists of rectangular waveguides and a sample holder for oil concentration. Figure 2 displays the section of the rectangular waveguide cell, featuring a wide edge size of 4.8 mm and a narrow edge size of 2.8 mm. The waveguide design is suitable for frequencies ranging from 4.00 to 6.00 GHz. Figure 2a,b display the side and top views of the SRR cell structure. The MTM comprises a dielectric substrate, Rogers RT 5880, and a metal layer of copper (Cu). The dimensions of the components are as follows: L is 10 mm, W is 10 mm, G1 is 0.60 mm, G2 is 0.60 mm, and S(L, W) is 0.4 mm. The dielectric substrate has a thickness of 1.57 mm, while the metal layer is 0.035 mm thick. A sample holder, securely fixed at the other end of the substrate, measures 9 mm in thickness and is constructed from acrylic sheets. The sensor layer has a low loss tangent of 0.0040 and a permittivity of 2.40. The side wall of the acrylic sheet has an overall thickness of 1 mm. In CST software, various boundary conditions can be set during the simulation to measure the waveguide for the proposed structure with realistic dimensions. For scattering parameter measurements during the simulation, a sample holder was placed on the back side of the unit, with electrical boundary conditions at the x-axis and magnetic conditions at the y-axis. The z-axis was treated as the propagation direction (added space), as depicted in Fig. 2b.

Fig. 2
figure 2

(a) Top view geometrical dimension parameters and (b) Simulation boundary conditions, including the unit cell and sample holder.

Full size image

Proposed design of MM structure

Designing SRR and analyzing resonance

The control variable technique was used to optimize the structural properties of the metamaterial because these parameters significantly affect the sensor’s performance. During the analysis of the structural properties, we focused on the evolution of the design configuration and the split gap width in both rectangular and star-shaped SRR structures. We also examined the impact of various substrates on the resonance frequency. An SRR is an artificial structure capable of inducing magnetic susceptibility in different types of metamaterials up to 200 THz51. Therefore, we precisely and responsively adjust the resonance frequency by changing the split gap in square and star shapes in response to vibration amplitude, making it an excellent choice for the proposed sensor among various SRR structures.

Figures 3 and 4 illustrate the reflection coefficient (S11) for the different design stages of the MTM-based SRR sensor. In the first stage of the design, drawing a square box on a substrate resulted in a sloped line without any resonance frequency. A resonance frequency of 4.31 GHz with a magnitude of − 38.079 dB was achieved in the 2nd stage by making cuts on the upper right corner of the first quadrant and the lower left corner of the third quadrant of the square. Figure 4 shows the scattering parameters for the third and final design. In the 3rd stage, as depicted in Fig. 4, the square was transformed into a star shape with an inner radius of 3 mm, resulting in a resonance point at 3.89 GHz with a magnitude of − 39.107 dB. During the 4th and final stage of the design, a 0.6 mm cut was implemented, and the star shape was rotated by 45°, leading to a resonance frequency of 3.335 GHz with a magnitude of − 41.583 dB.

Fig. 3
figure 3

Reflection coefficient value for first and second stage.

Full size image
Fig. 4
figure 4

Reflection coefficient value for the third and fourth stage.

Full size image

Figure 5 shows the S11 graph for different substrate materials. This study also explores how changing the dielectric material affects the overall performance of the MTM unit in sensing applications. Various materials, including Rogers models RT5880, RO4350, RT5870, and FR-4, were evaluated. The Rogers RT5880 substrate was selected as the most suitable option for the MTM-based SRR due to its superior performance in sensing applications compared to other substrates.

Fig. 5
figure 5

Impact of different substrates on the frequency response.

Full size image

Figure 6 displays the impact of different split gaps on the frequency response. A resonance frequency of 3.335 GHz with a magnitude of − 41.583 dB was observed with a split gap of 0.40 mm. In the second case, a resonance frequency of 3.14 GHz with a magnitude of − 41.236 dB was measured for a gap of 0.60 mm. In the third evaluation, using a gap of 0.80 mm, a magnitude of − 40.949 dB was recorded at 3.485 GHz. Ultimately, the MTM-based SRR sensor was designed with a split gap of 0.6 mm.

Fig. 6
figure 6

Impact of different Split Gaps on the frequency response.

Full size image

Experiments: testing for adulteration

In this section, we present an experimental assessment of the proposed sensor. Specifically, we test the designed 8-gon star-shaped sensor for its effectiveness in detecting adulteration in edible oil samples. Local cooking oil was selected as the sample to be tested for adulteration in this study. The experimental research focuses on testing branded cooking oil adulterated with local cooking oil, used here as a reference.

Local oil as adulterant

An experimental demonstration was conducted in a laboratory, as shown in Fig. 7, to test adulteration in branded cooking oil using local oil. Precautions were taken before starting the experiment, including maintaining room temperature and calibrating the PNA for the frequency range. Before starting the experiment, the PNA was calibrated using a calibration kit to cover the frequency range of 2 to 5 GHz. Figure 7 illustrates the comprehensive experimental setup used to determine the reflection coefficient (S11) of different liquids. Initially, the liquid sample was introduced into the sample holder using a syringe, and the reflection coefficient (S11) of each sample was assessed within the 2 to 5 GHz frequency range.

Fig. 7
figure 7

Experimental Setup for oil adulteration in a laboratory.

Full size image

Precautions were taken during the experiment to reduce errors. The sample holder was filled halfway with the liquid to ensure accurate results. Reproducibility and repeatability methods were adopted to minimize errors caused by environmental conditions. The sample holder was positioned between the waveguide ports during the experimental setup, and polyethylene foam was used to cover the space around the sample holder to minimize external environmental impact, as shown in Fig. 7. The figure depicts an experimental setup designed for precise measurement and analysis. In the upper left corner is a fabricated unit cell, which serves as the primary structure being studied. A waveguide port is present in the lower-left corner, acting as a crucial connection for transmitting signals. Moving to the upper right corner, the figure shows different samples, likely placed for comparison or testing under various conditions. Finally, the sample holder is located in the lower right corner, securely positioning the samples to ensure accurate and stable measurements during the experiment. This arrangement facilitates controlled experiments, likely focusing on the interaction between the unit cell, samples, and waveguide. The resulting data were then analyzed. These steps ensured that the experiment produced reliable and consistent results.

Different amounts of local oil were added to branded cooking oil as an adulterant, and the changes in operating frequency and return loss were observed. Five samples with varying concentrations of local oil in branded cooking oil were prepared for testing. These concentrations included 100% branded cooking oil, 80% branded cooking oil with 20% local oil, 60% branded cooking oil with 40% local oil, 40% branded cooking oil with 60% local oil, 20% branded cooking oil with 80% local oil, and 0% branded cooking oil with 100% local oil. The samples were prepared in separate beakers and mixed thoroughly to ensure uniformity. A measured quantity of the prepared mixtures was placed in the sample holder using a syringe to form a drop, allowing the MTM-based SRR characteristics to be examined. The operating frequency and return loss changed as test samples were added to the sample holder, with the amount and material characteristics of the adulterant in the loaded sample influencing these changes. Figures 8 and 10 illustrate the operating frequency and return loss variations for different cooking oil concentrations. By analyzing the results, the amount of local oil added to branded cooking oil as an adulterant can be determined.

Fig. 8
figure 8

Simulated and measured value of reflection coefficients for Sunflower oil.

Full size image

Conducting experiments to analyze the proposed device

Figure 8 shows the experimental results of adulterating sunflower oil with local oil. Five sunflower oil samples were prepared with local oil concentrations ranging from 0 to 100% in 20% increments. Figure 8 compares the simulated and measured values of the scattering parameter S11. Although there is a slight discrepancy, the simulated value for 100% sunflower oil is − 41.30 dB at a frequency of 3.413 GHz, while the measured value is − 40.97 dB at 3.188 GHz. Differences between the simulated and measured results can occur due to various factors, including the mutual coupling effect of the waveguide port, manufacturing limitations, and measurement errors.

It is important to note that the interaction between the transmitting and receiving terminals of the waveguide ports always affects the measurements. The measured values of the scattering parameter S11 for different local oil concentrations in sunflower oil are illustrated in Fig. 9a. The detailed graphical representation clearly shows that adjusting the local oil concentration in sunflower oil impacts both the resonance frequency and return loss. For instance, a mixture of 20% local oil and 80% sunflower oil results in a magnitude of − 33.56 dB at a frequency of 3.125 GHz. They were similarly, combining 40% local oil with 60% sunflower oil results in a magnitude of − 28.42 dB at 3.08 GHz, while a blend of 60% local oil with 40% sunflower oil achieves a magnitude of − 25.20 dB at 3.04 GHz. The graphical representation of the resonance frequency of dips for the different adulteration percentages for the sunflower oil is depicted in Fig. 9b. Figure 9b illustrates the relationship between notch amplitude and the adulteration percentage of sunflower oil. It shows how the notch amplitude varies as the adulteration percentage increases, likely reflecting the sensor’s sensitivity in detecting oil adulteration. As the adulteration level rises, the notch amplitude changes, indicating the presence and amount of adulterant in the oil. This data is crucial for assessing the sensor’s ability to detect oil quality accurately.

Fig. 9
figure 9

(a) Measured value of reflection coefficients for different amounts of adulteration in Sunflower oil (b) Respective notch amplitude shift for different adulteration percentage.

Full size image

The simulation and experimental results for pure coconut oil are shown in Fig. 10. For 100% coconut oil, the simulation shows a magnitude of − 41.30 dB at a resonance frequency of 3.4 GHz, while the measured result is − 39.855 dB at a resonance frequency of 3.29 GHz. The same procedure for sample preparation was followed as with sunflower oil. Figure 11a illustrates five samples of coconut oil with varying concentrations of local oil. When 20% local oil was mixed with coconut oil, a resonance frequency of 3.270 GHz was achieved with a magnitude of − 35.45 dB. Mixing 40% and 60% local oil with coconut oil resulted in resonance frequencies of 3.23 GHz and 3.16 GHz, with magnitudes of − 31.21 dB and − 25.81 dB, respectively. When 80% local oil was mixed with coconut oil, a magnitude of − 17.67 dB was achieved at 3.137 GHz. The graphical representation of the resonance frequency of dips for the different adulteration percentages for the coconut oil is depicted in Fig. 11b.

Fig. 10
figure 10

Simulated and measured value of reflection coefficients for Coconut oil.

Full size image
Fig. 11
figure 11

(a) Measured value of reflection coefficients for different amounts of adulteration in Coconut oil (b) Respective notch amplitude shift for different adulteration percentage.

Full size image

The shift in resonance frequency increases as the local oil concentration ranges from 0 to 100%. For sunflower oil, the change in resonant frequency as the local oil concentration rises from 0 to 100% results in a shift of 2.99 GHz, while for coconut oil, the shift is 3.11 GHz. This sensor demonstrates increased sensitivity in detecting contaminated solutions. The dielectric permittivity of the sample affects both the operating frequency and return loss. Figures 9 and 11 show the variations in frequency shift and return loss as the operating frequency values and the percentage of adulteration increase. The graphs clearly demonstrate a correlation between frequency shift, return loss, and adulteration rate. This process was repeated five times for both sunflower and coconut oil to analyze variations in resonance frequency and return loss, and the results were consistent. Based on the data from Figs. 9 and 11, the sensitivity, quality factor, and error can be calculated using formulas 3, 4, and 5 from reference52

$${\text{Q}} - {\text{factor}} = \frac{{{\text{f}}_{0} }}{{\Delta {\text{f}}}}$$
(3)
$${\text{Sensitivity}} = \left| {\frac{{({\text{f}}_{01} - {\text{f}}_{02} }}{{{\text{f}}_{01} \Delta \epsilon_{{\text{r}}} }}} \right|$$
(4)

where \({\text{f}}_{0}\) represents the centre frequency, while \(\Delta \text{f}\) indicates the bandwidth. Additionally, \({\text{f}}_{01}\) (first sample) and \({\text{f}}_{02}\)(second sample) frequency of the sample, while ∆εr denotes their permittivity difference. The measurement results indicate that the centre frequency for coconut oil is 3.29 GHz, while sunflower oil is 3.18 GHz.

Based on the calculation and measurement results, the sensor design demonstrates high sensitivity in detecting local oil concentrations in branded oils (such as sunflower and coconut oil) ranging from 0 to 100%, with great accuracy. Integrating this SRR-based sensor, as shown in Figs. 9 and 11, makes it suitable for use in industrial environments to evaluate the quality of edible oils. Table 1 compares the SRR-based sensor under consideration and those from prior studies, illustrating that the developed SRR-based sensor exhibits higher sensitivity and quality factors.

Table 1 Comparison with existing literature.
Full size table

Discussion

We conducted experimental comparisons between our proposed SRR-based sensor and traditional devices commonly used for detecting adulterated edible oil. In our study, we implemented an alternative approach to the conventional method. Instead of placing the oil solution above the metamaterial structure, we positioned it below in a sample holder. This configuration allows for the repeated substitution of the edible oil solution without affecting the metamaterial. Additionally, testing the oil solution inside the holder effectively reduces the influence of external environmental factors on the results.

Several factors influence the device’s performance, including operating frequency, bandwidth, response time, and sensitivity. Among these, sensitivity and quality factors are crucial for determining the device’s effectiveness. We measured the sensitivity of each case by analyzing the data obtained from experimental testing. To confirm the validity of our experiment, we focused on both reproducibility and repeatability. Reproducibility involved testing the sensor with the same sample in different environments or with different batches of sensors to ensure consistent performance. Table 1 presents a comparison between the newly developed MTM-based SRR sensor and previous studies, highlighting the proposed sensor’s superior sensitivity and quality factor. Furthermore, the sensor’s error is significantly reduced. The device’s accuracy was evaluated by comparing the measurement results with simulation data. A minimal discrepancy between the two indicates a small margin of error, which can be calculated using the following equation53:

$${\text{Error}} = \left| {\frac{{{\text{f}}_{{{\text{SM}}}} - {\text{f}}_{{{\text{ss}}}} }}{{{\text{f}}_{{{\text{ss}}}} }}} \right|*100$$
(5)

In comparison with the existing literature, the proposed metamaterial sensor demonstrates superior performance in several key areas. Operating at a frequency of 2.4 GHz, it matches the frequency range of several previous studies while offering a higher sensitivity of 0.92. The frequency shift of 760 MHz in this work is one of the highest reported, alongside47, indicating its strong detection capability. Additionally, the Q-factor of 149 significantly surpasses previous works such as (46.51) and41,44, ensuring better resonance and signal quality. The error rate of 3.1% is also a notable improvement over (~ 8%) and49 (~ 4%), leading to more accurate measurements. Moreover, while many existing studies focus solely on oil adulteration, the proposed sensor offers broader applicability, including liquid permittivity measurements, enhancing its versatility in industrial applications. This makes the current work a significant advancement in both performance and practical utility compared to the existing literature. Future work will focus on system miniaturization, integrating machine learning for real-time analysis, and enhancing environmental adaptability and cost efficiency. These additions provide a roadmap for improving performance and real-world applicability.

Conclusion

The compact, MTM-based SRR sensor developed in this study shows significant potential for detecting edible oils with high sensitivity and accuracy. By incorporating a star-shaped design enclosed in a square geometry and using low-cost substrates, this MTM-based SRR sensor offers a cost-effective solution without sacrificing performance. With a sensitivity of 90%, the sensor ensures reliable detection of edible oils, making it well-suited for food industry applications where accurate oil quality assessment is essential. The high Q-factor of 149 enhances the sensor’s ability to distinguish subtle differences between oil samples, contributing to its overall robustness and reliability. Additionally, with an error rate of just 3.1%, the sensor provides precise measurements for oil quality evaluation. Overall, this research lays the groundwork for developing practical and efficient sensors for food quality monitoring, benefiting consumers and the food industry. Future research could further optimize the metamaterial design and facilitate integrating this sensor into portable devices for real-world application.