A constitutive model for coal gangue coarse-grained subgrade filler incorporating particle breakage

Abstract

The accumulation and discharge amount of coal gangue are substantial, occupying significant land resources over time. Utilizing coal gangue as subgrade filler can generate notable economic and social benefits. Coal gangue coarse-grained soil (CGSF) was used to conduct a series of large-scale vibration compaction tests and large-scale triaxial tests. The results indicate that the maximum dry density of CGSF initially increases and then decreases with the increase in fractal dimension. The stress–strain curves of the samples exhibit a distinct nonlinear growth pattern. Analysis of the compaction effect suggests that the compaction degree of CGSF should not be lower than 93%. As the confining pressure increases, the extent of failure strength improvement due to increased compaction decreases. Additionally, the failure strength of samples initially increases and then decreases with the increase in coarse particle content. A modified quadratic polynomial fractal model gradation equation was proposed to describe the gradation of samples after particle breakage. Based on this, a new quantitative index for particle breakage was established. Analysis of particle breakage in samples revealed that higher confining pressure and greater coarse particle content lead to increased particle breakage. The breakage exhibited a significant size effect, and the impact of particle gradation on sample breakage was greater than that of confining pressure. The stress–strain relationship of CGSF was analyzed by using a logarithmic constitutive model, and the correlation between model parameters and the newly derived particle breakage index was generated. A constitutive model incorporating particle breakage for CGSF was established, and its accuracy was validated.

Introduction

Energy is not only the foundation of the global economy and sustainable development but a key factor for humanity’s continued survival. China is the world’s largest energy consumer, accounting for 23% of global energy consumption, with coal making up 62% of China’s total energy consumption¹. It is foreseeable that coal’s position in China’s energy structure will remain unchanged²; coal will remain the dominant energy source in China for the long term. Coal gangue is a solid waste generated during the construction, mining, and washing processes of coal mines³; China has vast reserves of coal gangue, and its annual increase is rapid^4,5. The large accumulation of coal gangue not only occupies land but poses a series of environmental risks, such as spontaneous combustion, landslides, and groundwater contamination^6,7,8. Using coal gangue as subgrade filler not only reduces the resource waste and environmental pollution caused by its accumulation but helps save the cost of subgrade construction. Therefore, research on the using coal gangue as subgrade filler holds significant economic and environmental benefits⁹.

It has gradually become a research hotspot to reuse mining waste in large-scale civil engineering, which can reduce environmental pollution and promote cleaner production in mining areas. In the research of using coal gangue as subgrade filler, Guo et al.¹⁰ conducted a serious of compaction test, unconfined compressive strength test, compression rebound modulus test, splitting strength test and splitting rebound modulus test, found that the cement stabilized macadam-gangue can be used in road base and Gradation 7 is recommended. Zhang et al. carried out the particle crushing tests of coal gangue coarse-grained subgrade filler to investigate the relationships between load and displacement, crushing strength, failure pattern, and gradation after crushing¹¹, conducted a series of cyclic triaxial tests using the large-scale dynamic and static triaxial apparatus to study the permanent deformation of coal gangue and propose a unified model of permanent deformation^12,13, obtain the well-graded limit for gradation curve and the optimal grading range of coal gangue subgrade filler through the large-scale vibration compaction test and large-scale triaxial tests and investigate the compaction and the mechanical behaviors of coal gangue as subgrade filler and constructing highway subgrade in practice¹⁴. Liu et al.¹⁵ used carbide slag (CS) and coal gangue (CG) powder to enhance the properties of the subgrade soil, and found that CS-CG stabilized soil shows favorable mechanical properties, durability, and environmental sustainability, indicating its potential as a substitute for traditional cement and lime treatments in subgrade soil reinforcement. Long et al.¹⁶ found that incorporation of coal gangue significantly improve the strength, stiffness and anti-corrosion ability of cement-soil mixture for foundation treatments.

As mentioned above, coal gangue has broad application value as a subgrade filler material. Li et al.¹⁷ carried out the chemical experiments of coal gangue and found that coal gangue could meet the relevant requirements of specifications and was able to be used in road base. As a soft coarse-grained filler, coal gangue is prone to particle breakage under external loads. In addition, there are limited researches on the particle breakage of coal gangue in existing studies, and there is insufficient research on the constitutive model of coal gangue subgrade fillers considering particle breakage. In view of this, this article conducts a series of large-scale vibration compaction tests and large-scale triaxial tests, analyzes the relationship between compaction and gradation, captures the effect of fractal dimension, compaction degree and confining pressure on the strength of coal gangue coarse-grained soil (CGSF) samples, investigate the particle breakage of samples, propose a modified quadratic polynomial fractal model gradation equation to describe the gradation of samples after particle breakage, and finally establish a constitutive model for CGSF incorporating particle breakage. The research conclusion has important guiding value for the reuse of coal gangue waste and the filling of coarse-grained subgrade.

Experimental materials and methods

Experimental materials

The coal gangue coarse-grained subgrade filler used in this investigation was collected from an abandoned coal mine (detailed coal mine information is unknown) in Xiangtan, Hunan Province (as shown in Fig. 1). The coal gangue discharged after coal mining was randomly stacked in the open space and had been mixed. The on-site sampling of test materials was randomly selected from the piled-up coal gangue. Nearly 15 tons of materials were transported to the laboratory for research. The surface of the coal gangue particles is grayish-black, relatively rough, and sharp-edged. The particles are prone to breakage under external forces. After being transported to the laboratory, all coal gangue was air-dried outdoors. To eliminate the influence of size effects, particles larger than 60 mm were removed by hand-picking. After natural air-drying, coal gangue was placed in an oven to dry completely. Then materials were sieved using standard sieving test with pore sizes of 0.075, 0.5, 2, 5, 10, 20, 40 and 60 mm. The particles after sieving test are shown in (Fig. 2).

Fig. 1

On site sampling of coal gangue materials.

Fig. 2

Coal gangue particles after sieving test.

Based on the Chinese scientific standards for Test Methods of Soils for Highway Engineering (JTG 3430–2020), basic property tests were conducted on coal gangue coarse-grained subgrade filler, and the following parameters were obtained, i.e., the natural moisture content ranged from 2.20 to 2.98%, with a liquidity index (IL) of 32% and a plasticity index (IP) of 21%. Note that, each group of experiments was conducted in parallel three times. Energy Dispersive Spectroscopy (EDS, JSM-6380LV) was used to analyze the elemental composition of the dried coal gangue (0.8 mm × 0.8 mm), which was independently completed by trained professionals. The average elemental composition of the samples is shown in (Table 1). As shown in Table 1, the primary element in coal gangue is oxygen (47.70%), followed by calcium (22.00%) and carbon (15.96%). In addition, Li et al.¹⁷ used coal gangue as railway roadbed construction in practice and obtained the dry density (2.41 g/cm³), natural water content (2.95%) and the chemical compositions, which were basically consistent with this test.

Table 1 The elemental composition of coal gangue.

Experimental methods

A vibrating compactor (as shown in Fig. 3) was used to capture the compaction parameters of the coal gangue coarse-grained subgrade filler. The sample sizes were Φ280mm × 350 mm, with a weight of approximately 34 kg. According to the Chinese scientific standards for Test Methods of Soils for Highway Engineering (JTG 3430–2020), the vibration frequency was set to 50 Hz, and the vibration time was 6 min. Four different gradations were selected for this test. The particle size groups for each gradation were as follows: < 0.075, 0.5–0.075, 2–0.5, 5–2, 10–5, 20–10, 40–20 and 60–40 mm.

Fig. 3

Vibration compactor.

In this study, the fractal model gradation equation i.e. Eq. (1), was used for gradation design^18,19,20. Based on this equation, four gradation curves for coal gangue coarse-grained subgrade filler were designed.

$$P_{i} = \left( {\frac{{d_{i} }}{{d_{\max } }}} \right)^{3 - D} = x^{3 - D}$$

(1)

where, P_i represents the passing percentage (%); D denotes the fractal dimension; x indicates the relative particle size, and x = d_i/d_max, d_i is the particle size (mm); d_max is the maximum particle size (mm), and d_max = 60 mm.

The control parameters of well-graded for subgrade are the coefficient of uniformity C_U = d₆₀/d₁₀ and the coefficient of curvature C_C = (d₃₀)²/(d₁₀*d₆₀). where ${d}_{60}$, ${d}_{30}$, and ${d}_{10}$ refer to the particle size corresponding to the passing percentage of 60%, 30% and 10% in the gradation curve, respectively (mm). Subgrade filler with well-graded meets C_U ≥ 5 and 1 ≤ C_C ≤ 3.Then, according to Eq. (1), the range of well-graded can be captured, i.e., 1.89 ≤ D ≤ 2.63, which was confirmed in¹². After that, four gradation curves with different fractal dimensions (D = 1.89, 2.13, 2.37, and 2.61) were designed in sequential order of increasing fractal dimension, as shown in (Fig. 4).

Fig. 4

Four gradation curves used in this test.

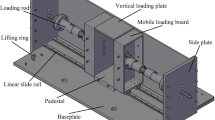
The DJSZ-150 large-scale dynamic and static triaxial testing machine (Fig. 5) was used to study the strength characteristics of coal gangue coarse-grained subgrade filler. The operation control panel offers two axial loading modes: constant stress loading control and constant strain loading control. The operation control system can automatically collect data on the axial load, axial displacement, confining pressure, pore pressure, back pressure, and volumetric strain of the specimen during the experiment. The sample has a diameter of 300 mm and a height of 600 mm. The instrument can perform various types of shear tests, including consolidated drained (CD), consolidated undrained (CU), and unconsolidated undrained (UU) tests.

Fig. 5

The DJSZ-150 large-scale dynamic and static triaxial testing machine: (a) computer control system, (b) pressure control system, (c) loading system.

Considering that the subgrade filler is typically shallow in actual engineering conditions, resulting in lower confining pressures. Thus, the confining pressures were set at 100, 200 and 300 kPa, with a shearing rate of 0.5 mm/min. According to the Chinese scientific standards for Specifications for Design of Highway Subgrades (JTG D30-2015), the compaction degrees of 90, 93, and 96% were used to conduct the consolidation undrained tests. Following the scientific standards, each group of experiments should be repeated 3 times to ensure the reliability of the test results. After testing, each test group was generally consistent. Considering the convenience of result analysis, one set of results from each group was selected for analysis, and the test design was shown in (Table 2).

Table 2 Test design.

Experimental procedure

The consolidated undrained (CU) triaxial test was carried out, following the methodology outlined in the Chinese scientific standards for Specifications for Design of Highway Subgrades (JTG D30-2015). The experimental procedure consists of (1) sample preparation, (2) sample saturation, (3) sample consolidation, and (4) sample loading, as illustrated in (Fig. 6). The specific operational steps are as follows:

Fig. 6

The large-scale triaxial testing process.

Sample preparation

The sample size is Φ300mm × 600 mm with the certain values of the maximum dry density and compaction degree, and the sample mass can be calculated. According to designed gradation (as shown in Fig. 4), the percentage of each particle group can be obtained. Then, weigh the materials of each particle group and mix them well. After that, place the mixed test materials into the sample preparation cylinder and compact it to the specified height (as shown in Fig. 6a) to obtain the prepared sample (as shown in Fig. 6b).

To ensure uniformity of specimen, each group of samples was divided into five equal portions, which were mixed thoroughly. The sample was prepared using the layer-by-layer tamping method, controlling the mass and height of each layer to achieve the designed compaction density. Each layer was compacted to a height of 120 mm using a tamper, with a total of five layers.

Sample saturation

After sample preparation, the specimen was placed in the loading apparatus within the triaxial test pressure chamber and saturated using a vacuum water permeation method. The specimen was saturated when the water level in the volumetric change tube increased to one-third or one-half of its capacity. After measuring, the pore pressure coefficient B > 0.95.

Sample consolidation

After saturation, the samples were consolidated using the equal pressure consolidation method. Enter the basic information and corresponding control parameters (sample number, stress and loading time) of the test on the operation control screen and when the water discharge stabilizes, it can be considered that the specimen solidification is completed.

Sample loading

The samples were loaded using displacement-controlled loading, with the shearing rate set to 0.5 mm/min. Since the stress–strain curve of coal gangue coarse-grained subgrade filler in the triaxial test does not exhibit a distinct peak, the samples were considered at failure when the axial permanent strain reached 15% (at which point the testing was stopped, reaching the failure strength). After testing, the specimen was removed from the pressure chamber. All samples are collected and naturally air-dried. Then, they were placed in an oven at 105 °C and dried for 24 h. After drying, the samples were cooled at room temperature. Subsequently, the standard sieving and weighing were carried out to determine the particle size distribution of the specimen after testing. The degree of particle breakage was assessed by comparing the particle gradation before and after the experiment.

Experimental results

Analysis of experimental results

The maximum dry density (ρ_dmax) for 4 gradation samples was measured using a vibrating compaction device, resulting in a curve showing the relationship between ρ_dmax and fractal dimension D. As shown in Fig. 7, the ρ_dmax initially increases and then decreases with the increase in fractal dimension D. The ρ_dmax reaches peak value of 2.1 × 10³ kg/m³ when D = 2.37.

Fig. 7

Relationship between maximum dry density (ρ_dmax) and fractal dimension (D).

Based on the results of large-scale triaxial tests, the relationship curves between axial stress (σ₁) and axial strain (ε₁) under different compaction degrees and gradation conditions were obtained, as shown in (Figs. 8, 9).

Fig. 8

Stress–strain curves of CGSF under different compaction degrees (D = 2.37).

Fig. 9

Stress–strain curves of CGSF under different gradations at 93% D_C.

As shown in Fig. 8, the stress–strain curves of the samples with D = 2.37 under different compaction degrees exhibit a clear nonlinear growth pattern. Under confining pressures of 100, 200 and 300 kPa, the stress–strain curves of samples with different compaction degrees show no peak values, indicating strain hardening behaviors. When the compaction degree is constant, as the confining pressure increases, the stress–strain curves shift upward, becoming steeper. The failure strength increases, and the strain hardening becomes more pronounced. This trend is observed under all three compaction conditions. Under a confining pressure of 100 kPa, when the compaction degree increases from 90 to 93%, the failure strength rises from 469.41 to 525.91 kPa, with an increase of 12.03%. However, when the compaction degree increases from 93 to 96%, the failure strength only increases from 525.91 to 550.85 kPa, showing a smaller growth of 4.74%. Under a confining pressure of 200 kPa, increasing the compaction degree from 90 to 93% improves the failure strength from 747.99 to 815.94 kPa, with an increase of 9.08%. When the compaction degree rises from 93 to 96%, the failure strength only increases from 815.95 to 831.11 kPa, showing an increase of just 1.86%, indicating minimal growth. Under a confining pressure of 300 kPa, increasing the compaction degree from 90 to 93% results in a rise in failure strength from 1053.42 to 1103.07 kPa, with an increase of 4.71%, showing minimal growth as well. When the compaction degree increases from 93 to 96%, the failure strength only increases from 1103.07 to 1153.03 kPa, with an increase of 4.53%. Additionally, as the confining pressure increases, the effect of increasing compaction on enhancing the failure strength diminishes. Therefore, for the subsequent analysis of the impact of gradation on large-scale triaxial test results, the compaction degree was consistently set at 93%.

As shown in Fig. 9, under a compaction degree of D_C = 93%, the stress–strain curves for 4 gradation samples of CGSF exhibit a significant nonlinear increase with confining pressures of 100, 200 and 300 kPa, which are characteristic of typical strain hardening behaviors. At the same confining pressure, as the fractal dimension D increases, the failure strength of the sample firstly increases and then decreases. This trend is closely related to the packing state of particles. When D is smaller (indicating a higher coarse particle content), the voids between coarse particles are not fully filled with fine particles, preventing the full development of the skeleton effect, which results in lower failure strength. When D is larger (showing a greater content of fine particles), the fine particles act as a lubricant between coarse particles, leading to lower failure strength. The maximum failure strength is achieved only when the packing state between coarse particles is optimal. This optimal state occurs when the voids between coarse particles are entirely filled with fine particles, forming a robust skeleton structure.

Constitutive model

Through large-scale triaxial tests, the relationship between vertical stress (σ₁) and vertical strain (ε₁) has been captured under different confining pressures (σ₃). Subsequently, an appropriate constitutive model can be employed to describe these relationships.

Based on the analysis of large-scale triaxial test results for CGSF in Section “Analysis of experimental results”, and considering the variation of the stress–strain curves of the samples, this paper employs a logarithmic constitutive model²¹ to describe the stress–strain relationship of the samples. For the triaxial test, the stress–strain relationship curve in the logarithmic constitutive model is expressed as:

$$\sigma_{1} - \sigma_{3} = a(1 - e^{{ - b\varepsilon_{1} }} )$$

(2)

where, σ₁ and σ₃ represent the maximum and minimum principal stresses, respectively; ε₁ denotes the axial strain; while a and b are model parameters.

When ε₁ → ∞, the limit strength is reached, at which point the ultimate deviatoric stress difference $(\sigma_{1} - \sigma_{3} )_{{\text{u}}}$ is given by:

$$(\sigma_{1} - \sigma_{3} )_{{\text{u}}} = a$$

(3)

where, (σ₁-σ₃)_u represents the ultimate deviatoric stress difference.

Therefore, the model parameter a represents the ultimate deviatoric stress. Then, the tangent deformation modulus can be expressed as:

$$E_{t} = \frac{{d\sigma_{1} }}{{d\varepsilon_{1} }} = b\left[ {\left( {\sigma_{1} - \sigma_{3} } \right)_{u} - \left( {\sigma_{1} - \sigma_{3} } \right)} \right] = b\left[ {a - \left( {\sigma_{1} - \sigma_{3} } \right)} \right]$$

(4)

where, E_t represents the tangent deformation modulus.

When ε₁ = 0, σ₁–σ₃ = 0, the initial deformation modulus can be expressed as:

$$E_{i} = ab$$

(5)

where, E_i represents the initial deformation modulus.

When ε₁ = 0,$(\sigma_{1} - \sigma_{3} ) = (\sigma_{1} - \sigma_{3} )_{{\text{u}}} = a$, the ultimate tangent modulus can be expressed as²¹:

$$E_{t} = - ab\left[ {\left( {\sigma_{1} - \sigma_{3} } \right)_{u} /a - 1} \right] = 0$$

(6)

According to the Mohr–Coulomb strength criterion:

$$\left( {\sigma_{1} - \sigma_{3} } \right)_{f} = \frac{{2c\cos \varphi + 2\sigma_{3} \sin \varphi }}{1 - \sin \varphi }$$

(7)

where, c represents cohesion (kPa), and φ denotes the internal friction angle (°).

The initial elastic modulus (E_i) can be expressed as:

$$E_{i} = Kp_{a} \left( {\frac{{\sigma_{3} }}{{p_{a} }}} \right)^{n}$$

(8)

where, P_a represents atmospheric pressure, which has the same dimensional unit as σ₃. K and n are experimental constants.

Substituting the above equations into Eq. (4), and then the tangent modulus equation can be obtained:

$$E_{t} = Kp_{a} \left( {\frac{{\sigma_{3} }}{{p_{a} }}} \right)^{n} \left[ {1 - \frac{{\left( {\sigma_{1} - \sigma_{3} } \right)\left( {1 - \sin \varphi } \right)}}{{2c\cos \varphi + 2\sigma_{3} \sin \varphi }}} \right]$$

(9)

The stress–strain curve after the large-scale triaxial test in Section “Analysis of experimental results” is analyzed using the aforementioned logarithmic constitutive model (Eq. 2). The comparison of the experimental results with the above model is shown in Fig. 10, and the model parameter values are provided in (Table 3).

Fig. 10

Comparison between experimental results and model: (a) D_C = 93% D = 2.61, (b) D_C = 93% D = 2.37, (c) D_C = 93% D = 2.13, (d) D_C = 93% D = 1.89.

Table 3 Logarithmic curve model parameters.

Figure 10 and Table 3 indicate that the stress–strain curves of CGSF obtained from large-scale triaxial tests align well with the curves of the logarithmic constitutive model, with a fitting correlation coefficient exceeding 0.99. This suggests that the model effectively describes the mechanical properties of CGSF and its strain-hardening behavior under varying gradations, confining pressures, and compaction conditions. However, under higher confining pressures, such as at 300 kPa, the experimental curves for D = 2.37 and D = 1.89 gradations exhibit slight deviations when compared to the experimental results obtained at lower confining pressures.

Particle breakage analysis

A new quantitative indicator of particle breakage

Currently, in the quantitative analysis of particle breakage for geotechnical materials, the breakage rate proposed by Hardin²² has been widely used due to its ease of calculation and accurate analysis. The study utilizes this breakage rate to quantitatively analyze the particle breakage of CGSF, where the breakage rate is defined as:

$$B_{r} = \frac{{B_{t} }}{{B_{p} }}$$

(10)

where, B_r represents the breakage rate; B_t denotes the breakage amount; and B_p indicates the breakage potential.

Based on the Eq. (10), the particle breakage rate can be calculated by the area enclosed by the gradation curve before and after the experiment and the coordinate axes²³, Then Eq. (10) can be expressed as:

$$B_{r} = \frac{{B_{t} }}{{B_{p} }} = \frac{{S_{i} - S_{o} }}{{S_{0} }}$$

(11)

where, S₀ and S_i represent the areas enclosed by the gradation curves of the sample before and after the experiment, bounded by d_i = d_min and d_i = d_max.

Schematic diagram of breakage rate calculation is shown in (Fig. 11). The relationship between the cumulative percentage content and particle size in the traditional gradation curve is converted into a relationship curve between the sieve passing rate P_i and particle size x_i in a relative coordinate system. Thus, Eq. (11) can be expressed as:

$$B_{r} = \frac{{\int_{{{\text{x}}_{\min } }}^{{{\text{x}}_{\max } }} {\left[ {P_{i} ({\text{x}}_{i} ) - P_{0} ({\text{x}}_{i} )} \right]} d{\text{x}}_{i} }}{{\int_{{{\text{x}}_{\min } }}^{{{\text{x}}_{\max } }} {P_{0} ({\text{x}}_{i} )} d{\text{x}}_{i} }}$$

(12)

where, P₀(x_i) and P_i(x_i) represent the sieve passing rates of the sample before and after the experiment respectively; x_imin = d_imin/d_max = 0.075/60 = 0.000125.

Fig. 11

Schematic diagram of breakage rate calculation.

To facilitate parameter control during experimental design and the analysis of test results, section “Experimental methods” of this paper uses a fractal model gradation equation for designing the experimental plan. However, particle breakage occurs in the coarse-grained soil after the experiment, leading to changes in the gradation. To enhance the descriptive ability of the fractal equation, it was modified by replacing the relationship in Eq. (1) with a quadratic polynomial form¹¹. Equation (1) can be rewritten as:

$$\ln P_{i} = (3 - D)\ln x_{i}$$

(13)

Then, Eq. (13) is expressed by a polynomial function following Taylor’s formula:

$$\ln P_{i} = \alpha_{0} + \beta \ln x_{i} + \alpha \ln^{2} x_{i} + \alpha_{3} \ln^{3} x_{i} + \alpha_{n} \ln^{n} x_{i}$$

(14)

According to the definition of gradation, P_i = 1 when x = 1, therefore a₀ = 0. To improve the widespread applicability of Eq. (14), the model parameters need to be reduced. Therefore, Eq. (14) can be written as:

$$P_{i} (x_{i} ) = e^{{\alpha_{i} \ln^{2} (x) + \beta_{i} \ln (x)}}$$

(15)

where, α_i and β_i are model parameters.

Combining Eq. (1) and Eq. (15), substituting $P_{i} (x_{i} ) = e^{{\alpha_{i} \ln^{2} (x) + \beta_{i} \ln (x)}}$ and $P_{0} (d_{i} ) = x^{3 - D}$ into Eq. (12), then:

$$B_{r} = \frac{{\int_{{x_{\min } }}^{{x_{\max } }} {e^{{\alpha_{{\text{i}}} \ln^{2} x + \beta_{{\text{i}}} \ln x}} dx} - \int_{{x_{\min } }}^{{x_{\max } }} {x^{3 - D} dx} }}{{\int_{{x_{\min } }}^{{x_{\max } }} {x^{3 - D} dx} }}$$

(16)

where, x_min = 0.075/60 = 0.000125, x_max = 60/60 = 1.

In Eq. (16), because $\int_{{x_{\min } }}^{{x_{\max } }} {e^{{\alpha_{{\text{i}}} \ln^{2} x + \beta_{{\text{i}}} \ln x}} dx}$ is difficult to calculate, a logarithmic transformation is applied to place the particle size distribution curve in a double-logarithmic coordinate system. The area under this curve in the double-logarithmic coordinate system is used to replace the area under the original function. By taking the logarithm of both sides of Eq. (15), the following result can be obtained:

$$\ln P_{i} (x_{i} ) = \alpha_{i} \ln^{2} x_{i} + \beta_{i} \ln x_{i}$$

(17)

Thus, the integral area S_i in the double-coordinate system is:

$$S_{{\text{i}}} = \int_{0.000125}^{1} {\ln P_{i} } dx_{i} = \int_{0.000125}^{1} {(\alpha_{i} \ln^{2} x_{i} + \beta_{i} \ln x_{i} )} dx_{i} = \left| {\left. {1.988\alpha_{i} - 0.999\beta_{i} } \right|} \right.$$

(18)

Similarly, ${S}_{0}$ is

$$\begin{aligned} S_{0} = & \int_{0.000125}^{1} {\ln P_{i} } dx_{i} = \left| {(3 - D)\int_{0.000125}^{1} {1nx} dx_{i} } \right| \\ = & \left| {(3 - D)x(\ln x - 1)_{0.000125}^{1} } \right| \\ = & \left| {D - 3 + (3 - D) \times ( - 1.28 \times 10^{ - 3} )} \right| \\ = & 3 - D \\ \end{aligned}$$

(19)

Substituting Eq. (18) and Eq. (19) into Eq. (16), the breakage rate B_r is obtained:

$$B_{{\text{r}}} = \left| {\frac{{\left| {\left. {1.988\alpha_{i} - 0.999\beta_{i} } \right| - 3 + D} \right.}}{3 - D}} \right|$$

(20)

Particle breakage analysis

Collect the sample particles after the large-scale triaxial tests, place them in a 105 °C oven for 24 h to dry, and then perform particle sieving and weighing. The particle gradation of the samples before and after breakage was respectively described using the fractal gradation Eq. (1) and the modified two-parameter gradation Eq. (15), as shown in (Fig. 12). The model parameters and breakage rate values calculated using Eq. (20) are listed in (Table 4).

Fig. 12

Comparison of gradation distribution and model calculation before and after experiment: (a) D_C = 93% D = 2.61, (b) D_C = 93% D = 2.37, (c) D_C = 93% D = 2.17, (d) D_C = 93% D = 1.89.

Table 4 Model parameters and particle breakage rate.

As shown in Fig. 12 and Table 4, there is a change in the particle gradation curve of the samples after the large-scale triaxial test. (1) Both the fractal gradation equation and the modified two-parameter gradation equation effectively describe the particle gradation distribution of the samples after the experiment. While, the modified two-parameter gradation equation offers superior descriptive capability. (2) Under the same gradation conditions, as confining pressure increases, the gradation curves gradually shift upwards, and the curves area increases. This indicates that particle breakage occurs within the samples, with larger particles breaking into smaller ones, reducing the size of coarse particles while increasing the number of fine particles. The degree of particle breakage increases progressively with the confining pressure. For example, the breakage rate (B_r) of the D = 2.61 sample increases from 3.48 to 9.95% with increasing confining pressure; for the sample with D = 2.37, the breakage rate increases from 14.25 to 25.08%; for the sample with D = 2.17, it increases from 20.81 to 31.12%; and for the sample with D = 1.89, it increases from 26.75 to 40.16%. The increase in breakage rate is consistently below 15%. (3) Under the same confining pressure, when the confining pressure is 100 kPa, the breakage rate of the sample increases from 3.48 to 26.75% as the gradation parameter D decreases from 2.61 to 1.89. At a confining pressure of 200 kPa, the breakage rate increases from 6.88 to 32.26%, and at 300 kPa, it increases from 9.95 to 40.16%. These increases in breakage rate exceed 20%. Therefore, the effect of confining pressure on particle breakage is less than the influence of particle gradation. (4) As the fractal dimension increases (indicating a decrease in coarse particle content), the degree of particle breakage in the sample gradually decreases, demonstrating a clear size effect in the particle breakage of coal gangue samples.

A Constitutive model considering particle breakage

Model establishment

The relationship curve between the particle breakage rate (B_r) and confining pressure (σ₃) was plotted, introducing P_a to normalize the x-axis. As shown in Fig. 13, as confining pressure increases, B_r for all samples gradually rises. The relationship between B_r and σ₃ is distinctly nonlinear, which can be described by the following equation:

$$B_{r} = \frac{{\sigma_{3} /p_{a} }}{{e_{1} + f_{1} \cdot \sigma_{3} /p_{a} }}$$

(21)

where, σ₃ represents the confining pressure; P_a is the atmospheric pressure; e₁ and f₁ are model fitting parameters, and the values of these parameters are shown in (Table 5).

Fig. 13

Relationship between B_r and σ₃/P_a.

Table 5 Model parameters.

From Fig. 13 and Table 5, it can be observed that Eq. (21) can accurately describes the relationship between breakage rate and confining pressure, with a correlation coefficient R² exceeding 0.98.

Based on the analysis of the logarithmic constitutive model in Section “Constitutive model”, the parameter a increases with the increase in confining pressure. Under the same gradation, there is a clear nonlinear relationship between confining pressure and the model parameter a (as shown in Fig. 14). The relationship between confining pressure and parameter a can be described by the following Eq. (22):

$$a = \frac{{\sigma_{3} /p_{a} }}{{e_{2} + f_{2} \cdot \sigma_{3} /p_{a} }}$$

(22)

where, e₂ and f₂ are model parameters and the values of these parameters are shown in (Table 6).

Fig. 14

Relationship between constitutive model parameter a and σ₃/P_a.

Table 6 Model parameters.

From the analysis above, it is evident that both gradation and confining pressure have significant impacts on particle breakage. Figures 13 and 14 illustrate that B_r and parameter a exhibit a distinct nonlinear relationship with confining pressure. Furthermore, the correlation between B_r and parameter a is analyzed, as shown in (Fig. 15). The following Eq. (23) effectively describes the relationship between B_r and the parameter a:

$$a = \frac{{B_{r} }}{{e_{0} + f \cdot B_{r} }}$$

(23)

where, e₀ and f are parameters of this model, and the values of these parameters are shown in (Table 7).

Fig. 15

Relationship between breakage rate B_r and constitutive model parameter a.

Table 7 Model parameters of breakage rate B_r and constitutive model parameter a.

As shown in Fig. 15, the model parameter a exhibits a nonlinear increase as the breakage rate B_r rises. The correlation coefficients R² for all the curves exceed 0.98.

By substituting Eq. (23) into Eq. (2), the constitutive model for CGSF can been obtained:

$$\sigma_{1} - \sigma_{3} = \frac{{B_{r} }}{{e_{0} + f \cdot B_{r} }}(1 - e^{{ - b\varepsilon_{1} }} )$$

(24)

Model verification

Based on Eq. (24), the analysis of the large-scale triaxial test results for CGSF presented in Section “Analysis of experimental results” is conducted, with a comparison between the experimental data and the model curve shown in (Fig. 16).

Fig. 16

Comparison between the modified model and the test curve.

As shown in Fig. 16, the constitutive model considering particle breakage can better describe the stress–strain relationship of the specimen.

To further validate the accuracy and applicability of the proposed model, experimental data from existing studies were selected for verification analysis. Chen et al.²⁴ conducted triaxial consolidated undrained (CU) tests on coarse gneiss under confining pressures of 500, 1000, 2000, and 3000 kPa, with initial gradation fractal dimensions D₀ = 2.3, 2.5, 2.6, and 2.7. The test results are compared with the curves of the proposed constitutive model Eq. (24) that considers particle breakage, as shown in (Fig. 17 and Table 8).

Fig. 17

Comparison between modified model and gneiss test curve in²⁴.

Table 8 Modified model fitting parameters.

Figure 17 shows that the modified model describes the experimental results of gneiss coarse-grained material well, with correlation coefficients all above 0.95, confirming the accuracy of the proposed modified model.

Conclusions

• (1) Large-scale vibration compaction tests revealed that the maximum dry density of CGSF first increases and then decreases as the fractal dimension rises. The results obtained from large-scale triaxial tests indicate that the stress–strain relationship of coal gangue samples exhibits a distinct nonlinear growth pattern. As confining pressure increases, the extent of strength gain from enhanced compaction decreases. Additionally, with increasing coarse particle content, the failure strength of coal gangue samples firstly rises and then declines.

• (2) A modified quadratic polynomial fractal model gradation equation was proposed to describe the particle size distribution of samples after particle breakage during testing. Based on this model, a new quantitative index for particle breakage was developed. Analysis of particle breakage indicates that a higher confining pressure and a higher content of coarse particles lead to a greater degree of particle breakage. The particle breakage exhibits a distinct size effect. Additionally, the influence of particle gradation on the extent of breakage is greater than that of confining pressure.

• (3) Based on the logarithmic constitutive model, the stress–strain relationship of CGSF was analyzed, and the correlation between model parameters and the derived new particle breakage index was analyzed. A new constitutive model for CGSF considering particle breakage was established, and the correctness of the model was verified. In addition, the established constitutive model is slightly insufficient to capture the response of strain-softening materials.