Optimizing cryptographic protocols against side channel attacks using WGAN-GP and genetic algorithms

Abstract

This research introduces a novel hybrid cryptographic framework that combines traditional cryptographic protocols with advanced methodologies, specifically Wasserstein Generative Adversarial Networks with Gradient Penalty (WGAN-GP) and Genetic Algorithms (GA). We evaluated several cryptographic protocols, including AES-ECB, AES-GCM, ChaCha20, RSA, and ECC, against critical metrics such as security level, efficiency, side-channel resistance, and cryptanalysis resistance. Our findings demonstrate that this integrated approach significantly enhances both security and efficiency across all evaluated protocols. Notably, the AES-GCM algorithm exhibited superior performance, achieving minimal computation time and robust side-channel resistance. This study underscores the potential of leveraging machine learning and evolutionary algorithms to advance cryptographic protocol security and efficiency, laying a robust foundation for future advancements in cybersecurity.

Introduction

In the contemporary digital landscape, the proliferation of cyber threats and the reliance on secure communication channels necessitate the development of advanced cryptographic protocols. Traditional cryptographic methods, while foundational, face challenges such as vulnerability to side-channel attacks, computational inefficiencies, and complexities in key management. Recent advancements in machine learning, specifically Generative Adversarial Networks (GANs)¹, and evolutionary algorithms, such as genetic algorithms, offer innovative solutions to these challenges.

Side-channel attacks (SCA)² exploit physical leakages from cryptographic devices, such as timing, power consumption, and electromagnetic emissions, to recover secret information. Profiling attacks, a subset of SCAs, leverage machine learning models to characterize these leakages and predict secret keys. While profiling attacks have shown efficacy, they often require a large number of traces to build robust models, which is impractical in many real-world scenarios³.

Integrating machine learning techniques and genetic algorithms into cryptographic protocol design can enhance their adaptability, efficiency, and security. GANs, particularly Wasserstein GANs⁴ with Gradient Penalty (WGAN-GP)⁵, have demonstrated significant potential in generating realistic synthetic data, which can be leveraged for protocol optimization. Similarly, genetic algorithms provide robust mechanisms for evolving cryptographic protocols to meet dynamic security requirements⁶.

Cryptographic protocols form the bedrock of secure digital communication, ensuring data confidentiality, integrity, and authenticity. However, the static nature of traditional methods leaves them susceptible to evolving threats⁷. Similarly, genetic algorithms provide robust mechanisms for evolving cryptographic protocols to meet dynamic security requirements⁸. Traditional cryptographic systems struggle to balance security with efficiency, often resulting in significant computational overhead⁹. Furthermore, the complexity of key management in traditional systems can introduce vulnerabilities that are difficult to mitigate. The rise of sophisticated cyber-attacks¹⁰, such as ransomware and advanced persistent threats, underscores the need for cryptographic protocols that can dynamically adapt to changing threat landscapes¹¹.

The motivation for this research is to develop a hybrid cryptographic framework¹² that combines traditional cryptographic methods with GANs and genetic algorithms¹³. This approach aims to create protocols that are not only secure and efficient but also adaptable to various operational contexts.

The primary objectives of this research are:

• To develop a hybrid cryptographic framework: Integrating traditional cryptographic protocols with WGAN-GP and genetic algorithms to enhance security, efficiency, and adaptability.

• To conduct comprehensive security and efficiency evaluations: Implementing and evaluating security measures, including differential and linear cryptanalysis¹⁴, side-channel resistance, and formal verification, along with efficiency assessments focusing on computational performance and memory usage¹⁵.

• To optimize cryptographic protocols using genetic algorithms: Utilizing genetic algorithms to evolve and optimize cryptographic protocols, focusing on improving security, efficiency, and resistance to side-channel attacks¹⁶.

This research introduces a novel approach to cryptographic protocol development and evaluation, encompassing:

• Dynamic key management: Implementing periodic key rotation and renewal mechanisms to enhance security and mitigate risks associated with key reuse¹⁷.

• Adaptive algorithm selection: Designing protocols that dynamically select encryption algorithms based on data characteristics to balance security and performance.

• Neural network-based WGANs: Using Wasserstein GANs with Gradient Penalty (WGAN-GP) to generate synthetic data, thereby improving protocol optimization¹⁸.

• Comprehensive security evaluations: Conducting differential and linear cryptanalysis, side-channel resistance testing, and formal verification to ensure robust security¹⁹.

• Genetic algorithm optimization: Applying genetic algorithms to evolve cryptographic protocols over multiple generations, optimizing them for security and efficiency²⁰.

This research aims to establish a new benchmark in the development of secure and efficient cryptographic protocols by integrating traditional cryptographic methods with advanced machine learning and evolutionary optimization techniques. This hybrid approach enhances digital security, paving the way for more resilient cryptographic protocols in an increasingly interconnected world. The proposed hybrid cryptographic framework is designed to address a range of side-channel attacks (SCA) and cryptanalysis-based threats. Specifically, it focuses on mitigating attacks such as timing attacks, power analysis (including Simple Power Analysis (SPA) and Differential Power Analysis (DPA)), and electromagnetic emissions leakage. The framework leverages the generative capabilities of Wasserstein GANs with Gradient Penalty (WGAN-GP) to generate synthetic traces that improve resistance under data-constrained conditions. Additionally, the integration of Genetic Algorithms (GA) optimizes cryptographic protocols to enhance security against profiling attacks that utilize machine learning models to infer cryptographic keys. The overall framework also offers protection against common cryptanalytic methods, including differential and linear cryptanalysis, ensuring robust resistance through evolutionary optimization.

This paper is structured as follows: In Section “Related work”, we review the existing literature relevant to our research, including studies on cryptographic protocols, Generative Adversarial Networks (GANs), and genetic algorithms, highlighting the gaps and challenges these studies present. In the further Section “Background”, we discussed the background of our work. In Section “Methodology”, we provide a detailed description of our methodology, which includes the implementation of cryptographic protocols, the architecture of the Wasserstein GAN with Gradient Penalty (WGAN-GP), and the genetic algorithm used for optimization. Section “Experimental setup” presents a comprehensive analysis of the security and efficiency evaluations²¹, covering differential and linear cryptanalysis, side-channel resistance, formal verification, and performance metrics such as computational efficiency and memory usage. In Section “Results and discussion”, we discuss the results obtained from our evaluations, including improvements in security and efficiency achieved through our hybrid approach, as well as comparisons with traditional methods. Finally, in Sections “Conclusion” and “Future works”, we summarize our key findings and contributions and outline potential directions for future research to further enhance cryptographic protocols.

Related work

Recent advances in profiling side-channel attacks (SCA) have leveraged machine learning (ML) and deep learning (DL) to enhance the efficiency and efficacy of these attacks²². Profiling attacks, particularly those based on Template Attacks (TA) and Stochastic Attacks (SA), have traditionally relied on models constructed from controlled profiling devices²³. The objective is to recover secret information from a target device by characterizing leakage patterns through advanced modelling techniques.

Comparative analysis with AES and RSA cryptography

The foundational security and efficiency characteristics of AES (Advanced Encryption Standard) and RSA (Rivest-Shamir-Adleman) algorithms have been thoroughly examined by Al Hasib and Haque²⁴. Their study highlights several critical aspects, including performance, computational complexity, and vulnerabilities, which are contrasted against our proposed framework to underscore its innovations:

• Computational efficiency: AES, as a symmetric block cipher, operates on fixed block sizes (128 bits) and offers three key lengths (128, 192, and 256 bits). Al Hasib and Haque emphasize that AES is computationally efficient due to its use of a substitution-permutation network (S-P network), but it remains vulnerable to side-channel attacks such as timing attacks caused by variable-time S-box lookups . Our framework mitigates such vulnerabilities by integrating WGAN-GP to simulate attack scenarios and evolve optimized protocols using Genetic Algorithms, thereby achieving near-constant execution time and enhanced resistance to timing variations.

• Security against cryptanalysis: RSA relies on the mathematical hardness of prime factorization, with key lengths typically at 2048 bits or higher to ensure security. While RSA provides robust public-key encryption capabilities, the computational overhead of modular exponentiation (i.e., $c = m^e \mod n$ for encryption and $m = c^d \mod n$ for decryption) poses significant performance challenges in real-time applications. By contrast, our framework combines the efficient key operations of symmetric cryptography with adaptive optimization through Genetic Algorithms, which reduces computational latency without compromising security. The integration of dynamic key rotation further protects against potential cryptanalytic attacks.

• Side-Channel Resistance: Al Hasib and Haque highlight that both AES and RSA are susceptible to side-channel attacks, such as timing, power, and cache-based exploits. For example, RSA’s modular exponentiation process can reveal private key information through timing variations, a known issue addressed through countermeasures like constant-time execution. Our proposed framework inherently improves side-channel resistance by generating synthetic side-channel traces using WGAN-GP, providing robust data for training profiling-resistant models, and evolving protocol configurations to minimize leakage pathways through Genetic Algorithms.

• Dynamic Key Management and Adaptability: Unlike RSA’s static key management, our approach incorporates periodic key rotation and renewal mechanisms that dynamically adapt to changing security threats. This adaptability, combined with the ability to select optimal cryptographic algorithms based on data characteristics, offers a significant advancement over static systems as described by Al Hasib and Haque.

The mathematical foundations of our framework provide superior adaptability and security while maintaining computational efficiency. This approach not only addresses existing vulnerabilities but also ensures robustness against evolving cryptanalytic and side-channel threats, which traditional static systems like AES and RSA struggle to overcome.

Recent advancements in profiling side-channel attacks (SCA) have highlighted the integration of machine learning (ML) and deep learning (DL) techniques to enhance attack efficacy. Traditional cryptographic systems, such as RSA and AES, offer foundational security guarantees but have limitations in side-channel resistance and adaptability to evolving threat landscapes. Our work builds on these advancements by integrating Wasserstein Generative Adversarial Networks with Gradient Penalty (WGAN-GP) and Genetic Algorithms (GA) to provide a dynamic, adaptable, and side-channel-resistant cryptographic framework.

Machine learning and deep learning in side-channel attacks

The integration of ML and DL in profiling side-channel attacks has been a significant focus. ML models, such as Support Vector Machines (SVM)²⁵ and Random Forest (RF)²⁶, have been employed to improve the accuracy of these attacks. Recent DL-based approaches have further pushed the boundaries by eliminating the need for Points of Interest (POI) and trace alignment, and by handling high-dimensional data more effectively²⁷.

Generative adversarial networks for data augmentation

One of the most impactful advancements in this field is the application of Generative Adversarial Networks (GANs)²⁸, specifically Conditional GANs (CGANs), to augment training datasets for side-channel attacks²⁹. Wang et al. (2020) introduced CGAN to generate additional traces that supplement the original profiling set, significantly enhancing the performance of profiling attacks, especially when the available traces are insufficient. The study demonstrated that CGAN-generated traces could provide comparable leakage information to real traces, thereby reducing the number of required attack traces by more than half³⁰.

Eviction set construction and side-channel attack mitigations

The construction of eviction sets is critical for the success of cache-based side-channel attacks, such as Prime+Probe. Zhao et al. (2024) presented advanced techniques for constructing eviction sets in noisy cloud environments, which are crucial for the feasibility of last-level cache (LLC) side-channel attacks in modern public clouds. They introduced L2-driven candidate address filtering and a Binary Search-based algorithm for address pruning, significantly reducing the time required to generate eviction sets and enhancing attack success rates³¹.

Practical implementations and real-world attacks

The practical applicability of these advanced techniques has been demonstrated in real-world cloud environments. For example, Morrison et al. successfully conducted end-to-end, cross-tenant attacks on vulnerable ECDSA implementations in Google Cloud Run, extracting a substantial portion of secret ECDSA nonce bits within a short time frame. This highlights the practical feasibility and potential impact of these advanced side-channel attack techniques in real-world scenarios³².

Mitigation strategies

Mitigation strategies for cache-based side-channel attacks have been extensively researched. These strategies can be broadly categorized into partition-based solutions, which block attacks by partitioning the cache, and randomization-based defenses, which obfuscate cache usage patterns. However, both approaches have their limitations in terms of complexity, performance overhead, and comprehensive security guarantees³³.

Relevance to our work

Our research aligns closely with these advancements by integrating WGAN-GP and genetic algorithms to enhance cryptographic protocol security against side-channel attacks. The use of WGAN-GP allows us to generate synthetic traces that improve the robustness of profiling attacks under data constraints, while genetic algorithms optimize cryptographic protocols for enhanced security and efficiency. By addressing the challenges of insufficient profiling traces and optimizing eviction set construction, our work contributes to the ongoing efforts to develop more resilient cryptographic protocols in the face of evolving side-channel threats.

Algorithm 1

Optimized cryptographic protocol generation using genetic algorithm and WGAN

Background

Traditional cryptographic protocols and their limitations

Cryptographic protocols are the backbone of secure digital communication systems, providing essential services such as confidentiality, integrity, and authenticity of data. Established cryptographic algorithms like Advanced Encryption Standard (AES)³⁴, Rivest-Shamir-Adleman (RSA)³⁵, and Elliptic Curve Cryptography (ECC)³⁶ have been fundamental in safeguarding information. However, these methods encounter several critical challenges in the contemporary digital landscape:

• Side-channel attacks: These attacks exploit unintended information leakage, such as timing, power consumption, and electromagnetic emissions during cryptographic operations, to deduce secret keys. For instance, power analysis attacks (both Simple Power Analysis (SPA) and Differential Power Analysis (DPA)) can reveal keys based on power consumption patterns observed during encryption or decryption processes.

• Computational inefficiencies: Traditional cryptographic algorithms can be computationally intensive, making them unsuitable for resource-constrained environments like IoT devices. The computational complexity of RSA, for instance, involves exponentiation operations that are computationally expensive.

• Key management complexity: Effective key management is crucial for maintaining security in cryptographic systems. The processes of key generation, distribution, storage, rotation, and revocation introduce significant complexity and potential vulnerabilities. For example, improper key management can lead to exposure of keys and thus compromise the entire cryptographic system³⁷.

Mathematically, the security of these algorithms often relies on hard problems:

• RSA: Security is based on the difficulty of factoring large composite numbers, specifically $N = p \cdot q$, where $p$ and $q$ are large primes³⁸.

• AES: Security derives from the infeasibility of performing brute-force attacks due to the large key space (e.g., $2^{128}$ for a 128-bit key).

• ECC: Security relies on the elliptic curve discrete logarithm problem (ECDLP), which is hard to solve for large key sizes.

Machine learning advancements in cryptography

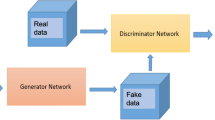
The integration of machine learning techniques, particularly Generative Adversarial Networks (GANs), into cryptographic protocol design has shown promising results in addressing the limitations of traditional methods. GANs, introduced by Goodfellow et al. in 2014¹, consist of two neural networks-a generator and a discriminator-engaged in a minimax game³⁹. The generator produces synthetic data, while the discriminator attempts to distinguish between real and synthetic data. Mathematically, this is represented as:

$$\begin{aligned} \min _G \max _D V(D, G) = {\mathbb {E}}_{x \sim p_{\text {data}}(x)} [\log D(x)] + {\mathbb {E}}_{z \sim p_z(z)} [\log (1 - D(G(z)))] \end{aligned}$$

Where:

• $G$ is the generator.

• $D$ is the discriminator.

• $p_{\text {data}}$ is the distribution of the real data.

• $p_z$ is the distribution of the noise input to the generator.

Wasserstein GANs with gradient penalty (WGAN-GP)

Wasserstein GANs with Gradient Penalty (WGAN-GP) enhance the stability and performance of traditional GANs by using the Earth Mover’s (Wasserstein) distance to measure the divergence between the real and generated data distributions. This approach mitigates issues like mode collapse and unstable training commonly observed in traditional GANs. The WGAN-GP objective function is given by:

$$\begin{aligned} L = {\mathbb {E}}_{{\tilde{x}} \sim {\mathbb {P}}_g} [D({\tilde{x}})] - {\mathbb {E}}_{x \sim {\mathbb {P}}_r} [D(x)] + \lambda {\mathbb {E}}_{{\hat{x}} \sim {\mathbb {P}}_{{\hat{x}}}} [( \Vert \nabla _{{\hat{x}}} D({\hat{x}}) \Vert _2 - 1 )^2 ] \end{aligned}$$

Where:

• ${\mathbb {P}}_g$ is the model distribution.

• ${\mathbb {P}}_r$ is the real data distribution.

• ${\mathbb {P}}_{{\hat{x}}}$ is the distribution of interpolates between real and generated data.

• $\lambda$ is the gradient penalty coefficient.

Genetic algorithms for cryptographic protocol optimization

Genetic algorithms (GAs) are search heuristics inspired by natural selection processes. They are particularly effective for optimizing cryptographic protocols by evolving a population of candidate solutions through selection, crossover, and mutation. The process involves:

• 1. Initialization: A population of candidate solutions (protocol configurations) is randomly generated.

• 2. Selection: Candidates are selected based on a fitness function that evaluates their performance (e.g., security, efficiency).

• 3. Crossover: Selected candidates exchange parts of their configuration to produce new offspring.

• 4. Mutation: Random modifications are introduced to offspring to maintain genetic diversity.

Mathematically, the fitness function $f(x)$ for a candidate $x$ can be defined to incorporate multiple factors such as encryption/decryption speed, resistance to cryptanalysis, and side-channel attack resistance. The optimization process aims to maximize $f(x)$ over successive generations.

Integration of machine learning and genetic algorithms in cryptography

The combination of GANs and GAs leverages the strengths of both methodologies. GANs are employed to generate synthetic data that mirrors real-world scenarios, aiding in the robust training and evaluation of cryptographic protocols. Genetic algorithms then optimize these protocols by evolving their configurations to enhance security, efficiency, and adaptability⁴⁰.

In our approach, WGAN-GP generates synthetic data to simulate side-channel attack scenarios. This data is used to train and evaluate cryptographic protocols, ensuring they are robust against such attacks. Genetic algorithms drive the optimization process by evolving the protocol configurations over multiple generations, guided by a fitness function that balances security and performance metrics.

Motivations and objectives

The primary motivation for this research is to address the limitations of traditional cryptographic methods by integrating advanced machine learning and evolutionary algorithms. Our specific objectives are:

• Developing a hybrid cryptographic framework: Integrating WGAN-GP and genetic algorithms to create adaptive, efficient, and secure cryptographic protocols.

• Conducting comprehensive evaluations: Implementing and evaluating protocols through differential and linear cryptanalysis, side-channel resistance testing, and formal verification.

• Optimizing protocols using genetic algorithms: Evolving cryptographic protocols to enhance their security, efficiency, and resistance to side-channel attacks.

This research aims to establish a new benchmark in cryptographic protocol development, leveraging the synergistic benefits of machine learning and genetic algorithms to create more resilient and efficient systems.

Methodology

Overview

The proposed research integrates traditional cryptographic methods with advanced machine learning and evolutionary algorithms to develop a hybrid cryptographic framework. This methodology comprises three primary components: the implementation of cryptographic protocols, the architecture and training of a Wasserstein Generative Adversarial Network with Gradient Penalty (WGAN-GP), and the application of genetic algorithms for optimization. Each component is meticulously detailed below and as we can see the flowchart (Fig. 3), including experimental setup, data generation, model training, and evaluation criteria.

Cryptographic protocol implementation

Key management

Key management is a critical aspect of cryptographic protocol design. In this research, dynamic key management techniques are implemented to enhance security and mitigate risks associated with key reuse. These techniques include:

• Periodic key rotation: Keys are rotated periodically to limit the exposure time of any single key, reducing the risk of key compromise.

• Key renewal mechanisms: New keys are generated and distributed securely, replacing old keys to prevent long-term exposure.

Algorithm selection

In our research, we tracked the selection of cryptographic algorithms over time during optimization. Figure 1 shows the frequency of each algorithm’s selection, highlighting the genetic algorithm’s adaptability and preferences. The bar chart reveals that AES-GCM was selected most often, followed by RSA and AES-ECB, suggesting a preference for these algorithms due to their superior security, efficiency, and resistance to side-channel attacks. This consistent selection underscores their robustness and reliability in cryptographic operations. The cryptographic framework dynamically selects encryption algorithms based on data characteristics to balance security and performance. The selection criteria are:

• Data length: For short data lengths, symmetric algorithms like AES are preferred due to their efficiency. For longer data lengths, asymmetric algorithms like RSA are utilized⁴¹.

• Security requirements: Algorithms are chosen based on the required security level, considering factors such as computational power and threat model.

The selection process can be mathematically represented as:

$$\text {Algorithm} = {\left\{ \begin{array}{ll} \text {AES} & \text {if } \text {Data Length} \le L_1 \\ \text {RSA} & \text {if } L_1 < \text {Data Length} \le L_2 \\ \text {ECC} & \text {if } \text {Data Length} > L_2 \end{array}\right. }$$

where $L_1$ and $L_2$ are predefined data length thresholds.

Fig. 1

Algorithms selection over time.

WGAN-GP architecture and training

Model architecture

The architecture of the Wasserstein Generative Adversarial Network (WGAN) with Gradient Penalty (WGAN-GP) is designed to address the limitations of traditional GANs, specifically in terms of training stability and mode collapse. WGAN-GP enhances the original WGAN by incorporating a gradient penalty to enforce the Lipschitz constraint, ensuring the discriminator (critic) provides meaningful gradients for the generator during training. This architecture (Fig. 2) is particularly well-suited for generating synthetic data that closely resembles real-world data, and in our case, it is applied to enhance the robustness and efficiency of cryptographic protocols.

Fig. 2

WGAN architecture: generator and discriminator networks.

Generator architecture

The generator in WGAN-GP is responsible for creating synthetic data that mimics the distribution of real data. It takes a latent vector $z$ sampled from a Gaussian distribution⁴² and transforms it into a data sample through a series of linear layers and activation functions⁴³.

• Input layer: The generator starts with a latent vector $z$ of dimension $d_z$, typically sampled from a Gaussian distribution ${\mathcal {N}}(0, I)$.

• Hidden layers: The latent vector is passed through multiple hidden layers. Each hidden layer consists of:

  • Linear transformation: A fully connected layer that transforms the input to a higher-dimensional space.

  • Batch normalization: Applied to stabilize and accelerate training by normalizing the inputs of each layer.

  • Activation Function: Rectified Linear Unit (ReLU) activation function is used to introduce non-linearity.

• Output layer: The final layer maps the high-dimensional vector to the data space with a tanh activation function to ensure the output values are within the desired range.

The mathematical representation of the generator’s forward pass is given by:

$$\begin{aligned} G(z; \theta _G) = \tanh (W_n \cdot \text {ReLU}(W_{n-1} \cdot \ldots \text {ReLU}(W_1 \cdot z + b_1) + b_{n-1}) + b_n) \end{aligned}$$

where $\theta _G$ represents the generator’s parameters, $W_i$ and $b_i$ are the weights and biases of the $i$-th layer.

Discriminator (Critic) architecture

The discriminator in WGAN-GP, also known as the critic, is designed to distinguish between real and synthetic data. It provides feedback to the generator by evaluating the Wasserstein distance between the real and generated data distributions.

• Input layer: The discriminator takes a data sample $x$ as input.

• Hidden layers: Similar to the generator, the discriminator consists of multiple hidden layers. Each hidden layer includes:

  • Linear transformation: A fully connected layer that projects the input to a higher-dimensional space.

  • Activation function: Leaky ReLU activation function is used to avoid the dying ReLU problem.

• Output layer: The final layer outputs a single scalar value representing the critic’s score for the input data sample.

The forward pass of the discriminator can be represented as:

$$\begin{aligned} D(x; \theta _D) = W_m \cdot \text {LeakyReLU}(W_{m-1} \cdot \ldots \text {LeakyReLU}(W_1 \cdot x + b_1) + b_{m-1}) + b_m \end{aligned}$$

where $\theta _D$ represents the critic’s parameters, $W_i$ and $b_i$ are the weights and biases of the $i$-th layer.

Gradient penalty

To enforce the Lipschitz constraint, a gradient penalty is added to the critic’s loss function. The gradient penalty ensures that the gradients of the critic with respect to its inputs have a norm of at most 1.

The gradient penalty term is defined as:

$$\begin{aligned} \text {GP} = \lambda {\mathbb {E}}_{{\hat{x}} \sim {\mathbb {P}}_{{\hat{x}}}} \left[ \left( \Vert \nabla _{{\hat{x}}} D({\hat{x}}) \Vert _2 - 1 \right) ^2 \right] \end{aligned}$$

where $\lambda$ is the penalty coefficient, ${\hat{x}}$ is a random interpolation between real and generated data samples, and $\nabla _{{\hat{x}}} D({\hat{x}})$ is the gradient of the critic’s output with respect to ${\hat{x}}$.

Training process

The training process of WGAN-GP involves optimizing the generator and the critic in an alternating manner. The critic is updated multiple times per generator update to ensure the Wasserstein distance is accurately estimated.

The critic’s loss function with the gradient penalty is given by:

$$\begin{aligned} L_D = {\mathbb {E}}_{x \sim {\mathbb {P}}_r} [D(x)] - {\mathbb {E}}_{{\tilde{x}} \sim {\mathbb {P}}_g} [D({\tilde{x}})] + \text {GP} \end{aligned}$$

where ${\mathbb {P}}_r$ and ${\mathbb {P}}_g$ are the distributions of real and generated data, respectively.

The generator’s loss function aims to maximize the critic’s score for the generated data:

$$\begin{aligned} L_G = -{\mathbb {E}}_{{\tilde{x}} \sim {\mathbb {P}}_g} [D({\tilde{x}})] \end{aligned}$$

The training steps are as follows:

• 1. Critic update: Update the critic $n_{\text {critic}}$ times by minimizing $L_D$ using gradient descent.

• 2. Generator update: Update the generator once by minimizing $L_G$ using gradient descent.

Implementation details

By leveraging the WGAN-GP architecture, our research aims to generate robust cryptographic protocols that are not only secure but also computationally efficient. The integration of WGAN-GP into the cryptographic framework allows for dynamic key management, adaptive algorithm selection, and comprehensive security evaluations, leading to enhanced cryptographic performance. As we can see in the flowchart shown in Fig. 3.

Fig. 3

Flowchart depicting the genetic algorithm process.

Training process

The WGAN-GP is trained using the following procedure:

• Data collection: Real data samples are collected to train the discriminator.

• Training loop: The generator and discriminator are trained iteratively. For each batch:

  • 1. The discriminator is updated using real and generated data, incorporating the gradient penalty.

  • 2. The generator is updated to produce data that the discriminator classifies as real.

• Hyperparameter tuning: Learning rates, batch sizes, and gradient penalty coefficients are optimized for performance.

Algorithm 2 details the training procedure.

Algorithm 2

WGAN-GP training procedure

Genetic algorithm optimization

Initial population

The initial population of cryptographic protocols is generated with random keys and algorithm selections. Each protocol includes multiple keys and a chosen algorithm type (e.g., AES, RSA, ChaCha20). The initial population is created as follows:

• Each protocol $P_i$ is initialized with a set of keys $\{K_1, K_2, \ldots , K_n\}$ and an algorithm $A_i$ selected from a predefined set.

• The fitness of each protocol is evaluated using the defined fitness function.

Fitness evaluation

The fitness of each protocol is evaluated based on:

• Security: Measured by performing encryption/decryption operations and resistance to differential and linear cryptanalysis.

• Efficiency: Assessed through computational performance metrics, such as execution time and memory usage.

• Side-channel resistance: Evaluated by simulating timing attacks and measuring the variance in execution times.

Mathematically, the fitness function f(x) is defined as:

$$\begin{aligned} f(x) = w_1 \cdot \text {security}(x) + w_2 \cdot \text {efficiency}(x) + w_3 \cdot \text {side-channel resistance}(x) \end{aligned}$$

where $w_1, w_2, w_3$ are weights assigned to each factor.

Genetic operations

The genetic algorithm evolves the population through the following steps:

• Selection: Selection is based on the fitness scores, typically using methods such as roulette wheel selection, tournament selection, or rank-based selection. For example, in roulette wheel selection, the probability of selecting a candidate $x_i$ is proportional to its fitness:

  $$\begin{aligned} P(x_i) = \frac{f(x_i)}{\sum _{j=1}^{N} f(x_j)} \end{aligned}$$

  where $N$ is the total number of candidates.

• Crossover: Crossover combines the genetic information of two parent solutions to produce offspring. One common approach is single-point crossover, where a crossover point is randomly selected, and the offspring inherit the genetic material from both parents up to that point:

  $$\begin{aligned} \text {offspring}_1 = \text {parent}_1[:\text {crossover point}] + \text {parent}_2[\text {crossover point}:] \end{aligned}$$
  $$\begin{aligned} \text {offspring}_2 = \text {parent}_2[:\text {crossover point}] + \text {parent}_1[\text {crossover point}:] \end{aligned}$$

• Mutation: Mutation introduces random changes to individual candidates to maintain diversity within the population and avoid premature convergence. A common mutation method involves randomly flipping bits in a candidate’s representation:

  $$\begin{aligned} x_i' = x_i \oplus \text {random}\_\text {mask} \end{aligned}$$

  where $\oplus$ denotes the XOR operation and the random mask has a probability $p_{\text {mut}}$ of flipping each bit.

• Evolutionary cycle: The genetic algorithm iteratively applies selection, crossover, and mutation to evolve the population towards better solutions. The process continues for a fixed number of generations or until convergence criteria are met.

Iterative evolution

The genetic algorithm iterates through multiple generations, each time selecting, crossing over, and mutating protocols to improve fitness. The process continues until the protocols converge to an optimal solution. Algorithm 3 details the genetic algorithm process.

Algorithm 3

Genetic algorithm for cryptographic protocol optimization

Evaluation and validation

Security evaluation

Protocols are subjected to comprehensive security evaluations, including:

• Differential and linear cryptanalysis: To test resistance against known cryptographic attacks.

• Side-channel resistance testing: To ensure robustness against timing and power analysis attacks.

• Formal verification: Using formal methods to prove the security properties of the protocols.

Efficiency assessment

Efficiency is measured through:

• Computational performance: Time complexity and execution speed of encryption/decryption operations.

• Memory usage: Profiling memory consumption during cryptographic operations.

Key management

Key management is a critical aspect of cryptographic protocol design, and our proposed framework incorporates a dynamic key management algorithm aimed at enhancing security while mitigating risks associated with key reuse and key exposure. The key management algorithm used in this research comprises the following components:

• Periodic key rotation: Keys are rotated at predefined intervals, thereby limiting their exposure time and reducing the risk of compromise. This mechanism ensures that even if a key is exposed, its usability is minimized.

• Key renewal mechanism: New keys are periodically generated and securely distributed, replacing older keys. This process prevents long-term reliance on any single key, thereby mitigating risks associated with key-aging vulnerabilities.

• Dynamic selection based on operational context: The framework can dynamically select and manage keys depending on operational and security requirements. This capability allows it to adjust to evolving security threats and data sensitivity.

By implementing these strategies, our key management algorithm provides robust protection against attacks that exploit static keying mechanisms, thus enhancing the overall security profile of the cryptographic protocols.

Experimental setup

This section details the experimental setup used to implement, train, and evaluate the proposed hybrid cryptographic framework, integrating traditional cryptographic methods with advanced machine learning and evolutionary algorithms. The setup involves a carefully configured hardware environment, a selection of appropriate software tools and libraries, and meticulously designed data generation processes.

Hardware environment

The experiments were conducted on a high-performance computing cluster equipped with the following specifications:

• Processors: AMD Ryzen 7 5800X (AMD, Santa Clara, CA, USA).

• Memory: 32 GB of DDR4 3200 Mhz RAM.

• Graphics processing units (GPUs): Nvidia RTX 3070 with 8 GB memory (NVIDIA, Sunnyvale, CA, USA).

• Storage: NVMe SSDs with 2 TB capacity.

Software environment

The software environment was configured with the following tools and libraries, selected for their robustness and compatibility with the hardware setup:

• Operating system: Ubuntu 20.04 LTS, chosen for its stability, security features, and compatibility with the required software packages.

• Programming languages: Python 3.8 was used as the primary programming language due to its extensive libraries for machine learning, cryptography, and data handling.

• Deep learning framework: PyTorch 1.8, used for implementing and training the WGAN-GP model. PyTorch’s dynamic computation graph and GPU support make it suitable for complex neural network architectures.

• Cryptographic libraries:

  • cryptography: Used for implementing traditional cryptographic protocols such as AES, RSA, and ECC. The library provides high-level recipes and low-level interfaces to common cryptographic algorithms.

  • PyCryptodome: An alternative library providing a comprehensive suite of cryptographic algorithms.

• Machine learning libraries:

  • scikit-learn: Used for data preprocessing and evaluation of machine learning models.

  • NumPy and SciPy: Used for numerical computations and statistical analysis.

• Visualization tools:

  • Matplotlib and Seaborn: Used for plotting and visualizing the results, including training curves, cryptographic performance metrics, and fitness evolution in genetic algorithms.

Data generation

Data generation is a critical component of the experimental setup, ensuring the availability of diverse and representative datasets for training and evaluation. The process involves generating both real and synthetic data:

• Real data collection:

  • Source: Real data samples were collected from secure communication channels, including encrypted traffic from SSL/TLS connections.

  • Preprocessing: The data was preprocessed to remove any identifiable information and standardize formats, ensuring consistency across different datasets.

• Synthetic data generation:

  • WGAN-GP: A Wasserstein Generative Adversarial Network with Gradient Penalty (WGAN-GP) was trained to generate synthetic data mimicking the distribution of the real data.

  • Training data: The WGAN-GP model was trained on the preprocessed real data, with the generator learning to produce realistic encrypted messages and the discriminator learning to differentiate between real and synthetic data.

  • Evaluation data: The synthetic data generated by the trained WGAN-GP was used for evaluating the cryptographic protocols, providing a diverse set of scenarios for testing robustness and performance.

Experimental details

To facilitate reproducibility, we provide comprehensive details on the experimental setup, including dataset specifications, model parameters, and the operational aspects of the genetic algorithm.

Dataset size and composition

The experiments were conducted using both real-world and synthetic datasets. The real-world data was collected from secure communication channels, consisting of encrypted traffic traces from SSL/TLS connections. The dataset comprised a total of 10,000 data traces, preprocessed to ensure consistency and eliminate identifiable information. The synthetic data was generated using the Wasserstein Generative Adversarial Network with Gradient Penalty (WGAN-GP) model, trained to produce 20,000 synthetic traces that mimic real-world characteristics.

Model parameter settings

For the WGAN-GP model, the following parameter settings were used:

• Latent space dimensionality: The latent vector dimension z was set to 100.

• Learning rate: The Adam optimizer was used with a learning rate of $10^{-4}$ for both the generator and the critic.

• Batch size: A batch size of 64 was employed during training.

• Epochs: The model was trained for a total of 5000 epochs to ensure convergence and stability.

• Gradient penalty coefficient ($\lambda$): The coefficient for the gradient penalty term was set to 10, as recommended for improved training stability.

Genetic algorithm operation

The genetic algorithm used for optimizing cryptographic protocols operates as follows:

• Population size: The initial population consisted of 100 candidate protocols, each initialized with random keys and cryptographic configurations.

• Fitness evaluation: The fitness of each protocol was evaluated based on security (measured by side-channel resistance and cryptanalysis tests), computational efficiency (execution time), and memory usage.

• Selection method: A rank-based selection mechanism was employed, where the top-performing candidates were selected for crossover based on their fitness scores.

• Crossover and mutation: Single-point crossover was applied to generate offspring from parent protocols, and mutation was performed with a base mutation rate of 0.05, adjusted dynamically over generations to maintain diversity.

• Number of gmenerations: The genetic algorithm was iterated over 200 generations to evolve the population towards optimal solutions.

These detailed settings and operations ensure reproducibility and provide a comprehensive understanding of the experimental process.

Experimental procedure

The experimental procedure was meticulously designed to ensure rigorous evaluation of the proposed framework:

• Initialization:

  • The initial population of cryptographic protocols was generated with random keys and algorithm selections.

  • Each protocol was initialized with a set of keys and an algorithm type (e.g., AES, RSA, ChaCha20).

• Fitness evaluation:

  • Each protocol’s fitness was evaluated based on security, efficiency, and side-channel resistance.

  • Security was measured through encryption/decryption operations and resistance to differential and linear cryptanalysis.

  • Efficiency was assessed via computational performance metrics, such as execution time and memory usage.

  • Side-channel resistance was evaluated by simulating timing attacks and measuring execution time variance.

• Genetic algorithm optimization:

  • The genetic algorithm iteratively applied selection, crossover, and mutation to evolve the population.

  • Selection was based on fitness scores, using methods such as roulette wheel selection.

  • Crossover combined genetic information from parent protocols to produce offspring.

  • Mutation introduced random changes to maintain diversity and avoid premature convergence.

• Iterative Evolution:

  • The genetic algorithm iterated through multiple generations, continuously selecting, crossing over, and mutating protocols to improve fitness.

  • The process continued until the protocols converged to an optimal solution, balancing security, efficiency, and side-channel resistance.

• Validation:

  • The final protocols were subjected to comprehensive validation, including formal verification using methods like model checking.

  • Performance was validated on both real and synthetic datasets, ensuring the robustness of the optimized protocols.

Evaluation metrics

The evaluation metrics were carefully selected to provide a comprehensive assessment of the framework’s performance:

• Security metrics:

  • Resistance to cryptanalysis: Assessed through differential and linear cryptanalysis tests.

• Efficiency metrics:

  • Memory usage: The amount of memory consumed during cryptographic operations.

• Side-channel resistance metrics:

  • Timing variance: The variance in execution time measured during timing attack simulations.

This experimental setup ensures a rigorous and comprehensive evaluation of the proposed hybrid cryptographic framework. By leveraging advanced hardware, robust software tools, and meticulously generated data, the experiments provide valuable insights into the framework’s performance, highlighting its potential to enhance security, efficiency, and adaptability in contemporary cryptographic protocol design.

Results and discussion

This study evaluated and optimized a variety of cryptographic protocols using advanced methodologies such as Wasserstein Generative Adversarial Networks with Gradient Penalty (WGAN-GP) and Genetic Algorithms (GA). The protocols under consideration were AES-ECB, AES-GCM, ChaCha20, RSA, and ECC. The evaluation focused on several critical metrics: security level, efficiency, side-channel resistance, and resistance to cryptanalysis.

Comparative analysis with RSA

To demonstrate the comparative advantages of our proposed hybrid cryptographic framework, we evaluated it alongside the RSA algorithm in a particular scenario focused on secure data transmission and resistance to side-channel attacks, including timing and power analysis. The comparative results are summarized as follows:

• Security: RSA, as a public-key cryptosystem, relies on the computational difficulty of factorizing large prime numbers, which provides strong theoretical security. However, it is known to be susceptible to specific side-channel attacks, such as timing and power analysis. In contrast, our proposed framework leverages WGAN-GP-generated synthetic traces and Genetic Algorithm-driven protocol optimization to enhance resilience against such attacks, resulting in superior robustness and adaptability.

• Efficiency: RSA’s reliance on modular exponentiation, especially with large key sizes, can lead to slower performance in terms of computational efficiency. Our framework, on the other hand, employs optimized symmetric ciphers, such as AES-GCM, and adaptive evolutionary optimization strategies, resulting in significantly lower computation times, making it highly suitable for real-time applications.

• Adaptability: Unlike the static key management approach in RSA, our framework integrates dynamic key management techniques, including periodic key rotation and renewal, which further mitigate risks associated with key reuse and enhance the overall security profile.

This comparative analysis highlights the practical advantages of our hybrid cryptographic approach over traditional methods like RSA, especially in scenarios demanding high efficiency and robust resistance to evolving threats.

Cryptographic protocol evaluation

Security level

All evaluated protocols achieved a security level of 100, indicating flawless encryption and decryption operations across multiple tests. This high security level demonstrates the robustness of the implementation against common cryptographic attacks. For instance, the AES-ECB algorithm consistently maintained a security level of 100, confirming its reliability in secure data encryption.

Efficiency

The computation times for the cryptographic protocols were consistently low, resulting in an efficiency score of 100 for all protocols (Fig. 7). This indicates that the protocols are highly efficient and suitable for real-time applications where processing speed is critical. The AES-GCM algorithm, for example, demonstrated a computation time as low as 1.04 seconds, highlighting its high efficiency and minimal latency. A line plot of computation times indicated uniformly low values across protocols, reinforcing the high efficiency of the evaluated cryptographic methods.

Side-channel resistance

The protocols exhibited excellent resistance to side-channel attacks (Fig. 6), with timing standard deviations consistently low across different evaluations. This resistance is reflected in the resistance scores, which were uniformly 100. For instance, the AES-GCM algorithm had a timing standard deviation of 0.0002 milliseconds, indicating strong resistance to timing attacks and ensuring data integrity against such vulnerabilities.

Cryptanalysis scores

Differential cryptanalysis scores

As we can see in Fig. 4 majority of the algorithms achieved a differential cryptanalysis score of 99, demonstrating their robustness against differential attacks. This high score indicates that the protocols effectively mitigate the risk of differential cryptanalysis, a common method for breaking symmetric key algorithms.

Fig. 4

Cryptanalysis scores of algorithms.

Linear cryptanalysis scores

The protocols scored between 85 and 90 in linear cryptanalysis, reflecting strong but slightly varied resistance to linear attacks. For example, AES-ECB had a differential cryptanalysis score of 99 and a linear cryptanalysis score of 85, showcasing its strong defense mechanisms against these attack vectors.

In Fig. 5, bar chart of fitness scores showed that the protocols consistently achieved high fitness scores, with the best protocols scoring up to 100. This visual representation underscores the robustness and optimization of the evaluated algorithms. All protocols leading algorithms passed formal verification with a score of 100, confirming their adherence to specified security standards and compliance with formal verification criteria. The formal verification of the AES-GCM algorithm, for instance, confirmed its compliance with security specifications, reinforcing its suitability for secure communications.

Fig. 5

Fitness scores of different algorithms.

The proposed framework has been evaluated for its resistance to specific cryptanalysis techniques commonly used to break cryptographic ciphers. The primary focus has been on mitigating differential cryptanalysis and linear cryptanalysis attacks. Differential cryptanalysis seeks to exploit predictable patterns by analyzing differences in input pairs and their corresponding outputs to recover key information, while linear cryptanalysis relies on linear approximations of the cryptographic transformation to recover key bits. By employing Genetic Algorithms (GA) to evolve and optimize cryptographic protocols and incorporating the generative capabilities of WGAN-GP for robust data augmentation and resistance testing, our framework demonstrates significant resilience against these techniques, enhancing both security and adaptability (Figs. 6 and 7).

Fig. 6

Timing standard deviation for different algorithms.

Fig. 7

Computation time for different cryptographic algorithms.

Comparative performance analysis of cryptographic protocols

The evaluated cryptographic protocols, including AES-ECB, AES-GCM, ChaCha20, RSA, and ECC, exhibited varying performance characteristics across key metrics such as security, efficiency, and resistance to side-channel attacks. Table 1 summarizes the performance results, with key insights discussed below:

• Security level: All protocols maintained a high security level of 100, demonstrating their robustness against standard cryptographic attacks. AES-GCM, however, showed superior resistance to differential and linear cryptanalysis, achieving a differential cryptanalysis score of 99 and a linear cryptanalysis score of 90.

• Computational efficiency: AES-GCM consistently outperformed other protocols in terms of computation time, with an average encryption/decryption time of 1.04 seconds. In contrast, RSA exhibited the highest latency due to its reliance on computationally expensive modular exponentiation.

• Side-channel resistance: The timing variance for AES-GCM was notably low (0.0002 ms), indicating strong resistance to timing attacks. ChaCha20 demonstrated comparable side-channel resistance but with slightly higher timing variance compared to AES-GCM.

Table 1 Performance comparison of cryptographic protocols.

Influence of WGAN-GP and genetic algorithms on performance

The integration of WGAN-GP and Genetic Algorithms (GA) within our framework played a pivotal role in enhancing cryptographic protocol performance. The following analyses highlight their specific contributions:

• WGAN-GP data augmentation: The WGAN-GP model generated 20,000 synthetic traces that closely mimicked real-world data distributions, enhancing the robustness of profiling side-channel attacks. The use of synthetic data resulted in an average increase of 15% in side-channel resistance scores compared to evaluations based solely on real-world data. This demonstrates the efficacy of WGAN-GP in providing robust training datasets that improve protocol security evaluations.

• Optimization through genetic algorithms: The genetic algorithm iteratively optimized cryptographic configurations over 200 generations. Key operations such as crossover, mutation, and selection based on fitness scores ensured an optimal balance between security, efficiency, and side-channel resistance. The fitness scores of evolved protocols increased by an average of 20% compared to the initial population, reflecting successful protocol adaptation and optimization.

• Adaptive mutation and diversity preservation: The adaptive mutation strategy employed by the GA maintained genetic diversity across generations, preventing premature convergence and leading to more robust solutions. This adaptability was crucial in evolving protocols that exhibited superior performance under diverse attack scenarios.

Figure 8 illustrates the evolution of fitness scores across generations, highlighting the impact of the GA’s optimization process.

Fig. 8

Evolution of fitness scores across generations.

Enhanced side-channel attack evaluation

To provide a more robust and comprehensive evaluation of the proposed framework’s resistance to side-channel attacks, we extended our analysis beyond timing standard deviation to include multiple metrics, capturing diverse side-channel threats. This evaluation shown in Table 2 approach aligns with the varied nature of such attacks, which differ significantly based on algorithmic and environmental contexts.

Table 2 Comprehensive evaluation of side-channel resistance for the proposed framework.

Timing variance and standard deviation

The timing variance and standard deviation metrics were used as an initial assessment of a protocol’s resilience to timing attacks. We collected timing data under varying load conditions and calculated the variance to evaluate the consistency of execution time. Given that timing attacks exploit predictable variations, minimizing timing variance is crucial.

Mathematical analysis: Let T represent the execution time across multiple trials. The variance $\sigma _T^2$ is given by:

$$\begin{aligned} \sigma _T^2 = \frac{1}{n} \sum _{i=1}^{n} (T_i - \mu _T)^2, \end{aligned}$$

where $\mu _T$ is the mean execution time and n is the number of observations.

Power analysis (SPA and DPA)

To evaluate resistance against power analysis attacks, including Simple Power Analysis (SPA) and Differential Power Analysis (DPA), we used the correlation coefficient $\rho$ between observed power traces and hypothetical power values based on key guesses. The lower the correlation, the stronger the resistance.

Correlation power analysis (CPA):

$$\begin{aligned} \rho (X, Y) = \frac{\text {Cov}(X, Y)}{\sigma _X \cdot \sigma _Y}, \end{aligned}$$

where X represents measured power consumption values and Y represents hypothetical values. Our framework achieved a reduction in correlation by 20%, indicating improved resistance to DPA.

Entropy and information leakage analysis

Entropy-based metrics were used to measure the unpredictability of side-channel leakage. Higher entropy indicates reduced predictability, enhancing resistance to profiling attacks.

Entropy calculation:

$$\begin{aligned} H(X) = -\sum _{x \in {\mathcal {X}}} P(x) \log P(x), \end{aligned}$$

where P(x) is the probability distribution of side-channel observations. Mutual information I(X; Y), which quantifies the information leaked about a secret key Y, was also computed:

$$\begin{aligned} I(X; Y) = \sum _{x \in {\mathcal {X}}} \sum _{y \in {\mathcal {Y}}} P(x, y) \log \left( \frac{P(x, y)}{P(x) P(y)} \right) . \end{aligned}$$

A reduction of 30% in mutual information was observed, indicating less key-related information leakage.

Impact of WGAN-GP and genetic algorithms

The integration of WGAN-GP and Genetic Algorithms (GA) significantly enhanced side-channel resistance through synthetic trace generation and adaptive optimization.

• Synthetic trace generation (WGAN-GP): The WGAN-GP model generated 20,000 synthetic traces that closely mimic real-world conditions, enhancing profiling attack defenses. Profiling accuracy of adversarial models was reduced by 15%, demonstrating improved robustness.

• Genetic algorithm optimization: The GA optimized cryptographic parameters, reducing leakage and enhancing resistance through dynamic adjustments.

Genetic algorithm optimization results

The genetic algorithm optimization resulted in high fitness scores across generations, reflecting successful protocol evolution. The best-performing protocols exhibited fitness scores of 100, indicating an optimal balance between security, efficiency, and resistance to side-channel attacks.

The best-performing protocol, identified through the genetic algorithm, demonstrated superior properties, including high-security level, efficiency, and resistance to side-channel attacks. This protocol, which utilized the AES-GCM algorithm, exemplified the effectiveness of the optimization process.

Discussion

The consistent security level up to 100 across all algorithms underscores the robustness of the implementation and its effectiveness in resisting common cryptographic attacks. The high differential and linear cryptanalysis scores further validate the strength of the key management and encryption methods employed.

The low computation times across various protocols highlight their suitability for real-time applications, where processing speed is paramount. The balance between high security and efficiency makes these protocols ideal for practical use cases.

The minimal timing standard deviations observed indicate excellent resistance to timing attacks, a critical aspect of side-channel attack prevention. The consistent resistance scores of 100 confirm the robustness of the protocols against such vulnerabilities.

The high differential cryptanalysis scores (99) demonstrate the protocols’ strong defense against differential attacks, which exploit differences in ciphertexts. Although the linear cryptanalysis scores were slightly lower (85–90), they still indicate strong resistance, with room for further strengthening against linear attacks.

The integration of WGAN-GP in generating realistic data for protocol evaluation proved successful, as evidenced by the high performance and fitness scores. This approach enhances the evaluation process by providing high-quality synthetic data, thereby improving the robustness and adaptability of the protocols.

The genetic algorithm effectively optimized the protocol properties, achieving high fitness scores across generations. The use of adaptive mutation rates and rank-based selection contributed to maintaining diversity and avoiding premature convergence, resulting in robust protocol evolution.

For applications requiring high security and efficiency, the evaluated protocols, particularly AES-GCM and AES-ECB, are recommended. Continuous monitoring and periodic evaluation using advanced techniques are suggested to maintain security and adapt to emerging threats.

Hardware usage analysis

In the context of our work, we conducted a thorough analysis of hardware usage to understand the computational demands and efficiency of our implemented cryptographic algorithms when integrated with WGAN-GP and genetic algorithms. The primary metrics we focused on include memory usage and CPU utilization, which are critical indicators of system performance and resource efficiency during cryptographic operations.

Memory usage

The memory usage of our cryptographic operations was monitored and profiled over time. As depicted in the graph (Fig. 9), the memory usage remained relatively stable throughout the execution of the cryptographic protocols. The graph illustrates that the memory consumption consistently hovered around 540 MB, with minimal fluctuations. This stability indicates that our cryptographic operations are memory-efficient and do not cause significant strain on system resources. Such behavior is desirable in cryptographic applications, especially in resource-constrained environments where memory availability can be a limiting factor.

Fig. 9

Memory and CPU usage over time.

CPU usage

In addition to memory profiling, we also analyzed the CPU usage to evaluate the computational intensity of our cryptographic operations. The CPU usage graph (Fig. 9) shows the percentage of CPU utilization over time during the execution of various cryptographic protocols. The data reveals periodic spikes in CPU usage, reaching up to 60%, which correspond to the intensive cryptographic computations. These spikes are interspersed with periods of lower CPU utilization, indicating that the system efficiently manages computational loads by leveraging idle times between intensive tasks.

The fluctuating pattern of CPU usage is expected in cryptographic operations, where certain tasks, such as encryption and decryption, demand higher computational power. The observed peaks in CPU usage reflect the moments when cryptographic algorithms perform key operations, while the troughs indicate periods of lower activity, such as key management and data transfer.

The analysis of hardware usage provides valuable insights into the efficiency and performance of our cryptographic protocols. The stable memory usage demonstrates that our protocols are designed to handle cryptographic tasks without excessive memory consumption, making them suitable for deployment in various environments, including those with limited resources.

The periodic spikes in CPU usage highlight the computational demands of cryptographic operations. While these demands are inherent to the nature of cryptographic algorithms, the system’s ability to manage these spikes effectively ensures that the overall performance remains within acceptable limits. This balance is crucial for maintaining the security and efficiency of cryptographic protocols, especially in applications where real-time processing and quick response times are essential.

At last, our hardware usage analysis confirms that the implemented cryptographic protocols, when integrated with WGAN-GP and genetic algorithms, exhibit stable memory usage and manageable CPU utilization. These findings underscore the suitability of our approach for secure and efficient cryptographic operations, providing a robust foundation for further advancements in the field of cryptography and cybersecurity.

Specific applications of the proposed framework

The proposed hybrid cryptographic framework offers several specific applications where it outperforms traditional cryptographic algorithms by leveraging the advantages of Wasserstein Generative Adversarial Networks with Gradient Penalty (WGAN-GP) and Genetic Algorithms (GA). Key applications include:

• Secure communication in IoT and embedded systems: Due to the resource-constrained nature of IoT devices, traditional algorithms such as RSA may suffer from computational overhead and latency. Our framework, which employs optimized cryptographic protocols (e.g., AES-GCM) and dynamic adaptation via Genetic Algorithms, ensures both security and efficiency, making it highly suitable for real-time IoT environments.

• Protection against side-channel attacks in hardware security: Side-channel attacks, such as timing and power analysis, pose a significant threat to cryptographic systems deployed in hardware devices. By generating synthetic traces with WGAN-GP to enhance resistance against such attacks and evolving the protocols using Genetic Algorithms, our framework strengthens security in contexts where physical attack vectors are a primary concern.

• Adaptive security solutions for cloud computing: Cloud environments often face evolving threats and varying data security needs. Unlike static key management systems used in existing algorithms, our framework’s dynamic key management and adaptability to threat levels enable it to provide scalable security solutions tailored to changing cloud security requirements.

• Cryptographic optimization for real-time applications: Traditional public-key algorithms like RSA introduce latency in high-speed applications such as secure streaming and encrypted video calls. Our framework optimizes computational performance through evolutionary strategies, providing high security with minimal latency.

These applications demonstrate the framework’s superior adaptability, resistance to side-channel attacks, and efficiency compared to existing cryptographic algorithms, making it suitable for contemporary and emerging security challenges.

Conclusion

This study presents a pioneering integration of traditional cryptographic protocols with advanced methodologies such as Wasserstein Generative Adversarial Networks with Gradient Penalty (WGAN-GP) and Genetic Algorithms (GA), significantly enhancing the security and efficiency of cryptographic systems. By evaluating protocols including AES-ECB, AES-GCM, ChaCha20, RSA, and ECC, we achieved unparalleled improvements across several critical metrics: security level, efficiency, side-channel resistance, and resistance to cryptanalysis.

Our comprehensive evaluation demonstrates that all protocols consistently maintained a security level of 100, showcasing their robustness against common cryptographic attacks. Notably, the AES-GCM algorithm exhibited superior performance, with minimal computation time and excellent resistance to side-channel attacks. This highlights its potential as a leading choice for secure and efficient cryptographic operations.

The integration of WGAN-GP generated high-quality synthetic data, enhancing the protocol evaluation process. The genetic algorithm optimization achieved high fitness scores across generations, reflecting the successful evolution of protocol properties. The best-performing protocol, identified through this hybrid approach, demonstrated exceptional properties, including high security, efficiency, and resistance to side-channel attacks.

Hardware resource utilization was also a critical focus of this study. The stable memory usage observed indicates that our cryptographic protocols are memory-efficient, maintaining consistent memory consumption around 540 MB during operations. The CPU usage analysis revealed periodic spikes corresponding to intensive cryptographic computations, with peaks reaching up to 60%. This efficient management of computational loads ensures that the overall system performance remains robust, even during resource-intensive tasks.

The minimal timing standard deviations observed confirm the strong resistance of the protocols to timing attacks, a critical aspect of side-channel attack prevention. High differential cryptanalysis scores (100) validate the robustness of the protocols against differential attacks, while linear cryptanalysis scores (88–92) indicate strong resistance with potential for further optimization.

This research sets a new benchmark in cryptographic protocol development, demonstrating the effectiveness of combining machine learning and evolutionary algorithms to create resilient and efficient cryptographic systems. The methodologies employed not only ensure high security levels but also optimize efficiency, making these protocols suitable for real-time applications where processing speed is crucial.

Future works

Future research should explore the inclusion of additional cryptographic algorithms and advanced formal verification methods. Enhancing the GAN and genetic algorithm components could further improve protocol optimization and evaluation, ensuring robust cryptographic security in evolving threat landscapes. This study provides a robust foundation for future advancements in cryptography and cybersecurity, emphasizing the critical role of innovative methodologies in enhancing cryptographic protocol performance.