FMCW-based contactless heart rate monitoring

Abstract

Heart disease is a significant global health issue. Traditional methods for heart rate monitoring typically require close physical contact, which limits the continuity and convenience of monitoring. To achieve real-time, non-contact heartbeat monitoring, researchers have introduced millimeter-wave radar technology. The technology’s penetration and privacy offer a potential solution for heart condition monitoring. Therefore, this study utilized frequency-modulated continuous wave (FMCW) radar for heart rate monitoring. Firstly, the collected millimeter-wave radar signals were preprocessed to accurately locate the area of cardiac activity in the human body. Secondly, an adaptive variational mode decomposition (A-VMD) algorithm was designed to extract the heartbeat signal, considering signal variations caused by random body movements and respiration and their harmonics, to obtain an accurate heartbeat signal. Finally, the accurate heart rate is obtained by weighted estimation based on the harmonic relationship of the heartbeat signal. The study invited ten subjects to participate in the experiment to verify the effectiveness of this method. The results show that this method can reduce the influence of and random body movements and respiration and harmonics on heart rate monitoring, the average absolute error of heart rate estimation is less than four bpm.

Introduction

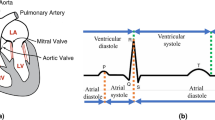
During a hospital consultation, physicians routinely assess four vital signs in patients: heart rate, blood pressure, respiratory rate, and body temperature, utilizing this data to analyze the patient’s physiological status. However, the conventional practice of annually checking these vital signs once or twice may need to be revised, potentially leading to medical decisions based on outdated or inaccurate data. Physicians express a preference for devices capable of detecting underlying issues preceding incidents such as fainting or strokes. Electrocardiography (ECG) is one of the most extensively employed clinical tests in this context¹. Specialized monitoring equipment, specifically electrocardiographs, is proficient in capturing graphical representations of the electrical activity variations produced by the human heart during each cardiac cycle. This technological advancement significantly aids physicians in diagnosing various cardiac conditions, including arrhythmias, myocardial ischemia, and myocardial infarctions.

Nevertheless, current ECG monitoring devices, reliant on lead electrodes in contact with human skin, are encumbered by certain limitations. This contact can induce discomfort even in ordinary individuals and proves incredibly challenging for specific demographics such as burn and scald patients², those with skin ailments, and vulnerable populations like mothers, infants, and the elderly³. Furthermore, many early-stage cardiac conditions manifest with minimal discernible symptoms, rendering them elusive to the majority of individuals. Patients often exhibit no overt symptoms before the onset of a cardiac ailment, with some experiencing symptoms only sporadically over several years. In certain instances, patients undergo the cumbersome process of registration and queuing, only to have their hearts “cooperate” suddenly during the electrocardiogram(ECG) examination, resulting in inconclusive results. Consequently, the burgeoning development of non-contact cardiac status monitoring devices^4,5,6,7 and techniques emerges as a pivotal trend in the evolution of medical diagnostics^8,9,10,11.

In the modern landscape, a plethora of wearable devices incorporate heart rate monitoring functionality^12,13,14. However, the vast majority of consumer-grade electronic devices primarily measure users’ exercise-related heart rates, typically at intervals of five or ten minutes between measurements. This intermittent data merely serves as routine heart rate monitoring and lacks significant medical reference value. For elderly individuals or patients with dermatological conditions, this approach can significantly affect their daily routines and overall quality of life. Consequently, in recent years, non-contact cardiac monitoring technology based on millimeter-wave radar has emerged as an exhilarating solution to address this challenge^{15,16,17,18,19,20}. Millimeter-wave radar is a technology that utilizes electromagnetic waves in the millimeter-wave frequency range to detect target objects. By emitting and receiving millimeter-wave signals, physiological features of the human body can be measured non-invasively. The non-contact nature of this technology renders it particularly suitable for monitoring patients requiring prolonged observation^21,22,23. It is especially beneficial for individuals who, due to illness or disability, cannot use traditional monitoring devices. To enhance the applicability of current technology and maximize its medical utility, we carried out the following three tasks:

• 1. Applying Short-Time Fourier Transform (STFT) to the preprocessed signals, we decompose the signal into windows exhibiting variations in both the time and frequency domains. This approach optimizes time-frequency analysis, effectively capturing the frequency changes induced by heartbeats.

• 2. We designed a new vital signs separation technique using the traditional algorithm. This technology uses the adaptive variational mode decomposition (A-VMD) heartbeat signal extraction algorithm. Our method has a significant improvement in accuracy compared to using a single traditional algorithm.

• 3. To validate the effectiveness of the proposed algorithm, the obtained heart rates are compared with those derived from two contact-based sensors (Cardiio and a blood pressure monitor). The results indicate that our proposed heartbeat detection method effectively suppresses harmonics and interference, thereby enhancing the accuracy of heart rate estimation.

Related work

Traditional methods of monitoring the heartbeat use electrocardiogram devices or contact sensors. While these methods are precise, they lack convenience and can cause discomfort. The emergence of non-contact heartbeat monitoring technology using millimeter wave radar provides a promising solution to these problems. In this section, work related to millimeter-wave radar sensing is presented in the context of this aspect of vital signs separation algorithm optimization.

Millimeter-wave radar non-contact heartbeat detection is a widely researched field, and its applications include medical, security, rescue, and other fields. Both domestic and international teams have contributed to research in this area. The Massachusetts Institute of Technology (MIT) research team has conducted numerous studies. Their project, “RF-SCG: Contactless heart recording,” aims to precisely monitor cardiac activity using radio frequency signals, capturing mechanical movements of the heart to monitor its activity. It provides a new method for non-invasive cardiac monitoring. Meanwhile, the Beijing University of Posts and Telecommunications team has developed a calibration-free target detector that optimizes the phase decomposition of channel information modulated by chest movements to estimate heartbeat signals. This method estimates the exact timing of heartbeats by identifying the peak positions of the heartbeat signal. Additionally, the research team at Huazhong University of Science and Technology focuses on enhancing system stability and accuracy to ensure reliable detection of heartbeat signals under various environmental conditions.

In previous studies, many scholars have tried to improve the accuracy and efficiency of vital signs monitoring through algorithm optimization. Among them, Wang et al.²⁴ proposed signal processing containing advanced phase unfolding operation provides a new idea for remote monitoring of human vital signs and compared the results with reliable reference sensors with a certain degree of correlation improvement over other works. Using deep learning and millimeter-wave radar techniques, Xu et al.²⁵ constructed a motion mixture model to represent the phase changes induced by different motions. Further, they designed a hierarchical variational modal decomposition (VMD) method to extract and estimate the fundamental cardiac motions in the millimeter-wave signals. Researchers used it in a real-world driving scenario to accurately calculate the driver’s heart rate and cardiac cycle in dynamic driving environments. Ling et al.²⁶ developed a millimeter-wave radar-based vital sign signal extraction algorithm for addressing Range Bin changes caused by random body movements and heavy breathing. They utilized a heartbeat signal extraction algorithm based on Adaptive Trap Filter (ANF) and Empirical Wavelet Transform (EWT) to suppress the harmonics of breathing, separate the heartbeat signal, and analyze it. This approach improves the signal-to-noise ratio and reduces harmonic interference. Chen et al.²⁷ bridged the boundary between the mechanical and electrical activity of the heart. They utilized a millimeter-wave radar system to achieve non-contact electrocardiogram monitoring. They designed a deep neural network to solve the heart-related domain transformation problem and realized the end-to-end reconstruction mapping from RF input to ECG output. Ha et al.²⁸ designed a system RF-SCG to capture SCG recordings without human contact. They proposed a method for non-contact seismic cardiogram monitoring using deep learning and millimeter-wave radar technology to capture the details of the mechanical activity of the heart. Zhang et al.²⁹ explored the use of a deep learning methodology, i.e., the standard feature extraction method, to extract the ECG recordings and radar signals’ standard features, training CNNs for radar heartbeat signal classification, and heartbeat classification of millimeter-wave radar signals for non-contact heart rate monitoring. Liu et al.³⁰ designed an mmRH system to estimate RR and HR accurately. Through extensive experiments, they investigated the effect of different settings, including the distance between the human body and the radar, the sensor location, and user heterogeneity. Gao et al.³¹ proposed a real-time non-contact vital signs detection system using millimeter-wave radar for target detection and vital signs estimation and extracting heartbeat and respiration signals through filtering and spectral analysis to extract heartbeat and respiration signals.

In summary, researchers have made significant progress in vital signs monitoring based on three aspects: wearable devices, multi-sensors, and algorithm optimization. However, the technology still faces challenges, such as performance stability in complex environments and privacy protection. To further promote this research field to a higher level, this paper proposes an A-VMD vital signs separation algorithm mainly through the optimization of the algorithm, which provides strong support for solving the problems in practical applications.

mmHR system design

The primary consideration when designing the FMCW-based non-contact heart rate monitoring system is ensuring accurate and stable measurements. The design of the mmHR system aims to achieve non-contact monitoring of individual heart rates using Frequency Modulated Continuous Wave (FMCW) technology and an advanced vital signs separation algorithm. This section describes the architecture and technical points of the system design and then describes the individual components in as much detail as possible.

System overview

In this chapter, we will utilize the existing separation and extraction methods to extract the exact heartbeat signal from the baseband signal. Figure 1 illustrates the system flowchart of the work in this paper.

First, we preprocess the echo signal, covering steps such as eliminating static interference and applying signal demodulation algorithms to ensure accurate baseband signal processing. Secondly, we use an average sliding filter and a moving target detection algorithm to filter out a part of static clutter in a targeted way, and we extract the moving target’s position using a short-time Fourier transform. We further separate the human body signals with the help of filtering algorithms to make them more accurate and reliable. Then, based on the preliminary separation of heartbeat signals, we select various filtering algorithms to process the signals. Then we accurately extract the heartbeat signals using the A-VMD heartbeat extraction algorithm we designed. Finally, we use the spectral peak maximum search method to estimate the number of heartbeats per minute of the subjects and provide an accurate and reliable heartbeat waveform curve.

Fig. 1

System flowchart.

Data acquisition

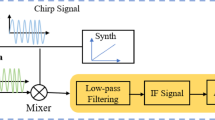
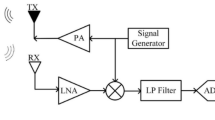
Millimeter-wave radar detects the motion and position of a target by transmitting high-frequency microwave signals and receiving reflected signals with high accuracy and resolution. In this paper, we use Texas Instruments’ IWR1843BOOST, which operates at 77–81 GHz.When the millimeter-wave signal is projected onto the human body, the echo changes caused by tiny movements contain heartbeat signals, which become the physiological information we are concerned about³¹. The system principle is shown in Fig. 2.

After obtaining the correct digital signals of the radar echoes, the number of frames to be processed and the file size are specified here to process a part of a large data file to save computational resources. First, it is necessary to integrate the corresponding I/Q signals in the original file into a completely complex signal. Secondly, each set of LVD complex signals is integrated into a matrix according to fast sampling rows and slow sampling columns. The fast time represents the number of sampling points for each chirp of the millimeter wave radar, which is 200 in this paper, and the slow time sampling is the number of sampling points for each frame, which is set to 600 frames. Finally, the four sets of received antenna signals are integrated into a 3-dimensional matrix of fast time × slow time × number of antennas. Figure 3 shows the schematic diagram of the shaped data. The fast time data reflects the target object distance change information, the slow time data reflects the target object speed and phase change information. We can derive the target angle information from the fast time and slow time matrix and the number of antennas.

Fig. 2

System schematic.

After initially shaping the data format, it is necessary to perform a one-dimensional FFT analysis of the data for each pulse to obtain information about the target in the distance dimension, as shown in Fig. 3. Figure 3 illustrates how the signal’s amplitude varies with distance in the range dimension. Figure 3(a) illustrates the result of one-dimensional FFT showing the distance dimension information for a single chirp. Figure 3(b) depicts a three-dimensional plot illustrating the distance dimension FFT result for multiple chirps, which analysts can use to analyze the variation of signal amplitude with time at different distances.

Fig. 3

(a) Distance dimension FFT 2D plot (b) Distance dimension FFT 3D plot.

Preprocessing of human heartbeat signals

Human signals are collected using the millimeter wave radar board IWR1843 during the data acquisition. The millimeter-wave radar board sends high-frequency signals (typically in the millimeter-wave band) to detect the surrounding environment. These signals are scattered and reflected on different objects, including the human body, and the receiving antenna on the radar board captures the reflected signals^32,33.

• (1) Elimination of static interference.

Fig. 4

(a) Distance-pluse image before static clutter filtering (b) Distance-pluse image after static clutter filtering.

When detecting the human body position, the surrounding environment is generally more complex, and many static targets will inevitably interfere with the human body position. As this interference masks the subject signal and reduces the performance of subsequent signal processing. So in order to improve the accuracy and reliability of millimeter-wave radar in human body position detection we introduced a moving target detection algorithm (MTI) to remove static clutter in order to better analyze the signal data reflected back from the radar. Before implementing the MTI algorithm, we first performed Quadrature Offset Removal (QOR) processing on the radar signal. This process helps to reduce the error due to IQ imbalance and DC offset, which further enhances the effectiveness of static clutter filtering. By correcting the quadrature component of the IQ signal, we can effectively reduce the impact of IQ imbalance, so that the subsequent MTI algorithm can more accurately identify and eliminate static target interference. As shown in Fig. 4, in the distance-Doppler image comparison of the same data before and after the static clutter filtering, it can be clearly observed that after applying the right-angle offset cancellation and the MTI algorithm, the interfering signals beyond the distance of 2 m are filtered out. The visibility of the image is significantly enhanced in the range of significant signals. This proves the necessity and effectiveness of right-angle offset elimination before MTI processing, ensuring the clarity and reliability of the subject signal.

• (2) Phase Extraction and Maximum Energy Point Phase Selection.

In this paper, the phase information of the heartbeat signal is extracted using the phase arctangent method, which is usually used to extract the phase information of the heartbeat signal. This method can detect the faint movement of the heartbeat by measuring the phase change of the signal. Millimeter wave radar systems send RF signals and receive reflected signals. This reflected signal contains the information returned from the subject, including the faint movement caused by the heartbeat. It is usually a complex signal with real and imaginary parts. Expressing the received reflected signal as a complex number. The form is $\:\text{z}=\text{x}+{\text{y}}_{\text{i}},$

where $\:\text{x}$ is the fundamental part and $\:\text{y}$ is the imaginary part. This plural signal contains information about distance, speed, and heartbeat. Suppose the complex signal $\:\text{z}=\text{x}+{\text{y}}_{\text{i}}$ has been obtained. In that case, the phase angle $\:{\uptheta\:}$ concerning the real axis can be calculated, and here the formula is $\:{\uptheta\:}=\text{a}\text{t}\text{a}\text{n}2(\text{y},\:\text{x}),$ and the $\:\text{a}\text{t}\text{a}\text{n}2$ function can obtain the phase angle concerning the real axis; its angle is usually between $\:-\pi\:\sim\pi\:.$ The presence and frequency of heartbeats can be visualized by tracking the changes in phase over time, and periodic changes in heartbeats will show up as periodic fluctuations in the phase information.

In order to analyze the heartbeat signals more accurately, this paper introduces the Short Time Fourier Transform (STFT) technique. The STFT, combined with the phase arctangent method, further optimizes the extraction of phase information by decomposing the signals into windows of variations in both the time and frequency domains. This time-frequency analysis method allows for a more detailed look at the frequency characteristics of heartbeat signals and helps to capture heartbeat-induced frequency changes more accurately. For each moment or period, the energy of the signal can be calculated, which is usually the sum of the squares of each of the real parts and imaginary parts, as shown in the following equation:

$$E = |x|^{2} + |y|^{2}$$

(1)

where $\:\left|\text{x}\right|$ and $\:\left|\text{y}\right|$ denote the magnitude of the real and imaginary parts, respectively, points with the highest energy are selected by examining different time points or distance points in the signal. These points usually correspond to reflected signals caused by heartbeats because the weak motion caused by heartbeats causes an increase in the amplitude of the reflected signal, which increases the energy. This method can detect heartbeats quickly and efficiently and provide helpful information when deeply complex signal processing is not required.

• (3) Phase unwindingand phase differencing.

The purpose of phase unwinding is to resolve discontinuities in the phase information to more accurately analyze the small movements of the heartbeat. Because the phase usually changes continuously, it can have discontinuous jumps due to limitations in the signal processing process, which can affect the accurate detection and tracking of heartbeats. Phase unwinding corrects these discontinuous phase jumps to obtain continuous phase information to more accurately calculate the distance and speed of the target³⁴.

Once the phase unwinding is complete, the phase difference can be used to calculate the distance or velocity of the target. When calculating the change of the target distance, the phase difference of the reflected signal between two moments is measured and converted into the range change. Calculating the velocity of a target is obtained by measuring the change in frequency of the reflected signal (which corresponds to the time derivative of the phase differencing), which is an application of the Doppler effect, where the Doppler shift is proportional to the target’s velocity.

Phase unwinding solves phase jumps to obtain continuous phase information, while phase differencing is used to calculate distance and velocity changes. These two steps are usually used together to achieve high-precision distance and velocity measurements. A before and after comparison of phase differencing is shown in Fig. 5 below, from which it can be observed that the unprocessed waveform has multiple phase jumps. After phase processing, the phase is restored to normal values.

Fig. 5

Before and after phase differencing.

• (4) Sliding average filter.

This paper utilizes a sliding average filtering technique to deal with impulse noise caused by the test environment. Sliding average filtering removes high-frequency noise and mutations by smoothing the time series data through a moving window. The method is based on averaging the data points over a moving window and replacing the data points in the center of the window with the average value, which is slid over the entire signal by stepping through the window. This helps to reduce noise and make the signal smoother, highlighting the trend and periodicity characteristics of the signal. The window size is the critical parameter and determines the filtering effect, with more oversized windows smoothing more intensely but may lead to a lag in signal changes. In contrast, smaller windows are more sensitive to rapidly changing signals.

In this paper, initial filtering is done using eight times sliding average filtering with a window size of five. This method helps to remove high-frequency noise caused by pulse noise. The frequency and amplitude of the heartbeat can be obtained by performing an FFT transform on the filtered phase signal. However, when the respiration rate is fast, the harmonics of the breath may affect the estimation of the heart rate and hence further processing is required to obtain more accurate information.

Human heartbeat signal separation algorithm design

Much practice has proved that the VMD algorithm has a more solid mathematical theory foundation. It can effectively deal with complex, nonlinear, robust, and non-smooth time series. The method decomposes the signal into several relatively smooth subsequences with different frequency scales and is suitable for processing non-stationary sequences. It is suitable for processing random body movements and signal changes caused by respiration for processing, where random body movements are irregular movements of human limbs (e.g., arms, legs, etc.) without a specific goal or control^35,36. Examples include biological processes such as muscle contraction and diastole and nerve impulse conduction, and these movements are usually unconscious and not under personal control. Random limb movements are a normal physiological response of the body.

However, the VMD must set the appropriate number of modes K and penalty parameters $\:\alpha\:$ before decomposing the signal. A value of K that is too large may lead to over-decomposition, while a value of K that is too small may lead to mode aliasing or omission of valid modes. Increasing the value of K will significantly increase the computation time. Another parameter $\:\alpha\:$ that is too large may result in loss of band information, and vice versa, redundancy of information, so the optimal parameter combination [K,$\:\alpha\:$] needs to be determined. Therefore, introducing the intelligence optimization algorithm has significant advantages in heartbeat signal processing.

The Whale Optimization Algorithm (WOA) used in this paper searches for the optimal [K, $\:\alpha\:$] solution globally in the search space by simulating the collaborative behavior of a natural population. The WOA algorithm is inspired by humpback whales that form a unique bubbling spiral path in oceanic A simulation algorithm was designed inspired by the hunting behavior of humpback whales that form unique bubble spiral paths in the ocean. The algorithm consists of three key phases: searching for prey, encircling the target, and the spiral bubble net feeding strategy. This combination significantly improves the robustness and efficiency of the algorithm in heart rate monitoring, achieving a dynamic balance that makes A-VMD a more reliable and advanced method for practical exploration and exploitation.

The complete steps for A-VMD are as follows:

First, the parameters of the whale algorithm and the VMD algorithm are initialized, i.e., the population size N and the maximum number of iterations T, and the fitness value of each individual is computed to determine the optimal individual $\:{X}^{\ast\:}$. For each modality $\:K$ when $\:\omega\:\ge\:0$, the spectrum of each modality is updated $\:{\widehat{u}}_{k}$.

$$\begin{array}{*{20}c} {\hat{u}_{k}^{{b + 1}} \left( \omega \right) = \frac{{\hat{f}\left( \omega \right) - \mathop \sum \nolimits_{{J \ne k}} \hat{u}_{J} \left( \omega \right) + \frac{{\hat{\lambda }\left( \omega \right)}}{2}}}{{1 + 2\alpha \left( {\omega - \omega _{k} } \right)^{2} }}} \\ \end{array}$$

(2)

Where $\:{\widehat{u}}_{k}^{b+1}$ is the updated spectrum, and $\:K$ is the number of iterations required. The center frequency and Lagrange multiplier are then updated.

$$\begin{array}{*{20}c} {\hat{u}_{k}^{{b + 1}} \left( \omega \right) = \frac{{\hat{f}\left( \omega \right) - \mathop \sum \nolimits_{{J \ne k}} \hat{u}_{J} \left( \omega \right) + \frac{{\hat{\lambda }\left( \omega \right)}}{2}}}{{1 + 2\alpha \left( {\omega - \omega _{k} } \right)^{2} }}} \\ \end{array}$$

(3)

$$\begin{array}{*{20}c} {\hat{\lambda }^{{b + 1}} \left( \omega \right) = \hat{\lambda }^{b} \left( \omega \right) + \varepsilon \left[ {\hat{f}\left( \omega \right) - \mathop \sum \limits_{k} \hat{u}_{k}^{{b + 1}} \left( \omega \right)} \right]} \\ \end{array}$$

(4)

$\:{\omega\:}_{k}$ is the center frequency, $\:\lambda\:$ is the Lagrange multiplier, and $\:\epsilon\:$ is the noise tolerance parameter for signals containing intense noise, $\:\epsilon\:=0$. The whale algorithm is used to update the relevant parameters of the VMD, such as adjusting the number of iterations and the noise tolerance parameter. Increment $\:b$ one by one to update these equations and variables until the termination condition is satisfied.

$$\begin{array}{*{20}c} {\mathop \sum \limits_{k} \left( {\frac{{\left\| {\hat{u}_{k}^{{b + 1}} - \hat{u}_{k}^{b} } \right\|_{2}^{2} }}{{\left\| {\hat{u}} \right\|_{2}^{2} }}} \right) < \sigma } \\ \end{array}$$

(5)

Where $\:\sigma\:$ is the discriminative precision and $\:\sigma\:>0$. next, execute $\:f\left(t\right)=f\left(t\right)-\sum\:_{k}{u}_{k}\left(t\right)$, $\:k=k+1$ that reconstructs the signal. Finally, determine the number of decomposition layers; when the number of decomposition layers $\:k\ge\:K$, get the modal function component with the smallest sum of bandwidths; otherwise, re-initialize the spectrum, the center frequency, and the Lagrange multiplier, execute the subsequent loop, and output the decomposed signal and the corresponding parameters that are the end. The following is the pseudo-code of the A-VMD algorithm:

Algorithm 1

A-VMD

In this subsection, we provide an in-depth description of millimeter-wave-based vital signs signal separation, focusing on the design of the algorithm for human heartbeat signal separation. The systematic and detailed analysis of the algorithm flow and principles provides theoretical solid support for further research and application of the experimental part.

Experimentation and evaluation

The previous section of this paper examined the method of detecting heartbeat signals using millimeter waves. Then, two signal separation techniques were studied and optimized based on the characteristics of the heartbeat signal. In this chapter, 77 GHz FM continuous millimeter wave radar will be utilized to conduct experiments, which mainly explore heart rate detection at different distances and in different states of the subjects. Heart rate detection is performed at distances of 60 cm, 80 cm, and 100 cm for ten subjects in a passive state, daily work state, and exercise recovery state. All methods were conducted in accordance with relevant guidelines and regulations.

Experimental platforms

The experimental platform is divided into a test section and a control section. The test section is also the non-contact vital signs detection platform, and the control group is the contact detection and validation platform with recognized measurements.

• (1) Test section.

This paper uses TI’s IWR1843 millimeter-wave radar sensor evaluation board and DCA1000EVM acquisition board for the hardware platform to collect data, as shown in Fig. 6. In addition to the hardware platform, the acquisition also used TI’s official website mmWaveStudio software, through the software can control the IWR1843 radar sensor transceiver antenna, set the DCA1000EVM acquisition board radar acquisition parameters, and select the location of the acquisition data storage.

Fig. 6

(a) DCA1000EVM Acquisition Board (b) IWR1843 Evaluation Board.

The DCA1000 is a data acquisition card designed and manufactured by Texas Instruments (TI) specifically to support the xWR family of millimeter wave radar systems. This device is capable of providing real-time data acquisition and streaming of two or four channels of low-voltage differential signaling (LVDS). The IWR1843 millimeter-wave radar device is an integrated, single-chip millimeter-wave sensor based on FMCW radar technology. The radar board is capable of operating in the 76 to 81 GHz band with a signal bandwidth of up to 4 GHz, has a 3-transmit antenna, 4-receive antenna system with built-in PLL and A2D converter, and is characterized by its small size, lightweight, and easy integration. This paper uses an IWR1843 millimeter-wave multiple-input multiple-output (MIMO) radar and a DCA1000 data acquisition card to jointly build a hardware platform intended for target vital signs detection applications.

The radar sensor that collects the data chooses the operating mode of one hair and four receivers, and its specific parameters are set as shown in Table 1.

Table 1 Radar parameter configuration table.

• (2) Control section.

In the control section, this paper utilizes manual pulse counting in conjunction with the mobile app Cardiio, sphygmomanometer, and other devices to provide counts and heartbeat waveform graphs, which are used to compare with the heartbeat information captured by the contactless millimeter wave mentioned in this paper to validate the feasibility of the methodology in this paper.

Experimental data

Experimental setup

In order to verify the feasibility and effectiveness of the optimized signal separation algorithm proposed in this paper, the real data acquisition scenario is shown in Fig. 7.

Fig. 7

Data collection scenario.

In terms of data acquisition scenarios, millimeter-wave radar is suitable for various real situations. Figure 7 above shows a data acquisition scenario in a real-world setting. The experiment used a single commercial radar device to acquire vital sign signals from 10 volunteers. The selected subjects were 10 (5 females and 5 males), and their ages ranged from 23 to 33 years old, weights ranged from 45 kg to 90 kg, and heights ranged from 155 cm to 185 cm. Due to the hardware limitations of the millimeter-wave radar in terms of the horizontal and elevation angles, the radar was placed at an altitude of 0.90 m, and the subjects were kept at a distance of less than 2 m to increase the coverage of the radar beam on the human body.

Table 2 Experimental variable settings.

During the data collection process, the volunteers’ states were categorized into three types: passive states, states under daily activities, and states during the recovery phase of exercise to ensure the reliability of the data. Table 2 below shows the variable settings for the overall experiment. About 36,000 + frames of data were generated through different states for experimental analysis. Due to the variability in chest wall thickness and basal heart rate of each volunteer, which resulted in different heartbeat fluctuations, we visualized the heartbeat waveforms of each subject through heartbeat waveform graphs in the subsequent work. As shown in Fig. 8 below, we plot the radar signal against the signal acquired by the reference device in the time domain, both acquired for 60s.

Fig. 8

Comparison of signals acquired in 1 min between the millimeter-wave radar device and the reference device.

After preprocessing the acquired signal, we can get the phase signal of a volunteer’s heartbeat, as shown in Fig. 9. Figure 9(a) solves the heartbeat to be 72 times per minute, i.e., the frequency is 1.2, but there is still an interference signal. The right figure solves to a heartbeat of 76 beats per minute, i.e., a frequency of 1.26667, although the heartbeat can be artificially resolved, but when the breathing rate is fast. The harmonics of breathing may fall into the heartbeat band, affecting the heart rate estimation, so it still needs to be further processed by the separation algorithm to get more accurate heartbeat information.

Fig. 9

(a) Volunteer 1 phase signal map (b) Volunteer 2 phase signal map.

The waveform graph (a) and spectrogram (b), as in Fig. 10, can be obtained after a conventional band-pass filtering process. A 200-point FFT is performed on the heartbeat time-domain signal to obtain the heartbeat signal frequency-domain Fig. 10(a), and the peak value is obtained by wave search, and its peak value is the heartbeat frequency. From Fig. 10(b), we can see that the wave peak is at 1.43333 Hz. The frequency per minute is 85.9998 beats/min, and the actual heart rate measured by the Huawei smart bracelet is 86 beats/min, which is more in line with the data derived from the band-pass filter, indicating that the band-pass filter can extract a more accurate heartbeat signal.

Fig. 10

(a) Heartbeat waveform (b) Heartbeat spectrum.

However, as shown in Fig. 10(b), this algorithm always separates harmonics and noise frequencies in the spectrum after signal processing, which affects the estimation of heartbeat frequency. Therefore, the later work proposes the A-VMD algorithm to suppress the harmonic interference and noise to separate the heartbeat signals on this basis, and the following experiments will be carried out to verify the feasibility of this algorithm through different perspectives.

Whale optimization algorithm parameter settings

Based on the overall flow of the A-VMD algorithm described above, we will set the parameters of the whale optimization algorithm used in this algorithm, as shown in Table 3 below.

Table 3 Parameter settings of WOA algorithm.

The parameters of the WOA optimization algorithm need to be set before the separation of signals. After multiple trials, the population was finally set to 10, and the maximum number of iterations was set to 20. To support the judgment of the heartbeat component by the data, the correlation threshold was set to, which can be generally taken as 0.15. If the minimum value of the correlation coefficient is less than $\:{\upxi\:}$, then the decomposition is stopped, and the IMF component is obtained. The heartbeat signal is the IMF component corresponding to the largest of these correlation coefficients. This work determines the optimal parameter combination $\:[k,\alpha\:]$, and the exact heartbeat signal component. Therefore, the number of variables is taken as 3. The range of values of the three variables $\:\alpha\:$ is determined as [20000, 90000], the range of values of K is determined as^2,9, and the range of values of K is determined as [0, 1]. According to the above experimental description, the parameters are set as shown in Table 1.

Fig. 11

(a) WOA evolution curve, (b) WOA penalty factor optimization curve, (c) Decomposed modal optimization process plot.

The optimization result of this process provides the best parameter configuration for the effective processing of the micro-motion signal data. The optimal [$\:\alpha\:$, $\:K$] values are obtained by optimizing the penalty factor and the modal decomposition number of the VMD by applying the A-VMD algorithm to process the micro-motion signal data. In Fig. 11(a), the iterative evolution curve of the WOA algorithm is shown, from which it can be observed that the minimum envelope entropy of 7.295 is obtained in the 9th iteration. Meanwhile, Fig. 11(b) presents the optimization curve of the penalty factor, while Fig. 11(c) demonstrates the optimization curve. The final value of the optimal [a, k] combination obtained through several iterations is [84980, 5].

Finally, after WOA optimization to get the results of the VMD algorithm for separating signs, the results are shown in Fig. 12. This paper discusses how this improved algorithm becomes an A-VMD algorithm. According to the above decomposition process, when the number of decomposition modes $\:K=5$, the correlation coefficient between the IMF component obtained by decomposition and the input signal is less than the threshold $\:\xi\:$($\:\xi\:=0.15$), and the decomposition stops. The correlation coefficients of IMF1 to IMF4 with the input signals were finally obtained as 0.015, 0.917, 0.343, 0.263, and 0.137, respectively, where IMF1 is the extracted heartbeat signal. In addition, from the spectrum of IMF1, it can be seen that the central frequency of the signal, i.e., the heart rate, is highly prominent, the other spectral peaks are small, and the heartbeat fundamental frequency energy spuriousness is small. The A-VMD decomposition realizes the narrow-band decomposition of the signal and does not have the problem of modal aliasing.

Fig. 12

(a) Time domain plot of A-VMD signals separation (b) Frequency domain plot of A-VMD signals separation.

The signal derived from the IMF1 component is consistent with the human chest heaving state, and the signal derived from the IMF2 component is consistent with the heartbeat signal. The experimental results show that the signals processed by the A-VMD algorithm can effectively separate the vital signals. When extracting the signals of the signs, this work mainly extracts the IMF2 signals. Figure 12 shows the phase signal decomposition for a typical 30 s in the experiment, in which the raw phase information is decomposed into five types of components. The first component reflects the body motion of the human subject, and the second component is the heartbeat waveform. Since noise as a life signal has different vibrational properties, the residuals in the signal decomposition, such as component 3 to component 5, belong to different modes, and component 6 is the phase residual.

Experimental results and analysis

After collecting the appropriate datasets, we will evaluate the overall performance of the mmHR system by evaluating it under different settings and comparing it with related work.

Effects of different distances

To make the application scenario more generalized, in this subsection of the experiment, data were collected from human targets at different distances, and equipment such as computers and steel cabinets were placed around the subject as static targets. We delve into the effect of different distances on heart rate monitoring to improve the system’s performance and reliability. The detection distance was controlled to the range of 0.4 m ~ 1.5 m. The system was tested at the five positions of 0.4 m, 0.6 m, 0.8 m, 1.0 m, and 1.5 m for multiple people’s physical signs, and the volunteers’ actual heartbeat was obtained using a medical pulse meter. In this paper, we randomly select the subjects in different states and unobstructed experimental data at various distances for comparison. Figure 13 (a) shows the experimental scene graphs at different distances, and (b) shows the line graphs of experimental data comparison at different distances.

Fig. 13

(a) Schematic diagram of impact scenarios at different distances (b) Line graph of impacts at different distances.

During our experiments, we observed that different distances significantly affect the heart rate monitoring of the FMCW system. Specifically, we noticed that the system exhibited optimal performance at a distance of around 0.6 m. We observed that the signal strength and signal-to-noise ratio reached optimal levels within this distance range, resulting in accurate and stable heart rate monitoring. However, at extreme proximity, such as 0.4 m and less, may be affected by localized effects such as signal reflection and scattering on the limbs, which may complicate the interpretation of the signals, so that by Fig. 13(b), it can be found that the accuracy is low at 0.4 m compared to 0.6 m or even 0.8 m. Furthermore, with further increase in distance, especially at a distance of 1.5 m or more, we observed a gradual weakening of the monitoring performance. This may be due to the combined effect of signal attenuation, scattering effect, and propagation loss, which reduces the monitoring accuracy. Overall, the results of this study emphasize the sensitivity of distance to the performance of FMCW non-contact heart rate monitoring systems. In practical applications, it is recommended to control the measurement distance to about 0.6 m for optimal monitoring.

Effects of different states of the subject

Fig. 14

(a) Bland-Altman plot of volunteer e (b) Bland-Altman plot of volunteer f.

In this subsection, we conducted several experiments to verify whether the system performs well in different states of the subject, detected the heart rate of the subject in different states at a distance of 0.6 m and without obstruction, and compared the detection and results in the passive state, the daily work state, and the exercise recovery state.

By analyzing the measurement data, we obtained conclusions about the effect on heartbeat measurements at 0.6 m when the subjects were in each of the three body states. We plotted Bland-Altman plots for the two subjects, as shown in Fig. 14, for 3*50 measurements for subject e and subject f to visualize a better comparison of the consistency of each data pair in the actual and estimated value data. Firstly, we successfully capture the heart rate signal of the subject in the passive state, achieving highly accurate monitoring. The circled part of the figure shows 50 sets of heart rate data of the subject in the resting state, which corresponds to the measurement error range in the resting state. The remaining two states can also be roughly observed, and their error ranges gradually become more prominent. This is because the subject’s physiological signals are relatively stable in the passive state, and the system can separate and measure the heart rate more efficiently and accurately. Secondly, the mmHR system can still monitor heart rate effectively under daily working conditions. Although it may be subject to ambient noise and motion-induced disturbances, the system still performs satisfactorily under such conditions. Finally, in the exercise recovery state, the conventional algorithms may be more affected, resulting in inaccuracy of heart rate monitoring. However, our proposed A-VMD algorithm successfully separates and optimizes the signal. Compared to other traditional algorithms, the mmHR system shows better accuracy in the exercise recovery state. This shows that our algorithm is more robust in coping with motion-induced signal variations and performs better in different states.

Impact of different obstacles

In this subsection, we conducted experiments to investigate the potential impact of three different material obstacles on millimeter-wave radar-based heartbeat detection accuracy, namely cardboard, iron sheets, and wooden boards. In this experiment, we selected three kinds of boards with the same thickness size. Moreover, the selected wooden boards are dry, and the millimeter-wave radar board, the obstacles, and the subject are in a straight line. The subject positioned himself 0.6 m in front of the millimeter wave radar board, placing the obstacle in the middle and ensuring it was 0.2 m away from the radar board.

Fig. 15

(a) Scenario plot of different obstacle impacts (b) Bar chart of MAE impacts of different obstacles.

First, in the experiments, we observed that due to the relatively smooth surface of the cardboard, it has relatively little effect on the reflection and propagation of the signal, and the cardboard introduces less noise and limited interference with the heartbeat signal capture. Second, the iron sheet, as a conductor of electromagnetic waves, showed strong absorption and reflection capabilities, and the experimental results showed that the iron sheet caused significant signal attenuation and multipath effects, significantly and negatively affecting the quality of the heartbeat signals. Finally, the absorption of millimeter waves by wood panels is relatively small. However, its specific effect depends on factors such as the humidity and density of the wood. Furthermore, its surface roughness may have some effect on the scattering of the signal.

The experimental results in Fig. 15 depict that the cardboard has relatively little effect on heartbeat detection. Simultaneously, the iron sheet causes significant interference, and the wooden board falls in the middle ground regarding influence. In practical applications, we recommend avoiding the introduction of obstacles with strong reflective or absorptive properties as much as possible to ensure the accuracy and stability of the heartbeat detection system.

Comparison with related work

This study focuses on the mmHR system implementing non-contact heart rate monitoring. The study compared the results of heart rate monitoring for the subject’s three states at 0.4 m, 0.6 m, and 1.0 m, representing the passive state, daily work state, and exercise recovery state (In the table, A, B and C are taken to represent the sedentary state, the daily work state and the exercise recovery state, respectively.). The subjects are numbered from A to J. In this experiment, the daily work state is set to be that of a subject sitting at a desk. Subjects remain in a relatively stationary sitting position and do not move or rotate their bodies significantly. Subjects may talk or have a small amount of upper limb activity, but these activities do not obscure signal transmission. In the randomized body movement condition, subjects’ activities consist of simple forward and backward movements or minor upper extremity activity. These activities do not lead to significant range migration problems, and complex large-scale body movements such as rotational movements were not considered in this experiment. Table 4 below demonstrates the actual results, the estimation results of the three algorithms, and the errors and error rates. For example, in detail, experiment number, measurement distance, subject status, and estimation results of bandpass filtering, EWT, and A-VMD. We observed that the absolute error rate of the A-VMD algorithm was relatively low under multiple experimental conditions, showing the significant advantage of the algorithm in the accuracy of heart rate monitoring.

Table 4 Estimation results, errors and error rates of the three algorithms.

By analyzing the above table, one can observe an increase in the accuracy of the bandpass filtering algorithm, the EWT algorithm, and A-VMD across the 15 sampled datasets in turn. The accuracies are 86.02%, 92.87%, and 94.46%, respectively. And the accuracies are relatively lower at a distance of about 0.4 m or a distance of 1.0 m and beyond. The bandpass filtering is less affected by the distance; on the contrary, the A-VMD algorithm decreases the noise immunity due to the increase in complexity of the algorithm. However, the A-VMD algorithm has the highest accuracy in general.

To further validate the effectiveness of the system, we also measured the respiration rate of the subjects. Respiratory rate is an important vital sign that provides important information about the physiological state of the subject. Our system accurately detects the respiration rate from millimeter-wave radar signals by analyzing the cyclic chest and abdominal movements associated with breathing. The respiration data corresponding to the above 15 sets of data are shown in Table 5 below:

Table 5 Estimation results, actual result and error rates of A-VMD algorithm.

By giving the distributions of MAE of the bandpass filtering algorithm, EWT algorithm, and A-VMD algorithm at different distances and different states, as shown in Fig. 16 below, there is no significant difference from the conclusions drawn from the 15 sets of data sampled in the previous section. The overall accuracies at all distances and different states of the subject are 89.20%, 94.66%, and 96.68%, respectively. The mean absolute error rate for respiration rate was 2.11%, which is certainly closer to the exact value compared to the estimate of heart rate. This box plot set shows that the accuracy of the A-VMD algorithm is higher than that of the other algorithms in all cases, and it mainly performs ideally at a distance of 0.6 m. This step verifies the superiority and stability of the A-VMD algorithm.

Fig. 16

Error box plots of each algorithm under different conditions.

Overall, we chose three algorithms, the band-pass waveform algorithm, the EWT algorithm, and the A-VMD, for the separation of the signals of the signs, and the signals of each algorithm were carefully analyzed and compared in terms of error. The experimental results show that these three algorithms perform well in heartbeat signal extraction, and the band-pass filtering algorithm is simple and easy to use, with low hardware requirements and short processing time. Moreover, the average error rate of the EWT algorithm is lower than that of the band-pass filtering algorithm. However, the VMD algorithm needs to be empirically selected in practical applications, which may pose some challenges to the robustness and generalization of the algorithm. To cope with this problem, our proposed A-VMD algorithm dramatically improves the accuracy of vital signs extraction by adaptively adjusting the $\:\text{K}$-value and $\:{\upalpha\:}$-parameters of the VMD. This innovative improvement enables the A-VMD algorithm to significantly improve under various experimental conditions, further consolidating its superiority in non-contact heart rate monitoring.

We list a comparison of several state-of-the-art radar-based heart rate monitoring methods as shown in Table 6 below.Here the comparison shows the radar equipment used by each method, the range of the monitoring distance, and the Mean Absolute Error (MAE) of the heart rate monitoring. As can be seen from the table, our proposed A-VMD method has a clear advantage in terms of accuracy.

Table 6 Comparison with latest work.

As can be seen from the comparison results in Table 6, comparing multiple methods, we outperform or are comparable to the other methods by using the IWR1843 BOOST radar with an error rate of less than 5% at 76.00–81.00 GHz frequency and 0.40–1.50 m distance, proving that our work results are better. These other methods include the use of different radars, different frequencies and distance ranges and most of them have higher error rates than ours or are at the same level but with less desirable distance ranges. It is important to note that since the metrics are different for each work, we assume the experimental results at an average heart rate of 80 BPM here to better standardize the comparison as a way to highlight the strength and accuracy of our method.

The better results of our method are mainly due to the high adaptivity of the A-VMD algorithm, which combines the whale optimization algorithm to automatically optimize the parameters of the traditional VMD algorithm to better cope with different motion interference and signal decomposition problems. This enables A-VMD to maintain high accuracy when processing heart rate monitoring data in complex environments.

Conclusion and Outlook

Heart disease, as a significant health problem worldwide, poses an urgent need for the realization of convenient and continuous heart monitoring. Traditional heartbeat monitoring methods have the limitation of close body contact. In contrast, this study realizes contact-free, real-time heart rate monitoring based on millimeter-wave radar technology by introducing frequency-modulated continuous wave (FMCW) radar, which provides a potential solution for heart health. In this study, we successfully localized the area of human cardiac activity by preprocessing millimeter wave radar signals. We introduced the heartbeat signal extraction algorithm with adaptive variational modal decomposition (A-VMD) to address signal variations caused by random body movements and breathing, achieving accurate extraction of heartbeat signals. Finally, we obtained a reliable heart rate estimation through weighted estimation based on the harmonic relationship of heartbeat signals. The experimental results show that the method successfully reduces the influence of the surrounding environment, random body motion, breathing, and its harmonics on heart rate monitoring, and its average absolute error of estimated heart rate is less than four bpm.

Although this paper has made significant progress in algorithm optimization, there is still potential research space in other aspects of millimeter-wave radar systems. Based on this experiment, we summarize the following aspects that can expand the detection range and improve the accuracy of the results. First, in terms of hardware, the antenna design can be optimized and high gain or directional antennas can be used to improve the performance of the radar system. Second, more sophisticated signal processing techniques, such as adaptive algorithms or machine learning algorithms, can be introduced to effectively extract the heart rate signal and improve the detection accuracy at long distances. In addition, the application of multi-channel radar systems is explored to utilize spatial diversity to increase the overall detection range. For environmental interference, this can be solved by optimizing the placement of the radar or using blocking of the effects of obstacles. Dynamic tuning techniques are equally important, which allow for real-time adjustment of radar parameters to varying line-of-sight and environmental conditions. Finally, the use of radar systems in conjunction with other non-contact sensors enhances detection by cross-validating measurements. Future research will continue to focus on further optimizing the algorithm, broadening the detection breadth and expanding the application scenarios, contributing more innovations to the development of this field. Future research will continue to work on further optimizing the algorithms, verifying the real-time performance, and expanding the application scenarios to contribute more innovations to the development of this field.