Back analysis of mechanical parameters based on GPSO-BP neural network and its application

Abstract

Rock mass mechanical parameters are essential for the design and construction of underground engineering projects, but parameters obtained through traditional methods are often unsuitable for direct use in numerical simulations. The back analysis method, based on displacement monitoring, has emerged as a new approach for determining rock mass parameters. In this study, an experimental scheme was developed using orthogonal and uniform experimental designs to obtain training samples for the neural network. A GA-PSO-BP neural network model (GPSO-BP) was proposed, combining the fast convergence of the particle swarm optimization (PSO) algorithm and the global optimization capability of the genetic algorithm (GA). This model was applied to invert the rock mass parameters E, μ, φ, and c for deep-buried tunnels. The results indicate that the GPSO-BP neural network model outperforms the BP, GA-BP, and PSO-BP neural network models in terms of faster convergence and higher accuracy. It also shows superior performance in handling small datasets and complex problems, achieving better data fitting and the highest score in rank analysis. The DDR curve further confirms the GPSO-BP model’s computational efficiency. When the rock mass parameters derived from this model are applied to forward numerical simulations, the average error across four monitoring projects is only 4.34%, outperforming the other three models. Thus, this study provides an effective method for improving the accuracy of rock mass parameter inversion in underground engineering.

Introduction

The mechanical parameters of rock masses are crucial for the design and construction of underground engineering, which directly impacts both the safety and cost-effectiveness of the project^1,2,3. Typical methods for determining these parameters include in-situ testing, geophysical exploration, laboratory testing, and so on^4,5. However, the inherent discontinuity, heterogeneity, and anisotropy of rock masses introduce a degree of subjectivity and conservatism in parameter estimation^6,7,8,9. Furthermore, parameters obtained through traditional methods are frequently unsuitable for direct use in numerical simulations; instead, they must be converted using empirical formulas before being applied in numerical calculations^10,11,12,13.

In response to these challenges, a growing number of scholars are turning to the extensive monitoring data collected on-site to conduct back analysis of rock mechanics parameters^14,15,16. The three main aspects of this approach are displacement back analysis, stress back analysis, and load back analysis^17,18. Among these, the displacement back analysis method is frequently used as the recommended technique for back analysis of rock parameters because it benefits from more intuitive, easily obtained, and large quantities of displacement data. This method can be traced back to the 1970s when Kavanagh et al.¹⁹ introduced the theory of displacement back analysis and used finite element analysis and measured displacement values to conduct back analysis of the elastic modulus of the rock mass. Following its creation, displacement back analysis incorporated the BP neural network, which soon gained popularity as a technique for this use case²⁰.

The iterative process in displacement back analysis is mostly solved by an optimization algorithm²¹. With advancements in intelligent technologies, methods such as genetic algorithms (GA)^22,23,24,25, particle swarm optimization (PSO)^26,27,28,29, simulated annealing (SA)³⁰, etc. have been integrated into back analysis, significantly enhancing the speed and accuracy of these processes. Feng et al. incorporated GA into artificial neural networks, establishing an evolutionary neural network method, which they successfully validated through a typical case³¹. Deng et al. replaced the time-consuming finite element method with a BP neural network and used GA as an optimization tool to improve global search capabilities, successfully applying this approach to the back analysis of the slope rock mass at the permanent ship lock of the Three Gorges Project³². Zhuang et al. improved GA by incorporating absolute percentage error as the target parameter while considering weights. They proposed an IAGA-BP inversion analysis method that effectively addressed the problem of displacement weight allocation between the dam foundation and the dam shoulder. This method was successfully applied to the inversion of the dam body and foundation parameters at the Yangfanggou Hydropower Station³³. Hashash et al. compared the advantages of GA and SelfSim algorithm in inverting soil material properties, indicating that GA optimization is more constrained by the soil constitutive model, while SelfSim optimization is less constrained by the soil constitutive model. This leads to GA often overestimating surface settlement, while SelfSim calculates more accurately²³. Moreira et al. evaluated the performance of evolutionary strategies in the inversion of mechanical parameters of underground structures, finding that GA demonstrates beneficial robustness and efficiency, thus alleviating some limitations of classical algorithms³⁴. Rechea et al. compared the performance of two minimization algorithms, gradient descent, and GA, in the analysis of deep excavation displacement data. The results demonstrated that both methods are capable of producing smooth and unique solutions³⁵. Ma et al. proposed a discrete element mechanics parameter back analysis method based on PSO, validated through typical landslide cases³⁶. Li et al. optimized PSO and combined it with support vector machines (SVM) for rock mechanics parameter inversion, achieving an error margin of just 0.91% compared to the assumed actual parameters²⁷. Miranda et al. compared traditional optimization algorithms with evolutionary optimization techniques in the back analysis of mechanical parameters for the hydroelectric powerhouse cavern of Venda Nova II built in Portugal, showing that both methods can effectively obtain optimal parameter sets and offer insights into the characteristics of the rock mass³⁷. Wang et al. combined GA with SA to form a modified GSA algorithm, which improved the ability and solution quality of optimization problems. The model has been applied in the rock mechanics parameter back analysis of the underground powerhouse on the right bank of Wudongde Hydropower Station and has achieved good results³⁰.

With the development of machine learning and algorithms, more and more novel methods are being proposed and applied in the inversion of surrounding rock parameters. Gao et al. introduced a novel neural network based on the black hole algorithm as an alternative to traditional neural networks. Their comparison revealed that the new network is an effective approach for determining the mechanical parameters of surrounding rock masses in underground tunnels¹⁷. Tang et al. developed a non-linear optimization technique (NOT) that demonstrated the capability to accurately and efficiently predict deformation caused by subsequent excavation in the provided cases³⁸. He et al. enhanced the non-dominated sorting genetic algorithm II (NSGA-II) by integrating it with the GA for application in slope stability assessment. The improved model exhibited a significant Pareto front shift and yielded smaller errors compared to the original NSGA-II model³⁹. Huang et al. proposed a deep learning method called Long short-term memory (LSTM) to invert slope stability with five control factors. The results showed that LSTM overcomes the problem of traditional machine learning being difficult to extract global features⁴⁰.

Based on the existing literature, this study establishes a GA-PSO-BP neural network model (GPSO-BP) for mechanical parameters by integrating GA, PSO, and BP neural networks. First, the orthogonal and uniform experimental designs are employed to design experimental schemes that simulate excavation to construct learning samples. Thereafter, the GA and PSO are integrated into the BP neural network to optimize the weights and thresholds. The surrounding rock parameters are passed through the model inverted using displacement monitoring data collected on-site and then fed into numerical simulation software for forward analysis. Finally, a comparison between the simulation results and the data from the on-site monitoring shows that the suggested approach produces good results.

Construction of back-analysis method

BP neural network

The BP neural network, a type of feedforward neural network, operates through a process of information forward propagation and error backpropagation^13,33. The basic principle involves calculating the deviation between the predicted output and the actual value during forward propagation, followed by backpropagating the error using gradient descent to adjust the network’s weights and thresholds. Through repeated training, the network’s error is minimized until it meets the desired criteria. Studies have shown that a three-layer BP neural network can approximate nonlinear functions with high accuracy, which is why the BP neural network in this study adopts a three-layer structure. The diagram of the three-layer BP neural network structure is shown in Fig. 1.

Fig. 1

Three-layer BP neural network structure.

Where, ${x}_{i}$ is the input layer node, ${H}_{j}$ is the hidden layer node, ${O}_{k}$ is the output layer node, ${\omega }_{ij}$ is the weight from the input layer to the hidden layer, ${\omega }_{jk}$ is the weight from the hidden layer to the output layer, ${a}_{j}$ is the threshold of the hidden layer, ${b}_{k}$ is the threshold of the output layer, ${Y}_{k}$ is the expected output value, ${e}_{k}$ is the error between the expected output and the actual output of the neural network, $m$ is the number of input layer nodes, $l$ is the number of hidden layer nodes, $n$ is the number of output layer nodes, ${f}_{1}$ is the transfer function from the input layer to the hidden layer, ${f}_{2}$ is the transfer function from the hidden layer to the output layer, where $i=\text{1,2},\dots ,m;j=\text{1,2},\dots ,l;k=\text{1,2},\dots ,n$.

The evolution steps of a BP neural network are as follows: (1) Determine the structure of the BP neural network. (2) Input the learning samples, randomly generate the weights and thresholds, and calculate the output. (3) Calculate the prediction error. (4) Backpropagate the error to adjust the weights and thresholds of the neural network. (5) Repeat steps (2) to (4), continuously refining the mapping relationship until the error reaches the predetermined target or other termination conditions are met.

However, the BP neural network also has some limitations: (1) It takes a lot of sample data to achieve high training accuracy; (2) Under some initial conditions, it is prone to get trapped in local optima; (3) The rate of convergence is comparatively slow.

Improvement methods

To solve the problem of the large sample demand in BP neural networks, scholars frequently employ orthogonal experimental design to construct a sample database, from which a subset of data is randomly selected for training and the remaining part for testing^13,41. However, this randomness leads to variability in the samples used by the BP neural network in each iteration, making it challenging to ensure reproducibility. To overcome this challenge, this study introduces uniform experimental design alongside orthogonal experimental design. In this approach, orthogonal experimental design is used to generate the learning samples for the BP neural network, while uniform experimental design provides the testing samples. This method significantly reduces the number of required experiments while maintaining accuracy and comparability by choosing representative test points instead of in-depth experiments.

PSO can reduce the learning time required for BP neural network training and enhance accuracy. However, standard PSO is prone to issues such as getting stuck in local optima and premature convergence. On the other hand, GA is a random search algorithm that explores multiple feasible solutions within the solution space of a problem through selection, crossover, and mutation operations, aiming to find the global optimal solution. By combining GA with PSO, the weights and thresholds of the BP neural network can be optimized, resulting in a prediction model that benefits from low computational complexity, fast convergence speed, and robust global convergence performance.

Orthogonal uniform design GA-PSO-BP neural network model

The orthogonal uniform design GA-PSO-BP neural network model (GPSO-BP) mainly includes orthogonal experimental design, uniform experimental design, GA, PSO, and BP neural network. The flowchart is shown in Fig. 2, and the specific implementation steps are as follows:

• (1) Construct learning samples. The range of parameter values needs to be determined first. Orthogonal experimental design and uniform experimental design are used to construct simulation schemes. These schemes are calculated using numerical software to generate displacement values, which serve as learning samples for the neural networks.

• (2) Determine the structure of the BP neural network. The weights and thresholds of the neural network are the parameters to be optimized, and they are used to generate the initial population $U$.

• (3) Introduce PSO to optimize the population $U$. The mean square error (MES) between the neural network’s output and the on-site measured value is used as the fitness evaluation index. A smaller fitness value indicates a smaller error and better adaptability. After each update of the population, the fitness values are sorted in ascending order and divided into three groups: ${U}_{1}$, ${U}_{2}$, ${U}_{3}$.

  $$Fitness=\frac{1}{n}\sum_{i=1}^{n}{({t}_{i}-{a}_{i})}^{2}$$

  (1)

  where, $Fitness$ is the fitness function, ${t}_{i}$ is the actual output value of the i-th training sample, ${a}_{i}$ is the expected value of the i-th training sample, $n$ is the number of training sets.

• (1)(1)(1)(4) Introduce GA to enhance the global search capability. The standard GA uses the roulette wheel method, which has a high degree of randomness and may eliminate better individuals. Therefore, for ${U}_{1}$ with the best adaptability, the replication is directly performed. For ${U}_{2}$ with moderate fitness, crossover operation is performed with crossover probability $pc$, which includes velocity crossover and position crossover, as shown in the following equation. For ${U}_{3}$ with the worst adaptability, mutation operation is performed with mutation probability $pm$. The fitness values of the offspring particles after crossover and mutation operations will be compared with those of parent particles, retaining the particles with smaller fitness values for the next iteration⁵⁰.

  $$\left\{\begin{array}{c}{v}_{i}\left(t+1\right)={\uptheta }_{1}{v}_{i}\left(t\right)+(1-{\uptheta }_{1}){v}_{j}(t)\\ {v}_{j}\left(t+1\right)=(1-{\uptheta }_{1}){v}_{i}\left(t\right)+{\uptheta }_{1}{v}_{j}(t)\end{array}\right.$$

  (2)
  $$\left\{\begin{array}{c}{x}_{i}\left(t+1\right)={\uptheta }_{2}{x}_{i}\left(t\right)+(1-{\uptheta }_{2}){x}_{j}(t)\\ {x}_{j}\left(t+1\right)=(1-{\uptheta }_{2}){x}_{i}\left(t\right)+{\uptheta }_{2}{x}_{j}(t)\end{array}\right.$$

  (3)

  where, ${\theta }_{1}$ and ${\theta }_{2}$ are random values between [0, 1].

• (5) Update individual extremum and global extremum. The fitness of the new particle will be compared with those of individual and global extremum, which will preserve better fitness.

• (6) Repeat steps (3) to (5) until the accuracy requirements are met or other termination conditions are satisfied.

• (7) Train and test the GPSO-BP neural network. The optimal weights and thresholds are fed into the BP neural network for training and testing. After repeated iterations, the desired neural network is achieved.

• (8) Evaluate the inversion effect. The displacement measurement data are input into the model to obtain the optimal inversion parameters. Forward calculations are then performed using these parameters to obtain displacement values, which are compared with the measured data.

Fig. 2

Flow chart of the GPSO-BP Neural Network Model.

Numerical example

To verify the superiority and effectiveness of the GPSO-BP neural network, a widely used tunnel excavation model was used for simulation. The circular tunnel has a radius of 3 m, and the analysis area extends to 15 m, which is five times the tunnel radius. Due to symmetry, only 1/4 of the cross-section was analyzed. The model grid and measure points are shown in Fig. 3. The initial ground stress was set as ${\sigma }_{x}={\sigma }_{y}=10.0 \text{MPa}$, and the mechanical parameters of the surrounding rock were $E=1.9 \text{GPa}$, $\mu =0.32$, $\varphi =27^\circ$, and $c=1.1 \text{MPa}$. The forward analysis was calculated in Flac3D software, and the displacement at the measure points is shown in Table 1.

Fig. 3

Tunnel excavation grid model and measure points layout diagram.

Table 1 Displacements of measure points.

The range of surrounding rock parameters in the back analysis is as follows: $1.5 \text{GPa}<E<2.5 \text{GPa}$, $0.2<\mu <0.4$, $27^\circ <\varphi <40^\circ$, and $0.7 \text{MPa}<c<1.7 \text{MPa}$. These parameters are divided into five equal parts, and experimental schemes are constructed through orthogonal and uniform experimental design. The displacement values are then calculated using Flac3D to generate training and testing samples for the neural network. The displacement monitoring values at the measure points are used as input data, while the surrounding rock parameters as output data for back analysis. According to Formula (4), the number of hidden layer nodes is determined to be 12 through the trial-and-error method. The BP neural network structure is defined as 9-12-4. The learning factors of PSO are set to $c1=c2=1.49$, the population size is 60, and the number of iterations is 400. The crossover probability for GA is set to 0.4, and the mutation probability is set to 0.1. All other parameters are kept at their default values.

$$l=\sqrt{m+n}+a$$

(4)

where, $l$ is the number of hidden layer nodes, $m$ is the number of input layer nodes, $n$ is the number of output layer nodes, $a$ is a constant between 1 and 10.

A comparison was made between BP, GA-BP, PSO-BP, and GPSO-BP neural networks. The relative error calculation results for the rock mechanics parameters are displayed in Table 2. According to the table, the GPSO-BP back analysis produces smaller errors compared to BP, GA-BP and PSO-BP neural networks, with an average relative error of only 3.32% across the four parameters, significantly lower than 11.14% for BP, 5.17% for GA-BP and 6.03% for PSO-BP neural networks. The fitness curves for the GA-BP, PSO-BP and GPSO-BP neural networks are illustrated in Fig. 4. It can be seen that as the number of iterations increases, the fitness values of all GA-BP, PSO-BP and GPSO-BP decrease. Moreover, the fitness of the GPSO-BP converges faster, with a smaller final fitness value, indicating that the GPSO-BP neural network proposed in this study offers faster convergence and higher accuracy in inverse analysis.

Table 2 Computed result of back analysis.

Fig. 4

The fitness curve of numerical example varies with the number of iterations.

Application in Zhaotong tunnel project

The GPSO-BP neural network is applied to the back analysis of surrounding rock parameters in the Zhaotong Tunnel, offering predictions and guidance for subsequent construction.

Engineering background

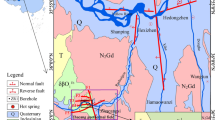
The Zhaotong Tunnel, a key project connecting the Chongqing and Kunming high-speed railways, has a total length of 16.26 km. The DK377 + 300 ~ 350 section of the main tunnel belongs to the gas outburst zone, where conventional geophysical detection equipment cannot be used. And the surrounding rock mainly composed of shale with well-developed joints and fissures, presents challenges for sampling. Consequently, the mechanical parameters of this section’s surrounding rock must be determined using a displacement back analysis method. The regional location of the Zhaotong Tunnel and the palm surface are shown in Fig. 5.

Fig. 5

The regional location of the Zhaotong Tunnel and the palm surface⁵¹.

On-site monitoring plan and data

The main tunnel of this section is constructed using the three-step method. After completing the excavation and initial support of the tunnel face, reflective monitoring points are installed at the arch crown and 80 cm above each of the three steps. A total station is then used to measure the settlement of the surrounding rock at the arch crown and the convergence at both sides after the initial support. The layout of the tunnel construction sections and monitoring points is shown in Fig. 6. The on-site monitoring of section DK377 + 330 is shown in Fig. 7.

Fig. 6

Tunnel construction section and monitoring points layout diagram.

Fig. 7

The on-site monitoring of section DK377 + 330.

Tunnel excavation alters the initial stress field of the surrounding rock, leading to displacement that can be divided into three parts, as shown in Fig. 8. Before excavation reaches the monitoring point, an initial deformation, denoted as S₀, has already occurred. After the excavation reaches the monitoring points but before the installation of monitoring instruments, an additional instantaneous deformation, referred to as S₁, takes place. Once the monitoring points are installed and until the displacement eventually stabilizes, the measured deformation corresponds to the actual deformation of the tunnel observed on-site, identified as the S₂ deformation segment. The relative displacement simulated by Flac3D is recorded starting from the moment of excavation, referred to as S₁ + S₂. Since the installation of on-site displacement monitoring points typically occurs after the completion of the initial support—usually lagging behind the tunnel face by half a day to a full day—determining S₁ is difficult to determine. Therefore, this study omits the S₁ deformation segment to maintain a consistent relationship between the relative deformation obtained from Flac3D simulations and the on-site measured displacement.

Fig. 8

The whole process curve of surrounding rock deformation.

Establishment and calculation of numerical models

The horizontal diameter of the Zhaotong Tunnel’s main tunnel is 15.04 m, and the vertical diameter is 13.23 m. The numerical calculation model of the tunnel typically spans 3–5 times the tunnel’s span. Considering the presence of a parallel guide tunnel located 35 m to the left and 70 m ahead of the main tunnel, the model’s analysis scope is appropriately expanded. The model dimensions are 200 m in the horizontal direction, 160 m in the vertical direction, and 50 m in the axial direction. It is divided into 299,013 nodes and 289,600 elements, as shown in Fig. 9. The average burial depth of this section is 900 m. Based on on-site hydraulic fracturing stress testing and stress inversion analysis of the Zhaotong Tunnel, the maximum horizontal principal stress ${\sigma }_{H}$ is determined to be 35.9 MPa, the minimum horizontal principal stress ${\sigma }_{h}$ is 20.3 MPa, and the vertical principal stress ${\sigma }_{v}$ is 28.6 MPa. The displacement of the bottom surface of the model boundary is fixed in the x, y, and z directions, and the normal displacement is constrained around it. The top surface is a free surface with no displacement constraints.

Fig. 9

The mesh for computation model.

The tunnel excavation employs a three-step excavation method, with excavation progressing in 2 m increments per cycle. The middle interface of the model is chosen for displacement monitoring to minimize boundary effects in the simulation. Cable elements are used for the anchoring, while shell elements are used for initial support. The material constitutive model is based on the Mohr–Coulomb criterion. The schematic diagram of the excavation and support is shown in Fig. 10.

Fig. 10

The schematic diagram of the excavation and support.

The surrounding rock in this section is situated at the boundary between Grade IV and Grade V rock. Based on the "Code for Design of Railway Tunnels" (TB 1003-2016), as well as geological conditions, geological exploration data, and design data for the Zhaotong Tunnel, the range of mechanical parameters for the surrounding rock has been established. To simplify the simulation, the strengthening effects of steel mesh and steel arches on the initial support are incorporated into the initial support concrete⁴². The calculation formula is as follows.

$$E^{\prime} = E_{c} + \frac{{A_{s} + E_{s} }}{{A_{c} }}$$

(5)

where, $E{\prime}$ is the elastic modulus of the converted initial support concrete, ${E}_{c}$ is the elastic modulus of the original initial support concrete, ${E}_{s}$ is the elastic modulus of the steel, ${A}_{s}$ is the cross-sectional area of the steel arch, and ${A}_{c}$ is the cross-sectional area of the concrete.

After calculation, the mechanical parameters of the surrounding rock, initial support, and bolt are presented in Table 3.

Table 3 Mechanical parameters of different materials.

Learning sample construction

To develop a mature GPSO-BP neural network, it is essential to train and test the network with a certain number of learning samples. Based on the defined range of surrounding rock parameters, 5 levels are designed for each parameter. A total of 25 mechanical parameter schemes are constructed as training samples for the neural network using the L₂₅ (5⁴) orthogonal experimental design table. Additionally, 5 mechanical parameter schemes are created as test samples for the neural network using the U₅ (5⁴) uniform design table. These 30 sets of mechanical parameter schemes are imported into the Flac3D model for excavation calculations, generating the apparent displacement values of the tunnel for various mechanical parameters. The learning samples of neural network are presented in Table 4.

Table 4 The processed learning samples of neural network.

Back analysis of surrounding rock parameters

The performance of the regression prediction in the algorithm is significantly impacted by the number of nodes in the hidden layer. According to Formula (1), the number of hidden layer nodes is determined to be 10. The transfer function from the input layer to the hidden layer is set to the logsig function, while the transfer function from the hidden layer to the output layer is set to the purelin function. The grid training function is set to the improved L–M algorithm. The parameters of BP, PSO, and GA were selected through extensive exploratory experiments and grid search methods in the early stage. The learning rate ($\alpha$) for the neural network is set to 0.01, with a network error threshold of 0.0001. The learning factors for PSO parameters are set to $c1=c2=1.49$, with a population size of 60 and 400 iterations. For the GA parameters, the crossover probability is set to 0.6, and the mutation probability is set to 0.2. All other parameters are maintained at their default values. The apparent displacement values are used as input samples for the neural network, while the rock mechanics parameters are used as output samples. The BP, PSO-BP, GA-BP and GPSO-BP neural networks are trained separately.

Performance evaluation of different neural network models

The fitness evolution curves of the GA-BP, PSO-BP, and GPSO-BP neural networks are shown in Fig. 11. It can be observed that the fitness curves are consistent with the numerical examples, with the GPSO-BP model converging the fastest and achieving the highest accuracy. Additionally, after 200 iterations, the fitness curves for all three models plateau, indicating no further reduction in error. This confirms that 400 iterations are sufficient for effective optimization.

Fig. 11

The fitness curve of engineering varies with the number of iterations.

To assess the performance of different models, seven widely used performance indices, namely Coefficient of determination (R²), Variance account for (VAF), Willmott’s Index of agreement (WI), Mean absolute error (MAE), Mean bias error (MBE), Root mean square error (RMSE), Mean absolute percentage error (MAPE) are calculated. Their mathematical expressions are provided in Eqs. (6) to (12). MAE, MBE, and RMSE are based on the error category, while R², VAF, and WI are based on the accuracy category. The correlation between the predicted and expected values for the test set was computed and presented in Table 5 to evaluate the models. However, the overall assessment is based on Rank Analysis^43,44. In this system, each model is assigned a score based on its accuracy ranking for each output parameter^45,46. The model with the highest accuracy receives 4 points, while the least accurate receives 1 point. The overall performance of each model is determined by summing the scores for all parameters in the test set. The final ranking of each model is then calculated based on its total score.

$${R}^{2}=\frac{{\sum }_{i=1}^{n}{({y}_{i}-{y}_{mean})}^{2}-{\sum }_{i=1}^{n}{({y}_{i}-{\widehat{y}}_{i})}^{2}}{{\sum }_{i=1}^{n}{({y}_{i}-{y}_{mean})}^{2}}$$

(6)

$$VAF\left(\text{\%}\right)=\left(1-\frac{var({y}_{i}-{\widehat{y}}_{i})}{var({y}_{i})}\right)\times 100$$

(7)

$$W=1-\left[\frac{{\sum }_{i=1}^{n}{({y}_{i}-{\widehat{y}}_{i})}^{2}}{{\sum }_{i=1}^{n}{\left\{\left|{\widehat{y}}_{i}-{y}_{mean}\right|+\left|{y}_{i}-{y}_{mean}\right|\right\}}^{2}}\right]$$

(8)

$$MAE=\frac{1}{n}\sum_{i=1}^{n}\left|\left({\widehat{y}}_{i}-{y}_{i}\right)\right|$$

(9)

$$MAPE=\frac{1}{n}\sum_{i=1}^{n}\left|\frac{{y}_{i}-{\widehat{y}}_{i}}{{y}_{i}}\right|\times 100$$

(10)

$$MBE=\frac{1}{n}\sum_{i=1}^{n}\left({\widehat{y}}_{i}-{y}_{i}\right)$$

(11)

$$RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{\left({y}_{i}-{\widehat{y}}_{i}\right)}^{2}}$$

(12)

where, ${y}_{i}$ and ${\widehat{y}}_{i}$ represent the $i$-th expected value and predicted value, respectively; $n$ denotes the number of samples in the dataset.

Table 5 Rank analysis for different neural networks.

As shown in the Table 5, the GPSO-BP model achieves the highest rank with a total score of 98 points, followed by the GA-BP and PSO-BP models. The BP model performs the worst, with only 45 points. When analyzing the scores for individual output parameters, GPSO-BP remains the best-performing model for the outputs $E$, $\mu$, and $c$. However, it is noteworthy that for the $\varphi$ output, the GA-BP model scores 27 points, outperforming GPSO-BP’s score of 20 points. Considering the overall performance of the models, GPSO-BP still demonstrates the best results.

In terms of the coefficient of determination (R²), all four models show good fitting performance for output parameters $E$ and $\varphi$, with values greater than 0.82. However, the R² value for output $c$ in the BP model is only 0.1619, which could be attributed to insufficient training samples. While the GA-BP and PSO-BP models improve the R² for $c$, it still remains below 0.5. In contrast, the GPSO-BP model achieves an R² of 0.66 for $c$, indicating that GPSO-BP has a better ability to handle complex models with small datasets compared to the other models. The value of VAF also well illustrates this viewpoint. Overall, the GPSO-BP model delivers the best fitting performance, followed by the GA-BP and PSO-BP networks, while the BP neural network exhibits the poorest fit.

To provide a more intuitive representation of the performance metrics, an accuracy matrix for the test set was constructed⁴⁴, as shown in Fig. 12. Each value in the figure represents the accuracy achieved relative to its ideal value, expressed as a percentage. For example, the ideal values for R² and MAE are 1 and 0, respectively. For the BP model, the R² and MAE values for $E$ output are 0.83 and 0.36, respectively. This can be interpreted as the model achieving 83% ($0.83/1\times 100\%=83\%$) accuracy for R² and 64% ($(1-0.36)\times 100\text{\%}=64\text{\%}$) accuracy for MAE. The accuracy for the other metrics follows Kardani’s definition⁴⁴. It should be noted that for the $\varphi$ output, the MAE and RMSE values for the four neural network models exceed 1, therefore, normalization should be performed before calculation. As shown in Fig. 12, except for a few instances where other models perform better, the GPSO-BP model consistently achieves the highest accuracy.

Fig. 12

Accuracy matrix.

The comparison between the predicted and expected values for the four output parameters is shown in Fig. 13. It can be observed that among the four outputs, the GPSO-BP model deviates the least from the expected values. The mean absolute percentage errors (MAPE) of the GPSO-BP neural network for predicting the four rock parameters are 8.10%, 4.96%, 5.15%, and 28.55%, respectively, outperforming the other three models. For the first three parameters, the MAPE is below 10%, with the exception of the cohesion parameter. All three neural networks struggle to fit the cohesion parameter, primarily due to its expected range of 0.05 to 0.5 MPa. The minimum value is as low as 0.05, meaning that even small absolute errors lead to large relative errors. For example, if the predicted value is 0.1, the relative error for an expected value of 0.05 is 100%, significantly raising the overall MAPE. Despite this, the GPSO-BP model still performs the best, with a MAPE of 28.55%, compared to 66.67% for the BP network, 49.42% for the PSO-BP network, and 38.00% for the GA-BP network.

Fig. 13

The comparison between the expected and predicted values and the MAPE. (a) Elastic modulus, (b) Poisson’s ratio, (c) Internal friction angle, and (d) Cohesion.

This study also uses the Developed Discrepancy Ratio (DDR), a metric proposed by Noori et al. in 2010. The formula for calculating DDR is provided in formula (13). While the standard error offers an average measure of error, it does not provide information about the error distribution. Therefore, DDR is used to assess the efficiency of the model during its development phase^47,48,49. Figure 14 presents the DDR results for different models across the four output parameters. The deviation of the GPSO-BP model’s DDR curve is the smallest for all four outputs, staying closest to the zero line. This indicates that, based on the DDR metric, the GPSO-BP model demonstrates the highest efficiency.

Fig. 14

The DDR of test data with four output parameters. (a) Elastic modulus, (b) Poisson’s ratio, (c) Internal friction angle, and (d) Cohesion.

$$DDR=\left(\frac{Predicted value}{Expected value}\right)-1$$

(13)

Positive analysis and comparison based on inversion results

The measured displacement values on site were input into the trained neural network, and the back analysis results of the surrounding rock parameters are shown in Table 6.

Table 6 The back analysis results of the surrounding rock parameters.

The surrounding rock parameters obtained from different neural networks were input into Flac3D for forward calculation, yielding values for roof settlement and horizontal convergence. These results were compared with the on-site measured values, as shown in Fig. 15. The displacement predictions obtained from the forward calculations using the inversion parameters of the GPSO-BP neural network model exhibited the smallest errors when compared to the measured values. The relative errors for roof settlement and the convergence of the three steps were 1.11%, − 6.88%, − 0.41%, and − 8.97%, respectively, which are significantly better than those produced by BP, GA-BP and PSO-BP neural networks.

Fig. 15

Comparison of displacement between different algorithms.

As shown in Fig. 8, the deformation S₁ was disregarded. The displacement at the moment of exposing the monitoring points on the upper step is 0 and gradually increases as the excavation processes. The displacement change curve obtained from the forward calculation using the GPSO-BP neural network is compared with the on-site measured values, as shown in Fig. 16. The trends of the four curves are generally consistent. However, some discrepancies exist in the convergence curves of the upper and middle steps. These differences may be due to various factors affecting the excavation, where the upper, middle, and lower steps might not have advanced simultaneously as assumed. In contrast, the Flac3D simulations were conducted with all three steps advancing simultaneously, leading to some variation in the middle portion of the curve. Nonetheless, the final deformation from the numerical simulation closely matches the field measurements, indicating that the parameter identification and back analysis results of the proposed GPSO-BP neural network inversion model are reliable.

Fig. 16

Comparison chart of displacement trend with excavation steps. (a) Roof settlement, (b) Upper step convergence, (c) Middle step convergence and (d) Lower step convergence.

Conclusions and discussion

Conclusions

This study proposes a displacement back analysis model based on the GPSO-BP neural network, which integrates the advantages of orthogonal experimental design, uniform experimental design, GA, PSO, and BP neural network. This model has been successfully applied to the inversion of surrounding rock parameters in the Zhaotong Tunnel.

• (1) To address the issues of slow convergence and susceptibility to local optima in the original BP neural network, the selection, crossover, and mutation operations of GA were improved and embedded into each iteration of PSO, resulting in the proposed GPSO-BP neural network model. This model enhances global search capabilities while preserving the best particles. The fitness curves indicate that the GPSO-BP model achieves faster convergence and higher accuracy compared to PSO-BP and GA-BP.

• (2) Traditional BP, GA-BP, and PSO-BP neural network models perform well with small datasets and simple models (numerical examples), but struggle with more complex models such as the Zhaotong Tunnel. In the back-analysis of rock parameters for the Zhaotong Tunnel, the R² for the parameter $c$ using the BP model was only 0.1619. For the GA-BP and PSO-BP models, the R² values were also less than 0.5, whereas the GPSO-BP achieved an R² of 0.66. Additionally, the GPSO-BP model achieved R² values above 0.8 for the other three output parameters, demonstrating superior performance when dealing with small datasets and complex models. This suggests that the GPSO-BP model is more suitable for application in complex rock engineering scenarios.

• (3) A rank analysis of the test sets for the BP, PSO-BP, GA-BP, and GPSO-BP models indicates that, although GA-BP performed best for the parameter $\varphi$, GPSO-BP achieved the highest overall score when considering total performance, and was therefore identified as the best model among the four. The back-analysis method provided in this study is shown to be reliable.

• (4) The GPSO-BP model was successfully applied to the displacement back analysis of the Zhaotong Tunnel case. The rock parameters obtained from this model were used in forward analysis through numerical simulation, resulting in an average relative error of only 4.34% across four monitoring points. The predicted trends closely aligned with the observed displacement values, outperforming the BP model (17.10%), PSO-BP (15.92%), and GA-BP (14.78%). Since the Zhaotong Tunnel is a typical deep-buried, large-section, high-stress tunnel, it is indicated that the GPSO-BP model provides valuable insights for similar underground engineering projects.

Discussion

Training a neural network requires a large dataset, but generating such data through numerical simulation software is an extremely time-consuming and labor-intensive process. This is why only 30 samples were used in this study. Although the GPSO-BP model shows improvements over the other three methods in handling small datasets and complex models, its generalization ability remains limited. In future work, it is planned to replace the time-consuming numerical simulation process with a BP neural network, which will generate additional data based on the existing dataset. This will expand the training samples and improve the model’s generalization ability.

Additionally, a grid search method was used to determine the parameters for BP, PSO, and GA, which introduced a level of empiricism. This led to high computational costs and long training times to obtain optimal parameters, and the selected parameters may not represent the best combination. Future research will focus on conducting sensitivity analysis of hyperparameters and implementing algorithms that enable adaptive adjustment of neural network hyperparameters to enhance model stability.

Statement attesting

For the images and information presented in this manuscript, informed consent was obtained from all study participants and/or their legal guardians for the publication of identifying information/images in an online open-access publication. All patient names and other personal identifiers have been removed, in compliance with ethical standards.