Deep learning model based prediction of vehicle CO₂ emissions with eXplainable AI integration for sustainable environment

Abstract

The transportation industry contributes significantly to climate change through carbon dioxide ($\hbox {CO}_{2}$) emissions, intensifying global warming and leading to more frequent and severe weather phenomena such as flooding, drought, heat waves, glacier melting, and rising sea levels. This study proposes a comprehensive approach for predicting $\hbox {CO}_{2}$ emissions from vehicles using deep learning techniques enhanced by eXplainable Artificial Intelligence (XAI) methods. Utilizing a dataset from the Canadian government’s official open data portal, we explored the impact of various vehicle attributes on $\hbox {CO}_{2}$ emissions. Our analysis reveals that not only do high-performance engines emit more pollutants, but fuel consumption under both city and highway conditions also contributes significantly to higher emissions. We identified skewed distributions in the number of vehicles produced by different manufacturers and trends in fuel consumption across fuel types. This study used deep learning techniques to construct a CO₂ emission prediction model, specifically a light multilayer perceptron (MLP) architecture called CarbonMLP. The proposed model was optimized by hyperparameter tuning and achieved excellent performance metrics, such as a high R-squared value of 0.9938 and a low Mean Squared Error (MSE) of 0.0002. This study employs XAI approaches, particularly SHapley Additive exPlanations (SHAP), to improve the model interpretation ability and provide information about the importance of features. The findings of this study show that the proposed methodology accurately predicts CO₂ emissions from vehicles. Additionally, the analysis suggests areas for further research, such as increasing the dataset, integrating additional pollutants, improving interpretability, and investigating real-world applications. Overall, this study contributes to the design of effective strategies for reducing vehicle CO₂ emissions and promoting environmental sustainability.

Introduction

In the 21st century, climate change poses a significant challenge to humanity, as it harmfully affects ecosystems, the economy, and human welfare. Carbon dioxide (CO₂) emission is the primary cause of climate change. Additionally, the reasons for this epidemic include various human activities such as industrial processes, energy production, and transportation. While CO₂emissions are a global concern, countries such Canada face unique challenges due to their reliance on fossil fuel-based transportation across vast geographical landscapes. Canada’s transportation sector accounts for a significant portion of the country’s overall greenhouse gas (GHG) emissions, making it a priority for policy interventions aimed at reducing environmental impacts¹. Moreover, these emissions threaten the environment and negatively affect human health. Exposure to air pollution from traffic can aggravate respiratory problems such as asthma and chronic obstructive pulmonary disease (COPD) and may increase the risk of developing heart disease or stroke².

Transportation is a crucial foundation of contemporary society, enabling economic transactions, worldwide interconnections, and individual movement. However, reliance on fossil fuels has resulted in a substantial and increasing environmental predicament, namely, a surge in CO₂ emissions. These emissions are a major cause of the increase in greenhouse gases, which accelerate climate change and lead to environmental problems such as higher sea levels, extreme weather conditions, and disruptions to ecosystems. Motor vehicles have a significant impact on the transportation sector, and are a major contributor to CO₂ emissions. In 2020, cars accounted for approximately 23% of global CO₂emissions³. An average passenger automobile produces 4.6 metric tonnes of carbon dioxide annually⁴. Different transports also emit nitrogen oxides and other pollutants, which also contribute to smog formation and acid rain and are harmful to ecosystems⁵. The World Counts emphasize the significant influence of cars on the condition of the air, highlighting them as a primary contributor to air pollution⁶.

Figure 1 shows the distribution of CO₂emissions by vehicle type for the year 2022 worldwide⁷. The graph highlights the percentage contribution of each vehicle category to total global CO₂ emissions. Comprehending and forecasting these emissions are essential for formulating efficient measures to combat climate change.

Fig. 1

Transportation Emissions by Vehicle Type Contributing to total CO₂ Emissions.

The complex interplay of these factors influences vehicle CO₂ emissions. The most significant contributors are the fuel type, engine characteristics, driving behavior, road conditions, vehicle weight, and aerodynamics. The level of CO₂ emissions produced by vehicles is directly influenced by the type of fuel used.

Biofuels, hydrogen, and electricity produce less CO₂than fossil fuels such as gasoline and diesel⁸. Biofuels have a lower carbon footprint, while hydrogen fuel vehicles produce only water vapor as a byproduct⁹. Engine displacement, power output, and technology are factors that influence CO₂ emissions. Although advancements in engine technology, such as direct injection and turbocharging, can enhance fuel efficiency and reduce emissions, it is important to note that larger and more powerful engines often generate higher levels of CO₂¹⁰. Fuel consumption and CO₂emissions also significantly depend on the gearbox mechanism, whether manual or automatic¹¹. CO₂emissions can be decreased by eco-driving strategies such as maintaining steady speeds, activating traffic lights, and moderately accelerating. Conversely, aggressive acceleration, rapid braking, and frequent idling contribute to higher emissions¹². Vehicle fuel consumption and CO₂emissions are influenced by traffic congestion, road surface conditions, and inclines. Stop-and-go traffic results in heightened engine idle and suboptimal fuel use, whereas uneven road surfaces can generate extra friction, thus affecting fuel efficiency¹³. Furthermore, severe temperatures and the level of winds also affect fuel consumption and emissions¹⁴. A higher vehicle weight requires increased energy consumption, which results in higher levels of CO₂emissions. Moreover, the presence of aerodynamic drag affects cars because their streamlined structures encounter reduced air resistance, which results in lower emissions¹⁵. The development of policies and strategies is important for reducing climate change by estimating vehicle CO₂ emissions. To promote cleaner and more fuel-efficient vehicles, the prediction and monitoring of CO₂emissions from vehicles remains a difficult task. Traditional methods for estimating emissions, such as emission factors and vehicle testing, have limitations in accuracy, scalability, and adaptability to dynamic driving conditions¹⁶. In addition, regulatory bodies have established emission factors based on criteria such as vehicle type, fuel type, and other pertinent variables. Although useful, these parameters frequently offer a generic approximation and fail to consider the dynamic interaction of factors that influence actual emissions in the real world¹⁷.

This research was motivated by the pressing need to address the environmental impact of vehicle emissions and enhance our comprehension of the processes that cause variations in emissions. Policymakers can make well-informed judgements about emission reduction methods, sustainable transportation policies, and infrastructure expenditures by creating accurate forecasting models¹⁸. Furthermore, precise forecasts of CO₂ outflows can empower consumers to make clear choices when selecting vehicles, emphasize eco-friendly driving practices and support sustainable transportation.

This study aimed to address the limitations of existing methods for estimating vehicle CO₂ emissions by developing a lightweight deep learning (DL) model that leverages real-world data and offers several key advantages:

• 1. Build and train a lightweight DL model using advanced techniques to predict vehicle CO₂ emissions accurately from comprehensive datasets. Multiple algorithms are compared to select the most accurate and robust predictors.

• 2. We integrate real-world data to train the deep learning model with eXplainable Artificial Intelligence (XAI) integration, enhancing realism and accuracy in predicting vehicle CO₂ emissions.

• 3. Ensure computational efficiency and scalability by developing a DL model with minimal data preprocessing, thereby promoting real-world applicability for widespread adoption in on-board emission estimation and regulatory use.

Although the dataset used in this study is specific to Canadian vehicles and emissions data, the developed model and techniques can be generalized and applied to similar datasets from other countries and regions. Vehicle CO₂ emissions are a global issue and are influenced by factors such as engine size, fuel consumption, and vehicle type. The predictive techniques and insights gained from this research apply to various geographic contexts, as they leverage universal vehicle characteristics. Furthermore, the methods demonstrated in this study provide a framework that can be easily adapted to account for regional differences in emissions standards, vehicle types, and driving conditions, making it relevant for national and international efforts to reduce CO₂ emissions.

This study analyzed recent CO₂ emissions trends for a variety of vehicle types and models from multiple manufacturers. This study uses data from the Canadian government’s official open data website to show how various car features affect CO₂ emissions. The data preparation process comprises rigorous cleaning, data engineering, and transformation procedures to increase dataset quality and prediction accuracy. This study employs advanced deep learning techniques, specifically a multilayer perceptron (MLP) architecture, to improve the prediction accuracy of CO₂ emissions. Although traditional machine learning models are mentioned for performance comparison, the primary focus of this study is on the deep learning approach, which leverages its strengths to achieve more accurate CO₂ emission projections. Furthermore, XAI methodologies, such as Shapley Additive exPlanations plots, are used to improve model interpretability. This integration not only enhances model transparency but also provides more detailed insights into the impact of numerous vehicle characteristics on CO₂ emissions predictions, allowing for the creation of more effective emission reduction plans.

In this paper, we present an in-depth analysis of the forecasting CO₂ emissions from vehicles using deep learning and XAI techniques. Section ’Related Work’ review important literature on the topic to provide a context for our research. Section ’Method’ describes the approach used, which included data collection, preprocessing, model development, and evaluation techniques. Section ’Result Analysis’ presents the results and discussions that evaluate the performance of the proposed model and discuss valuable achievements. The ’Conclusion and Future Work’ closes by summarizing the main contributions, identifying shortcomings, and suggesting areas for future research.

Related work

Artificial intelligence (AI) models have shown promise in reducing carbon dioxide (CO₂) emissions through various mechanisms. Studies have shown that AI can notably lower CO₂emissions, particularly in regions with advanced industrial structures^19,20. AI algorithms enhance the Measurement and Verification (MV) protocols for energy-efficient infrastructure, leading to substantial reductions in both energy consumption and emissions²¹. For example, AI techniques, such as multi-gene genetic programming, have been effectively applied to model and optimize CO₂capture in coal-fired power plants, achieving over 99% accuracy in emission predictions²². These AI models provide valuable insights for improving the design and operational strategies of CO₂capture systems, contributing to long-term decarbonisation efforts²². Additionally, AI strategies have been successfully implemented at the city level to further reduce carbon emissions and support carbon neutrality goals²³.

The application of AI in the chemical industry has also gained recognition for its ability to optimize processes, predict emissions, and support sustainable practices. This contribution is essential for the industry’s transition toward net-zero emissions and overall²⁴. The impact of AI on carbon reduction varies across countries, with more pronounced effects observed in high-carbon emission and high-income nations. This variation underscores the importance of considering industrial and demographic structures when designing strategies for emission reduction²⁵. Collectively, these findings highlight the vital role that AI plays in advancing carbon neutrality and offer insights for policy recommendations and sustainable development strategies.

The transportation sector, which is responsible for approximately 16.2% of global CO₂emissions, has also benefited from AI-driven advancements²⁶. Machine learning (ML) algorithms, such as Random Forest, Decision Tree, and Regression Models, have been employed to accurately predict CO₂emissions²⁷. Among these, Gradient Boosting Regression (GBR) has been proven to be the most effective . These ML algorithms consider both socioeconomic and transportation-related factors when predict emissions²⁸. Supervised machine learning regression approaches, validated through metrics such as the Root Mean Square Error (RMSE), have been used to enhance the accuracy of CO₂emission forecasts²⁹. In particular, the real-time forecasting of CO₂emissions from automobiles in India has demonstrated the effectiveness of constructing ML models and optimizing hyperparameters to achieve precise predictions³⁰.

Deep Neural Networks (DNNs) have gained popularity for estimating CO₂emissions becuase of their ability to analyze complex patterns and correlations in large datasets. Advanced deep-learning algorithms, such as Long Short-Term Memory (LSTM), Gated Recurrent Units (GRU), and Recurrent Neural Networks (RNN), have been successfully utilized to forecast vehicle emissions with notable success³¹. Integrated models combining these algorithms have shown promise for enhancing the accuracy of emission predictions. For instance, LSTM and BiLSTM models have been effectively employed to predict CO₂emissions based on vehicle characteristics, such as engine size, fuel type, and consumption rates³². Additionally, ensemble learning techniques that utilize deep neural networks have been suggested to reduce uncertainty in predicting vehicle energy efficiency, further improving the accuracy and robustness³³.

Ensemble approaches, which combine multiple models and algorithms, have proven to be highly interpretable, accurate, and robust in predicting carbon-related parameters. These models are invaluable tools for policymakers and environmental decision-making^34,35.For example, models trained using real-time sensor data collected through OBD-II ports in vehicles have provided scalable and efficient methods for monitoring emissions at the vehicle level³⁶. One particular machine learning model, UWS-LSTM, has demonstrated precise predictions of CO₂emissions in hybrid vehicles, making it highly effective for smart vehicle applications that require fast and efficient results³⁷.

explainable AI models have demonstrated varying levels of precision in estimating CO₂emissions from vehicles. Studies have indicated that advanced non-linear multivariate models, such as ENGM(1,4), are more effective than conventional statistical models in forecasting transportation sector emissions, achieving superior accuracy³⁸. Furthermore, advanced AI approaches, such as feed-forward neural networks (FFNN), adaptive network-based fuzzy inference systems (ANFIS), and LSTM, have been employed to forecast CO₂emissions, with LSTM exhibiting particularly high accuracy³⁹. Additionally, the use of Shapley Additive ExPlanations (SHAP) for lane-change decisions has provided clear and understandable explanations for the factors influencing AI model decisions, thereby improving the interpretability and trustworthiness of these models⁴⁰.

In summary, AI’s potential to reduce CO₂ emissions is widely recognized across various sectors, including energy, chemicals, and transportation. AI not only optimizes processes and predicts emissions but also supports sustainable practices and informs policy-making. The integration of AI in emission reduction efforts represents a critical pathway toward achieving carbon neutrality and addressing climate change on a global scale An overview of the Literature Review is given in Table 1

Table 1 Overview of the literature review.

Methods and materials

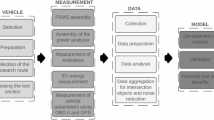
The methodology of this study centers exclusively on deep learning techniques to comprehensively forecast CO₂ emissions from vehicles. The process began with preprocessing and data collection, followed by the creation of the MLP model. Additionally, explainable AI (XAI) methods, particularly Shapley Additive Explanations (SHAP), have been utilized to enhance the interpretability and reliability of predictions. An overview of the methodology used in this study is shown in Figure 2.

Fig. 2

Methodology Diagram Illustrating the Entire Process Described in the Paper, from Data Collection to Model Evaluation and Interpretation.

Data collection and exploration

This study’s dataset, which was obtained from Kaggle, provides extensive information on how CO₂ emissions vary depending on various vehicle parameters. The dataset compiles data from the Canadian government’s official open data website, spanning a period of seven years Dataset. The dataset, which includes 12 columns and 7385 rows across a 7-year span is an extensive information source. Information on vehicle models, fuel types, transmissions, city and highway fuel consumption ratings, and CO₂ emission levels is all included. Table 2 presents an overview of the characteristics, explanations, and associated values of the dataset.

The “uel Consumption Comb (mpg)” column in the dataset was originally added to represent fuel consumption in miles per gallon (mpg). However, additional analysis revealed that the reported values did not match the normal conversion from litres per 100 km (L/100 km) to miles per gallon (mpg)⁵¹. The correct conversion formula is as follows:

$$\begin{aligned} \text {mpg} = \frac{235.215}{L / 100 Km} \end{aligned}$$

(1)

Due to the disparity between the reported “Fuel Consumption Comb (mpg)” values and the expected values estimated using the conversion procedure, this column was removed from the dataset. Instead, the column reflecting fuel usage in litres per 100 km (L/100 km) will be used for additional analysis and modelling.

Table 2 Description of dataset features.

A distinct pattern emerged from the analysis of CO$_2$ emissions by vehicle model: vehicles with high-performance engines, such as SRT, Rolls Royce, and Lamborghini, had the highest emissions, whereas fuel-efficient models, such as Smart and Honda, exhibited the lowest emissions. This observation is consistent with the theory that large engines produce more CO$_2$.

To quantify these observations, we calculated the mean CO$_2$emissions for 41 distinct car models displayed in the visualization. The mean was estimated by grouping the dataset by vehicle maker and applying the following formula⁵²:

$$\begin{aligned} \text {Mean CO}_{2} \text { Emissions } = \frac{1}{n} \sum _{i=1}^{n} \text { CO }_{2i} \end{aligned}$$

(2)

where $n$ represents the total number of entries for a specific vehicle model, and $\text {CO}_{2i}$ denotes the CO$_2$ emissions for each entry.

This analysis, illustrated in Figure 3, provides insightful information on how vehicle design influences the environmental impact and underscores the importance of considering emissions in feature selection for predictive analysis.

Fig. 3

Mean CO₂ Emissions by Vehicle Make: This figure shows the relationship between vehicle models and CO₂ emissions, helping identify designs that contribute to higher emissions and guiding feature selection in our predictive analysis.

The distribution of vehicles manufactured by each company was skewed when analyzing the dataset collected over a period of seven years in Canada. Ford had the highest number of cars (623); however, its average CO₂ emissions were relatively moderate. This distinction highlights that while Ford’s large vehicle count (623 cars $\times$ 270 g/km/car = 168,210 g/km CO₂ emissions) significantly contributes to total emissions, it does not result in the highest average emissions per vehicle. In contrast, SRT had the fewest automobiles in the dataset, whereas Chevrolet was the second-largest manufacturer in terms of vehicle count. Figure 4 provides an overview of the number of vehicles produced by each manufacturer, demonstrating their contributions to overall CO₂ emissions.

Fig. 4

Number of Vehicles Made by Maker (Company): This figure shows the distribution of vehicles by manufacturer, highlighting their impact on overall CO₂ emissions. This insight guides our handling of manufacturer-related categorical variables in the modelling phase.

The analysis of the fuel usage trends for various fuel types revealed some notable patterns, as shown in Figure 5. Among the fuel types, ethanol (denoted as “E”) exhibited the highest fuel consumption. This increased consumption may be attributed the lower energy density of ethanol compared to that of gasoline. In contrast, fuels labelled “X” (regular gasoline), “Z” (premium gasoline), and “D” (diesel) demonstrated lower fuel consumption levels. Although natural gas, represented by “N”, is included in the dataset, only one vehicle utilized this fuel, and therefore it is not prominently displayed in Figure 6 due to its limited representation.

Figure 6 illustrates that despite the higher fuel consumption of ethanol, its CO₂ emissions are comparable to those of other fuels, particularly gasoline and diesel. This suggests that while ethanol may require more fuel per kilometer, it does not produce proportionally higher CO₂ emissions. Most vehicles in the dataset emit CO₂ in the range of 200 to 300 g/km, regardless of fuel type, with ethanol slightly overlapping this range.

Fig. 5

Histogram of Fuel Consumption by Fuel Type: This figure illustrates how fuel types affect fuel consumption, a key predictor of CO₂ emissions. Analyzing these trends enhances our understanding of the impact of fuel type choices on model predictions and emissions.

Fig. 6

Scatter Plot of CO₂ Emission by Fuel Consumption: This figure compares CO₂ emissions across fuel types, highlighting their environmental impact.

A summary of the CO₂ emissions dataset shown in Table 3 is provided using descriptive statistics. Important details including the engine size (ES) litres, number of cylinders, fuel consumption (FC) in city, highway, combination (litres per 100 km), CO₂ emissions (grams per kilometer), and the total number of observations are listed in the table. As we can see, there is a standard deviation of 1.35 litres and an average engine size of 3.16 litres. A variety of engine sizes, ranging from 0.9 litres to 8.4 litres, are also shown by the statistics. This table also provides information on the differences in CO₂ emissions and fuel usage between the different cars. This synopsis establishes the framework for additional investigation into the variables impacting CO₂ emissions.

Table 3 Descriptive statistics of vehicle parameters.

Interesting trends were found by analyzing the links between the features (apart from the object features) using the correlation heatmap in Figure 7. Engine size demonstrates a robust positive correlation with cylinder count (0.93), and a moderately strong correlation with fuel consumption measures: city (0.83), highway (0.75), and combined (0.81), as well as CO₂ emissions (0.85). This indicates that larger engines with more cylinders (0.93) typically lead to higher fuel consumption, with city consumption exhibiting the strongest association. Additionally, vehicles with higher city fuel consumption generally have higher highway and combined fuel consumption, as demonstrated by the high correlations between these measures (all above 0.94). This reinforces the idea that greater fuel consumption during city driving is associated with higher consumption on highways and overall. Correlation analysis was conducted using Python, with Pandas for data handling and Seaborn for generating the heatmap.

Fig. 7

Correlation Heatmap of Vehicle Characteristics: The correlation heatmap shows strong relationships among key numerical features, particularly engine size, cylinder count, and fuel consumption metrics. This suggests multicollinearity that can affect model performance and assists in feature selection for better interpretability.

Data Pre-processing

Data pre-processing is a crucial step in any deep learning modelling, as it directly affects the quality of the model’s predictions. In this study, we carried out a comprehensive and methodical pre-processing phase to ensure that the dataset was clean, structured, and ready for analysis. Pre-processing involves handling missing values, transforming variables, addressing outliers, and preparing the data for the deep learning pipeline. The goal of this process was to eliminate any inconsistencies or anomalies that might hinder the model’s performance. The pre-processing workflow involved several key steps, which are outlined below:

Data cleaning

• Missing and null values: Missing or null values in the dataset can lead to bias or inaccuracies in model training, especially when important variables are incomplete. The dataset was checked for both the values.

• Duplicate Values: Duplicate records in the dataset can skew results, leading to incorrect model outcomes by over-representing certain observations. A thorough check was conducted to identify any duplicate rows. After determining whether any entries in the data were duplicates, values were eliminated. This prevents the analysis from being skewed and guarantees that each data point represents a distinct observation.

Data engineering and transformation

Data engineering is crucial for improving the predictive capability of deep learning models. In our study, we used a variety of strategies to prepare and modify the dataset, ensuring that the model could accurately forecast CO₂ emissions based on different vehicle features.The following methods were applied to prepare the dataset:

• Outlier Detection and Removal: Outliers were identified using z-score analysis and eliminated from the dataset. This phase is critical for avoiding skewed model predictions induced by extreme values that could affect the learning process. Data points with a z-score greater than 2.6 were declared outliers and eliminated, ensuring that the model was trained on clean data.

  $$\begin{aligned} z_i = \frac{x_i - \mu }{\sigma } \end{aligned}$$

  (3)

  Where $x_i$ is an individual data point, $\mu$ is the mean of the data, and $\sigma$ is the standard deviation.

• Categorical Feature Encoding: To transform categorical variables (such as make, model, vehicle class, transmission, and fuel type) into numerical representations suitable for the model, we first used one-hot encoding. This approach divides each category into binary columns, allowing the model to effectively learn from these variables. However, we also assessed target encoding, which calculates the mean target value for each category and replaces it with mean values. Although target encoding can reduce dimensionality, we discovered that one-hot encoding improved the interpretability of the SHAP values in our models.

• Normalization and Scaling: To ensure that every feature contributes equally to the model’s performance, the numerical features were min-max scaled. This scaling method converts each feature to a common range (0 to 1), thereby reducing the impact of varying units and magnitudes. This was particularly crucial for features such as fuel consumption and engine size, which had different scales. The equation for min-max scaling is:

  $$\begin{aligned} x_{\text {scaled}} = \frac{x - x_{\text {min}}}{x_{\text {max}} - x_{\text {min}}} \end{aligned}$$

  (4)

  where $x_{\text {max}}$ and $x_{\text {min}}$ are the minimum and maximum values, respectively.

In summary, the data engineering process was thorough and aimed at enhancing the predictive capabilities of the model. By detailing the methods used for data preparation and their resultant effects on the dataset, we provide a clearer understanding of how these techniques contribute to overall analysis and modelling efforts.

Dataset splitting and validation

The performance and robustness of the model were rigorously assessed in this study using a 5-fold cross-validation technique. This approach successfully generalizes the model to unseen data, lowering the possibility of overfitting and enhancing the accuracy of our findings. The dataset was systematically partitioned into five equal sections, denoted as $D_1, D_2, D_3, D_4,$ and $D_5$. In each iteration of the cross-validation process, four of these sections were used for training the model and the remaining section served as the validation set. This process can be mathematically represented as follows:

$$\begin{aligned} \text {Training Set} = D_{i} \quad \text {for} \quad i \in \{1, 2, 3, 4, 5\} \end{aligned}$$

(5)

$$\begin{aligned} \text {Validation Set} = D_{j} \quad \text {for} \quad j \in \{1, 2, 3, 4, 5\}, \quad j \ne i \end{aligned}$$

(6)

This cross-validation procedure was repeated five times to ensure that each subset was used once as the validation set. The overall process is summarized as follows:

• 1. Iteration 1:

  • Training on $D_2, D_3, D_4, D_5$

  • Validation on $D_1$

• 2. Iteration 2:

  • Training on $D_1, D_3, D_4, D_5$

  • Validation on $D_2$

• 3. Iteration 3:

  • Training on $D_1, D_2, D_4, D_5$

  • Validation on $D_3$

• 4. Iteration 4:

  • Training on $D_1, D_2, D_3, D_5$

  • Validation on $D_4$

• 5. Iteration 5:

  • Training on $D_1, D_2, D_3, D_4$

  • Validation on $D_5$

The 5-fold cross-validation method provides a more legitimate estimate of model generalization by testing multiple data partitions, thereby reducing the potential for overfitting. By averaging the performance metrics across all five iterations, we comprehensively evaluated the performance of the model. This approach ensures that the findings are not unduly influenced by a specific train-test split, offering a more reliable assessment of the model’s predictive capabilities.

Model building

Deep learning is a subset of machine learning that uses artificial neural networks and is a useful method for discovering intricate patterns and relationships in data⁵³. Deep learning models are distinct from typical machine-learning algorithms in that they are composed of numerous layers of interconnected neurons, which allows them to automatically extract meaningful features from raw data⁵⁴. Deep learning models can be especially useful in CO₂emission prediction because of their capacity to manage non-linear correlations between vehicle features and emissions. Owing to their multi-layered architecture, deep learning models can capture these complicated interactions more efficiently than traditional machine learning models, which makes it difficult to handle such complexities⁵⁵. A variety of deep learning architectures are appropriate for regression problems such as CO₂emission prediction⁵⁶. This section presents the proposed architecture and its development procedures.

Proposed model development

This study introduced a novel approach for predicting CO₂ emissions from vehicle attributes. We constructed a light deep learning model using a multilayer perceptron (MLP) architecture. MLPs, which are neural network foundations, are composed of interconnected neuronal layers. This method harnesses the power of deep learning to identify intricate connections between input features and the target variable (CO₂ emissions).

Input Format: The input data for the proposed deep learning model consists of a dataset with multiple features related to vehicle attributes, as described in Table 2. These features include attributes such as Make (vehicle manufacturer), Model, Vehicle Class (VC), Engine Size (ES), Cylinders, and Fuel Type (FT), along with various measures of fuel consumption city (FCCity), fuel consumption highway (FCH), and fuel consumption combined (FCcomb).

In this study multiple densely connected layers were used, each with ReLU activation for non-linearity. The design consists of an input layer, three hidden layers with 128, 64, and 32 neurons each, and a single regression (linear activation) neuron in the final output layer.

The model was built using the Adam optimizer, which is a highly efficient tool known for its effectiveness, especially in large-scale models. The mean squared error (MSE) loss function is also employed. The design was facilitated using TensorFlow’s Keras Application Programming Interface (API). Figure 8 provides a visual representation of the architecture of the proposed deep learning model.

Fig. 8

Architectural Diagram of the Proposed CarbonMLP Model: Shows the input layer with three hidden layers (128, 64, and 32 neurons, respectively), and the output layer with a single regression neuron. Each layer uses ReLU activation functions, except for the final output layer, which uses linear activation.

The goal of the proposed model is to forecast CO₂ emissions using the provided dataset. In its formulated form, the model architecture is:

$$\begin{aligned} \text {Input:} \quad x_{\text {train}} \quad (\text {shape: } (n,m)) \end{aligned}$$

(7)

$$\begin{aligned} \begin{aligned}&\text {Hidden 1:} \quad h^{(1)} = \text {ReLU} \left( x_{\text {train}} \cdot W^{(1)} + b^{(1)} \right) \\&\qquad \qquad \qquad \qquad \qquad (\text {shape: } (n, 128)) \end{aligned} \end{aligned}$$

(8)

$$\begin{aligned} \begin{aligned}&\text {Hidden 2:} \quad h^{(2)} = \text {ReLU} \left( h^{(1)} \cdot W^{(2)} + b^{(2)} \right) \\&\qquad \qquad \qquad \qquad \qquad (\text {shape: } (n, 64)) \end{aligned} \end{aligned}$$

(9)

$$\begin{aligned} \begin{aligned}&\text {Hidden 3:} \quad h^{(3)} = \text {ReLU} \left( h^{(2)} \cdot W^{(3)} + b^{(3)} \right) \\&\qquad \qquad \qquad \qquad \qquad (\text {shape: } (n, 32)) \end{aligned} \end{aligned}$$

(10)

$$\begin{aligned} \begin{aligned}&\text {Output:} \quad Y_{\text {pred}} = h^{(3)} \cdot W^{(4)} + b^{(4)} \\&\qquad \qquad \qquad \qquad \qquad (\text {shape: } (n, 1)) \end{aligned} \end{aligned}$$

(11)

In the given neural network architecture, the entire process from input to output can be traced through several equations, each detailing a specific layer or operation. The input layer defined in Equation (7), uses the training data $x_{\text {train}}$ which has $n$ samples and $m$ features. Equation (8) describes the first hidden layer $h^{(1)}$ where the ReLU activation function is employed after combining the inputs with weights $W^{(1)}$ and biases $b^{(1)}$. Further transformations occurred in subsequent hidden layers. The second hidden layer $h^{(2)}$ is represented by Equation (9), again using the ReLU function. However, the outputs from the first hidden layer are processed with a new set of weights $W^{(2)}$ and biases $b^{(2)}$. The third hidden layer followed a similar pattern, as detailed in Equation (10), processing the output of the second hidden layer using the weights $W^{(3)}$ and biases $b^{(3)}$. The network output $Y_{\text {pred}}$, which predicts $\text {CO}_2$ emissions, was calculated using Equation (11). This output is the result of processing the activation of the third hidden layer using the final set of weights $W^{(4)}$ and biases $b^{(4)}$. Each step relies on weights $W^{(i)}$ and biases $b^{(i)}$ for each layer, driving forward the network’s ability to learn and make accurate predictions based on input data.

Optimized parameters

Our deep learning model underwent extensive fine-tuning using various hyperparameters to ensure reliable and consistent CO$_2$ emissions forecasts. After evaluating the multiple configurations, we identified the optimal settings for the proposed architecture. The selected design employs ReLU activation for non-linearity and consists of three hidden layers striking an effective balance between efficiency and complexity. The Mean Squared Error (MSE) loss function aligns well with our regression objectives, whereas the Adam optimizer enhances training efficiency.

In order to mitigate overfitting, the model was trained for 100 epochs with a batch size of 8, using a 5-fold cross-validation approach to ensure effective learning from the data. These carefully selected hyperparameters significantly improved the robustness and accuracy of the model in predicting CO$_2$ emissions. Table 4 provides a comprehensive overview of the strategies employed to optimize performance, detailing the various hyperparameters involved in the model optimization process.

Table 4 Optimized hyperparameters of the proposed CarbonMLP model.

Explainable AI interpretation

explainable AI (XAI) methods are designed to enhance the interpretability of models and provide insights into the elements that influence predictions. In this study, we employed robust XAI techniques, specifically SHapley Additive exPlanations (SHAP), to gain insight into the impact of features on CO₂ emission projections. We used a series of visualizations, including SHAP Summary, waterfall, force, and dependence plots.

SHAP (SHapley Additive exPlanations)

The SHAP values offer a robust framework for explaining individual predictions by quantifying the contribution of each the $i^\text {th}$ feature to the output of the model. The SHAP value for feature is calculated using the following equation:

$$\begin{aligned} SHAP_i = \phi _0(f) + \sum _{j=1}^{M} \frac{(M-j)! \cdot j!}{M!} \left( \phi _j(f) - \phi _{j-1}(f) \right) \end{aligned}$$

(12)

where; $SHAP_i$ represents the SHAP value for the $i^\text {th}$ feature, $\phi _0(f)$ denotes the baseline contribution of the model output, $f$ is the proposed CarbonMLP model that maps the input features to the predicted CO₂ emissions, $M$ is the total number of features.

To calculate the contribution of the features, the SHAP method considers all possible combinations of feature values and their respective outputs, providing a fair distribution of the model’s prediction among the input features. This means that each feature’s contribution is evaluated in the context of all other features, ensuring that the interactions are properly accounted for. The features used in this study and their descriptions are listed in Table 2. These include attributes such as make (vehicle manufacturer), Model, Vehicle Class, Engine Size, Cylinders, and Fuel Type, as well as various measures of fuel consumption (city, highway, combined), which are essential to understanding how vehicle characteristics affect CO₂ emissions. The SHAP value explains the impact of each feature on model output predictions. SHAP values not only quantify the contributions of individual features but also allow for a deeper understanding of how vehicle characteristics influence $\hbox {CO}_{{2}}$ emission predictions. This methodology enhances model transparency and aids stakeholders in making informed decisions based on analysis.

SHAP summary plot

The SHAP summary plot provides a global view of the importance of the mean absolute SHAP value of each feature. This helps with model interpretation and validation by enabling the identification of important predictors and their particular effects on model predictions. In Equation (13), Where $N$ represents the number of features. The plot was calculated as follows:

$$\begin{aligned} \text {SHAP Summary Plot}=\sum _{i=1}^{N} |SHAP_i |\end{aligned}$$

(13)

SHAP waterfall plot

The SHAP waterfall plot shows how each feature contributes to the variation in the base value, providing detailed insights into individual predictions. This makes it easier to interpret certain forecasts by emphasizing the variables that influence model outputs and possible areas for development. In Equation (14), is calculated as follows:

$$\begin{aligned} \text{ SHAP } \text{ Waterfall } \text{ plot }=\text {Base Value} + \sum _{i=1}^{N} SHAP_i \end{aligned}$$

(14)

SHAP force plot

The SHAP force plot illustrates how each characteristic affects a single prediction, and shows how the model determines the output for a given instance. This allows feature impacts to be examined, highlighting how each contributes to the final prediction and improves model transparency. In Equation (15), is calculated for the force plot as:

$$\begin{aligned} \text{ SHAP } \text{ Force } \text{ plot }=\text {Base Value} + \sum _{i=1}^{N} SHAP_i \end{aligned}$$

(15)

SHAP dependence plot

The SHAP dependence plot considers the relationships with other variables and shows the relationship between a feature and the model output forecast. It provides important insights into the feature behavior and model performance by assisting in the discovery of complex patterns and nonlinear relationships. The plot was calculated using Equation (16):

$$\begin{aligned} Output Prediction = \text {f(x)}+ \sum _{i=1}^{N} SHAP_i \end{aligned}$$

(16)

Evaluation metrics

Evaluation metrics are crucial for evaluating the effectiveness and performance of predictive models in practical applications. This component contained the metrics used to assess the performance of the proposed model. The metrics included the Mean Squared Error (MSE), Root Mean Squared Error (RMSE), R-squared (R2), and Mean Absolute Percentage Error (MAPE).

Mean Squared Error (MSE)

The efficacy of the model was assessed using Mean Squared Error (MSE), which measures the average squared difference between the predicted and observed results. This calculation is expressed by the following equation:

$$\begin{aligned} \text {MSE} = \frac{1}{n} \sum _{i=1}^{n} (y_i - \hat{y}_i)^2 \end{aligned}$$

(17)

where, $n$ are the number of samples, $y_i$ represents the target value, and $\hat{y}_i$ denotes the target value, respectively.

Root Mean Squared Error (RMSE)

The square root of the Mean Squared Error (MSE), also known as the Root Mean Square Error (RMSE), is the mean difference between the observed and predicted outcomes. The RMSE was calculated as follows :

$$\begin{aligned} \text {RMSE} = \sqrt{\frac{1}{n} \sum _{i=1}^{n} (y_i - \hat{y}_i)^2} \end{aligned}$$

(18)

R-squared (R$^2$)

The R-squared (R$^2$) statistic illustrates the extent to which the independent variables account for the variance in the dependent variable. On the scale, which goes from zero to one, higher numbers denote a better model fit.The R$^2$ formula is as follows:

$$\begin{aligned} R^2 = 1 - \frac{\sum _{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum _{i=1}^{n} (y_i - \bar{y})^2} \end{aligned}$$

(19)

where, $\bar{y}$ represents the mean of the observed values.

Mean Absolute Percentage Error (MAPE)

The average percentage variation between the actual and anticipated values is measured by the Mean Absolute Percentage Error (MAPE), which sheds light on the accuracy of the predictions of the magnitude of the actual value. It is calculated as:

$$\begin{aligned} \text {MAPE} = \frac{1}{n} \sum _{i=1}^{n} \left| \frac{y_i - \hat{y}_i}{y_i} \right| \times 100\% \end{aligned}$$

(20)

where, $y_i$ denotes the actual value, $\hat{y}_i$ the predicted target value of the $i^\text {th}$ sample, $n$ the number of samples.

Experimental results

Hardware setup and model training

The proposed deep learning model was trained using a powerful GPU P100 accelerator in a Kaggle notebook environment to enhance the processing efficiency. This platform offers a scalable solution for computationally intensive tasks, including deep neural network training. The Keras API was employed for the model training.

Batches of pre-processed data were fed through the model during training, and the Adam optimizer was used to minimize the Mean Squared Error (MSE) loss function. After fine-tuning various hyperparameters, the optimal values were selected: a batch size of 8 and training for 100 epochs with 5-fold cross-validation to ensure robust generalization and avoid overfitting. This carefully designed training procedure allows the model to effectively capture the intricate relationships between vehicle attributes and CO₂ emissions, resulting in highly reliable prediction capabilities. The complexity of the model over time, as measured by the number of trainable parameters, is shown in Figure 9.

As the training progressed, Figure 9 shows a significant initial drop in the number of trainable parameters within the first two epochs, followed by stabilization across subsequent epochs. This indicates that the model was quickly adjusted to optimally represent the relationships between vehicle attributes and CO₂ emissions, without over-complicating the structure.

This gradual reduction in model complexity helps to avoid overfitting, demonstrating that the model learns efficiently from the data without increasing unnecessary parameters. The modest increase in trainable parameters in the first few epochs reflects the model’s capability to represent intricate patterns, after which it stabilizes, reinforcing the robustness of the model.

Fig. 9

Model complexity over time of CarbonMLP model.

Computational efficiency comparison

To further justify our selection of the proposed CarbonMLP model, we conducted a detailed computational efficiency comparison with more complex LSTM⁵⁷and BiLSTM⁵⁸ models. The comparison was based on major performance measures, such as training time, inference time, memory usage, parameter count, and latency. We chose LSTM and BiLSTM models because they are widely used for time-series prediction as well as sequence modeling tasks like CO₂ emissions, making their computational effectiveness benchmark suitable for comparing with the current deep learning models. These measures are calculated under equal conditions to ensure fairness. The results of this comparison are presented in Table 5.

Table 5 Computational efficiency and performance comparison.

Training and inference time

Compared to LSTM and BiLSTM, the proposed CarbonMLP model significantly reduces the training and inference times. These reductions make CarbonMLP better suited for real-time and large-scale deployment. CarbonMLP requires 54.7% less time for training than LSTM and 43.5% less time than BiLSTM. Similarly, the inference time for CarbonMLP was 34.8% shorter than LSTM and 25% shorter than BiLSTM, indicating its computational efficiency in production environments.

Memory usage and model size

Memory usage and model size are critical in contexts with limited computational resources. CarbonMLP had a significantly reduced footprint in both measurements. CarbonMLP consumes 3% less memory than LSTM and BiLSTM. Additionally, the model size of CarbonMLP was 76.6% smaller than that of LSTM and 88.7% smaller than that of BiLSTM, making it highly efficient for deployment in devices with limited storage capacity.

Latency and batch processing time

Latency and batch processing times are crucial for models to make quick predictions. CarbonMLP outperforms LSTM and BiLSTM in these areas. The proposed CarbonMLP offers a 61.5% reduction in latency compared with LSTM and a 31.8% reduction compared with BiLSTM. Similarly, its batch processing time is 19% faster than that of LSTM and 15% faster than that of BiLSTM, further demonstrating its efficiency in high-throughput environments.

Model complexity and number of parameters

A model with fewer parameters is easier to train, deploy, and maintain, particularly in cases with limited computational power. CarbonMLP was developed to be lightweight while still providing a competitive performance. CarbonMLP contained 76.8% fewer parameters than the LSTM model and 88.8% fewer parameters than the BiLSTM model, making it highly efficient in terms of model complexity without sacrificing performance.

Performance evaluation

Finally, the predictive performance of the models was evaluated based on the Mean Squared Error (MSE), with the proposed CarbonMLP outperforming both the LSTM and BiLSTM models in this metric. The proposed CarbonMLP outperformed both the LSTM and BiLSTM models in terms of prediction accuracy, as evidenced by its reduced MSE value. This demonstrates the usefulness of the model, despite its relatively simplistic development.

The computational efficiency comparison establishes that the proposed CarbonMLP model is highly efficient in terms of training and inference time, memory utilization, latency, and model size, while still providing competitive predictive performance. The capabilities of CarbonMLP make it the best choice for real-world CO₂ emission prediction tasks, particularly in contexts with limited computational resources.

Performance evaluation of the proposed model

The proposed deep learning model can fully represent the complex relationships between CO₂ emissions and vehicle attributes. After conducting 5-fold cross-validation, excellent performance metrics were obtained. The average R-squared value was 0.9938, demonstrating a 99.4% explained variation, with an extremely low Mean Squared Error (MSE) of 0.0002 and a Root Mean Squared Error (RMSE) of 0.0142. Additionally, the model’s Mean Absolute Percentage Error (MAPE) was 2.5%, indicating that the predictions were, on average, within 2.6% of the actual values.

These metrics are summarized in the performance curve shown in Figure 13, where R-squared, MSE, RMSE, and MAPE are depicted, providing a holistic view of the model’s predictive accuracy and its ability to generalize across all cross-validation folds.

The results are further supported by the training and validation loss curves shown in Figure 10, which display the loss trends for each of the five folds. The consistency across these curves highlights the ability of the model to generalize across validation sets without overfitting. Figure 11 presents a summary of these loss curves, further demonstrating that both training and validation losses decreased steadily throughout the training process.

Moreover, the accuracy of the model was confirmed by the actual versus predicted plot in Figure 12, where the data points were closely clustered around the diagonal line, reinforcing the high correlation between the predicted and actual CO₂ emissions. While an isolated outlier with a significantly lower actual value compared to its prediction was observed, this may be attributed to data anomalies, underrepresented patterns, or the model’s limitations in capturing edge cases. Importantly, the predicted values were restored to their original scale after normalization, ensuring that the performance metrics accurately reflected the true CO₂ emissions. These compelling performance indicators, combined with insightful visualizations, underscore the robustness of the model and its potential for practical applications in CO₂ emission prediction tasks.

Fig. 10

Training and validation loss curves for each of the five folds during 5-fold cross-validation. Each subplot shows the trend of the loss function across epochs for both the training and validation datasets, demonstrating consistent convergence and the model’s generalization ability across the different folds. The loss curves show a steady decrease, indicating effective training and no significant overfitting.

Fig. 11

Average training and validation loss curve of CarbonMLP model.

Fig. 12

Actual vs predicted plot of CarbonMLP model.

Fig. 13

CarbonMLP model’s performance curve.

To entirely evaluate the “CarbonMLP” model’s effectiveness in estimating CO₂ emissions, we used a Taylor diagram, as shown in Figure 14. This useful picture summarizes three critical metrics: correlation coefficient (R), standard deviation (SD), and centered root mean square difference (RMSD). R denotes the linear relationship between the expected and observed emissions, with a value of one indicating complete agreement. The correlation coefficient (R) was calculated as follows:

$$\begin{aligned} \text {R} = \frac{\sum _{i=1}^{n} (x_i - \overline{x})(y_i - \overline{y})}{\sqrt{\sum _{i=1}^{n} (x_i - \overline{x})^2 \sum _{i=1}^{n} (y_i - \overline{y})^2}} \end{aligned}$$

(21)

where, $x_i$ and $y_i$ represent the individually predicted and observed values, respectively. $\overline{x}$ and $\overline{y}$ denote the respective means.

The radial distance from the origin should be close to the observed standard deviation (SD) is calculated as follows:

$$\begin{aligned} \text {SD} = \sqrt{\frac{1}{n} \sum _{i=1}^{n} (x_i - \overline{x})^2} \end{aligned}$$

(22)

Finally, the smaller angle between the data point and the reference point for the centered root mean square difference (RMSD) reflects a good alignment of cyclical patterns in emissions. The centered RMSD was calculated as follows:

$$\begin{aligned} \text {RMSD} = \sqrt{\frac{1}{n} \sum _{i=1}^{n} (x_i - y_i)^2} \end{aligned}$$

(23)

We can acquire significant information by analyzing the exact location of our “CarbonMLP” model’s data point on the Taylor diagram in Figure 14. Ideally, the data point should be close to the circle displaying a correlation coefficient of one, suggesting a high level of agreement between the predictions and observations. Furthermore, the radial distance from the origin should be similar to the reported standard deviation, indicating that the model adequately captured the variability. Finally, a lower angle between the data point and the reference point for the centered RMSD indicates good synchronization of cyclical patterns in emissions. By examining these characteristics of the Taylor diagram, we may accurately assess the “CarbonMLP” model’s ability to estimate CO₂ emissions from automobiles.

Fig. 14

Taylor diagram for “CarbonMLP” model performance.

Comparison of model performance with existing approaches

In predicting CO₂ emissions, our proposed deep learning model outperformed complex deep learning architectures and traditional machine learning algorithms. As the metrics of performance shown in Table 6, the proposed model has the highest R-squared value of 0.9938 and the lowest MSE value of, 0.0002 signifying the high accuracy of the model and the higher correlation of the predicted values with the observed actual CO₂ emissions.

In the machine learning module, various algorithms such as Decision Trees, K-Nearest Neighbors (KNN), Support Vector Machines (SVM), and XGBoost were applied to compare their performance. These algorithms played different roles in the analysis⁵⁹. Decision Trees are simple, interpretable models that can handle both the linear and non-linear relationships between vehicle attributes and CO₂ emissions. They segment the data into smaller, more manageable chunks, allowing for an intuitive understanding of which features lead to different levels of emissions. However, they may lack the flexibility to capture complex patterns in the data when used alone. K-Nearest Neighbors (KNN) regressor works by measuring the proximity of data points in the feature space. It is useful in scenarios where the relationship between features is non-linear. However, KNN’s performance can degrade when faced with high-dimensional data or large datasets, as seen by its relatively higher MSE and lower R-squared in Table 6. The Support Vector Machine (SVM) regressor aims to find a hyperplane that best fits the data points, minimizing the prediction error. While effective in some cases, SVM struggled to handle the intricacies of the CO₂ emission data in this study, resulting in higher errors compared to the deep learning approaches. XGBoost, a highly efficient gradient boosting algorithm, is well-suited for complex, non-linear problems. It showed relatively strong performance but still fell short of the proposed deep learning model due to its inability to capture deeper patterns in the data without overfitting.

These models were also combined in an ensemble approach, integrating the strengths of Decision Trees, KNN, and XGBoost to improve the generalization and accuracy. By leveraging the diversity of predictions from these models, the ensemble achieved a lower MSE (0.0003) and higher R-squared (0.9889) than individual machine learning algorithms, although it still did not outperform the proposed deep learning model. The outcomes show that even though such basic techniques, such as Decision Trees or KNN, provide satisfactory predictions, they are not able to embrace the non-linearity of the factors inside the CO₂ emission.

The superiority of these models in sequential data processing was considered when using the LSTM and BiLSTM models in our deep learning module. By their nature, LSTM models cover distances in the sequence and implement memory over long intervals, making them suitable for time-series forecasting. This is important for establishing a relationship between vehicle characteristics and CO₂ emissions over time. BiLSTM improves the above in the sense that word sequences are analyzed in forward and backward ways, capturing contexts in past and future data points. This split view is most helpful in emissions predictions, where the coefficients may be a function of prior and subsequent values. LSTM and BiLSTM are used because they are among the best algorithms that work for sequential data, and sequential data is which are required for prediction tasks. The emission data obtained always have temporal characteristics related to things, such as the specifications of the automobile and changes in legislation. These dynamics can be captured using these models and hence provide better forecasts of CO₂ emissions. It is also important for a predictive model to be built with data pattern changeability so that it can adapt to current data patterns. This is evident in the proposed CarbonMLP model where the deep learning approach efficiently captures these complex interactions and is therefore the best approach towards achieving highly precise CO₂ emission prediction in real environments.

Table 6 Performance comparison among all models.

XAI interpretation using SHAP

We employed the (SHAP) values to acquire a better understanding of the underlying mechanics of the advanced deep learning model and how different features influence its predictions. This model-agnostic technique allows us to understand how each variable affects the model’s CO₂ emission forecasts. With an impressively low Mean Squared Error (MSE) of 0.0002 and a high R-squared value of 0.9938, our proposed model performed well, establishing it as the best option for SHAP explanation. Analyzing the SHAP values associated with each prediction allowed us to determine which features had the greatest positive or negative impact on the model’s CO₂ emission predictions.

SHAP summary plot: Global feature importance for CO₂ emission prediction

The SHAP summary plot in Figure 15 provides a comprehensive view of how different features affect the CO₂ emissions predictions across the entire dataset. The features were ranked by their importance, and the plot shows the distribution of their impact on the model’s output. The key elements of the SHAP summary plot are as follows:

• Feature Importance (Y-axis): The features are ordered by importance, with the most impactful features listed at the top. The top three features in this plot are Fuel Consumption City (L/100 km), Fuel Consumption Comb (L/100 km), and Fuel Consumption Hwy (L/100 km), indicating that fuel consumption metrics are critical predictors of CO₂ emissions.

• SHAP Value (X-axis): SHAP values represent the contribution of each feature to the prediction. Positive SHAP values increased the predicted CO₂ emissions, whereas negative SHAP values decreased it. A SHAP value of 0 indicates no impact on the prediction for that instance.

• Color Gradient (Feature Value): The colors represent feature values, with blue indicating low values and red indicating high values. For example, low fuel consumption values (blue) tend to decrease CO₂ predictions, whereas high fuel consumption values (red) increase the predictions.

• Distribution of Impact: The spread of points for each feature indicates how much variation exists in its impact. Features such as Fuel Type_X and Cylinders_6 show a wide distribution of SHAP values, indicating that their impact can vary significantly depending on the vehicle configuration.

The summary plot reveals that the fuel consumption metrics, engine size, number of cylinders, fuel type, and vehicle class are among the most important predictors of CO₂ emissions. Features such as Fuel Consumption City and Fuel Consumption Comb have a consistent positive relationship with CO₂ emissions-vehicles with higher fuel consumption produce more CO₂. Additionally, the impact of certain features, such as Fuel Type_X and Transmission_AS6, varies depending on the vehicle configuration, highlighting the importance of feature interactions in the model’s predictions.

Fig. 15

SHAP Summary Plot: Visualization of feature importance, with Fuel Consumption Combined (L/100 km) as the highest ranking feature. Red represents a greater impact on CO₂ emissions, and blue represents a lower impact.

SHAP waterfall plot: Instance-Level explanation for CO₂ emission prediction

To explain the contribution of each feature to the prediction of a specific vehicle (index 0), we used SHAP to generate a waterfall plot, as shown in Figure 16. The SHAP waterfall plot provides an instance-level explanation of how different features contribute to the final CO₂ emission prediction for a specific data point. The key elements in the SHAP waterfall plot are as follows:

• Baseline Value $E[f(x)] = 0.506$: The expected value of the prediction, which is the mean CO₂ emission prediction across all instances in the dataset. This baseline served as the starting point of the plot.

• Model Output $f(x) = 0.543$: The final predicted value for this particular instance (vehicle), after accounting for the contributions of all features. This represents the CO₂ emission prediction for the 0th index in the dataset.

• Feature Contributions: Each horizontal bar represents the contribution of a feature to the final prediction. Features that increase the predicted value are shown in red (positive contributions), whereas features that decrease the prediction are shown in blue (negative contributions). For example, Fuel Type_X contributes +0.02 to the final prediction, slightly increasing the CO₂ emission prediction. On the other hand, Cylinder_6 has a negative contribution (−0.01), reducing the prediction.

• Cumulative Impact: The contributions from all features were accumulated, starting from the baseline $E[f(x)] = 0.506$, and the final prediction was reached at $f(x) = 0.543$. This small contribution of each feature adds to shifting the prediction from the baseline value to the final result.

• Many Small Contributions: The plot shows that a large number of smaller features (grouped as “2099 other features”) have a combined contribution of +0.02, which also affects the prediction. These grouped features individually have small impacts but collectively influence the final output.

The SHAP waterfall plot visually demonstrates the effect of each feature on prediction. Features such as Fuel Type_X and Fuel Consumption Comb push the prediction upward, while features such as Fuel Type_Z and Cylinders_6 have a negative impact. The cumulative effect of all these feature contributions led to a final prediction of 0.543 from the baseline value of 0.506. By visualizing the individual feature contributions, the SHAP waterfall plot provides an interpretable and transparent view of how the model arrives at specific CO₂ emission predictions. This transparency aids in understanding the features that significantly influence the prediction of each vehicle.

Fig. 16

SHAP Waterfall Plot: Detailed analysis showing the relative contributions of each characteristic to variations from the base value. Highlights the significant impact of fuel consumption in the city, combined fuel consumption, and highway fuel consumption on the model’s CO₂ emissions prediction.

SHAP force plot: Instance-Level explanation for CO₂ emission prediction

The SHAP Force Plot in Figure 17 provides a detailed explanation of the individual predictions made by the model for the 0th index in the dataset. It visualizes the contributions of each feature, demonstrating whether they push the prediction higher or lower than the baseline.

• Baseline Value $E[f(x)]$: The baseline value, representing the expected value of the model’s output without any feature information, is $E[f(x)] = 0.50$. This is the mean prediction of CO₂ emissions across all instances.

• Model Output $f(x) = 0.543$: The final predicted value for the 0th index is $f(x) = 0.543$, which is slightly higher than the baseline, indicating a higher predicted CO₂ emission for this instance.

• Positive Contributions (Red): Features such as Fuel Consumption City (L/100 km) and Fuel Type_E significantly increased the prediction, contributing positively to the final output. These are represented by red sections on the left side of the plot.

• Negative Contributions (Blue): Features such as Fuel Type_Z and Cylinders_6 decrease the prediction, pulling it lower than it would otherwise. These are represented by the blue sections on the right hand side of the plot.

• Cumulative Impact: The plot illustrates the transition from the baseline value to the final predicted value by balancing the positive and negative contributions. The overall effect of these features led to a final predicted value of 0.543, as shown on the right end of the force plot.

This visualization provides an intuitive understanding of the model’s decision-making process, highlighting how various features interact to produce the final prediction.

Fig. 17

SHAP Force Plot: In-depth analysis of individual predictions illustrating how each feature affects the model’s output. Emphasizes the notable impact of city fuel consumption, combined fuel usage, and highway fuel consumption on CO₂ emissions predictions.

SHAP dependence plots: Analysis of feature impact on CO₂ emissions

The SHAP dependence plots in Figure 18 provide a detailed visualization of how specific features affect predicted CO₂ emissions and how they interact with other variables in the model.

• Engine Size: The dependency plot in Figure 18a demonstrates a positive relationship between engine size and CO₂ emissions, suggesting that larger engines contribute to higher emissions. However, the narrower range of SHAP values compared to other features indicates that engine size has a relatively lower impact on CO₂ emissions. This aligns with the nature of the data, where fuel consumption metrics (City, Combined, and Highway) are more directly tied to emissions, making them more influential predictors in the model.

• Fuel Consumption (City): The dependency plot in Figure 18b reveals that fuel consumption under city driving conditions is strongly correlated with CO₂ emissions. Higher fuel consumption in urban environments leads to increased CO₂ predictions, making city fuel efficiency an important target for emission reduction strategies.

• Fuel Consumption (Combined): The combined fuel consumption dependence plot in Figure 18c shows a similar trend, where increased overall fuel consumption results in higher CO₂ emissions. This emphasizes the importance of improving fuel efficiency across different driving conditions to reduce environmental impact.

• Fuel Consumption (Highway): The highway fuel consumption plot in Figure 18d also demonstrates a positive relationship with CO₂ emissions. While highway driving is generally more fuel-efficient than city driving, fuel consumption in this condition still contributes significantly to emissions, highlighting the role of efficiency improvements in reducing emissions.

Overall, the SHAP dependence plots provide a comprehensive and insightful analysis of how engine size and fuel consumption metrics, specifically in city, combined, and highway driving conditions, play significant roles in predicting vehicle CO₂ emissions. The lower variation and smaller magnitude of SHAP values for Engine Size suggest that it has a weaker effect on the target variable when compared to the Fuel Consumption features. While fuel consumption metrics exhibit a wider range of SHAP values, underscoring their dominant influence on the model’s predictions, the smaller range observed for engine size indicates its relatively lower importance in comparison. This distinction highlights that fuel efficiency improvements, particularly in urban and combined driving conditions, are critical drivers for reducing CO₂ emissions. Nonetheless, engine size remains a contributing factor that cannot be entirely overlooked.

These findings highlight the potential for substantial reduction in CO₂ emissions through targeted improvements in vehicle design and fuel efficiency. By focusing on developing engines with smaller displacements, optimizing fuel consumption across different driving conditions, and employing advanced technologies to enhance efficiency, manufacturers can make significant strides toward minimizing emissions. This not only aids in complying with environmental regulations but also supports the broader goal of mitigating climate change and achieving a sustainable future. Ultimately, SHAP analysis provides actionable insights that can inform both policymakers and automotive engineers, encouraging the adoption of strategies that prioritize energy efficiency and emission reduction in the transportation sector. This will lead to the development of greener vehicles and cleaner environments, contributing meaningfully to global efforts to combat climate change.

Fig. 18

SHAP Dependence Plots for various features: (a) Engine Size, (b) Fuel Consumption (City), (c) Fuel Consumption (Combined), and (d) Fuel Consumption (Highway).

Comparison with previous work

This analysis expands on the findings of the literature review by comparing the proposed Custom Deep Learning Model with existing models for estimating CO₂ emissions. As shown in Table 7, many studies cited in the literature review used models such as BilSTM and XGBoost for this task.

Our proposed method outperforms existing methods for predicting CO₂ emissions. It had the lowest Mean Squared Error (MSE) and Root Mean Squared Error (RMSE) of the models in the table, implying a better fit between the anticipated and actual CO₂ emission data. Furthermore, the proposed model had a high R-squared value, indicating a significant connection between the predictions and actual data. While admitting potential constraints resulting from differences in the datasets and assessment measures used in previous studies, the proposed approach outperformed these important parameters. Furthermore, it has SHAP values that improve its interpretability. Using SHAP values, we obtained insights into how different features influence the model’s predictions, improving its overall transparency and dependability. In conclusion, the high performance and interpretability of our custom deep learning model make it an effective tool for predicting CO₂ emissions.

Table 7 Comparison with previous work.

Discussion

The proposed deep learning model outperformed existing carbon dioxide (CO₂) emission prediction models with a low Mean Squared Error (MSE) of 0.0002, Root Mean Squared Error (RMSE) of 0.0142, and high R-squared value of 0.9938. These indicators show a better match between the model predictions and actual CO₂ emissions, indicating a significant correlation with the real-world data. While highlighting the possible limitations derived from the differences in previous research approaches, the model’s clear outperformance establishes it as a powerful tool for precise CO₂ emission prediction. Our key contribution is the development of a model that not only predicts CO₂ emissions but also provides interpretability by utilizing SHAP values. This transparency helps us to better understand which elements, such as vehicle characteristics, fuel consumption, and engine size, have the greatest impact on CO₂ emissions. By identifying these main factors, the model can inform vehicle-related CO₂ emissions reduction plans. For example, insights gained from the interpretability features of the model can be used to target efforts aimed at improving engine performance, promoting fuel-efficient vehicles, and encouraging environmentally responsible driving practices. This study improves CO₂ emission forecasts and provides useful information to environmental authorities, regulators, and the automobile sector. These stakeholders can use the model’s capabilities to create and implement successful plans to reduce CO₂ emissions from automobiles, thus paving the way for a more maintainable environment.

Conclusion and future work

This study explored the efficacy of a deep learning model for predicting carbon dioxide (CO₂) emissions from vehicles. The proposed model demonstrated outstanding performance, outperforming the previous techniques in terms of accuracy and interpretability. In summary, this study developed a deep learning model with eXplainable AI (XAI) integration to estimate CO₂ emissions from vehicles using a Multilayer Perceptron (MLP) architecture. The model was trained using a dataset consisting of 7,385 rows and 12 columns, which included vehicle characteristics such as Make, Model, Vehicle Class, Engine Size (L), Cylinders, Transmission, Fuel Type, Fuel Consumption ratings (City, Highway, and Combined), and CO₂ emissions (g/km). The model was extremely successful, as evidenced by a high R-squared value of 0.9938 and low Mean Squared Error (MSE) of 0.0002. Further studies using assessment metrics and visualizations validated the capacity of the model to represent the complex links between vehicle features and CO₂ emissions. Additionally, SHapley Additive exPlanations (SHAP) values were applied to obtain the influence of different features on the model’s CO₂ emission predictions of the model. Despite these optimistic findings, this study has some limitations that require further investigation. The proposed model’s performance was influenced by the dataset used. If trained using data from a specific region or vehicle type, its applicability to different populations or geographical locations may be limited. Furthermore, this study’s emphasis on CO₂ emissions, although important, addresses only one aspect of the environmental challenge. Including other pollutants, such as nitrogen oxides (NOx) and particulate matter (PM), would provide a more complete view of the environmental impact of a vehicle. In addition, the model analysis was constrained to the features found in the training data. A more in-depth look at the external elements that may influence CO₂ emissions, such as driving behavior, weather conditions, and road infrastructure, could provide useful insights for future model modifications.

Future endeavors can build on this study and explore new avenues for creating a more sustainable environment. Expanding the dataset to cover a broader and more diverse range of geographical regions would improve the model’s generalizability. Incorporating more contaminants into the analysis of CO₂ emissions would provide a more comprehensive understanding of the environmental impact of vehicles. Exploring sophisticated interpretability techniques may yield further insights into the decision-making process of the model. However, the most significant future advancements will involve real-world applications. Consider vehicles outfitted with sensors that measure CO₂ emissions based on the same parameters that the model identifies as important. These real-time data can be fed back into the model to drive continual improvement and inform drivers of eco-driving advice. Our journey toward a sustainable environment goes beyond the conceptual framework. Future studies should consider incorporating additional variables, such as driving habits, road conditions, and environmental factors. Real-time monitoring systems and vehicle sensor data are essential for improving pollution forecasts. Moreover, investigating sophisticated deep learning architectures and ensemble approaches may enhance the prediction capabilities of the model. By taking these steps, we can capitalize on the power of this science to create a cleaner and more sustainable future for our planet. This study lays the groundwork for more precise and understandable CO₂ emissions forecasting models for vehicles. This knowledge will enable public officials, automobile manufacturers, and drivers to develop a more sustainable future for transportation by resolving restrictions and exploring new opportunities. The proposed approach, which combines advanced modeling with interpretability, makes a substantial contribution to establishing sustainable transportation systems, protecting the environment, and reducing vehicle emissions.