Neural network backstepping control of OWC wave energy system

Abstract

This paper investigates the application of Neural Network Backstepping Control (NN-BSC) for enhancing the rotational speed control of Oscillating Water Column (OWC) wave energy systems. Traditional control methods face limitations when dealing with nonlinearities, irregular wave conditions, and actuator disturbances. To address these challenges, this research paper introduces a Chebyshev NN within the BSC framework, leveraging its high approximation accuracy and computational efficiency. The design of the NN-BSC involves estimating the disturbance term using the Chebyshev NN and validating the stability OWC control system through Lyapunov analysis. The proposed NN-BSC law effectively handles nonlinearities and improves system robustness under dynamic conditions. Numerical simulations have been conducted using MATLAB/SIMULINK to compare the performance of the uncontrolled OWC system, conventional PI and BSC, and NN-BSC, under scenarios with and without actuator disturbances. The parameters for PI, BSC, and NN-BSC are optimized using a Particle Swarm Optimization (PSO) algorithm, which minimizes a fitness function defined by the Integral Squared Error (ISE). Results indicate that NN-BSC achieves smoother rotor speed tracking, particularly under actuator disturbances, where the conventional PI and BSC exhibits significant performance degradation in terms of ISE. Under actuator disturbance scenarios: (1) NN-BSC achieved the lowest ISE value of 22.5433, outperforming PI (40.6381) and BSC (37.1192), and (2) NN-BSC demonstrated the lowest maximum peak overshoot (0.9651 rad/s) and fastest settling time (0.0561 s).

Introduction

Ocean wave energy refers to the process of harnessing the energy generated by the movement of ocean waves to produce electricity or perform mechanical work. This form of renewable energy has the potential to provide a significant amount of clean power due to the vast and consistent nature of ocean waves. Wave energy technology is still in the developmental and early commercial stages. Several pilot projects and small-scale installations are being tested around the world, particularly in Europe, North America, and Australia. Continued advancements in technology, along with supportive government policies, are crucial for the future growth of this renewable energy source¹.

There are several types of wave energy converters, each designed to capture energy in different ways based on their interaction with the waves. Some of the main types include²: Point Absorbers, Oscillating Water Columns (OWCs), Attenuators, Oscillating Wave Surge Converters, Overtopping Devices, and Submerged Pressure Differential Devices. OWCs are among the most studied and deployed wave energy conversion systems due to their relatively simple design and ability to be integrated into coastal structures³. Control systems for OWCs play a crucial role in optimizing the performance, efficiency, and reliability of these wave energy converters⁴. The control system manages the turbine, airflow, and overall dynamics of the OWC to maximize energy capture from the waves under varying sea conditions⁵. The airflow and rotor speed control are the two main control schemes employed in OWCs for managing the electrical power generation from ocean waves.

A brief review of these control schemes is presented next. Initially, few theoretical studies on airflow and rotor speed control appeared in^6,7,8 and ⁹. In⁶ and ⁷, a theoretical model suggested that using a control valve in an OWC plant with a Wells turbine can notably enhance energy production by mitigating aerodynamic stall losses. The paper in⁸ and ⁹ explored the rotor speed control strategy for an OWC wave energy plant with a Wells turbine and variable speed generator, which focused on adjusting electric torque to optimize turbine efficiency and meet grid power quality requirements. Later in¹⁰ and¹¹, the Indian Wave Energy Program focused on an OWC system with a twin Wells turbine and 55 kW generator, where a MATLAB/SIMULINK model and controller were used to optimize turbine power output, with simulations and experiments showing improved performance over an uncontrolled module.

After establishment of Nereida project plant, located in the Basque coast of Mutriku, several studies on control of OWC systems were conducted, which could be found in^{12,13,14,15,16,17}, and¹⁸. In¹² and¹³, a control scheme was proposed to improve the performance of the Wells turbine by adjusting rotor resistance in response to pressure drops, effectively managing stalling behaviour and maximizing power generation as the turbine approaches critical flow coefficient levels. In^14,15,16 and¹⁷, the studies examined stalling behaviour in Wells turbines and compared two control strategies: one adjusted the rotational speed of the induction generator based on pressure drop, while the other used airflow control via a modulation valve. Both methods effectively prevented stalling and optimized turbine performance. In¹⁸, a robust sliding mode control (SMC) scheme for OWC plants was presented, demonstrating improved power extraction and disturbance rejection compared to traditional proportional-integral (PI) based control.

Expanding on the aforementioned studies, the fractional order proportional-integral-derivative (FOPID) for airflow control and backstepping rotational speed control strategies were proposed later in^{19,20,21,22,23,24}, and²⁵. In¹⁹, the paper proposed using a FOPID controller, optimized by particle swarm optimization (PSO), for air flow control in OWC wave power plants, showing improved power output and turbine performance compared to conventional PID control under varying sea conditions. In²⁰, a control scheme was presented for maximizing turbine output power in an OWC wave power plant using a Wells turbine and doubly fed induction generator (DFIG), which combined fuzzy maximum power point tracking (MPPT) and backstepping control (BSC) for improved efficiency and stability. In²¹, the paper proposed three nonlinear control strategies for OWC wave power-take-off systems, demonstrating that the proposed controllers enhance the output power of the system under realistic sea wave conditions. In²², the paper presented event-triggered nonlinear controllers for an OWC wave energy plant, which demonstrated that the event-triggered BSC outperforms the event-triggered SMC in maximizing turbine output power while minimizing control updates. In²³, a centralized airflow control scheme was proposed for a complex ocean energy network of OWCs, significantly reducing output power variation using a two-stage controller optimized by PSO. In²⁴, a type 2 fuzzy logic controller for rotor speed control in OWC wave power plants was designed to maximize electrical output, with simulations showing improved performance using the irregular wave model. In²⁵, the paper presents an ocean wave energy control strategy using aquila optimization (AO) to optimize BSC parameters for MPPT in an OWC wave energy converter. The AO demonstrated superior performance over PSO and genetic algorithm (GA) techniques.

Several other significant studies on control of OWC have also been conducted, which are discussed next. In²⁶, the MPPT-based control approach was validated through case studies, showing its ability to consistently achieve optimal rotational speed and maximize active power generation and also highlighted its potential for enhancing the commercialization of OWC power plants. In²⁷, an adaptive SMC scheme for OWC plants using Wells turbines and DFIGs was designed, which demonstrated through simulations that it improved power generation efficiency and robustly handles system uncertainties and disturbances. In²⁸, an optimized higher-order SMC was proposed, enhancing turbine performance by improving efficiency and reducing the peak-to-average power ratio under varying sea conditions. In²⁹, the paper introduced a fuzzy gain scheduled PI controller for the Nereida wave power plant that demonstrated the optimized power generation and maintained robustness under varying input conditions compared to conventional PI controllers. In³⁰, again a fuzzy gain scheduled SMC was presented for OWC with Wells turbines, effectively preventing stalling, enhancing power generation, and outperforming standard SMC in reducing power fluctuations under varying wave conditions. In³¹, the paper presented a state-space model of an OWC and demonstrated that second-order SMC, combined with valve control, improves electric energy conversion, particularly in less energetic sea states. In³², the study proposed using deep learning algorithms using long short-term memory and convolutional neural network (NN) to predict the rotational speed in an OWC to improve rated power control and operational efficiency. In³³, a generalized predictive control scheme was proposed to enhance wave energy conversion efficiency by optimizing flow coefficient, preventing turbine stalling, and integrating system limitations, validated through simulations and experiments. In³⁴, the paper proposed an adaptive second-order SMC to enhance energy conversion efficiency in oscillating water column wave energy systems, which demonstrated superior performance over standard control strategies.

The advanced control strategies discussed above, such as SMC proposed in¹⁸, adaptive SMC proposed in³⁴, and generalized predictive control proposed in³³, require sophisticated design and tuning, making them more complex to implement and maintain in real-world applications. Control techniques like FOPID designed in¹⁹ and deep learning-based methods as developed in³² can be computationally intensive, potentially leading to higher processing requirements and longer response times. Although these control strategies (e.g.¹⁸ and²⁷) are designed to address uncertainties and disturbances, their effectiveness may still be affected by parameter variations and environmental changes, especially in the presence of highly irregular wave conditions.

Given these considerations, this paper introduces the use of Chebyshev NN to design the BSC for rotational speed control of OWC. Chebyshev NN offers high approximation accuracy, robustness to nonlinearities, and adaptability to varying conditions³⁵, making it particularly well-suited for addressing the challenges of complex and dynamic systems such as OWCs. Chebyshev NN simplifies the control design, reduces computational demands, and provide smooth control actions, making them particularly well-suited for addressing the challenges of complex and dynamic systems such as OWCs. The Chebyshev neural network has been widely explored in various studies for its applicability in diverse control schemes across different applications, e.g. robotic systems³⁶, spacecrafts^37,38 and³⁹, twin rotor control systems⁴⁰, electric vehicles⁴¹, power converters⁴², and solar powered devices⁴³.

As compared to data driven control methods (such as in^44,45,46), the NN-BSC combines a structured model-based framework with NN adaptability to ensure robust performance and moderate computational demands, even in scenarios with bounded uncertainties. A brief comparison between NN-BSC and data-driven control schemes is discussed as follows:

• Model Dependence: NN-BSC relies on a mathematical model of the system for control design, while data-driven control methods eliminate this dependency by directly leveraging system data for controller design.

• Training Requirements: NN-BSC employs a NN for estimating disturbances, requiring proper training and parameter tuning, whereas data-driven approaches often optimize performance using empirical data without explicit system modelling.

• Generalization: NN-BSC can generalize to unmodeled dynamics within the framework of the existing model, whereas data-driven control excels in adapting to varying operating conditions by directly learning from real-time data.

• Implementation Complexity: NN-BSC integrates a functional link network with the control law, making it computationally lightweight, whereas data-driven methods may require extensive data preprocessing and computation, increasing implementation complexity.

While data-driven methods excel in handling significant modelling uncertainties, they often require: (1) Extensive and high-quality datasets for effective learning, (2) Computationally intensive optimization processes, and (3) Careful tuning to avoid issues like overfitting. Therefore, NN-BSC is preferred over data-driven control in this study as it avoids the need for extensive, high-quality datasets, computationally intensive optimization, and overfitting concerns, which might not be suitable all real-world scenarios.

Additionally, unlike disturbance observers, which require precise system models and disturbance knowledge, the NN-based approach offers adaptability without such prerequisites. The NN integration with BSC enables robust closed-loop stability analysis using Lyapunov stability theory to ensure system stability and asymptotic convergence of tracking errors under dynamic and uncertain conditions. This integration compensates for inaccuracies in the OWC system model by adaptively approximating unknown dynamics in real-time, bridging gaps between the simplified model and practical applications.

Building on these advantages and its proven versatility across various applications, this paper employs the Chebyshev NN to design a BSC for controlling the rotational speed of OWC systems. Therefore, this paper proposes following novel contributions:

• The Chebyshev NN is utilized to develop a novel NN-BSC for regulating the rotational speed of OWC, offering superior approximation accuracy, robustness to nonlinearities, and adaptability to dynamic conditions.

• The NN-BSC law is formulated and validated using Lyapunov stability analysis to ensure stability and enhanced performance for OWC systems under varying operational scenarios.

The design process for the NN-BSC scheme begins with a thorough description of the OWC wave energy system, which includes an overview of ocean waves and JONSWAP irregular wave model, the OWC chamber and Wells turbine, and the electrical generator. Following this, the process covers the conventional BSC design and its Lyapunov stability analysis to establish a baseline for comparison. The focus then shifts to the NN-BSC design, starting with an overview of the Chebyshev NN and its role in the scheme. This is followed by the design of the NN-BSC law. Asymptotic tracking is a critical challenge in nonlinear control systems. Recent advancements, including Adaptive RISE control with neural networks, model-based reinforcement learning, and hybrid-driven approaches, offer potential solutions^47,48,49). Based on these, Lyapunov stability analysis is conducted to ensure robust performance of NN-BSC in this study. The final stage involves numerical simulations and results, where the performance of an uncontrolled OWC system is first evaluated. This is followed by a comparison of the PI, BSC and NN-BSC performance, both without and with actuator disturbances. The parameters for PI, BSC, and NN-BSC were determined through an optimization process that utilized a PSO algorithm to minimize a fitness function based on Integral Squared Error (ISE). These evaluations assess the effectiveness of the conventional PI and BSC as compared to NN-BSC in controlling the rotational speed of the OWC system under varying conditions.

The remainder of this paper is structured as follows: section “OWC wave energy system description” provides a detailed description of the OWC wave energy system. Section “Conventional BSC design and stability analysis” focuses on the conventional BSC design and its associated Lyapunov stability analysis. In section “NN-BSC design and stability analysis”, the design and stability analysis of the NN-BSC are discussed, including the application of Chebyshev Neural Networks. Section “Numerical simulations and results” presents the numerical simulations and results, offering a comparative analysis of system performance. Finally, section “Concluding remarks” concludes with remarks summarizing the findings and implications of the study.

OWC wave energy system description

The OWC system typically consists of a partially submerged chamber with an opening below the waterline, allowing waves to enter and cause the water column inside to oscillate as shown in Fig. 1. This oscillation creates an alternating airflow, which drives a bi-directional turbine, such as a Wells turbine, to convert the kinetic energy of the air into mechanical energy. The turbine is connected to a generator, which then converts the mechanical energy into electrical power.

Fig. 1

OWC system description.

Ocean wave description

Ocean waves are often modelled using irregular wave models to simulate real-world conditions. These models account for the randomness and complexity of natural waves. Such models help in understanding and predicting wave behavior, crucial for optimizing energy conversion and coastal management. The JONSWAP model is a prominent example⁵⁰, designed to represent the statistical characteristics of sea waves, particularly for generating realistic wave spectrum as shown in Fig. 2 and assessing wave energy conversion efficiency in various conditions. This model has been selected for use in this study to generate irregular wave profiles.

OWC chamber and wells turbine description

The air velocity inside OWC chamber is mathematically represented by the equation given in⁵¹:

$${V_x}=\left( {\frac{{{A_o}}}{{{A_d}}}} \right)\frac{{\partial {h_w}\left( t \right)}}{{\partial t}}$$

(1)

Here, ${A_o}$ represents the cross-sectional area of the OWC (in ${m^2})$, ${A_d}$ denotes the cross-sectional area of the turbine duct (in ${m^2}$), ${h_w}\left( t \right)$ indicates the wave height (in meters), and ${V_{air}}$is the air velocity (in $(m/s$). The expression for air velocity, as given in Eq. (1), serves as the input to the Wells turbine.

Fig. 2

JONSWAP wave spectrum.

Fig. 3

Wells turbine schematic diagram.

Next, the Wells turbine⁵², invented by Alan Wells, is a specialized turbine used in OWC wave energy converters. It features a symmetrical air-foil shape that allows it to operate efficiently in both directions of airflow, converting bidirectional wave-induced airflow into rotational mechanical energy as shown in Fig. 3.

The turbine torque, ${T_{tur}}$, is defined as⁵¹:

$${T_{tur}}=f\left( {{\phi _{tur}}} \right)V_{{air}}^{2}$$

(2)

where $f\left( {{\phi _{tur}}} \right)$ is a function of the turbine flow coefficient, ${\phi _{tur}}$, expressed as:

$$f\left( {{\phi _{tur}}} \right)={C_{tur}}{k_{tur}}r\left( {1+\phi _{{tur}}^{{ - 1}}} \right)$$

(3)

Here, ${C_{tur}}$represents the characteristics of the Wells turbine, which vary with ${\phi _{tur}}$ as depicted in Fig. 4. ${k_{tur}}$ represents the turbine constant and r is the turbine radius (in m). The turbine flow coefficient, ${\phi _{tur}}$, is calculated as:

$${\phi _{tur}}={V_{air}}{\left( {r{\omega _{rot}}} \right)^{ - 1}}$$

(4)

As shown in Fig. 4, when the flow coefficient ${\phi _{tur}}$ is at or below the threshold value ${\phi _{th}}=0.3$, the torque coefficient is maximized, resulting in the highest turbine torque and, consequently, the greatest power output. Here, ${\phi _{th}}$ represents the flow coefficient threshold limit. If the flow coefficient remains below this threshold, turbine torque and output power continue to increase. However, when ${\phi _{tur}}$ exceeds ${\phi _{th}}$, both turbine torque and output power begin to decline.

Fig. 4

Wells turbine characteristics.

Next, the Wells turbine is linked to a DFIG, and as a result, the equation that describes the turbo-generator interaction can be formulated as follows:

$$\frac{{d{\omega _{rot}}}}{{dt}}=\frac{1}{J}\left( {{T_{tur}} - F.{\omega _{rot}} - {T_{gen}}} \right)$$

(5)

where ${\omega _{rot}}$ represents the rotor speed, F denotes the frictional coefficient, and ${T_{gen}}$ is the electromagnetic torque of the DFIG.

Electrical generator description

A DFIG type electrical generator has been considered in this study, which is widely utilized in wind and wave energy systems. It consists of a stator connected to the grid and a rotor linked to a variable frequency converter. This configuration allows the DFIG to operate efficiently at variable speeds, optimizing energy capture and enhancing grid stability¹⁸. Its ability to control both active and reactive power makes it versatile and effective for renewable energy applications. The DFIG direct-quadrature (dq) dynamics in differential equation form are as follows²²:

$$\frac{{d{\lambda _{ds}}}}{{dt}}= - \frac{{{R_s}{L_r}}}{Q}{\lambda _{ds}}+{\omega _e}{\lambda _{qs}}+\frac{{{R_s}{L_m}}}{Q}{\lambda _{dr}}+{v_{ds}}$$

(6)

$$\frac{{d{\lambda _{qs}}}}{{dt}}= - {\omega _e}{\lambda _{ds}} - \frac{{{R_s}{L_r}}}{Q}{\lambda _{qs}}+\frac{{{R_s}{L_m}}}{Q}{\lambda _{qr}}+{v_{qs}}$$

(7)

$$\begin{aligned} \frac{{d{\lambda _{dr}}}}{{dt}} & =\frac{{{R_r}{L_m}}}{Q}{\lambda _{ds}} - \frac{{{R_r}{L_s}}}{Q}{\lambda _{dr}} \\ & \;\; - ({\omega _{rot}} - {\omega _e}){\lambda _{qr}}+{v_{dr}} \\ \end{aligned}$$

(8)

$$\frac{{d{\lambda _{qr}}}}{{dt}}=\frac{{{R_r}{L_m}}}{Q}{\lambda _{qs}}+({\omega _{rot}} - {\omega _e}){\lambda _{dr}}+{v_{qr}}$$

(9)

Where, In this framework, Q is defined as $Q={L_s}{L_r} - L_{m}^{2}$. The flux linkages ${\lambda _{ds}}$, ${\lambda _{qs}}$, ${\lambda _{dr}}$ and ${\lambda _{qr}}$ represent the direct and quadrature axis fluxes for the stator and rotor, respectively, within the DFIG. The resistive parameters ${R_s}$ and ${R_r}$ correspond to the stator and rotor resistances, while ${L_s}$, ${L_r}$ and ${L_m}$ denote the stator inductance, rotor inductance, and mutual inductance of the DFIG. The stator supply angular frequency is denoted by ${\omega _e}$, and the DFIG voltages are characterized by ${v_{ds}}$, ${v_{qs}}$, ${v_{dr}}$ and ${v_{qr}}$. The initial conditions for the flux states are specified as ${\lambda _{ds0}}$, ${\lambda _{qs0}}$, ${\lambda _{dr0}}$ and ${\lambda _{qr0}}$, respectively. The formulations for electromagnetic torque and output power are delineated as follows:

$${T_{gen}}= - M\left( {{\lambda _{qs}}{\lambda _{dr}} - {\lambda _{ds}}{\lambda _{qr}}} \right)$$

(10)

$${P_{gen}}={T_{gen}}{\omega _{rot}}$$

(11)

where, $M=\left( {\frac{3}{2}} \right)\left( {\frac{p}{2}} \right)\left( {\frac{{{L_m}}}{Q}} \right)$. p is number of poles of DFIG.

The mathematical model of the OWC system stated above (Eqs. 1–11) has been validated in prior experimental studies (e.g. in^17,51) that demonstrates its reliability and accuracy for control design purposes in this study.

To design BSC, Eq. (5) through (10) are transformed into a state-space model in strict feedback form as per the process underlined in²². The state equations for the OWC plant are provided as follows:

$${\dot {\alpha }_1}={k_1}{\alpha _1}+{k_2}{\alpha _2}+{D_{tur}}$$

(12)

$${\dot {\alpha }_2}={k_3}\left( {{\alpha _1} - {\omega _e}} \right)+{k_4}{\alpha _2}+{u_r}$$

(13)

where, ${k_1}= - \frac{F}{J}$; ${k_2}= - \frac{M}{J}$; ${\text{~}}{k_3}=\frac{{{L_r}}}{{{L_m}}}{\psi _S}$; ${k_4}= - \frac{{{R_r}{L_s}}}{Q}$; ${u_r}={v_{qr}}$; ${D_{tur}}=\frac{{{T_{tur}}}}{J}$; ${\alpha _1}={\omega _{rot}}$ and ${\alpha _2}={\lambda _{qr}}$. The state ${\alpha _1}~$represents the rotor speed, which serves as the output of the OWC system targeted for control. The term ${u_r}$ acts as the control input for the OWC system.

Fig. 5

Block diagram of OWC wave energy system with MPPT and BSC/NN-BSC.

Conventional BSC design and stability analysis

The block diagram in Fig. 5 depicts OWC wave energy system integrated with MPPT and BSC/NN-BSC modules. Wave height, ${h_w}\left( t \right)$, data is supplied to both the OWC wave energy system and the MPPT module. The implementation of the MPPT module in this study adheres to the design methodology outlined in²². The OWC system transmits state signals, ${\alpha _1}$ and ${\alpha _2}$, to the BSC/NN-BSC module, which processes these inputs and generates control signal, ${u_r}$, to control the OWC system. Simultaneously, the MPPT module sends the reference signal, ${\alpha _{1{\text{d}}}}$, to the BSC/NN-BSC block, guiding the controller to ensure maximum energy extraction.

A step-by-step approach is employed for the design of the BSC. The controller for the second-order system, described by Eqs. (12) and (13), is developed in two stages. First, a virtual controller, ${\alpha _{2d}}$, is designed. This ${\alpha _{2d}}$ is then used to formulate the final control law ${u_r}$.

The design of the virtual controller, ${\alpha _{2d}}$, takes into account the error component, expressed as:

$${\tilde {\alpha }_1}={\alpha _{1d}} - {\alpha _1}$$

(14)

The next step involves differentiating Eq. (14), which results in the following expression:

$${\dot {\tilde {\alpha }}_1}={\dot {\alpha }_{1d}} - {\dot {\alpha }_1}={\text{~}}{\dot {\alpha }_{1d}} - {\text{~}}{k_1}{\alpha _1} - {D_{tur}} - {k_2}{\alpha _2}$$

(15)

At this point, we add and subtract the ${k_2}{\alpha _{2d}}$ term, and Eq. (15) is rewritten as:

$${\dot {\tilde {\alpha }}_1}={\dot {\alpha }_{1d}} - {\text{~}}{k_1}{\alpha _1} - {D_{tur}} - {k_2}{\alpha _2}+{k_2}{\alpha _{2d}} - {k_2}{\alpha _{2d}}$$

(16)

The virtual controller ${\alpha _{2d}}$ is chosen as:

$${\alpha _{2d}}=k_{2}^{{ - 1}}\left( {{{\dot {\alpha }}_{1d}} - {\text{~}}{k_1}{\alpha _1} - {D_{tur}}+{\sigma _1}{{\tilde {\alpha }}_1}} \right)$$

(17)

where, ${\sigma _1}>0$.

Taking the derivative of ${\alpha _{2d}}$ produces:

$${\dot {\alpha }_{2d}}=k_{2}^{{ - 1}}\left( {{{\ddot {\alpha }}_{1d}} - {\text{~}}{k_1}{{\dot {\alpha }}_1} - {{\dot {D}}_{tur}}+{\sigma _1}{{\dot {\tilde {\alpha }}}_1}} \right)$$

(18)

Subsequently, the second error component is formulated as:

$${\tilde {\alpha }_2}={\alpha _{2d}} - {\alpha _2}$$

(19)

Substituting Eqs. (17) and (18), the Eq. (16) can be expressed as:

$${\dot {\tilde {\alpha }}_1}= - {\sigma _1}{\tilde {\alpha }_1}+{k_2}{\tilde {\alpha }_2}$$

(20)

The subsequent step involves computing the derivative of Eq. (19), yielding:

$${\dot {\tilde {\alpha }}_2}={\dot {\alpha }_{2d}} - {\dot {\alpha }_2}={\dot {\alpha }_{2d}} - {\text{~}}{k_3}\left( {{\alpha _1} - {\omega _e}} \right) - {k_4}{\alpha _2} - {u_r}$$

(21)

By substituting ${\dot {\alpha }_{2d}}$ into Eq. (21), the following expression is obtained:

$${\dot {\tilde {\alpha }}_2}=k_{2}^{{ - 1}}\left( {{{\ddot {\alpha }}_{1d}} - {\text{~}}{k_1}{{\dot {\alpha }}_1} - {{\dot {D}}_{tur}}+{\sigma _1}{{\dot {\tilde {\alpha }}}_1}} \right) - {\text{~}}{k_3}\left( {{\alpha _1} - {\omega _e}} \right) - {k_4}{\alpha _2} - {u_r}$$

(22)

Solving Eq. (22) by substituting Eqs. (12) and (20) produces the following result:

$${\dot {\tilde {\alpha }}_2}=\left( {{k_3} - {k_1}{k_4}k_{2}^{{ - 1}} - \sigma _{1}^{2}k_{2}^{{ - 1}}} \right){\tilde {\alpha }_1}+\left( {{k_1}+{k_4}+{\sigma _1}} \right){\tilde {\alpha }_2} - {u_r}+{f_d}$$

(23)

where, ${f_d}$ is treated as a disturbance function and is represented as:

$${f_d}=k_{2}^{{ - 1}}{\ddot {\alpha }_{1d}} - \left( {{k_1}k_{2}^{{ - 1}}+{k_4}k_{2}^{{ - 1}}} \right){\dot {\alpha }_{1d}} - \left( {{k_3} - {k_1}{k_4}k_{2}^{{ - 1}}} \right){\alpha _{1d}}+{k_4}k_{2}^{{ - 1}}{D_{tur}} - k_{2}^{{ - 1}}{\dot {D}_{tur}}+{k_3}{\omega _e}$$

(24)

.

To develop a control strategy that ensures the closed-loop stability of the OWC system, a suitable Lyapunov function candidate, denoted as ${V_{lf1}}$, is selected as follows:

$${V_{lf1}}=\frac{1}{2}\left( {\tilde {\alpha }_{1}^{2}+\tilde {\alpha }_{2}^{2}} \right)$$

(25)

The expression in Eq. (25) is subjected to differentiation and subsequently reformulated as:

$${\dot {V}_{lf1}}={\tilde {\alpha }_1}{\dot {\tilde {\alpha }}_1}+{\tilde {\alpha }_2}{\dot {\tilde {\alpha }}_2}$$

(26)

By substituting $\dot{\tilde{\alpha }}_{1}$ and $\dot{\tilde{\alpha }}_{2}$ from Eqs. (20) and (23) into Eq. (26), the following expression is derived:

$${\dot {V}_{lf1}}= - {\sigma _1}\tilde {\alpha }_{1}^{2}+{\tilde {\alpha }_2}\left\{ {{k_2}{{\tilde {\alpha }}_1}+\left( {{k_3} - {k_1}{k_4}k_{2}^{{ - 1}} - \sigma _{1}^{2}k_{2}^{{ - 1}}} \right){{\tilde {\alpha }}_1}+\left( {{k_1}+{k_4}+{\sigma _1}} \right){{\tilde {\alpha }}_2} - {u_r}+{f_d}} \right\}$$

(27)

Next, the control law ${u_r}$:

$${u_r}={k_2}{\tilde {\alpha }_1}+\left( {{k_3} - {k_1}{k_4}k_{2}^{{ - 1}} - \sigma _{1}^{2}k_{2}^{{ - 1}}} \right){\tilde {\alpha }_1}+\left( {{k_1}+{k_4}+{\sigma _1}} \right){\tilde {\alpha }_2}+{f_d}+{\sigma _2}{\tilde {\alpha }_2}$$

(28)

results in:

$${\dot {V}_{lf1}}= - {\sigma _1}\tilde {\alpha }_{1}^{2} - {\sigma _2}\tilde {\alpha }_{2}^{2} \leqslant 0$$

(29)

where, ${\sigma _2}>0$.

Equation (29) is shown to be negative semi-definite, indicating that the derivative of the Lyapunov function, ${\dot {V}_{lf1}}$, does not permit non-trivial error state trajectories for ${\tilde {\alpha }_1}$ and ${\tilde {\alpha }_2}$ beyond the trivial solution ${\tilde {\alpha }_1}={\tilde {\alpha }_2}=0$. Consequently, these error states asymptotically converge to zero. Therefore, the system described by Eqs. (12) and (13), when governed by the control law ${u_r}$ in Eq. (24), is asymptotically stable.

The final closed-loop state error dynamics of the OWC system under BSC framework are given by:

$${\dot {\tilde {\alpha }}_1}= - {\sigma _1}{\tilde {\alpha }_1}+{k_2}{\tilde {\alpha }_2}~$$

(30)

$${\dot {\tilde {\alpha }}_2}=\left( {{k_3} - {k_1}{k_4}k_{2}^{{ - 1}} - \sigma _{1}^{2}k_{2}^{{ - 1}}} \right){\tilde {\alpha }_1}+\left( {{k_1}+{k_4}+{\sigma _1}} \right){\tilde {\alpha }_2} - {u_r}+{f_d}$$

(31)

where, ${u_r}$ denotes the backstepping control law, and ${f_d}$ represents the disturbance function. These are expressed as:

$${u_r}={k_2}{\tilde {\alpha }_1}+\left( {{k_3} - {k_1}{k_4}k_{2}^{{ - 1}} - \sigma _{1}^{2}k_{2}^{{ - 1}}} \right){\tilde {\alpha }_1}+\left( {{k_1}+{k_4}+{\sigma _1}} \right){\tilde {\alpha }_2}+{f_d}+{\sigma _2}{\tilde {\alpha }_2}$$

(32)

$$f_{d} = k_{2}^{{ - 1}} \ddot{\alpha }_{{1d}} - \left( {k_{1} k_{2}^{{ - 1}} + k_{4} k_{2}^{{ - 1}} } \right)\dot{\alpha }_{{1d}} - \left( {k_{3} - k_{1} k_{4} k_{2}^{{ - 1}} } \right)\alpha _{{1d}} + k_{4} k_{2}^{{ - 1}} D_{{tur}} - k_{2}^{{ - 1}} \dot{D}_{{tur}} + k_{3} \omega _{e}$$

(33)

There, the Eqs. (30–33) represent the final state space model of OWC in terms of state error dynamics with BSC law. Equations (30) and (31) provide a comprehensive representation of the closed-loop state-space dynamics of the OWC system in terms of state errors.

Figure 6 illustrates the architecture of the BSC scheme for the OWC system. The inputs include the reference input $\:{\alpha\:}_{1d}$, system states $\:{\alpha\:}_{1}$ and $\:{\alpha\:}_{2}$, and $\:{D}_{tur}$. The BSC output $\:{u}_{r}$ is computed using Eqs. (17), (32), and (33). The model explicitly incorporates the control law (Eq. 32) and disturbance function (Eq. 33), aligning the inputs and outputs for subsequent NN-BSC implementation. These dynamics serve as the foundation for analyzing stability and tracking performance under the proposed NN-BSC framework in the next section.

Fig. 6

Architecture of BSC scheme for the OWC system.

NN-BSC design and stability analysis

Disturbance term ${f_d}$ in BSC design introduces uncertainty and unpredictability that makes it difficult to model and compensate for its effect accurately. It is also has nonlinear or time-varying behaviour, which complicates the controller performance. This terms is also very difficult to measure in real scenario. Hence, in this study, the disturbance term ${f_d}$ is estimated using Chebyshev NN and the stability of NN-BSC law is analysed subsequently.

Chebyshev NN overview

The Chebyshev NN leverages the orthogonal properties of Chebyshev polynomials³⁵ to efficiently approximate nonlinear system dynamics with high accuracy and computational efficiency. In this study, the Chebyshev NN integrates seamlessly into the BSC framework, combining the adaptive learning capabilities of NNs with the systematic control design of BSC.

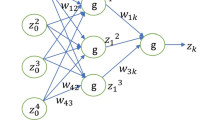
The NN architecture employed in this study is a single-layer Chebyshev NN, illustrated in Fig. 7, and categorized as a functional link network leveraging Chebyshev polynomials⁴⁰. The architecture involves:

• Input Layer: Inputs to the NN are the system states ${\alpha _1}$, ${\alpha _2} \cdots$, ${\alpha _j}$, which are functionally expanded using Chebyshev polynomials.

• Functional Expansion: This expansion transforms the input variables into a higher-dimensional feature space to enhance approximation capability.

• Output Layer: The expanded terms are linearly combined using weights (${\hat {W}^T}$) to generate the estimated disturbance ${\hat {f}_d}$ which is critical for improving the control accuracy of the OWC system.

Fig. 7

Structure of Chebyshev NN.

One approach to function approximation is through a truncated power series expansion, which provides minimal error near the expansion point but incurs significant error as the evaluation distance increases. Chebyshev series, on the other hand, offer superior computational efficiency, particularly when power series exhibit slow convergence. As a result, Chebyshev series are frequently employed for function approximation, delivering greater efficiency compared to power series of the same degree. The Chebyshev polynomials, ${T_n}\left( \alpha \right),$ are defined recursively as follows:

$${T_0}\left( \alpha \right)=1$$

(34)

$${T_1}\left( \alpha \right)=\alpha$$

(35)

$${T_{n+1}}\left( \alpha \right)=2\alpha {T_n}\left( \alpha \right) - {T_{n - 1}}\left( \alpha \right)$$

(36)

The output of weighted sum of each neuron in the hidden layer is computed as follows:

$${f_d}={W^T}{\phi _{NN}}\left( {{\alpha _1},{\alpha _2}} \right)+ \in$$

(37)

where, W represent the weight matrix of the NN having dimension $m \times 1$, and m represents number of neurons. The ideal weights are limited by specified positive bounds such that ${\left\| W \right\|_F} \leqslant {W_M}$. The notation ${\left\| W \right\|_F}$ represents the Frobenius norm of the weight matrix W and is represented as:

$${\left\| W \right\|_F}=\sqrt {\mathop \sum \limits_{{i=1}}^{m} {{\left| {{w_i}} \right|}^2}}$$

(38)

where, ${w_i}$ is the weight of the i-th neuron. Next, $\in$ denote the functional reconstruction error vector of the Chebyshev NN. The error $\in$ is bounded such that $\in \leqslant { \in _M}$. The function ${\phi _{NN}}\left( {{\alpha _1},{\alpha _2}} \right)$ serves as a basis function, formulated using Chebyshev polynomials as defined in Eqs. (34–36) and is expressed as follows:

$$\left. {\begin{array}{*{20}{c}} {{\phi _{NN}}\left( {{\alpha _1},{\alpha _2}} \right)=\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1&{{T_1}\left( {{\alpha _1}} \right)} \end{array}}&{\begin{array}{*{20}{c}} {{T_2}\left( {{\alpha _1}} \right)}& \cdots \end{array}} \end{array}} \right.} \\ {~~~~~~~~~~~~~~~~~~~~~~~~~~~\left. {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \cdots &{{T_1}\left( {{\alpha _2}} \right)} \end{array}}&{{T_2}\left( {{\alpha _2}} \right)}& \cdots \end{array}} \right]} \end{array}} \right\}$$

(39)

where, the basis function, ${\phi _{NN}}\left( {{\alpha _1},{\alpha _2}} \right)$, vector has the dimension $1 \times m$. Henceforth, ${\phi _{NN}}\left( {{\alpha _1},{\alpha _2}} \right)$ will be denoted as ${\phi _{NN}}$ for notational simplification.

Moreover, an estimation of the function ${f_d}$ can be expressed as:

$${\hat {f}_d}={\hat {W}^T}{\phi _{NN}}$$

(40)

where, $\hat {W}$ is the estimated weight matrix of the ideal weight matrix W.

Choose an error function as:

$${\tilde {f}_d}={f_d} - {\hat {f}_d}={W^T}{\phi _{NN}}+ \in - {\hat {W}^T}{\phi _{NN}}$$

(41)

The Eq. (37) is further simplified as:

$${\tilde {f}_d}={\tilde {W}^T}{\phi _{NN}}+ \in$$

(42)

where, $\tilde {W}=W - \hat {W}$.

NN-BSC law and stability proof

To design the NN-BSC law, the term $\:{f}_{d}$ has been replaced by its estimate $\:{\widehat{f}}_{d}$ in the expression of BSC law, $\:{u}_{r}$, in Eq. (32), which is expressed as follows:

$$\:{u}_{r}={k}_{2}{\stackrel{\sim}{\alpha\:}}_{1}+\left({k}_{3}-{k}_{1}{k}_{4}{k}_{2}^{-1}-{\sigma\:}_{1}^{2}{k}_{2}^{-1}\right){\stackrel{\sim}{\alpha\:}}_{1}+({k}_{1}+{k}_{4}+{\sigma\:}_{1}){\stackrel{\sim}{\alpha\:}}_{2}+{\widehat{f}}_{d}+{\sigma\:}_{2}{\stackrel{\sim}{\alpha\:}}_{2}$$

(43)

The NN-BSC law, as formulated in Eq. (43), is substituted into Eq. (31), resulting in the following

expression:

$$\:{\dot{\stackrel{\sim}{\alpha\:}}}_{2}=-{k}_{2}{\stackrel{\sim}{\alpha\:}}_{1}-{\sigma\:}_{2}{\stackrel{\sim}{\alpha\:}}_{2}+{f}_{d}-{\widehat{f}}_{d}$$

(44)

An additional actuator disturbance term $\:{\Delta\:}$ such that $\:{\Delta\:}\le\:{{\Delta\:}}_{M}$, is added in Eq. (44) to study the robustness of the proposed controller. $\:{{\Delta\:}}_{M}$ is the upper bound on actuator disturbance. Hence, the Eq. (44) is now written as:

$$\:{\dot{\stackrel{\sim}{\alpha\:}}}_{2}=-{k}_{2}{\stackrel{\sim}{\alpha\:}}_{1}-{\sigma\:}_{2}{\stackrel{\sim}{\alpha\:}}_{2}+{f}_{d}-{\widehat{f}}_{d}+{\Delta\:}=-{k}_{2}{\stackrel{\sim}{\alpha\:}}_{1}-{\sigma\:}_{2}{\stackrel{\sim}{\alpha\:}}_{2}+\stackrel{\sim}{f}+{\Delta\:}\:\:\:=-{k}_{2}{\stackrel{\sim}{\alpha\:}}_{1}-{\sigma\:}_{2}{\stackrel{\sim}{\alpha\:}}_{2}+{\stackrel{\sim}{W}}^{T}{\varphi\:}_{NN}+\in\:+{\Delta\:}$$

(45)

Next, the weight update mechanism is designed to ensure system stability. This update process is governed by an adaptive learning rule, which enhances the robustness of the learning process. In this regard, a cost function is considered as follows:

$$\:Y=\frac{1}{2}{\stackrel{\sim}{\alpha\:}}_{2}^{2}$$

(46)

The adaptive learning rule to update of neural network weights is defined as follows:

$$\dot{\hat{W}} = - \eta \frac{{\partial Y}}{{\partial \hat{W}}} - \frac{{\eta \rho }}{{\sigma _{2} }}\left\| {\tilde{\alpha_{2} }} \right\| \hat{W}$$

(47)

where, $\:\eta\:$ represents learning rate and $\:\rho\:$ represents damping coefficient.

The differentiation of $\:Y$ can be represented as follows:

$$\:\frac{\partial\:Y}{\partial\:\widehat{W}}=\frac{\partial\:Y}{\partial\:{\stackrel{\sim}{\alpha\:}}_{2}}\frac{\partial\:{\stackrel{\sim}{\alpha\:}}_{2}}{\partial\:{\widehat{f}}_{d}}\frac{\partial\:{\widehat{f}}_{d}}{\partial\:\widehat{W}}$$

(48)

Substituting, $\:\frac{\partial\:Y}{\partial\:{\stackrel{\sim}{\alpha\:}}_{2}}={\stackrel{\sim}{\alpha\:}}_{2}$ and $\:\frac{\partial\:{\widehat{f}}_{d}}{\partial\:\widehat{W}}={\varphi\:}_{NN}$ in Eq. (48), the $\:\frac{\partial\:Y}{\partial\:\widehat{W}}$ is expressed as:

$$\:\frac{\partial\:Y}{\partial\:\widehat{W}}={\stackrel{\sim}{\alpha\:}}_{2}{\varphi\:}_{NN}\frac{\partial\:{\stackrel{\sim}{\alpha\:}}_{2}}{\partial\:{\widehat{f}}_{d}}$$

(49)

Referencing Eq. (44) and differentiating it with respect to $\:{\widehat{f}}_{d}$ yields the following result:

$$\:\frac{\partial\:}{\partial\:{\widehat{f}}_{d}}\left({\dot{\stackrel{\sim}{\alpha\:}}}_{2}\right)=\frac{\partial\:}{\partial\:{\widehat{f}}_{d}}(-{k}_{2}{\stackrel{\sim}{\alpha\:}}_{1}-{\sigma\:}_{2}{\stackrel{\sim}{\alpha\:}}_{2}+{f}_{d}-{\widehat{f}}_{d}+{\Delta\:})$$

(50)

Equation (50) is solved further and results in:

$$\:\frac{\partial\:}{\partial\:{\widehat{f}}_{d}}\left({\dot{\stackrel{\sim}{\alpha\:}}}_{2}\right)=-{\sigma\:}_{2}\frac{\partial\:{\stackrel{\sim}{\alpha\:}}_{2}}{\partial\:{\widehat{f}}_{d}}-1\approx\:0$$

(51)

From Eq. (51), the following expression is derived:

$$\:\frac{\partial\:{\stackrel{\sim}{\alpha\:}}_{2}}{\partial\:{\widehat{f}}_{d}}=-\frac{1}{{\sigma\:}_{2}}$$

(52)

Hence, the final expression for $\:\frac{\partial\:Y}{\partial\:\widehat{W}}$ after substituting $\:\frac{\partial\:{\stackrel{\sim}{\alpha\:}}_{2}}{\partial\:{\widehat{f}}_{d}}$ in Eq. (49) is:

$$\:\frac{\partial\:Y}{\partial\:\widehat{W}}=-\frac{{\stackrel{\sim}{\alpha\:}}_{2}{\varphi\:}_{NN}}{{\sigma\:}_{2}}$$

(53)

Which further modifies Eq. (47) in the following form:

$$\dot{\hat{W}} = \frac{\eta }{{\sigma _{2} }}\tilde{\alpha }_{2} \phi _{{NN}} - \frac{{\eta \rho }}{{\sigma _{2} }}\left\| {\tilde{\alpha }_{2} } \right\|\hat{W}$$

(54)

In this context, Eq. (54) serves as the final weight update mechanism for the NN-BSC law defined in Eq. (43).

The stability analysis of the NN-BSC law is now conducted. For this purpose, a Lyapunov function candidate is introduced as follows:

$$\:{V}_{lf2}=\frac{1}{2}\left({\stackrel{\sim}{\alpha\:}}_{1}^{2}+{\stackrel{\sim}{\alpha\:}}_{2}^{2}\right)+\frac{1}{2}tr\left\{{\stackrel{\sim}{W}}^{T}\left(\frac{{\sigma\:}_{2}}{\eta\:}\right)\stackrel{\sim}{W}\right\}$$

(55)

The expression in Eq. (55) is subjected to differentiation and subsequently reformulated as:

$$\:{\dot{V}}_{lf1}={\stackrel{\sim}{\alpha\:}}_{1}{\dot{\stackrel{\sim}{\alpha\:}}}_{1}+{\stackrel{\sim}{\alpha\:}}_{2}{\dot{\stackrel{\sim}{\alpha\:}}}_{2}+tr\left\{{\stackrel{\sim}{W}}^{T}\left(\frac{{\sigma\:}_{2}}{\eta\:}\right)\dot{\stackrel{\sim}{W}}\right\}$$

(56)

The expression for $\:\dot{\stackrel{\sim}{W}}$ is required in Eq. (56). It can be obtained by differentiating $\:\stackrel{\sim}{W}=W-\widehat{W}$, resulting in $\:\dot{\stackrel{\sim}{W}}=\dot{W}-\dot{\widehat{W}}$. Since the ideal weights are constant, $\:\dot{W}=0$, leading to $\:\dot{\stackrel{\sim}{W}}=-\dot{\widehat{W}}$. Thus, $\:\dot{\stackrel{\sim}{W}}$ is given by:

$$\dot{\tilde{W}} = - \frac{\eta }{{\sigma _{2} }}\tilde{\alpha }_{2} \phi _{{NN}} + \frac{{\eta \rho }}{{\sigma _{2} }}\left\| {\tilde{\alpha_{2} }} \right\| \hat{W}$$

(57)

Next, $\:{\dot{\stackrel{\sim}{\alpha\:}}}_{1}$ from Eq. (30), $\:{\dot{\stackrel{\sim}{\alpha\:}}}_{2}$ from Eq. (45), and $\:\dot{\stackrel{\sim}{W}}$ from Eq. (57) are substituted into Eq. (56). This results in:

$$\begin{aligned} {{\dot {V}}_{lf2}} & ={{\tilde {\alpha }}_1}\left( { - {\sigma _1}{{\tilde {\alpha }}_1}+{k_2}{{\tilde {\alpha }}_2}} \right) \\ & \;\;+{{\tilde {\alpha }}_2}\left( { - {k_2}{{\tilde {\alpha }}_1} - {\sigma _2}{{\tilde {\alpha }}_2}+{{\tilde {W}}^T}{\phi _{NN}}+ \in +{\text{\varvec{\Delta}}}} \right) \\ & \;\;+tr\left\{ {{{\tilde {W}}^T}\left( {\frac{{{\sigma _2}}}{\eta }} \right)\left( { - \frac{\eta }{{{\sigma _2}}}{{\tilde {\alpha }}_2}{\phi _{NN}}+\frac{{\eta \rho }}{{{\sigma _2}}}{{\left\| {\tilde {\alpha_2 }} \right\|}}\hat {W}} \right)} \right\} \\ \end{aligned}$$

(58)

Equation (58) is further modified as follows:

$${\dot {V}_{lf2}}= - {\sigma _1}\tilde {\alpha }_{1}^{2} - {\sigma _2}\tilde {\alpha }_{2}^{2}+{\tilde {\alpha }_2}\left( { \in +{\text{\varvec{\Delta}}}} \right)+\rho {\left\| {\tilde {\alpha_2 }} \right\|}tr\left\{ {{{\tilde {W}}^T}\hat {W}} \right\}$$

(59)

Consider the following inequality³⁶:

$$tr\left\{ {{{\tilde {W}}^T}\hat {W}} \right\} \leqslant {W_M}{\left\| {\tilde {W}} \right\|_F} - \left\| {\tilde {W}} \right\|_{F}^{2}$$

(60)

Inserting the inequality presented in Eq. (60) into Eq. (59) results in:

$${\dot {V}_{lf2}} \leqslant - {\sigma _1}\tilde {\alpha }_{1}^{2} - {\sigma _2}\tilde {\alpha }_{2}^{2}+{\left\| {\tilde {\alpha_2 }} \right\|}\left( {{ \in _M}+{{\text{\varvec{\Delta}}}_M}} \right)+\rho {\left\| {\tilde {\alpha_2 }} \right\|}\left( {{W_M}{{\left\| {\tilde {W}} \right\|}_F} - \left\| {\tilde {W}} \right\|_{F}^{2}} \right)$$

(61)

Further solving Eq. (61) results in the following form:

$${\dot {V}_{lf2}} \leqslant - {\sigma _1}\tilde {\alpha }_{1}^{2} - {\sigma _2}\tilde {\alpha }_{2}^{2} - \rho {\left\| {\tilde {\alpha_2 }} \right\|}\left[ {{{\left( {{{\left\| {\tilde {W}} \right\|}_F} - \frac{1}{2}{W_M}} \right)}^2} - \frac{1}{4}W_{M}^{2} - \frac{{{ \in _M}+{{\text{\varvec{\Delta}}}_M}}}{\rho }} \right]$$

(62)

Equation (62) remains negative semi-definite provided the following condition is satisfied:

$${\left\| {\tilde {W}} \right\|_F} \geqslant \frac{1}{2}{W_M}+\sqrt {\left( {\frac{{{ \in _M}+{{\text{\varvec{\Delta}}}_M}}}{\rho }+\frac{1}{4}W_{M}^{2}} \right)}$$

(63)

Consequently, the dynamical OWC system described by Eqs. (30) and (31), when controlled by the NN-BSC control law defined in Eq. (43), with the weight update mechanism outlined in Eq. (54) and under the condition specified in Eq. (63), establishes asymptotic stability. This completes the stability proof. Following the detailed derivation, the architecture of the NN-BSC is illustrated in Fig. 8. It clearly depicts the reference input, system states, control signals, and the incorporation of the Chebyshev NN into the OWC control system. Next, the parameters of PI, BSC, and NN-BSC were determined by minimizing ISE using PSO as per the process employed in²⁵. The ISE expression is as follows:

$$\:\text{I}\text{S}\text{E}\:={\int\:}_{t=0}^{{T}_{sim}}{\stackrel{\sim}{\alpha\:}}_{1}^{2}dt$$

(64)

where, $\:{T}_{sim}$ is the simulation time.

Other advanced optimization techniques are not employed in this study, as the primary focus is to integrate the Chebyshev NN with BSC for OWC control and validate system stability through Lyapunov analysis. However, in²⁵, some advanced optimizers, such as the AO and GA including PSO, were successfully used to determine optimal BSC parameters for OWC systems. This highlights the potential for such methods to achieve globally optimal parameter values. The application of similar optimization algorithms to further refine NN-BSC parameters may also be explored in future work.

Fig. 8

Architecture of NN-BSC scheme for the OWC system.

Numerical simulations and results

In this section, numerical simulations are presented to evaluate the performance of the NN-BSC applied to the OWC wave energy system. The simulations include performance analysis of the uncontrolled OWC to establish a reference for comparison. Additionally, the NN-BSC is compared with traditional PI and BSC under scenarios with and without actuator disturbances. These comparisons aim to demonstrate the ability of NN-BSC to enhance wave energy capture, maintain system stability, and improve robustness against disturbances. Numerical simulations were conducted using MATLAB/SIMULINK. Simulation parameters for the OWC system have been adopted from²². The simulation parameters and corresponding ISE values for PI, BSC, and NN-BSC, determined using the PSO optimizer, are presented in TABLE I. The simulation time, $\:{T}_{sim}$, is taken as 50 s. The PI controller expression used is as follows:

$$\:{u}_{r}={K}_{p}{\stackrel{\sim}{\alpha\:}}_{1}+{K}_{i}{\int\:}_{t=0}^{{T}_{sim}}{\stackrel{\sim}{\alpha\:}}_{1}dt$$

(65)

where, $\:{K}_{p}$ is the proportional gain and $\:{K}_{i}$ is the integral gain of PI.

Irregular wave profiles or heights are generated using the JONSWAP spectrum model, depicted in Fig. 9. The air velocity inside the OWC is computed from Eq. (1), with wave height serving as the input, as illustrated in Fig. 10. The function $\:{\varphi\:}_{NN}$ has been formulated using Chebyshev polynomials as defined below:

$$\:{\varphi\:}_{NN}=[1\:\:\:{\alpha\:}_{1}\:\:\:2{\alpha\:}_{1}^{2}-1\:\:\:{\alpha\:}_{2}\:\:\:2{\alpha\:}_{2}^{2}-1]$$

(66)

Table 1 Optimization results for controller gains and ISE values.

The optimization results in Table 1 indicate a clear progression in performance, with the NN-BSC significantly outperforming the PI and BSC methods in terms of ISE. This improvement can be attributed to the adaptive learning capabilities of the Chebyshev NN within the NN-BSC framework, enabling better handling of nonlinearities, disturbances, and dynamic conditions.

Fig. 9

Wave profile generated using JONSWAP.

Fig. 10

Air velocity generated using Eq. (1).

Performance evaluation of uncontrolled OWC

In this subsection, the performance of the uncontrolled OWC plant is analysed, which emphasizes key performance limitations. First, the flow coefficient often exceeds the critical threshold of 0.3, as shown in Fig. 11, which indicates stalling in Wells turbine. Additionally, the rotor speed in the uncontrolled OWC system fluctuates around the stator supply frequency of $\:50\pi\:$ rad/s, as seen in Fig. 12. A considerable rotor speed error appears when comparing the actual rotor speed to the reference speed generated by the MPPT block, as presented in Fig. 13.

Fig. 11

Well turbine flow coefficient waveforms for uncontrolled OWC system.

Fig. 12

Rotor speed waveforms for uncontrolled OWC system.

Fig. 13

Rotor speed error waveforms for uncontrolled OWC system.

The turbine torque in the uncontrolled OWC system shows stalling effects, with visible stalling regions around 5s and 20s (refer red encircled regions) in Fig. 14, which reduces system efficiency. Due to this stalling, the output power remains below 50 kW, as shown in Fig. 15. It indicates the overall unsatisfactory performance of the uncontrolled OWC system. The observations in rotor speed, power output, and turbine torque highlight the need for an effective control strategy to address these issues and improve system performance.

Fig. 14

Well turbine torque waveforms for uncontrolled OWC system.

Fig. 15

Output power waveforms generated for uncontrolled OWC system.

Performance evaluation of BSC and NN-BSC without actuator disturbance $\left( {i.e.{\text{~~}}\Delta \left( t \right) = 0} \right)$

In this subsection, the performance of the PI, BSC, and NN-BSC controlled OWC wave energy system without actuator disturbances is evaluated. Firstly, as shown in Fig. 16, the actual rotor speed satisfactorily tracks the MPPT reference speed for all three control methods. However, as seen in the zoomed section, significant steady state error is observed in the actual rotor speed for PI between 18.9s and 26.9s, which are notably absent in BSC and NN-BSC.

Fig. 16

Rotor speed waveforms for BSC and NN-BSC controlled OWC system without actuator disturbance.

Similarly, Fig. 17 illustrates that the rotor speed error settles more quickly and without transients for NN-BSC, particularly noticeable between 26.5 s and 26.9 s, whereas significant transients are present with PI and BSC. Further, the q-axis rotor flux error in NN-BSC, as depicted in Fig. 18, settles to zero without any transients, demonstrating a smoother control response compared to PI and BSC, where error variations remain significant, especially during the same time frame.

Fig. 17

Rotor speed error waveforms under BSC and NN-BSC controlled OWC system without actuator disturbance.

Fig. 18

q-axis rotor flux error waveforms under BSC and NN-BSC controlled OWC system without actuator disturbance.

Fig. 19

Control voltage waveforms under BSC and NN-BSC controlled OWC system without actuator disturbance.

Fig. 20

Flow coefficient waveforms under BSC and NN-BSC controlled OWC system without actuator disturbance.

Fig. 21

Wells turbine torque waveforms under BSC and NN-BSC controlled OWC system without actuator disturbance.

Fig. 22

Output power waveforms under BSC and NN-BSC controlled OWC system without actuator disturbance.

Rotor control voltages, shown in Fig. 19, reveal that during abrupt changes in the MPPT reference, substantial control efforts are required to minimize rotor speed and q-axis rotor flux errors. The Wells turbine flow coefficient, depicted in Fig. 20, remains consistently below the critical threshold of 0.3 for all three control methods, which ensures stable operation. Additionally, the Wells turbine torque and output power, shown in Figs. 21 and 22 respectively, are significantly enhanced in all three control methods as compared to the uncontrolled OWC system. These results demonstrate that NN-BSC outperforms or is at least on par with the conventional PI and BSC, providing superior control by minimizing transients, achieving faster error settling, and maintaining critical operational thresholds.

Performance evaluation of BSC and NN-BSC with actuator disturbance $\left( {i.e.{\text{~~}}\Delta \left( t \right)=10sin\left( {2\pi t} \right)} \right)$

In this subsection, the performance of the PI, BSC and NN-BSC controlled OWC wave energy system under actuator disturbance is analysed, which highlights the advantages of NN-BSC over conventional PI and BSC. As illustrated in Fig. 23, the actual rotor speed for NN-BSC satisfactorily follows the MPPT reference speed without noticeable transients. In contrast, PI and BSC exhibits significant transients in rotor speed throughout the response, particularly visible between 18.8s and 24.8s in the zoomed portion.

Fig. 23

Rotor speed waveforms for BSC and NN-BSC controlled OWC system with actuator disturbance.

Fig. 24

Rotor speed error waveforms under BSC and NN-BSC controlled OWC system with actuator disturbance.

The rotor speed error, shown in Fig. 24, settles faster without transients in the NN-BSC case, especially between 26.4s and 36.4s, whereas PI and BSC consistently shows prominent transients throughout the response. The q-axis rotor flux error, depicted in Fig. 25, demonstrates superior control by NN-BSC as it smoothly settles to zero without any transients. In contrast, PI and BSC shows significant error variations throughout, as seen during 26.4s to 36.4s in the zoomed section. Figure 26 highlights rotor control voltages, indicating that during sudden changes in the MPPT reference, all control methods require substantial efforts to minimize rotor speed and flux errors. Additionally, all controllers need continuous control efforts to counteract actuator disturbances.

Fig. 25

q-axis rotor flux error waveforms under BSC and NN-BSC controlled OWC system with actuator disturbance.

Fig. 26

Control voltage waveforms under BSC and NN-BSC controlled OWC system with actuator disturbance.

Fig. 27

Flow coefficient waveforms under BSC and NN-BSC controlled OWC system with actuator disturbance.

The Wells turbine flow coefficient, shown in Fig. 27, remains consistently below the critical threshold of 0.3 for PI, BSC, and NN-BSC, even under actuator disturbances, maintaining the turbine operational safety. Figures 28 and 29 illustrate the Wells turbine torque and output power, respectively. It shows significant enhancements for all control methods compared to the uncontrolled OWC system, even in the presence of disturbances.

Fig. 28

Wells turbine torque waveforms under BSC and NN-BSC controlled OWC system with actuator disturbance.

Fig. 29

Output power waveforms under BSC and NN-BSC controlled OWC system with actuator disturbance.

Table 2 Time response performance specifications of rotor speed error.

The Table 2 compares the time response performance specifications of rotor speed for three control methods—PI, BSC, and NN-BSC—under two scenarios: $\Delta \left( t \right)=0$ and $\Delta \left( t \right)=10sin\left( {2\pi t} \right)$. Key metrics include maximum peak overshoot and settling time. The NN-BSC demonstrates the best performance, achieving the lowest maximum peak overshoot (0.962488 rad/s for $\Delta \left( t \right)=0$ and 0.965075 rad/s for $\Delta \left( t \right)=10sin\left( {2\pi t} \right)$ and the shortest settling time (0.0323s and 0.0561s, respectively). This highlights its ability to minimize transient errors and stabilize quickly, even under disturbances. The BSC offers moderate improvement over PI, with reduced maximum peak overshoot and faster settling time. However, the PI controller exhibits the highest maximum peak overshoot (2.02206 rad/s for $\Delta \left( t \right)=0$) and longest settling time (8.8658s), reflecting its limitations in managing transient behaviour and achieving rapid stabilization compared to the more advanced methods.

Overall, the results indicate that NN-BSC outperforms conventional PI and BSC when subjected to actuator disturbances, providing superior transient-free control and quicker error settling. The NN-BSC enhances robustness and control precision under disturbance conditions that ensures more reliable and efficient energy capture.

Concluding remarks

An NN-BSC scheme for rotational speed regulation in OWC wave energy systems was designed in this study. By integrating Chebyshev NNs into the BSC framework, this study addresses key limitations of conventional control methods, such as the inability to handle nonlinearities, disturbances, and variations in ocean wave conditions effectively. By offering smoother rotor speed tracking and reducing transient errors, the NN-BSC provides improved control stability, faster convergence, reduced transients and efficient power generation, as validated by numerical simulations. The NN-BSC, particularly under actuator disturbances, demonstrates robustness and adaptability, which makes it a superior alternative to conventional PI and BSC. The simulation results highlight that the NN-BSC maintains the critical operational thresholds of the Wells turbine, enhances the turbine torque and output power levels.

Suggested future scopes of this study are as follows:

• Investigate advanced neural network architectures, such as deep learning, to enhance system adaptability under uncertain sea conditions.

• Conduct experimental validation of the proposed control strategy using a physical OWC prototype to complement simulations.

• Explore advanced nonlinear control schemes like sigmoid PID and intelligent PID controllers for managing nonlinearities and uncertainties.

• Apply advanced optimization algorithms to further refine NN-BSC parameters and achieve globally optimal performance.