Introduction

High entropy alloys (HEAs), also known as multi-principal element alloys (MPEAs) or complex concentrated alloys (CCAs), are solid solution alloys containing five or more elements in equiatomic or near equiatomic proportions (between 5% and 35% atomic concentration). The increase in configurational entropy of mixing elements overcomes the enthalpies of compound formation, inhibiting intermetallic formation, which stabilises the solid solution in a single phase with high configurational entropy1,2.

Cantor alloy (CrMnFeCoNi) was among the first reported MPEA in 2004 that showed exceptional properties in the race of CCAs3. However, Alx(CrFeCoNiCu) with varying Al concentration (x = 0 to 3) was also developed at the same time by Yeh4 and it was after this effort that the name high-entropy alloy (HEA) was coined. Since then, various CCAs/MPEAs/HEAs have emerged due to their exceptional mechanical properties over conventional alloys.

Various refractory HEAs (RHEAs) such as NbMoTaW5, TixNbMoTaW (x = 0, 0.25, 0.5, 0.75, 1)5 VxNbMoTa (x = 0.25, 0.5, 0.75, 1.0)6, Nb40Ti25Al15V10Ta5Hf3W27, NbMoTaW(HfN)x (x = 0, 0.3, 0.7, 1.0)8, MoNbTaVW9, HfNbTaZr9, Re0.1Hf0.25NbTaW0.410 and some 3d transition metal HEAs such as Al10.3Co17Cr7.5Fe9Ni48.6Ti5.8Ta0.6Mo0.8W0.411, Al10.2Co16.9Cr7.4Fe8.9Ni47.9Ti5.8Mo0.9Nb1.2W0.4C0.412 have been developed for high-temperature applications in aerospace, gas turbine, and nuclear power plants. Other MPEAs such as CoCrFeNiTax (x = 0, 0.1, 0.2, 0.3, 0.4, 0.5, and 0.75)13, CoCrFeNiNbx (x = 0, 0.103, 0.155, 0.206, 0.309 and 0.412)14 and CoCrFeNiNbx (x = 0.1, 0.25, 0.5 and 0.8)15 have also shown a remarkable combination of high strength and ductility for their eutectic counterparts such as CoCrFeNiTa0.4 and CrFeCoNiNb0.5 respectively. However, it is noticeable that these alloys are reliant on the use of critical raw materials (CRMs) such as Ta, W, Nb and Hf16. The availability of Hf powder is extremely limited17. Rizzo et al.16 have alluded to the importance of having a flawless supply chain of raw materials to maintain a sustainable circular economy. Thus, the exigency of minimizing the use of CRMs to mitigate the excess of imports and reducing the need for excessive mining to accelerate the transition to net zero became the prime focus of this study.

The classification of CRM is an important distinction in the realization of this research. Accordingly, various CRMs identified in the past and present were tabulated and classified under three categories (see Fig. 1).

Fig. 1
figure 1

The severity scale of materials listed in the category of CRMs by the EU18,19,20,21,22.

Full size image

CRMs that appeared three or more times and remained a current concern were classed as 1st Tier. This includes elements such as Be, Bi, Co, Ga, Ge, Hf, Mg, Nb, Sb, Sc, Si Metal, Ta, V and W which are considered most critical in their usage. The 2nd Tier CRMs include elements such as Al, Cu, He, Li, Mn, Ni, P, Sr, and Ti, which have appeared recently as CRMs for more than once. Materials such as Cr and In are not considered CRMs as they were excluded from the 2023 list of CRMs and therefore are not considered as CRM in this study. An exception was made in the algorithm to include Co and V which are although classed as 1st Tier CRMs were not treated as critical. This is due to the ongoing advances made in the recovery and recycling methods and it is expected that the Co and V will become non-critical over time23,24,25,26.

A description of strategies adopted in recovering and recycling Co and V has been discussed in Section “Data collection using Thermo-Calc 2024a”. Henceforth, we considered Co and V as non-CRM for the current investigation and included them in the database for our current investigation. Accordingly, we report:

  • Preparation of a fresh database reporting Vickers hardness of unary (pure) and binary-based compositions for non-CRM (Al, Cr, Cu, Fe, Ni, Ti, Mo, Mn, Sn, Zn, Zr) and CRM elements (Co and V- treated as non-critical in this study) using Thermo-Calc 2024a property model calculator based on CALPHAD approach. A total of 3,608 instances were recorded and no experimental data was incorporated to keep the database free from experimental uncertainty arising from the manufacturing process.

  • Training and testing of various tree-based regression models: Decision Tree Regressor (DTR), Random Forest Regressor (RFR), AdaBoost Regressor (ABR), Gradient Boost Regressor (GBR), XGBoost Regressor (XGBR) and Extra Tree Regressor (ETR) based on the developed database and their performance evaluation based on various regression metrics such as coefficient of determination (R2_score), mean absolute error (MAE), mean squared error (MSE), root mean squared error (RMSE), and mean absolute percentage error (MAPE) for finding the robust regression model (best predictor) to correctly predict hardness of an unseen instance.

  • Optimisation of the best regression model using metaheuristic optimisation techniques such as Particle Swarm Optimisation (PSO), Genetic Algorithm (GA), Ant Colony Optimisation (ACO), Cuckoo Search Optimisation (CSO) and Whale Optimisation Algorithm (WOA) in search of new multicomponent compositions to generate Reduced-CRM multi-principal element alloys (R-CRM-MPEAs) with target Vickers hardness values. Other optimization algorithms such as Artificial Bees Colony (ABC) and Simulated Annealing (SA) were also optimised for the same objective, but they both failed to generate the desired compositions.

  • The ML-predicted hardness values were benchmarked to the corresponding predictions obtained from the Thermo-Calc calculator to test the robustness of the optimization models and compare the percentage error between ML and Thermo-Calc prediction of hardness value for the same compositions.

  • A thorough evaluation was performed on experimentally synthesized CRM-laden MPEAs from the literature to benchmark the predicted R-CRM-MPEAs compositions generated in this study. This comparison aimed to demonstrate the feasibility of partially or fully replacing CRMs while preserving the hardness of the alloy.

  • As a test case, Vickers hardness of a newly predicted composition (Al6.25Cu18.75Fe25Co25Ni25) developed by our group27,28,29 was measured experimentally and compared with the corresponding Thermo-Calc and ML predicted values successfully which lends credence to the computational prediction.

Methodology

Most recent HEAs developed have been obtained by adjusting the composition percentages or substituting one element from an already established HEA. For example, various research articles built the new composition based on cantor alloy (CoCrFeMnNi) either by replacement of (CrFeCoNiCu30 and TiCrFeCoNi31), variation (CrMnFeCoxNi and CrMnFeCoNix with x = 0–232), or by addition (CrMnFeCoNiCu3, CrMnFeCoNiAlx33) of an element2. Additionally, reduction-based alloys have spawned lower-order systems such as binaries, ternaries and quaternary alloys- termed low and medium-entropy alloys2. Ten binaries, ten ternaries and five quaternaries’ compositions can be made from a cantor alloy. Among two of the ten possible binaries (FeNi and CoNi), five of the ten possible ternaries (CoFeNi, CrFeNi, FeMnNi, CoCrNi and CoMnNi), and three of the five possible quaternary (CoCrFeNi, CoFeMnNi and CoCrMnNi) are single phase FCC solid solution34,35. Interestingly, equiatomic CoCrNi medium entropy alloy shows better mechanical properties than the CoCrFeMnNi HEA, which demonstrates that configurational entropy (increasing the number of elements in an alloy) does not necessarily improve the mechanical property of an alloy36. Moreover, numerous research articles employed various state-of-the-art ML strategies in designing and developing novel MPEAs37,38,39,40.

Apart from these compositions, various MPEAs have been developed by utilising elements such as Al, Cu, Cr, Ti, V, W, Ta, Hf, Nb, Mo, Zn, Zr, Si extensively, while certain precious metal HEAs incorporate elements such as Ag, Pt, Au, Ru, Rh, Pd. However, many of these elements (Hf, Nb, Ta, Pt, Pd, Ru, Rh, W) have been marked as critical and have reached an alarming stage41. Consequently, when considering MPEAs comprised solely of non-CRMs elements, the available experimental data in the literature is scarce which limits the training and testing of the machine learning models. Therefore, we extracted a fresh database using Thermo-Calc 2024a software, which is based on a CALculation of PHAse Diagram (CALPHAD) approach. This database contains Vickers hardness values for unary (pure) and binary compositions of materials extracted from Thermo-Calc software using the TCHEA7 database. The work aimed to discover R-CRM-MPEAs compositions (from unary and binary composition databases) with mechanical properties comparable to CRM-laden MPEA compositions.

In recent years, CALPHAD has played a crucial role in designing transition alloys from a completely serendipitous process to a well-established method seeking a thermodynamic rationale36. CALPHAD has been extensively utilised in literature for phase prediction and rapid screening of potential alloys by estimating their compositional and microstructural properties which are validated experimentally36,42. However, no study can be seen in the literature with a focus on mechanical property prediction solely from the CALPHAD method. This is because predicting mechanical properties is not as straightforward as phase prediction. Phase prediction relies solely on the Gibbs free energy for lower-order compositions. For more complex or higher-order compositions, phases are predicted by extrapolating Gibbs free energy from the lower-order systems43. Unlike phase prediction, mechanical property prediction requires rigorous research into the manufacturing (processing) routes, processing parameters, post-processing treatments, testing parameters and extensive knowledge or expertise in the field. Thermo-Calc 2024a offers a property model calculator, which allows the prediction of yield strength and hardness of a composition based on the phases present at a particular temperature44.

Currently, Thermo-Calc does not account for factors such as processing history, parameters, time and other crucial variables for accurately predicting mechanical properties under specific experimental conditions. However, its hardness prediction tool still provides a solid foundation for making informed estimations. To assess the discrepancy between experimentally obtained mechanical properties and Thermo-Calc predictions, we extracted the Vickers hardness values of various alloys, including medium- and high-entropy alloys, from experimental literature across different processing methods (casting, additive manufacturing, powder metallurgy, rolling, and severe plastic deformation techniques such as High-Pressure Torsion (HPT) and Equal Channel Angular Pressing (ECAP)). These were then compared to Thermo-Calc predictions, as shown in Fig. 2. A detailed comparison is provided in tabular form in supplementary Table 1s. Thermo-Calc predictions were seen to be insensitive to the strain rate applied during the manufacturing process which can lead to different hardness values based on the manufacturing process. For a few compositions, the CALPHAD hardness value matched the experimental values, however, it is difficult to generalize which experiments led to the values that are closest to the CALPHAD predictions. For instance, the hardness values obtained from CALPHAD for CoCrNi match with the ECAP processed (for 3 passes) and post-deformation annealed (at 700 °C) samples. As for the FeMnNi medium entropy alloy, its CALPHAD value was closest to the alloy processed via rolling (90% rolled) and then annealed at 1073 K for 1 h (see Fig. 2). Thus, generalizing which experimental processing route leads to hardness values that closely match those predicted by CALPHAD is arduous.

Fig. 2
figure 2

Vickers hardness comparison for selective MPEAs based on the experimental results obtained from various manufacturing methods (black dots) vs. CALPHAD predicted values (in red dots).

Full size image

Data collection using Thermo-Calc 2024a

Despite cobalt’s inclusion in the 1st tier CRM category, its production is not a concern. The Democratic Republic of Congo (DRC) is the world’s largest producer of Co, with its production projected to increase from 11,000 MT in the year 2000 to 98,000 MT by 202045. However, the market of Co presents a considerable risk due to supply-chain complexities. China, which has limited domestic cobalt production has significantly increased its imports from the Democratic Republic of the Congo (DRC) and controls cobalt processing in the region through various Chinese firms. This initiative by China was aimed at securing a competitive advantage in regulating the electric vehicle market.

A potential remedy here would be to recover Co from waste batteries. Suriyanarayanan et al.24 recently introduced an innovative and efficient approach for Co extraction with an extraction efficiency > 97%, using a nonionic deep eutectic solvent (ni-DES) comprised of N-methylurea and acetamide. Zhang et al.25 developed a supercritical fluid extraction process using supercritical CO2 solvent with tributyl phosphate–nitric acid and hydrogen peroxide adduct to recover Li, Co, Mn and Ni with a 90% extraction efficiency. Moreover, Yang et al.26 in 2024 estimated the sales volume of new energy passenger vehicles (NEPV) from 2023 to 2035 based on the historical NEPV sales data from 2013 to 2022. Utilizing Weibull distribution to analyze different sales scenarios, they estimated the potential of recycling Co for maintaining a balance between supply and demand. Their analysis predicted the peak potential of recycling of Co to be about 0.167 MT with an economic value ranging from 49.01 billion to 94.60 billion RMB in 2035. Consequently, they concluded that recycling Co is necessary to alleviate the supply risk pressure and take Co off of the CRM list.

Similarly, Petranikova et al.23 summarized the efforts in the recovery of Vanadium by selecting more sustainable technologies with lower generation of harmful by-products. They highlighted the importance of combining hydrometallurgical and pyrometallurgical approaches to increase the material recovery rates. With ongoing strategic advancements in recovery and recycling, Cobalt (Co) and Vanadium (V) are expected to transition from their current status as CRMs to non-CRMs. As these management methods evolve, the associated risks related to these materials are anticipated to gradually decrease.

In this context, a large dataset of Vickers hardness values for unary and binary element-based compositions using the property model calculator in Thermo-Calc 2024a (Version 2024.1.132110-55) was compiled by focusing on elements Al, Cr, Cu, Co, Fe, Ni, Ti, V, Mo, Mn, Sn, Zn and Zr.

While extracting the data, it was observed that the property predictor module relies on certain assumptions. Those assumptions are: (i) the material is homogeneous i.e., with no imperfections or defects (ii) it considers only local equilibrium and neglects long-range diffusion. Therefore, to calculate the mechanical properties, it uses simplified theoretical models and databases (containing thermodynamic and kinetic data), which do not capture the complexities related to processing (as-cast, heat-treated, homogenized, or severely deformed samples) and testing conditions (the amount of load and time required in hardness testing). Thermo-Calc predictions can therefore be expected to carry a certain percentage of error when compared to the experimentally synthesized specimen based on its processing history.

For determining the hardness value of a particular composition using Thermo-Calc, the phases present in the system were first identified using their corresponding phase diagram observed at a range of temperatures, computed using an equilibrium calculator. Based on the available features within the software, by considering the system size of 1 mol at a temperature of 300 K and 1 bar pressure, the hardness value was estimated. In some cases, the identified phases in the phase diagram could not be marked while calculating Vickers hardness due to their unavailability in the property model calculator, highlighting one of the several limitations of Thermo-Calc 2024a that needs to be improved.

Consequently, a total of 3,608 instances of different compositions were extracted. This database contains only compositional information and the hardness value of each instance. The highest hardness value obtained was in the range of 400–405 HV. Some of the interesting compositions with higher Vickers hardness values in the database were Cr42Ti58, Ti74Zn26, Ni24Ti76, Cu16Ti84 with a hardness value of 405HV, 404 HV, 403 HV and 402 HV respectively. The complete dataset is provided as supplementary data. It’s worth noting that no experimental data was considered in this database to avoid mixing synthetic data into the prediction model.

Data sorting

The database was first checked to avoid repetition. The screened dataset was divided into 80:20 (2,886 and 722 instances) ratio for training, evaluation and verification.

Tree-based ML model evaluation

Various tree-based regression algorithms such as Decision Tree Regressor (DTR), Random Forest Regressor (RFR), AdaBoost Regressor (ABR), Gradient Boost Regressor (GBR), XGBoost Regressor (XGBR) and Extra Tree Regressor (ETR) were employed. A detailed description of each algorithm with its flowchart is provided in Section “Methodology” as Supplementary information.

The performance of a machine learning (ML) model is influenced by hyperparameters, which are adjustable settings that govern various aspects of the model’s learning process, such as complexity, regularisation, and convergence. Examples of hyperparameters include the maximum depth of trees in decision tree models, the number of trees in ensemble models like Random Forest and Gradient Boost, as well as the number of hidden layers in neural networks and the penalty term used in support vector machines. Proper tuning of these hyperparameters is essential for achieving an optimal balance between model accuracy and generalisation.

To optimize the hyperparameters of the selected algorithms, Random Search CV was employed. Unlike Grid Search, which systematically evaluates all possible combinations of hyperparameter values, Random Search, samples a fixed number of hyperparameter combinations from a defined distribution. This approach significantly reduces computational costs while still allowing the exploration of a diverse range of values, making it particularly advantageous for complex models with many hyperparameters.

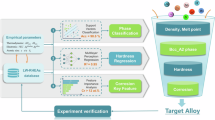
Each hyperparameter configuration was evaluated using a 5-fold cross-validation approach, where the dataset was divided into five subsets. Each subset was used once as a validation set while the others served as the training set, ensuring a thorough and unbiased assessment of the model’s generalization capabilities. The coefficient of determination (R² score), mean absolute error (MAE), root mean squared error (RMSE), and mean absolute percentage error (MAPE), as detailed in Eq. 1 to 4, were used as performance indicators to quantify the difference between predicted values and observed outcomes. The optimized hyperparameters for each regressor model are listed in Table 1. This methodology helped in identifying the best-performing hyperparameter settings, ensuring that the model would perform consistently across different data splits. The working principle of this investigation is illustrated in Fig. 3.

$${\text{R}}^{2} \_{\text{Score}} = \frac{{\sum {\left( {y_{i} - \hat{y}_{i} } \right)^{2} } }}{{\sum {\left( {y_{i} - \mu } \right)^{2} } }}$$
(1)
$${\text{MAPE = }} = \frac{1}{n}\sum\nolimits_{{i = 1}}^{n} {\frac{{\left| {\left( {y_{i} - \hat{y}_{i} } \right)} \right|}}{{\left( {y_{i} } \right)}}}$$
(2)
$${\text{MAE}} = \frac{1}{n}\sum\nolimits_{{i = 1}}^{n} {|y_{i} - \hat{y}_{i} |}$$
(3)
$${\text{RMSE}} = \sqrt {\frac{1}{n}\sum\nolimits_{{i = 1}}^{n} {\left( {y_{i} - \hat{y}_{i} } \right)^{2} } }$$
(4)
Table 1 Summary of the optimized hyperparameters for the chosen ML algorithms.
Full size table
Fig. 3
figure 3

Workflow of the current study: (a). data collection and processing; (b). training, testing and evaluation of tree-based models; (c). classification of optimization models (full-length image is provided in Section “Optimisation techniques”) and selection of best optimization model (models in red font were selected for this study) for obtaining our objective; (d). generated novel compositions; (e). comparison of the predicted hardness with Thermo-Calc ones for validation; hardness of novel HEA (Al6.25Cu18.75Co25Fe25Ni25) prepared in the earlier study was measured and compared with Thermo-Calc one for reinforcing the present study.

Full size image
Fig. 4
figure 4

(a) Performance of various tree-based ML models: R2_score (in light orange), MAPE (in green), (b) actual vs. predicted hardness of test data for the ETR model.

Full size image

The results obtained from various algorithms are presented in Fig. 4a. The Extra Trees Regressor (ETR) demonstrated a superior performance and achieved an R² score of 0.82 and Mean Absolute Percentage Error (MAPE) of 0.17, utilizing optimized hyperparameters determined through Random Search Cross-Validation (see the scatter plot in Fig. 4b). It is important to note that while several studies report even higher R² scores, those models typically incorporate numerous descriptors, such as atomic size difference (δ), electronegativity difference (∆χ), valence electron concentration (VEC), mixing enthalpy (∆Hmix), mixing entropy (∆Smix), melting temperature (∆Tm), Young’s modulus (E), shear modulus (G), differences in shear modulus (δG), lattice distortion energy (µ), the Peierls-Nabarro factor (F), and other parameters (Ω-parameter, ϕ-parameter, and γ-parameter), which together enhance performance metrics. In contrast, our approach relies solely on compositional information and hardness values, achieving an R² score of 0.82. This underscores the model’s robustness to predict hardness values without requiring any additional descriptors.

To explore novel multi-component compositions, we employed a metaheuristic optimization strategy aimed at generating alloys with superior hardness compared to those in the training and testing datasets, which consisted exclusively of unary and binary compositions. The optimization techniques that facilitate the exploration of more complex and high-performance MPEAs are detailed in the subsequent sections. The hardness values of the newly optimized MPEAs were then compared against CALPHAD-based predictions, and these findings are discussed comprehensively in Section “Results and discussions”.

Optimisation techniques

The classification of various optimisation models followed in this work is shown in Fig. 3c with red fonts highlighting the algorithms used in this investigation. Traditional optimisation techniques, which include general methods and non-general or specified methods tailored for specific types of problems, have certain limitations such as the requirement of the objective function to be differentiable and lack of ability to obtain a globally optimum solution. Some of the popular traditional optimisation techniques such as Newton Raphson, Successive Quadratic Programming algorithm, Steepest Descent Algorithm, Stochastic Newton optimisation method and Sequential Unconstrained Minimization technique46,47 are well known. Recently, some non-traditional methods of optimisation popularly known as meta-heuristic optimisation techniques have gained increasing popularity in solving complex problems. The term metaheuristic combines meta and heuristic, both originated from Greek. Meta symbolizes higher or beyond, and heuristic signifies intelligent guesswork based on past experience or intuitive solution of a problem. Therefore, metaheuristic optimisation can be considered as something beyond intuitive, combined with certain mathematical rules or higher-level frameworks. It can broadly be classified into two categories: single trajectory-based and population-based optimisation. Single-trajectory based optimisation (such as Hill Climbing, Gradient Descent, Tabu Search, Random Search etc.) starts with a single solution at each iteration, and the current solution is replaced by another best solution found in the neighbourhood for that iteration. Contrarily, population-based optimisation techniques are inspired by natural-selection and biological evolution, where a set of solutions are randomly initialized and updated through an iterative process. Genetic algorithm, Differential evolution and others belong to evolutionary optimisation techniques, while Particle swarm optimisation, Ant colony optimisation, Cuckoo search and others are examples of swarm-intelligence-based optimisation techniques47,48. These techniques are exploration-and-exploitation oriented, which introduces diversification in the search space, resulting in the attainment of global optimum solutions by avoiding local optimum solutions for complex real-world problem49.

Among all available various nature-inspired metaheuristic optimisation techniques, genetic algorithms, particle swarm optimisation, Cuckoo search and a few others have been proven to successfully solve a wide range of complex real-world problems. However, some of the recently introduced metaheuristic optimisation techniques such as Ant colony optimisation, Artificial Bee Colony optimisation, Spotted Hyena optimisation, whale optimisation need substantiation for their convergence. Rao50 in his book chapter has highlighted that the fundamental idea of these methods is the same while naming them differently. In this work, we compared which optimisation technique works best for our ETR model to discover new multicomponent compositions from the unexplored compositional space of nearly 8,008 types (see Fig. 5) as per combination theory while only ternary to decenary-based compositions were considered for 13 elements. Figure 6 describes five metaheuristic optimization techniques used in this study. A detailed description of each optimization technique with its working principle is elaborated in section 3s of the supplementary information.

Fig. 5
figure 5

Total possible compositions from selected 13 elements.

Full size image
Fig. 6
figure 6

Various metaheuristic optimisation models applied in this work: (1). Genetic Algorithm (GA), (2). Particle Swarm Optimisation (PSO), (3). Cuckoo Search Optimisation (CSO), (4). Whale Optimisation Algorithm (WOA) (5). Ant Colony Optimisation (ACO).

Full size image

Results and discussions

Evaluation of several reduced-CRM-MPEAs

Optimisation function was set up to obtain novel multi-principal element alloys with Vickers hardness > 400 HV, by enforcing composition constraint such that the sum of 3, 4, 5, 6, 7, 8, 9, or 10 elements become 100, while keeping the proportion of each element equal or near equal to generate multicomponent compositions.

Among all the optimisation models, cuckoo search optimisation (CSO) provided predictions near the Thermo-Calc predictions. Recent literature suggests that the cuckoo search optimisation (CSO) performs better than PSO, GA, ACO, ABC and WOA51,52,53,54. Gandomi et al.51 provided an extensive comparison and concluded that CSO performs better than GA and PSO, as GA requires a higher number of iterations and its implementation is computationally expensive53. On the other hand, PSO requires less computational effort but considerable execution time to find a solution from a large space for a complex optimisation problem. Civicioglu and Desdo8 suggested that CSO provides more robust results than PSO and ABC. Bhargava et al.55 showed that CSO offers a reliable method for solving thermodynamic calculations for complex phase equilibrium applications.

The ternary to decenary multicomponent compositions generated by the various algorithms, including GA, PSO, WOA, ACO and CSO, are presented in Tables 2, 3, 4, 5 and 6, respectively. These compositions were subsequently validated using the property model calculator in Thermo-Calc (TC) software. By comparing the hardness values of the newly generated compositions to those predicted by TC, it is evident that the CSO algorithm produced the most reliable multicomponent compositions, with a prediction error of less than ± 20%. Furthermore, compositions generated by CSO exhibited superior hardness compared to those derived from other optimization methods.

For instance, CSO successfully generated compositions such as Cu4Fe4Ni4Zn4Zr4Co10Cr10V20Ti20Mo20 (10 elements), Zn5Cr10Zr10Mo25Ti25V25 (6 elements), Zr6.25Zn18.75Ti25V25Mo25 (5 elements), Ti0.01111NiFe0.4Cu0.4 (4 elements), which achieved hardness values of 477 HV, 443 HV, 434 HV and 488 HV respectively. In contrast, while GA, PSO, and WOA demonstrated consistency in their predictions for several compositions, they often failed to accurately predict compositions with higher hardness values. Notably, these algorithms became increasingly erroneous with the inclusion of more elements in the alloy design.

ACO method proved to be reliable for ternary and quaternary compositions, yielding relatively low prediction errors. However, as the complexity escalated from quinary to decenary compositions, the percentage error substantially increased, and ACO was unable to generate viable compositions with more than seven elements.

As a result, CSO emerged as the most reliable algorithm among those tested, capable of generating multicomponent compositions with reduced CRM content and enhanced hardness values. Figure 7 illustrates the hardness values generated by each algorithm in comparison to those evaluated by Thermo-Calc for ternary to decenary compositions, providing a comprehensive overview of algorithm performance across varying levels of compositional complexity.

Table 2 Compositions generated using GA optimisation.
Full size table
Table 3 Compositions generated using PSO optimisation.
Full size table
Table 4 Compositions generated using WOA optimisation.
Full size table
Table 5 Compositions generated using ACO optimisation.
Full size table
Table 6 Compositions generated using CSO optimisation.
Full size table
Fig. 7
figure 7

Comparison of hardness value for newly generated MPEA compositions compared for ML and Thermo-Calc predictions using various techniques: (a) Genetic algorithm (GA), (b) Particle swarm optimisation (PSO), (c) Whale optimization (WOA), (d) Ant colony optimization (ACO), (e) Cuckoo search optimization (CSO).

Full size image

We further compared the hardness values of the newly generated R-CRM-MPEAs with those of CRM-containing MPEAs reported in the literature to assess the feasibility of partially substituting CRMs. Figure 8 provides a comparison of the mechanical properties between experimentally synthesised CRM-laden alloys reported in the literature and the newly predicted R-CRM-MPEAs in this work.

Fig. 8
figure 8

Comparison of R-CRM-MPEA with CRM-laden MPEAs to demonstrate the feasibility of partially substituting CRMs with readily available elements while attaining comparable mechanical properties.

Full size image

The results indicate that the proposed approach can yield comparable hardness. For example, CoCrFeNb0.309Ni containing two 1st-Tier CRMs exhibits a hardness of 480 HV, whereas the newly predicted composition, Ti0.0111NiFe0.4Cu0.4, achieves a superior hardness of 488 HV without including any 1st-Tier CRMs. The computational approach employed using ML in this work has great potential to design R-CRM-MPEA compositions. This approach can be leveraged to eliminate the use of CRMs in diverse applications such as catalysis, semiconductors, transportation and other carbon-intensive sectors.

Benchmarking of the newly synthesised alloy Al6.25Cu18.75Fe25Co25Ni25

To test our predictions, a random and a new FCC phase alloy, Al6.25Cu18.75Fe25Co25Ni2527,28,29 was selected for experimental validation. Vickers hardness testing was performed utilising a Wilson hardness testing apparatus, with a load of 0.1 kgf. The Vickers hardness value was determined by averaging the measurements from nine indents on a polished surface. The experimentally measured Vickers hardness of Al6.25Cu18.75Fe25Co25Ni25 was subsequently compared with the hardness values evaluated by Thermo-Calc (TC) and our ML model (refer to Table 7). It was observed that both the TC-evaluated and ML-predicted hardness values were in strong agreement with the experimentally measured hardness with an error of less than 20%.

Table 7 Comparison of experimentally measured hardness with TC and ML predicted hardness.
Full size table

While numerous studies in the literature on MPEAs have used machine learning, a majority of these remain concentrated on developing algorithms for phase classification56,57,58 or predicting mechanical properties, such as hardness, yield strength, or elastic modulus59,60,61,62,63. Relatively few investigations have aimed to generate or optimize novel MPEA compositions. Most of these efforts have concentrated on achieving high hardness values which differs from the focus of this investigation where the main objective was to develop substitute alloys to eliminate the use of CRMs and hardness was used as an indicator to demonstrate that comparable properties can still be obtained.

Ren et al.64 used a dataset of 205 HEA samples featuring 19 characteristics commonly employed in HEA property prediction. They implemented a tree-based machine learning model to predict hardness and integrated it with Particle Swarm Optimization (PSO) for component optimization. Due to the limited availability of real experimental data, they resorted to synthetic data through random oversampling to improve the performance of their Component Optimization Model (COM), which raises concerns about the reliability of their prediction. Their database primarily included Al, Co, Cr, Cu, Fe and Ni.

Similarly, Wen et al.65 focussed on the same Al-Co-Cr-Cu-Fe-Ni HEA family and its subgroups but worked with a limited dataset of only 155 samples. They proposed a property-oriented materials design strategy that combined machine learning with the Design of Experiments (DOE) to discover alloys with high hardness within this HEA system. Their resulting alloy exhibited a hardness approximately 10% higher than the best value found in the original training set.

In contrast, Yang et al.66 used a dataset of 370 HEAs, including compositions such as Al-Co-Cr-Cu-Fe-Ni, Al-Co-Cr-Fe-Mn-Ni, and their derivatives, along with vanadium-containing alloys, which are recognised for their high hardness. They applied techniques such as Inverse Projection (IP) and High-Throughput Screening (HTS) and encountered substantial prediction errors of up to 58% due to the risks associated with extrapolation beyond the boundaries of the training dataset and insufficient data diversity.

To effectively navigate the design space for alloys with high hardness, it is essential to enrich the training datasets with refractory alloys, given their inherent high-temperature stability and robust mechanical properties. However, a major impediment to the reliable application of ML in materials science continues to be the scarcity of relevant data, particularly for HEAs/MPEAs. Roy et al.67 addressed this issue by employing a generative adversarial network (GAN) to explore an 18-dimensional design space involving Co-Fe-Ni-Si-Al-Cr-Mo-Ti-Nb-V-Zr-Mn-Cu-Sn-Ta-Hf-W-Zn MPEAs using a limited dataset of 241 alloys. They successfully designed two new MPEAs with hardness values exceeding 941 HV.

In contrast to these studies, our research emphasizes sustainable materials design by assessing whether compositions with reduced or no CRMs can achieve competitive hardness values. This objective addresses a critical gap in the current alloy design landscape—the need for environmentally sustainable materials that minimize reliance on CRMs while maintaining desirable mechanical properties. This approach not only advances sustainability goals but also enhances supply chain resilience, representing a significant step forward in alloy innovation.

Conclusion

This study represents a significant effort to support Net-Zero initiatives by developing new compositions with reduced critical raw materials (CRMs). The research relies on a computational framework that involves sourcing a dataset of Vickers hardness values for unary (pure) and binary material compositions from Thermo-Calc 2024a and the TCHEA7 database. This dataset was used to build machine learning models to identify complex compositions of alloys with reduced-CRM without negating the mechanical properties.

Among all regression models, the Extra Trees Regressor (ETR) demonstrated superior performance, achieving an R² score of 0.82 and a MAPE of 0.17 for the test data. Various metaheuristic optimization techniques were subsequently employed to inversely predict novel multicomponent alloy compositions free of critical raw materials (CRMs) but with hardness comparable to CRM-containing multi-principal element alloys (MPEAs). Of all the optimization models, Cuckoo Search Optimization (CSO) demonstrated a high level of concordance with Thermo-Calc predictions, with an average deviation of ± 20%. A literature-sourced CRM-laden composition, CoCrFeNb0.309Ni, containing two 1st -Tier CRMs (Co and Nb), showed a hardness value of 480 HV and a new alloy was generated using a machine learning method namely, Ti0.01111NiFe0.4Cu0.4, with a hardness of 488 HV that showed great opportunity to eliminate CRMs in developing MPEAs.

The validity of this study was reinforced by comparing computational predictions—derived from our machine learning methodology and Thermo-Calc evaluations—with the experimentally measured Vickers hardness of a test alloy Al6.25Cu18.75Fe25Co25Ni25, which contains a single 1st-Tier CRM, cobalt (Co). Therefore, this investigation offers valuable insights into the potential for designing novel MPEAs with reduced or even no CRMs, significantly contributing to sustainable materials innovation to support Net Zero in the metal sector. Future research will focus on further experimental validation to corroborate the findings for the newly generated compositions.