Introduction

Caenorhabditis elegans (C. elegans) is a soil-dwelling worm with a transparent body, a short life cycle, rapid reproduction, and a relatively simple nervous system structure1. With these characteristics, C. elegans is considered one of the most important model organisms. Therefore, C. elegans is widely used in many fields, including developmental biology2, neuroscience3, aging4 and lifespan research5, and drug screening6. It is currently known that many potential factors, such as genes, the nervous system, age, and environmental pollutants, can affect the motor behavior of freely moving C. elegans7, and the motor behavior of C. elegans has been observed to reflect a number of different behaviors, including feeding behavior8, escape behavior9, and chemotaxis behavior10. In order to obtain objective and accurate data on the movement behavior of C. elegans, researchers have developed various C. elegans tracking algorithms11.

The current C. elegans tracking algorithms can be classified into two categories: computer vision methods and end to end methods. Computer vision methods consist of intra-trajectory method and inter-trajectory method12. Among them, the intra-trajectory method outputs a single-worm trajectory based on the worm detector, and the inter-trajectory method outputs the optimal solution for multiple-worm trajectory based on the correlation of the single-worm trajectory. However, due to the considerable degree of similarity between individual worms, recognition errors caused by collisions between bodies represent a major challenge for worm tracking algorithms13. Figure 1 shows the several typical C. elegans tracking algorithms and their classification. As shown in the section A of Fig. 1, the model-based C. elegans tracking method was initially proposed as an inter-trajectory approach for detecting worm using morphological14 or probabilistic algorithm15. The detection response is fitted to a variety of worm models, including plane models16,17, motion models18, articulated models15,19, and deformable models20,21, and combined with recursive Bayesian filtering methods to obtain the worm tracking trajectory. However, some of these methods do not consider collisions18, while the rest require the construction of an accurate worm model15,16,17,21,22, which leads to high computational costs, especially when there are a large number of worms. In order to reduce the calculation time, the Multi-Worm Tracker (MWT) was proposed to achieve high-throughput worm tracking, as shown in section B of Fig. 123. As one of the most popular intra-trajectory methods, it detects worm responses through morphological processing and directly correlates responses between frames based on the appearance and position features of the worm, which also enables online tracking. However, while MWT is capable of identifying instances of worm collisions, the identity of the worm is lost following the collision, resulting in the output of MWT comprising a significant number of trajectory segments24.

The inter-trajectory method has been proposed to improve the output results of MWT. The network method based on dynamic programming integrates the trajectory segments generated by MWT into complete tracks, in which the trajectory of collision worms is processed by trimming and merging, as shown in section C of Fig. 124. However, the more accurate intra-track method obviously produces better results than the trimmed results. Subsequently, the Multi-animal Tracker (MAT)25, which is also a high-throughput tracker, and it based on machine learning methods, attempts to obtain the collision trajectory of the worm within the trajectory through the Kalman filter method, as shown in section B of Fig. 1. Similarly, end-to-end methods have also been proposed for collision worm tracking26,27,28,29, such as fully convolutional neural network and transformer neural network, which can effectively segment colliding worms in videos, as shown in section D of Fig. 1. However, learning-based worm tracking methods require a significant amount of labeling and training to achieve optimal results, which can be costly in terms of computational resources and hardware requirements. Furthermore, the operational logic of learning-based methods is challenging to elucidate, which impedes the ability of biological researchers to comprehend and hinders the adoption of this method on a broader scale. In conclusion, our objective is to design a collision C. elegans tracking intra-trajectory method with low computational cost, and the method should be more easily understood for generalization to more C. elegans laboratories or coupling to worm tracking algorithms that are unable to handle collisions.

In this paper, an improved particle filter method combined with a cultural algorithm are proposed for collision C. elegans tracking. Among them, the particle filter improved by the sine cosine algorithm (SCA) can continuously track the C. elegans, while the cultural algorithm can identify the target C. elegans after collides. Benefiting from the characteristics of particle filtering, an accurate C. elegans model is not required, which results in lower computational costs. We believe that this method offers a novel, friendly and convenient solution for tracking of collision C. elegans.

Fig. 1
figure 1

Diagram of typical C. elegans tracking methods and their classification. Among them, section A is model-based worm tracking methods, section B is high-throughput worm tracking methods, section C is an inter-trajectory worm tracking method, and section D is end-to-end tracking methods.

Full size image

Methods

The strain and culture conditions of C. elegans

The strain of C. elegans involved in this study is wild-type N2 and RB1579. The RB1579 strain carries a mutation in the sptl-3 gene, which encodes a protein involved in the biosynthesis of sphingolipids, in particular ceramide and sphingomyelin. The sptl-3 has serine C-palmitoyltransferase activity and is a key component of the serine C-palmitoyltransferase complex, which plays a key role in sphingolipid metabolism. In terms of locomotion, during the L4 stage, the locomotion ability of RB1579 is significantly lower than that of the wild type, which is manifested by the mutant crawling more slowly, at about 40% of the speed of the wild type. In terms of development, at the L4 stage, the body length of the mutant was significantly larger than that of the wild type. Therefore, the wild type and the RB1579 mutant are selected as experimental objects to evaluate the performance of the proposed method in worms with different locomotor abilities. The worm eggs were placed in agar petri dishes that had been coated with E. coli OP50. In order to ensure the consistency of experimental conditions, the temperature of the incubator was maintained at 20 degrees Celsius. The images of the worms were collected at 12, 24, 36, 48, 60, and 72 h after hatching, corresponding to four larval stages (L1, L2, L3, L4) and two adult stages young adult (YA) and day 1 adult (D1), respectively.

C. elegans image acquisition system

A 1.6-megapixel complementary metal oxide semiconductor camera was selected, which has a pixel size of 3.45 μm * 3.45 μm, a resolution of 1440*1080, and a maximum frame of 65.2 per second. An industrial lens with a focal length of 35 mm was chosen for imaging, which has an aperture size (F#) range of 4–16 for adapting to live variations. The lens and the camera are connected via C-mount. The working distance is set to 233 mm, with an area of 22.9 mm * 17.3 mm of the petri dish being captured. A 65 mm * 65 mm white Light Emitting Diode light source is employed as the illumination source, and the backlight illumination technology ensures uniform and stable illumination. During the experiment, the researchers took the petri dish out of the incubator, and then placed it in the image acquisition system for photography. Under this set of conditions, a C. elegans with a body length of 1 mm and a width of 0.15 mm is presented in an image with an area of 62 pixels * 9 pixels.

Improved particle filter tracker with sine cosine algorithm

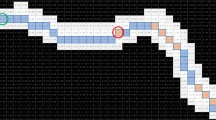
Particle filter, also known as sequence importance sampling (SIS), is a Monte Carlo method (MC) that represents probability density function (PDF) through \(\:N\) particles \(\:\left\{{x}_{t}^{i},{w}_{t}^{i}\right\}\)30. Figure 2 shows a schematic diagram of the traditional particle filter tracking method applied to a worm. The white outline is the worm, and the yellow border is the bounding box of the worm. Particle filter involves particle \(\:{x}_{t}^{i}\) generate, particle update, weight \(\:{w}_{t}^{i}\) calculate and resample. First, a target point is selected, as indicated by the green circle in Fig. 2a. The features of the target point are extracted, and then particles \(\:{x}_{t}^{i}\) are evenly generated within the bounding box of the worm. At this time, each particle has an equal weight and the sum is 1. Then, the position of the particles is updated by the pre-set speed of the worm, as shown in the cross symbols in Fig. 2b. The weight of each particle \(\:{w}_{t}^{i}\) can be obtained by comparing it with the features of the target point. Since the target point is located within the worm outline, the weight of the particles within the worm outline will be much greater than those in the background, as indicated by the red and gray crosses in Fig. 2b respectively. Finally, resampling is performed based on the weight of the particles, and particles with high weights are copied, which means that particles will accumulate within the worm contour as the iteration progresses, as shown in Fig. 2c. The calculation process of particle filter is shown in the supplementary document. However, the resampling step can lead to a concentration of weight on a single particle, which is known as the sample impoverishment problem31. To address this challenge, the SCA was introduced to improve the particle filter32.

Fig. 2
figure 2

Flow chart of particle filter tracking C. elegans. Among them, blue area indicates the background, white area indicates the worm blob, the yellow rectangle indicates the bounding box of the worm, the red and gray cross markers indicate the high-weight and low-weight particles, and the green marker indicates the centroid of the worm.

Full size image

The SCA is a swarm intelligence optimization algorithm that explores solution space by simulating triangular functions, thereby enabling the resolution of complex optimization problems32. In this research, SCA is used before the resampling stage to increase the number of high weight particles. The principle of the SCA algorithm is shown in Fig. 3. The green circle represents the target point, and the red cross symbol represents a particle. The particles move randomly according to the parameters, as detailed in the supplementary file. When the particle moves into the white area, it moves closer to the target point, and if the particle moves into the yellow area, it moves away from the target point. The SCA algorithm can improve the diversity of particles, which can avoid the problem of sample impoverishment.

Fig. 3
figure 3

Flow chart of SCA applied on particles. Among them, the green circle is the target point, the red cross is the particle point, the white area is the area close to the target point, and the yellow area is the area away from the target point. The particle searches for the target point through sine or cosine motion.

Full size image

In contrast to the Trigonometric Particle Filter previously proposed33, the SCA algorithm utilized in this study features a redesigned workflow for particle filter. In this research, the SCA algorithm was executed on four occasions prior to resampling, and all particles were retained for the cultural algorithm screening, which further augmented the diversity of the particles.

Cultural algorithm

The cultural algorithm is a knowledge-based double-layer evolution system34, and the principle of cultural algorithm applied on particle filtering is shown in Fig. 4. The yellow area is the particle space, where particles are generated, and the blue area is the belief space, where knowledge is stored. The Select function is used to take the top particles from the particle population to generate new particles, which corresponds to the resampling process of particle filter, and the Objective function is used to evaluate the weight of the particles. The individual experience of the top particle is transferred to the belief space through the Accept function, and population experience is formed according to certain rules. The population experience adjusts the rules for particle generation through the Influence function.

In this research, the blob of the C. elegans is used as the situational knowledge of the belief space, which allows the algorithm to find the correct C. elegans after a collision. Furthermore, in each frame, the top 20 particles with the highest weights are extracted into the belief space, and a feature range are extracted as the normative knowledge. The particles generated by SCA are filtered according to the feature range, and the particles within the feature range are retained as the input particles for the resampling step. Wherein, the top 20 particles extracted in each frame have the gray-scale features that are closest to the target point, and these features form a gray-scale range that continues to iterate as the number of frames increases. When the worm moves to a background with uneven brightness, the particle selection can be guided by the normative knowledge formed. This method reduces the influence of illumination change areas in the Petri dish, thereby enhancing the robustness of the tracking algorithm.

Fig. 4
figure 4

Flow chart of the cultural algorithm for particle filter. The yellow area is the particle space, and the blue area is the belief space. New particles are constantly generated in the particle space through the Select and Objective functions. The characteristics of the particles are accepted by the belief space to form situational knowledge and normative knowledge. This knowledge is used to influence particle generation and determine the correct worm.

Full size image

Proposed tracking method

The process of tracking collision worm is illustrated in Fig. 5, while a physical diagram is presented in Fig. 6. The tracking of collision worm is divided into three stages: pre-collision, in-collision, and post-collision. This stage is judged by the worm blob area, and the worm blob is obtained by a morphological algorithm. Parameter \(\:{Thre}_{col}\) is set as 1.8 times of the worm blob area. As the number of frames increases, when the blob area is greater than \(\:{Thre}_{col}\), the worm is judged to be in in-collision stage, and when the blob area is less than \(\:{Thre}_{col}\), the worm is judged to be in post-collision stage.

To improve the efficiency of the algorithm, the image is down-sampled before the experiment. In order to solve the problem of the computational cost of high-resolution images, we set the down-sampling rate to 0.5, which can reduce the amount of calculation with less impact on accuracy. In the first frame, the target point is manually selected, as indicated by the blue cross in Fig. 6a. Concurrently, the features of target point are recorded, the supplementary file illustrates the method employed for the extraction of target point features. Subsequently, a set of \(\:N\) particles are generated uniformly within the worm bounding box, as shown in Fig. 6b. Considering the balance between tracking accuracy and computational cost, we have selected an appropriate number of particles based on experimental results, which improves the efficiency of the algorithm while ensuring accuracy, and the number of \(\:N\) is set to 50 in this paper. Then, the particle positions are updated according to the random walk model, which is shown in the supplementary file. The likelihood of the particles is calculated based on the Bhattacharyya distance to the target point feature, and is fitted to a Gaussian distribution to generate weights. At this point, the likelihoods of the 20 particles with the highest weights are transferred to the belief space and stored as normative knowledge. The information of the worm blob is transferred to the belief space and stored as situational knowledge. Then, the SCA algorithm is applied to the updated particles, resulting in the acquisition of \(\:N\) particles after four iterations. The number of input particles in the resampling stage is related to the number of iterations of the SCA algorithm. More iterations can lead to more particles with high weights, but will increase the computational cost. Based on the experimental results, a moderate resampling stage with an input particle number of 4N was selected. Ultimately, the likelihood of the 4N particles is calculated, and the 4N particles whose likelihood range aligns with the normative knowledge are retained for the resampling stage. In the resampling stage, particles with high weights are selected, which causes the particles to cluster around the worm body, as shown in Fig. 6c. This process is iterated continuously to achieve worm tracking in the pre-collision stage, as shown in Figs. 5 and 6d.

In the in-collision stage, the culture algorithm ceases to receive information of the worm blob, which is then set as feature X. At this point, the improved particle filter algorithm continues to track the worm collision blob, as shown in Fig. 6e,f. In the post-collision stage, the improved particle filter tracks the two worms for three frames. The blob information of the two worms is saved as features \(\:A\) and \(\:B\). The target with the smallest Bhattacharyya distance is identified as the correct worm target by comparing features \(\:A\) and \(\:B\) with \(\:X\), as shown in Fig. 6g,h. Wherein, the blue and yellow particles and bounding box represent two worms.

Fig. 5
figure 5

Flowchart of the proposed collision worm tracking method.

Full size image
Fig. 6
figure 6

The physical images of the proposed collision worm tracking method. (a) Manually mark the target point. (b) Particles are generated uniformly and updated in the bounding box of worm. (c) After the SCA and resampling stages, the particles aggregate in the worm body. (d) In the pre-collision stage, the particles continuously tracking worm. (e) In the in-collision stage, the particles tracking collision worm area. (f) The particles continuously tracking collision worm. (g) In the post-collision phase, the two worms are tracked separately. (h) Correct worm is determined based on the situational knowledge of the cultural algorithm. Among them, the blue cross represents the target point, the green rectangle is the bounding box of the target worm, and the red dot is the particle. The yellow and blue rectangles are the bounding box of the worms that have not been judged, and the yellow and blue dots are the corresponding particles. The scale bar in (a), (b), (c), (e), (g) and (h) is 2 mm, and the scale bar in (d) and (f) is 3 mm.

Full size image

Results

Experimental setup and evaluation index

To verify the applicability of the algorithm, the wild type N2 and RB1579 strains were selected for experiments on C. elegans of six ages: L1, L2, L3, L4, young adult, and D1, and fifty collision fragments were taken at each age for different worm strains. The experiment results are shown in Fig. 7. In the figure, the green rectangle represents the bounding box of the target worm, the red dot denotes the particle, and the orange rectangle indicates the other worm involved in the collision.

The experimental results show that the worms in the L1, L2, and L3 stages are very small, while the worms in the L4, young adult, and D1 stages have significantly increased in size. Therefore, the parameters of morphological processing method need to be adjusted for worms at different age stages, as shown in the supplementary file. In addition, since the algorithm is not sensitive to the speed of worm movement, tracking can be achieved without adjusting the parameters when the age of the two strains worms selected for the experiment is the same.

Fig. 7
figure 7

Experimental result figures of the proposed collision worm tracking method. The worm strains are N2 wild type and RB1579, and the ages of worm are L1, L2, L3, L4, Young adult and D1. The green rectangle is the bounding box of the target worm, the red dot is the corresponding particle, and the orange rectangle is the bounding box of the colliding worm. The scale bar of the first three columns is 0.4 mm, and the scale bar of the last three columns is 1 mm.

Full size image

To evaluate the performance of proposed algorithm, three typical evaluation metrics for tracking algorithm: processing time, average error and harmonic mean F-measure30. The processing time is given by the timing function of the Matlab software. The average error is obtained from the Euclidean distance between the expert path and the algorithm path, as shown in Eq. (1):

$$\:{error}_{ave}=\frac{\sum\:_{k=1}^{K}\sqrt{{({x}_{2}-{x}_{1})}^{2}+{({y}_{2}-{y}_{1})}^{2}}}{K}$$
(1)

where \(\:{x}_{1},{y}_{1}\) and \(\:{x}_{2},{y}_{2}\) are the expert path and algorithm path, respectively. \(\:k\) and \(\:K\) represent the current and total number of frames in the collision fragment. The harmonic mean F-measure is introduced to evaluate the performance of the algorithm in the precision-recall space, and the equation can be expressed as Eq. (2):

$$\:F=\frac{1}{\alpha\:*\frac{1}{P}+\left(1-\alpha\:\right)*\frac{1}{R}}$$
(2)

in this formula, \(\:\alpha\:\) is a constant that represents the weight of precision \(\:P\) and recall \(\:R\). In this research, \(\:\alpha\:\) is set to 0.5 based on experience. The formula of precision \(\:P\) and recall \(\:R\) can be expressed as Eq. (3):

$$\:\begin{array}{c}P=\frac{{N}_{TP}}{{N}_{TP}+{N}_{FP}}\\\:R=\frac{{N}_{TP}}{{N}_{TP}+{N}_{FN}}\end{array}$$
(3)

wherein, \(\:{N}_{TP}\) is the number of pixels correctly identified by the algorithm, \(\:{N}_{FP}\) is the number of pixels that have the background as target, and \(\:{N}_{FN}\) is the number of pixels that could not be classified successfully.

Average process time

The average processing time of the proposed method in this paper is shown in Fig. 8, and the results of different ages worms are represented by different colors. The code was executed on a desktop computer with the Windows 10 operating system, an Intel Core i9-13900 K processor, and 32 GB of RAM. The processing times of data for each age in Fig. 8a and b were obtained by 50 collision fragments. As illustrated in the figure, the median of the process time of all ages is between 0.02 and 0.04 s, indicating that the algorithm is capable of achieving 30 frames per second. The standard deviations from L1 to D1 in Fig. 8a are 0.0136, 0.0077, 0.0109, 0.0159, 0.0810, and 0.0090, respectively, and the standard deviations from L1 to D1 in Fig. 8b are 0.0105, 0.0157, 0.0114, 0.0092, 0.0150, and 0.0139. As illustrated in the figure, the processing time of some images is between 0.05 and 0.06 s. This is attributed to the presence of impurities of petri dish, which result in particles gathering at these impurities during tracking, thereby waste some performance. Moreover, the processing time for some images reaches approximately 0.09 s. It was observed that these images are the initial frames of the video, indicating that the algorithm requires more performance during particle generation.

Fig. 8
figure 8

The average processing time of collision fragments by different strains. (a) RB1579. (b) N2 wild type. The mean value is between 0.02 and 0.04 s, the maximum value is 0.09 s, and the standard deviation of RB1579 is 0.0136, 0.0077, 0.0109, 0.0159, 0.08 10, and 0.0090, and the standard deviation of N2 wild type is 0.0105, 0.0157, 0.0114, 0.0092, 0.0150, and 0.0139.

Full size image

Average error

The average error of the method is obtained by the average Euclidean distance between the expert path and the algorithm path. The path of the proposed method and the traditional particle filter method were obtained. The results of the experiment are presented in Fig. 9a–l. The data for each age in Fig. 9m,n are obtained by averaging the error of 50 collision fragments. The average error standard deviations from L1 to D1 of N2 wild type are 1.5246, 1.4010, 1.5559, 1.4379, 1.6530, and 1.5367, and the average error standard deviations from L1 to D1 of RB1579 are 1.2464, 1.347, 1.2531, 1.2337, 1.2950, and 1.2732, respectively. The green points in the figure are used to represent the expert path, the blue points represent the proposed method path, and the magenta points represent the traditional particle filter path. It can be seen that when the age of the worm is L1, L2, due to the small worm body, the traditional particle filter is unable to maintain a stable tracking of the worm, instead being drawn towards the impurities present in the figure, as shown in Figures (a)-(d). When the age of the worm is greater than L3, the traditional particle filter can track the worm, but in the post-collision stage, the tracking trajectory is frequently lost, as shown in Figures e-l. The proposed algorithm can track collision worm at different ages. The middle part of some of the orange trajectories in the figure deviates from the green trajectory. This is because during the in-collision stage, the proposed method uses the collision blob as the target, and at this time, the trajectory has a certain error with the expert path. In addition, it can be seen that the proposed method path is smoother, while the expert path fluctuates is similar to a trigonometric function. This is because the proposed method uses the center of the bounding box as the path point, while the expert path uses the center of the skeleton of worm as the path point, which brings a certain error with expert path. The above two errors have caused a certain average error, as shown in Fig. 9m,n. The experimental results show that the average error value is between 8 and 20 pixels, while the median error value is between 13 and 15.

In addition, the number of ID switch (IDS) is an important evaluation indicator of target tracking performance, which measures the ability of algorithm to handle target identity consistency. In the experiment, a total of 60 collision segments from two strains at six ages are analyzed, which contained a total of 5,850 frames and 573 IDS events are recorded. Most of these IDS were caused by impurities in the background being misidentified as targets, which was a major interfering factor in the experimental environment. The remaining IDS were mainly caused by interference from other worms with highly similar gray scale and blob features to the target worm.

Fig. 9
figure 9

Average error of collision fragments by different strains. (a), (c), (e), (g), (i), (k) The physical images of the N2 strain of L1, L2, L3, L4, Young adult, and D1. (b), (d), (f), (h), (j), (l) The physical images of the RB1579 strain of L1, L2, L3, L4, Young adult, and D1. (m) Average error figure of N2 strain. (n) Average error figure of RB1579 strain. In figures (a) to (l), the green dots represent the expert path, the blue dots represent the proposed method path, and the magenta dots represent the traditional particle filter path. In Figures (m) and (n), the mean is 13 to 15 pixels, the maximum is 20 pixels, and the standard deviation of N2 is 1.5246, 1.4010, 1.5559, 1.4379, 1.65 30, and 1.5367, and the standard deviation for RB1579 is 1.2464, 1.347, 1.2531, 1.2337, 1.2950, and 1.2732. The scale bar in figures (a)–(l) is 1 mm.

Full size image

Harmonic mean

The F-measure experiments are performed on two strains of different age worm to evaluate the tracking efficiency of the proposed algorithm, as shown in Fig. 10. The data for each age in Fig. 10a and b were obtained by averaging the F-measure of 50 collision fragments. The harmonic mean standard deviations from L1 to D1 of RB1579 are 0.0482, 0.0436, 0.0460, 0.0465, 0.0538, and 0.0487, and the harmonic mean standard deviations from L1 to D1 of N2 wild type are 0.0467, 0.0422, 0.0433, 0.0430, 0.0452, and 0.0518, respectively. As can be seen from the figure, the F-measure values range from 0.65 to 0.98, with a median between 0.8 and 0.9, which means that the proposed method exhibits robust tracking capabilities. Furthermore, the F-measure values for worms in the L1 and L2 stages are comparatively low. This is due to the relatively diminutive worm bodies in these two stages, in comparison to those in stages subsequent to L3, and the difference in gray level characteristics between the body and the background is small, which leads to more particle recognition errors.

Fig. 10
figure 10

The F-measure of collision fragments by different strains. (a) RB1579. (b) N2 wild type. The median value is between 0.8 and 0.9, the maximum value is 0.98, and the standard deviation of RB1579 is 0.0482, 0.0436, 0.0460, 0.0465, 0.0538, and 0.0487, and the standard deviation of N2 is 0.0467, 0.0422, 0.0433, 0.0430, 0.0452, and 0.0518.

Full size image

Discussion

In order to verify the improvement of proposed method over existing methods, the advantages and disadvantages of proposed method and other related methods are summarized, and the results are shown in Table 1. It can be seen that the method proposed in this paper does not require the construction of a worm model or pre-training before tracking, and is capable of tracking collision worms, which is a feature not found in existing worm tracking methods. This evidence substantiates the assertion that the method proposed in this paper is a more comprehensive and implementable approach. According to the experimental results, the proposed method in this paper exhibits a process time ranging from 0.020 to 0.040 s per frame, which is analogous to the recently proposed deep learning-based method, which has an average worm tracking time of 0.027 s per frame29. Furthermore, the proposed method exhibits a mean F-measure ranging from 0.8 to 0.9, which demonstrates high tracking accuracy. In contrast, the existing deep learning-based worm tracking methods usually require a dedicated workstation to run, while proposed method can achieve the same accuracy and speed as existing methods on common computer configurations. This feature confers a substantial advantage to proposed method in scenarios involving single worm tracking tasks.

Table 1 Comparison of the method proposed in this paper with existing methods for worm tracking.
Full size table

The tracking method proposed in this paper is also applicable to images with different resolutions, as shown by the experimental results of the csb-1 dataset in the supplementary file. In the csb-1 dataset, a single worm is represented by about 90*15 pixels, which is about 1.5 times the image used in this paper. Without down-sampling, the processing time and F-measure did not change significantly, but the average error increased due to the increased image resolution. This means that the proposed method is effective for images with different resolutions. It should be noted that the down-sampling method is recommended when the amount of data is significantly increased. Furthermore, an increased image bit depth can provide richer grayscale details. However, this does not lead to a notable enhancement in tracking precision, given that the grayscale contrast between the worms and the background is already sufficiently obvious. Changes in image brightness can affect the accuracy of morphological processing. The segmentation threshold of the image needs to be adjusted to cope with different brightnesses. Finally, an image sampling rate of more than 3 frames per second is acceptable, because the method is stable enough to track the free moving worm due to the slower speed of target worm.

The proposed method in this paper should be regarded as a separate module that can be used to improve the existing multi-worm tracking method. In theory, this method can be applied to any worm video with gray scale features. In our opinion, this method can be integrated into a multi-worm tracking method to obtain the identity and trajectory of the worms before and after the collision. Alternatively, the method can be integrated into online single-worm tracking, combined with a microscope and displacement platform to achieve high-resolution video capture. To assess the efficacy of the proposed method, the experiments presented in this paper are primarily designed to track a single collision, and the worms need to be manually marked during the initialization phase. It is evident that the worm detection method has the potential to enhance the efficiency of the experiment when integrated proposed method with the existing worm tracking method. Regarding the collision of three or more worms, in theory, the method in this paper can handle this situation, but at present, this method has not been integrated, which is also a future focus of optimization for this method. Furthermore, instances of tracking failure may occur when the target worm collides with a worm that exhibits a high degree of similarity, this is mainly due to the fact that the cultural algorithm judges the target worm in the post-collision stage based on the blob information. It is our contention that a more accurate method of worm feature extraction represents a crucial direction for future work.

The proposed method still has some deficiencies. As evidenced by the experimental results, the proposed method is primarily concerned with the tracking of individual worms in the context of collisions. In the pre-collision stage, proposed method only extracts the worm blob information as the judgment criterion for the cultural algorithm. In order to further improve the accuracy of the algorithm, we believe that more worm features should be collected, such as the movement speed of the worm body, the amplitude and the frequency of the sinusoidal movement, as the input of the cultural algorithm. In addition, for particle filtering, the processing time is directly proportional to the number of particles. Therefore, we believe that an adaptive method can be introduced to adjust the number of particles in each frame of the image according to the complexity of the image. Finally, the development of more efficient algorithms and hardware architectures is also a crucial aspect that can enhance the parallelization capability of the algorithm and facilitate the processing of larger tracking tasks.

Conclusion

This research proposes a particle filter algorithm that combines the SCA and the culture algorithm for the purpose of tracking a single C. elegans in the event of a collision. In contrast to previous worm tracking methodologies, the approach presented in this research is a model-free method. In this method, the SCA is employed primarily for the precise tracking of the target C. elegans, while the culture algorithm is utilized for the identification of the target C. elegans in post-collision stages. At last, the experiment is conducted on the collision fragments, with the objective of calculating the average processing time, average error, and F-measure of the proposed method. The experimental results demonstrate that the proposed method is capable of accurately tracking the target C. elegans and identifying it in post-collision stage. In conclusion, the advantages of the proposed method in comparison to existing methods are presented, and the limitations of the proposed method and potential avenues for future research are outlined. It is our hope that this method will provide researchers with a way to process information about collision worms, thereby encouraging the development of worm tracking algorithms.