Introduction

Infertility affects approximately one in six couples worldwide1. Assisted reproductive technology (ART) is recommended for couples with unresolved infertility. However, achieving a satisfactory pregnancy rate remains challenging. It indicates that the live birth rate (LBR) per initiated cycle was 40.1% for women under 35 and 4.5% for women over 42 in the United States in 20132. Previous research3 has highlighted key factors—including weight, ovarian function, and comorbidity—that significantly impact the success of assisted reproduction programs4. Recently, additional research has highlighted ethnic origin5, male age6, and embryo cryopreservation durations7 as potential variables. However, identifying the key influencing factors remains challenging.

Machine learning techniques offer a promising solution. By extracting insights from historical data, machine learning allows for comprehensive analysis and ranking of factors influencing ART outcomes. This cutting-edge discipline leverages complex big data to acquire valuable knowledge efficiently8 and has found extensive applications across various fields, including healthcare9. For instance, dynamic systems design and control in applications such as robotics, autonomous vehicles, and industrial process plants10. In the medical domain, machine learning has demonstrated its utility in tasks such as COVID-19 diagnosis and epidemic forecasting11, medical image analysis12, cancer diagnosis and treatment selection13, and electronic health record management14. This technology enables pattern recognition and prediction of disease risk, treatment responses, and patient outcomes15. Within the realm of ART, machine learning has been used to assess embryo quality16, analyze sperm characteristics17, and explore predictive models for ovarian reserve function (such as anti-Mullerian hormone(AMH) level, follicle-stimulating hormone(FSH) level, and age)18. However, despite these advancements, the relative importance of different influencing factors in the in vitro fertilization and embryo transfer (IVF-ET) process has not been thoroughly studied.

To address this gap, we propose the use of a clustering ensemble approach to analyze the significance of each feature in the IVF-ET algorithm model. Cluster analysis, an unsupervised machine learning technique, is particularly employed to extract insights from unlabeled data19. Effective clustering algorithms are widely applied across various fields, including Vehicular Ad hoc Networks (VANETs)20 and other contexts where search efficiency and coverage of critical scenarios are key considerations21. Ensemble classifiers distinguish themselves in reducing false positives in high-risk scenarios22, thereby enhancing clustering accuracy. Their adaptability to various datasets23, and robustness against data noise, bolstered by integrating multiple deep networks, further underscore their superiority24.

Effective clustering algorithms such as non-negative matrix factorization (NMF)25, accelerated multiplicative updates for non-negative matrix factorization (AMU-NMF)26, generalized deep learning clustering (GDLC) algorithm based on NMF27, Multi-view clustering (MVC) algorithm based on deep semi-NMF28, generalized deep learning algorithm based on NMF for multi-view clustering29, Meta-CLustering Algorithm (MCLA)30, and dense representation based ensemble clustering (DREC) algorithm31 have been developed. These algorithms have been applied to identify signature genes associated with recurrent implantation failure (RIF)32 and gene co-clusters in two species33, demonstrating their potential in complex biological datasets.

Given the existing gaps in the literature and the promise of machine learning techniques, we conducted a retrospective study to assess the significance of various influencing factors in the IVF-ET process. Data comprising clinical characteristics and live birth outcomes of IVF-ET patients at Sichuan Jinxin Xi’nan Women’s and Children’s Hospital between January 2022 and December 2022 were collected and analyzed using a self-developed ensemble algorithm called NMF-based ensemble algorithm (NMFE). This algorithm combines the strengths of NMF, AMU-NMF, and GDLC, aiming to improve the efficiency of data clustering and provide valuable insights aimed at enhancing the success rate of IVF-ET.

Results

Comparison between different algorithms

We conducted a comparison of the NMFE with some well-known effective algorithms. The algorithms used in the comparison are NMF17, AMU-NMF18, GDLC19, MCLA22 and DREC23. The accuracy (ACC) and purity (PUR) values serve as metrics to assess the performance and effectiveness of different algorithms34. A higher accuracy value indicates a greater proportion of correct predictions, whereas a higher purity value indicates a higher percentage of instances that are accurately classified. The accuracy and purity value of NMFE are 0.7912 and 0.8605 respectively, surpassing those of other algorithm models. This indicates that NMFE is more effective (Table 1; Fig. 1).

Table 1 Results of accuracy and purity value on the IVF dataset by different clustering algorithms. The accuracy and purity value of NMFE are 0.7912 and 0.8605 respectively, surpassing those of other algorithm models. *The maximum value in the same group.
Full size table
Fig. 1
figure 1

Area diagram integrating ACC and Purity on the dataset IVF-ET. The algorithm becomes more efficient as the area increases. The NMFE algorithm has the largest area (Area: 3404.13), indicating that its effectiveness is the highest among the above algorithms.

Full size image

Ranking analysis of influencing factors

In our study, we extended our analysis to compare the efficacy of NMF, AMU-NMF, GDLC, and NMFE algorithms. Following the random masking of the original data by three different sets of random numbers, NMFE consistently exhibited higher accuracy and purity values compared to other algorithms across the majority of cases (Table 2).

Table 2 Accuracy and purity values of different algorithms by masking each feature group by three different sets of random numbers. NMFE consistently demonstrated higher accuracy and purity values compared to other algorithms in the majority of cases. *The maximum value in the same group.
Full size table

To further investigate the impact of specific feature groups on the IVF-ET model, we masked the data for groups such as Therapeutic Interventions, Embryo Transfer Outcomes, and Ovarian Response Assessment Indicators with random numbers. This manipulation resulted in a significant decrease in the overall accuracy value of the IVF-ET model, suggesting that these feature groups exert a substantial influence on the model’s performance.

To quantify the influence of various feature groups on the IVF-ET outcome, we computed ACC-GAP and PUR-GAP values by summing the accuracy and purity values after masking the data with the three sets of random numbers. Smaller calculated values for these gaps indicated a more robust influence of the feature group on the overall model and a greater effect on the IVF-ET outcome (Table 3; Fig. 2.). Among the feature groups, Therapeutic Interventions exhibited the smallest ACC-GAP and PUR-GAP values, suggesting that they contribute the most significantly to the model.

Table 3 The ACC-GAP and PUR-GAP values for each feature group were calculated using NMFE. The feature group therapeutic interventions demonstrated the lowest ACC-GAP and PUR-GAP values. Conversely, the male Basic Information feature group had the highest ACC-GAP value. The female Basic Information feature group had the highest PUR-GAP value. *The maximum value in the same group, # the minimum value in the same group.
Full size table
Fig. 2
figure 2

Rank each feature group according to the ACC-GAP and PUR-GAP values. The top 5 groups that have the greatest influence on the IVF-ET results identified are Therapeutic Interventions, Embryo Transfer Outcomes, Ovarian Response Assessment Indicators, Embryo Transfer-Related Indicators, and Complications During Pregnancy.

Full size image

Based on our influence analysis, we identified the top five groups with the greatest influence on the IVF-ET result: Therapeutic Interventions, Embryo Transfer Outcomes, Ovarian Response Assessment Indicators, Embryo Transfer-Related Indicators, and Complications During Pregnancy. Within the Therapeutic Interventions group, factors such as the ovarian stimulation protocol, ovulation stimulation drugs, and pre-cycle and intra-cycle acupuncture were found to be particularly influential. To gain a deeper understanding of the impact of each treatment plan on the IVF-ET result, we conducted a separate analysis for each intervention factor (Table 4; Fig. 3).

Table 4 ACC-GAP and PUR-GAP value of different intervention factors group by NMFE. Ovarian stimulation protocols, ovulation stimulation drugs, and pre-and intra-cycle acupuncture ranked 7th, 8th, 12th, and 14th based on ACC-GAP values, and 4th, 6th, 13th, and 14th based on PUR-GAP values. * the maximum value in the same group, # the minimum value in the same group.
Full size table
Fig. 3
figure 3

Rank of different intervention factors in the IVF-ET model. Ovarian stimulation protocols, ovulation stimulation drugs, and pre-and intra-cycle acupuncture significantly declined in the rankings of IVF-ET models.

Full size image

Upon further analyzing the clinical features within the Therapeutic Interventions separately, we observed a shift in the rank of influential factors. Specially, ovulation-stimulating drugs dropped to seventh place, ovarian stimulation protocol dropped to eighth place, and acupuncture treatment was further behind. Whether this shift indicates a synergistic effect among multiple therapies will require further validation to confirm.

Discussion

In this study, we have proposed an ensemble clustering algorithm model to assess the influence of clinical characteristics on IVF-ET live births of fresh embryo transfer. This algorithm surpasses other algorithms in terms of accuracy and purity, demonstrating its robustness and reliability in handling the IVF-ET dataset. The results revealed that the five leading feature groups with the most substantial impact on live births in IVF-ET are Therapeutic Interventions, Embryo Transfer outcomes, Ovarian Response Assessment Indicators, Embryo Transfer-related Indicators, and Complications During Pregnancy. Conversely, factors such as basic male and female information, female diagnosis, and obstetric history had a relatively minor influence.

Among these, Therapeutic interventions as the most influential factor, encompassing multiple aspects of the treatment plan, including ovulation stimulation drugs (recombinant human follicle-stimulating hormone (rFSH) and human menopausal gonadotropin (hMG)), the ovarian stimulation protocol, and the utilization of acupuncture before and during the IVF cycle. The European Society for Human Reproduction (ESHRE) guideline on ovarian stimulation in IVF/ICSI recommends both rFSH and hMG as viable options35. However, the initial dosage of gonadotrophin is pivotal in determining the outcome of controlled ovarian stimulation (COS) and subsequent IVF outcomes36. Thus, it’s crucial to consider an individual’s ovarian potential before initiating stimulation, as a standardized prescription may adversely affect women’s outcomes37. For example, low doses may result in insufficient follicular development in women with normal or high ovarian reserve while excessive doses could lead to ovarian hyperstimulation syndrome (OHSS)38.

Once the follicle has reached a certain size, gonadotropin-releasing hormone (GnRH) -agonists can be used to stimulate the maturation and increase ovum count. On the other hand, recombinant GnRH -antagonists can be employed to inhibit the release of natural luteinizing hormone, thereby preserving eggs for further development. The selection of the ovarian stimulation protocol closely correlates with OHSS occurrence and clinical pregnancy rate39. In the general IVF population, GnRH antagonists were associated with a lower ongoing pregnancy rate after fresh embryo transfer compared to long-protocol agonists with lower OHSS rates. This underscores the challenge of selecting the most suitable protocol for individual patients. Individualizing treatment in IVF aims to maximize pregnancy chances while minimizing ovarian stimulation risks38.

Thus, the selection of ovarian stimulation drugs and protocols is a crucial factor for IVF-ET outcomes, and treatment should be individualized based on ovarian response35. Our model highlights ovarian response as a key factor, recommending antral follicle count (AFC) or AMH for predicting high or poor ovarian response26. Since age and BMI inversely correlate with AMH, they are also important considerations when personalizing treatment plans40,41,42,43.

Acupuncture, as traditional adjuvant therapy, is being increasingly chosen by subfertility couples to improve the success rate of IVF-ET44,45. In the United States, 44% of infertile women undergoing IVF-ET administrate acupuncture46. However, the potential of acupuncture to enhance the live birth rate of IVF-ET remains debatable47,48. Recent clinical studies have indicated several positive effects of acupuncture. It has been found to reduce anxiety during embryo transfer49, improve oocyte quality50, and enhance endometrial blood flow and receptivity51, ultimately leading to improved outcomes in IVF-assisted pregnancy.

Additionally, when examining the impact of the ovulation stimulation drugs, ovarian stimulation protocols, and acupuncture (pre-cycle and intra-cycle), we observed a significant decrease in their influence on the IVF-ET model, with acupuncture showing the least effect. To investigate this further, we conducted additional analysis and data mining. We found that the majority of patients in our dataset did not receive acupuncture treatment. Only 198 patients received intra-cycle acupuncture and 144 patients received pre-cycle acupuncture. It is important to note that the efficacy of acupuncture is closely related to the number of sessions52,53 Therefore, the limited use of acupuncture in our dataset may not accurately reflect its true potential in enhancing IVF-ET outcomes. Hence, concluding that acupuncture is ineffective based solely on our findings would be premature. Upon comprehensive consideration of the intervention factors, their combined influence remains significant, hinting at potential synergistic effects among multiple therapies. However, further validation is required to substantiate this observation.

Our results indicated that multiple clinical features after embryo transfer significantly impact the IVF-ET model. Specifically, we considered the Embryo Transfer Outcomes group and the Complications During Pregnancy group. The Embryo Transfer Outcomes group encompassed conditions such as ectopic pregnancy, miscarriage, and premature delivery, while the Complications During Pregnancy group included gestational hypertension, gestational diabetes, intrahepatic cholestasis of pregnancy, fetal transfusion, and premature rupture of membranes. These findings aligned with established clinical patterns54,55,56,57, suggesting good validity for our model in analyzing the IVF-ET dataset. Additionally, the Embryo Transfer-related Indicators group comprised factors like endometrial thickness, transferred embryo count, and transferred good-quality embryo count. These factors are widely acknowledged as critical determinants of live birth outcomes in the context of IVF-ET58,59.

Our research findings emphasize the significance of various factors in IVF-ET outcomes. While obstetric history, which includes past pregnancies and deliveries, is generally considered relevant to IVF success, our data mining model does not assign it significant importance compared to other features. A history of successful pregnancies may suggest fertility capability, while previous failed pregnancies or miscarriages could indicate underlying fertility issues. Similarly, cesarean sections or uterine surgeries may affect uterus shape and integrity, potentially impacting embryo implantation. However, our model found that prior obstetric history did not significantly affect IVF-ET outcomes. It is important to note that patients seeking ART assistance often face significant fertility challenges and may have compromised natural conception abilities. Although past reproductive history may influence future pregnancies, it is not decisive in determining IVF-ET success. Our model also indicates that the cause of a woman’s infertility does not play a significant role in IVF-ET outcomes. Additionally, we considered the ethnicity of both partners in our analysis, given China’s multi-ethnic nature. Our dataset included patients from 30 ethnic groups, with the largest representation being Han (n = 2006), followed by Tibetan (n = 52) and Yi (n = 138). Other ethnicities, such as Hui, Tujia, Qiang, and Miao, were less prevalent. Interestingly, our results show minimal impact of ethnicity on the model. Furthermore, the educational background and occupation of both partners had minimal influence on the model, indicating that these factors may not significantly affect IVF-ET success.

Conclusions

Our data mining results indicate that therapeutic intervention, ovarian function, and embryo quality are the primary factors influencing pregnancy outcomes in fresh embryo transfer. Conversely, ethnic background, occupational status, educational levels, female infertility cause, and previous pregnancy history do not significantly impact pregnancy outcomes. Using NMFE, we evaluated and ranked the influence of various factors on patients undergoing fresh embryo transfer.Several limitations point to avenues for future research. Firstly, we did not explore in detail how specific characteristics impact IVF-ET outcomes. For instance, we did not determine optimal ovarian stimulation protocols tailored to individual patients. Similarly, we did not investigate the efficacy of acupuncture administered before and during the IVF cycle, nor did we establish the ideal number of acupuncture sessions. Furthermore, our model did not establish optimal dosages for medications or guide combining clinical interventions to achieve the best results. As such, our next steps involve enriching the dataset and conducting an in-depth analysis of these issues. Additionally, we plan to develop an artificial intelligence-driven personalized IVF support model to assist clinicians in selecting better treatment plans. Moreover, insights from this study will be used to further investigate matters related to frozen embryo transfer, with the ultimate goal of reducing economic costs for patients seeking assisted reproduction.

Materials and methods

Dataset

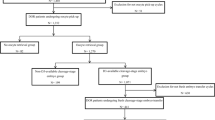
From January 2022 to December 2022, a total of 9539 patients underwent IVF at Sichuan Jinxin Xi’nan Women’s and Children’s Hospital, of which 3695 patients received fresh embryo transfer and 2238 patients observed pregnancy outcomes (Fig. 4). This study was approved by the Medical Ethics Management Committee of Sichuan Jinxin Xinan Women and Children’s Hospital (Ethnic number: No.2023-043) and was conducted according to all relevant guidelines and regulations. Since the data collected is anonymous, the requirement for informed consent was waived by the committee.

Fig. 4
figure 4

Flowchart of patient inclusion.

Full size image

The dataset used in this study contains clinical features before and after IVF-ET. It consists of a total of 85 independent features, 69 clinical features before fresh embryo transfer, and 16 clinical features after transfer. Based on the correlation between features, we grouped them into 13 categories: Female Basic Information (3 items), Male Basic Information (5 items), Menstrual History (3 items), Obstetric History (12 items), Previous History of Assisted Reproduction (3 items), Ovarian Response Assessment Indicators (10 items), Therapeutic Interventions (4 items), Factors Associated with Embryo Quality (13 items), Female Diagnosis (10 items), Embryo Transfer-related Indicators (6 items), Hormone Levels After Transplantation (2 items), Embryo Transfer Outcomes (9 items), and Complications During Pregnancy (5 items) (Table 5; Fig. 5). The dataset contains one dependent feature, referred to as “Result”, which is divided into categories such as no pregnancy, miscarriage, and live birth. Of the cases in the dataset, 1,660 were not pregnant, 298 were miscarriages including ectopic pregnancy, biochemical pregnancy, and abortion, and 280 were live births. A comparative analysis of statistical differences in clinical features between groups with and without live births after fresh embryo transfer is shown in Supplementary Tables 1 & Supplementary Table 2.

Table 5 Features in IVF-ET dataset. The dataset used in this study contains 85 independent clinical features. Based on the correlation between features, we grouped them into 13 categories.
Full size table
Fig. 5
figure 5

The clinical features in the dataset. All the clinical features were grouped into 13 categories and calculated the fraction of features in each group relative to the total number of features. Female Basic Information (5 items, 6%), Male Basic Information (5 items, 6%), Menstrual History (3 items, 4%), Obstetric History (12 items, 14%), Previous History of Assisted Reproduction (3 items, 14%), Ovarian Response Assessment Indicators (8 items, 9%), Therapeutic Interventions (4 items, 5%), Factors Associated with Embryo Quality (13 items, 15%), Female Diagnosis (10 items, 12%), Embryo Transfer-related Indicators (6 items, 7%), Hormone Levels After Transplantation (2 items, 2%), Embryo Transfer Outcomes (9 items, 11%), and Complications During Pregnancy (5 items, 6%).

Full size image

Proposed ensemble algorithm

In this paper let \(X=\left\{ {{x_1},{x_2}, \ldots {x_n}} \right\} \in {{\mathbb{R}}^{M,N}}\) us denote the dataset of IVF-ET. \({x_n}\)denotes the n-th sample in the dataset. M denotes the feature dimension of each sample, and each feature is to portray a sample effective attribute. N denotes the sum of all samples involved in this modeling. In this paper, we use non-negative matrix factorization (NMF)60 and its two variants algorithms to construct an ensemble model.

NMF works by approximating the high-dimensional target matrix using two low-dimensional matrices. We obtain effective low representations through multiple variants of the NMF algorithm, and then the ensemble model is constructed by fusing the low-dimensional feature matrices obtained from the training of multiple models. The objective function of NMF is shown in Eq. (1).

$$\mathop {\arg \hbox{min} }\limits_{{U,V}} {J_1}\left( {U,V} \right)=\left\| {X - UV} \right\|_{F}^{2},s.t.{\text{ }}U \geqslant 0,V \geqslant 0.$$
(1)

where U, V are two low-dimensional matrices. U is the weight matrix and V is the feature matrix, and \(U \in {{\mathbb{R}}^{M,K}},V \in {{\mathbb{R}}^{N,K}}\). K is the dimension of the low-dimensional matrix, in which\(K \ll \hbox{min} \left\{ {M,N} \right\}\). In Eq. 1, \({\left\| {{\text{ }} \cdot {\text{ }}} \right\|_F}\) is the Frobenius norm. To obtain U and V that approximate the original matrix X. The corresponding update rules are usually obtained using multiplicative updating. Furthermore, to accelerate NMF update and improve the effectiveness of the algorithm, a significant acceleration algorithm AMU-NMF was proposed by Gillis et al.26. It improves the efficiency of the algorithm while ensuring convergence. Further, to improve the representation ability and convergence speed of the algorithm. Wang et al. proposed a deep matrix factorization representation learning algorithm GDLC based on element update. Its objective function is shown in Eq. (2).

$$\begin{gathered} \mathop {\arg \hbox{min} }\limits_{{U,V}} {J_1}\left( {U,V} \right)=\left\| {X - UV} \right\|_{F}^{2}+\alpha \left\| U \right\|_{F}^{2}+\beta \left\| V \right\|_{F}^{2},s.t.{\text{ }}U \geqslant 0,V \geqslant 0. \hfill \\ ={\sum\limits_{{m=1}}^{M} {\sum\limits_{{n=1}}^{N} {\left( {{x_{m,n}} - \sum\limits_{{k=1}}^{K} {{u_{m,k}}{v_{n,k}}} } \right)} } ^2}+\alpha \cdot {\sum\limits_{{m=1}}^{M} {\sum\limits_{{k=1}}^{K} {\left( {{u_{m,k}}} \right)} } ^2}+\beta \cdot {\sum\limits_{{n=1}}^{N} {\sum\limits_{{k=1}}^{K} {\left( {{v_{n,k}}} \right)} } ^2} \hfill \\ \end{gathered}$$
(2)

To optimize the objective function, a stochastic gradient descent algorithm61,62 and an alternate iterative update strategy63 are used to minimize the objective function.

To better improve the effectiveness of the algorithm, we fused the feature matrices obtained from the learning of the three algorithms NMF, AMU-NMF, and GDLC to construct an NMF-based ensemble algorithm (NMFE). Since the feature matrices are all non-negative matrices, to satisfy the effectiveness of the fusion algorithm and to ensure non-negativity, we propose a deep fusion-based method. The objective function of the method is shown below .The algorithm framework for NMFE is shown in Fig. 6.

Fig. 6
figure 6

Algorithmic framework for NMFE. It is constructed by fusing the feature matrices that are obtained from NMF, AMU-NMF, and GDLC algorithms.

Full size image
$$\begin{gathered} \mathop {\arg \hbox{min} }\limits_{{U,V}} {J_1}\left( {U,V} \right)=\sum\limits_{{i=1}}^{I} {\left\| {{V^{(i)}} - E} \right\|_{F}^{2}} +{\alpha _1}\left\| E \right\|_{F}^{2},s.t.{\text{ }}U \geqslant 0,V \geqslant 0. \hfill \\ =\sum\limits_{{i=1}}^{I} {{{\sum\limits_{{n=1}}^{N} {\sum\limits_{{k=1}}^{K} {\left( {v_{{n,k}}^{{(i)}} - {e_{n,k}}} \right)} } }^2}} +{\alpha _1} \cdot {\sum\limits_{{n=1}}^{N} {\sum\limits_{{k=1}}^{K} {\left( {{e_{n,k}}} \right)} } ^2} \hfill \\ \end{gathered}$$
(3)

Where I denote the number of models that are used to construct the ensemble model. \({\text{i}} \in \left\{ {1,2,3} \right\}\),\({V^{(1)}}\),\({V^{(2)}}\),\({V^{(3)}}\) denote the feature matrices obtained by algorithm NMF, AMU-NMF, and GDLC respectively. The objective function of the matrix is written in elemental form and then the SGD is used to optimize the objective function, which can be obtained as follows concerning the variable\({e_{n,k}}\).

$${J_2}\left( {{e_{n,k}}} \right)={\left( {v_{{n,k}}^{{(i)}} - {e_{n,k}}} \right)^2}+{\alpha _1} \cdot {\left( {{e_{n,k}}} \right)^2}$$
(4)

Based on SGD its update rule can be obtained as follows.

$$e_{{n,k}}^{{\left( t \right)}} \leftarrow e_{{n,k}}^{{\left( t \right)}} - \eta \left( {\left( {v_{{n,k}}^{{(i)}} - {e_{n,k}}} \right) \cdot \left( { - 1} \right)+{\alpha _1}{e_{n,k}}} \right)$$
(5)

There is a subtraction operation in Eq. (5), which does not guarantee that the update value is non-negative. For this reason, we use an activation function with a non-negative value domain to constrain in Eq. (4), rewriting (4) as

$${J_2}\left( {{e_{n,k}}} \right)={\left( {v_{{n,k}}^{{(i)}} - f\left( {{{\hat {e}}_{n,k}}} \right)} \right)^2}+{\alpha _1} \cdot {\left( {f\left( {{{\hat {e}}_{n,k}}} \right)} \right)^2}$$
(6)

We let \(f\left( \cdot \right)=sigmoid\left( \cdot \right)\). Based on the work in (6), the element’s SGD-based gradient values are transformed into weights for constructing the deep network for the update, and we can obtain the following update rule.

$$\left\{ \begin{gathered} {\left( {{{\hat {e}}_{n,k}}} \right)^T}={\left( {{{\hat {e}}_{n,k}}} \right)^1}+\eta {\left( {\Delta {e_{n,k}}} \right)^r}{\text{ }}r<R \hfill \\ {\left( {{{\hat {e}}_{n,k}}} \right)^1}\mathop \leftarrow \limits^{{r+1}} f\left( {{{\left( {{{\hat {e}}_{n,k}}} \right)}^T}} \right){\text{ }}r<R \hfill \\ {e_{n,k}}={\left( {{{\hat {e}}_{n,k}}} \right)^1}+\eta {\left( {\Delta {e_{n,k}}} \right)^r}{\text{ }}r=R \hfill \\ {\left( {\Delta {e_{n,k}}} \right)^r}=\sum\limits_{{t=1}}^{T} {\left( {\left( {v_{{n,k}}^{{(i)}} - f{{\left( {{{\hat {e}}_{n,k}}} \right)}^t}} \right) \cdot \left( { - 1} \right)+{\alpha _1} \cdot f{{\left( {{{\hat {e}}_{n,k}}} \right)}^t}} \right) \cdot f{{\left( {{{\hat {e}}_{n,k}}} \right)}^t} \cdot \left( {1 - f{{\left( {{{\hat {e}}_{n,k}}} \right)}^t}} \right)} \hfill \\ \end{gathered} \right.$$
(7)

Where R denotes the total number of rounds for training, and T denotes the number of times that the element \({\hat {e}_{n,k}}\) is updated in a round. \(\eta {\left( {\Delta {e_{n,k}}} \right)^r}{\text{ }}\) denotes the cumulative value of the gradient for update the element \({\hat {e}_{n,k}}\) in the r-th round. By using the update rule of Eq. (7), we can learn to obtain the matrix E, which will be clustered using the k-means algorithm, and the clustering results of the NMFE model can be obtained.