Introduction

Accrual success is a dominant determining factor for the success of clinical trials (CT). Global data analysis of all terminated trials reported 55% of trials terminated due to low accrual rate1. An Institute of Medicine report found 71% of phase III trials approved by the National Cancer Institute’s (NCI’s) Cancer Therapy Evaluation Program closed without meeting their accrual goals2. Failed accrual dramatically affects costs for sponsors (Pharma, National Institutes of Health), academic institutions, investigators, and society.

The ability to predict CT accrual success with high precision before the trials start is highly valuable. It allows for early identification of trials that are unlikely to meet accrual goals before allocating critical resources. Moreover, identifying these trials enables more focused and targeted efforts to improve accrual.

While several methods for predicting accrual are available, limitations exist. For example, Cohort identification tools3,4,5 forecast “best case scenario” accrual by estimating the number of available subjects that meet inclusion/exclusion criteria using electronic health record (EHR) data. This method estimates the upper limit for accrual but fails to consider factors that limit accrual, such as the probability of consent, the complexity of the trial design, and the effectiveness of recruitment strategy. Existing accrual forecasting tools estimate accrual based on an estimated accrual rate (a parameter that is hard to determine before the start of the trial) or a limited number of associated factors6,7,8,9,10,11,12,13. Some commercial vendors14,15,16 have recently offered such tools, but these products often lack sufficient evidence supporting their efficacy. Academic studies are typically much more rigorous, have detailed description of methods and clearly stated statistical assumptions. Many studies address complex clinical trial designs such as the multi-center trials, considers accrual as well as randomization, and allows for adaptive adjustment as the trial progresses. Many of the studies leverages the Bayesian approach for predicting the average and variation of accrual (see Anisimov, 202017 for a comprehensive review). Earlier Bayesian approaches model the enrollment process as Poisson processes with accrual rate from a uniform distribution12. A more sophisticated approach, the Poisson-gamma model, was introduced to account for variations among accrual rate in different centers in multi-center trials, where the prior distribution of accrual rate is a gamma distribution7,13. This was further extended to capture the situations where clinical centers can be initiated with random delays and also can be closed earlier6 and to model accrual in specific centers, regions, or countries18. For predicting accrual prior to the trial start, the main limitation of these and related approaches6,7,8,9 is that they rely on estimated accrual rate (or specifying a prior distribution), which can be difficult to obtain. Additionally, studies that investigate the relationship between accrual and trial-related factors often only examine a small number of trial-related factors. Also, these studies are often descriptive, without assessing the joint predictive capacity of these factors for accrual success10,11. In addition, many studies focus on trials from a specific medical domain where recruitment is particularly challenging, or for specific recruitment methods and scenarios19,20,21. A third category is the manual academic administrative review22,23,24. This approach uses experienced scientists and research staff to subjectively predict accrual success (i.e., in the context of feasibility assessment). However, it frequently suffers from incomplete knowledge and is susceptible to undesirable variability due to varying composition of committees and other biases. In addition, this method is resource intensive and not scalable.

A large number of barriers and facilitators for CT accrual have already been identified1,22,23,24,25, including trial design and complexity, number of eligible and available participants, experience of trial investigators, and characteristics of the institution hosting the trial (e.g. size, location, recruitment performance in prior trials). In principle, a model based on these factors can be constructed for predicting accrual failure. However, only a small fraction of the previously identified barriers and facilitators were examined simultaneously in prior quantitative studies6,7,8,9,10,11,26, partially because many of these factors are hard to obtain from a large number of CTs. Also, these studies are commonly based on trials that are collected in a single organization, which can result in bias. Moreover, prior studies on accrual failure risk utilized relatively simple statistical methods (e.g. parametric models capturing additive relationships, such as generalized linear models) that may not fully capture the complex relationships among the predictors and the prediction target. Furthermore, these studies focus on identifying the factors associated with accrual, but did not evaluate the predictive capacity of the derived models formally. Therefore, the ability of these models to assess accrual failure risk in the real world remains unclear.

To address the above challenges, we leveraged information reported on clinicaltrials.gov website and external sources, utilized both rule-based and data-driven machine learning natural language processing (NLP) methods to create a dataset for predicting clinical trial accrual failure. Our sample covers CTs across a large variety of disease types conducted in different regions in the US from 1995 to 2022. Importantly, we manually reviewed failed trials reported on clinicaltrials.gov and identified trials that failed due to accrual. These efforts make modeling accrual failure possible. To assess the generalizability of the model over time, we employed a pseudo-prospective validation design, where models were built using historical data and validated on future data. We employed state-of-the-art predictive modeling techniques and protocols to capture complex, non-linear, interactive relationships among a large number of variables available before the trial starts, eliminating the need to estimate accrual rate, and to optimize predictive performance while avoiding overfitting. Further, we explored several methods to enable robust and cost-effective translation of the predictive model into the real world. We employed Markov boundary based feature selection methods which choose a minimum number of features with maximal predictive performance27,28, enabling the cost-effective implementation of decision support tools (DST). We examined and improved model calibration such that the model predicted probability of success better aligns with the actual probability of accrual failure. We also implemented prediction with reject option to improve predictive performance in the predicted cases.

Several recent publications also used clinicaltrial.gov information to construct predictive models for related tasks such as, predicting accrual rate categories (low, median, vs. high)29 and predicting trial termination30,31. The individual accrual rate categories from the study by Bieganek et al.29 were relatively broad, with low accrual rates defined as ≤ 25 participants/year, medium accrual rates defined as 25 < r ≤ 100 participants/year, and high accrual rates defined as > 100 participants year. This limits the models’ applicability in practical settings. The models reported by Elkin et al. and Kavalci et al.30,31 predict trial termination due to any reason, not specifically because of accrual failure. To the best of our knowledge, the current work is the first to focus on building a model specifically for predicting the binary outcome of trial failure due to accrual failure, which is defined as accrual that was too slow to meet accrual goals within a defined period. Accurately gauging the risk of trial failure due to accrual failures enables interventions to improve recruitment specifically for the trials that need them the most, ultimately enhancing the probability of trial success.

The accrual models developed here have resulted in good predictive performance that is stable over time, with predictive performance of cross-validation AUC = 0.744+/-0.018 and prospective validation AUC = 0.737+/-0.038. Furthermore, these models are also enhanced by improving calibration and implementing prediction with reject option, which enables model translation into DST suitable for a variety of real-world settings. These models, which use less than fifty easy-to-construct features, demonstrated good predictive performance and calibration.

Method

Goal

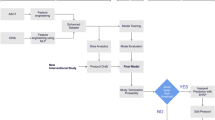
The primary goal of our study was to construct and evaluate models for clinical trial accrual failure risk assessment using information available before the start of the trial. A high-level summary of the analytical processes used to achieve this goal is visualized in supplemental Fig. S1.

Data

A total number of 111,494 clinical trials in the format of XML are collected from ClinicalTrial.gov, downloaded on 9/12/2022. We selected trials with four criteria: (1) U.S.-based; (2) interventional clinical studies; (3) the trial was initiated between 1995 and 2022; and (4) The trial recruitment status is either “Completed” or “Terminated”, this removes trials that are on-going, suspended, or withdrawn. The application of these criteria resulted in 57,846 trials in total.

Target of interest

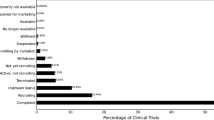
The primary target of interest for this study was whether a trial is terminated due to accrual issues. To construct the target of interest, we first examined the recruitment status field from ClinicalTrials.gov. We started with all trials that have recruitment status of “Completed” and “Terminated”. The trials marked as “Completed” are the trials that ended normally, and participants are no longer being examined or treated (that is, the last participant’s last visit has occurred). None of these trials were terminated due to accrual issues. The trials that were marked as “Terminated” are the trials that have stopped early and will not start again. For the terminated trials, a text field provides unstructured data on reasons for termination provided by the responsible party. We manually reviewed the reason for termination for the remaining 7,965 terminated trials to determine if they were terminated due to accrual issues. One reviewer reviewed and labeled all 7,965 terminated trials, and a second reviewer randomly reviewed 1,000. The agreement between the two reviewers is 100%. The annotated outcomes of the 7,965 trials are described in supplemental Table S1.

We examined additional data fields on ClinicalTrials.gov to further assess if the outcome categories we assigned to the trials were valid. Specifically, we looked at the data fields “actual enrollment” and “estimated enrollment”. The estimated enrollment is the number of participants the trial planned to enroll. The actual enrollment is the actual number of participants enrolled, updated after the trial is completed or terminated. We computed for each trial the ratio of estimated enrollment minus actual enrollment over estimated enrollment (see Fig. 1 for distribution of the ratio for completed trials and terminated trials). For terminated trials, we expect this ratio to be positive. For completed trials, we expect this ratio to be fairly close to zero. There are 4,583 trials out of the 49,881 completed trials with the ratio greater than 0.5. We flagged these trials as abnormal since it is unlikely that a completed trial only recruited less than half of the participants originally planned.

Fig. 1
figure 1

The number (a) and percentages (b) of the three type of trials over time. To access the generalizability of our models over time, we used a prospective cross-validation design (c) where historical data were used as discovery data (yellow) for model training and selection, whereas future data were used as validation data (red). x-axis represents time.

Full size image

We generated two datasets: one with the flagged abnormal trials included, one without the flagged abnormal trials. Our modeling procedure was conducted on both of the datasets as a sensitivity analysis. The model performance was very similar. We reported the results based on the dataset without the flagged abnormal trials in the main text. This dataset has 53,263 trials, consisting of 45,298 completed trials, 4,986 trials terminated due to non-accrual issues, and 2,979 trials terminated due to accrual issues. And the results on the other dataset in the supplemental file.

Feature construction

We are interested in predicting termination due to accrual failure before the trial starts. Therefore, we used information available before the initiation of the trials for feature construction. Some of the features constructed were informed by prior literature on related tasks30,31. Novel features were also constructed for this study. We categorize the constructed features into two broad categories: (1) Design Features: a small set of features capturing trial characteristics using hand-crafted feature construction methods designed specifically for this study. (2) Text Features: a large set of features capturing information in the text description of the trials using text and natural language processing methods.

The 87 Design Features (Table 1) are constructed to capture factors that have been previously reported to correlate with clinical trial accrual success. All of them are derived from the ClinicalTrials.gov XML data, except for the study population and institutional score. The study population feature represents the size of the population from which participants can be recruited32.The institutional score33 estimates the research capacity and output of the institution responsible for the clinical trial which was considered to be a facilitator of accrual success23,34,35,36. Detailed descriptions of the construction methods for these features are presented in our prior study29. Given the reported positive correlation between the complexity of eligibility criteria and risk for accrual failure23,25,37, we included features to capture high-level characteristics of the eligibility criteria of trials, such as average number of words per eligibility criteria, number of eligibility criteria, etc. We adopted the method for constructing these features from a related study on predicting trial termination30. All other design features were directly extracted from structured fields of ClinicalTrials.gov data, capturing information such as study design and study administration.

Table 1 Distribution of design features and the top 5 most frequent MeSH terms for completed trials, trials that terminated due to other reasons, and trials that terminated due to accrual reasons.
Full size table

The 6,085 text features consist of 5,985 Medical Subject Headings terms (MeSH), and 100 word embedding vectors. We included the MeSH terms since they contain information regarding the research topic or target disease of the clinical trial, a factor reported to be related to accrual success in prior literature23,25,35,38. The word embedding features are constructed to capture the information contained in the “Detailed Description” field of ClinicalTrial.gov. The party responsible for a trial is instructed to provide the following information in this field: “Extended description of the protocol, including more technical information, if desired. Do not include the entire protocol; do not duplicate information recorded in other data elements, such as Eligibility Criteria or outcome measures”. NLP methods are ideal for capturing information in this field since it contains unstructured textual data. We used BioWordVec39, a pre-trained Doc2Vec model, to embed the “Detailed Description” of the trial into vectors of length 100. BioWordVec was derived from a biomedical corpus based on PubMed data contains 27,599,238 articles and MeSH terms. Benchmarking indicated that BioWordVec demonstrated superior performance to other embeddings for tasks in the biomedical domain.

Analytical strategy for predictive modeling

Overall design

To evaluate the performance of predicting future accrual failure based on historical data, we implemented a prospective cross-validation design, where clinical trial data from 1995 to 2022 were divided into discovery data and validation data. The discovery data consists of data from clinical trials that occurred earlier in time, whereas the validation data consists of data from clinical trials that occurred later in time. To evaluate the model performance over time, we evaluated five pairs of discovery and validation datasets. The five discovery datasets are all trials initiated during and before 2012, 2014, 2016, 2018, and 2020. Their corresponding validation datasets are all trials initiated in 2013–2014, 2015–2016, 2017–2018, 2018–2020, and 2021–2022 (Fig. 1).

Classification

We considered the following classification methods: multinomial logistic regression, random forest (mtry = sqrt(number of variables), number of trees = 500), and Adaptive Boosting, i.e. Adaboost (number of trees = 500). We used the multi-class version of these algorithms to categorize the outcome into three categories: completed (class 0), terminated for reasons unrelated to accrual (class 1), and terminated due to accrual failure (class 2). We chose the multi-class setup since it gives better performance compared to directly predicting the binary outcome of if the trial terminated due to accrual in our initial exploration (Supplemental Table S2).

We provide brief descriptions of the three classification method below, and also supplied reference to more detailed discussions of them.

Multinomial logistic regression40 is a classification method that generalizes logistic regression to multiclass problems, where the outcome of the prediction is a categorical with more than two classes. The Multinomial logistic regression describe the probability of outcome \(\:Y\) being in class \(\:c\) with a generalized linear combination of the predictors\(\:\:\varvec{X}\). \(\:P\left(Y=c\right)=\:\frac{{e}^{{\varvec{\beta\:}}_{\varvec{c}}\varvec{X}}}{{\sum\:}_{i}{e}^{{\varvec{\beta\:}}_{\varvec{i}}\varvec{X}}\:},\:i\le\:C\), where \(\:C\) is the total number of outcome class.

The random forest41 is an ensemble learning method. It constructs an ensemble of decision trees and the prediction is made by voting using the ouput of all the decision trees. Specifically, the random forest is a ensemble \(\:e\left(\varvec{X}\right)\) of \(\:K\) decision Trees \(\:{T}_{1}\) to \(\:{T}_{K}\): \(\:e\left(\varvec{X}\right)=({T}_{1}\left(\varvec{X}\right),{T}_{2}\left(\varvec{X}\right),\dots\:,\:{T}_{K}\left(\varvec{X}\right))\), The estimated probability of an observation being associated with class \(\:c\) is determined by the proportion of the trees that returns class \(\:c\) as output, i.e., \(\:P\left(Y=c\right)=\frac{{\sum\:}_{i}{(T}_{i}\left(\varvec{X}\right)=C)}{K}\) .The random in random forest comes from the fact that it uses bootstrap samples to build each decision tree and randomly select a subset of features when considering a candidate split.

AdaBoost42 is also an ensemble learning method where the predictions of many weak learners are combined into a weighted sum that represents the final output of the boosted classifier, i.e. \(\:e\left(\varvec{X}\right)=\:{\alpha\:}_{1}{T}_{1}\left(\varvec{X}\right)+{\alpha\:}_{2}{T}_{2}\left(\varvec{X}\right)+{\alpha\:}_{3}{T}_{3}\left(\varvec{X}\right)\)…+ \(\:{\alpha\:}_{K}{T}_{K}\left(\varvec{X}\right)\), where \(\:T\) represent each individual weak learner and \(\:\alpha\:\) represents their weights. We used decision tree as the weak learner (hence the notation \(\:T\)), since our outcome is categorical. AdaBoost is adaptive in the sense that subsequent weak learners are constructed to focus on those instances misclassified by previous classifiers.

Feature selection

For the feature selection, we use all features, fisher’s test43, and generalized local learning (GLL). The fisher’s test assesses the univariate correlation between the outcome and individual candidate predictors, whereas the GLL assesses the conditional dependence among the outcome and a candidate predictor conditioned on combinations of other candidate predictors. Under broad assumptions, GLL guarantees the selection of the most compact (i.e., minimal) set of variables that contain the maximal information regarding the prediction target. GLL in addition to being theoretically optimal, has also been shown to be highly successful in real world benchmarks and applications, and finally possesses causal interpretability under well-defined conditions27,28. Specifically, we used the GLL variant GLL-PC (K= 1, 2, 3).

Model selection and performance estimation

The models were developed on the discovery data. The performance of the models was validated with cross-validation in the discovery data to estimate the model performance on data with a similar distribution as the discovery data. To test the generalization performance of these models to future data, the models were applied to validation data. To select the model that results in the best predictive performances among several model families and tune parameters for each, and obtain unbiased performance estimation on the discovery datasets, we used a five-fold nested-cross-validation procedure (NCV). The inner loop of the NCV is used to select the best classification, feature selection, and their hyperparameter combinations, and the outer loop of the NCV evaluates the performance of the selected models. The nested-cross validation procedures were repeated four times (we refer to each of them as a NCV repeat) to reduce the variation related to random cross-validation splits (see the “Imbalance” subsection below) and splitting the data into five folds. We conducted model selection and performance estimation based on the model’s ability to determine if the trial terminated due to accrual (e.g. AUC for distinguishing class 2 vs. the rest), since this is our outcome of interest. For detailed description of the NCV protocol can be found in here44.

Missing values

Treatment for missing values was incorporated into the modeling pipeline so that imputation on the validation data is done according to the distribution of the discovery data. This prevents information leakage (i.e., to ensure that the error estimates are not biased). Median imputation was used for the continuous variables, and missing indicator columns were added to retain the missingness information. For the categorical variables with missing data, we added a “missing” level to the categories for that variable to represent the missingness information. Mesh and embedding variables are free of missingness. Out of 87 design variables the percentage of missingness ranges from 2 to 33%, among which 80 variables do not have any missing value. More than 91% of the variables have missingness less than 2%. The missingness are due to the corresponding values not being reported in clinicaltrials.gov.

Information content analysis

To examine the predictive performance of the two different types of features in the dataset (design features and text features), we trained classifiers on them individually and compared the predictive performances to the model trained with all features.

Imbalance

The proportion of trials that terminated due to accrual failure in our dataset is 2,979, constituting 5.59% of the total number of trials. An imbalance in the proportions of different outcome classes often results in suboptimal performance45,46. Therefore, we explore if subsampling, a common technique to handle imbalanced data, improves performance. We explored four subsampling settings when training the models: (1) C1TO1TA1: sampling equal number of trials that were completed (C), terminated due to other reasons (TO), and terminated due to accrual issues (TA). (2) C2TO1TA1: sampling twice as many completed trials, compared to terminated due to other reasons, and terminated due to accrual issues (3) C5TO1TA1: sampling five times as many completed trials, compared to terminated due to other reasons, and terminated due to accrual issues (4) No subsampling. For the first three subsampling settings, the number of TA trials is the smallest of the three categories, so all of them were always sampled. For C trials and TO trial, a random subset of observations were sampled in each NCV repeat. For the last subsampling setting, i.e. no subsampling, all observations are used. The subsampling was only conducted on the discovery data when training the model. The validation data were not subsampled.

Performance metrics

We used area under the receiver operating characteristic curve (AUC), sensitivity, specificity, precision, and negative predictive value to evaluate the predictive performance of the models. We used the Brier score to evaluate model calibration. The perfect prediction will have AUC of 1, Brier score of 0. Random guess will result in AUC of 0.5 and Brier score of 0.25.

Improving predictive models for translation into decision support tools

Model calibration

The close correspondence between model predicted risk vs. observed risk is important if the model is to be deployed in a real world setting47. The deviation of model predicted risk from the actual risk can result in model misinterpretation and misuse. Therefore, we evaluated the calibration of our models with the Brier Score48. To improve model calibration, we applied isotonic regression, Platt scaling and spline calibration49 to recalibrate models prediction on the discovery data, and evaluated model calibration on the validation data with Brier Score.

Prediction with reject option

Prediction with reject option is a framework aiming to prevent misclassification by not making a prediction for a subset of observations50,51,52. When the cost of misclassification exceeds that of withholding a decision, prediction with reject option is preferred. In our application, the costs of misclassification include the cost of starting a trial when it would fail accrual and the cost of not starting a trial when it would succeed in accrual. The cost of withholding decision is the additional cost associated with deciding if the trial is to be started, such as, the cost of manual review by a group of experts that will lead to a decision outside the scope of the model. To explore if prediction with reject option improves predictive performance, we implemented a method termed “double threshold”. The intuition underlying this method is that, the model predicted score relates to the confidence of model prediction. And the confidence of model prediction are lower for observations with predicted scores that fall in the midrange of the predicted values. We empirically evaluate this by withholding prediction for the observations with predicted scores in the midrange and examine if the predictive performance improves for the rest of the observations. To achieve this, we introduced two thresholds on the predicted score, such that the trials with scores between these thresholds are classified as undecided. The trials with scores under the lower threshold are predicted to succeed in accrual. And the trials with scores higher than the upper threshold are predicted to fail in accrual. The selection of the thresholds is done by a grid search on the discovery data. The performance of the double threshold is evaluated on the validation data.

Results

Characteristics of the data

Our dataset contains 45,298 completed trials, 4,986 trials terminated due to non-accrual issues, and 2,979 trials terminated due to accrual issues. Figure 1 shows the number and the distribution of the three trial categories: completed (C), terminated due to other reasons (TO), and terminated due to accrual issues (TA). It is notable that the percentages of trials in the three categories changed over time. This could be due to a combination of the following factors: (1) actual percentages of trials in different categories changed over time, (2) changes in the reporting requirements for clinical trials over time53,54, and (3) many of the trials that started in the more recent years are still ongoing, resulting in a bias in the estimated percentages of trials in different categories. For example, out of all the trials that started in 2021, we observed them for less than 2 years (up to the point of our data download on Sep, 2022). Supplemental Table S3 shows the percentages of trials that are completed or terminated till our data collection time out of the total number of trials started in a particular year. Table 1 shows descriptive statistics for key characteristics of the trials in our study.

Predictive modeling results

In this section we present predictive modeling results for predicting trial termination due to accrual. We first present sensitivity analysis for different level of potential noise in the outcome and for different subsampling. We than focused on reporting results for the dataset with low noise level in the outcome without subsampling. We presented results from models using all features, and compared that the models using design features and text feature respectively to assess the information content in different feature types.

Influence of noise in outcome category and subsampling on model performance

As stated in the method section, we faced two choices when deciding what trials to include when training our models. First, whether to include data from trials that potentially contain errors related to the outcome category. Second, whether to use subsampling to address class imbalance.

To assess the influence of potential noise in outcome category on predictive performances, we ran models based on data excluding and including the potentially problematic trials. The average validation AUC over all subsampling schema for the selected models determined by the model selection procedure on the discovery dataset was 0.714+/-0.033 and 0.706+/-0.022 respectively, for models built on data excluding or including the potentially problematic trials.

To assess the influence of subsampling on predictive performances, we applied different ratios of subsampling on the discovery datasets and evaluated the performance on the validation data where the proportion of different outcome categories were unaltered. We observed that when we train our models without subsampling (i.e. preserving the original proportion of outcome where 5.59% of trials terminated due to accrual), the performance on the validation data is on average nominally higher compared to when the three subsampling procedures were applied. Specifically, the average AUC for the model determined by the model selection procedure applied to validation datasets without subsampling is 0.732+/-0.028. Whereas, the average AUC for C1TO1TA1, C2TO1TA1, C5TO1TA1 are 0.693+/-0.032, 0.701+/-0.03, 0.721+/-0.015, respectively.

Given that excluding potentially problematic trials and without subsampling achieved nominally the best results, we focus on reporting results based on these models. The results on the dataset including potentially problematic trials, with subsampling C1TO1TA1, C2TO1TA1 and C5TO1TA1 can be found in supplemental Table S4.

Predictive performance of models built with all features

We first assess what is the best predictive performance can be achieved using all features. Using all 6,172 features, the model selected by the model selection procedure achieved good cross-validation predictive performance in the discovery datasets. The average cross-validation AUC over all discovery datasets are 0.733+/-0.03. The cross-validation performance is stable over the five discovery data sets, indicating consistent performance over time (Fig. 2c). Applying the models derived from the discovery dataset to the validation data resulted in similar performance. The average AUC for the prospective validation datasets are 0.732+/-0.028. The performance on the validation datasets increases over time (Fig. 2c). We hypothesize that this is largely due to the change of trial composition over time. Specifically, the more recent validation data contains more trials with shorter duration. When we applied our model to subsets of trials that completed or terminated within 2,4,6, and 8 years, the predictive performances decreased as the timespan increased, with average AUCs of 0.747, 0.728, 0.718, and 0.704, respectively (details can be found in supplemental Table S5). This result is consistent with our hypothesis.

Fig. 2
figure 2

Predictive performance of Models Built with Different Feature Types: (a) Design Features, (b) Text Features, and (c) All Features (Design + Text Features). The AUC of the model selected by the models selection procedure were estimated with cross-validation on the discovery datasets (yellow lines) and prospectively on the validation datasets (red lines). X-axis tick label on top of the subplots indicate the timespan of the discovery datasets. X-axis tick label on the bottom of the subplots indicate the timespan of the validation datasets.

Full size image

Information content in models with different feature types

To assess the information contained in the design features and the text features regarding accrual failure, we built models using features from these domains respectively. The performance of the models using the text features resulted in cross-validation AUC = 0.682+/-0.029 and prospective validation AUC = 0.681+/-0.029 over all the discovery datasets. It is significantly worse compared to the models using all features, with cross-validation AUC = 0.733+/-0.029 and prospective validation AUC = 0.732+/-0.028 (cross-validation AUCs: t=-11.2, p < 0.01; prospective validation AUCs: t=-2.87, p = 0.02). The performance of the models using design features resulted in cross-validation AUC = 0.744+/-0.018 and prospective validation AUC = 0.737+/-0.038, it is not statistically significantly different from the models using all features (cross-validation AUCs: t = 0.33, p = 0.756; validation AUCs: t=-0.19, p = 0.851). As shown in Fig. 2, the cross-validation performance of models using different feature types are also stable over time. These results indicate that the hand-crafted design features representing factors previously reported in the literature contain more information compared to the text features (mesh terms and embedding vectors) we constructed. Further, models using both the design and text features do not result in better performance for accrual failure prediction compared to models using only the design features alone.

Improving models for decision support

In this section we describe several methods we employ to enhance various aspects of model translation, including reducing model size, refining model calibration, and improving predictive performance by introducing prediction with reject option.

Identifying models with a smaller set of input features

The models selected by our models selection procedure for all discovery datasets typically contain all 6,172 features. These models can be converted to a decision support tool. However, the decision support tool requires relatively high resource commitment. It will require all 6,172 features as input, extracted and computed from raw data, adequate computational resources to store and execute the prediction model, and expert monitoring and maintenance. Though missing imputation can be conducted at prediction time if not all features are available, but that may reduce model performance55,56.

To improve the model with the goal of obtaining a cost-effective decision support tool, we examined if there are models with smaller numbers of features that achieve similar predictive performance. As mentioned in the previous section, using the design features achieved predictive performance that is not statistically significantly different from using all features. Therefore, using only design features is one solution to reducing the number of features while retaining model performance. In this section, we explore potential further reductions of the number of features in the model using GLL-PC feature selection. We chose the GLL-PC feature selection since in principle GLL-PC can identify the smallest feature set that preserves the maximal information regarding the target of interest27,28. As shown in Fig. 3b and d, the GLL-PC models applied to all 6,127 features resulted in models with, on average, 718 features, resulting in average cross-validated AUC = 0.722+/-0.003 (as compared to cross-validated AUC = 0.733+/-0.029 from the model with all 6,127 features) and prospective validation AUC = 0.706+/-0.029 (as compared to AUC = 0.732+/-0.028 from the model with all 6,127 features). The predictive performance difference between the GLL-PC vs. the full model is not statistically different on both cross-validation set, with t = -1.52, p = 0.138 and prospective validation set, with t = 1.9306, p = 0.064. As shown in Fig. 3a and c, The GLL-PC models applied to the design features resulted in models with on average 42 features, resulting in average cross-validated AUC = 0.724+/-0.003, (statistically significantly different as compared to cross-validated AUC = 0.744+/-0.018 from the model with all 87 design features, t = -11.476, p < 0.01) and prospective validation AUC = 0.705+/-0.029 (not statistically significantly different compared to prospective validation AUC = 0.737+/-0.0383 from the model with all 87 design features t = 1.4972, p = 0.1753). Moreover, the GLL-PC models also demonstrated stable performances over time. Our results suggests that, reduction of the number of features can be achieved by using the GLL-PC feature selection impacting model performance marginally or not at all. Selected AUCROC (area under the receiving operating curve) plots are shown in Fig. 3e and f. The features selected in the most compact models (design features selected by GLL-PC) and feature importance are presented in supplemental Table S6a and b.

Fig. 3
figure 3

Models Constructed with the GLL Feature Selection Showed Similar Predictive Performances Using a Smaller Number of Features. This is observed both in the cross-validated performance estimation in the discovery datasets (a, b) and the prospective validation performances (c, d). For models using design features (a, c) and all features (b, d). For (a–d), X-axis tick label on top of the subplots indicate the timespan of the discovery datasets. X-axis tick label on the bottom of the subplots indicate the timespan of the validation datasets. Panel (e), (f) shows ROC curves for model performance on the validation sets with design features and all features respectively. For legibility, we only show ROC curves for year 2017–2018, ROC curves on the other validation datasets looks similar and are included in supplemental Fig. S2.

Full size image

Model calibration

Another important consideration for a decision support tool is model calibration, which is how closely the model predicted probability of failure due to accrual aligns with the actual probability47. To assess the model calibration, we computed the Brier Score. The average Brier score for the models selected by the model selection procedure is 0.274+/- 0.005 and for GLL-PC is 0.274+/-0.005 on the validation data. To improve the calibration we applied the isotonic regression method, this resulted in significant improvement in calibration (p < 0.01). After model calibration, the average Brier score for the models is 0.068+/-0.017 and for GLL-PC is 0.071+/-0.021 on the validation data. We also applied two other calibration methods Platt scaling and spline calibration. The three methods work similarly well, we report isotonic regression in the main result section and the results of other methods in the supplementary Table S7.

Prediction with reject options

To further improve model performance and applicability in real-world decision support settings, we investigated the model performance under learning with reject option (LRO). Specifically, we consider three potential decision-support recommendations given the prediction output of the predictive model: (1) model prediction has low reliability, recommend expert review; (2) model predicts with high confidence for accrual success, recommend proceeding with current accrual plan; (3) model predicts with high confidence for accrual failure, recommend delay the initiation of accrual and explore additional resources to improve accrual. We examined one simple method to categorize model predictions into the above three categories, i.e., implementing two threshold values on model prediction. The predictions that are lower than the lower threshold are considered to be in category (2), the predictions that are higher than the higher threshold are considered to be in category (3), and the predictions that are between the two thresholds are considered to be in category (1). Different values of the thresholds would result in different predictive performances for the trials in (2) and (3), and will also affect the number of trials needing manual review, increasing institutional burden. Therefore, the optimal threshold for different institutions might be different application settings, depending on the expectation of model performance and available resources, i.e. the trade-off between misclassification cost and rejection cost.

We illustrate this method by applying different thresholds to the model using all features, at 20%, 30%, and 40% rejection rate of the total number of trials. In general, we found that as the percentage of rejects increases the predictive performance of the model also increases. The rejection rate of 20%, 30%, and 40% are AUC = 0.730+/-0.018, 0.747+/-0.019, and 0.759+/-0.022, respectively, averaged over the five prospective validation dataset. Among three rejection rates, 40%+/-2% showing significant improvement over that without rejection (AUC 0.732+/-0.028, p = 0.0498). These results indicate that model performance can be further improved by withholding decisions on trials with low prediction reliability. Supplemental Table S8 shows the AUC, sensitivity, specificity, positive predictive value (PPV) and negative predictive value (NPV) for all prospective validation data and different rejection rates. Performances are stable over time except for year 2021–2022. This is likely related to this validation set is small and has different trial proportions compared to the other validation sets (Fig. 1a and b).

Discussion

The key contributions of this study are threefold. First, we constructed a dataset for predicting clinical trial failure due to accrual based on the clinicaltrial.gov data with information for 57,846 trials. We manually annotated the reasons for failure for 7,965 failed trials to construct our outcome of interest. We also extracted and constructed features informed by prior literature and using data-driven NLP methods. This dataset can benefit future studies with similar goals. Secondly, we successfully constructed models for predicting clinical trial accrual failure with good performance that generalizes well to prospective data through a 10-year span. To the best of our knowledge, this is the first study to develop models for predicting clinical trial failure due to accrual based on a large dataset with a comprehensive set of trial features. Thirdly, we demonstrated that enhancements can be made to the models to further improve their performance and applicability in real-world decision support settings.

Several directions for future work can address the limitations of the current study and may result in improved prediction performances. The first direction for future work is to evaluate the models built in the current study in a dataset with percentages of trials failed due to accrual that better approximate that of the real world. Our dataset, extracted from clinicaltrial.gov, has an accrual failure rate of 5.59%, which may not reflect the accrual failure rate in the real world due to bias in reporting53,54. We expect the model performance to hold if the trials failed due to accrual reported on clinicaltrial.gov was representative of all trials that failed due to accrual. Otherwise, our models are biased due to the bias in the data and may result in reduced model performance when applied in a real-world setting. Further, building models de-novo in a dataset with percentages of failed trials that better approximate the real-world can result in improved predictive performances. Secondly, constructing additional features regarding the trials can potentially improve the predictive performance. Many barriers and facilitators of accrual identified in prior literature were not captured in clinicaltrial.gov. Examples include patient compensation25,35,] patient burden25,35,57,58,59, the effectiveness of communication to patients23,35,57,58,60,61,62 and among the trial team35,36,57,58,61,63, concurrent trials competing for participants and the trial team25,35. These data are available and can be constructed from enterprise-level databases such as the clinical trial management systems. We are not aware of an existing dataset that is representative of the real-world accrual failure rate, contains a large variety of trials covering many diseases and geographical areas, and has a comprehensive set of trial characteristics. Constructing such a dataset can greatly enhance the ability to predict accrual failure. Thirdly, our models only flag the trials that are more likely to fail due to accrual, but do not point to interventions that can potentially lead to accrual improvement. The identification of intervention requires the knowledge of causal factors impacting accrual. In general, models and risk factors derived solely for predictive purpose are associative, and are not guaranteed to be causally relevant due to the potential presence of observed and hidden confounding. Applying computational causal modeling techniques64,65 to a dataset that contains a large number of potential remediable causal factors for accrual can reveal trial-specific interventions for improving accrual. Lastly, our study identified models with good predictive performance and a small set of parameters that are cost effective to implement and maintain. In addition, adding the prediction with reject option further enhances the models performance. Our study provides a set of models that can be implemented in the real-world setting, however, the specific model of choice (e.g. percent of reject) depends on several aspects in the application setting that might be intertwined, including what decisions are to be made given the model output, the expected model performance, and the available resource. For example, an institution that have ample existing resource for improving accrual may choose a larger percent of reject value such that more trials will go through an expert review process for potential improvement of accrual. In general, institution-specific information about the cost of the following items can be leveraged to formally guide the choice of models44 : false positive (model judge the trial to be able meet accrual goal but in fact the trial would not), false negative (model judge the trial to not be able to meet accrual goal but in fact the trial would), expert review for the reject trials, and the institution’s goals and budget for clinical trials. The financial implications of model implementation in specific institutions should be evaluated in a case by case manner.

Conclusion

The current study produced predictive models for accrual failure with good predictive performance that is stable over a ten year period. We also identified models that are better suited for translation into a real-world decision support tool, characterized by great calibration, cost-effectiveness for implementation and maintenance, and an option to withhold prediction. This study demonstrated a first step towards a decision support tool for clinical trial resource allocation.