Introduction

In the present scenario, the growth of Internet facilities and the establishment and propagation of social platforms, namely Reddit, Instagram, and Facebook, have enabled an essential influence on the amount of content spreading in social media1. In many cases, the content distributed is unique or is deployed for entertaining reasons; in other instances, the manipulation could be directed onto deception principles, with criminal and governmental results, such as applying the fake content as a digital sign in a crime analysis2. Manipulation of Images or Video mentions some actions carried out on digital content with software editing devices. Notably, the copy-move model duplicates a portion of an image and then pastes it toward similar imageries3. With the development of editing devices, features of fake images have risen, making them seem like the original images for human vision. Moreover, post-processing manipulations like JPEG brightness modifications, equalization, or compression can decrease the hints missed by manipulation and make it challenging to identify4. Respecting how simple it is to generate fake images as a portion of a false news broadcast, there are crucial requirements for finding models that could be maintained using modern technologies in fraud assistance5. The reliability of an image is confirmed over more than one tactic, either individually or in combination, testing an image for reality. A common approach is CMFD, which includes cloning or duplicating an image patch into the same image. These patches to be cloned or copied are both regular and irregular arrangements6. CMFD is growing in reputation owing to a larger portion of its convenience. As its new expansion nearly the turn of the present day, the primary reason for copy-move forgery detection (CMFD) was verifying when the imaging analysis in question, also called the queried features some parts, which are cloned, and whether these clonings were implemented with malevolent intention. The three major kinds of CMFD are affine, complex, and plain7.

The initial CMFD examinations typically dealt with basic cloning. Intriguingly, in preceding research, the investigators establish that human decisions overcome machine learning (ML) concerning computerized copies. This may be produced by the recent absence of photorealism, discovered in most computer graphics devices. A considerably deep learning (DL) model is presented to resolve this problem8. As the collection of video control processes propels and extends, the engineered and altered video becomes unclear from the unique video. According to the assessment of several models, novel methods are needed, including arranging changed video to adapt to its changing type and performing changing recognition independent of altering. Maintain faith in the reliability of video content, and it is essential to make processes that can differentiate and control video processing. The methods to tackle one sort of damage are mostly undeserving and prone to various simulations. The functioning of this method depends on the codecs applied for video content and the compression8. The rapid expansion of digital content and the rise of online platforms have significantly improved the amount of shared media, making it easier for manipulated content to spread. As editing tools become more advanced, detecting digital forgeries, particularly in videos, has become increasingly difficult9. The ability to alter and manipulate exact video content poses serious challenges to content authenticity, specifically in crime investigations or news reporting. Identifying these manipulations promptly and accurately is significant to maintaining trust in digital media. Therefore, developing advanced techniques for detecting video forgeries is vital to safeguard the integrity of online content and prevent misuse10.

This manuscript presents an Enhancing Copy-Move Video Forgery Detection through Fusion-Based Transfer Learning Models with the Tasmanian Devil Optimizer (ECMVFD-FTLTDO) model. The objective of the ECMVFD-FTLTDO model is to perceive and classify copy-move forgery in video content. At first, the videos are transformed into distinct frames, and noise is removed using a modified wiener filter (MWF). Next, the ECMVFD-FTLTDO technique employs a fusion-based transfer learning (TL) process comprising three models: ResNet50, MobileNetV3, and EfficientNetB7 to capture diverse spatial features across various scales, thereby enhancing the capability of the model to distinguish authentic content from tampered regions. The ECMVFD-FTLTDO approach utilizes an Elman recurrent neural network (ERNN) classifier for the detection process. The Tasmanian devil optimizer (TDO) method is implemented to optimize the parameters of the ERNN classifier, ensuring superior convergence and performance. A wide range of simulation analyses is performed under GRIP and VTD datasets. The major contribution of the ECMVFD-FTLTDO approach is listed below.

  • The ECMVFD-FTLTDO method begins by transforming videos into individual frames, then noise removal using a MWF technique to improve image quality. This preprocessing step enhances the clarity of the frames for enhanced analysis. Refining the visual data, the method prepares the input for more precise feature extraction and detection tasks.

  • The ECMVFD-FTLTDO approach utilizes a fusion-based TL approach that integrates ResNet50, MobileNetV3, and EfficientNetB7 models. This integration captures a wide range of spatial features across diverse scales, improving the method’s capability to recognize intrinsic patterns. By implementing the merits of multiple models, the approach enhances feature extraction and overall detection performance.

  • The ECMVFD-FTLTDO model utilizes an ERNM classifier to detect tampered regions within videos. This approach uses the temporal dependencies in video frames to detect inconsistencies indicative of tampering. By integrating ERNN, the methodology improves its capability to capture dynamic patterns and improve detection accuracy.

  • The ECMVFD-FTLTDO technique utilizes the TDO method to fine-tune the parameters of the ERNN classifier, improving its performance. By optimizing the model’s weights, TDO confirms more accurate detection of tampered regions in videos. This optimization process significantly enhances the classifier’s efficiency and overall detection accuracy.

  • The novelty of the ECMVFD-FTLTDO method is in integrating multiple pre-trained models within a fusion-based TL framework, incorporating ResNet50, MobileNetV3, and EfficientNetB7 to capture diverse features. Furthermore, the TDO model is optimized to optimize the ERNN classifier parameters, improving the model’s capability to detect tampered video content. This integration of advanced techniques significantly enhances the accuracy and robustness of the detection process.

Literature survey

Sabeena and Abraham11 developed a novel AI method using the DL theory for progressive copy-move image counterfeit localization and detection. In this paper, image segmentation, feature extraction, and restricting the fake part in an image utilize the Convolutional Block Attention Module (CBAM). In particular, channel and spatial attention features were merged by the CBAM to take context information completely. Moreover, deeper matching was applied to calculate Atrous Spatial Pyramid Pooling (ASPP), and feature mapping self-correlation was used to combine the scaled correlation mappings to build the coarse mask. Lastly, bi-linear upsampling was completed to resize the forecast output to dimensions similar to the new image. Maashi et al.12 presented a reptile search algorithm with a deep TL-based CMFD (RSADTL-CMFD) technique. The proposed method utilizes NASNets to extract features. This method additionally uses the RSA for parameter tuning. This model enhances the network’s hyperparameter, allowing the technique to rapidly adjust to various tasks of forgery detection and attain better performance. Eventually, XGBoost successfully uses the features removed from the DL technique to classify areas inside the images. Timothy and Santra13 introduced a new DL technique that utilizes the structural strengths of CNNs, GNNs, ResNet50, VGG16, and Mobile Net. These networks are improved by extracting their novel classifier and applying a novel one specially created for binary forgery classification. Vaishnavi and Balaji14 implemented a new intellectual DL-based CMIFD detection (IDL-CMIFD) model. This model includes the Adam optimizer with an EfficientNet to develop a valuable collection of feature vectors. Furthermore, a chaotic monarch butterfly optimizer (CMBO) with the DWNN method was employed for classifier principles. The CMBO model has been applied to the optimum tuning of the parameter convoluted in the DWNN method. Amiri et al.15 designed a method (SEC), a three-way model depending on a developmental model, which might identify fake blocks well. During this initial portion, suspicious points were detected with the assistance of the SIFT technique. Next, they are discovered using the equilibrium optimizer method. Finally, colour histogram matching (CHM) equals questionable blocks and points. Zhao et al.16 proposed an effectual end-wise DL model for CMFD, applying a span-partial architecture and attention mechanism (SPA-Net). This technique removes features approximately with a preprocessing unit. It subtly removes deep feature mapping with attention mechanism and span-partial architecture as the SPA-Net component of the feature extractor. This span-partial architecture has been calculated to decrease the redundant feature information. A feature upsampling unit has been used to up-sample the features to new dimensions and generate a copy-move mask.

Zhao et al.17 utilized enhanced DL models and presented a strong localization method using a convolutional neural network (CNN)-based spectral study. The feature extraction module removes deep features from Mel-spectrograms during this localization method. However, the Correlation Detection Module spontaneously selects the correlation among this deep feature. Lastly, the module of Mask Decoding graphically discovers the forged parts. Mohiuddin et al.18 presented an ensemble-based model for detecting fake frames from a video. In this approach, initially, the frames were preprocessed, and 3 various types of features—Local Binary Pattern (LBP), Haralick, and custom Haralick were removed from every video. Then, lexicographical sorting was carried out to successfully organize the frames by taking related feature values. A filter model was employed to remove the false recognition. Alhaji, Celik, and Goel19 present a novel approach to deepfake video detection by combining ant colony optimization–particle swarm optimization (ACO-PSO) features with DL models. ACO-PSO extracts spatial and temporal characteristics from video frames to identify subtle manipulation patterns, which are then used to train a DL classifier. Nagaraj and Channegowda20 aim to enhance video forgery detection by employing spatiotemporal averaging for background information extraction, feature vector reduction with ResNet 18, and a stacked autoencoder for improved forgery detection and reduced dimensionality. Chaitra and Reddy21 present a TL-based method for CMF detection using a Deep Convolutional Neural Network (Deep CNN) with pre-trained GoogLeNet parameters. A novel optimization algorithm, Fractional Leader Harris Hawks Optimization (FLHHO), is used to adjust the Deep CNN’s weights and biases for improved accuracy. Sekar, Rajkumar, and Anne22 propose an optimal DL method for deepfake detection, comprising face detection with Viola–Jones (VJ), preprocessing, texture feature extraction with a Butterfly Optimized Gabor Filter, spatial feature extraction using Residual Network-50 with Multi Head Attention (RN50MHA), and classification with Optimal Long Short-Term Memory (LSTM), optimized by the Enhanced Archimedes Algorithm (EAA). Alrowais et al.23 introduce the Deep Feature Fusion-based Fake Face Detection Generated by Generative Adversarial Networks (DF4D-GGAN) technique for detecting real and deepfake images, using Gaussian filtering (GF) for preprocessing, feature fusion with EfficientNet-b4 and ShuffleNet, hyperparameter optimization via an improved slime mould algorithm, and classification with an extreme learning machine (ELM).

Girish and Nandini24 introduce a novel video forgery detection model using video sequences from the SULFA and Sondos datasets. The model applies spatiotemporal averaging for background extraction, uses GoogLeNet for feature extraction, and selects discriminative features with UFS-MSRC to improve accuracy and reduce training time. An LSTM network is then employed for forgery detection across different video sequences. Almestekawy, Zayed, and Taha25 develop a stable and reproducible model for Deepfake detection by integrating spatiotemporal textures and DL features, utilizing an improved 3D CNN with a spatiotemporal attention layer in a Siamese architecture. Zhu et al.26 propose a Contrastive Spatio-Temporal Distilling (CSTD) approach, utilizing spatiotemporal video encoding, spatial-frequency distillation, and temporal-contrastive alignment to improve detection accuracy. Uppada and Patel27 present a framework for detecting fake posts by analyzing visual data embedded with text. Using Flickr’s Fakeddit dataset and image polarity data, the framework employs separate architectures to learn visual and linguistic models, extracting features to flag fake news. Xu et al.28 introduce a novel forgery detection GAN (FD-GAN) with two generators (blend-based and transfer-based) and a discriminator, using spatial and frequency branches. Srivastava et al.29 propose a copy-move image forgery detection method integrating Gabor Filter and Centre Symmetric Local Binary Pattern (CS-LBP) for feature extraction, followed by key point matching using Manhattan distance and classification with Hybrid Neural Networks with Decision Tree (HNN-DT). Yang et al.30 introduce AVoiD-DF, an audio-visual joint learning approach for detecting deepfakes using audio-visual inconsistency. It uses a Temporal-Spatial Encoder for embedding information, a Multimodal Joint-Decoder for feature fusion, and a Cross-Modal Classifier to detect manipulation. The paper also introduces a new benchmark, DefakeAVMiT, for multimodal deepfake detection. Yan et al.31 propose a Latent Space Data Augmentation (LSDA) model to enhance deepfake detection. MR, Kulkarni, and Biradar32 introduce an Enhanced Flower Pollination-Adaptive Elephant Herd Optimization (EFP-AEHO) model for optimizing Deep Belief Network (DBN) weights. It improves performance by using Eigenvalue Asymmetry (EAS). Liao et al.33 propose the facial-muscle-motions-based framework (FAMM) model. It locates faces, extracts facial landmarks, and models facial muscle motion features. Dempster-Shafer theory is used to fuse forensic knowledge for final detection results.

Proposed methodology

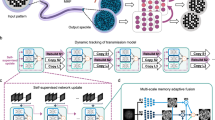
This manuscript presents an ECMVFD-FTLTDO model. The model’s major aim is to detect and categorize copy-move forgery in video content. It comprises various stages, such as preprocessing, TL model fusion, ERNN detection, and TDO-based parameter tuning. Figure 1 reveals the complete process of the ECMVFD-FTLTDO technique.

Fig. 1
figure 1

Overall process of ECMVFD-FTLTDO approach.

Full size image

Stage I: preprocessing

In the first stage, the videos are converted into individual frames, and noise removal is done using MWF. The MWF-based preprocessing is a powerful technique for improving image quality before further analysis, specifically in video forgery detection. Unlike conventional filtering methods, MWF adapts to varying noise levels across the image, improving noise reduction while preserving crucial details. This capability to adjust to local image characteristics makes MWF highly effective in handling diverse noise types, which is common in real-world videos. The adaptability of the filter ensures that fine features, significant for detecting forgeries, remain intact while noise is minimized. Compared to other techniques, such as GFs, which apply uniform smoothing, MWF gives more precise and context-sensitive noise removal. This results in an enhanced performance during subsequent detection stages, resulting in more accurate detection of tampered regions in videos. Figure 2 illustrates the MWF architecture.

Fig. 2
figure 2

Overall structure of the MWF model.

Full size image

Convert videos into frames

Preprocessing by adapting videos into frames involves removing individual image frames from the video, allowing frame-by-frame study for tasks like object classification or detection34. This step shortens the processing by breaking the video into handy static images for further investigation or model input. The video is initially transformed into frames formulated below in the mathematical formulation.

$$I = \left\{ {f_{1} ,f_{2} ,f_{3} ,{ } \ldots ,f_{n} } \right\}$$
(1)

Here \(I\) represent the video frameset, and \(f_{n}\) denotes the ‘n’‐amount of frames.

Removal of noise

In this phase, the salt and pepper noise was removed utilizing MWF, giving a superior outcome to the usual WF. It is a Pixel-wise linear filter designed to assess the variance and mean of every pixel. The image \(I_{p}\) \(\left( {u,{ }v} \right)\) is formulated below,

$$I_{E} = I_{p} \left( {u,{ }v} \right) = \eta + \frac{{\left( {\sigma^{2} - r^{2} } \right)}}{{\sigma^{2} }}\left( {I_{i} \left( {u,{ }v} \right) - \eta } \right)$$
(2)

The formulation mentioned above specifies that \(\eta\) is the mean, \({\sigma }^{2}\) indicates the variance, \({r}^{2}\) refers to noise variance, \({I}_{i}\) denotes an image for noise removal, and \({I}_{E}\) is the improved image employed for further steps.

Stage II: feature extraction using fusion of TL models

Next, the ECMVFD-FTLTDO technique employs a fusion-based TL procedure comprising 3 methods: ResNet50, MobileNetV3, and EfficientNetB7. This is highly effective due to the unique merits each model brings to the table. ResNet50, with its deep architecture, outperforms capturing complex features through residual connections, making it ideal for handling complex patterns in images and videos. MobileNetV3, known for its effectiveness and lightweight design, is appropriate for real-time applications, giving fast processing without compromising accuracy. EfficientNetB7, on the contrary, balances both high performance and computational efficiency, making it a robust choice for large-scale data. By incorporating these models, the approach employs their complementary merits, enabling improved feature extraction across diverse scales and improving the overall detection capability. This fusion outperforms individual models by improving accuracy and efficiency in detecting forgeries, particularly in resource-constrained environments.

ResNet50

Average pooling was employed at first, and then the activation function of softmax was applied to generate a fully connected (FC) layer with 1000 nodes35. ResNet-50’s structure depends on the unique concept of the bottleneck residual block, which unites 1 × 1 convolutions, occasionally mentioned as a bottleneck, to decrease the matrix multiplication and the number of parameters. This design selection allows quicker training of individual layers. The structure contains numerous important modules and begins with a 7 × 7 kernel convolutional and 64 extra kernels utilizing a 2-sized stride. Then, a layer of max pooling with a 2-sized stride is practised. Furthermore, this design is improved by nine other layers, each consisting of a multiple repetition of 3 × 3 convolutional with 64 kernels, 1 × 1 convolutions with 256 kernels, and 1 × 1 convolution with 64 kernels. Next, an extra 12 layers were inserted, which contained 3 × 3 convolutional with 128 kernels, 1 × 1 convolution with 512 kernels, and four repetitions of 1 × 1 convolutions with 128 kernels. This sequence endures with 18 more layers containing varied convolutions, repeated 6 times, and succeeded by nine more layers featuring iteration of convolutions with fluctuating kernel dimensions. Lastly, this network used the softmax activation function to attain average pooling and an FC layer with 1000 nodes.

MobileNetV3

MobileNetV3 is the baseline method due to its trivial structure and creation. It is mainly suitable for resource‐constrained atmospheres without negotiating on performance36. This technique includes depth-wise separable convolution and effective constructing blocks, permitting it to extract significant features from imaging. The MobileNetV3 is employed to deploy the data joint throughout the training. This TL application allows the method to simplify the individual features accurately. The system perfectly exploits its vital size by involving pre-trained weight to distinguish related features. The traditional model made alterations to refine the MobileNetV3 technique to remove the related image feature. The first stage concerned is substituting the highest dual output layer of the MobileNet technique with a \(1\text{x}1\) point‐wise convolutional, enabling feature extraction from imageries.

This convolutional helps as a multi-layer perceptron and includes numerous non-linear processes for reducing dimensionality and image classification. Furthermore, \(1\text{x}1\) point‐wise convolutions were inserted at the topmost to adjust the weight for dissimilar databases depending on the classification task. Next, an output from the \(1\text{x}1\) point‐wise convolution employed for feature extraction was compacted, resulting in a 128-pixel image feature for all images. The MobileNetV3 technique concerns the attention mechanism deployed to the final and intermediate layer features of MobilenetV3. Both experience average and \(\text{max}\) pooling processes. Figure 3 depicts the infrastructure of MobileNetV3.

Fig. 3
figure 3

Framework of MobileNetV3.

Full size image

EfficientNetB7

The EfficientNet method is an effective method of classification. The compound coefficient is a simple and effective technique. Rather than randomly enhancing the depth, resolution, or width, compound scaling utilizes a pre-determined collection of scaling coefficients for measuring every dimension evenly. The EfficientNet structure contains a baseline system, represented by EfficientNet B0, which is the initial point for creating a compound scaling model. This method includes altering 3 main sizes: depth (\(\alpha\)), resolution \(\left(\beta \right),\) and width \(\left(\varphi \right)\). It uses a depth‐wise separable convolution block as its main block that involves depth‐ and point‐wise convolutions. This block aids in decreasing the difficulty of computational when upholding indicative power Compound scaling of numerous EfficientNet techniques, namely BO to B7, each having an increased ability. This structure balances performance and model size, making it effective for an extensive range of applications, chiefly in situations with limited computational sources.

Stage III: detection using ERNN classifier

For the detection process, the ECMVFD-FTLTDO approach utilizes an ERNN classifier37. This classifier is appropriate for video forgery detection because it can capture temporal dependencies between frames, which is crucial for analyzing dynamic video content. Unlike conventional feedforward networks, ERNN integrates feedback loops, allowing it to retain information from previous frames and better comprehend the sequence of events in video data. This makes ERNN effective at detecting subtle inconsistencies or tampering across multiple frames. Furthermore, ERNN can learn intrinsic patterns in sequential data, which is beneficial for detecting forgeries that may span several frames or involve minor alterations. Compared to other techniques, such as CNNs, which primarily concentrate on spatial features, ERNN’s capacity to process temporal relationships gives a distinct advantage in detecting video manipulations. Figure 4 depicts the structure of the ERNN model.

Fig. 4
figure 4

Architecture of the ERNN technique.

Full size image

The ERNN attains the selected feature and models intrusions devouring them. In the ERNN model, a buffering layer has been recognized as the recurrent layer that allows the hidden layer (HL) outputs to respond to themselves. ERNN permits the responses to be learned, identified, and given spatial and temporal tendencies. Therefore, the HL condition one through the former is repeated in the recurrent layer. As an outcome, the recurrent neuron counts are equivalent to the HL counts. Finally, the ERNN includes an input, output, a recurrent layer, and a HL that provides layered data. Every layer is offered in more than one neuron, and they utilize the computation of a non-linear function.

ERNN contains \(m\) and \(n\) neurons within the HL and input layer and a solitary output component. Assume \({x}_{it}(i=\text{1,2},\dots , m)\) indicates the set of neuron’s input vector at \(t th\) time. The output of the network at time \(t+1\) is signified by \({y}_{t+1}\), the output of the HL neuron at \(t th\) time is streamlined by \((0=\text{1,2},\dots ,\) \(n\)), and the recurrent layer neuron’s accomplishing has been characterized by \(({r}_{jt}=\text{1,2},\dots ,n\)). Node \(i\) within the neurons of the input layer is associated with node \(j\) in the HL by a weight called \({w}_{ij}\). The node is associated with the node \(j\) in the HL neurons and output by weights \(v_{j}\) and \(cj\), respectively. Nevertheless, all neurons’ inputs in the HL are accompanied by:

$$net_{jt} \left( l \right) = \mathop \sum \limits_{i = 1}^{n} w_{ij} x_{ij} \left( {l - 1} \right) + \mathop \sum \limits_{j = 1}^{m} c_{j} r_{jt} \left( l \right)$$
(3)
$$r_{jt} \left( l \right) = x_{jt} \left( {l - 1} \right),i = 1,2, \ldots ,n,j = 1,2, \ldots ,m.$$
(4)

During the output of hidden neurons as:

$$x_{jt} \left( l \right) = f_{H} \left( {net_{jt} \left( l \right)} \right) = f_{H} \left( {\mathop \sum \limits_{i = 1}^{n} w_{ij} x_{ij} \left( l \right) + \mathop \sum \limits_{j = 1}^{m} c_{j} r_{jt} \left( l \right)} \right)$$
(5)

Here, the activation function \(f_{H} \left( x \right) = 1/\left( {1 + e - x} \right)\) within the HL is specific to the sigmoid. The specified by an output of HL:

$$y_{t + 1} \left( l \right) = f_{T} \left( {\mathop \sum \limits_{j = 1}^{m} v_{j} z_{jt} \left( l \right)} \right)$$
(6)

Now, \(f_{T} \left( x \right)\) appears as the function of activation and is a mapping of individuality.

The training phases contain the primary weight initialization phases, which take various arbitrary information, propagate ERNN forward and backwards, and compute original weights. They utilize the EHBA process to tune these hyperparameter networks. The ERNN hyperparameter, comprising momentum, batch size, dropout rate, and learning rate, is allotted depending on the finest solutions.

Stage IV: TDO-based parameter tuning

To optimize the parameters of the ERNN classifier, the TDO model is implemented, ensuring superior convergence and performance38. This method is chosen for its robust global search capabilities, enabling it to efficiently explore a large solution space and identify optimal parameter configurations. Unlike conventional optimization methods, such as gradient descent, which can get stuck in local minima, the TDO outperforms at avoiding such traps through its exploration and exploitation balance. Its capability to adaptively search through diverse regions of the parameter space allows it to optimize complex models more effectually. Furthermore, TDO’s heuristic search approach is highly appropriate for optimizing parameters in non-convex and high-dimensional spaces, making it ideal for intrinsic ML tasks. Compared to other techniques, such as grid or random search, TDO needs fewer evaluations to attain superior results, improving efficiency and accuracy. Figure 5 demonstrates the steps involved in the TDO approach.

Fig. 5
figure 5

Steps involved in the TDO model.

Full size image

TDO is a population‐based stochastic technique that uses Tasmanian Devils as its search agents. The initial population is produced randomly, depending on the problem’s restraints. The population members of TDO help as hunters in the solution space, delivering candidate values depending upon their locations in the search space. So, the set of TDO members can be demonstrated utilizing a matrix, as signified in Eq. (7).

$$X = \left[ {\begin{array}{*{20}l} {X_{1} } \hfill \\ \vdots \hfill \\ {X_{i} } \hfill \\ \vdots \hfill \\ {X_{N} } \hfill \\ \end{array} } \right]_{N \times m} = \left[ {\begin{array}{*{20}l} {x_{1,1} } \hfill & \ldots \hfill & {x_{1,j} } \hfill & \ldots \hfill & {X_{1,m} } \hfill \\ \vdots \hfill & \ddots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {x_{i,1} } \hfill & \ldots \hfill & {x_{i,j} } \hfill & \ldots \hfill & {x_{i,m} } \hfill \\ \vdots \hfill & \ddots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {x_{N,1} } \hfill & \ldots \hfill & {x_{N,j} } \hfill & \ldots \hfill & {x_{N,m} } \hfill \\ \end{array} } \right]_{N \times m}$$
(7)

Here, \(X\) signifies the Tasmanian devil population, \(X_{i}\) represents the \(ith\) candidate solution, and \(x_{i,j}\) refers to the candidate’s value for \(the j^{th}\) variable of the \(i^{th}\) solution. \(N\) is the number of searches, and \(m\) designates the number of variables.

The objective function is calculated by positioning every candidate solution of the variables. So, the computed value of the objective function can be demonstrated utilizing the vector in Eq. (8).

$$F\left( X \right) = \left[ {\begin{array}{*{20}l} {F_{1} } \hfill \\ \vdots \hfill \\ {F_{i} } \hfill \\ \vdots \hfill \\ {F_{N} } \hfill \\ \end{array} } \right]_{N \times 1} = \left[ {\begin{array}{*{20}l} {F\left( {X_{1} } \right)} \hfill \\ \vdots \hfill \\ {F\left( {X_{i} } \right)} \hfill \\ \vdots \hfill \\ {F\left( {X_{N} } \right)} \hfill \\ \end{array} } \right]_{N \times 1} .$$
(8)

Here, \(F\) denotes an objective function vector value; \(F_{i}\) signifies the value of the aim function attained over the \(ith\) candidate solution. The finest member is upgraded at every iteration depending upon the newly attained values. The updating procedure depends upon dual foraging strategies such as scavenging and hunting for prey.

Exploration phase: scavenging for carrion

Tasmanian devils sometimes scavenge carrion when prey is too large to digest fully or lacks sufficient nourishment. This behaviour reflects the Tasmanian Devil Optimizer (TDO) search strategy, where the devil chooses a target solution (carrion) and moves towards it if the objective function improves or away if it worsens. This process, reflecting the search for optimal solutions, is modelled in Eq. (9) to Eq. (11). Whereas Eq. (9) pretends the random collection of one such situation where the \(i^{th}\) Tasmanian devil selects the \(k^{th}\) population member as the objective carrion. So, \(k\) should be chosen randomly among one and \(N,\) while \(i\) is picked oppositely.

$$C_{i} = X_{k} , i = 1,2, \ldots , N, k \in \{ 1,2, \ldots , N|k \ne i\}$$
(9)

Here, \(C_{i}\) denotes the carrion preferred by the ith Tasmanian devil.

Based on the chosen carrion, a new location is computed. If the objective function improves, the Tasmanian devil moves toward it; otherwise, it moves away. After analyzing the new position, the devil accepts it if the objective function is better; otherwise, it stays at the previous location. This process is modelled in Eq. (10) and Eq. (11).

$$x_{i,j}^{new,S1} = \left\{ {\begin{array}{*{20}l} {x_{i,j} + r \times \left( {c_{i,j} - I \times x_{i,j} } \right),} \hfill & {F_{{C_{i} }} < F_{i} } \hfill \\ {x_{i,j} + r \times \left( {x_{i,j} - c_{i,j} } \right), } \hfill & {otherwise} \hfill \\ \end{array} } \right..$$
(10)
$$X_{i} = \left\{ {\begin{array}{*{20}l} {X^{new,\;S1} ,} \hfill & {F_{i}^{new^{\prime}S1} < F_{i} } \hfill \\ {x_{i}^{i} ,} \hfill & {Otherwise} \hfill \\ \end{array} } \right.$$
(11)

While \(X_{i,j}^{new, S1}\) denotes the novel state of ith Tasmanian devil, \(x_{i,j}^{new, S1}\) refers to the value of its jth variable, \(F_{i}^{new, S1}\) indicates a novel value of an objective function, \(F_{{C_{i} }}\) means an objective function value of the chosen carrion, \(r\) denotes a produced value at random in the range of \([\text{0,1}]\), and \(I\) is a randomly produced variable in the interval of 1 or 2.

Exploitation phase: feeding through hunting prey

The second feeding tactic of Tasmanian devils contains hunting and eating prey. The behaviour of Tasmanian devils throughout the attack procedure is separated into dual phases. In the 1st phase, it picks prey by scanning the region and starts an attack. Next, after getting near to the prey, it hunts the prey, catches it, and commences feeding. The 1st modelling phase is equivalent to the first approach, i.e., carrion collection. The first phase is demonstrated by utilizing Eq. (12) to Eq. (14). The \(i^{th}\) population member is nominated randomly as the prey. At the same time, \(k\) refers to a natural random number dissimilar from \(i\), which ranges from 1 to N. The process of prey selection is formulated in Eq. (12).

$$P_{i} = X_{k} ,i = 1,2, \ldots ,N,k \in \left\{ {1,2,{ } \ldots { },{ }N{|}k \ne i} \right\}$$
(12)

where \(P_{i}\) signifies the prey nominated by the \(ith\) Tasmanian devil.

Once the location of the prey is defined, a novel location is formulated for the Tasmanian devil. When computing this novel location, if the chosen prey objective function value is superior, the Tasmanian devil travels near it; or else, it travels far away from that location. The mathematical process is formulated in Eq. (13). The newly calculated position will substitute the preceding location if it enhances the objective function value. This stage is exhibited in Eq. (14).

$$x_{i,j}^{new,S2} = \left\{ {\begin{array}{*{20}l} {x_{i,j} + r \times \left( {c_{i,j} - I \times x_{i,j} } \right),} \hfill & {F_{{p_{i} }} < F_{i} } \hfill \\ {x_{i,j} + r \times \left( {x_{i,j} - p_{i,j} } \right),} \hfill & {otherwise} \hfill \\ \end{array} } \right..$$
(13)
$$X_{i} = \left\{ {\begin{array}{*{20}l} {X^{new,S2} ,} \hfill & { F_{i}^{new,S2} < F_{i} } \hfill \\ {x_{i}^{i} ,} \hfill & {Otherwise} \hfill \\ \end{array} } \right.$$
(14)

where \(X_{i,j}^{new, S2}\) denotes the novel state of the \(ith\) Tasmanian devil depending upon the 2nd strategy \(S2,\) \(x_{i,j}^{new, S2}\) refers to the value of its \(j^{th}\) variable, \(F_{i}^{new, S2}\) is its novel value, and \(F_{{p_{i} }}\) is the objective function value.

This strategy differs from the first, mainly in the second phase, where Tasmanian devils simulate a local search by hunting prey near the attack position. The hunting phase is modelled using Eq. (15) to Eq. (17). In this phase, the devil’s position is determined as the midpoint of its neighbourhood, and the radius defines the range within which it chases prey. The new position is calculated based on this chasing process, and if it improves the objective function, the devil accepts it. The update procedure is represented by Eq. (17).

$$R = 0.01 \times \left( {1 - \frac{t}{T}} \right)$$
(15)
$$x_{i,j}^{new} = x_{i,j} + \left( {2 \times r - 1} \right) \times R \times x_{i,j}$$
(16)
$$X_{i}^{{{\text{new}}}} = \left\{ {\begin{array}{*{20}l} {X^{new} , } \hfill & {F_{i}^{new} < F_{i} } \hfill \\ {x_{i} ,} \hfill & {Otherwise} \hfill \\ \end{array} } \right.$$
(17)

Here, \(R\) signifies the neighbourhood radius of the attacked position, \(t\) represents an iteration count, \(T\) denotes a maximum iteration count, \(X_{i}^{new}\) represents the novel state of the \(ith\) Tasmanian devil in the district of \(X_{i} ,\) \(x_{i,j}^{new}\) refers to the value of its \(j^{th}\) variable, and \(F_{i}^{new}\) represents its objective function value.

Fitness selection is a substantial factor in the performance of the TDO technique. The hyperparameter range procedure comprises the solution-encoded technique to assess the effectiveness of the candidate solution. Here, the TDO model considers precision the key to projecting the fitness function. Its mathematical formulation is mentioned below.

$$Fitness = {\text{ max }}\left( P \right)$$
(18)
$$P = \frac{TP}{{TP + FP}}$$
(19)

Here, \(TP\) signifies the positive value of true, and \(FP\) denotes the positive value of false.

Performance validation

In this section, the empirical validation of the ECMVFD-FTLTDO technique is verified under dual databases such as GRIP39,40 and VTD41. The GRIP dataset contains 637 images, and the VTD dataset has 731 images, as illustrated in Table 1. Figure 6 represents the sample images of the original and forged.

Table 1 Details of dataset.
Full size table
Fig. 6
figure 6

Sample images (a) Original and (b) forged.

Full size image

Figure 7 provides confusion matrices generated by the ECMVFD-FTLTDO method on the GRIP dataset. The approach’s performance requires that it accurately detects and identifies all classes.

Fig. 7
figure 7

Confusion matrices of ECMVFD-FTLTDO technique (a–f) Epochs 500–3000.

Full size image

The classifier result of the ECMVFD-FTLTDO technique is represented below distinct epochs on the GRIP dataset in Table 2 and Fig. 8. The table values state that the ECMVFD-FTLTDO model correctly recognized all the samples. On 500 epochs, the ECMVFD-FTLTDO model delivers an average \(acc{u}_{y}\) of 94.72%, \(pre{c}_{n}\) of 94.74%,\(rec{a}_{l}\) of 94.72%, \(F{1}_{score}\) of 94.51% and MCC of 89.46%. Further, on 1000 epochs, the ECMVFD-FTLTDO technique provides an average \(acc{u}_{y}\) of 94.07%, \(pre{c}_{n}\) of 94.07%,\(rec{a}_{l}\) of 94.07%, \(F{1}_{score}\) of 93.88% and MCC of 88.15%. Afterwards, on 2000 epochs, the ECMVFD-FTLTDO technique acquires an average \(acc{u}_{y}\) of 82.87%, \(pre{c}_{n}\) of 86.19%,\(rec{a}_{l}\) of 82.87%, \(F{1}_{score}\) of 81.79%, and MCC of 68.98%. Eventually, on 3000 epoch counts, the ECMVFD-FTLTDO technique presents an average \(acc{u}_{y}\) of 91.40%, \(pre{c}_{n}\) of 91.86%,\(rec{a}_{l}\) of 91.40%, \(F{1}_{score}\) of 91.04%, and MCC of 83.26%.

Table 2 Classifier outcome of ECMVFD-FTLTDO technique under dissimilar epochs on GRIP dataset.
Full size table
Fig. 8
figure 8

Average of ECMVFD-FTLTDO method on GRIP dataset.

Full size image

Figure 9 depicts the training \(acc{u}_{y}\) (TRAAC) and validation \(acc{u}_{y}\) (VLAAC) performances of the ECMVFD-FTLTDO model on the GRIP dataset. The \(acc{u}_{y}\) values are computed for 0–1500 epoch counts. The figure featured that the TRAAC and VLAAC values show rising tendencies, which reported the capabilities of the ECMVFD-FTLTDO technique with maximum performance through several iterations. Moreover, the TRAAC and VLAAC kept closed across the epoch counts, indicating lesser overfitting and demonstrating the ECMVFD-FTLTDO technique’s superior performance, assuring stable prediction on hidden samples.

Fig. 9
figure 9

\(Acc{u}_{y}\) curve of ECMVFD-FTLTDO method on GRIP dataset.

Full size image

Figure 10 exposes the TRA loss (TRALS) and VLA loss (VLALS) graph of the ECMVFD-FTLTDO approach on the GRIP dataset. The loss values are figured under 0–1500 epoch counts. The TRALS and VLALS values illustrate decreasing tendencies, reporting the proficiency of the ECMVFD-FTLTDO method in balancing a trade-off between data fitting and generalization. The incessant decline in loss values, too, promises the maximal outcome of the ECMVFD-FTLTDO method and tuning the prediction outcomes after a bit.

Fig. 10
figure 10

Loss curve of ECMVFD-FTLTDO method on GRIP dataset.

Full size image

Figure 11 states that the ECMVFD-FTLTDO methodology on the VTD dataset made the confusion matrix. The analysis identifies that the ECMVFD-FTLTDO model specifically has effectual detection and identification of all classes.

Fig. 11
figure 11

Confusion matrices of ECMVFD-FTLTDO technique (a–f) Epochs 500–3000.

Full size image

The classifier study of the ECMVFD-FTLTDO approach can be resolved beneath distinct epochs on the VTD dataset in Table 3 and Fig. 12. The table values state that the ECMVFD-FTLTDO approach is appropriately renowned for all the samples. On 500 epochs, the ECMVFD-FTLTDO model delivers an average \(acc{u}_{y}\) of 92.67%, \(pre{c}_{n}\) of 93.50%,\(rec{a}_{l}\) of 92.67%, \(F{1}_{score}\) of 92.83%, and MCC of 86.16%. Further, on 1000 epochs, the ECMVFD-FTLTDO model provides an average \(acc{u}_{y}\) of 89.94%, \(pre{c}_{n}\) of 91.65%,\(rec{a}_{l}\) of 89.94%, \(F{1}_{score}\) of 90.14%, and MCC of 81.58%. In the meantime, on 2000 epochs, the ECMVFD-FTLTDO method becomes average \(acc{u}_{y}\) of 89.33%, \(pre{c}_{n}\) of 91.65%,\(rec{a}_{l}\) of 89.33%, \(F{1}_{score}\) of 89.54%, and MCC of 80.95%. Lastly, on 3000 epochs, the ECMVFD-FTLTDO method provides an average \(acc{u}_{y}\) of 91.45%, \(pre{c}_{n}\) of 91.59%,\(rec{a}_{l}\) of 91.45%, \(F{1}_{score}\) of 91.24%, and MCC of 83.03%.

Table 3 Classifier outcome of ECMVFD-FTLTDO technique under dissimilar epochs on VTD dataset.
Full size table
Fig. 12
figure 12

Average of ECMVFD-FTLTDO method on VTD dataset.

Full size image

Figure 13 demonstrates the TRAAC and VLAAC outcomes of the ECMVFD-FTLTDO model on the VTD database. The \(acc{u}_{y}\) values are computed for 0–500 epoch counts. The figure showcased the TRAAC and VLAAC values showing rising tendencies, which reminded the ability of the ECMVFD-FTLTDO technique with enhanced performance above numerous iterations. Likewise, the TRAAC and VLAAC remain closer upon the epoch counts, which specifies minimal overfitting and exhibits the higher performance of the ECMVFD-FTLTDO approach, encouraging stable prediction on undetected instances.

Fig. 13
figure 13

\(Acc{u}_{y}\) curve of ECMVFD-FTLTDO method on VTD dataset.

Full size image

In Fig. 14, the TRALS and VLALS graph of the ECMVFD-FTLTDO technique on the VTD dataset is validated. The loss values are calculated over 0–500 epoch counts. The TRALS and VLALS values establish declining tendencies, reporting the ability of the ECMVFD-FTLTDO methodology to balance a trade-off between generality and data fitting. The continual reduction in loss values also pledges the superior outcome of the ECMVFD-FTLTDO methodology and tuning the prediction outcomes on time.

Fig. 14
figure 14

Loss curve of ECMVFD-FTLTDO method on VTD dataset.

Full size image

Table 4 and Fig. 15 compare the ECMVFD-FTLTDO approach with the existing models on the GRIP dataset42. The solution emphasized that the PatchMatch-DFAVCMDL, LSTM-EnDec, CRF-Layer, High-pass FCN, Dense Moment Extraction, and VCMFD models have reported minimum performance. At the same time, the CNN-CMVFD model has obtained closer outcomes with \(acc{u}_{y}\) of 86.16%, \(pre{c}_{n}\) of 79.95%,\(rec{a}_{l}\) of 79.91%, \(F{1}_{score}\) of 79.32%, and MCC of 76.55%. In Addition, the ECMVFD-FTLTDO model reported enhanced performance with a maximum \(acc{u}_{y}\) of 95.26%, \(pre{c}_{n}\) of 95.17%,\(rec{a}_{l}\) of 95.26%, \(F{1}_{score}\) of 95.13% and MCC of 90.43%.

Table 4 Comparative analysis of ECMVFD-FTLTDO method on GRIP dataset42.
Full size table
Fig. 15
figure 15

Comparative analysis of ECMVFD-FTLTDO method on GRIP dataset.

Full size image

Table 5 and Fig. 16 investigate the comparative solution of the ECMVFD-FTLTDO method with the existing models on the VTD dataset. The results emphasized that the PatchMatch-DFAVCMDL, LSTM-EnDec, CRF-Layer, High-pass FCN, Dense Moment Extraction, and VCMFD models have reported lesser performance. Afterwards, the CNN-CMVFD technique obtained closer outcomes with \(acc{u}_{y}\) of 81.87%, \(pre{c}_{n}\) of 82.75%,\(rec{a}_{l}\) of 91.84%, \(F{1}_{score}\) of 91.60%, and MCC of 77.35%. Simultaneously, the ECMVFD-FTLTDO technique reported superior performance with maximal \(acc{u}_{y}\) of 92.67%, \(pre{c}_{n}\) of 93.50%,\(rec{a}_{l}\) of 92.67%, \(F{1}_{score}\) of 92.83%, and MCC of 86.16%.

Table 5 Comparative analysis of ECMVFD-FTLTDO method on VTD dataset42.
Full size table
Fig. 16
figure 16

Comparative analysis of ECMVFD-FTLTDO method on the VTD dataset.

Full size image

In Table 6 and Fig. 17, the comparative solution of the ECMVFD-FTLTDO approach is specified in terms of time on GRIP and VITD datasets. The results suggest that the ECMVFD-FTLTDO model has improved performance. On the GRIP dataset, the ECMVFD-FTLTDO approach provides lesser time of 13.5 s whereas the PatchMatch-DFAVCMDL, LSTM-EnDec, CRF-Layer, High-pass FCN, Dense Moment Extraction, VCMFD and CNN-CMVFD models attain greater time of 21.3 s, 45.8 s, 42.4 s, 69.6 s, 39.6 s, 31.4 s, and 21.0 s, respectively. On VTD dataset, the ECMVFD-FTLTDO approach provides lesser time of 10.2 s whereas the PatchMatch-DFAVCMDL, LSTM-EnDec, CRF-Layer, High-pass FCN, Dense Moment Extraction, VCMFD and CNN-CMVFD models attain greater time of 75.8 s, 68.7 s, 46.6 s, 91.3 s, 53.1 s, 33.7 s, and 29.8 s, respectively.

Table 6 Time outcome of ECMVFD-FTLTDO technique on GRIP and VTD datasets.
Full size table
Fig. 17
figure 17

Time outcome of ECMVFD-FTLTDO technique on GRIP and VTD datasets.

Full size image

Conclusion

In this manuscript, an ECMVFD-FTLTDO model is presented. The primary aim of the ECMVFD-FTLTDO model is to classify and detect copy-move forgery in video content. It comprises stages such as preprocessing, fusion of TL models, ERNN detection, and TDO-based parameter tuning. Primarily, the videos are transformed into individual frames and noise removal using MWF. Next, the ECMVFD-FTLTDO technique employs a fusion-based TL process comprising three models, ResNet50, MobileNetV3, and EfficientNetB7, to capture diverse spatial features across various scales, thus enhancing the model’s abilities to distinguish authentic content from tampered regions. For the detection process, the ECMVFD-FTLTDO approach utilizes an ERNN classifier. The TDO approach is implemented to optimize the parameters of the ERNN classifier, ensuring superior convergence and performance. A wide range of simulation analyses is performed under GRIP and VTD datasets. The performance validation of the ECMVFD-FTLTDO technique portrayed a superior accuracy value of 95.26% and 92.67% compared to existing approaches under GRIP and VTD datasets.