Abstract
Hybrid energy systems (HESs) are integrated systems that have successfully addressed the problems of meeting the increasing demand for electrical power. Like all known power systems, the energy and stream quality are among the most important issues in addition to the durability of the HES. In this study, the battery-powered HES is presented, where this designed system consists of a wind system and a photovoltaic (PV) system. The strategy of maximum power point (MPP) tracking (MPPT) based on the adaptive neuro-fuzzy inference system (ANFIS) method is used to command the PV system and the wind system, and the MPPT based on the neural method is used. These proposed strategies do not need the mathematical model of the studied system and augment the robustness and stability, where the system performance is great. Also, the fractional-order proportional-integral regulator and the integral sliding mode control approach are combined to control the battery-based storage system, and the particle swarm optimization approach was used to estimate the gain values of the resulting controller. The HES was realized using MATLAB, where the competence is tested under different work scenarios. The results showed excellent efficacy of the designed control and were compared with conventional control. The simulation results showed that using the neural MPPT strategy in the case of the wind speed being 12 m/s, the values of rise time, response time, MPP, and steady-state error (SSE) are improved by rates estimated at 99.32%, 60%, 1.5%, and 60%, respectively compared to the perturbations and observations-based MPPT approach. Compared to the traditional strategy, the ANFIS-MPPT strategy improves the values of MPP, response time, SSE, and rise time in the case of irradiation, which takes the value of 1000 W/m2, by percentages estimated at 18%, 60%, 94.70%, and 69.23%, respectively. Also, the PSO-FOPI-ISMC strategy improves the harmonic distortion of the current value in the second test by 55.20% and 72.90% for mode 1 and mode 2, respectively, compared to the traditional approach. These results make the designed approach of great importance in the future in other industrial applications.
Similar content being viewed by others
Introduction
The challenges currently facing the world are the phenomenon of global warming and the rising demand for electrical energy (EE), as it has become necessary to think seriously about how to save energy and make it accessible to everyone while providing it for the future1. As is known, EE generation across the world relies heavily on traditional energy sources (ESs), such as coal, natural gas, and crude oil2. Relying on these ESs causes numerous undesirable cons such as the spread of toxic gases, high costs of producing EE, and environmental pollution, etc. In addition, the energy demand is constantly increasing due to rapid economic growth and rising population growth, which has made traditional ESs unable to meet this large demand3. However, the increase in demand for EE leads to an increase in the consumption of traditional ESs, which makes the demand for these ESs constantly increase and thus leads to an insane rise in the prices of these sources. The rise in prices of traditional ESs inevitably leads to disruptions in EE generation and raises the costs of producing and consuming EE4. Energy sources such as gas and oil are limited and not widely available, as their presence is limited to some countries only. This in turn affects the stability of EE production and future generations and their energy demand. Among the problems that are affecting some countries around the world is the phenomenon of climate change due to global warming, where these two problems have become major issues in the field of environment and global economy5. These two problems have an important impact on access to energy and its high cost. The increasing demand for electricity across the world has already raised concerns about supply difficulties and significant environmental impacts, such as climate change and global warming. According to reference6, it is concluded that energy generated from traditional ESs causes an augment in the emission of greenhouse gases, which may affect the phenomenon of climate change. Substantial attempts to minimize the volume of toxic gas emissions led to the Kyoto Agreement on reducing global greenhouse gas creation. This international agreement was established to limit the use of conventional ESs in the creation of EE and to search for other, more efficient solutions to protect the atmosphere. This agreement has been ratified by developing and developed countries, where the matter has been taken seriously to take strict measures and apply possible international sanctions on countries that have ratified this agreement that do not respect this agreement to get better and develop ESs. As is known, effective ESs in terms of their protection of the environment, non-spreading of toxic gases, and low charge are among the most important features of these sustainable ESs that must be focused on to obtain highly efficient electrical networks7. The increased use of EE has led to a significant development of ESs, so at present several ESs have been developed to include various energy sources. In line with this development, which has many benefits like other fields, new issues have been discussed in the field of ESs, such as economic distribution. Over several decades, with the increasing consumption of EE, its supply systems have increased such that today the distribution of loads between energy-producing units at the lowest cost is one of the most widespread and complex issues in the use of the ES.
The solutions that have been relied upon across the world and have received great interest from governments and researchers are natural resources, represented by renewable energy sources (RESs) such as solar energy (SE), hydropower, wind energy (WE), etc. These ESs are considered among the most prominent appropriate, useful, and effective solutions for generating EE, through which we can overcome climate change and significantly reduce the phenomenon of global warming8. Several countries around the world have led a large network of partners and researchers to create new technology and take advantage of the latest existing technologies to provide EE at a lower cost than systems based on traditional ESs. Relying on ESs that use WE and SE as primary sources of energy generation will reduce the use of fossil fuels in generating EE, which will lead to a reduction in toxic gas emissions and production and consumption costs at the same time9. As is known, RESs offer an effective solution in generating EE, as they are free and available throughout the year, which leads to reducing the cost of power production compared to usual ESs, as no gaseous or water pollutants are released during generation10. Accordingly, WE and SE are considered among the most famous sources that have been relied upon in the area of generating EE.
In WE, turbines called wind turbines (WTs) are used to generate EE, where the WTs convert WE into mechanical power (MP), which is then transformed into EE by generators11. The energy produced by WTs depends on wind speed (WS) and the WT size, with larger WTs generating more power12. WTs are classified into horizontal-axis and vertical-axis types, with differences in design and energy output13. Additionally, WTs can operate at fixed or variable speeds. Fixed-speed WTs generate constant energy regardless of WS, while variable-speed WTs adjust output based on WS changes, increasing efficiency14,15. Recent advancements, like multi-rotor WTs, combine multiple WTs to reduce land use, construction challenges, and costs while improving overall energy production16. In this knowledge, numerous WTs are used to form one WT to minimize the area of wind farms and thus reduce charges. Also, the use of this technology contributes considerably to minimizing the dimensions of WTs and the difficulty of constructing giant WTs on the ground17.
Traditionally, SE is considered one of the most important sources used to generate EE and defeat global warming. In these systems, photovoltaic (PV) cells are used to translate the light beam into a stream using PV cells18. Therefore, to obtain greater energy, many PV cells must be used in the form of sheets or panels called PV panels19. So, the solar system for generating EE differs from the WE system for generating EE, as one WT can be used to replace the use of a large farm of PV panels, which makes WE one of the most effective solutions that can be relied upon in the future to meet the increasing demand for EE20. On the other hand, the disadvantage of relying on these ESs is their irregular and random nature, as disturbances in the generation of EE occur in difficult weather conditions, which creates several undesirable problems21. Therefore, RESs such as WE and SE cannot fully control the increasing demand for EE, especially in difficult weather conditions. These RESs are characterized by a variable nature, so to overcome this problem, these systems must be combined with the use of an energy storage system (ESS)22. This proposed solution leads to significantly improving and increasing the effectiveness of ESs, with continuous and permanent energy supply reliability despite bad weather conditions. Therefore, it is necessary to use WE systems with SE systems in one system to generate EE, while using the surplus energy to store to use it in critical times or where there are bad weather conditions. The use of this combination of the two systems is called hybrid energy systems (HESs), as the importance of these HESs lies in their ability to defeat the crisis of rising demand and reduce dependence on traditional ESs of EE generation. In these HESs, the greater the number of ESs, the greater the cost and the ability to significantly save EE. Therefore, it is necessary to use batteries with these systems to store surplus energy. The quality of power is based on the quality of current and voltage, as in the work23 the author conducted a comparative study between serial voltage injection and parallel current injection in an ES connected to the grid. Series voltage injection is considered more effective than parallel current injection in terms of improving the quality of the voltage on the load side. The stability improvement of a 13-bus wind farm system was studied using a dynamic voltage recovery device (DVR) and a static distribution synchronous compensator (DSTATCOM) to save the required power. DVR is an efficient and modern device used in parallel within the network and can protect sensitive loads from voltage problems in the network by voltage injection. DVR and D-STATCOM were used to improve fault voltage stability. Simulation results showed that single- and three-phase overloads significantly changed the system voltage, making it necessary to use compensators to improve voltage stability. DVR and D-STATCOM showed similar performance under normal conditions and improved somewhat under grid voltage unbalance. However, the DVR outperformed the D-STATCOM under asymmetric fault conditions and resulted in lower voltage variations. In24, the topic of HESs was addressed using artificial intelligence (AI) methods, where smart approaches were used to get better competence and overcome the defects found in the HES. This work gives an image of how to use smart approaches in managing HESs to obtain good operation and increase energy quality on the other hand. As is known, power quality is one of the most important defects that must be paid attention to obtain a network with high durability. In25, the author used a modified bald eagle search algorithm, integrated with the grasshopper optimization algorithm to improve the characteristics of an HES. The studied ES consists of two wind farms, two PV farms, and flexible loads. Using the proposed approach led to significantly improving the characteristics of the studied ES. Moreover, simulation results reveal that uncertainties lead to an increase in cost and emissions, while the inclusion and sharing of flexible loads in the UC program can effectively mitigate the cost and emission levels. The author believes26 that ESs based on RESs have a set of restrictions, such as the balance of production and consumption in the system, production limits, rates of increase and decrease, production costs, and environmental pollution and losses that limit their spread. In this work, the author studied the issue of load distribution to improve the effectiveness and performance of the ES. This issue is one of the most important issues in the system today. A mutant version of the honey bee mating optimization algorithm based on collective intelligence is proposed for economic emission transmission (E-ED) of the ES. The proposed algorithm was used to solve the E-ED problem with nonlinear cost functions. Also, a nonlinear adaptive ES was used to increase the efficiency and balance of the standard algorithm for local and final searches. The simulation results showed that the efficiency of this algorithm in solving the economic load distribution problem is better than other algorithms. In27, the author made a comparative study of four different controllers namely FACTS STATCOM, TCSC, static synchronous series compensator, and unified power flow controller on static voltage stability in ESs. The use of these control strategies has a different impact on the performance and effectiveness of the control ES. DC power flow is used to evaluate the effects of these strategies on the load potential of the ES. In this work, the effect of these strategies on the maximum loading point is determined. The author believes28 that generating electricity close to consumption gives more flexibility in ESs to provide various services to consumers in addition to reducing system losses. These losses are among the most prominent issues that must be addressed and appropriate solutions proposed. Also, global warming and the limitation of fossil fuels are among the main incentives for the development of ESs. Therefore, it is necessary to combine distributed generation resources with the power grid, as well as well and highly efficient control of these resources. Therefore, the microgrid (MG) is one of the methods that have been proposed to combine distributed generation sources. Also, one of the topics that is of great importance in this regard is the proper management of distributed generation resources in small grids to reduce the costs of electricity generation and reduce the phenomenon of global warming. Resource management in an MG is a completely nonlinear and first-order problem. A multi-objective genetic algorithm (NSGAII) was used to study the optimal programming of the MG taking into account the available capacities in the electricity market while simultaneously minimizing pollution and cost. An MG consisting of solar, wind, microturbine, fuel cells, and battery resources was studied using three different scenarios. Also, uncertainty about load and solar and wind generations were taken into account. In this work, the probability distribution function (PDF) and the roulette wheel were used to generate variables with uncertainty. The goal of the first scenario was to reduce costs by optimizing the particle swarm optimization (PSO), genetic algorithm (GA), and ABC algorithms. In the second scenario, contamination and duplication of studies were reduced using these three algorithms. In the third scenario, there was a simultaneous reduction in pollution and cost by these three algorithms (PSO, GA, and ABC), taking into account the weight coefficients as well as the NSGAII algorithm. In29, a new modified version of grey wolf optimization (MGWO) is proposed to solve the unit commitment (UC) problem in an ES under uncertainty. Market price variation is the main source of uncertainty in the UC program. Therefore, there is a model based on the normal probability density function (PDF) to reduce the effect of market price uncertainty in the model. Simulations of a standard 10-BTU power system are performed, and the optimization results by the proposed MGWO are compared with the previous version of the GWO algorithm and the results of the PSO algorithm. The simulation results confirm the superiority of the proposed MGWO algorithm over the PSO and GWO algorithms in improving the characteristics of the studied ES.
The stability of ESs is one of the most important policies that must be paid attention to and focused on. Determining the maximum load margins is an important issue in the operation of ESs, as ES operators must take appropriate preventive measures to avoid stability problems. In the work30, the effectiveness of both parallel FACTS devices and series FACTS devices on steady-state voltage and power stability was studied. Steady-state modeling and its effects on ES performance are studied. Also, improving the static stability of the ES and thus improving the power flow in the network was studied. In this work, the effects of using different types of FACTS on the loadability and stability of the ES were studied. To compare FACTS devices it was proposed to use a method based on the concept of maximum load point index. MATLAB was used to compare different types of FACTS on the stability of an ES based on the use of the IEEE 14 bus test system. The simulation results showed that using parallel FACTS devices is more appropriate than serial FACTS devices in terms of the stability of the studied ES. In31, the optimal energy management of an MG with parking lots (PL) and distributed generation (DG) units is studied using a modified version of the Imperial Competitive Algorithm (ICA). 24-h scheduling for the engagement of DG units and EV PLs was implemented in two scenarios. The PLs are divided into seven groups, each group having a different flight behavior. Therefore, energy management must be done in a way that minimizes operating costs depending on the state of charge of EVs as well as the production capacity of distributed generation sources. The effectiveness and performance of the proposed ICA algorithm with both GA and PSO algorithms. This proposed ES was implemented in the MATLAB environment, where simulation results demonstrated the effectiveness of the proposed method. Simulation results show a reduction in the operating cost of the MG by approximately 63%. Also, the simulation results showed the effectiveness and high performance of the proposed algorithm in improving the characteristics of the studied ES compared to the GA and PSO algorithms.
In32, a hybrid fuzzy-logic-based power management system is proposed for RESs with a multiport quasi-Z source converter. Fuzzy logic (FL) is used to manage power modes, preventing switching losses and simplifying system operation. The Mamdani FL reasoning system captures non-linear behavior without relying on a mathematical model (MM), delivering high efficiency and resilience during faults. The system’s performance, verified through MATLAB simulations and experiments, shows improved energy quality. However, the challenge with FL lies in determining the optimal number of rules, as too many can slow the system down. In33, HESs are described as combining different power generation, storage, and conversion technologies to enhance capacity, minimize charges, and get better environmental and operational efficiency compared to standalone systems. Hybridization is seen as a solution to augment flexibility, reduce production costs, and integrate RESs for cleaner energy production. The work provides a comprehensive overview of HESs, focusing on their design and applications in buildings, with attention to environmental, economic, and technical aspects. It also highlights current and future trends in HESs for buildings, aiming to promote energy-efficient networks and sustainable technologies. The author emphasizes that the high flexibility of integrated HESs enhances the integration of RESs, stressing the need for effective control techniques to optimize performance. In34, the growing global energy demand has led to excessive exploitation of non-renewable resources, increasing toxic gas emissions and raising global temperatures. The rising costs of traditional energy sources have prompted a shift toward RESs, particularly solar (SE) and WE. The author suggests that due to the intermittent nature of SE and WE, hybridizing them with systems like batteries can enhance reliability and efficiency. This work provides an overview of hybrid SE and WE systems, their configurations, models, and control techniques. MATLAB simulations show the system’s importance in energy storage, but highlight a drawback in power quality, as large ripples were observed due to a lack of focus on control strategies. In35, a feasibility analysis of a solar-diesel hybrid MG in Nigeria was conducted, focusing on the Gbamu-Gbamu system in Ogun State. The study evaluated the installation of an 85 kW solar PV system to enhance energy access and support sustainable development in rural areas. Using RETScreen expert software and NASA climate data, the technical, economic, and environmental viability of the ES was assessed. Results showed a 92.9% reduction in greenhouse gas emissions, a positive net present value, and an average monthly solar radiation of 4.78 kWh/m2. The ES provided a payback period of four years and enabled the annual export of 203 MWh, underscoring its benefits for power access and local economic growth. In36, the author explored the environmental impact of a hybrid SE and biomass ES using a life cycle assessment. The study revealed that while the construction and recycling phases have a minimal environmental impact, the solar subsystem contributes the most emissions during construction, followed by the anaerobic reactors. This highlights that an excessive focus on SE can lead to greater environmental issues. However, the HES effectively minimizes non-renewable energy use; mitigates climate change, acidification, and eutrophication, and replaces harmful alternatives like lignite coal. Additionally, it generates clean thermal energy, minimizes organic waste, and produces valuable agricultural by-products. A HES proposed in37 is based on the use of a proportional-integral (PI) controller to compensate for the impact of communication time delay (CTD) and intelligent FL-assisted robust ratio control-based virtual inertia (VI) is implemented for handling the Denial-of-Service (DoS) attacks. In this proposed ES, Fick’s law optimization strategy was used to determine the gain values of the used controls. The proposed control has been evaluated for its effectiveness and performance in terms of different practical scenarios such as gradient load disturbances, cyber-attacks, CTD variation, random WE fluctuations, parametric uncertainties, industrial and domestic loads, and the presence of nonlinearities in the system such as generator dead band, valve limits, and generator rate constraint. The simulation results showed the high performance of the designer’s approach in improving the characteristics of the studied ES in various scenarios compared to the traditional approach. It was proposed in38 a HES based on the use of thermal power plants, a WE plant, and a SE plant to generate EE. In order to control this ES, it was proposed to use intelligent fractional-order fuzzy-proportional derivative plus fractional-order-integral (FOF-PD + FOI) control and VI control for frequency regulation. The proposed approach is an integration of several different controllers, where the strategy Archimedes optimization algorithm (AOA) was used to determine the gain values of the proposed controller. The proposed FOF-PD + FOI approach is compared with PI, proportional-integral-derivative (PID), and fuzzy-PD + I (F-PD + I) in terms of steady-state error (SSE), improved power quality, and dynamic performance. To replicate the robust operation of the AOA-tuned FOF-PD + FOI and VIC controller, differences in virtual inertia of both regions as well as differences in network parameters are taken into account. The simulation results showed the high performance of the proposed approach compared to other controllers, especially in terms of improving power quality and reducing the THD of current. The disadvantage of this proposed controller lies in its complexity and the presence of a significant number of gains. In39, the author addresses the complexities of deploying RES due to uncertainties in WS and fluctuations in load demand. To enhance reliability in island MGs, a HES was developed using WTs, a lithium-ion battery for electrical storage, a PEM hydrogen storage system, and a diesel generator. Model predictive command (MPC) was employed to optimize the system’s durability and performance by maintaining the state of charge (SOC) and level of hydrogen (LOH) within safe limits. MATLAB simulations under varying weather conditions indicated SOC levels ranging from 20% to 88.52% and LOH levels from 10% to 90.06%. The MPC strategy aimed to prevent degradation and energy outages while minimizing construction costs for network integration. In40, the problem of frequency deviation of HES based on a PV system and a diesel generator was addressed. This problem can be attributed to the random nature of the source or uncertain load demand. In this work, power is generated through a PV system, and the MPPT strategy based on modified incremental conductivity (MIC) is used to control it. This strategy has its behavior comprehensively compared with classical perturbation and observation (P&O) and incremental conduction (IC) techniques. Also, an optimal-fuzzy-proportional-integral-derivative (O-F-PID) controller for load frequency control (LFC) is proposed. The proposed O-F-PID approach compared optimal PID (O-PID) controllers and conventional PID (C-PID) controllers under different source and load demand conditions. The results showed the effectiveness and strength of the O-F-PID approach in reducing the problem of system frequency deviation compared to other strategies. In41, an artificial gorilla troops optimizer was used to improve the effectiveness and performance of HES based on the use of both WE and a diesel generator. This strategy is characterized by simplicity and ease of use, as it was used to determine gain values for both integral type sliding mode control (I-SMC) and PID frequency controller. The results reveal the effectiveness of using the proposed approach compared to modern methodologies in terms of improved frequency deviations, shorter settlement time, and minimal integral errors. Storage systems are necessary for systems that generate energy from renewable sources, as they are considered one of the most prominent systems that are currently being addressed and attempted to be developed. In the work42, the author addressed the topic of control of an energy storage system (ESS). In this work, it is proposed to use both PSO and GA to calculate the minimum and maximum load in the network with ESSs. Using these two strategies greatly improved the effectiveness of the ESS. In43, the author emphasizes the need for energy storage technologies in RESs due to the randomness and intermittency of solar and WE. While pumped hydro storage (PHS) is a common storage solution, its capacity is often limited by geographical conditions. The paper proposes a HES that integrates SE, WE, hydropower, and dual-energy storage (PHS-TES), utilizing a high-advantage operational strategy. It addresses challenges such as optimal sizing and loss of power supply probability (LPSP) using multi-objective PSO while considering seasonal uncertainties in RESs. A case study demonstrated the effectiveness of this coordinated approach in terms of economics and reliability. The results showed that the PV-wind-CSP-PHS reduces the levelized cost of energy (LCOE) by 19.1% compared to a PV-wind-CSP with the same LPSP, highlighting the economic and reliability benefits of the dual-energy storage approach over single storage systems. The designed system was successfully realized in MATLAB. In44, a new methodology for evaluating hybrid ESSs within HESs is proposed, utilizing wavelets to decompose net load into time segments. The study introduces the stretched filament technique for assessing the ESS effect, moving beyond traditional optimization methods to provide a visual strategy. Proper selection of ESS technologies within specific time frames enhances the evaluation of various sizes of storage systems. The research, realized in MATLAB, reveals that ESSs effectively store surplus power and release it during deficits, thus reducing intermittency. Additionally, it highlights that costs are directly related to storage capacity and inversely related to management time, indicating a strategic allocation of storage capacities based on speed and efficiency. In45, the author discusses how an MG comprises various distributed power resources and local loads, with their integration leading to HES. The focus of the work is on enhancing the profit, security, economy, and dynamic performance of integrated HES through a four-level hierarchical multi-agent management strategy. Level 1 implements optimal bidding strategies for maximizing overall system profit, while Level 2 optimizes power management commands for the cost-effective operation of each MG. The Level 3 agent coordinates switching commands to ensure the security of each MG, and Level 4 facilitates local hybrid commands for the dynamic performance of distributed power sources. The proposed ES was validated in MATLAB with various scenarios, showing impressive performance. However, the study did not address energy quality or total harmonic distortion (THD), which is a crucial indicator of the effectiveness and durability of any HES. Therefore, improving command strategies to enhance these aspects should be prioritized alongside ES management.
In this work, a HES different from the above-mentioned systems is addressed. The HES system studied consists of a PV system, a WE system, and a storage system based on batteries. In this studied system, EE is generated from PV and WE systems, which makes it one of the systems that work to protect the environment and are therefore of great importance in the energy field. The use of energy storage gives this system an advantage that overcomes the disadvantages of traditional systems. The stored energy can be used in critical circumstances and situations to compensate for energy shortages or high energy demand, especially at peaks. On the other hand, the work done focuses on improving the quality of energy produced by HES, using new strategies with high performance and great durability. To control the PV system, the MPPT approach based on adaptive neuro-fuzzy inference systems (ANFISs) was used, comparing the results with the MPPT strategy based on the perturbations and observations (P&O) algorithm. Therefore, the MPPT-ANFIS strategy is considered the first main contribution of this paper. The MPPT-ANFIS strategy is characterized by simplicity, ease of implementation, outstanding performance, high durability, and lower costs. In the WE system, an MPPT strategy based on artificiel neural networks (ANNs) was used to control the operation of the boost converter. This converter is used to connect the existing WE system to a permanent magnet synchronous generator (PMSG)-type generator. This boost converter has several advantages such as simplicity, lower costs, ease of implementation, and ease of control. The ANN-MPPT strategy is the second major contribution of this paper. The results of the ANN-MPPT strategy were compared with the PO-MPPT approach in terms of response time (RT), SSE, and rise time. To charge the surplus energy in the batteries, a buck-boost converter is used, as it has several advantages, including simplicity, ease of control, and lower costs. This converter was relied upon because it allows the charging and discharging of the battery. PI control was used to control the battery converter. In this completed work, a three-phase inverter was used to connect the studied system to the load. Therefore, to control this inverter, both fractional-order PI controllers based on the PSO (PSO-FOPI) technique and integral SMC technique based on the PSO (PSO-ISMC) technique were used to improve the power quality and reduce the THD of current. Therefore, the use of both PSO-FOPI and PSO-ISMC controllers is considered the third main contribution of this paper. The use of both PSO-FOPI and PSO-ISMC controllers does not require precise knowledge of the MM of the system being studied. MATLAB was used to implement these proposed strategies under different working conditions. The completed tests demonstrate the effectiveness, durability, and efficiency of the proposed strategy in improving power quality compared to the traditional strategy. Also, the results obtained highlight the extent of integration of the three systems in the studied HES. The objectives achieved by this work can be summarized in the following points:
-
Overcoming the problems and disadvantages of the MPPT strategy of PV system.
-
Significantly improved power quality compared to using traditional strategies.
-
Improving the stream THD value compared to classical technique and other works.
-
Significantly improve the dynamic response of PV energy.
-
Overcoming the disadvantages of using PI control.
-
The value of SSE and rise time is significantly reduced when using both ANN-MPPT and ANFIS-MPPT compared to using the traditional strategy.
-
Improve MPP value compared to using the traditional MPPT method.
There are six sections of this article. The second section discusses the components of the HES proposed for the study. In this section, the MM is given for each of the PV, WE, and ESS. The third section discusses the proposed control strategies, giving the necessary details for each MPPT, ANFIS-MPPT of PV, NN controller of WE system, battery controller, and three-phase inverter controller. In the fourth section, the management power flow system was discussed, and the necessary algorithm was given. In the fifth and sixth sections, the results of the simulation of the studied ES and the conclusions drawn from this completed work are presented.
Hybrid renewable energy system components
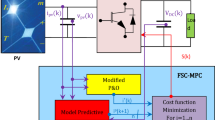
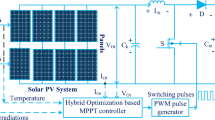
This study introduces a HES architecture designed specifically for stand-alone applications in remote areas, as illustrated in Fig. 1. The proposed system integrates a PV generator and a WE system equipped with a PMSG, which serve as the primary energy source to supply an AC electrical load. To ensure reliable operation, a lithium-ion battery storage system is included as a backup to compensate for energy deficits when the PV and WE subsystems cannot fully meet the load demands. The system requires various power converters, including a DC/DC converter, a bi-directional DC/DC converter, and a three-phase DC/AC inverter for efficient load integration. The focus of this study is on enhancing the energy efficiency of the HES through three key aspects. First, an MPPT approach is developed using two intelligent techniques to optimize power extraction from the PV and WE subsystems. Second, power flow management is implemented via an advanced battery control strategy. Finally, a novel approach combining PSO, fractional-order proportional-integral (FOPI), and integral sliding mode control (ISMC) is employed to improve power quality. The mathematical formulations for these methods are detailed in the subsequent sections.
Photovoltaic system
The designed energy conversion PV system, as described in Fig. 2, consists of a PV generator, a DC/DC boost converter (DC/DC-BC), and its controller of MPPT. The PV systems play a pivotal role by converting sunlight into EE based on cells linked in series and parallel to create an energy demand. The DC/DC-BC is used to obtain the desired level of voltage and to get the maximum energy of the PV system under variable conditions of weather.
PV system modeling is a crucial aspect of designing, analyzing, and optimizing the competence of solar ESs. Modeling a PV system involves creating mathematical equations that represent the behavior of its various components. A common approach is to use the single-diode equivalent circuit model, which describes the electrical performance of a PV array. The basic equations for this model are46,47:
The energy of PV array is given as following:
where, Ipv and Vpv represent the output stream and voltage of the PV array, respectively. Iph denotes the photo-stream (A) of the PV cell, which depends on the solar irradiation G and the temperature T as described in Eq. (2). Io is the reverse saturation stream (A), which varies with temperature as given in Eq. (3). Rs and Rsh are the series and shunt resistances, respectively. Ns are the number of series-connected cells, and Np is the number of parallel-connected PV modules; q is the electron charge (1.602 × 10−19C), and K is the Boltzmann constant (1.3 × 10−23J).
Figure 3 illustrates the electrical behavior characteristics of a PV array. These characteristics reveal that the system has an operating point where the energy is maximized, even with changes in irradiation and temperature. This underscores the importance of employing a DC/DC-BC with an MPPT to keep the PV at its optimal energy point. In our study, we utilized ANFIS and P&O techniques to address this challenge.
WE conversion system
The WT is the mechanism that converts kinetic energy to mechanical energy. This power will be transferred to an electrical three-phase wave based on PMSG. After that, the electrical stage transfers the three-phase electrical to different applications by a PWM-controlled rectifier48. This is then controlled by a BC to step up the voltage to the DC link voltage value. In addition, the BC is also used to extract the maximum power from the WE conversion system at variable speeds. A block diagram of the suggested WE translation system is shown in Fig. 4. According to reference48, the available power from the variable WS can be determined as.
where, \(P_{m}\) is the ME in watts, ρ is the air density in g/m3, \(R\) is the rotor blade radius, \(V_{w}\) is WS, \(\beta\) is pitch angle, \({\uplambda }\) is the tip speed ratio, \(\Omega_{t}\) is the WT speed, and \(C_{p}\) is the energy conversion coefficient that was discovered by physicist Albert Betz in 1919s and named by the Betz limit, where Betz limit says that no WT can translate more than 59.3% of the kinetic power of the wind into ME49. According to our WT model, can be modeled with the following equations:
In this model the PMSG is associated directly with the WT to reduce the fluctuation of the gearbox. The dynamic equations are given as in50,51.
Here \(f\) represents the rotational damping and J is the equivalent inertia of WT and generator, \(\psi_{dq}^{T}\) is the generator permanent flux intensity, (\(L_{d}\) = \(L_{q}\)) are the (d-q) axis inductances, Rs is the stator phase resistance, \(p\) is the number of the pole pairs, \(T_{e} {\text{ and }}T_{m}\) is the electromagnetic torque and the mechanical torque developed by the WT, and \(\Omega_{m}\) is the generator speed.
Figure 5 shows the WT characteristics of Pm (\(\Omega_{t}\)) with the variable value of a WS and \(\Omega_{t}\). Based on this characteristic curve, it’s evident that the system reaches an operational state where the output energy is maximized for various WS values. This underscores the necessity of employing an MPPT to regulate the DC/DC-BC and ensure that the optimal power point is tracked regardless of the prevailing WS conditions.
Energy storage system model
In this section, the modeling of ESSs is presented. The ESSs are utilized to satisfy the load’s energy demands, offer regulation in voltage and frequency stability, and protect electronic devices from energy problems, harmonic reduction, and transient stability38,52. In our proposed standalone system, a lithium-ion (LI-ION) battery is used as an ESS because of its various advantages of the fast charge–discharge features, along with the quick response and great cycle life53. The bi-directional buck-BC is also used to incorporate the ESS into the DC link bus to maintain the DC link voltage at a constant value as well as to ensure the balance between the energy battery and HRESs to require the load demands, as depicted in Fig. 6. Figure 6 gives a picture of the control used in the battery, where the PI controller is used to generate the pulses necessary to operate the buck-boost converter of the battery. Also, simplicity, ease of implementation, rapid DR, and lower costs are the most prominent features that distinguish the battery control system. What’s more, the battery has two modes of operation: discharging and charging modes. During the charging mode, the stream of the battery is negative (buck converter), and during the discharging mode, the stream of the battery is positive (boost converter). The equations of battery ESS are determined in the following equations54.
The battery power is given by53:
With:
The battery power is described by its state of charge carried out by52:
where the SOC of the battery has the following constraint54:
Microgrid connected 3-phase inverter mathematical model
The inverter connects the hybrid source’s DC side to the grid’s AC side. The primary objectives of the voltage source inverter (VSI) are to convert DC energy to AC and regulate voltage under changing weather conditions. The electrical behavior of a grid-connected 3-phase inverter is effectively represented in the synchronous a, b, and c frames, as shown below55.
where, \({ }V_{i} = { }\left[ {\begin{array}{*{20}c} {V_{id} } & {V_{iq} } \\ \end{array} } \right]^{{\text{T}}} { }\) et \(I_{i} = { }\left[ {\begin{array}{*{20}c} {I_{id} } & {I_{iq} } \\ \end{array} } \right]^{{\text{T}}} { }\) represent the output voltage and stream vectors of the VSI, respectively; \(V_{L} = { }\left[ {\begin{array}{*{20}c} {V_{Ld} } & {V_{Lq} } \\ \end{array} } \right]^{{\text{T}}} { }\) et \(I_{L} = { }\left[ {\begin{array}{*{20}c} {I_{Ld} ,} & {I_{Lq} } \\ \end{array} } \right]^{{\text{T}}}\) represent the load voltage and current vectors, respectively; \(L_{f}\) and \(C_{f}\) denote the inductance and capacitor of the LC filter, respectively.
Control methods of the studied system
The main purpose of controlling HESs is to ensure efficient integration and management of energy sources. It balances energy supply and demand, maintains stability, and ensures reliable power delivery while maximizing efficiency, minimizing environmental impact, and handling RE variability. Advanced algorithms enhance performance and adaptability in standalone setups. The designed control ES, depicted in Fig. 1, encompasses several key components: the optimization of MPPs for both PV and WE sources, management of the ESS and DC link voltage regulator, and control over the load inverter. The primary role of the MPPT regulators is to ensure optimal energy extraction from the WT and PV array, adjusting the duty cycle signal to the BC accordingly. This facilitates the load conditions to be met effectively. Meanwhile, the ESS and DC link voltage regulator oversee the regulation of the DC link voltage and manage the discharge/charge process of the ESS. Lastly, the load inverter regulator is responsible for maintaining the stability of the frequency and voltage of the load inverter within the desired parameters. Further elaboration on the design and realization of these controllers will be provided in subsequent subsections.
MPPT technique
The MPPT is a crucial component in optimizing the performance of HESs that combine WE and PV systems. Over the years, various research efforts have focused on developing and implementing MPPT techniques tailored to these systems56,57. One widely adopted approach is the Perturb and Observe (P&O), known for its simplicity and straightforward realization. However, the P&O is prone to large oscillations around the optimal operating point and has a slow convergence time. For that, two AI methods are employed to enhance the competence of our proposed ES. Specifically, an ANN approach is utilized for the WE system, while an ANFIS is employed for the PV system. These AI-based MPPT approaches calculate the duty cycle switch value for their respective boost converters, aiming to extract optimal and efficient power from the HESs.
-
(a)
ANFIS-MPPT for PV system.
The ANFIS is a powerful tool for modeling complex systems, such as nonlinear systems for MPPT. ANFIS is an intelligent technique that leverages the learning and parallel data processing capabilities of ANNs, along with the interpretability of Takagi–Sugeno FL, to create a hybrid model58,59. Figure 7 represents the internal structure of the ANFIS controller used in this paper. From this figure, it can be seen that the ANFIS controller has a structure consisting of 5 layers. This architecture uses square and circular nodes to represent distinct adaptive functions. The five-layer ANFIS system consists of two inputs (x1 and x2) and one output (Y). The node functions within the various layers of a 5-layered ANFIS are as follows60:
Layer 1-fuzzification layer: This layer is responsible for mapping the input variables (such as voltage and current) to FL sets. It computes the degree of membership for each input variable in each FL set:
Layer 2-rule layer: This layer computes the firing strength of each rule by combining the degree of memberships of the input variables. The firing strength of a rule ii can be calculated as:
Layer 3-normalization layer: This layer normalizes the firing strengths of the rules. The normalized firing strength \(w_{i}\) for rule ii is calculated as:
Layer 4-consequent parameter layer: This layer computes the consequent parameters (Coefficients) of the FL system. The output of this layer is a linear combination of the input variables with the parameters \(p_{i}\), \(q_{i} ,\) for rule i and input j:
Layer 5-defuzzification layer: This layer aggregates the outputs of all rules to generate a single crisp output. This is typically done using a weighted average method.
where, i represents the number of rules; o1,i, o2,i, o3,i, o4,I, and y are the outputs of the five layers; x1 and x2 are inputs; μA and μB are MFs; wi is the output of the second layer, namely firing strength; pi, qi, and ri are consequent parameters and fi .is the consequent function.
In this presented work, the ANFIS-based MPPT approach for maximizing the energy output of a PV module in varying weather conditions is implemented (Fig. 7). The method utilizes irradiation (G) and T as input variables, with the output being the reference value of VPV*. This reference value is compared with the voltage in the PV system VPV, and any resulting error is managed by a PI regulator to generate the duty cycle (D) as depicted in Fig. 2. This duty cycle is then applied to command the DC-DC converter, ensuring that the system maintains optimal power tracking. Figure 8 represents the proposed control algorithm for controlling the PV system. Through this form, the basic points or stages that must be followed to implement and use the proposed control strategy are known. Also, based on Fig. 8, it is possible to know the optimal energy tracked from the PV units by the MPPT strategy based on the ANFIS controller. The data for this control consists of outputs and inputs that are obtained through the parameters of the PV model and are used to train the model of the MPPT approach. Figure 9 represents the membership function for input variable T and output variable G used to implement the ANFIS controller. From this figure, it is noted that the number of functions used for both input and output is 7 functions. A trigonometric function was used to represent the membership function of the ANFIS controller.
b) ANN controller for WE system.
ANNs have been widely applied in MPPT for HES systems, including WE conversion systems. In the context of a DC-DC-BC connected to a WE system, an ANN can be utilized to track the MPP of the WT, ensuring optimal power conversion61.
One common approach is to use a feed-forward NN, where the inputs are the DC WE voltage, DC wind current, and other relevant parameters, and the output is the duty cycle of the BC. The ANN is trained using historical data or results to approximate the relationship between the input parameters and the optimal D for maximum power extraction. Mathematically, the ANN model for MPPT can be represented as follows62:
The output of the hidden layer can be calculated as:
The output of the output layer can be calculated as:
where Let x = [× 1, × 2] be the input vector representing the relevant parameters (e.g., DC wind voltage and DC wind current). Let \(\fancyscript{w}_{ij}^{\left( 1 \right)}\) be the weight matrix of the ANN, where \(\fancyscript{w}_{ij}^{\left( 1 \right)}\) represents the weight connecting the i-th input neuron to the j-th hidden neuron. Let b = [b1, b2, …bm] be the bias vector, where bj is the bias term for the j-th hidden neuron. Let f be the activation function of the hidden layer neurons (e.g., sigmoid, tanh). Let g be the activation function of the output neuron (e.g., linear, sigmoid). \(\fancyscript{w}_{ij}^{\left( 2 \right)}\) is the weight connecting the j-th hidden neuron to the output neuron, and c is the bias term for the output neuron. Figure 10 represents the ANN structure used to estimate the value of D in this paper. From Fig. 10, it is noted that the ANN structure has several layers, where each layer has several nodes, except for the outer layer, which contains one node.
During training, the weights and biases of the ANN are adjusted using an optimization algorithm (e.g., gradient descent) to minimize the difference between the predicted D and the actual D for a given set of input parameters.
Battery controller design
The management of the power in and out of the battery is achieved through the control of DC voltage and SOC as depicted in Fig. 11. In this approach, two loops (external and internal) have been used to create the gate signals for switches Sb1 and Sb2 of the DC/DC converter. Figure 11 presents the process of the control technique. The error between the actual value of the DC link voltage and its reference value is used as an indicator for the battery operation. When the main ESs are greater than the load requirements, the DC link voltage becomes greater than the reference value, and then the battery is charged, and the discharging mode is opposed to the previous case. The external loop used to determine the reference current of a battery by the error between the actual DC voltage and the reference set value is processed through the PI regulator. This signal is then compared with the stream flowing through the battery, and the error is controlled through the hysteresis regulator. The parameters of the PI regulator are given in the following equations52.
The transfer function from Vdc to Pb is given as54.
For constant battery voltage, the equation can be written as Eq. (27)52.
Three phase inverter controller design
The regulator’s main goal is to convert DC energy from hybrid RESs into AC energy for load demand while maintaining voltage and frequency stability and minimizing THD. To achieve this, a PI control strategy based on direct current transformation (DCT) is used, with two control loops: the outer voltage control loop, which tracks the MPP by controlling the direct and quadrature components of the voltage (Vd and Vq), and the inner current control loop, which ensures a unity power factor by regulating the load current components (Id and Iq). The system begins by measuring the three-phase load voltages (Vabc), which are transformed into the d-q frame using a phase-locked loop (PLL) for synchronization. These voltages are then compared to reference values, generating reference currents (Id* and Iq*) and correcting any discrepancies via the PI controller. Figure 12 represents the control used to control a three-phase inverter. From this form, it is noted that the control used is characterized by simplicity, inexpensive, easy to implement, and does not require an MM of the ES studied.
However, traditional PI control struggles with active and reactive power ripples, prompting the use of advanced methods such as fractional-order PI control, artificial intelligence techniques (ANNs, GAs, and PSO), FL control, and nonlinear methods like SMC approach to improve accuracy, robustness, and performance, ensuring better power quality, system stability, and reduced THD value.
In our work, to address this method’s limitations, a novel approach combining PSO-FOPI-ISMC is used in this work, featuring inner and outer command loops. The inner loop employs a PSO-FOPI controller to regulate voltages Vd and Vq, ensuring constant voltage and efficient energy transfer from the HES to the MG. The outer loop uses a PSO-ISMC controller to manage direct and quadrature current components, allowing synchronization between the inverter and grid voltages.
a. FOPI Controller concept for voltage loop.
Over the last two decades, fractional-order proportional-integral-derivative \(({\text{PI}}^{ \propto } \;{\text{D}}^{\upbeta } )\) approaches have gained significant attention. Since the 1990s, the research conducted by Oustaloup and Podlubny on fractional-order controllers (FOC)63,64 applied to dynamic system control, has demonstrated their superior performance and greater adaptability compared to traditional controllers. These studies have shown that FOCs offer substantial advantages in controlling and optimizing complex systems, outperforming conventional controllers across various applications65. The FOPID or \(({\text{PI}}^{ \propto } \;{\text{D}}^{\upbeta } )\) regulators have the following forms of the transfer function, respectively66.
where, \({\text{ K}}_{{\text{p}}}\), \({\text{K}}_{{\text{i}}}\), and \({\text{K}}_{{\text{d}}}\) represent the proportional, integral, and derivative gain constants, respectively. Meanwhile, \(\propto { }\) and \(\upbeta\) denote the fractional orders of the integral and derivative terms. In the case of a classical PID regulator, these values are both equal to 1. As illustrated in Fig. 13, this compares the control domains of the traditional PID regulator and the FOPID regulator.
In the voltage control loop of the inverter, the quadrature and direct voltage components are controlled by the FOPI is designed to improve system robustness and eliminate steady-state errors. The real component (vd) and the reactive component (vq) are controlled using FOPI technique control combined with a PSO algorithm to ensure precise tracking of reference currents (id-q).
-
(b)
ISMC technique for current loop.
The SMC approach is a highly robust and effective method for controlling nonlinear ESs by driving the system’s state toward a predefined sliding surface and ensuring it remains there. On this surface, the system exhibits desirable dynamic behavior, achieving stability and demonstrating strong resistance to disturbances and uncertainties in ES parameters. The control law in SMC comprises a discontinuous component, which provides high precision and ensures fast convergence to the sliding surface. This makes SMC particularly advantageous in applications requiring reliability and robustness, such as motor control, robotics, and power electronics. However, the inherent discontinuity in the control law can lead to a phenomenon known as "chattering," characterized by high-frequency oscillations that can negatively impact ES performance and hardware. We employ advanced techniques like introducing boundary layers, implementing higher-order sliding modes, or incorporating integral action to address this issue. These methods help reduce or eliminate chattering while retaining the robustness and accuracy of the SMC67,68,69. The basic control law for traditional SMC can be represented as:
where, \(u_{eq}\) is the equivalent control, which keeps the system on the sliding surface, and \(u_{dis}\) is the switching control, responsible for driving the system toward the sliding surface.
In this section, the stream control loop of the inverter, and the active and reactive power components are controlled by the integral ISMC. The ISMC is designed to improve ES robustness and eliminate steady-state errors. The sliding surface is given as:
From above equations, the following errors to control the grid-currents can be defined as:
According to reference70, the sliding surface and its derivative for inner current loop are chosen as
where, m1 and m2 are the positive constant.
The design of the sliding mode is based on two terms. Include the equivalent part \(I_{eq}\) and other discontinuous terms \(I_{dis}\) . Where the equivalent command is inserted to maintain the controlled variable on the sliding surface S(x) = 0, and for satisfy the convergence and stability, propose the discontinuous command. To determine the \(u_{eq}\), the derived sliding surface is placed \(\dot{S}_{dq}\) = 0 as shown by Eq. (35).
where, \(s_{dq}\) is the sliding surfaces for \(I_{d - q}\), respectively. This structure allows the ISMC to deliver fast and accurate control of both direct and quadrature current components, ensuring stable inverter operation even under varying load and weather conditions.
The direct component (Id) and the quadrature component (Iq) are controlled using SMC method to ensure precise to create the control (ud-q). The equivalent control input is derived using the invariance condition, represented by the following relationship: \(s_{dq}\) and \(\dot{s}_{dq} = 0\) imply that \(u = u_{eq}\), the sign function approach law provides for control. The equivalent term of the system is described as follow:
And to ensure that the ES can achieve its stability and convergence we are chosen the discontinuous equation as follow:
where, \(u_{dq }\) is the control input applied to the inverter, \(m_{1,2 } {\text{and}} k_{dq1,2 }\) are the sliding gains, \(e_{dq } = I_{dqref} - I_{dq}\) is the sliding surface (the difference between the reference and actual stream), is \(sgn\left( {S_{dq} } \right)\) the sign function.
The ISMC for three phase inverter connected to AC-MG system is typically defined as70:
-
(c)
PSO algorithm.
PSO strategy is a population-based optimization approach inspired by the social behavior of birds flocking or fish schooling. It was introduced by Kennedy and Eberhart in 199571. The algorithm is used to solve complex optimization problems by iteratively improving a candidate solution concerning a given measure of quality, known as the fitness function. PSO operates by initializing a group of particles (Potential solutions) randomly within the search space (Fig. 14). Each particle moves within the space based on its own experience and the collective experience of the swarm.
The PSO algorithm mimics swarm behavior to find optimal solutions by adjusting particle positions based on personal and global best experiences as described in Fig. 14. Each particle updates its velocity \(V_{i} ^{t}\) and position \(X^{t}\) considering inertia, personal best \(P_{i}^{best}\), and swarm knowledge (global best \(G_{i}^{best}\)). This iterative process balances exploration and exploitation until a satisfactory solution is found72,73.
To enhance the performance and accuracy of the PSO algorithm, key parameters have been meticulously chosen. The population size is set to 20, with a maximum of 100 iterations. The acceleration coefficients, c1, and c2, are both set to 2, while the acceleration constants, a1 and a2, and are assigned values of 0.02. The initial value of x is configured at 0.7 for optimized results. The primary goal of the PSO algorithm is to minimize the objective function. To accomplish this, we will utilize the objective function based on the integral of absolute errors (IAE). The mathematical representation of the integral of absolute errors (IAE) is as follows:
where, \(e_{{I_{d} }} \left( t \right) = \smallint \left( {I_{d }^{*} - I_{d} } \right)^{2} dt\); \(e_{{I_{q} }} \left( t \right) = \smallint \left( {I_{q }^{*} - I_{q} } \right)^{2} dt\).
This study treats the tuning of FOPI-ISMC controller parameters as an optimization task to ensure accurate reference tracking. Using the PSO algorithm, the optimal values for FO-ISMC parameters (\(k_{p } ,k_{i} ,\) \(\propto\) \(m_{1,2 } {\text{and}} k_{dq1,2 }\)) are determined to command the DC bus voltage and grid stream in PV grid-connected systems, improving simulation performance. Figure 15 shows the optimization process.
Management power flow system
The management strategy for the HESs integrated into standalone aims to ensure the consistent delivery of high-quality power in alignment with the specific ESS format and weather conditions. Moreover, the battery serves dual roles as a power sink or supply. Depending on weather conditions, it must discharge or charge within defined limits in response to surplus or insufficient HES. In this research, excess energy resulting from high SE and WE conditions initially charges the battery bank until it reaches its upper charge limit, after which the dump load absorbs any additional energy. In our model, the duty ratio of the buck converter is dependent on the DC bus voltage as shown in Fig. 16. The equation of the HES is determined in Eq. (6)52.
With:
Then
When the HRES connected in parallel with ESS Eq. (4) is given
These are the governing equations of the energy balance in the DC link, where the sign \(\pm\) defines the mode of operation of battery charge or discharge52.
Based on our proposed model, a flowchart is presented in Fig. 17, which illustrates the coordination strategy among the various RESs, including the battery storage system and the dump load. To ensure optimal and efficient operation, the SOC of the battery is maintained within a specified range, with a lower limit of 25% and an upper limit of 80%. Based on this flowchart, the system’s operation can be described through the following cases:
Case 1: When the total power generation from the PV system and WECS exceeds the load demands, the principal and additional loads will be exclusively supplied by HESs.
Case 2: When the energy generated by HESs exceeds the load demand and the SOC is below 80%, surplus power is utilized to charge the batteries.
Case 3: When PV and WE sources are insufficient to meet the load requirements, the principal and additional loads will be powered by the HESs and batteries, provided the SOC is above 25%.
Case 4: When the total energy generated by HESs exceeds the load demands and the SOC is above 80%, the supervisory controller activates the Dump load to absorb the surplus power from the HES.
Case 5: When the PV and WE sources are unable to meet the load requirements, and the SOC is above 80%, the battery ESS begins supplying the loads and disconnects the dump load.
Results
The simulation model of the designed standalone SE and WE hybrid system with ESS has been developed using MATLAB, considering various weather and load conditions. The parameters of the standalone system, PV array, WT, and battery ESS are detailed in Table 1. This section examines the ES performances through two cases:
-
1.
In the first case, the HES are regulated to maintain MPPT operation, taking into account variable weather conditions such as WS and irradiation.
-
2.
In the second case, the system is regulated to mitigate harmonic streams generated by variable AC linear loads under different weather conditions, based on the SOC of the battery.
Performances of subsystem PV/WE with intelligent MPPT approaches
First, the performance of the PV/WE subsystem is studied using smart MPPT methods, where the results obtained are represented in Figs. 18 and 19. Figure 18 represents the results of the PV generator under varying irradiation levels with P&O and ANFIS-MPPT techniques. Figure 18a represents the DC output energy in the case of using the two strategies (P&O and ANFIS) compared with the PV generator output power, as there are ripples in this energy. This power is related to the value of irradiation, as the higher the value of irradiation, the greater the value of this power, and vice versa. In the case of using ANFIS, energy with fewer fluctuations and a fast dynamic response is obtained compared to the P&O strategy.
Figure 18b represents the duty cycle if both P&O and ANFIS are used. Through this form, the duty cycle value is significantly affected by the irradiation value, as its value increases and decreases as the irradiation value increases and decreases. Also, it is noted that there are fluctuations at the duty cycle level, as these fluctuations are much less when using ANFIS compared to P&O.
Figure 18c represents the change of PV voltage as a function of time if both P&O and ANFIS are used. It is noted that the value of the PV voltage does not change with time, as its value remains constant regardless of the irradiation value in the presence of ripples. The PV voltage value when using P&O and ANFIS follows the reference value well. However, the value of the PV voltage ripples is lower when using ANFIS compared to P&O, which indicates the ability of the designed control approach to reduce the PV voltage ripples, which is desirable.
PV stream in the case of using both P&O and ANFIS is represented in Fig. 18d, where it is noted that the value of this current is associated with the value of irradiation with the presence of fluctuations at the level of this stream. These fluctuations are larger when using P&O compared to ANFIS. This current takes constant values during each phase or irradiation value, where these values are positive.
Figure 19 represents the simulation results of the WE conversion system under varying WS levels with P&O and ANN-MPPT strategies. In Fig. 19a, the change in the shape of WE as a function of time is given in the case of using both P&O and ANN, where the value of this power increases and decreases for the two controls with the presence of fluctuations. The latter is lower in the case of using ANN compared to using P&O. Also, it is noted that using ANN provides a faster dynamic response that is better than using P&O.
The change in duty cycle in the case of using both P&O and ANN is represented in Fig. 19b, where it is noted that the duty cycle is better in the case of using ANN compared to using P&O, as its value is constant and approximately equal to 0.6 without undulations in the case of using ANN. But if P&O is used, its value is not constant throughout the simulation period, it changes.
In Fig. 19c, the change in wind current as a function of time is given in the case of using both ANN and P&O. Through this form, the value of this stream changes according to the change in WS, as it increases and decreases with the augment and decrease in WS, with the presence of undulations. The fluctuations of this current are lower when using ANN compared to using P&O, which indicates the ability of the ANN strategy to enhance the system’s features and its efficiency.
In Fig. 19d, the variation of generator speed as a function of time is given in the case of using both ANN and PO. This speed is constant during each period, reaching its maximum value of 300 rad/s during the periods 0 to 0.5 s and 2 to 2.5 s.
Random profile of irradiation and WS with varying load
The following results verify the competence of the command employed. The ES was tested under two primary conditions: normal operation (25 < SOC < 80) % and overcharging (SOC > 80) %.
Scenario 1: If 25% < SOC < 80%.
In Fig. 20, the reference values are given for each of the profile WS, profile irradiation, and profile load used in the first test to study the competence of the designed strategies.
The results of this test are represented in Fig. 21. In Fig. 21a, the shape of the change in the constant voltage line is given, where it is noted that the value of this Vdc voltage follows the reference well and takes a constant value throughout the simulation period, with the presence of ripples. Also, it is observed that the limit value is exceeded during the time moments of 0, 0.5, 1, 1.5, and 2 s due to the change in the reference values of irradiation.
Figure 21b illustrates the energy flow management in the designed HES under varying weather conditions, including WS and irradiation levels, with load profiles. The RES power curves depict the MPP extracted from the PV and WE systems using smart approaches (ANFIS MPPT, ANN-MPPT, and PSO-FOPI-ISMC for VSC). The battery energy curve shows energy changes during charge and discharge operations. Energy flow distribution in the designed MG between generation sources and load consumption is divided into three different modes:
Mode 1: (Charging Operation), from t = 0 to t = 1 s, the total power generation from the PV and WE system exceeds the principal and additional loads, and the SOC is less than 80%. In this mode, the principal and additional loads are supplied only by the RESs, and the excess power is used to charge the battery storage (The battery operates in charging mode). In case 1, from t = 0 to 0.5 s, Pload = 60 kW, Ppv = 50 kW, Pw = 40 kW, and Pb = -30 kW (Charge mode). In case 2, from t = 0.5 to 1 s, Pload = 90 kW, Ppv = 100 kW, Pw = 10 kW, and Pb = -20 kW (Charge mode).
Mode 2: (Disconnected operation) From t = 1 to 1.5 s, the RESs’ generation energy (110 kW) is equal to the load demand energy (110 kW), and the battery is completely disconnected from the ES. Here, Pload = 110 kW Ppv = 80 kW, Pw = 30 kW, and Pb = 0 kW.
Mode 3: (Discharging operation) from t = 1.5 to 2.5 s, the total generation power from the PV generator system and WE generator system is insufficient to meet the load demand (Less than 80 kW), and the battery supplies the deficiency in energy generated by the RESs to the loads (The battery operates in discharging mode). In case 1 (Mode 3), from t = 1.5 to 2 s, Pload = 80 kW, Ppv = 40 kW, Pw = 30 kW, and Pb = + 10 kW (Discharge mode). In case 2 (Mode 3), from t = 2 s to 2.5 s, Ppv = 20 kW, Pw = 30 kW, and Pb = + 24 kW (Charge mode).
Figure 21c shows the variation of the direct current component over time. It can be observed that the current value closely follows the reference for all methods (PI, PSO-FOPI-ISMC), though some ripples are present. The current value is not constant but varies over time with ES conditions changes. However, the proposed method demonstrates better RT and reduced oscillations compared to the PI method.
In Fig. 21d, the change of three-phase load voltage and stream as a function of time is given. These currents and tensions take a sinusoidal shape, with the value of the stream changing according to the three modes.
Figure 21e represents the change in battery current as a function of time, as the value of this current follows the reference well, with fluctuations at the level of this stream. This current is negative in the time range from 0 to 1 s and is non-existent in the time range from 1 to 1.5 s. Also, this current is positive in the time range of 1.5 to 2.5 s. So this current has three different states depending on the mode changes, which is normal.
In Fig. 21f, the change in battery SOC as a function of time is given, where battery SOC increases in the time range from 0 to 1 s to reach a maximum value of 60.60%. After that, the battery SOC remains at the maximum value for a time range of 1 to 1.5 s. After this time frame, the battery SOC begins to decrease, reaching around the value of 60.30% at the time point of 2.5 s.
The battery voltage is represented in Fig. 21e, where this voltage varies in value according to time frames with ripples at its level. The value of this effort decreases with time.
THD is a key metric for assessing power quality. According to international standards, it must be maintained below 5%. In our designed solution, a control scheme combining three techniques is implemented: PSO-FOPI-ISMC, across the three previously defined modes. The THD of the load stream, after filtering, is shown in the following figures. Figures 22 and 23 depict the load source streams and voltage curves along with the associated THD for both the PSO-FOPI-ISMC and PI techniques. From these figures, it can be observed that the THD in all modes is below the 5% threshold required by international standards while achieving a unity power factor for both techniques. Additionally, in the case of energy injection from HRE to the load without a battery (Mode 2), the THD was observed to be at its lowest. In modes 1 and 3, where the battery was active, the THD increased. Specifically, the THD values for the PI technique were 1.90%, 1.89%, and 2.15% for modes 1, 2, and 3, respectively. The fundamental (50 Hz) current amplitudes for these modes were 192.9 A, 235.9 A, and 170.5 A, respectively. For the PSO-FOPI-ISMC technique, the THD values were 0.70%, 0.56%, and 0.72% for modes 1, 2, and 3, respectively. The corresponding fundamental current amplitudes were 192.6 A, 237.3 A, and 169.6 A. These figures indicate that the designed approach is superior in terms of achieving lower THD values and maintaining a good waveform quality for both supply current and voltage.
Scenario 2: If SOC > 80%
In another simulation run, the battery SOC is initially set to 81.25% to analyze the operation of the dump load. Figure 24 illustrates the ES in two modes of operation. In mode 1, from time t = 0 to t = 0.5 s, the total energy generation exceeds the load demand. During this period, the battery does not contribute to the power supply, and the dump load operates to balance the power. The power values are as follows: Pload = 90 kW, Ppv = 100 kW, Pw = 28 kW, Pb = 0 kW, and P (Dump load) = 35 kW (Disconnected mode).
In mode 2, from time t = 0.5 s to t = 1 s, energy generation is lower than the load demand, leading to battery discharge to supply the deficit energy. Figure 25 represents the change in the battery SOC value as a function of time, as well as the change in the battery voltage value as a function of time. The change in the SOC value of the battery is represented in Fig. 25a. It is noted that the SOC value of the battery changes with time. Also, the SOC value of the battery remains within safe limits to prevent overcharging. Figure 25b represents the change in battery voltage as a function of time. This voltage changes and does not take a fixed value throughout the simulation period with the presence of ripples. The battery voltage value is affected by the change in the SOC value, as it is noted that when the SOC value decreases, the battery voltage decreases. The power values for mode 2 are Pload = 130 kW, Ppv = 80 kW, Pw = 40 kW, Pb = 13 kW, and P (Dump load) = 0 kW (Discharge mode). The energy difference represents losses consumed in the filter.
Figure 26 represents three-phase load current and voltage. From this figure, it is observed that voltages and currents take a sinusoidal shape with ripples. Also, it is noted that the value of these currents and voltages changes depending on the situation.
Figures 27 and 28 illustrate the load current and voltage, along with the current THD. From these figures, it can be observed that the voltage and current are closely correlated, as an augment in voltage is accompanied by a corresponding rise in current. At 0.39 s, the THD values were 1.43% for the PI controller and 0.64% for the proposed method, while at 0.69 s, they were 1.74% for the PI controller and 0.47% for the proposed controller. These THD values are satisfactory and indicate that the current quality is acceptable. However, the proposed solution consistently achieves lower THD values, with an improved waveform for both current and voltage.
Robustness tests
In practical operation, the parameters of HESs can be affected by various factors, including temperature fluctuations, magnetic material saturation, and frequency variations. Despite these changes, the performance of the inverter control system should remain stable and robust. To evaluate robustness, simulations were conducted under the same conditions as Scenario 2, with updated parameters for the PMSG and the filter of the inverter, the new values of the parameters are \(R_{g}^{`} = R_{g} *2\), \(L_{g}^{`} = L_{g} /2,\) \(R_{f}^{`} = R_{f} *2\), \(L_{f}^{`} = L_{f} /2\). The results of this test are included in Figs. 29 through 31.
Figure 29 represents both the change in current and Ps as a function of time. Figures 29a,b demonstrate that both controllers enable the Ps and direct current to accurately track their desired values. However, the results also reveal noticeable chattering in the case of the PI controller, as seen in Figs. 29a,b, compared to the proposed FOPI-ISMC controller based on the PSO algorithm. These findings indicate that the proposed FOPI-ISMC controller not only maintains the robustness of the classic PI controller but also significantly minimizes the chattering phenomenon. Moreover, the inclusion of an additional parameter (Integral order δ) in the fractional integrator enhances the flexibility and performance of the FOPI-ISMC controller compared to the traditional PI controller. Furthermore, Figs. 30 and 31 illustrate that the inverter currents exhibit smooth sinusoidal waveforms, free from ripples, ensuring clean energy without harmonic injection into the MG. The THD values of the output current for both the proposed and traditional control methods, as shown in Figs. 30 and 31, highlight that the FOPI-ISMC controller based on the PSO algorithm reduces the THD of the current by approximately 74.76%, 71.12%, and 73.38% compared to the traditional SMC method. This improvement can be attributed to the ability of the proposed controller to significantly reduce chattering, offering superior performance over the conventional PI strategy.
Comparative study
Within this study, advanced technologies of ANFIS and ANN outperform simpler methods like P&O due to their ability to handle nonlinearities, uncertainties, and dynamic changes, improving accuracy, RT, and efficiency. AI-based ESs adapt to environmental changes (e.g., irradiance, WS), reducing SSE and optimizing power tracking, while conventional methods struggle with rapid fluctuations. AI methods use historical and real-time data to predict system behavior, resulting in faster adjustments. ANFIS, in particular, excels in managing the nonlinear characteristics of RESs, ensuring stability and reduced power loss, while P&O lacks this capability. AI systems leverage NNs and FL approaches to make precise, adaptive control decisions, offering superior performance compared to rule-based traditional methods. This makes ANFIS and ANN particularly suitable for complex RESs, as it ensures optimal power extraction and system reliability. These findings are supported by the results presented in Tables 2 and 3.
Table 2 presents the numerical values for MPP, rise time, SSE, and RT under varying irradiation levels for both ANFIS-MPPT and P&O-MPPT. The data highlights the superior performance of ANFIS-MPPT across these indicators, demonstrating its effectiveness in enhancing the control system’s efficiency. Specifically, ANFIS-MPPT reduced rise time by 80%, 64.17%, and 69.23% at irradiation levels of 600 W/m2, 800 W/m2, and 1000 W/m2, respectively, compared to P&O-MPPT. Similarly, RT was minimized by 82%, 78.26%, and 60% under the same conditions. Furthermore, ANFIS-MPPT increased MPP by 28%, 24%, and 18% for the respective irradiation levels, achieving the most significant improvements at 600 W/m2.
In terms of SSE, ANFIS-MPPT outperformed P&O-MPPT with reductions of 66.66%, 80%, and 94.70% at irradiation levels of 600 W/m2, 800 W/m2, and 1000 W/m2, respectively. Notably, the reduction in SSE became more pronounced with increasing irradiation levels, showcasing ANFIS-MPPT’s ability to maintain higher accuracy as environmental conditions change. This detailed analysis not only confirms the efficacy of ANFIS-MPPT in optimizing key performance indicators but also emphasizes its adaptability and reliability in varying operational scenarios. These findings are supported by the results presented in Tables 2 and 3.
In Table 3, the values of RT, MPP, and rise time are given in different cases of WS for the proposed strategies. From this table, it is noted that the values of MPP, rise time, and RT are better when using the ANN-MPPT compared to using the P&O-MPPT, which is a good thing. Therefore, the ANN-MPPT minimized the rise time value compared to the P&O-MPPT by ratios estimated at 10%, 80%, and 99.32% when the WS was equal to 9 m/s, 11 m/s, and 12 m/s, respectively. The RT value was also minimized compared to the P&O-MPPT by ratios estimated at 57.14%, 68.75%, and 60% when the WS is equal to 9 m/s, 11 m/s, and 12 m/s, respectively. The P&O-MPPT strategy provided unsatisfactory results for MPP when the WS was equal to m/s, 11 m/s, and 12 m/s compared to the ANN-MPPT. The latter increased the MPP value by rates estimated at 6.4%, 4%, and 1.5% during the corresponding WS. The ANN-MPPT gave good values for SSE compared to the P&O-MPPT, and this appears through the calculated reduction ratios, where the SSE value was reduced by percentages estimated at 94.47%, 87.5%, and 60% in the case of WSs of 9 m/s, 11 m/s, and 12 m/s, respectively.
Table 4 summarizes the performance of the proposed method of PSO-FOPI-ISMC and the classical method (PI control) during steady-state conditions. The results demonstrate the superiority of the proposed control scheme across various scenarios, including SOC variations, weather changes, and charge profile test cases. The proposed method consistently achieves a lower percentage of load power output oscillation (ePL) compared to the conventional approach under all irradiation, WS levels, and SOC conditions. Furthermore, the PSO-FOPI-ISMC control scheme significantly reduces mean absolute current tracking errors (eId and eIq) in all modes compared to the traditional PI regulator. In terms of harmonic performance, the proposed method ensures lower THD and higher current quality. Specifically, the THD was reduced by 63.1%, 70.3%, and 66.5% in Scenario 1 (25% < SOC < 80%) and by 55.2% and 72.9% in Scenario 2 (SOC > 80%), clearly highlighting the effectiveness of the proposed approach over the conventional PI controller.
In Table 5, a comparison is made between the work done and some scientific papers in terms of the type of control strategy used, the components of the studied HES, the value of stream THD, and the contribution made. Through this table, the work completed differs from other work in terms of contribution and type of ES studied. Also, this paper differs from the rest of the mentioned works in terms of the kind of control strategy used, as it is noted that the paper is superior to other papers in terms of the stream THD, which indicates the effectiveness and high competence of the designed strategy.
Conclusions
In this paper, the design and control of a standalone MG with HES are presented. The HES-MG comprises a WT, two boost converters, a PV array, an ESS, a DC dump load, a bidirectional DC/DC-BC, and an AC loads inverter. After providing mathematical modeling for each element of the studied ES, this studied system is implemented using MATLAB. Various scenarios are proposed to verify the enhancement of characteristics of the renewable HES control system. Smart approaches using ANFIS and ANN extract the MPP from the PV generator and wind system, respectively. These approaches demonstrate superior effectiveness to the P&O technique under variable weather conditions, such as WSs and irradiation levels, regarding rise time, RT, MPP, and ESS efficiency. Additionally, the management of energy and charge/discharge operations of the battery ESS is presented to fulfill the load profile, prevent battery ESS overcharging, and reduce the intermittency and variation of renewable HESs. Simulation results confirm that the ES can supply EE to the load under variable changes in meteorological conditions and loads while maintaining the THD of the load current within acceptable limits. Through the work done and the results obtained, the following results can be concluded:
-
The use of both ANNs and the ANFIS approach leads to overcoming the problems and drawbacks of the traditional MPPT strategy.
-
Using the PSO-FOPI-ISMC approach leads to an improvement in the SSE value compared to the traditional approach in the second test by percentages of 61.90% and 63.60% for mod 1 and mod 2, respectively. Also, rates are estimated at 65.70%, 67.80%, and 69.70% for mod 1, mod 2, and mod 3, respectively.
-
The THD value of the current was reduced in the case of using the PSO-FOPI-ISMC approach by percentages estimated at 55.20% and 72.90% in the second test and by ratios estimated at 63.10%, 70.30%, and 66.50% in the first test compared to the traditional approach (PI control).
-
The values of rise time, RT, MPP, and SSE were improved if the ANN-MPPT approach was used when the wind speed was 12 m/s by 99.32%, 60%, 1.5%, and 60%, respectively, compared to P&O-MPPT.
-
The value of RT, MPP, SSE, and rise time was improved when using the ANFIS-MPPT approach when the radiation was equal to 600 W/m2, by percentages estimated at 82%, 28%, 66.60%, and 80%, respectively, compared to the P&O-MPPT approach.
These obtained results increase the importance of the proposed control system and the extent of its application in other industrial fields such as propulsion and traction. The completed work has limitations, as only the completed work was studied using simulation. Also, specific tests were used to study the efficacy and effectiveness of the proposed strategies. The effectiveness of the proposed strategies in the event of a network failure has not been studied, which gives less data on the effectiveness and efficiency of the proposed approach. On the other hand, this completed work has a set of challenges that limit its use and spread in the future. The most prominent of these challenges lies in (1) the presence of a significant number of control strategies, (2) Many components, (3) High costs, (4) Difficulty in completion, and (5) Complexity. These challenges will be reduced by creating new systems that are highly effective and have many features that make them applicable systems on the ground at very low costs.
In the future, this HES will be developed using other RESs, such as hydropower, to generate EE. Also, this work will be accomplished experimentally using real equipment, and the results will be compared with other nonlinear strategies such as backstepping control.
Data availability
Data available on request from the authors. The datasets used and/or analysed during the current study available from the corresponding author on reasonable request. In the event of communication, the fist author (Habib Benbouhenni, E-mail: habib.benbouhenni@enp-oran.dz) will respond to any inquiry or request.
Abbreviations
- THD:
-
Total harmonic distortion
- HES:
-
Hybrid energy system
- PV:
-
Photovoltaic system
- EE:
-
Electrical energy
- ES:
-
Energy system
- FL:
-
Fuzzy logic
- PSO:
-
Particle swarm optimization
- MM:
-
Mathematical model
- MG:
-
Microgrid
- ANFIS:
-
Adaptive neuro-fuzzy inference system
- SE:
-
Solar energy
- AI:
-
Artificial intelligence
- ISMC:
-
Integral sliding mode control
- NN:
-
Neural network
- WS:
-
Wind speed
- MPPT:
-
Maximum power point tracking
- WE:
-
Wind energy
- WT:
-
Wind turbine
- MP:
-
Mechanical power
- ESS:
-
Energy storage system
- BS:
-
Battery storage
- MPC:
-
Model predictive control
- SOC:
-
State of battery charge
- MPP:
-
Maximum power point
- P&O:
-
Perturbations and observations
- ANN:
-
Artificial neural network
References
Jain, N., Sharma, S., Thakur, V., Nutakki, M. & Mandava, S. Prediction and analysis of household energy consumption integrated with renewable energy sources using machine learning algorithms in energy management. Int. J. Renew. Energy Res. 14(2), 354–362. https://doi.org/10.20508/ijrer.v14i2.14577.g8893 (2024).
Zekrifa, D. M. S. et al. Optimized controller design for renewable energy systems by using deep reinforcement learning technique. Int. J. Renew. Energy Res. 14(1), 101–110. https://doi.org/10.20508/ijrer.v14i1.14362.g8854 (2024).
AlBusaidi, A. S., Al Lamki, H., AlHinai, A. & Kazem, H. A. Techno economic design and analysis of a hybrid renewable Energy system for Jazirat Al Halaniyat in Oman. Int. J. Renew. Energy Res. 13(3), 1039–1050. https://doi.org/10.20508/ijrer.v13i3.13679.g8778 (2024).
Fendzi, W. M., Dzonde, S. R. N., Jacques Molu, R. J. & Tsobze, S. K. Contribution into robust optimization of renewable energy sources: Case study of a standalone hybrid renewable system in Cameroon. Int. J. Renew. Energy Res. 13(3), 1093–1120. https://doi.org/10.20508/ijrer.v13i3.14103.g8802 (2024).
Abderrahim, S., Allouche, M. & Chaabane, M. A new robust control strategy for a wind energy conversion system based on a T–S fuzzy model. Int. J. Smart Grid 4(2), 88–99. https://doi.org/10.20508/ijsmartgrid.v4i2.103.g87 (2020).
Ifanda, I. et al. Optimizing turbine siting and wind farm layout in Indonesia. Int. J. Renew. Energy Res. 13(3), 1351–1363. https://doi.org/10.20508/ijrer.v13i3.14070.g8806 (2024).
Naseem, S. et al. Rural areas interoperability framework: Intelligent assessment of renewable energy security issues in PAKISTAN. Int. J. Smart Grid 4(2), 43–55. https://doi.org/10.20508/ijsmartgrid.v4i2.93.g89 (2020).
Elsayed, Y., Saad, N. H. & Zekry, A. Assessing wind energy conversion systems based on newly developed wind turbine emulator. Int. J. Smart Grid 14(4), 139–148. https://doi.org/10.20508/ijsmartgrid.v4i4.133.g101 (2020).
Opedare, I. M., Adekoya, T. M. & Longe, A. Optimal sizing of hybrid renewable energy system for off-grid electrification: A case study of University of Ibadan Abdusalam Abubakar Post Graduate Hall of Residence. Int. J. Smart Grid 14(4), 176–189. https://doi.org/10.20508/ijsmartgrid.v4i4.135.g110 (2020).
Mahesh, K., Muzamil, A. S., Amir, M. S., Syed Ali, A. K. & Aneel, K. Techno-economic comparative analysis of an off-grid PV-wind-hydrogen based EV Charging Station under Four Climatically Distinct Cities in Pakistan. Int. J. Hydrog. Energy 93, 1268–1282. https://doi.org/10.1016/j.ijhydene.2024.11.074 (2024).
Mansoor, A. S., Zubair, A. M., Mahesh, K. & Mazhar, H. B. Wind energy integration: Dynamic modeling and control of DFIG based on super twisting fractional order terminal sliding mode controller. Energy Rep. https://doi.org/10.1016/j.egyr.2021.09.022 (2021).
Kaloi, G. S. et al. An LVRT scheme for grid connected DFIG based WECS using state feedback linearization control technique. Electronics 8(7), 777. https://doi.org/10.3390/electronics8070777 (2019).
Farghaly, M. B. & Abdelghany, E. S. Study the effect of trailing edge flap deflection on horizontal axis wind turbine performance using computational investigation. Int. J. Renew. Energy Res. 12(4), 1942–1953. https://doi.org/10.20508/ijrer.v12i4.13433.g8617 (2022).
Francisco, J., Sarrias-Mena, R., Fernández-Ramírez, L. M. & García-Vázquez, C. A. Comparative study of wind farm integration on voltage stability. Trakia J. Sci. 14(3), 297–304. https://doi.org/10.5502/trakia.2016.0297 (2016).
Caglayan, R. Z., Kayisli, K., Zhakiyev, N., Harrouz, A. & Colak, I. A review of hybrid renewable energy systems and MPPT methods. Int. J. Smart Grid 6(3), 72–78. https://doi.org/10.20508/ijsmartgrid.v6i3.248.g243 (2022).
Elkodama, A., Ismaiel, A., Abdellatif, A. & Shaaban, S. Aerodynamic performance and structural design of 5 MW Multi Rotor System (MRS) wind turbines. Int. J. Renew. Energy Res. 12(3), 1495–1505. https://doi.org/10.20508/ijrer.v12i3.13343.g8535 (2022).
Benbouhenni, H., Gasmi, H. & Colak, I. Backstepping control for multi-rotor wind power systems. Majlesi J. Energy Manag. 11(4), 8–15 (2022).
Todeschini, G., Huang, H., Bristow, N., Wyn David, T. & Kettle, J. A novel computational model for organic PV cells and modules. Int. J. Smart Grid 14(4), 157–163. https://doi.org/10.20508/ijsmartgrid.v4i4.127.g105 (2020).
El Alami, Y. et al. Optimized controller design for renewable energy systems by using deep reinforcement learning technique, design and realization of a descretized PV system with an improved MPPT control for a better exploitation of the PV energy. Int. J. Renew. Energy Res. 14(2), 224–237. https://doi.org/10.20508/ijrer.v14i2.14354.g8884 (2024).
Walid, K., Sofiane, M., Benbouhenni, H., Hamza, G. & Es-saadi, T. Application of third-order sliding mode controller to improve the maximum power point for the photovoltaic system. Energy Rep. 9, 5372–5383. https://doi.org/10.1016/j.egyr.2023.04.366 (2023).
Pandey, N. K., Pachauri, R. K., Choudhary, S. & Thanikanti, S. B. Frequency locked loop-based control algorithm with enhanced second-order generalized integrator for PV-battery integrated system to improve power quality. Int. J. Renew. Energy Res. 14(1), 155–165. https://doi.org/10.20508/ijrer.v14i1.14241.g8870 (2024).
Qaid, K. A., Tee, W. H., Gan, C. K. & Tan, P. H. Modelling and sizing a grid-connected PV-battery system using DIgSILENT for powering UTeM Main Campus. Int. J. Renew. Energy Res. 13(3), 1200–1211. https://doi.org/10.20508/ijrer.v13i3.14042.g8792 (2024).
Mehrdad, A. K., Ilhami, C., Phatiphat, T. & Kei, E. Modeling and simulation of DVR and D-STATCOM in presence of wind energy system. Comput. Mater. Continua 74(2), 4547. https://doi.org/10.3970/cmc.2023.074.0205 (2023).
Zahraee, S. M., Khalaji Assadi, M. & Saidur, R. Application of artificial intelligence methods for hybrid energy system optimization. Renew. Sustain. Energy Rev. 66, 617–630. https://doi.org/10.1016/j.rser.2016.08.028 (2016).
Mostafa, M. L., Mehrdad, A. K. & Tohid, N. Stochastic unit commitment study in a power system with flexible load in presence of high penetration renewable farms. Int. J. Energy Res. 2023(1), 9979610. https://doi.org/10.1002/er.9979610 (2023).
Salman, H., Mehrdad, A. K., Hassan, S. & El Manaa, B. Economic dispatch optimization considering operation cost and environmental constraints using the HBMO method. Energy Rep. 10, 1718–1725. https://doi.org/10.1016/j.egyr.2023.01.017 (2023).
Mehrdad, A. K. & Hamid, L. Effects of STATCOM, TCSC, SSSC, and UPFC on static voltage stability. Int. Rev. Electr. Eng. 4(6), 1376–1384. https://doi.org/10.1002/iree.00405 (2011).
Mehrdad, A. K. et al. Optimum operation management of microgrids with cost and environment pollution reduction approach. IET Renew. Power Gener. https://doi.org/10.1049/rpg2.12202 (2022).
Hassan, S., Mehrdad, A. K., Ilhami, C. & Kei, E. Unit commitment for power generation systems based on prices in a smart grid environment. Sustainability 13(18), 10219. https://doi.org/10.3390/su131810219 (2021).
Mehrdad, A. K., Abolfazl, R. N., Mostafa, A., & Hamid, S. Comparison between parallel and series FACTS devices on static voltage stability using MLP index. In SPEEDAM 2010 (IEEE, 2010). https://doi.org/10.1109/SPEEDAM.2010.5533830.
Shokouhandeh, H., Ahmadi, K. M., Asghari, F., Colak, I. & Eguchi, K. Distributed generation management in smart grid with electric vehicle participation. Sustainability 14(8), 4770. https://doi.org/10.3390/su14084770 (2022).
Say, G., Hosseini, S. H. & Esmaili, P. Hybrid source multi-port quasi-Z-source converter with fuzzy-logic-based energy management. Energies 16, 4801. https://doi.org/10.3390/en16124801 (2023).
Nazari-Heris, M., Esfehankalateh, T. & Ifaei, A. Hybrid energy systems for buildings: A techno-economic-enviro systematic review. Energies 16, 4725. https://doi.org/10.3390/en16124725 (2023).
Chrifi-Alaoui, L., Drid, S., Ouriagli, M. & Mehdi, D. Overview of photovoltaic and wind electrical power hybrid systems. Energies 16, 4778. https://doi.org/10.3390/en16124778 (2023).
Elegeonye, H. I. et al. Techno-economic optimization of mini-grid systems in Nigeria: A case study of a PV–battery–diesel hybrid system. Energies 16, 4645. https://doi.org/10.3390/en16124645 (2023).
Zhang, C., Sun, J., Ma, J., Xu, F. & Qiu, L. Environmental assessment of a hybrid solar-biomass energy supplying system: A case study. Int. J. Environ. Res. Public Health 16, 2222. https://doi.org/10.3390/ijerph16122222 (2019).
Pathak, P. K., Yadav, A. K. & Kamwa, I. Resilient ratio control assisted virtual inertia for frequency regulation of hybrid power system under DoS attack and communication delay. IEEE Trans. Ind. Appl. 99, 1–9. https://doi.org/10.1109/TIA.2024.3482274 (2024).
Sneha, V. S., Vivek, P., Pawan, K. P. & AnilKumar, Y. Virtual inertia and intelligent control assisted frequency regulation of time-delayed power system under DoS attacks. Chaos Solitons Fractals 188, 115578. https://doi.org/10.1016/j.chaos.2024.115578 (2024).
Seedahmed, M. M. A., Ramli, M. A. M., Abusorrah, A. & Alqahtani, M. M. Control-oriented model of an optimally designed hybrid storage system for a standalone microgrid. IEEE Access 11, 119161–119186. https://doi.org/10.1109/ACCESS.2023.3326333 (2023).
Pawan, K. P., Sanjeevikumar, P., Anil, K. Y., Alvi, P. A. & Baseem, K. Modified incremental conductance MPPT algorithm for SPV-based grid-tied and stand-alone systems. IET Gener. Transm. Distrib. 16(4), 776–791. https://doi.org/10.1049/gtd2.12328 (2022).
Maloth, R., Anil, K. Y. & Pawan, K. P. Artificial Gorilla Troops optimizer for frequency regulation of wind contributed microgrid system. J. Comput. Nonlinear Dyn. 18(1), 011005. https://doi.org/10.1115/1.4056135 (2023).
Firas, M. M. et al. Optimal management of energy storage systems for peak shaving in a smart grid. Comput. Mater. Contin. 75(2), 3317–3337. https://doi.org/10.3970/cmc.2023.075.3317 (2023).
Guo, S. et al. Multi-objective sizing of solar-wind-hydro hybrid power system with doubled energy storages under optimal coordinated operational strategy. CSEE J. Power Energy Syst. 9(6), 2144–2155. https://doi.org/10.17775/CSEEJPES.2021.00190 (2023).
Santos, Y. A., Nunes, M. P. M., Lemes, L. A. C. & Bortoni, E. C. Evaluation of hybrid energy storage systems using wavelet and stretched-thread methods. IEEE Access 8, 171882–171891. https://doi.org/10.1109/ACCESS.2020.3024966 (2020).
Dou, C., Yue, D., Li, X. & Xue, Y. MAS-based management and control strategies for integrated hybrid energy system. IEEE Trans. Ind. Inform. 12(4), 1332–1349. https://doi.org/10.1109/TII.2016.2569506 (2016).
Villalva, M. G., Gazoli, J. R. & Filho, E. R. Comprehensive approach to modeling and simulation of photovoltaic arrays. IEEE Trans. Power Electron. 24(5), 1198–1208. https://doi.org/10.1109/tpel.2009.2013862 (2009).
Zebraoui, O. & Bouzi, M. Improved MPPT controls for a standalone PV/wind/battery hybrid energy system. Int. J. Power Electron. Drive Syst. 11, 988–1000. https://doi.org/10.11591/ijpeds.v11.i2 (2020).
Nguyen, H. V. P., Nguyen, V. T. & Nguyen, V. H. A combined strategy to improve operational efficiency of microgrids with high integration of solar and wind energy. Int. J. Renew. Energy Res. 13(3), 1247–1258. https://doi.org/10.20508/ijrer.v13i3.14194.g8797 (2024).
Alberizzi, A., Zani, A. & Di Barba, P. Analyzing the European Intraday Market: Statistical insights and strategies for continuous trading in renewable energy systems. Int. J. Renew. Energy Res. 13(4), 1515–1525. https://doi.org/10.20508/ijrer.v13i4.14208.g8825 (2023).
Marmouh, S., Boutoubat, M. & Mokrani, L. Performance and power quality improvement based on DC-bus voltage regulation of a stand-alone hybrid energy system. Electr. Power Syst. Res. 163, 73–84. https://doi.org/10.1016/j.epsr.2018.06.004 (2018).
Alahmadi, A. A. A. et al. Hybrid wind/PV/battery energy management-based intelligent non-integer control for smart DC-microgrid of Smart University. IEEE Access 9, 98948–98961. https://doi.org/10.1109/ACCESS.2021.3095973 (2021).
Poudel, R., Krishnan, V., Reilly, J., Koralewicz, P., Baring-Gould, I. Integration of storage in the DC link of a full converter-based distributed wind turbine. IEEE Power & Energy Society General Meeting, 1–5. https://doi.org/10.1109/pesgm46819.2021.9638225 (2021).
Abhishek, J. Lithium-ion battery based renewable energy solution for off-grid electricity: A techno-economic analysis. Renew. Sustain. Energy Rev. 72, 922–934 (2017).
Dhar, R. K., Merabet, A., Al-Durra, A. & Ghias, A. M. Y. M. Power balance modes and dynamic grid power flow in solar PV and battery storage experimental DC-link microgrid. IEEE Access 8, 219847–219858. https://doi.org/10.1109/ACCESS.2020.3042536 (2020).
Benadli, R., Bjaoui, M., Khiari, B. & Sellami, A. Sliding mode control of hybrid renewable energy system operating in grid connected and stand-alone mode. Power Electron. Drives 6(41), 144–166. https://doi.org/10.2478/pead-2021-0009 (2021).
Bollipo, R. B., Mikkili, S. & Bonthagorla, P. K. Hybrid, optimization, intelligent and classical PV MPPT techniques: Review. CSEE J. Power Energy Syst. 2020, 9–33. https://doi.org/10.17775/CSEEJPES.2019.02720 (2020).
Pande, J., Nasikkar, P., Kotecha, K. & Varadarajan, V. A review of maximum power point tracking algorithms for wind energy conversion systems. J. Mar. Sci. Eng. 9(11), 1–30. https://doi.org/10.1016/j.rser.2012.02.016 (2021).
Moyo, R. T., Tabakov, P. Y. & Moyo, S. Design and modeling of the ANFIS-based MPPT controller for a solar photovoltaic system. J. Sol. Energy Eng. 143, 041002. https://doi.org/10.1115/1.4048882 (2021).
Mahmud, N., Zahedi, A. & Mahmud, A. A cooperative operation of novel PV inverter control scheme and storage energy management system based on ANFIS for voltage regulation of grid-tied PV system. IEEE Trans. Ind. Inform. 13, 2657–2668. https://doi.org/10.1109/TII.2017.2651111 (2017).
Kulaksiz, A. A. ANFIS-based estimation of PV module equivalent parameters: Application to a stand-alone PV system with MPPT controller. Turk. J. Electr. Eng. Comput. Sci. 21, 2127–2140. https://doi.org/10.3906/elk-1201-41 (2013).
Karabacak, K. & Cetin, N. Artificial neural networks for controlling wind–PV power systems: A review. Renew. Sustain. Energy Rev. 29, 804–827. https://doi.org/10.1016/j.rser.2013.08.070 (2014).
Khan, H. S., Mohamed, I. S., Kauhaniemi, K., & Liu, L. Artificial neural network-based voltage control of DC/DC converter for DC microgrid applications. In 2021 6th IEEE Workshop on the Electronic Grid (EGRID). Presented at the 2021 6th IEEE Workshop on the Electronic Grid (eGRID) 1–6 (IEEE, 2021).
Asma, D., Jihed, H., Messaoud, A., Manel, C. & Hafedh, T. Robust fractional PI controller design for stand-alone microgrid under load variation: An optimization-based approach. Int. J. Renew. Energy Res. 13(4), 1526–1537. https://doi.org/10.20508/ijrer.v13i4.14540.g8826 (2023).
Sumanth Yampara, L. A., Lakshminarasimman, L. & Sambasiva, R. G. Optimal design of FoPID controller for DFIG based wind energy conversion system using Grey-Wolf optimization algorithm. Int. J. Renew. Energy Res. 12(4), 2111–2120. https://doi.org/10.20508/ijrer.v12i4.13446.g8594 (2022).
Srivishnupriya, A. P., Mohamed, T. A. M. & Vinoth Kumar, N. J. Automatic generation control of three area hybrid power system by sine cosine optimized dual mode fractional order controller. Int. J. Renew. Energy Res. 12(3), 1414–1426. https://doi.org/10.20508/ijrer.v12i3.13127.g8524 (2022).
Dharamalla, C. S. R., Rama Rao, P. V. V. & Kiranmayi, R. Improvement of power quality in grid integrated smart grid using fractional-order Fuzzy logic controller. Int. J. Renew. Energy Res. 12(2), 960–969. https://doi.org/10.20508/ijrer.v12i2.12948.g8483 (2022).
Abdelaziz, S., Kamel, C. & Kamel, B. S. Multiphase interleaved bidirectional DC–DC converter for electric vehicles and smart grid applications. Int. J. Smart Grid 4(2), 80–87. https://doi.org/10.20508/ijsmartgrid.v4i2.102.g86 (2020).
Yousfi, A., Tayeb, A. & Chaker, A. Power quality improvement based on five-level shunt APF using sliding mode control scheme connected to a photovoltaic. Int. J. Smart Grid 1(1), 9–15. https://doi.org/10.20508/ijsmartgrid.v1i1.4.g4 (2017).
Habib, B. Comparative study between direct vector control and Fuzzy sliding mode controller in three-level space vector modulation inverter of reactive and active power command of DFIG-based wind turbine systems. Int. J. Smart Grid 2(4), 188–196. https://doi.org/10.20508/ijsmartgrid.v2i4.24.g24 (2018).
Boutaghane, K., Bennecib, N., Benidir, M., Benbouhenni, H. & Colak, I. Performance enhancement of a three-phase grid-connected PV inverter system using fractional-order integral sliding mode controls. Energy Rep. 11, 3976–3994 (2024).
Muhammad, Z. M. et al. Strategic planning of renewable distributed generation in radial distribution system using advanced MOPSO method. Energy Rep. 6, 2872–2886. https://doi.org/10.1016/j.egyr.2020.10.002 (2020).
Mahesh, K., Nallagownden, P. & Elamvazuthi, I. Advanced Pareto front non-dominated sorting multi-objective particle swarm optimization for optimal placement and sizing of distributed generation. Energies 9, 982. https://doi.org/10.3390/en9120982 (2016).
Aman, I. N. & Anas, L. M. MPPT algorithms (PSO, FA, and MFA) for PV system under partial shading condition, case study: BTS in Algazalia, Baghdad. Int. J. Smart Grid 4(3), 100–110. https://doi.org/10.20508/ijsmartgrid.v4i3.113.g99 (2020).
Bandahalli Mallappa, P. K., Martínez-García, H. & Velasco-Quesada, G. Power quality improvements in grid-connected PV system using hybrid technology. Renew. Energy Power Qual. J. 19, 316–320. https://doi.org/10.24084/repqj19.284 (2021).
Roy, T. K., Mahmud, M. A., Oo, A. M. T., Bansal, R. & Haque, M. E. Nonlinear adaptive backstepping controller design for three-phase grid-connected solar photovoltaic systems. Electr. Power Compon. Syst. 45(20), 2275–2292. https://doi.org/10.1080/15325008.2018.1431334 (2018).
Somnath, D. & Akella, A. K. Power flow control of PV-wind-battery hybrid renewable energy systems for Stand-Alone application. Int. Renew. Energy Res. https://doi.org/10.20508/ijrer.v8i1.6534.g7278 (2018).
Al-Quraan, A., Al-Qaisi, A. & Modelling, M. Design and control of a standalone hybrid PV-wind micro-grid system. Energies 14(16), 4849. https://doi.org/10.3390/en14164849 (2021).
Albalawi, H., El-Shimy, M. E., AbdelMeguid, H., Kassem, A. M. & Zaid, S. A. Analysis of a hybrid wind/photovoltaic energy system controlled by brain emotional learning-based intelligent controller. Sustainability 14(8), 4775. https://doi.org/10.3390/su14084775 (2022).
Acknowledgements
This research was supported by King Khalid University, Research Project RGP.2/472/45.
Author information
Authors and Affiliations
Contributions
Conceptualization: K.B., H.B., N.B. methodology: K.B., H.B., N.B., I.C., Z.M.S.E., S.F.A. software: K.B., H.B. validation: K.B., H.B., N.B., I.C., Z.M.S.E., S.F.A. formal analysis: K.B., H.B., N.B., I.C., Z.M.S.E., S.F.A. investigation: K.B., H.B., N.B., I.C., Z.M.S.E., S.F.A. resources: K.B., H.B., N.B. data curation: K.B., H.B., N.B., writing—original draft preparation: K.B., H.B., N.B. writing—review and editing: K.B., H.B., N.B., Z.M.S.E., S.F.A. visualization: K.B., H.B., N.B., I.C., Z.M.S.E., S.F.A. supervision: K.B., H.B., N.B., I.C., Z.M.S.E., S.F.A. project administration: K.B., H.B. funding acquisition: H.B., Z.M.S.E., S.F.A. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Boutaghane, K., Benbouhenni, H., Bennecib, N. et al. Using new control strategies to improve the effectiveness and efficiency of the hybrid power system based on the battery storage system. Sci Rep 15, 4730 (2025). https://doi.org/10.1038/s41598-025-88804-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-88804-9