Introduction

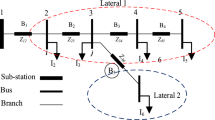
On a global scale, there is a pressing need to significantly expand power generation capacity to accommodate the increasing electricity demand and prevent potential power shortages. Failure to address this issue may have substantial economic consequences for any nation. As observed, the physical distance between power generation units and consumer sites often results in considerable power losses within the distribution networks1. Along with the above, problems such as deteriorated bus voltage profile and poor power factor are also observed in the distribution systems. In the past literature, various researchers have proposed that placing compensatory devices like distributed generation (DGs) and shunt capacitor (SCs) nearer to the load helps alleviate the above-mentioned issues. Moreover, owing to depleting fossil reserves, their escalating prices, and growing environmental concern, the world is witnessing a paradigm shift in transportation systems, i.e., from gasoline-based vehicles to electric vehicles (EVs). However, the rapidly growing use of EVs may present various challenges, such as increased peak load demand, large feeder currents, and degradation in the voltage profiles of the radial distribution networks (RDN). The proper placement of EV charging stations (EVCSs) along with the optimal deployment of DGs and SCs in the RDN might be helpful in fixing these issues. In addition to the above, in various literature, the optimal reconfiguration (ORC) of the RDN is also reported as one of the ways to reduce line losses further and improve system reliability. Network reconfiguration involves altering the topology of a RDN by selectively opening sectionalizing switches and simultaneously closing an equivalent number of tie-line switches, all while ensuring the network’s radial structure is preserved2.

It has been reported in the past literature that inappropriate placement of DG, SC, and EVCS units could lead to a rise in line losses, deteriorated voltage profile, and elevated back power flow within the system. Hence, to decipher the complex task of optimal placement and sizing (OPS) of DGs, SCs, and EVCSs in consort with the ORC in the RDNs, optimization techniques have been greatly emphasized in the past reported works3. A rigorous review of various strategies of DG allocations considering different objectives and constraints of RDN is highlighted in4,5. In6, using binary particle swarm optimization and shuffling frog leap algorithm (BPSO-SFLA), OPS of DG units are presented to minimize line losses and enhance the bus voltage profile. The stud krill herd algorithm (SKHA) and multi-objective (MO) optimization technique were employed by the authors in7 to determine the OPS of DGs. In8, a novel metaheuristic artificial hummingbird algorithm (AHA) is presented for the best possible planning of replenishable energy-based distributed generators (DGs) taking generation and load uncertainty into account. In9, the water flow optimization (WFO)-based algorithm has been used to find OPS of DG systems efficiently, demonstrating superior technical and economic benefits over other optimization techniques, including significant cost savings and reduced annual economic losses. Along with the above, the techno-economic benefits of all the assessed case studies are presented in a comparative manner. The authors of10 discovered the OPS of SCs in RDN using the multi-objective salp swarm algorithm (MOSSA). In11, the backward-forward sweep method and PSO algorithm are employed for OPS of SCs, which resulted in improved voltage stability and reduced power losses and costs in a 50-bus RDN. The optimal implantation of EVCSs utilizing a cross algorithm featuring chicken swarm optimization and teaching learning-based optimization algorithms (CSO-TLBO) is presented in12. From past research, it has been noted that the simultaneous OPS of DGs and SCs (OPS-DGSC) boosts the bus voltage profile and reduces line power losses more efficiently than their individual applications in the RDNs. The authors of13 have used multi-objective strength Pareto evolutionary algorithm 2 (SPEA2) to solve the simultaneous OPS-DGSC conundrum considering load uncertainty. The objective functions taken in this work consist of minimizing the system’s net cost, line losses for both reactive and active power considering a variety of operating constraints. In14, the authors have described a two-step method for improving the performance of a RDN through the determination of the OPS-DGSC, incorporating both single and MO functions. In step 1, two voltage sensitivity factors centered on voltage deviation and voltage stability index are computed to minimize the search space by identifying candidate buses for the optimal location of DGs and SCs. In step 2, the chaotic bat algorithm (CBA) is used to realize the ODGSCP. The authors of15 introduced an improved golden jackal optimization (IGJO) algorithm for optimally placing several SCs and different DGs in a RDN. The studied approach has demonstrated superior performance in terms of voltage enhancement, stability, and loss reduction.

The purpose of ORC is to obtain the best topology of RDN according to the considered objective functions. The optimization challenge associated with the ORC is characterized as a combinatorial, non-differentiable, and constrained conundrum due to the fact that there exist several possible switching combinations from which the optimal network topology is required to be found. A new meta-heuristic comprehensive teaching–learning harmony search optimization algorithm (CTLHSO) has been proposed by the authors in16 for optimal DG placements with ORC of RDNs to accomplish reduced line losses and improved bus voltage profile. An approach based on the social beetle swarm optimization algorithm (SBSOA) for DG integration considering ORC is presented in17. The work considers various objective functions such as active power line loss minimization, voltage deviation reduction, and improvement in load distribution. The coyote algorithm (COA) is used in18 to minimize the active power line losses in IEEE 69- and 119-bus RDNs considering two scenarios employing (i) ORC alone and (ii) simultaneous ORC and DG placement. The use of ant colony optimization algorithm (ACOA) for OPS of DGs with ORC is investigated in19. In comparison to techniques like the fireworks algorithm and adaptive shuffled frogs leaping algorithm, the ACOA significantly reduces power loss, improves voltage stability, and enhances system reliability when tested in IEEE 33- and IEEE 69-bus systems. A combined approach to improve DG placement and network reconfiguration utilizing the Andean condor algorithm (ACA) is presented in20. The goal was to lessen power losses and upsurge energy efficiency. MATLAB simulations performed on 33- and 69-bus networks exhibit the effectiveness of the ACA approach in attaining considerable decreases in reactive and active power line losses in comparison to the chaotic PSO (CPSO) method. The modified biogeography-based optimization algorithm (MBBOA) is offered in21 to evaluate the optimum location of SCs with ORC of RDN considering loss reduction and voltage profile enhancement as objectives. A simultaneous ORC and SC placement is proposed in22 to moderate the real power line loss and operational cost; and to improve the bus voltages. In this work, the authors used a combination of Johnson’s algorithm (JA) and adaptive whale optimization algorithm (AWOA) to simulate the formulated problem. Some researchers have studied the impact of simultaneous OPS-DGSC in RDN with ORC and found the combination more beneficial than the above-discussed methods. The authors use multi-criteria decision-making non-dominated sorting genetic algorithm II (MCDM-NSGAII) in23 to determine the best location for DGs and SCs under optimally reconfigured 33- and 69-bus RDNs. Quasi-reflection-based slime mould algorithm (QRSMA)-based approach for simultaneous OPS-DGSC units with ORC to minimalize line losses and voltage deviation in RDN is proposed in24. In25, an enhanced artificial ecosystem optimizer (AEO) technique is utilized to optimize DGs and SCs allocations alongside reconfiguration of power distribution systems. The suggested method has demonstrated superior performance over competing optimization algorithms with regard to reduced power losses in the Cairo distribution system. To reduce power loss and augment voltage profiles in a variety of distribution systems, a comparative research employing the grey wolf optimizer (GWO) algorithm for DG and SC implantation with ORC was conducted in26. This study showed that the GWO was more effective than other conventional and metaheuristic techniques.

Despite the numerous advantages, EVCSs may have a deleterious influence within the electrical grid if not planned properly and placed at suitable locations. As a result, numerous researchers have carefully examined the impact of EVCS implantation in RDN in the past. In27, the authors found the optimal integration of EVCS and DG units utilizing artificial intelligence (AI) method and the hybrid grey wolf optimization and particle swarm optimization, i.e., HGWOPSO technique giving due consideration to the reliability of RDN. A fuzzy MO method based on a two-stage grasshopper optimization algorithm (GOA) is presented in28 for simultaneous OPS of DGs, SCs, and EVCSs in the RDN. DG and SC sizing and allocation are optimized using the fuzzy-GOA approach in the first stage to increase the RDN’s voltage profile, real power line loss reduction, and substation power factor. Considering the pre-allocated DGs and SCs, the fuzzy-GOA technique is applied in the second step to find the best locations and number of EVCSs to be installed. Wang et al. have studied the impact of simultaneous optimal implantation of DGs and EVCSs with ORC of RDN in order to increase the cost–benefit and power quality of RDN. In this study, the stochastic nature of DG and EV units has been considered29. Using the Lévy flight and chaos disturbed beetle antennae search (LDBAS) algorithm, the model optimizes power loss, load balancing, and voltage deviation, with simulations on RDN showing enhanced system performance and increased EV penetration. In order to delineate the research contributions identified in the existing literature and to emphasize the contributions of the current study, along with the identified research gaps, Table 1 provides a comparative analysis of the existing literature and the proposed approach.

Table 1 A summary of comparison between existing literature and the proposed work.
Full size table

Based on the literature survey conducted, researchers have extensively explored various combinations of the placement of DG, SCs and EVCS in conjunction with the ORC of RDNs to augment overall system performance. However, there is a notable gap in the literature regarding comprehensive investigations on simultaneous consideration of OPS of DG, SC, and EVCS units accompanied by ORC of RDN. Furthermore, due to the complexity and high-level computations involved in the adopted approach, the utilization of a powerful meta-heuristic algorithm is imperative to achieve accurate and efficient results. Nevertheless,30 discloses that centroid-based oppositional learning (COL) is a relatively new technique applied in optimizer to improve its efficiency. The COL approach exhibits greater efficiency compared to opposition-based learning. It delivers a high likelihood of convergence close to the optimal global solution with less computational effort. The recently released AHA has a robust global search capability and has demonstrated excellent success in the past in resolving a variety of real-world issues31. On the other hand, early convergence has been observed in certain circumstances. This inspires the authors of this paper to suggest an enhanced AHA version that incorporates COL. Premature convergence is avoided by the proposed novel COL-based AHA, called COLAHA, which skillfully preserves a balance between the optimization process’s exploitation and exploration stages. Using a range of unimodal and multimodal benchmark test functions, the efficacy of the proposed COLAHA is evaluated, and the outcomes are contrasted with those attained by other well-known, potent algorithms, including the AHA, PSO, WOA, salp swarm algorithms (SSA), and teaching learning-based optimization (TLBO). Subsequently, in order to demonstrate its superiority, the problem of DG, SC, and EVCS unit placement and sizing in RDNs with ORC is solved using the proposed COLAHA and other investigated algorithms. The comparative results formulated confirm the preeminence of COLAHA more so than alternative algorithms. This study modifies the objective functions through the fuzzy logic technique in order to improve system performance. Then, it applies the suggested COLAHA to get the best possible outcomes.

The following summarizes the primary contributions of the suggested study:

A novel COL-based an enhanced version of AHA, called as COLAHA, is proposed for the first time.

The performance investigation of RDN under COLAHA-based simultaneous OPS of DGs, SCs and EVCSs along with ORC has been extensively carried out.

The fuzzy logic approach-based objective functions have been adopted to enhance the system performance.

A detailed performance comparison of the proposed approach is made with other existing methods.

The structure of the remainder of this paper is organized as follows. In Section "Problem formulation", the problem formulation, load flow analysis, objective functions, and the various constraints are presented as part of the proposed study. Section "Proposed and the studied optimization approaches" provides an in-depth examination of the AHA and COLAHA optimization techniques. The outcomes and interpretation are detailed in Section "Outcomes and Interpretation". Finally, the conclusion derived from this study is encapsulated in Section "Conclusion".

Problem formulation

In this work, various considered objective functions are first fuzzified and, thereafter, the adopted optimization algorithms are applied to obtain the optimal result. The subsequent subsections provide a detailed description of the objective functions considered in this study.

Fuzzy domain multi-objective function formulation

Fuzzy logic32 allows the user to select a value of interest from a wide range of possibilities. In this part, fuzzy membership functions are used to obtain the distribution system’s performance parameters that converge towards the predefined desired values.

Fuzzification of substation (S/S) power factor

The Eq. (1) can be utilized to determine the fuzzy membership function for substation (S/S) power factor (PF) illustrated in Fig. 1, where \(P{F}_{D}\) represents the desired power factor level. In this equation, the parameters are defined as follows: \({PF}_{min}=0.85\), \(P{F}_{D}\)=0.95 and \({PF}_{min}=1.0\) are considered.

Fig. 1
figure 1

S/S power factor.

Full size image
$${\mu }_{PF}=\left\{\begin{array}{c}0 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, {\text{f}}{\text{o}}{\text{r}} \, PF\le P{F}_{min}\\ \frac{\left(PF-P{F}_{min}\right)}{\left(P{F}_{D}-P{F}_{min}\right)} {\text{f}}{\text{o}}{\text{r}}P{F}_{min}\le PF\le P{F}_{D}\\ \frac{\left(P{F}_{max}-PF\right)}{\left(P{F}_{max}-P{F}_{D}\right)} {\text{f}}{\text{o}}{\text{r}}P{F}_{D}\le PF\le P{F}_{max}\end{array}\right.$$
(1)

Fuzzification of DG penetration

The right-angled triangle function is used to represent the DG’s penetration limit (shown in Fig. 2), which may be determined using (2) and (3). The DG penetration indicator (PDGI) is the fraction of the total DG output to the total active power load.

Fig. 2
figure 2

DG penetration limit.

Full size image
$$PDGI=\frac{\sum_{i=1}^{NDG} PD{G}_{i}}{\sum_{j=1}^{BN} P{L}_{i}}$$
(2)
$${\mu }_{PDGI}=\left\{\begin{array}{c}0 {\text{f}}{\text{o}}{\text{r}} PDGI\le PDG{I}_{min}\\ \frac{\left(PDGI-PDG{I}_{min}\right)}{\left(PDG{I}_{SP}-PDG{I}_{min}\right)}{\text{ for PDGI }}_{min}\le PDGI\le PDG{I}_{SP}\\ \frac{\left(PDG{I}_{max}-PDGI\right)}{\left(PDG{I}_{max}-PDG{I}_{SP}\right)}{\text{ for PDGI }}_{SP}\le PDGI\le PDG{I}_{max}\\ 0 {\text{f}}{\text{o}}{\text{r}} \, {\text{P}}{\text{D}}{\text{G}}{\text{I}} \, >PDG{I}_{max}\end{array}\right.$$
(3)

Here, the fuzzified design parameters are designated as \(PDG{I}_{max}\) and \(PDG{I}_{min}\). \(PDG{I}_{SP}\) is determined as a fraction of the total real power load selected to represent the desired amount of DG penetration for the required total DG capacity32. The value of \(PDG{I}_{min}, PDG{I}_{SP}\) and \(PDG{I}_{max}\) are set to 0.4, 0.5, and 0.6, respectively.

Fuzzification of active power line loss

The active power loss index (APLI) is calculated as the fraction of power loss with DGs and SCs to the base case as specified in (4).

$$\begin{array}{c}APLI=\frac{AP{L}^{DGSC}}{AP{L}^{BC}}\\ \end{array}$$
(4)

where \(AP{L}^{DGSC}\) and \(AP{L}^{BC}\) are active power loss with DGs and SCs, and with base case respectively. The right-angled triangle membership function, as illustrated in Fig. 3, is used to represent active power loss minimization as one of the objective component in the fuzzy domain. The goal of the current effort is to lower active power loss below a predetermined threshold. Hence, in line with32, to have the desired real power loss minimization \(APL{I}_{min}\) is chosen based on utility condition and \(APL{I}_{max}\) is considered as 1.

Fig. 3
figure 3

Active power line loss index.

Full size image
$${\mu }_{APLI}=\left\{\begin{array}{cc}1 & {\text{for}} \, APLI\le APL{I}_{min}\\ \frac{\left(\text{A}PL{I}_{max}-APLI\right)}{\left(APL{I}_{max}-\text{A}PL{I}_{min}\right)} \, & {\text{for}} \, APL{I}_{min}\le APLI\le APL{I}_{max}\\ 0 \, & {\text{for}} \, APLI>APL{I}_{max}\end{array}\right.$$
(5)

Fuzzification of bus voltage profile

The bus voltages in the distribution system are denoted by the fuzzy membership function (illustrated in Fig. 4), which is calculated as per (6).

Fig. 4
figure 4

Node voltage fuzzy membership.

Full size image
$${\mu }_{{V}_{i}}=\left\{\begin{array}{c} \, {0} \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, {\text{f}}{\text{o}}{\text{r}} \, {V}_{i}\le {V}_{L1}\\ \frac{\left({V}_{i}-{V}_{L1}\right)}{\left({V}_{min}-{V}_{L1}\right)} {\text{f}}{\text{o}}{\text{r}}{V}_{L1}<{V}_{i}<{V}_{min}\\ 1.0 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, {\text{f}}{\text{o}}{\text{r}} \, {V}_{min}\le {V}_{i}\le {V}_{max}\\ \frac{\left({V}_{max}-{V}_{i}\right)}{\left({V}_{max}-{V}_{L2}\right)} \, \, \, \, {\text{f}}{\text{o}}{\text{r}} \, {V}_{max}<{V}_{i}<{V}_{L2}\\ \, {0} \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, {\text{f}}{\text{o}}{\text{r}} \, {V}_{i}>{V}_{L2}\end{array}\right.$$
(6)

The distribution network’s fuzzified voltage profile performance index (\({\mu }_{{V}_{i}}\)) is defined as the least of all fuzzy membership values for all discrete node voltages and is denoted by (7).

$${\mu }_{VT}=\text{ min }({\mu }_{{V}_{i}})$$
(7)

Fuzzy objective function for optimum deployment of EVs

A fuzzy multi-objective function with fuzzy real power loss and fuzzy voltage profile objectives is employed to determine the optimal number of EVs and their placements while also taking into account the distribution system peak load. The power loss index with EVs (PLIEV) can be expressed as per (8).

$$\begin{array}{c}PLIEV=\frac{PLE{V}^{EVDGSC}}{PLE{V}^{DGSC}}\\ \end{array}$$
(8)

In the (8), \(PLE{V}^{EVDGSC}\) is the real power losses associated with EVs, DGs and SCs, and \(PLE{V}^{DGSC}\) is the real power loss of DGs and SCs. Referring Fig. 5, the fuzzy active power loss index can be obtained by (9).

Fig. 5
figure 5

Membership function for real power loss with EVs.

Full size image
$${\mu }_{PLIEV}=\left\{\begin{array}{c}0 {\text{f}}{\text{o}}{\text{r}} PLIEV\le PLIE{V}_{min}\\ \frac{\left(PLIEV-PLIE{V}_{min}\right)}{\left(PLIE{V}_{SP}-PLIE{V}_{min}\right)} for PLIE{V}_{min}\le PLIEV\le PLIE{V}_{SP}\\ \frac{\left(PLIE{V}_{max}-PLIEV\right)}{\left(PLIE{V}_{max}-PLIE{V}_{SP}\right)}{\text{ for PLIEV }}_{SP}\le PLIEV\le PLIE{V}_{max}\\ 0 {\text{f}}{\text{o}}{\text{r}} \, {\text{P}}{\text{L}}{\text{I}}{\text{E}}{\text{V}} \, >PLIE{V}_{max}\end{array}\right.$$
(9)

The power loss increases with EV load, hence, the PLIEV will always be greater than one. When compared to DGs and SCs, this allows for a 50% increase in power loss during peak hours. The values of \(PLIE{V}_{min}\), \(PLIE{V}_{SP}\) and \(PLIE{V}_{max}\) are 1.0, 1.5, and 2.0, respectively. The fuzzy multi-objective function (\({J}_{F}\)) expressed in terms of considered individual fuzzy objective functions is shown in (10).

$$Maximize {J}_{F}= {\mu }_{PF}+{\mu }_{PDGI}+ {\mu }_{APLI}+ {\mu }_{VT}+{\mu }_{PLIEV}$$
(10)

The fuzzified objective function effectively resolves these conflicts by normalizing and balancing the objectives using fuzzy membership functions. This ensures that no single objective dominates the optimization process, allowing for a holistic approach to system improvement.

Network constraints

In each iteration of the optimization technique, several constraints must be satisfied to find the solution for OPS of multi-units in RDNs. The constraints considered in this work are as follows.

Constraints for equality

The equality constraints for power balance are described as

$$\sum_{i=1}^{DG} {P}_{\text{dg}i}+{P}_{g}-APL={P}_{d}$$
(11)
$$\sum_{i=1}^{DG} {Q}_{\text{dg}i}+\sum_{i=1}^{SC} {Q}_{ci}+{Q}_{g}-RPL={Q}_{d}$$
(12)

where, APL is the active power line loss and RPL is the reactive power line loss. \({P}_{\text{dg}i}\) and \({Q}_{\text{dg}i}\) are the real and reactive powers generated, respectively, by the DG placed at bus i. \({P}_{g}\) and \({Q}_{g}\) are the generated real and reactive powers of the network, respectively. \({Q}_{ci}\) is the reactive power added at bus i. \({P}_{d}\) and \({Q}_{d}\) are the total real and reactive power demands, respectively.

Constraints for inequality

Bus voltage constraints

The voltages must be kept within the minimum (\({V}_{\text{min}}\)) and the maximum \(({V}_{max}\)) bounds of voltage at each bus as expressed below.

$${V}_{min}\le {V}_{i}\le {V}_{max}$$
(13)
DG size constraint

The active power injected by \({DG}_{i}\) at the ith bus must be within the minimum limit (\({DG}_{min}\)) and the maximum limit (\({DG}_{max}\)).

$${DG}_{min}\le {DG}_{i}\le {DG}_{max}$$
(14)
SC size constraint

Similarly, the size constraint of SC for reactive power compensation may be expressed as (15)

$${QC}_{min}\le {QC}_{j}\le {QC}_{max}$$
(15)

where, \({QC}_{min}\) and \({QC}_{max}\) signify the minimum and the maximum permissible kVAr limits for shunt capacitors.

Power factor constraint

The power factor should be within the allowable limits as presented by (16)

$${PF}_{min}\le {PF}_{j}\le {PF}_{max}$$
(16)

where, \({PF}_{min}\) and \({PF}_{max}\) denote the minimum and the maximum PF limits of the installed DGs.

Radiality constraint

This work creates an incident matrix (im) of order \((NB \times NB)\) to check the system’s radiality. Each element of (im) is found by (17).

$$i{m}_{i,j}= \left\{\begin{array}{cc}1& \text{if node i is directed towards node j}\\ 0& \text{otherwise}\end{array}\right.$$
(17)

Proposed and the studied optimization approaches

In this work, our research has been confined to population-based algorithms that include both swarm-inspired and evolution-inspired optimization approaches. The list includes the proposed COLAHA and the studied AHA, AOA, GA, and WOA. These approaches are used to discover OPS of DGs, SCs, and EVCSs in an optimally reconfigured network considering fuzzified objective functions. The proposed COLAHA is a novel approach and an improved version of the basic AHA, which is explained in detail in the following sections.

AHA

The AHA represents a cutting-edge bio-inspired optimization technique, introduced in 2021, tailored for solving a myriad of engineering applications31. Rooted in the intelligent behaviors of hummingbirds, AHA stands out among its peers due to its ability to emulate the intricate flight maneuvers and foraging strategies of these remarkable avian creatures. AHA, like other optimization algorithms, has distinct exploration and exploitation stages, which are aided by three main components: food sources, hummingbirds, and a visit table. In the AHA framework, each food source, represented by a solution vector, encapsulates attributes such as nectar quality, refill rate, and visit history. The fitness value associated with each food source reflects its nectar-refilling rate, with higher values indicating higher desirability. Each hummingbird is assigned a distinct food source to feed from, retaining crucial information such as the location and refill rate of its chosen source. This information is exchanged among hummingbirds to foster collaboration and efficiency within the population. The visit table serves as a repository for tracking the interaction history between hummingbirds and food sources. It records details such as the duration since a particular hummingbird’s last visit to a specific food source. With each iteration, the visit table is amended to reflect the latest visitation data, facilitating informed decision-making by hummingbirds during subsequent foraging attempts. The development of AHA is underpinned by three distinct foraging techniques: directed, territorial, and migrating foraging. These techniques leverage the innate abilities of hummingbirds to navigate and exploit resources efficiently in diverse environments. Mathematical models underpinning the three foraging methods provide a quantitative framework for understanding the dynamics of AHA. These models enable researchers and practitioners to analyze and optimize the algorithm’s performance across different scenarios and problem domains. The details of the mathematical equations mimicking the behavior of hummingbirds are described below stepwise:

Guided foraging: Among the family of birds, most can fly in omni-direction, but hummingbirds have the additional capability to glide axially and diagonally as well. The axial flight may be stated, mathematically, as (18).

$$D^{i} = \left\{ \begin{gathered} 0,\,\,\,\,\,\,\,if\,i = randi([1,d])\,\,\,\,\,\,\,\,\,\,\,i = 1,...,d \hfill \\ 1,\,\,\,\,\,\,\,\,else \hfill \\ \end{gathered} \right.$$
(18)

The diagonal flight may be stated mathematically as (19).

$$D^{i} = \left\{ \begin{gathered} 0,\,\,\,\,\,\,\,if\,i = P\left( j \right),\,j \in \left[ {1,k} \right]\,,\,P = randperm(k),\,k \in \left[ {2,\left[ {r_{1} \times \left( {d - 2} \right)} \right] + 1} \right] \hfill \\ 1,\,\,\,\,\,\,\,\,else \hfill \\ \end{gathered} \right.$$
(19)

The omnidirectional flight may be stated mathematically as (20)

$$D^{i} = 1\,\,\,\,\,\,\,\,\,i = 1,...,d$$
(20)

where, d is the dimension of the agent. \(r_{1}\) is a random value between 0 and 1. The mathematical equation simulating the guided foraging behaviour and a candidate food source is presented in (21)-(22)

$$\upsilon_{i} \left( {t + 1} \right) = Z_{i,tag} \left( t \right) + a \times D \times \left( {Z_{i} \left( t \right) - Z{}_{i,tag}\left( t \right)} \right)$$
(21)
$$a \sim N\left( {0,1} \right)$$
(22)

where, \(Z_{i} \left( t \right)\) is the position of ith food source at the current iteration t. \(Z_{i,tag} \left( t \right)\) is the position of the target food source that ith hummingbird intends to visit. a is a guide factor, which is subject to normal distribution with a mean value equal to zero and a standard deviation value of 1.

The position update of the ith food source is expressed as per (23)

$$Z_{i} \left( {t + 1} \right) = \left\{ \begin{gathered} Z_{i} \left( t \right)\,\,\,\,\,\,\,\,\,\,\,\,\,f\left( {Z_{i} \left( t \right)\,} \right) \le f\left( {\upsilon_{i} \left( {t + 1} \right)\,} \right) \hfill \\ \upsilon_{i} \left( {t + 1} \right)\,\,\,\,\,\,\,f\left( {Z_{i} \left( t \right)\,} \right) > f\left( {\upsilon_{i} \left( {t + 1} \right)\,} \right) \hfill \\ \end{gathered} \right.$$
(23)

where, \(f\left( . \right)\) denotes the function fitness value.

Territorial foraging: The hummingbirds’ territorial foraging behavior is mathematically expressed as follows

$$\upsilon_{i} \left( {t + 1} \right) = Z_{i} (t) + b \times D \times Z_{i} (t)$$
(24)
$$b \sim N\left( {0,1} \right)$$
(25)

where, b is a territorial factor, which is subject to a normal distribution.

Migration foraging: A hummingbird’s migratory foraging behavior to a destination is defined according to (26)

$$Z_{ior} (t + 1) = LB + (UB - LB) \times rand(0,1)$$
(26)

where, \(Z_{ior} (t + 1)\) is the food source with the worst nectar-refilling rate in the population. LB and UB are the lower and the upper bounds of the considered decision variables, respectively. By integrating the foraging strategies, memory capacity, and flight abilities of hummingbirds, AHA represents a versatile optimization tool with wide-ranging engineering applications. The more details on AHA may be referred from31. The AHA’s ability to mimic the intelligent behaviors of hummingbirds, coupled with its mathematical rigor and adaptability, qualifies it as a promising approach for addressing complex real-world engineering/non-engineering problems.

Proposed COLAHA

The opposition-based learning strategy, initially developed by Tizhoosh33, aims to enhance the search capabilities of existing algorithms. Later, several other improvements to the opposition-based strategy, such as quasi-opposition methods34, quasi-reflection-based approach35, etc., were proposed and blended with various algorithms to enhance their exploitation and exploration capabilities. However, all these opposition-based methods rely on the minimum and maximum bounds of the populations while generating new opposition points. Therefore, in36, Rahnamayan et al. introduced a centroid opposition-based computation strategy that considers all members of the population matrix rather than just the extreme points (i.e., the minimum and the maximum limits). This approach has been found to improve convergence speed and accuracy compared to its predecessors.

In this centroid opposition-based method, the centroid is calculated using (27)

$$M = \frac{{Z_{1} + Z_{2} + ... + Z_{n} }}{n}$$
(27)

where, M is the centroid and \(Z_{1} ,\,\,Z_{2} ,...,\,\,Z_{n}\) are the n points in D-dimensional search space.

So, the centroid of each solution/points may be calculated using (28).

$$M_{i} = \frac{{\sum\limits_{j = i}^{n} {X_{i,j} } }}{n}$$
(28)

The opposite point (COZ) of the current point (Z) using the centroid-based oppositional learning may be obtained by employing (29).

$$COZ_{i} = 2 \times M - Z_{i}$$
(29)

The proposed COLAHA utilizes the centroid-based oppositional learning concept both during population initialization and in the iterative phase. The steps associated with generating the initial population matrix using COLAHA are described below in detail.

Step 1: Initialize the population randomly according to the population matrix size (NP).

Step 2: Based on the population obtained in Step 1, generate centroid opposition-based solutions using Eqs. (27)-(29).

Step 3: All populations (marked in Step1 and Step 2) are merged and ranked by their fitness values. The top NP number of solutions among it is selected for the subsequent iterative process of the algorithm.

After initializing the population, the algorithm’s iterative process begins. In each iteration, a random number between 0 and 1 is generated and compared to the generation jumping factor (taken as 0.3 in this work). If the generating jumping factor value is greater than the randomly generated value, the centroid opposition approach is used to produce an equal number of centroid opposition solutions based on the current population matrix size using (29). Subsequently, the two population matrices are combined, and the best solutions, based on their respective fitness value, are selected for the next iteration according to the population matrix size. The generation jumping factor determines the frequency with which the centroid opposition concept is applied and, thus, enhances the diversity in the population matrix. At this stage, the lower and upper limits of a decision variable are determined as the lowest and highest values of each variable in the current population, respectively. The pseudo-code for the proposed COLAHA is described in Algorithm 1.

Algorithm 1
figure afigure a

Pseudo-code of COLAHA

Full size image

Outcomes and Interpretation

The proposed COLAHA is initially evaluated on various multimodal and unimodal benchmark test functions. The outputs generated by COLAHA are contrasted to those of recently announced algorithms to demonstrate its effectiveness and supremacy. Subsequently, COLAHA is utilised to determine the OPS of DGs, SCs, and EVCSs in the optimally reconfigured IEEE standard 69- and 118-bus RDNs. To analyze the performance of the studied COLAHA, five different case studies have been considered as mentioned below.

  • Case 1: Testing of COLAHA on the benchmark test functions.

  • Case 2: Simultaneous OPS of DGs and SCs.

  • Case 3: Simultaneous OPS of DGs, SCs, and EVCSs.

  • Case 4: Simultaneous OPS of DGs and SCs with ORC of RDN.

  • Case 5: Simultaneous OPS of DGs, SCs, and EVCSs with ORC of RDN.

The baseline values for voltage and power are established at 12.66 kV and 10 MVA, respectively, while performing the load flow simulation for IEEE 69-bus RDN. The total base load demand of the system is (3802.1 + j2694.6) kVA. A detail on the studied 69-bus RDN may be found in37. Similarly, the bus and load data of 118-bus RDN are taken from the work of38. The base values of voltage and power for the 118-bus distribution system are considered as 11 kV and 100 MVA, respectively. The total base load demand of the system is (22709.71 + j17040.97) kVA. In the proposed work, the maximum limit for SC sizing is taken as 600 kVAr for a single location with a step size of 100kVAr. The DG’s maximum limit is considered as 8 MW for a single location. The bus voltage constraint is considered within the limit 0.9 p.u. to 1.1p.u. The population size of 50 and the maximum iteration number as 100 have been considered for all the studied algorithms. The proposed solution to the identified problem is implemented using MATLABR software in Windows 10 64-bit system. The system used for running different algorithms consists of an intel core i5 processor of 8th generation with 8 GB RAM. The backward-forward sweep method is utilized for calculating the load flow parameters of the proposed work. This work considers a maximum of three DG units and the same number of SC units for optimal placements at a single location. Similarly, it is assumed that a maximum of 5 bus locations may be used for optimal EVCS deployment with a maximum charging capacity of 50 EVs per location.

For each of the mentioned case studies, five different optimization methods (referred as fuzzy-COLAHA, fuzzy-AHA, fuzzy-AOA, fuzzy-GA, and fuzzy-WOA) have been employed, and their respective outcomes are compared to evaluate their efficacies. Here, the word fuzzy appended ahead of each algorithm refers to their application in evaluating fuzzified objective function.

Case 1: Mathematical benchmark functions

The efficacy of the proposed COLAHA has been evaluated utilising a range of mathematical unimodal and multimodal benchmark test functions. The outcomes obtained employing it are matched to those of basic AHA and other algorithms to demonstrate its effectiveness and superiority. Table 2 presents the specifics of the benchmark test functions. Each function is independently run for 30 times considering 1000 iterations for each run. Thereafter, the mean and standard deviation (std) values for each benchmark test function are calculated. The convergence characteristics of COLAHA for the severals benchmark testing functions are illustrated in Figs. 6a-o. Table 3 exhibits the performance analysis of the proposed COLAHA with those of the basic AHA and several other algorithms referenced in31 when tested on benchmark functions. Table 3 presents that the proposed COLAHA outperforms the basic AHA and other algorithms in terms of mean and standard deviation values for most of the benchmark functions. Therefore, it may be concluded that COLAHA has superior solution searching capabilities compared to other counterparts.

Table 2 Details of benchmark test functions.
Full size table
Fig. 6
figure 6

Convergence curves obtained for different benchmark test functions f1 to f15 (Case 1). (a) f1 (b) f2 (c) f3 (d) f4 (e) f5 (f) f6 (g) f7 (h) f8 (i) f9 (j) f10 (k) f11 (l) f12 (m) f13 (n) f14 (o) f15.

Full size image
Table 3 Summary of results obtained for different benchmark functions (Case 1).
Full size table

Case 2: Simultaneous OPS of DGs and SCs in IEEE 69- and 118-bus RDNs

This case study examines the OPS of DGs and SCs and thoroughly demonstrates their impact on RDN performance. The outcomes of all the studied algorithms are then compared with each other with respect to base case scenario (i.e., without placement of DGs and SCs). The outcomes of the studied algorithms for the IEEE 69- and 118-bus distribution networks are displayed in Table 4 and Table 5, respectively. As shown in Table 4, the total active power compensation provided by DGs under fuzzy-COLAHA is 2252 kW, whereas, it is 2211 kW, 2900 kW, 2255 kW, and 2018 kW, respectively, for fuzzy-AHA, fuzzy-AOA, fyzzy-WOA, and fuzzy-GA for 69-bus RDN. Similarly, with COLAHA the reactive power compensation provided by DGs is 1091 kVAr, whereas, it is 1071 kVAr, 1405 kVAr, 1092 kVAr, and 977 kVAr for other compared algorithms (throughout the manuscript, the term “other compared algorithms” refers to fuzzy-AHA, fuzzy-AOA, fuzzy-WOA, and fuzzy-GA in the given order). The total reactive power compensation offered by SCs are 1100 kVAr, 1100 kVAr, 1000 kVAr, 1100 kVAr, and 1100 kVAr, respectively for fuzzy-COLAHA and other compared algorithms for 69-bus RDN. Because of the above-mentioned power compensations at optimal locations, the RDN performance is found to be improved from the base case scenario. The APL is improved by 93.26% in the case of fuzzy-COLAHA, whereas, the improvement of 92.11%, 88.71%, 86.76%, and 83.19% is observed, respectively, in the case of other compared algorithms for 69-bus RDN. Similarly, the RPL is improved by 89.20% under fuzzy-COLAHA, whereas, it is improved by 88.46%, 85. 03%, 84.00%, and 78.56%, respectively, for other compared algorithms. The minimum bus voltage is also enhanced to 0.99 p.u. employing fuzzy-COLAHA which shows the efficacy of the algorithm in providing a stable voltage profile to the RDN. The minimum bus voltage varies between 0.98 p.u. to 0.99 p.u. for other compared algorithms. The convergence curve and the comparative voltage profile of the 69-bus RDN are, respectively, displayed in Fig. 7a and Fig. 7b for 69-bus RDN.

Table 4 Summary of results of IEEE 69-bus RDN (Case 2).
Full size table
Table 5 Summary of results of IEEE 118-bus RDN (Case 2).
Full size table
Fig. 7
figure 7

Comparative performance results for IEEE 69-bus system (a) voltage profile (b) convergence curve (Case 2).

Full size image

In the case of IEEE-118 bus RDN, it may be observed from Table 5 that the optimally placed DGs offered active power compensation of 9134 kW under fuzzy-COLAHA and 9505 kW, 10,460 kW, 9408 kW, and 8727 kW, respectively, for other compared algorithms. Similarly, the DGs provided reactive power compensation of 4424 kVAr, 4604 kVAr, 5067 kVAr, 4557 kVAr, and 4227 kVAr, respectively, using fuzzy-COLAHA and other compared algorithms. Due to the optimal placement of SCs, the RDN gets the reactive power compensation as 700 kVAr, 1000 kVAr, 1600 kVAr, 1500 kVAr, and 400 kVAr, respectively, employing fuzzy-COLAHA and other compared algorithms. Because of this OPS-DGSC in 118-bus RDN, the APL is reduced by 71.72% in the case of fuzzy-COLAHA and 70.59%, 53.30%, 67.37%, and 62.48% under other compared algorithms. Similarly, the RPL is reduced by 71.36% for fuzzy-COLAHA and 70.59%, 59.49%, 69.18%, and 62.23% for other compared algorithms. The minimum bus voltage is also improved to 0.96 p.u. under fuzzy-COLAHA. This shows that the fluctuation in bus voltage is reduced and remained in the allowable range of ± 5% after the OPS-DGSC in 118-bus RDN. The system power factor is also improved from the base case scenario for all the studied algorithms. The Fig. 8a and Fig. 8b represent the convergence curve and the comparative voltage profile of the system for 118-bus RDNs, respectively. From Tables 4–5 and Figs. 7–8, it may be seen that the proposed fuzzy-COLAHA technique outperforms the fuzzy-AHA, fuzzy-AOA, fuzzy-GA, and fuzzy-WOA approaches for almost all the compared parameters for both 69-bus and 118-bus RDNs. It may also be observed from the figures that the COLAHA-based placement and sizing of DGs and SCs offered the best bus voltage profiles over other counterparts, resulting in the least voltage deviation from the nominal value. From the above observations, it may be concluded that the fuzzy-COLAHA technique performs better to other studied methods in terms of convergence specifications and improving the overall RDN’s performance for this case study.

Fig. 8
figure 8

Comparative performance results for IEEE 118-bus system (a) voltage profile (b) convergence curve (Case 2).

Full size image

Case 3: Simultaneous OPS of DGs, SCs, and EVCSs for 69- and 118-bus RDN

In this case study, the simultaneous OPS of DGs, SCs, and EVCSs are determined for IEEE standard 69- and 118-bus RDN. The achieved results employing the proposed and studied algorithms are demonstrated in a comparative manner in Table 6 and Table 7 for 69- and 118-bus RDN, respectively. From Table 6, it may be perceived that the total active power support offered by optimally placed DGs is 2546 kW for fuzzy-COLAHA, whereas, it is 2533 kW, 2420 kW, 1866 kW, and 1533 kW, respectively, for other compared algorithms. Similarly, the total reactive power compensation provided by optimally placed DGs is 1234 kVAr for fuzzy-COLAHA, whereas, for other compared algorithms it is 1227 kVAr, 1172 kVAr, 905 kVAr, and 743 kVAr, respectively. The total reactive power compensation given by optimally placed SCs is 800 kVAr for fuzzy-COLAHA, whereas, it is 900 kVAr, 800 kVAr, 900 kVAr, and 900 kVAr, respectively, for other compared algorithms. The optimal position and count of EVCSs obtained using the proposed and studied algorithms are shown in Table 6 for 69-bus RDN. The total active and reactive power load added to the RDN due to optimal EVCSs placement and sizing are 761 kW and 369 kVAr, respectively, for fuzzy-COLAHA. Similarly, for other compared algorithms, the total active power load added due to the optimal EVCSs placement are 455 kW, 846 kW, 793 kW, and 944 kW, respectively, and the total reactive power load added to RDN are 218 kVAr, 409 kVAr, 385 kVAr, and 457 kVAr, respectively. As a result of these OPS, the APL is reduced by 88.67%, 86.80%, 83.61%, 85.66%, and 73.44% for fuzzy-COLAHA and other compared algorithms, respectively. Similarly, the RPL is reduced by 85.31%, 84.04%, 79.09%, 79.27%, and 70.30% for fuzzy-COLAHA and other compared algorithms, respectively. The minimum bus voltage is also enhanced to 0.98 p.u. for fuzzy-COLAHA and lies within the range of 0.96–0.98 p.u. for other compared algorithms. The system power factor is also improved to 0.95 under the action of other compared algorithms. The convergence curve obtained under all the studied algorithms for 69-bus RDN is shown in Fig. 9a, whereas, the comparative voltage profiles are showcased in Fig. 9b.

Table 6 Summary of results of IEEE 69-bus RDN (Case 3).
Full size table
Table 7 Summary of results of IEEE 118-bus RDN (Case 3).
Full size table
Fig. 9
figure 9

Comparative performance results for IEEE 69-bus system (a) voltage profile (b) convergence curve (Case 3).

Full size image

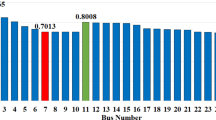
The optimal results for 118-bus RDN are comparatively represented in Table 7. As shown in Table 7, the fuzzy-COLAHA offers total active and reactive power compensations of 7693 kW and 3726 kVAr, respectively, due to the optimal DGs placement. The other compared algorithms offer total active power compensation of 8142 kW, 13,026 kW, 15,312 kW, and 11,162 kW respectively, whereas, the respective reactive power compensation are 3942 kVAr, 6308 kVAr, 7416 kVAr, and 5406 kVAr. Similarly, because of the optimal SCs placement, the reactive power compensation offered to the RDN are 1300 kVAr, 1300 kVAr, 1500 kVAr, 700 kVAr, and 600 kVAr, respectively, for fuzzy-COLAHA and other compared algorithms. The optimal position and the count of EVCSs are shown in Table 7 for all the studied algorithms along with their respective additional active and reactive power load demand to the RDN. The total active and reactive power load demand added to the RDN due to fuzzy-COLAHA is 1119 kW and 541 kVAr, respectively. Due to this OPS, the APL has been reduced by 69.08% for fuzzy-COLAHA, whereas, it is reduced by 66.41%, 61.15%, 57.06%, and 49.88%, respectively, in the case of other counterparts. Similarly, the RPL is reduced by 68.42%, 65.01%, 61.22%, 58.47%, and 54.30%, respectively, under fuzzy-COLAHA and other compared algorithms. The system power factor is improved to 0.8018, which is comparable to the base case scenario, whereas, it varies between 0.7 to 0.8 for other compared algorithms. Figure 10a shows the convergence curves of various studied algorithms. From Fig. 10a, it may be seen that fuzzy-COLAHA has improved convergence characteristics than other compared algorithms. The Fig. 10b, presents the comparative bus voltage profiles obtained under the proposed and the studied approaches. It is evident from the figure that almost all the algorithms bring the bus voltages within the allowable voltage deviation limit. However, the bus voltage profile found under fuzzy-COLAHA exhibits lesser deviations among all the compared algorithms, which shows its superiority over other counterparts. Moreover, in this case study, it may be observed that the performance of both RDNs deteriorated slightly compared to the previous case study. This is mainly due to the addition of extra loads due to the charging of EVs. However, the overall performance of the RDNs is still admirable because of the OPS-DGSC. Moreover, from the overall evaluation of results, it may be concluded that the fuzzy-COLAHA outperforms the fuzzy-AHA, fuzzy-AOA, fuzzy-GA, and fuzzy-WOA approaches for 69-bus and 118-bus RDNs.

Fig. 10
figure 10

Comparative performance results for IEEE 118-bus system (a) voltage profile (b) convergence curve (Case 3).

Full size image

Case-4: Simultaneous OPS of DGs and SCs with ORC of RDN for 69- and 118-bus system

In this case study, the optimal location and size of DGs and SCs are obtained simultaneously along with the ORC of the RDN. The outcomes obtained utilizing the adopted algorithms are presented in Table 8 and Table 9 for 69- and 118-bus RDNs, respectively. From Table 8, the optimal locations and their respective sizes obtained for DGs and SCs may be seen for various studied and proposed algorithms. The total active power compensation offered by DGs are 2882 kW, 2860 kW, 1720 kW, 2670 kW and 2263 kW, respectively, for fuzzy-COLAHA and other compared algorithms. Similarly, the reactive power compensation provided by DGs are 1396 kVAr, 1385 kVAr, 832 kVAr, 1293 kVAr, and 1097 kVAr, respectively, under fuzzy-COLAHA and other compared algorithms. The reactive power compensation offered by optimally placed SCs are 1000 kVAr, 1000 kVAr, 1200 kVAr, 1000 kVAr, and 1100 kVAr, respectively, for fuzzy-COLAHA and other studied algorithms. The information regarding the open tie-line switches is presented in Table 8 for all the studied and proposed algorithms. Due to these OPS-DGSC along with the ORC of 69-bus RDN, the system APL with respect to the base case get reduced to 9.48 kW for fuzzy-COLAHA and 14.16 kW, 16.79 kW, 20.10 kW, and 25.47 kW, respectively, for other compared algorithms. In terms of percentage, the APL is reduced by 95.79%, 93.71%, 92.54%, 91.07%, and 88.68%, respectively, for fuzzy-COLAHA and other studied algorithms. Similarly, the RPL get reduced to 7.35 kVAr, 7.78 kVAr, 13.71 kVAr, 12.94 kVAr, and 16.66 kVAr, respectively, employing fuzzy-COLAHA and other compared algorithms. In terms of percentage, the RPL is reduced by 92.80%, 92.38%, 86.58%, 87.33%, and 83.69%, respectively, for fuzzy-COLAHA and other studied algorithms. The system power factor also gets improved to nearly 0.95 lagging for almost all the studied and proposed algorithms. The minimum bus voltage of the system get improved to 0.99 p.u. utilizing fuzzy-COLAHA, whereas, it varies between 0.98 p.u. to 0.99 p.u. for other compared algorithms. But, the bus voltage variation is found to be much less in the case of fuzzy-COLAHA than its other counterparts (refer Fig. 11a). The comparative convergence characteristics of all the algorithms are shown in Fig. 11b.

Table 8 Summary of results of IEEE 69-bus RDN (Case 4).
Full size table
Table 9 Summary of results of IEEE 118-bus RDN (Case 4).
Full size table
Fig. 11
figure 11

Comparative performance results for IEEE 69-bus system (a) voltage profile (b) convergence curve (Case 4).

Full size image

The OPS-DGSC for 118-bus RDN are demonstrated in detail in Table 9. The total active power compensation obtained due to the OPS of DGs are 9457 kW, 8903 kW, 11,772 kW, 12,550 kW, and 9096 kW, respectively, for fuzzy-COLAHA and other compared algorithms. Similarly, the total reactive power compensation offered by the optimal DGs placement are 4579 kVAr, 4311 kVAr, 5700 kVAr, 6077 kVAr, and 4406 kVAr, respectively, for fuzzy-COLAHA and other compared algorithms. The total reactive power compensation yielded from optimally placed SCs are 1300 kVAr, 1100 kVAr, 800 kVAr, 1000 kVAr, and 1100 kVAr, respectively, under fuzzy-COLAHA and other compared algorithms. The details of open tie-line switches are mentioned in Table 9 for all the studied and proposed algorithms. Due to the OPS-DGSC along with ORC of RDN, the system APL with respect to the base case of 1298.15 kW is reduced to 139.87 kW for fuzzy-COLAHA, whereas, it is reduced to 228.89 kW, 287.23 kW, 350.76 kW, and 433.24 kW, respectively, for rest other algorithms. In terms of percentage, the APL is reduced by 89.23% for fuzzy-COLAHA and 82.37%, 77.87%, 72.98% ans 66.63%, respectively, for other studied algorithms. The RPL is reduced to 115.50 kVAr, 175.74 kVAr, 190.39 kVAr, 231.64 kVAr, and 310.94 kVAr, respectively, for fuzzy-COLAHA and other compared algorithms. In terms of percentage, the RPL is reduced by 88.20% for fuzzy-COLAHA and 82.04%, 80.55%, 76.33%, and 68.23%, respectively, for other compared algorithms. The system power factor observed to be 0.77 lagging for fuzzy-COLAHA, whereas, for other compared algorithms, it is found to be in the range 0.72–0.77 lagging. The comparative improvement in the bus voltage profile of the system may be observed from Fig. 12a, whereas, the convergence profile of the algorithms is presented in Fig. 12b. In this case study, it may be observed the RDN performance in terms of obtained results are the best in comparison to the previous case studies. This is because the ORC of RDN further improves the performance in addition to the OPS-DGSC. Moreover, in this case study also, the fuzzy-COLAHA outperforms other compared algorithms in almost all parameters.

Fig. 12
figure 12

Comparative performance results for IEEE 118-bus system (a) voltage profile (b) convergence curve (Case 4)

Full size image

Case-5: Simultaneous OPS of DGs, SCs and EVCSs with ORC of RDN for 69- and 118-bus system

In this case study, the impact of the simultaneous OPS of DGs, SCs, and EVCSs along with ORC on the performance of 69- and 118-bus RDNs has been investigated. The above problem statement is solved using the proposed fuzzy-COLAHA and other studied algorithms. The obtained results under each are compared to showcase the superiority of one over other. In a comparative format, the results employing these algorithms are presented Table 10 and Table 11, respectively, for 69- and 118-bus RDNs. It may be seen from these Table 10 that, the total active power compensation contributed by DGs for 69-bus RDN are 2798 kW, 3222 kW, 3327 kW, 3719 kW, and 2544 kW, respectively, for fuzzy-COLAHA and other compared algorithms. While, the total reactive power compensation offered are 1356 kVAr, 1561 kVAr, 1611 kVAr, 1802 kVAr, and 1233 kVAr, respectively, employing fuzzy-COLAHA and other compared algorithms. Similarly, the total reactive power compensation provided by SCs are 800 kVAr, 600 kVAr, 600 kVAr, 500 kVAr, and 900 kVAr, respectively, under the proposed fuzzy-COLAHA and other compared algorithms. Detail of EVCS locations and their respective counts are presented thoroughly in Table 10 along with the data of open tie-line switches. Due to this OPS along with the ORC of RDN, the system APL is reduced by 93.35, 92.47, 91.83, 87.84, and 87.94%, respectively, using fuzzy-COLAHA and other compared algorithms, whereas, the respective reactive RPL get reduced by 89.08, 86.53, 86.16, 85.74, and 78.76%. The power factor of the system has been improved to 0.95 lagging in case of fuzzy-COLAHA and found in the range of 0.94–0.95 lagging for other compared algorithms. Similarly, the minimum bus voltage of the system has been improved to 0.98–0.99 p.u. for all the studied and proposed algorithms. The comparative bus voltage profiles obtained under all the algorithms is presented in Fig. 13a. The convergence curves yielded under studied and the proposed algorithms are demonstrated in Fig. 13b. These figures confirms the superior performance of the proposed approach over others.

Table 10 Summary of results of IEEE 69-bus RDN (Case 5).
Full size table
Table 11 Summary of results of IEEE 118-bus RDN (Case 5).
Full size table
Fig. 13
figure 13

Comparative performance results for IEEE 69-bus system (a) voltage profile (b) convergence curve (Case 5).

Full size image

In case of 118-bus RDN, the active power compensation provided by fuzzy-COLAHA and other compared algorithms-based optimal placement of DGs are 10,828 kW, 8676 kW, 15,162 kW, 11,556 kW, and 11,783 kW, respectively. The respective reactive power compensations are 5244 kVAr, 2611 kVAr, 7343 kVAr, 5597 kVAr, and 5706 kVAr. The reactive power compensation offered by SCs are 900 kVAr, 1000 kVAr, 1200 kVAr, 1500 kVAr, and 900kVAr, respectively, for fuzzy-COLAHA and other compared algorithms. The optimal locations of EVCSs and their respective counts are presented in Table 11. The table also contains the additional active and reactive power load added by the EVs to the RDN, as well as the information regarding the open tie-line switches found under the proposed and other studied algorithms. As an effect of the OPS of the considered units with ORC of RDN, the APL has been reduced by 87.92%, 77.27%, 76.10%, 68.79%, and 65.41% under fuzzy-COLAHA and other compared algorithms, respectively. On the other hand, the respective RPL is reduced by 87.52%, 76.80%, 71.10%, 70.71%, and 66.37%. The minimum bus voltage is enhanced to 0.97 p.u. under fuzzy-COLAHA and found as 0.95 p.u., 0.96 p.u., 0.96 p.u., and 0.96 p.u. for other compared algorithms. The bus voltage profile for 118-bus RDN is demonstrated in Fig. 14a, whereas, Fig. 14b represents the convergence curves obtained under the adopted algorithms. From the outcome of this case study, it may be observed that the performance of RDN gets slightly depreciated because of the addition of extra load presented by the EVCSs. However, the overall performance obtained under all the studied approaches is found to be quite significant.

Fig. 14
figure 14

Comparative performance results for IEEE 118-bus system (a) voltage profile (b) convergence curve (Case 5).

Full size image

Referring to the results discussed under all case studies, an improved performance of RDN in terms of line loss reduction, bus voltage profile etc. has been observed under the optimal deployment of DGs and SCs. Due to the inclusion of EVCS placement (considering them as load) the performance deteriorates a bit, but it remains within the acceptable boundaries. However, the performance of the RDN is further enhanced due to the application of ORC of RDN. This further facilitates to add EVCS sustainably into the RDN, which is evaluated as the Case 5 in the presented work. Moreover, in all the case studies, the efficacy of the proposed fuzzy-COLAHA is found superior over other counterparts in achieving desirable RDN performance post optimal deployment of considered compensation devices. In addition, the effectiveness of the fuzzy-COLAHA is more visible in case of 118-bus RDN than the 69-bus RDN. This shows that the proposed fuzzy-COLAHA performs better than its other counterparts when the system becomes more complex.

Conclusion

In this work, firstly, a new modified and improved version of AHA is proposed which is termed as COLAHA. The proposed algorithm is tested over various unimodal and multi-modal benchmark functions and the outcome is compared with published literature to demonstrate its efficacy and superiority. Thereafter, a successful maiden application of fuzzy-COLAHA is made in conjunction with studied fuzzy-AHA, fuzzy-AOA, fuzzy-GA, and fuzzy-WOA in obtaining the OPS of DGs, SCs, and EVCSs in an optimally reconfigured RDN. Four different case studies are carried out to illustrate the effects of different combinations of OPS of DGs, SCs, and EVCSs along with ORC on the performance of the RDNs. The objective function taken in this work comprises of the reduction of active and reactive power supplies at the substation, the minimization of line losses and the enhancement of network voltage stability. Under the action of the proposed optimization approach, it has been perceived that for optimal DG and SC placement with ORC of RDN, system characteristics (such as line losses, voltage deviation, system power factor, etc.,) are improved relative to their base case values. Meanwhile, as a result of the increase in load demand caused by EV penetrations, the system performance deteriorated slightly. However, the OPS of DGs and SCs and ORC of RDN contributes to the overall improvement in the performance of the distribution system, which enables the placement of more EVCSs and facilitates additional charging of EVs. Based on the simulation results obtained, it is evident that the proposed fuzzy-COLAHA outperformed the other approaches in terms of the majority of performance parameters of the studied 69- and 118-bus RDNs. Finally, the present study infers that the fuzzy-COLAHA-based approach is superior in terms of performance. The proposed approach yields the best solution and converges significantly faster than the other studied AHA, AOA, GA and WOA-based strategies.