Introduction

Due to the rapid progression in human population and escalation in rural-urban migration, the demand for infrastructure continues to be a high challenge for most countries. Infrastructures such as roads, houses, hospitals, schools, bridges, dams, etc., are required for human lives. For the construction of all these infrastructures, concrete is the most important and most used man-made construction material due to many of its benefits which includes high compressive strength and more durable, cost-effectiveness, moldability to different shapes, ease of construction, high fire resistance and lower energy consumption during production1,2. On the contrary, the major shortcomings of concrete are its high rigidity and poor toughness, low tensile strength, and shrinkage. This causes a major drawback of using concrete and limits its applications for different construction purposes, especially in areas subjected to high tensile and fatigue loads. These drawbacks make cracking inevitable in the concrete throughout its service life, which often occurs at the adolescent stage of its lifespan. The cracks can significantly affect the durability, serviceability and safety of the structure depending on its nature i.e. either minor or major cracks1,3,4.

With the use of steel reinforcements in concrete to form the composite “reinforced concrete”, the steel gives the tensile strength, while the concrete contributes to compressive strength, and prevents the steel from exposure to fire, chemical attacks or other harmful compounds that can cause corrosion or damage the steel5,6,7. However, still with the use of steel reinforcements, the reinforced concrete structures are susceptible to cracking due to poor toughness and shrinkage of the concrete. For example, it has been reported that in concrete bridges, more than 90% of the major defects occur due to cracking in the concrete due to its poor shrinkage and toughness8. To address these deficiencies of concrete and improve its toughness, cracking and shrinkage resistance, the idea of micro-level reinforcement was invented, i.e. by adding different types of short discontinuous fibers into the concrete9,10. The fibers enhance the fracture properties of the fibers by preventing and inhibiting the growth of micro-cracks to macro-cracks, improving the mechanical properties of the concrete, and averting damage and failure of the concrete structures due to cracking1. Fibers added to concrete have also been reported to improve its impact and fatigue resistance, enhance ductility, and toughness, prevent or decrease shrinkage cracking and creep, and delay post cracking failure3,11,12,13. Fiber has also been found to improve the fire and high temperature resistance of concrete by preventing spalling and reducing the loss in weight and strength of the concrete when exposed to elevated temperature14,15,16. Fiber can be classified as natural or synthetic; the latter is commonly used in concrete. Synthetic fibers such as steel fiber, polypropylene fiber, polyvinyl alcohol fiber, basalt fiber, carbon fiber, glass etc. have been added to cementitious materials like concrete and mortar, and have been reported to improve one or more properties of the composites1,8,17,18,19. Natural fibers are obtained from natural sources such as plants, animals, and minerals. Plant-based natural fibers include coir fiber, DPF, hemp fiber, kenaf fiber, jute fiber, sisal fiber, abaca fiber, etc. Animal-based natural fibers include sheep wool fiber, horsehair fiber, angora fiber etc. The mineral-based natural fibers include glass fiber, asbestos fiber, graphite fibers etc19. The natural fibers have some benefits over synthetic fibers which include lower cost, availability, more environmentally sustainable, high tensile strength with lower elasticity, superior alkaline resistance and thermal/acoustic properties, and inferior abrasiveness and density20,21,22. The foremost deficiencies of using natural fibers in concrete include reduction in strength, meagre bond between the cement paste and fiber surface, caused by the hydrophilicity of the fiber, high water absorption and wettability of the fiber triggering escalation in pore volume in the concrete5,21,23.

Date palm fiber (DPF) is a plant-based material which is extracted from the mesh of date trees. The date trees are available in abundance in the MENA countries, especially Saudi Arabia24,25. The date tree wastes including its mesh and trunk leaves are normally truncated minimum once a year, with more than 20 kg of waste generated which is mostly discarded into landfills without being utilized or recycled21,26,27. The mesh of the date trees is washed thoroughly, treated, and cut into smaller sizes for use as the DPF. The DPF is also employed as a fiber material in cement composites5,28,29,30. The DPF has been found to have a lower cost-to-strength ratio when compared to other synthetic and natural fibers26. Some studies have utilized DPF as an additive in concrete and mortar and have reported significant enhancements in the properties of the cementitious composites. Althoey et al.29 used DPF to substitute synthetic fibers: steel fiber (SF) and polypropylene fibers (PPF) on high-strength concrete. The concrete was produced concrete using 0%, 0.2%, 0.4%, 0.6%, and 1% volumes of DPF, SF and PPF each. It was found that the DPF showed higher improvement with regards to density, ultrasonic pulse velocity and permeability compared to SF and PPF. With the addition of 1% DPF, a substantial gain in tensile strength by 17% and flexural strength by 60–85% compared to the plain high-strength concrete was noticed. Ozerkan et al.23 reported an escalation in setting times and water absorption of mortar with the addition of 0.5–2% DPF. There was a reduction in drying shrinkage and enhancement in the tensile and compressive strengths of the mortar with the incorporation of up to 1% DPF due to proper dispersion of the fibers and adequate homogeneity achieved in the fresh mix. Alatshan et al.31 added 0.5–2.5% DPF of different lengths (50, 60 and 70 mm) to concrete. They noticed a decline in bending and compression resistance of the concrete with an increase in fiber content and length. However, the addition of 0.5%-50 mm DPF slightly enhanced the compressive strength, and 0.5% DPF with any length also improved the flexural strength of the concrete. Tioua et al.32 added two volume fractions of 0.1% and 0.2% of DPF to Roller Compacted concrete (RCC). They used two lengths of the DPF (10 and 20 mm). A reduction at the early age of drying shrinkage with the addition of DPF was observed, where up to 50% reduction was recorded with the addition of 0.1%- 20 mm DPF. Furthermore, DPF lowered the risk of cracking in the RCC. However, the DPF was found to cause a depletion in the compression resistance of the concrete. Zanichelli et al.33 incorporated between 2 and 10% DPF by volume to cement mortar. The DPF was found to reduce the compressive strength, fracture toughness and elastic modulus of the mortar. However, the energy absorption capacity and ductility of the mortar improved with the addition of DPF. Vantadori et al.34 reported a significant gain in the ductile behavior and energy absorption of mortar with adding between 2 and 10% DPF. Other studies have also reported improvement in acoustic, thermal properties, toughness, impact resistance, tensile strength, and crack resistance with the addition of DPF to cementitious composites21,23,35,36.

The main disadvantage of using natural fibers, especially DPF, is poor adhesion between the fiber and cement matrix which is caused by the presence of chemicals and impurities which include lignocellulose, hemicellulose, cellulose, and wax in the DPF. This poor bonding causes a reduction in the mechanical properties and durability of the composite. Additionally, the DPF is hydrophilic in nature, making it easily absorb water and becomes more wettable, thereby causing poor compatibility and consistency when missing, leading to increased porosity and reduction in strength and durability of the composite24,37. Moreover, the DPF is easily affected by thermal and moisture absorption degradation due to its hemicellulose content. This also causes the weakening of the cement paste and a reduction in the properties of the cement composite24. The high wettability and absorption of the DPF mostly result in a balling effect during mixing, which reduces the consistency and increases the porosity in the hardened microstructure21,36. Therefore, to lessen the undesirable effects of DPF on the mechanical strengths of concrete, silica fume was employed as a SCM in the concrete. The silica fume is used as a SCM in concrete, and is a byproduct obtained from the production of silicon and silicon alloys. The silica fume rich in silica (Si) produces calcium silicate hydrates (C-S-H) as the main hydration product during the hydration process with cement in the concrete. The C-S-H has a similar layered structure to tobermite, which gives it the ability to bond the aggregates together with the cement paste38,39. With C-S-H accounting from more than 60% of the hydration products formed during hydration reaction, it therefore significantly affects the general mechanical properties of the composite40. With the high SiO2 in silica fume, during the hydration reaction the Ca(OH)2 will be consumed to produce surplus C-S-H. With such properties, the silica fume when used as a SCM in the DPF reinforced concrete, it is expected to enhance the bonding between the fiber and the cement matrix/aggregate, thus improving the mechanical and thermal performance of the concrete16,21.

Mathematical and statistical modelling have been utilized for concrete applications to generate the relationships between the variables added to modify the concrete’s properties and the properties of the concrete41,42. Among the statistical approaches used, multivariable regression analysis (MRA) has been employed for many years in civil engineering applications such as in the building and construction fields. The MRA is a representational model, which makes it easier to understand and apply using methods like sensitivity analysis, graphical approaches, giving it some advantages over black-box models like ANN43,44. Different computer-based intelligence techniques such as genetic programming, ANN, multi-criteria-based decision methods (MCDM) and MRA have been utilized to investigate the influence of multiple variables on the properties of concrete42,45,46,47,48. However, there is deficiency of relevant prediction models for DPF reinforced concrete, especially when subjected to high temperature conditions. Therefore, in this study silica fume was added as a SCM to the DPF reinforced concrete to mitigate the detrimental effects of the DPF on the mechanical and thermal properties of the concrete. Additionally, MRA and MCDM analysis methods were employed to develop the relationship between multiple variables (DPF and silica fume) and the properties of the concrete under normal and elevated temperature exposure.

Materials and methodology

Materials

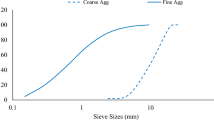
The materials used in this study include cement, silica fume, aggregates, DPF, water and superplasticizer. The cement was fresh, dry, and free from any lump or agglomerate when using it, and it agree with the requirements of ASTM C150/C150M49, and its properties are displayed in Table 1. Micro silica fume was employed as a SCM in this study. The properties of the silica fume are highlighted in Table 1. For the fine aggregate, natural river sand which was free of dirt and impurities was utilized. The aggregate was well-graded and conformed with ASTM C33/C33M50 specifications for aggregate gradation for use in concrete as given in Fig. 1. The aggregate properties are displayed in Table 2. Crushed gravel with a maximum size of 19 mm, which was clean and free from impurities was utilized as the coarse aggregate. Its particle gradation in Fig. 1 showed that it followed the requirements of ASTM C33/C33M50 for gradation of coarse aggregate in concrete. The summary of its properties is displayed in Table 2.

Raw DPFs in the form of rectangular interwoven mesh were obtained from nearby date tree farms within the Riyadh region of Saudi Arabia. The sizes of the mesh range between 30 and 50 cm in length and 20 to 30 cm in breadth. Prior to adding to the concrete, the raw DPF was treated and processed into single individual fibers. The treatment involves first soaking in a 3% NaOH solution for 2 h to remove dirt and impurities and enhance the roughness of the fibers. After soaking, the DPFs were extensively washed with clean water and detached into single fibers. The DPF was dried under the sun for about 72 h until it was dried. The dried DPFs were then cut into small single fibers with lengths varying between 2 and 3 cm, and diameter of 0.1–0.3 mm. The properties of the DPF summarized in Table 3.

Table 1 Properties of cementitious materials21,28.
Full size table
Fig. 1
figure 1

Particle size gradation of aggregates.

Full size image
Table 2 Properties of aggregates.
Full size table
Table 3 Properties of the DPF used21.
Full size table

Mix proportioning

Proportioning of the control concrete mix was accomplished by utilizing the procedures explained in ACI 211.1R51. Superplasticizer was added in a dosage of 1% by weight of cementitious materials to minimize the impact of the variations in the water-to-binder ratios. The varying proportions of DPF added were 0%, 1%, 2% and 3% by weight of binder. Cement was partially replaced with silica fume in doses of 0%, 5%, 10% and 15%. The mix proportions based on the combinations of DPF, and silica fume is shown in Table 4.

Table 4 Mix proportioning21,28.
Full size table

Test methods

The dry basic materials were weighed, batched, and sampled according to the guidelines outlined in ASTM C192/C192M52. Similarly, the mixing of the fresh concrete was done in the laboratory in accordance with the ASTM C192/C192M52 method. Subsequently, the slump and fresh density tests were conducted on fresh concrete before casting the fresh concrete into the desired molds. The fresh concrete was allowed to harden in the laboratory by keeping it for at least 24 h prior to demolding. The hardened concrete was then cured in water for 28 days before testing.

The experiments for the concrete at normal temperature were already conducted in our previous studies as reported in Ibrahim, et al.21. The fresh and hardened densities tests were performed in accordance with the guidelines of BS-EN 12350-653 and BS EN 12390-754 respectively. The compressive strength testing was conducted using 100 mm cubes after 28 days curing period by adopting the methods in BS EN 12390-355. The split tensile strength was evaluated using 100 mm by 200 mm cylindrical samples after subjecting them to 28 days curing period, following the BS EN 12390-625 guidelines. The flexural strength was measured using prismatic-shaped samples of 100 × 100 × 500 mm3 sizes after curing for 28 days in water in accordance with ASTM C293/C293M56 specifications. The water absorption test was executed using 100 mm cubes, by following the methodology listed in ASTM C64257, after 28 days curing.

The experiments at elevated temperatures were conducted in our previous research reported in Adamu et al.16. Cubic specimens (100 mm) were first exposed to normal water curing for 28 days before testing. The samples were dried completely after curing and weighed. The weight of the dried sample is recorded as Mi. The samples were then exposed to high temperatures in an electric furnace for 2 h at the rate of 10 °C/min. Heating temperatures of 200 °C and 800 °C were adopted. Subsequently, the samples kept inside the furnace in closed condition to cool. The samples were weighed again and recorded as MT. The weight loss of the samples was computed using Eq. 1. The samples then underwent compressive strength testing in accordance with BS EN 12390-355 specifications

$$\:{W}_{L,T}=\frac{{M}_{i}-{M}_{T}}{{M}_{i}}\times\:100$$
(1)

where WL, T is the weight loss at temperature T in %, Mi is the weight of the sample prior to heating in g, MT is the weight of sample after heating at temperature T in g.

MCDM

The significance of Multi-Criteria Decision Making (MCDM) lies in identifying the best mix based on the various criteria under investigation. After meticulous analysis, the date palm fiber reinforced concrete must undergo scrutiny based on a range of performance metrics including workability, physical properties, mechanical properties, and thermal performance parameters. While environmental considerations were excluded from this study due to the variability of material exposure conditions across applications, they can be addressed in a separate investigation.

In this study, 12 parameters were investigated, encompassing Fresh Density, Unit Weight, Compressive Strength, Flexural Strength, Split Tensile Strength, Compressive Strength at 200 °C and 800 °C, Mass Loss at 800 °C, Slump, and Water Absorption. Each parameter, post-analysis, suggests different potential mixes, underscoring the necessity of identifying the optimal mix.

The utilization of various MCDM methods offers several advantages. Firstly, it enhances resilience, enabling decision-makers to adapt to changing circumstances effectively. Secondly, it increases precision by incorporating multiple dimensions of performance simultaneously, providing a comprehensive evaluation. Thirdly, it fosters a deeper understanding of the trade-offs between different mixes, facilitating informed decision-making. Finally, it offers flexibility, allowing stakeholders to prioritize criteria based on specific project requirements or constraints. Thus, MCDM methodologies serve as invaluable tools in navigating the complex landscape of material selection, ensuring that the chosen mix aligns optimally with project objectives and performance criteria.

The adoption of four MCDM methodologies—TOPSIS, EDAS, WSM, and WPM—ensures a comprehensive and robust decision-making process. This diverse selection allows for the exploration of various perspectives, cross-validation of results, and comprehensive analysis of the decision landscape.

All four methods require weights for criteria analysis, which were determined using the entropy method. The MCDM technique begins with establishing weights for each criterion, facilitated by the entropy method. By employing MCDM, it becomes convenient to assess a wide range of options based on various parameters, easing well-informed decision-making. The entropy method enables decision-makers to appropriately weigh individual parameters, providing a comprehensive understanding of the decision-making challenge along with its trade-offs and consequences.

The formulae utilized for calculating the entropy weight (\(\:{H}_{j}\)) are presented in Eq. (2):

$$\:{H}_{j}=-\sum\:_{i=1}^{n}{p}_{ij}\text{l}\text{o}\text{g}\left({p}_{ij}\right)$$
(2)

Where n is assigned for number of alternatives, and pij denotes the normalized value of the ith alternative of criterion j.

Additionally, the entropy reduction (\(\:{R}_{j}\)) for criteria’s (j) is determined using Eq. (3):

$$\:{R}_{j}=H-{H}_{j}$$
(3)

where H signifies the entropy of the decision matrix encompassing criteria under evaluation.

The weight (\(\:{w}_{j}\)) assigned to each criterion is based on its entropy reduction relative to the total entropy reduction and is computed by Eq. (4):

$$\:{w}_{j}=\:\frac{{R}_{j}}{\sum\:_{j=1}^{m}{R}_{j}}$$
(4)

Here, m stands for the number of criteria under evaluation.

The determined weights were subsequently applied to MCDM analysis. To offer a comprehensive understanding of the calculation process, further elaboration is provided on all four MCDM approaches.

TOPSIS

The first method employed was the TOPSIS method, aimed at identifying the optimal composition for the DPF reinforced concrete (DPFRC) integrated with silica fume (SF). In addition to pinpointing the ideal composition, TOPSIS provided rankings for the mixes developed in the study based on various performance parameters.

The TOPSIS method facilitates the simultaneous consideration of multiple criteria crucial for assessing the viability and efficacy of mixes of DPFRC. This is executed by systematically normalizing the decision matrix, the TOPSIS technique ensures that various performance metrics are weighted proportionally to their relative importance in the evaluation process. In the first step, the normalized value of the performance of alternative was calculated using Eq. (5).

$$\:{r}_{ij}=\:\frac{{x}_{ij}}{\sqrt{\sum\:_{i=1}^{n}{x}_{ij}^{2}}}$$
(5)

In the Eq. (4) above, \(\:{r}_{ij}\) represents the normalized value of the performance of alternative i on criteria (j), \(\:{x}_{ij}\) denotes the raw performance value, and n represents number of alternatives.

In the second step, the weighted normalized value was calculated using Eq. (6).

$$\:{v}_{ij}={w}_{j}\:\times\:\:{r}_{ij}$$
(6)

Here, \(\:{v}_{ij}\) signifies the weighted normalized value of alternative (i) on criteria (j), \(\:{w}_{j}\) represents the weight assigned to criterion j, and \(\:{r}_{ij}\:\)denotes the normalized value.

In the next step, the computation of the Positive Ideal Solution (PIS) and Negative Ideal Solution (NIS) was computed by using Eqs. 7 and 8. The PIS and NIS allow for the identification of optimal and suboptimal performance benchmarks. In this step, Euclidean distances are computed from each alternative to both the PIS and NIS, effectively measuring their closeness from optimal solution.

$$\:{S}_{i}^{+}=\:\sqrt{\sum\:_{j=1}^{n}{\left({v}_{ij}-{a}_{j}^{+}\right)}^{2}}$$
(7)

In the equation above, \(\:{S}_{i}^{+}\)represents the Euclidean distance from alternative i to the PIS, and \(\:{a}_{j}^{+}\)signifies the maximum value of criterion j across all alternatives.

$$\:{S}_{i}^{-}=\:\sqrt{\sum\:_{j=1}^{n}{\left({v}_{ij}-{a}_{j}^{-}\right)}^{2}}$$
(8)

Similarly, \(\:{S}_{i}^{-}\)represents the Euclidean distance from alternative i to the NIS, and \(\:{a}_{j}^{-}\)signifies the minimum value of criterion j across all alternatives.

Finally, the closeness coefficient (\(\:{C}_{i}\)) is computed to determine the relative performance of each concrete mix design using Eq. 9. This coefficient reflects the proximity of an alternative to the ideal solution, with a higher \(\:{C}_{i}\) values indicating superior performance.

$$\:{C}_{i}=\:\frac{{S}_{i}^{-}}{{{S}_{i}^{+}+S}_{i}^{-}}$$
(9)

Moreover, utilizing the closeness coefficient (\(\:{C}_{i})\:\)values, each criterion is ranked, ultimately leading to the identification of the optimal mix.

EDAS

EDAS offers a comprehensive means of assessing multiple criteria simultaneously, aligning with the complex considerations involved in sustainable construction materials. Through a systematic process, EDAS ensures the normalization of the decision matrix, thus enabling fair and equitable comparisons across diverse performance metrics. Criteria such as compressive strength, flexural strength, and water absorption are judiciously weighted to indicate their relative importance in the evaluation process.

In the initial step, the average solution is calculated based on the decision matrix using Eq. (10) provided below.

$$\:Avg=\:\frac{1}{n}\:\sum\:_{j=1}^{n}{x}_{j}$$
(10)

Where, \(\:{x}_{j}\) signifies the performance value of each alternative on criteria (j).

Moreover, the computation of positive (PDA) and negative (NDA) distance from the average matrices varies depending on the nature of the criteria. When maximizing criteria are applied, PDA and NDA are computed using Eq. (11) correspondingly. Conversely, for minimization criteria, Eq. (12) is utilized.

$$\:PDA=\:\frac{{x}_{j}-Avg}{\text{max}\left(x\right)-Avg}$$
(11)
$$\:NDA=\:\frac{{Avg-\:x}_{j}}{\text{Avg}-\text{\:min}\left(x\right)}$$
(12)

In the next step, the determination of weighted sum of PDA and NDA for all alternatives, utilizing Eqs. 13 and 14 are performed.

$$\:Sp=\:\sum\:_{j=1}^{n}{w}_{j}\:\times\:\:PDA$$
(13)
$$\:Sn=\:\sum\:_{j=1}^{n}{w}_{j}\:\times\:\:NDA$$
(14)

In the next step, the normalization of the values of Sp and Sn for various mixes is calculated as shown in Eqs. 15 and 16.

$$\:{NSp}_{i}=\:\frac{{Sp}_{i}}{\sum\:_{i=1}^{n}{Sp}_{i}}$$
(15)
$$\:{NSn}_{i}=\:\frac{{Sn}_{i}}{\sum\:_{i=1}^{n}{Sn}_{i}}$$
(16)

In the last step, the calculation of appraisal score (AS) was computed using Eq. 17. Then, based on the appraisal score (AS), the ranking was performed to determine the best outcome.

$$\:{AS}_{i}=\:\frac{{NSn}_{i}}{{NSp}_{i}+\:{NSn}_{i}}$$
(17)

WSM

WSM provides a comprehensive means of assessing multiple criteria simultaneously, aligning with the multifaceted considerations inherent in sustainable construction materials. Through a structured process, WSM assigns weights to each criterion, indicating their relative significance in the methodology. The overall score based on the developed mixes is computed using Eq. 18.

$$\:{Swsm}_{i}=\:\sum\:_{j=1}^{m}{w}_{j}\:\times\:\:{x}_{ij}$$
(18)

In the equation above, \(\:{S}_{wsmi}\:\)represents the score of alternatives (i), with \(\:{w}_{j}\) denoting the weight assigned to criteria (j) and \(\:{x}_{ij}\:\)representing the performance value of alternatives (i) on criteria (j). Following the aggregation of scores, WSM enables the ranking of alternatives based on their overall performance scores. Alternatives with higher scores are deemed to exhibit superior performance across the evaluated criteria.

WPM

WPM provides a comprehensive means of assessing multiple criteria simultaneously, aligning with the multifaceted considerations inherent in sustainable construction materials. Similar to WSM, this method also assigns weights to each criteria. The assessment of the overall score for the developed mixes is computed using Eq. 19.

$$\:{Swpm}_{i}=\:{\prod\:}_{j=1}^{m}{x}_{ij}^{{w}_{j}}$$
(19)

In the equation above, \(\:{S}_{wpmi}\:\)represents the overall score of alternative i, with xij denoting the performance value of alternative i on criterion j and wj representing the weight assigned to criterion j. Following the calculation of the product scores, WPM facilitates the ranking of choices based on their cumulative performance scores. The highest rank alternative is considered to exhibit superior performance across the assessed criteria.

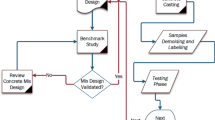
The flowchart (Fig. 2) illustrates the entire research process, providing a clear and systematic visualization of the steps involved. It effectively outlines the raw materials, product development, testing phases, as well as the application of MCDM and MRA analysis, offering a comprehensive understanding of the research approach.

Fig. 2
figure 2

Adopted methodology flowchart.

Full size image

Results and discussions

Experimental findings

The experimental results for the effect of DPF as a natural fiber and silica fume as a partial substitute to cement in DPF reinforced concrete have been presented in our previous studies in Ibrahim et al.21 and Adamu et al.28, and the results summary are presented in Table 5. Both slump, fresh density and unit weight decreased with the addition of both DPF and silica fume. The reduction in slump due to DPF addition is due to its high moisture absorption and wettability, hence reducing some proportion of mixing water. While silica fume due to its larger surface area compared to cement it replaced also absorbs part of the mixing water and reduces the workability of the fresh concrete. The reduction in fresh density and unit weight triggered by the DPF is due to its hydrophilic nature. This causes an escalation in entrapped air during mixing, and pores in the hardened cement matrix, thus causing a decline in the density of the concrete21,28. The reduction in density due to silica fume addition is ascribed to the lower specific gravity of the lower density of the silica fume in comparison to the cement it partly substituted21,28. The compressive strength and water absorption were negatively affected by the increased addition of DPF to the concrete due to the poor adhesion between the fiber and cement matrix, and increased porosity in the cement matrix due to the air entrapment effect of the DPF21,58. The flexural and tensile strengths increased by up to 3% DPF as shown in Table 5, in mixes M1, M2 and M3. The increment in the tensile strengths can be ascribed to the fibrous nature of the DPF, giving it bridging properties, slowing the crack propagation before and after loading, enhancing post-cracking strength, and hence higher tensile strengths21. The addition of silica fume improved the strengths and reduced water absorption of the DPF reinforced concrete. This is due to the high pozzolanic reaction of the silica fume resulting from its finer sizes and high SiO2 content. The SiO2 reacts through pozzolanic reaction with the Ca(OH)2 from cement hydration to form excess hydration products for strength development and densification of the concrete microstructure.

Table 5 Experimental results for DPF reinforced concrete at normal temperature.
Full size table

The experimental results for the DPF reinforced concrete integrated with different dosages of DPF and silica fume under elevated temperatures of 200 °C, 400 °C, 600 °C and 800 °C were presented in our previous research and published in Adamu et al.16 and it is presented in Table 6. The weight loss escalated with an increase in temperature, and DPF content. For the mixes without any silica fume, the weight loss of the control was 0.59%, 0.94%, 3.52% and 4.47% at 200 °C, 400 °C, 600 °C and 800 °C respectively. With the addition of DPF to control, weight loss increases. When the concrete was subjected to a temperature of 200 °C, the weight loss of the mixes containing 1% DPF (M1), 2% DPF (M2) and 3% DPF (M3) were increased by 6.78%, 27.12% and 62.17% respectively in comparison to the control mix. Similarly at 400 °C, the weight loss of mixes M1, M2, and M3 were greater than that of the control by 21.28%, 51.06% and 88.30% respectively in comparison to the control mix. At 800 °C, the weight loss with the addition of DPF was very severe, where the values for mixes M1, M2 and M3 were higher by 54.58%, 76.06% and 112.75% respectively in relation to the control mix. This escalation in weight loss is due to the degradation of both the concrete microstructure and the DPF due to the heat effect. As the DPF is a natural fiber containing high content of cellulose, hemicellulose and lignin24, when subjected to a very high temperature, it can easily degrade and leaves voids in the concrete matrix, thereby promoting weight loss16. At exposure temperature up to 400 °C, up to 10% cement replacement with silica fume resulted in a decline in the weight loss of the concrete containing 1% and 2% DPF. For the mix containing 5% silica fume with 1% DPF, i.e. M4, its weight loss was lower than that of the control mix by 13.56% and 9.57% at 200 °C and 400 °C respectively. For mix M5 (5% silica fume and 2% DPF), its weight loss was lower than that of the control by 6.78% and 3.19% at 200 °C and 400 °C respectively. For the mixes, containing 10% silica fume, mix M7 (10% silica fume and 1% DPF), weight loss was lower than the corresponding control mix by 45.76% and 10.64% at 200 °C and 400 °C respectively. Mix M8 (10% silica fume with 1% DPF), its weight loss was lower by 27.12% and 13.83% at 200 °C and 400 °C respectively in comparison to the control mix. The weight loss of M9 containing 10% silica fume and 3% DPF was lower than that of the control mix by 1.69% at 200 °C. For the mixes containing 15% silica fume, only mix M10 containing 15% silica fume and 1% DPF has lower weight loss compared to the control mix by 18.64% and 20.21% at 200 °C and 400 °C respectively. However, at temperature above 400 °C, the partial replacement of cement with silica fume does not reduce the weight loss of the mixes containing any dosage of DPF. The reduction of weight loss with the partial replacement of cement with silica fume was ascribed to the superior thermal resistance of silica fumes compared to cement. Also, as the silica fume densified the concrete’s microstructure, it slowed down the moisture evaporation and deterioration of the cement matrix during heating, hence lowering the weight loss16. The residual strengths of the concrete increased when heated to a temperature of 200 °C and 400 °C regardless of the added DPF or silica fume content. As an illustration, for the control mix, its residual compressive strengths were higher by 3.07% and 15.92% at 200 °C and 400 °C respectively compared to its strength at normal temperatures. Similar trends can be seen on the mixes containing only DPF. Mix M1 has higher strengths at 200 °C and 400 °C by 4.92% and 13.27%, while M2 has higher strengths at 200 °C and 400 °C by 13.18% and 15.78%, respectively compared to their respective strengths at normal temperatures. This improvement was also noticed on the mixes containing 5%, 10% and 15% silica fume. Compared to their compressive strengths at normal temperature, the compressive strengths of M4 were higher by 6.53% and 16.9% at 200 °C and 400 °C respectively, and the strength for M5 was higher by 10.32% and 16.9% at 200 °C and 400 °C respectively. Similar improvements can be seen in other mixes containing 10% and 15% silica fume like M7, M8, M9, M10, M11 and M12. This increment is related to the acceleration of the hydration reaction during heating, thereby escalating the hydrothermal reactions in the concrete, where surplus tobermorite is formed from the reactions between the hydration and pozzolanic compounds. Furthermore, the evaporation of moisture when subjected to high temperature causes the Van der Waals forces between the particles to rise, thereby improving the strength of the concrete16,59,60. The residual strength of the concrete decreased with increment in addition of DPF to the concrete when heated at any temperature between 200 and 800 °C. This reduction was ascribed to the increase in pore volume caused by the DPF in the cement matrix and the degradation of the DPF under heating, creating weak and porous paths for premature failure to occur16,61. Silica fume addition to the DPF reinforced concrete caused an increment in the residual strength when heated to a temperature up to 400 °C, and this was due to the escalation of hydrothermal pozzolanic reaction between the SiO2 from silica fume with the cement hydration products to produce more gels with stronger Van der Waals forces, thereby boosting the residual strength16,59,60.

Table 6 Experimental results for DPF reinforced concrete at elevated temperature.
Full size table

Multivariable regression analysis

In accordance with statistical analysis, based on the null hypothesis, no direct relationship exists between the input variables (DPF and Silica fume) and the mechanical properties of the DPF reinforced concrete at both normal and elevated temperatures. To justify the falsity of the null hypothesis and derive the relationship between input parameters (DPF and silica fume) and the output/independent parameters (properties of the DPF reinforced concrete), nonlinear multivariable regression analysis (NLMRA) was selected.

The relationship between the input parameters and the properties of the concrete as output parameters can be derived in the form of a single linear regression (SLR). When the input parameter is only one, a linear relationship is the best for the relationship. The relationship can also be in the form of single nonlinear regression (SNLR), when there is curvature and the linear relationship is not suitable, then nonlinear polynomial, power, logarithmic or other forms are the most suitable. When the number of input variables is two or more, then the multivariable regression analysis (MRA) is used. The MRA can be linear MR (LMRA) or nonlinear MRA (NLMRA). The NLMRA is used to develop a nonlinear mathematical relationship between two or more input parameters with a single dependent variable. This method of analysis is mostly used to develop relationships between different input parameters with the compressive strength of concrete in the field of civil engineering due to the nonlinear (curvature) nature of the strength results62,63.

The general form for all the single regression analysis types is displayed in Eqs. 20 and 21 Below.

$$\:SLR\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:Y=c+MX\pm\:\in\:$$
(20)
$$\:SNLR\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:Y={c+{M}_{1}X}^{2}+{M}_{2}X\pm\:\in\:$$
(21)

Where Y represents the denotes the response/dependent variable, c denotes the Y intercept for which X=0, M, M1 and M2 are the slopes/coefficients of the variables, X is the independent variable, and ∈ is the error in the models5,46,64.

The general form for all the multivariable regression analysis types is displayed in Eq. 22 and Eq. 23.

$$\:Y=c+{M}_{1}{X}_{1}+{M}_{2}{X}_{2}+\dots\:+{M}_{n}{X}_{n}\pm\:\in\:$$
(22)
$$\:Y=c+\sum\:_{i=1}^{k}{M}_{i}{X}_{i}+\sum\:_{i=1}^{k}{M}_{ii}{X}_{i}^{2}+\sum\:_{i<}\sum\:_{j}{M}_{ij}{X}_{i}{X}_{j}\pm\:\in\:$$
(23)

In Eq. 3 and Eq. 4, Y denotes the independent variable, c represents the Y-intercept, and ∈ is the error in the models. While in Eq. 3, M1, M2, Mn are the slopes/coefficients of X1, X2 and Xn respectively. and X1, X2 and Xn are the independent variables. In Eq. 4, i and j denotes the linear and quadratic coefficients respectively. Xi and Xj are the independent variables, Mi, Mii and Mij are the coefficients of regressions5,42,46,65.

In this study, the NLMRA technique was used to derive the statistical relationship between DPF and Silica fume as the input parameters and the properties of the DPF reinforced concrete under normal and elevated temperatures, as the dependent variables. The properties of the DPF reinforced concrete considered under normal temperature include fresh density, unit weight, compressive strength, split tensile strength, flexural strength, and water absorption. The properties of the concrete under elevated temperatures considered were weight loss at 200 °C and 800 °C and residual compressive strengths at 200 °C and 800 °C. The developed models are presented as Eq. 24 to Eq. 33.

$$\:{M}_{F}=2488.807-55.9994\times\:D-23.9225\times\:S+3.0573\times\:D\times\:S+2.38766\times\:{D}^{2}+0.3653\times\:{S}^{2}$$
(24)
$$\:{M}_{D}=2402.593-83.7323\times\:D-16.2247\times\:S+0.46306\times\:D\times\:S+14.5248\times\:{D}^{2}+0.38436\times\:{S}^{2}$$
(25)
$$\:{F}_{CK}=43.0914-0.33183\times\:D+3.26915\times\:S-0.01238\times\:D\times\:S-1.2255\times\:{D}^{2}-0.2445\times\:{S}^{2}$$
(26)
$$\:{F}_{ST}=3.07514+0.23757\times\:D+0.174225\times\:S-0.00453\times\:D\times\:S-0.02592\times\:{D}^{2}-0.01357\times\:{S}^{2}$$
(27)
$$\:{F}_{F}=5.49068+0.41336\times\:D+0.25506\times\:S-0.004641\times\:D\times\:S-0.01835\times\:{D}^{2}-0.021336\times\:{S}^{2}$$
(28)
$$\:WA=3.28959+0.32427\times\:D-0.286333\times\:S+0.000713\times\:D\times\:S+0.007201\times\:{D}^{2}+0.0194\times\:{S}^{2}$$
(29)
$$\:{w}_{200}=0.58687+0.06931\times\:D-0.07104\times\:S-0.00015\times\:D\times\:S+0.01458\times\:{D}^{2}+0.00403\times\:{S}^{2}$$
(30)
$$\:{w}_{800}=4.80994+1.80668\times\:D+0.22034\times\:S-0.04719\times\:D\times\:S-0.083735\times\:{D}^{2}-0.001314\times\:{S}^{2}$$
(31)
$$\:{F}_{R,200}=44.51602-0.58401\times\:D+3.99371\times\:S-0.087195\times\:D\times\:S-1.01794\times\:{D}^{2}-0.25181\times\:{S}^{2}$$
(32)
$$\:{F}_{R,800}=23.0719-5.60933\times\:D-0.23323\times\:S+0.22939\times\:D\times\:S+0.452242\times\:{D}^{2}-0.040084\times\:{S}^{2}$$
(33)

where MF stands for fresh density in kg/m3, MD denotes the hardened density/unit weight in kg/m3. FCK, FST and FF stand for the compressive, split tensile and flexural strengths respectively, in MPa, WA represents the water absorption in %. w200 and w800 represents the weight loss at 200 °C and 800 °C respectively in %. FR,200 and FR,800 represent the residual strengths at 200 °C and 800 °C respectively, in %. D and S represents DPF and silica fume respectively, in %.

The developed models were analyzed, assessed, and validated using the ANOVA summary summarized in Table 7. The null hypothesis set must be false for any model to be acceptable and used. This can be done by checking the statistical significance of the model. If the model has a Probability (P-value) less than 0.05, then the model is said to be significant5,66. From the ANOVA summary in Table 6, the P-values for all the models at both normal and elevated temperatures are very significant, as their P-values were extremely low. Therefore, the null hypothesis that states that no relationship exists between the variables (DPA and ESP) and the models (responses) at both normal and elevated temperatures is found to be false. In addition, the coefficient of determinations (R2) was used to assess the accuracy and correlation of the models with the experimental data. R2 values for any model range between 0 and 1, with 0 zero no correlation between the model and the experimental data, and 1 signifying a perfect correlation between the models and the data67,68. From Table 7, all the models have reasonably high R2 values, which were all greater than 0.70. The model for weight loss at 800 °C has the best correlation amongst all the models with R2 value of 0.902, which is very close to 1. Hence the model is said to have a very high correlation and predictability, with only 9.8% of the total data not perfectly fitted into the model. The model for water absorption has the lowest degree of correlation, with R2 value of 0.708. Therefore, the model for water absorption can be said to have a reasonably high degree of correlation and predictability, with only about 29.2% of the total data not perfectly fitted into the model. Hence, the developed model equations in Eq. 3 to Eq. 8 can be used to predict the properties of the DPF reinforced concrete modified with silica fume at normal and elevated temperature conditions.

Table 7 ANOVA summary for multivariable regression models.
Full size table

To check the predictability, preciseness, and accuracy of each model, their predicted versus actual values were plotted graphically. Each of the predicted responses were estimated using their respective equations developed, whereas the actual values were the experimental data utilized to develop the models. For a good and accurate model, there should be a high correlation between its predicted and actual value. The predicted against actual charts for the established models at normal temperature are presented in Fig. 3, while for the models at elevated temperature are depicted in Fig. 4. All the models have good to high correlations between their respective predicted and actual plots, as the data points were reasonably aligned across the straight trendline. The model for weight loss at 800 °C has the best fitness and correlation in terms of its predicted versus actual plots as shown in Fig. 4d. This justifies its highest R2 value obtained from the ANOVA summary. On the other hand, the model for water absorption has the most dispersed and least correlated data points on its predicted versus actual plots as shown in Fig. 3f. This gives further clarification and justification of its lowest R2 value amongst the established models.

Fig. 3
figure 3

Predicted against actual plots at normal temperature.

Full size image
Fig. 4
figure 4

Predicted versus actual plots at elevated temperature.

Full size image
Fig. 5
figure 5

Normal probability plots at elevated temperature.

Full size image

The normal probability plots for all the models were drawn and presented in Figs. 5 and 6 for normal temperature and elevated temperature exposures respectively. Since the experimental data were random, there is a need to check whether they are normally distributed or not. Checking for the normality of the models is very important, as non-linear regression was built on the assumption that the residuals follow a normal distribution function. This assumption explains the established aim of the regression, which is minimizing the sum of the squats of the Y-value or vertical distances between the data points and the regression curve69. For a model/data to be normally distributed, the data points plotted on the distribution plots should theoretically form approximately a linear pattern. From the normal probability distribution plots in Figs. 5 and 6, the data points were aligned approximately across the straight reference line drawn. Hence, the properties of the DPF reinforced concrete at normal and elevated temperatures all follow the normal probability distribution.

Fig. 6
figure 6

Normal probability plots at elevated temperature.

Full size image

Multicriteria optimization

Based on the data collected from experiments, various MCDM methodologies were adopted to determine the optimal mix based on their performance in each criterion. These methods enable decision-makers to evaluate multiple alternatives while considering various criteria, thus aiding in informed decision-making. The analysis begins with assigning the weights using an entropy method. Computing entropy weights, as outlined in Eqs. (1–3) in the methodology section, is a crucial step in the MCDM technique. Table 8 displays the raw data used for analysis, while Table 9 presents the normalized decision matrix to facilitate weight determination. Lastly, Table 10 showcases entropy weights, which are essential for ranking alternatives across different MCDM techniques.

Table 8 Raw decision matrix.
Full size table
Table 9 Normalized decision matrix.
Full size table
Table 10 Entropy weight of each parameter.
Full size table

TOPSIS and EDAS ranking

The TOPSIS method utilizes Relative Closeness Coefficient (RCC) values to differentiate between the best and worst alternatives (mixes), with the highest RCC indicating the optimal choice. Table 11 presents detailed calculations of parameters used in both the TOPSIS and EDAS techniques to rank mixes based on their performance metrics. In TOPSIS, (Si+), (Si−), and (Ci) values are employed for mix assessment and ranking. As shown in Table 11, Mix No. M7 ranks 1st based on its (Ci) value computation, indicating superior performance across various metrics. Similarly, the EDAS technique identifies M7 as an ideal mix with high Appraisal Scores (ASi). Despite minor ranking discrepancies between TOPSIS and EDAS for some mixes, both methods concur on M7’s outstanding performance. Additionally, M4 emerges as the second-ranked ideal mix in both techniques. These rankings underscore M7’s balanced performance across physical, mechanical, thermal, and fresh performance criteria, conforming to its position as the optimal mix according to both TOPSIS and EDAS evaluations.

Table 11 Ranking of mixes based on TOPSIS and EDAS technique.
Full size table

WSM and WPM ranks

Table 12 displays the computed values of Swsm and the ranking of mixes using the WSM method, alongside Swpm and rankings using the WPM method. Both methods utilize normalized weights to calculate Swsm and Swpm, facilitating a fair comparison across criteria. Notably, both methods yield similar rankings for Date Palm Fiber Reinforced Concrete (DPFRC) mixes. M7 emerges as the top-performing mix in both WSM and WPM, mirroring the outcomes seen in TOPSIS and EDAS techniques. This consistency underscores M7’s superior performance across various evaluation methodologies, highlighting its efficacy as the optimal mix to be adopted for developing Date Palm Fiber Reinforced Concrete (DPFRC).

Table 12 Ranking of mixes based on WSM and WPM technique.
Full size table

Comparative ranking

The provided Fig. 7 showcases the rankings of various mix designs for Fiber reinforced concrete (FRC) using four different multi-criteria decision-making (MCDM) methods: Weighted Sum Model (WSM), Weighted Product Model (WPM), Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), and Evaluation Based on Distance from Average Solution (EDAS). Each mix design (M1 through M12) is evaluated across these methods, and their respective rankings are illustrated.

Fig. 7
figure 7

Comparative ranking.

Full size image

Starting with mix design M1, it is consistently ranked 5th across all four methods, indicating a strong consensus on its performance. Mix design M2, however, shows slight variability, being ranked 7th by both WSM and WPM, and 8th by TOPSIS and EDAS. Similarly, mix design M3 is ranked 10th by WSM, WPM, and EDAS, but 12th by TOPSIS, showcasing some disagreement among the methods.

Mix design M4 is uniformly ranked 2nd by all methods, reflecting high agreement on its superior performance. A similar pattern is observed with mix design M5, which is ranked 4th across the board. Mix design M6 experiences some variation, being ranked 8th by WSM, WPM, and EDAS, and 9th by TOPSIS. Notably, mix design M7 achieves unanimous top ranking (1st) from all methods, indicating it is the best-performing mix design among the evaluated options.

For mix design M8, there is complete agreement with a 3rd place ranking from all methods. Mix design M9 shows slight discrepancies, being ranked 6th by WSM, WPM, and EDAS, and 7th by TOPSIS. Mix design M10 presents more variability, ranked 9th by WSM, WPM, and EDAS, and 6th by TOPSIS. Mix design M11 is consistently ranked near the lower end, with WSM placing it at 11th, WPM at 10th, and both TOPSIS and EDAS at 11th.

Lastly, mix design M12 is generally considered the least favourable, ranked 12th by WSM, WPM, and EDAS, and 11th by TOPSIS. This analysis highlights a strong consensus for certain mix designs, particularly those ranked at the extremes (like M7 and M12), while intermediate rankings show some variability, reflecting the inherent differences in the evaluation criteria of each MCDM method.

Sensitivity analysis

The sensitivity analysis conducted using the TOPSIS, EDAS, WSM, and WPM methods offers critical insights into the performance evaluation of concrete mixes incorporating Eggshell Powder (ESP) and Date Palm Ash (DPA). Table 13 outlines the weight scenarios assigned to each criterion, with each scenario representing different priority settings to simulate realistic decision-making conditions faced by stakeholders. Figure 8 provides a detailed visualization of the sensitivity analysis for Fiber Reinforced Concrete (FRC) mix designs (M1 to M12) across the four MCDM methods. The radar charts demonstrate the performance rankings of each mix under varying evaluation criteria, highlighting their relative sensitivity to changes in priority weights. This analysis underscores the robustness and reliability of the selected methods in identifying optimal mix designs under diverse decision-making scenarios.

Table 13 Assigned weights for sensitivity analysis.
Full size table
Fig. 8
figure 8

Sensitivity analysis.

Full size image

For mix design M1, the radar chart shows a relatively balanced performance across all methods, indicating stability and robustness in its evaluation. The rankings are consistent, reflecting its moderate standing among the mix designs. In contrast, mix design M2 reveals some divergence among the methods, with WSM and WPM showing similar trends while TOPSIS and EDAS differ slightly, indicating that M2’s ranking is sensitive to the criteria emphasized by each method.

Mix design M3 displays significant variability, especially in the TOPSIS method, which ranks it lower compared to WSM, WPM, and EDAS, suggesting that M3’s evaluation is highly influenced by the specific method used, particularly the criteria of TOPSIS. Conversely, mix design M4 shows consistent high rankings across all methods, confirming its strong performance and stability, making it a reliable choice.

M5’s radar chart indicates consistency, with all methods closely aligning in their evaluation, suggesting M5 is a solid performer with little sensitivity to the choice of evaluation method. For M6, the radar chart shows some variability, particularly in the TOPSIS method, which ranks it slightly lower than the others, indicating that M6’s ranking is moderately sensitive to the evaluation criteria.

Mix design M7 stands out with all methods ranking it at the top, highlighting its dominance and underscoring its exceptional performance and robustness. Similarly, M8 exhibits consistency with all methods closely aligned, suggesting that M8 is a reliable performer with stable rankings across different methods.

In the case of M9, the chart shows some variation, particularly with TOPSIS ranking it lower compared to WSM, WPM, and EDAS, indicating a moderate sensitivity in M9’s evaluation depending on the method used. M10 reveals significant differences, especially with TOPSIS ranking it higher while WSM, WPM, and EDAS show lower rankings, suggesting that M10’s ranking is highly method-dependent and particularly sensitive to TOPSIS criteria.

M11’s radar chart displays consistent low rankings across all methods, reflecting agreement on its relatively poor performance, with uniformity suggesting little sensitivity to the evaluation method. Similarly, M12 shows consistent low rankings, indicating a robust consensus on its inferior performance.

The sensitivity analysis using radar charts provides a comprehensive view of how different mix designs for FRC are ranked across four MCDM methods. While some mix designs, such as M4, M5, M7, and M8, show consistent performance and low sensitivity to the evaluation method, others, like M2, M3, M6, M9, and M10, exhibit variability and are more sensitive to the criteria of specific methods. Overall, M7 stands out as the top performer across all methods, while M11 and M12 are consistently ranked lowest. This detailed sensitivity analysis helps us in understanding the robustness and stability of the rankings, helping to identify the most reliable mix designs for FRC.

Conclusions

The following conclusions were formulated based on the experimental work, multivariable regression analysis and MCDM analysis conducted.

  1. (1)

    Based on the experimental results, the addition of DPF as a natural fiber in the concrete led to reductions in density and compressive strength. The tensile strengths of the concrete were improved with the addition of DPF as natural fiber up to 2% dosage.

  2. (2)

    Incorporating silica fume as SCM helped in mitigating the loss in strengths and also boosts the mechanical strengths of the DPF.

  3. (3)

    Non-linear regression analysis was carried out to develop models for predicting the mechanical properties of the DPF reinforced concrete at normal and elevated temperature conditions. The models developed were found to have excellent significance, with a reasonably high degree of correlation and predictability.

  4. (4)

    Mix design M7 containing 1% DPF and 10% silica fume consistently achieves the highest ranking across all evaluation methods, establishing it as the top-performing option among those analyzed. Despite containing 1% of DPF and 10% of silica fume, M7 demonstrates superior thermo-mechanical performance compared to other mixes. However, its slump value is relatively lower than that of mixes without fibers, this might affect its workability and ease of placement. More superplasticizers can be used for M7 to improve its workability. Additionally, M7 exhibits superior thermal performance under various exposure conditions compared to the other mixes evaluated.

  5. (5)

    The developed models can be useful in eliminating the need for experiments to determine the properties of the DPF reinforced concrete in normal and high temperature conditions, which will lead to savings in cost and time, and promoting environmental sustainability.