Introduction

In the era when the Internet was not yet popularized, intellectual property transactions primarily relied on traditional carriers such as books, magazines, films, patents, and trademarks. They were conducted through third-party institutions with high transaction costs and prone to disputes. The rise of the Internet has brought new opportunities for intellectual property transactions, and networked transactions have broadened the transaction channels and lowered the transaction threshold. However, at the same time, the infringement of intellectual property rights in the network environment has become increasingly rampant, and its low-cost and highly covert characteristics have posed a challenge to the traditional intellectual property protection mechanism. Blockchain technology provides a new solution for intellectual property protection1 with its data non-tampering and decentralized characteristics. It can ensure the authenticity of transaction data, effectively prevent fraud, and realize the traceability of transactions and the clear division of responsibility. The alliance chain stands out among the many branches of blockchain with its efficient transaction performance and superior privacy protection2 capabilities. By limiting the participating nodes, the alliance chain safeguards the transaction efficiency while considering the participants’ privacy rights and interests. Applying alliance chain technology to intellectual property transactions is expected to fundamentally improve the security and transparency of transactions, reduce transaction costs, shorten the transaction cycle, and simplify the rights protection process.

Identity authentication is a critical link in intellectual property transactions, ensuring that the property rights and property rights owners are authentic and reliable. However, identity authentication has problems and challenges that need to be solved, such as identity authentication centrality, low security of single-factor authentication, incomplete protection of identity privacy, and low efficiency of identity authentication3,4. In the current research on identity authentication, Li Xiangyang et al.5 realized a blockchain-based intellectual property transaction platform in which the identity authentication link ensures identity security and data tampering in intellectual property transactions through digital certificates and digital signatures, etc. Still, it needs to rely on a trusted third party, and when the third party is attacked, it will impact the identity authentication system. Zhuang et al.6 introduced a blockchain-powered platform for intellectual property transactions, incorporating an enhanced Shamir secret-sharing method to ensure privacy protection and traceability of identities. Wu Fei et al.7 proposed an identity authentication scheme based on face recognition, which gives a new idea of identity authentication using biometric features. Niu Xiaolin et al.8 proposed a music copyright protection and transaction system based on an alliance chain, applying music fingerprints to copyright authentication. Si Haiping et al.9 relied on a trusted third party by distributing digital certificates applied to the identity authentication of agricultural intellectual property. Xi Xin et al.10 used the ECDH algorithm for information encryption in the digital authentication process. Still, the ECDH algorithm has the problem of impersonation of identity by intermediaries, and there is no identity authentication to guarantee the authenticity of the identity. Yuan et al.11 proposed a privacy-preserving intellectual property identity authentication method based on blockchain, which uses zero-knowledge proof for privacy protection. Zhang Guangzong et al.12 proposed an improved zero-knowledge algorithm for privacy protection, which reduces the computation of generating proof. However, there is still the problem of authenticity and reliability of identity. Y. Cheng et al.13 proposed an efficient anonymization authentication and privacy-preserving reliability assessment scheme, which protects the privacy of vehicle identities through anonymization techniques while assessing the reliability of crowdsourced data. However, it lacks integration with emerging technologies and fails to incorporate blockchain for better performance. X. Feng et al.14 proposed the PBAG protocol, which utilizes blockchain and global update commitments to achieve privacy-preserving authentication, improve authentication efficiency and solve the certificate revocation problem. However, as the number of vehicles increases, the updating and management of global commitments may become complicated. H. Sun et al.15 proposed a MTDCAP protocol to secure CAN bus authentication against potential attacks using mobile target defense. However, the increase in mobile target defense and authentication process may lead to an increase in communication delay and authentication time, which affects the real-time performance of the system.

To summarize, scholars have done a lot of work on improving the security of identity authentication, but there are still problems, such as low security of one-factor authentication, low efficiency of identity authentication, etc. There is little research on using a two-factor identity authentication mechanism in the identity authentication of intellectual property transactions. Not enough attention is paid to the privacy protection problem in the identity authentication process. In view of the issues and challenges of identity authenticity, security, privacy protection, and authentication efficiency in the identity authentication of intellectual property transactions, this paper designs a two-factor identity authentication model for intellectual property transactions based on improved zero-knowledge proof, aiming to construct a comprehensive identity authentication framework that integrates the characteristics of alliance blockchain and intellectual property transactions, which is composed of three core entities: the regulator, the demand side and the supply side. The work of this article is as follows:

  1. 1.

    An authentication method combining improved zero-knowledge proof with fingerprint biometrics and property right feature identification technology is designed to complete authentication without revealing the identity mark and protect privacy.

  2. 2.

    Designed a two-factor authentication mechanism combining ID password with fingerprint and property right feature identification to improve the security and reliability of authentication.

  3. 3.

    The zero-knowledge proof is improved to reduce the proof computation and size and improve the efficiency of proof generation and verification.

  4. 4.

    This design uses alliance chain technology to construct a decentralized identity authentication model and combines smart contracts to execute the corresponding authentication process automatically.

The biggest innovation of this paper is to design a two-factor authentication model based on an alliance chain for intellectual property transactions. A two-factor authentication mechanism combining ID passwords with physiological and property rights characteristics is proposed. The integration of alliance chain technology and smart contracts constructs a decentralized and automated authentication process that improves the security and efficiency of intellectual property transactions. Combining improved zero-knowledge proof with fingerprint biometrics and property rights characterization, this approach ensures authentication without revealing sensitive information, thereby protecting privacy. In addition, improved zero-knowledge proofs reduce computational complexity and proof size, thereby increasing the efficiency of proof generation and verification.

Next, a two-factor authentication model for intellectual property transactions based on improved zero-knowledge proof will be presented, model analysis and experiments will be conducted, and conclusions will be drawn.

Two-factor authentication model for intellectual property transactions based on improved zero-knowledge proof

Overall framework model

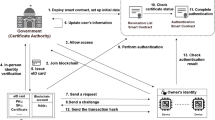
The overall framework model design is shown in Fig. 1. The model contains five entities: supply side, demand side, regulator, chain of alliance, and database, which play the following roles in this model:

  1. (1)

    Supply-side: It refers to the entity that owns intellectual property rights, including patents, trademarks, or copyrights, or an entity that has the right to authorize the disposal thereof and may put its intellectual property resources on the market for trading or licensing.

  2. (2)

    Demand-side: A person or organization needs to use or access intellectual property and wants to hide who they are and what they do.

  3. (3)

    Supervisors: Supervisors are responsible for supervising the process of intellectual property transactions to ensure their legality and compliance.

  4. (4)

    Alliance Chain: A platform for conducting intellectual property transactions, which ensures the proper conduct of transactions by incorporating intelligent contracts. It can be used to record transaction information and ensure the integrity and authenticity of data. It also combines cryptography and other technologies to protect identity privacy.

  5. (5)

    Database: Used to store user identity information, i.e., hashed fingerprint biometrics.

Fig. 1
figure 1

General framework model of two-factor authentication for intellectual property transactions based on improved zero-knowledge proof.

Full size image

Two-factor authentication primary process for intellectual property transactions

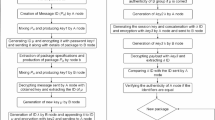
As shown in Fig. 2, the total two-factor authentication process is divided into four stages: the ID password identity registration stage, fingerprint and intellectual property identity registration stage, ID password identity authentication stage, and fingerprint and intellectual property identity authentication stage. The two-factor authentication stage is carried out through the two-factor authentication of ID password, fingerprint, and property rights recognition; firstly, according to the registered ID password to log in to the account belongs to the first factor of authentication, and then through the collection of fingerprint biometrics and intellectual property identity features to generate a zero-knowledge proof to the verifier for the second factor of authentication.

Fig. 2
figure 2

Two-factor authentication general flow.

Full size image

ID password identity registration phase

The transaction parties first register their identity information on the alliance chain, and this model proposes a two-factor identity registration mechanism with an ID password combining physiological and property rights characteristics. The identity registration stage first needs to carry out the design of ID password registration, enter the user ID and password, and determine whether it is empty; if it is empty, then registration failure, not empty, continue to determine whether the ID has been registered, if it has been registered, registration failure, if it is not registered, hash encrypted storage on the alliance chain, return “Success” indicates that Successful registration.

Fingerprinting and title identity registration phase

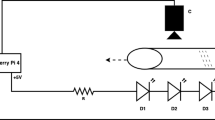
ID password identity registration after both parties go through the optical fingerprint identification module in accordance with the prompts to enter the fingerprint and extract the fingerprint features to generate a template to determine whether it is empty; if it is empty, then the registration fails, not empty, then the fingerprint biometrics encrypted with Poseidon hash function. Encrypting the fingerprint data first ensures that the fingerprint information is always processed and stored in an encrypted form, thus protecting the user’s privacy and improving data security. Then, determine whether the encrypted fingerprint has been enrolled; if it has been enrolled, the enrollment fails; if it has not been enrolled, the hash-encrypted fingerprint will be stored in the database and return “Success” to indicate successful enrollment. The supplier provides the intellectual property transaction certificate consisting of intellectual property introduction, encrypted intellectual property feature information, transaction money, and access time and publishes it on the alliance chain to complete the registration of intellectual property identity after the regulator’s audit.

ID password authentication phase

A transaction is initiated after the two-factor identity is registered and the two-factor identity authentication phase is entered. The demand side checks the intellectual property transaction certificate on the chain. If it wants to carry out a transaction, it initiates the transaction and then enters the identity authentication stage. In the authentication stage, it is necessary to design ID and password authentication first, input the user ID and password, and determine whether they are empty; if they are empty, the authentication fails; if they are not empty, then continue to query whether the ID has been registered on the alliance chain, if not, the authentication fails, if it has been registered, then verify whether the ID and password match and if it matches. It returns “Success. Successful matching will return “Success.”

Fingerprint and title identification phase

After successfully completing ID password authentication, the next step is to perform fingerprint and property rights authentication. In this phase, a zero-knowledge proof algorithm is used to handle biometric and intellectual property features for identification. This algorithm can generate and verify the required proof without revealing personal privacy information. Specifically, the system will ask for proof generated by the zero-knowledge proof algorithm, and if this proof passes the validation, the system will return “true,” indicating that the fingerprint and intellectual property identity verification was successful.

Improved zero-knowledge algorithm design for two-factor authentication in intellectual property transactions

The relevant notations are defined in Table 1.

Table 1 Notations definition.
Full size table

In the fingerprinting and title authentication phase, an improved Plonk zero-knowledge proof algorithm is designed to generate zero-knowledge proof and validate it through regulators and counterparties. Plonk (Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge) is a zero-knowledge proof algorithm for generalized trusted settings. The general trusted setup allows the same SRS to be used for all circuits of a certain bounded size, and it can be updated by new parties without compromising security. And the soundness of the system requires only the honesty of one of all updates before that point in time. This feature removes a major obstacle to deploying zk-SNARKs in the real world. Polynomial commitments are a crucial part of PlonK, allowing the prover to commit to a polynomial and later prove evaluations of that polynomial at specific points. Plonk algorithm uses a batched version of the KZG polynomial commitment scheme to efficiently commit to and evaluate polynomials. Furthermore, Plonk is a non-interactive zero-knowledge proof protocol, meaning that no multiple rounds of interaction between the prover and the verifier are required.

The design of the improved zero-knowledge algorithm for two-factor authentication of intellectual property transactions is divided into three phases: initialization, generation of zero-knowledge proof, and verification of zero-knowledge proof. Firstly, initialization is carried out to design the private input carrying the private identity information of both parties of the transaction, such as fingerprint biometrics and intellectual property characterization information, and the public input is the encrypted fingerprint biometrics and encrypted intellectual property characterization information of both parties of the transaction, and the final output is the circuit to judge whether the private input and the public input are equal or not so as to generate the public parameter. Second, Plonk zero-knowledge proof is generated based on the public parameters, and a constraint compression strategy based on Poseidon hashing is designed to reduce the workload. Finally, the regulator and the counterparty view the zero-knowledge proof and verify it.

  1. 1.

    Initialization: the circuit needs to be set up initially SRS (Structure Reference String). Since Plonk’s zero-knowledge proof algorithm is generalized and trustworthy, only one trustworthy communication setup is needed for the circuit. Then, the public parameter PP is generated based on the circuit’s design, which includes the initial setup and circuit parameters.

$$PP=\left\{ {X,w,srs,{q_L}\left( x \right),{q_R}\left( x \right),{q_M}\left( x \right),{q_O}\left( x \right),{q_C}\left( x \right),{S_{{\sigma _1}}}\left( x \right),{S_{{\sigma _2}}}\left( x \right),{S_{{\sigma _3}}}\left( x \right)} \right\}$$
  1. 2.

    Generating zero-knowledge proof: generating zero-knowledge proof based on the public parameter PP is divided into five steps as follows:

  1. (a)

    Compute polynomials a(x), b(x), c(x) over the multiplicative subgroup group H of order n, where a(x) is the private input of the private identity information of the two parties to the transaction, b(x) is the public input of the hashed encrypted identity information of the encrypted fingerprint biometrics in the database or of the intellectual property features in the intellectual property transaction certificates, and c(x) is the output for determining whether or not the outputs are equal if the output is 0 then it is equal, and if it is not 0, then it is not equal.

  1. (b)

    Perform permutation substitution constraint construction z(x).

  2. (c)

    The total constraint of Eq. (1) is constructed by transforming the gate constraint and the permutation substitution constraint into a polynomial t(x).

$$\begin{aligned} t\left( x \right) & =\left( {a\left( x \right)b\left( x \right){q_M}\left( x \right)+a\left( x \right){q_L}\left( x \right)+b\left( x \right){q_R}\left( x \right)+c\left( x \right){q_O}\left( x \right)+PI\left( x \right)+{q_C}\left( x \right)} \right)\frac{1}{{{Z_H}\left( x \right)}} \\ & \;\;+\left( {\left( {a\left( x \right)+\beta x+\gamma } \right)\left( {b\left( x \right)+\beta {k_1}x+\gamma } \right)\left( {c\left( x \right)+\beta {k_2}x+\gamma } \right)z\left( x \right)} \right)\frac{\alpha }{{{Z_H}\left( x \right)}} - (\left( {a\left( x \right)+\beta {S_{{\sigma _1}}}\left( x \right)+\gamma } \right) \\ & \;\;\;\left( {b\left( x \right)+\beta {S_{{\sigma _2}}}\left( x \right)+\gamma } \right)\left( {c\left( x \right)+\beta {S_{{\sigma _2}}}\left( x \right)+\gamma } \right)z\left( x \right))\frac{\alpha }{{{Z_H}\left( x \right)}}+\left( {z\left( x \right) - 1} \right){l_1}\left( x \right)\frac{{{\alpha ^2}}}{{{Z_H}\left( x \right)}} \\ \end{aligned}$$
(1)
  1. (d)

    The construction of the critical intermediate function r(x) is represented in Eq. (2). This function encapsulates the components that need to be kept secret during the proof process. Because the polynomial promises the highest height of n + 2, we need to perform the power reduction operation; here, the Poseidon hash function is used to improve and simplify the size of the proof.

$$\begin{aligned} r\left( x \right) & =Poseidon\left( {\left( {\bar {a}\bar {b}} \right.} \right. \cdot {q_M}\left( x \right)+\bar {a} \cdot {q_L}\left( x \right)+\bar {b} \cdot {q_R}\left( x \right)+\bar {c} \cdot {q_O}\left( x \right)+PI\left( \theta \right) \\ & \;\;\;+{q_C}\left( x \right))+\left( {\left( {\bar {a}+\beta \theta +\gamma } \right)\left( {\bar {b}+\beta {k_1}\theta +\gamma } \right)\left( {\bar {c}+\beta {k_2}\theta +\gamma } \right) \cdot z\left( x \right)} \right)\alpha - \left( {\left( {\bar {a}+\beta {{\bar {S}}_{{\sigma _1}}}+\gamma } \right)} \right. \\ & \;\;\;\left( {\bar {b}+\beta {{\bar {S}}_{{\sigma _2}}}+\gamma } \right)\left( {\bar {c}+\beta {{\bar {S}}_{{\sigma _3}}}+\gamma } \right){{\bar {z}}_\omega })\alpha +\left( {z\left( x \right) - 1} \right){l_1}\left( \theta \right)\left. {{\alpha ^2}} \right) - Poseidon\left( {\bar {t} \cdot {Z_H}\left( \theta \right)} \right) \\ \end{aligned}$$
(2)
  1. (e)

    Construct polynomial commitments at \(\:{\uptheta\:}\),\(\:{\uptheta\:}{\upomega\:}\)two points to generate Plonk zero-knowledge proof \(\:{\uppi\:}\). Equation (3) denotes a polynomial over \(\:{\uptheta\:}\) points and Eq. (4) denotes a polynomial over \(\:{\uptheta\:}{\upomega\:}\).

$$~{W_\theta }\left( x \right)=\frac{1}{{x - \theta }}\left( {\begin{array}{*{20}{c}} {r\left( x \right)} \\ {+v\left( {a\left( x \right) - \bar {a}} \right)} \\ {+{v^2}\left( {b\left( x \right) - \bar {b}} \right)} \\ {+{v^3}\left( {c\left( x \right) - \bar {c}} \right)} \\ {+{v^4}\left( {{S_{{\sigma _1}}}\left( x \right) - {{\bar {S}}_{{\sigma _1}}}} \right)} \\ {+{v^5}\left( {{S_{{\sigma _2}}}\left( x \right) - {{\bar {S}}_{{\sigma _2}}}} \right)} \end{array}} \right)$$
(3)
$${W_{\theta \omega }}\left( x \right)=\frac{{{v^6}\left( {z\left( x \right) - {{\bar {z}}_\omega }} \right)}}{{x - \theta \omega }}$$
(4)

The final proof of generation:

$$\pi = \left( {\left[ a \right]_{1} ,\left[ b \right]_{1} ,\left[ c \right]_{1} ,\left[ z \right]_{1} ,\left[ {Poseidon\left( {t\left( x \right) \cdot Z_{H} \left( x \right)} \right)} \right]_{1} ,\left[ {W_{\theta } } \right]_{1} ,\left[ {W_{{\theta \omega }} } \right]_{1} ,\bar{a},\bar{b},\bar{c},\bar{S}_{{\sigma _{1} }} ,\bar{S}_{{\sigma _{2} }} ,\bar{z}_{\omega } } \right)$$
  1. 3.

    Verifying zero-knowledge proof: The regulator and the counterparty check that the elements in the generated proof \({{\uppi}}\) satisfy the properties of the group and the domain.Calculated to validate the relevant commitments as in Eqs. (5–7).

$${\left[ D \right]_1}=[Poseidon{\left( {t\left( x \right) \cdot {Z_H}\left( x \right)} \right]_1}+{v^6}u \cdot {\left[ z \right]_1}$$
(5)
$${\left[ F \right]_1}={\left[ D \right]_1}+v \cdot {\left[ a \right]_1}+{v^2} \cdot {\left[ b \right]_1}+{v^3} \cdot {\left[ c \right]_1}+{v^4} \cdot {\left[ {{S_{{\sigma _1}}}} \right]_1}+{v^5} \cdot {\left[ {{S_{{\sigma _2}}}} \right]_1}$$
(6)
$${\left[ E \right]_1}={\left[ {Poseidon\left( {\bar {t} \cdot {Z_H}\left( \theta \right)} \right)} \right]_1}+v\bar {a}+{v^2}\bar {b}+{v^3}\bar {c}+{v^4}{\bar {S}_{{\sigma _1}}}+{v^5}{\bar {S}_{{\sigma _2}}}+u{\bar {z}_\omega }~$$
(7)
$$e\left( {{{\left[ {{W_\theta }} \right]}_1}+u \cdot {{\left[ {{W_{\theta \omega }}} \right]}_1},{{\left[ X \right]}_2}} \right)=e\left( {\theta \cdot {{\left[ {{W_\theta }} \right]}_1}+u\theta \omega \cdot {{\left[ {{W_{\theta \omega }}} \right]}_1}+{{\left[ F \right]}_1} - {{\left[ E \right]}_1},{{\left[ 1 \right]}_2}} \right)$$
(8)

Finally, through the Eq. (8) bilinear mapping verification proof, if the equation is valid, then it means that the input authentication information is consistent with the actual and successfully passes the fingerprint and title identity authentication stage; if the equation is not valid then it means that the input authentication information is inconsistent with the actual, and there may be the behavior of fake identity, and the regulator will be further regulated. Among them, a constraint compression strategy based on Poseidon hash is designed to generate zero-knowledge proof, which reduces the workload and complexity of zero-knowledge proof and, at the same time, improves the efficiency of generating and verifying zero-knowledge proof, thus improving the efficiency of the whole model.

Model analysis

Model security analysis

This model provides unforgeability, reliability, zero-knowledge, and completeness applicable to identity authentication by designing an improved Plonk algorithm for identity privacy protection and using two-factor authentication with ID password and fingerprint. Table 2 shows the comparison of security of authentication models, comparing this model with models of other schemes. As can be seen from the table, literature16,17,18 do not support two-factor authentication and perform poorly in terms of reliability, zero knowledge, and completeness. Literature19 and 20perform better in terms of identity unforgeability, reliability, zero-knowledge, and completeness but do not support two-factor authentication. Literature16,18 do not design algorithms for identity privacy preservation, and literature17,20 do not implement identity unforgeability.

Table 2 Comparison of authentication model security.
Full size table

Model performance analysis

Tables 3 and 4 show the model proof generation and validation performance analysis, respectively, where m denotes the number of wires, n denotes the number of multiplication gates, and a denotes the number of addition gates, \(\:{\mathbb{G}}_{1}\) and \(\:{\mathbb{G}}_{2}\) are groups defined on different elliptic curves, \(\:\mathbb{F}\) is a finite prime number field, \(\:\mathcal{l}\) indicates the number of public inputs, and \(\:\text{P}\) indicates the number of pairwise operations. As shown in Table 3, the Groth16 algorithm has some limitations in the general trusted setup, the Auroralight algorithm lacks simplicity, and in terms of the workload of the certifiers, it can be seen that the Sonic algorithm has an enormous amount of workload of the certifiers, while our algorithm has some advantages in terms of the relatively low workload of the certifiers. Among them, seven times in our algorithm perform exponential operation operations on the group \(\:{\mathbb{G}}_{1}\)defined by elliptic curves and compute the number of domain multiplications by eight FFTs of scale 4n, five FFTs of scale 2n, and twelve FFTs of scale n. Since n is related to a in the actual circuits, here n and a are combined and denoted as (n + a), which ultimately approximates to 7n + 7a and 54(n + a ) log(n + a) results. Our algorithm, onic algorithm, and Plonk algorithm all have a general trusted setup and simplicity, and as can be seen from the table, our algorithm is relatively small in terms of proof size. As shown in Table 4, there is Additional ancillary work for the Auroralight algorithm, in terms of the workload of validators, Plonk’s algorithm and our algorithm perform two matching operations and our algorithm performs relatively fewer exponential operations on group \(\:{\mathbb{G}}_{1}\) defined by elliptic curves.

Table 3 Model proof generation performance analysis.
Full size table
Table 4 Model proof validation performance analysis.
Full size table

Test

Experimental environment

The model is implemented by Snarkjs, the circuit is written by Circom language, the model implementation process is simulated, and finally, the verified smart contract is deployed in the Remix test. The experimental environment is as follows: host model ASUS ROG Strix Scar 7, Intel(R) Core(TM) i5-9300 H CPU @ 2.40 GHz.

Experimental process

First, the design of the circuit is carried out with private inputs for private information and public inputs for encrypted private information and outputs are equal if they are zero, as shown in Fig. 3.

Fig. 3
figure 3

Circuit design.

Full size image

The model circuit is designed, and the circuit is compiled, as shown in Fig. 4.

Fig. 4
figure 4

Circuit compilation.

Full size image

Generation and validation of the required public parameters and setup files through the Plonk zero-knowledge proof framework, as shown in Figs. 5 and 6.

Fig. 5
figure 5

Public parameters and setup files.

Full size image
Fig. 6
figure 6

Validation results.

Full size image

This command is used to export the validation key from the generated .zkey file, which is the file used to validate the proof during the zero-knowledge proof process, as shown in Fig. 7.

Fig. 7
figure 7

Export the validation key.

Full size image

Then, the property owner private inputs the intellectual property characterization information, such as the application number of the patent, and the regulator public inputs the encrypted property feature information obtained from the certificate of the intellectual property transaction, as shown in Fig. 8.

Fig. 8
figure 8

Inputs for zero-knowledge proof.

Full size image

This command is used to verify that a given zero-knowledge proof witness file is consistent with the circuit, as shown in Fig. 9.

Fig. 9
figure 9

Witness checking.

Full size image

Perform 100 experiments for generating proofs and 100 experiments for verifying proofs and put the records in files, as shown in Fig. 10. The specific values are shown in Figs. 11 and 12.

Fig. 10
figure 10

Records.

Full size image
Fig. 11
figure 11

Time to generate proofs.

Full size image
Fig. 12
figure 12

Time to verify proofs.

Full size image

The time for zero-knowledge proof generation is shown in Fig. 13, and the experiment was conducted to generate 100 proofs with an average proof generation time of 0.42346 s.

Fig. 13
figure 13

Proof generation time.

Full size image

The time for verification of zero-knowledge proof is shown in Fig. 14; the experiment was carried out for 100 proofs, and the average proof verification time was 0.19119 s.

Fig. 14
figure 14

Proof validation time.

Full size image

As shown in Fig. 15, for the verification pass, the verification experiment is carried out by deploying the verification smart contract to the chain, and the final output “true” indicates that the verification passes and the experiment is completed.

Fig. 15
figure 15

Verification passed.

Full size image

As shown in Table 5, as in the case of the same size of the circuit input data, this model improves the authentication time in the fingerprint authentication stage, thus improving the efficiency of identity authentication for intellectual property transactions.

Table 5 Model efficiency analysis.
Full size table

Conclusions

In view of the problems of false property rights and difficulties in identity authentication in intellectual property transactions, this paper proposes an identity authentication model for property rights transactions based on the alliance chain, aiming to improve the security and credibility of the transactions. Firstly, by constructing a two-factor identity authentication model, the responsibilities, functions, and authentication process of each role in the model are clarified, which provides a theoretical basis for the realization of the model. On this basis, this paper proposes a two-factor authentication mechanism that combines ID passwords, individual physiological features, and property rights features and utilizes fingerprint biometrics and intellectual property features to generate identity markers, which ensures the uniqueness and authenticity of the identity of the subject of the transaction. In order to further enhance the efficiency and security of the authentication process, this paper designs a constraint compression strategy based on the Poseidon hash algorithm, which effectively reduces the computational burden of the zero-knowledge proof algorithm in the execution process and optimizes the performance of the authentication model. In addition, this paper also combines the models used in other kinds of literature to carry out a comparative analysis of the security of the authentication model, ensuring that this model is applicable to the characteristics of unforgeability, reliability, zero-knowledge, and completeness of identity authentication, and verifies the model performance. Through comparison and verification, the study shows that the two-factor identity authentication model based on the alliance chain can not only effectively reduce the risk of false identity and property right information forgery in intellectual property transactions but also ensure the accuracy of identity authentication of the two parties in the transaction while carrying out privacy protection, and improve the security and efficiency of the transaction process. This model has a wide range of potential applications, especially in the fields of digital assets and smart contracts, and can provide a more secure and reliable solution for the protection and transaction of intellectual property rights in the future.

In summary, the identity authentication model based on the alliance chain proposed in this paper shows strong advantages in intellectual property transactions, and its security, reliability, and efficiency make it an important technological breakthrough in the field of intellectual property protection, which provides strong support for further promoting the application of blockchain technology in intellectual property protection.