Solving the problem of power ripples for a multi-rotor wind turbine system using fractional-order third-order sliding mode algorithms

Abstract

Power quality is one of the most prominent challenges hindering the spread and use of direct power control (DPC) in the field of control, especially for induction generator (IG) control. The lower power quality in the case of using the DPC approach is due to the use of hysteresis comparators. This work proposes a new controller to overcome the drawbacks of the DPC approach, such as low robustness and high total harmonic distortion (THD) value of current for IG present in multi-rotor wind turbine (MRWT) based power system. The proposed controller is fractional-order third-order sliding mode control (FOTOSMC), as this controller is used to determine reference values ​​for a voltage. In addition to using the FOTOSMC controller, the pulse width modulation strategy is used to control the operation of the machine inverter. The proposed approach differs from the traditional DPC approach and existing controls. This proposed approach is characterized by high robustness and high performance in improving power quality. The DPC approach based on the FOTOSMC controller was implemented in MATLAB with a comparison to the traditional DPC approach and some related works in terms of response time, jitter, steady-state error, and overshoot. Simulations under different wind conditions are performed to evaluate the designed strategy’s performance and robustness against conventional methods, revealing substantial improvements in dynamic response and stability. The results show the superior dynamic performance of the developed algorithm in terms of enhancing the quality of active power (37.99%, 55.04%, and 44.44%) and reactive power (49.17%, 27.27%, and 30.87%) in the two tests compared to the DPC. This control method effectively reduces the THD by 42.35%, 41.25%, and 31.36% compared to the DPC, resulting in a more efficient and reliable wind energy conversion system. This research confirms the effectiveness and efficiency of the proposed approach in renewable energy applications. It promotes the most efficient and sustainable energy solutions, making it a promising solution in other industrial applications.

Introduction

With the depletion and environmental detriments associated with fossil fuels such as oil, gas, and coal, there is an increasing focus on developing alternative energy sources. These alternatives are essential for mitigating the environmental impacts, particularly greenhouse gas emissions, associated with traditional fossil fuel extraction¹. Renewable energy sources (RESs), such as solar, hydro, and wind energy (WE), are highlighted for their cleaner electricity generation and potential to reduce reliance on finite resources. Among these, WE stands out due to its vast potential and relatively low environmental footprint. WE harness natural wind currents, converting kinetic energy into electricity without emitting harmful pollutants².

RESs offer a viable solution despite the difficulty of handling their inherently fluctuating and occasionally unpredictable outputs. A significant advancement in clean power is the use of variable-speed wind turbine (WT) systems for electricity production, which have become progressively more cost-competitive^3,4,5. This transition plays a critical role in lowering greenhouse gas emissions and promoting sustainable energy practices.

The conventional WT, characterized by a single horizontal axis and three blades, has been the conventional choice for generating electrical energy. The use of these traditional WTs in wind farms causes several problems and defects, the most prominent of which is the effect of the WTs in wind farms on the wind generated between the WTs, which reduces the yield of the wind farm. The energy gained from wind using WTs is affected by a factor called the coefficient of power. This coefficient has a value of less than 1, with its largest value being 0.59, which makes the energy gained less compared to WE. In addition, the use of these traditional WTs does not resist strong winds, which leads to large losses and thus high costs for re-maintenance. In order to obtain more energy, giant WTs must be used. These giant WTs are difficult to accomplish and require very advanced technology and equipment, which makes it difficult to spread and use WTs. Therefore, researchers had to search for appropriate solutions to overcome the problems and defects of traditional WTs and try to increase the performance of the WTs, especially in the case of strong winds. A design that has been proposed as an alternative to the WT is the dual-rotor WT (DRWT). DRWT is considered an improvement over traditional WTs and an effective and reliable solution in the field of renewable energies to overcome the problem of high energy demand and the disadvantages of WT. In⁶, the aerodynamic performance and structural design of a 5 MW multi-rotor turbine were discussed. Also, a mathematical model of this WT was given, mentioning its advantages and disadvantages. The use of a DRWT turbine offers several advantages, including improved aerodynamic efficiency, suitability for lower wind speeds (WSs), and increased mechanical power output gained from the wind compared to a conventional WT. The design of the DRWT differs from that of conventional WTs, as it consists of two WT units. In DRWT, there is often a main WT that has a larger capacity and an auxiliary WT that has a lower capacity than the main WT. The main WT and the auxiliary WT are fixed on one axis and rotate in the opposite direction. Most often, this DRWT is referred to as a multi-rotor WT (MRWT). DRWT turbines are in continuous and permanent development, as new technologies and ideas have recently emerged that have given WTs great importance in the energy field. By optimizing the capture of WE, DRWTs can significantly contribute to the overall efficiency and effectiveness of WE generation. Numerous studies have been conducted on this technology to harness WE^7,8,9,10, consistently demonstrating that the energy extracted using these advanced systems surpasses that generated by conventional WTs. Specifically, these turbines yield 20–35% more energy compared to standard WTs^8,9. The use of DRWT allows the dimensions of WTs to be significantly reduced, which helps to accomplish them with ease, which reduces costs. Also, the use of this type reduces the size of wind farms, as some DRWT turbines can be used to finance the network with the necessary energy, which makes this technology of great importance. The use of DRWT in wind farms is not affected by the wind generated between the WTs, which allows for an increase in the yield of the wind farm compared to traditional WTs. These WTs are resistant to strong winds and have high durability compared to traditional WTs, which reduces losses resulting from strong winds. Thus, the use of this technology allows power generation to continue despite the presence of strong winds. MRWT is a more expensive technology compared to conventional WTs. Compared to conventional WTs, this technology is complex to control. Also, it contains many mechanical components, which makes it require more regular maintenance than traditional WTs. Despite these challenges, continued developments and innovations in MRWT technology point to a promising future role in the field of renewable energies. As research advances and technology improves, MRWTs are expected to become more efficient and cost-effective, contributing significantly to the renewable landscape and the global shift towards sustainable energy solutions. Due to the many advantages of MRWT compared to conventional WTs, it is relied upon in this paper to convert WE into mechanical energy.

In addition to WTs, generators, particularly induction generators (IGs)¹¹, are widely utilized, particularly in variable WS conditions. The doubly-fed induction generator (DFIG) is notably the most suitable for WE applications because of its robustness, low cost, simple algorithm, and overall cost-effectiveness^12,13. This generator’s unique capability to control both power output and rotational speed by feeding the rotor allows it to adapt efficiently to different WSs, making it highly desirable. In¹⁴, permanent magnet synchronous generators (PMSGs) were used to convert energy gained from wind into electrical energy. In this energy system, the PMSG is connected to the grid using two inverters. Also, the use of a PMSG does not allow controlling the output power or changing the speed of the PMSG as is the case with IG.

Compared to other types of generators, such as synchronous generators, direct current (DC) generators, and PMSGs, IGs offer several advantages. SGs require more complex control systems and can be less stable under varying WSs. DC generators are less efficient and require more maintenance. PMSGs, while efficient, tend to be more expensive and less durable in harsh environments. In contrast, IGs, and particularly DFIGs, combine the benefits of cost-effectiveness, durability, and operational simplicity¹⁵.

To power a DFIG, two specific converters are required: the rotor side converter (RSC), which then changes this direct voltage into an alternating voltage of lower value compared to the grid voltage, and the grid side converter (GSC), which converts alternating voltage into direct voltage¹⁶. This dual conversion process ensures efficient energy transfer and adaptability to changing wind conditions, further solidifying the DFIG’s position as the optimal choice for WE generation.

In energy systems based on renewable sources, power quality, and frequency are among the most important features that must be paid attention to. In these energy systems, energy quality is closely linked to the control strategy. Control strategy plays an important role in improving power quality, frequency, and current. Also, the control strategy used has a prominent role in the costs of the energy system and the ease of its implementation. Therefore, it is necessary to choose a control approach with high specifications, such as robustness, ease of adjustment, outstanding performance, rapid dynamic response (DR), ease of implementation, and a lower degree of complexity. In the work¹⁷, the author believes that voltage and frequency stability are among the most prominent indicators that should be focused on in small AC networks. The author proposed a distributed secondary control scheme based on binary threshold smoothing of frequency recovery, medium voltage recovery, and active and reactive power (Ps and Qs) sharing between DGs in AC blocks subject to irregular communication delays and drive saturation to maintain stability of grid frequency and bus voltage. To obtain efficient and robust performance, he designed a strategy based on state transformation, based on the prior information of the control inputs. This strategy has the ability to handle irregular delays and has the potential to completely mitigate the harmful effects of communication delays. In addition, a hyperbolic tangent function is introduced to approximate the non-smooth saturation function, and a time-invariant anti-saturation controller is designed, which can alleviate the effect caused by engine saturation. This proposed strategy was implemented in a MATLAB environment, where, several simulation cases were conducted to evaluate the performance of the proposed strategy on the microgrid test system. The results obtained were compared with other existing methods. These results along with the comparison reveal the validity, effectiveness, robustness, and flexibility of the proposed method in recovering the microgrid frequency/average bus voltage and achieving accurate active/reactive power sharing.

Numerous research studies have concentrated on developing efficient control strategies for WE conversion systems (WECS) in the existing literature. The conventional approach in WECS frequently involves vector control using proportional-integral (PI) methods. Nevertheless, these linear control methods are particularly vulnerable to variations in model parameters and show limited robustness against uncertainties and external disturbances¹⁸. Additionally, PI control methods require precise tuning of their parameters, which can be challenging and time-consuming. They also tend to perform poorly under non-linear and time-varying conditions, often leading to suboptimal performance. The PI controllers struggle with DR, resulting in slower reaction times and potential instability under rapid changes in WS.

Recently, efforts have been made to address these shortcomings, with direct power control (DPC) emerging as a simpler and more direct alternative. Despite its benefits, DPC has its limitations, including issues with current total harmonic distortion (THD) and energy fluctuations caused by the discontinuous nature of its hysteresis controllers (HCs)¹⁹. Additionally, DPC suffers from high switching losses due to the frequent on-off actions of power electronic devices, and it can result in significant electromagnetic interference. These drawbacks can lead to reduced efficiency and potential reliability concerns in the system. Research has indicated that the use of HCs in DPC leads to power fluctuations and reduced current quality. To tackle these problems, various solutions have been suggested to enhance competence²⁰. Many of these approaches remove the switching table (ST) and HCs, replacing them with alternative techniques. Although these alternatives can mitigate the drawbacks of DPC, they often add complexity, making them harder to implement and less desirable. One prominent solution among these alternatives is a nonlinear control, such as SMC (sliding mode control).

SMC has received significant attention and proven highly effective, especially in the realm of power electronic control²¹. However, its optimal application is hindered by chattering, a phenomenon stemming from the discontinuous nature of its switching control. This chattering can cause excessive mechanical wear and high-frequency oscillations in electrical systems, thereby diminishing overall system performance and efficiency. Moreover, precise system modeling is essential for SMC design, as inaccuracies can markedly affect control effectiveness. To overcome these challenges, recent literature has proposed several advanced strategies. For instance, global SMC²²aims to enhance robustness by considering a broader system perspective, thereby improving stability across varying operational conditions. Fractional-order nonsingular terminal SMC²³introduces fractional calculus to mitigate chattering and enhance transient response, resulting in smoother control actions. Integral-type terminal SMC²⁴integrates integral action into SMC to bolster tracking accuracy and disturbance rejection capabilities. In the work²⁵, the author used the SMC approach based on a fast Markov system (MJS) to overcome the problems and shortcomings of power networks located in remote areas. These power grids in remote areas have the disadvantages of high power penetration fed by the inverter, weak maintenance forces, low grid strength, and high risks of natural disasters. The author argues that enhancing the integrity and resilience of the vulnerable grid in remote areas is critical to the operation and expansion of the overall energy system in the long term. The proposed approach to improve the effectiveness and efficiency of the power grid is characterized by high performance, great durability, and the great ability to accurately overcome system dynamics problems after the occurrence of major emergencies, including the failure of distributed generators, damage to transmission lines, and short circuit accident. Using the SMC-MJS approach allows the system to be stabilized after emergencies occur. This proposed approach was implemented in a MATLAB environment, where the results showed that using the SMC-MJS approach ensures that the studied system recovers to a stable state in a faster manner. In²⁶, the author used the super-twisting sliding mode (STSM) strategy to improve the performance and effectiveness of the maximum power point tracking (MPPT) approach while comparing the results with traditional strategies such as incremental conductance algorithm. The effectiveness and competence of the STSM approach were verified using MATLAB, where several different tests were used to confirm the effectiveness and strength of the STSM approach. Simulation results showed the effectiveness, high performance, and efficiency of using the STSM technique in improving the characteristics of the MPPT strategy compared to other strategies. According to the work done in²⁷, the SMC approach provided satisfactory results compared to the PI controller in terms of improving the DFIG properties. The SMC approach significantly improves the degree of robustness compared to the PI controller, as it gives satisfactory results in terms of power ripples and THD of current. A comparative study was completed in²⁸between the SMC and vector control approaches to determine the best strategy in terms of performance and effectiveness in improving power quality. The comparison showed that using the SMC approach is much better than the vector control approach in terms of response time (RT), reducing torque ripples, and improving power quality. However, using the SMC approach causes the phenomenon of chattering, which creates several problems and defects at the level of the studied system. In addition, using the SMC approach does not eliminate power ripples, as ripples are observed at the torque and current levels if this approach is used, which is undesirable. The author in²⁹ compared some backstepping and SMC strategies for a DFIG-type generator used in WE conversion systems. These two strategies were used to control the two power converters. The backstepping control (BC) strategy is considered asymptotically stable in the context of Lyapunov’s theorem. The BC strategy is considered more complex and contains a large number of gains compared to the SMC approach. This comparison was performed using MATLAB, where variable WS was used to complete the study. Simulation results showed good performance of the system under the proposed control strategies. Compared with the BC strategy, the SMC approach offers the best performance. Due to the importance of the SMC approach, researchers have focused on it, and several effective solutions have been created to overcome the problems of the SMC approach. One of the most prominent solutions adopted is integrating the SMC approach with other strategies (Hybrid control). Using these solutions gave satisfactory results.

In the domain of hybrid SMC methods, passivity-based SMC³⁰emphasizes energy considerations to ensure system stability and efficiency, particularly in energy conversion applications. Enhanced fuzzy fractional-order SMC³¹combines fuzzy logic (FL) with fractional-order calculus to achieve robust control under uncertain and varying conditions. Backstopping-SMC (BSMC) was used as a suitable solution to overcome the problems of SMC strategy³². This strategy was used to control the power of DFIG, as it is characterized by high performance and great durability. This strategy was proposed to improve stability and performance in nonlinear systems. MATLAB was used to implement this strategy and compare it with the traditional approach and some existing controls. The results showed that the BSMC approach is characterized by a very fast DR and high durability. Moreover, the use of the BSMC approach led to a significant reduction in power and current ripples compared to the traditional approach. Despite these good results, the BSMC approach is characterized by many drawbacks, including a large degree of complexity and the presence of a significant number of gains, which makes it difficult to use smart strategies in determining the values ​​of these gains.

Additionally, proportional-integral-derivative (PID) terminal SMC³³integrates PID control with SMC principles to achieve precise tracking and disturbance rejection, leveraging the strengths of both approaches. Neuro-FL SMC³⁴, on the other hand, utilizes adaptive neuro-FL inference systems to dynamically adjust control parameters, optimizing performance in dynamic and uncertain environments. Despite their potential to address the limitations of traditional SMC, these advanced methods often introduce greater complexity and computational demands, which can pose challenges in real-time implementation and practical application.

Certain studies indicate that elevating the relative degree of the sliding surface derivative in SMC reduces chattering, enhancing operational performance in energy generation applications. To tackle this challenge, recent research has investigated the efficacy of a third-order SMC (TOSMC) based on the super-twisting (ST) algorithm. This method has shown promising results, particularly in WECS, as documented in^35,36,37,38.

In³⁹, a TOSMC technique is proposed to achieve the MPPT technique in a photovoltaic (PV) system operating under varying climate conditions. This method enhances the overall competence of the PV panel by ensuring it operates at its optimal power output. Additionally, it effectively minimizes the steady-state error (SSE) in the generated energy, leading to more stable and reliable energy production. In⁴⁰, the authors introduce an innovative third-order ST-like integral SMC designed for tracking nanopositioning trajectories. This advanced controller provides continuous control inputs, significantly enhancing its practicality for real-world applications. The controller’s simulation results show that it delivers a smooth and rapid transient response, successfully mitigating chattering, a common issue in SMCs. Furthermore, it performs effectively under external disturbances and model uncertainties in a piezoelectric nanopositioning system, ensuring precise and reliable positioning.

In⁴¹, researchers focus on enhancing the control of a WECS equipped with a 5-phase PMSG, specifically targeting disturbance-related challenges. This study addresses the issues of the traditional ST-SMC by introducing an advanced control method called ATOCSTC (adaptive third-order continuous ST control). This controller combines a smoothly continuous switching control term, an adaptation law, and a third-order sliding mode surface. Unlike the traditional ST-SMC, which depends on discontinuous “sign” functions, the proposed controller uses tangent hyperbolic functions to dynamically adjust gains, providing a more continuous and efficient control mechanism. Simulation results show that ATOCSTC greatly improves performance under various disturbances, including parameter variations, grid voltage sag, and WS fluctuations. However, this approach has some drawbacks, such as implementation complexity and reduced robustness due to the smooth function employed, potentially impacting the practicality and overall effectiveness of ATOCSTC in real-world applications. In⁴², the author used the TOSMC approach based on the grey wolf optimization (GWO) strategy to control the power and improve the THD of current value for an energy system based on the WE system. This proposed strategy is characterized by high performance, great durability, and efficiency in significantly reducing energy ripples compared to both indirect field-oriented control (IFOC) and the IFOC-SMC approach. The TOSMC-GWO controller was used to improve the effectiveness and efficiency of the IFOC approach. MATLAB was used to complete this study and compare the results with the SMC controller. The simulation results showed that the TOSMC-GWO controller has high performance compared to the SMC controller, as the TOSMC-GWO controller reduces the values ​​of overshoot, rise time, RT, and SSE by percentages estimated at 96.25%, 10.73%, 8.82%, and 80%, respectively, compared to the SMC controller. Also, the TOSMC-GWO controller reduces torque and current ripples by 84.61% and 82.23%, respectively, compared to the SMC controller.

In this research, a novel control is developed to significantly enhance the performance and robustness of the WE. This new control technique utilizes both fractional-order (FO) and TOSMC approaches to manage the Qs and Ps of a 1500 kW IG-MRWT. The fractional-order technique is crucial as it offers greater flexibility and precision in system control by generalizing the conventional integer-order calculus. This allows for better handling of system dynamics and improved control performance. TOSMC provides significant advantages over conventional SMC. While conventional SMC effectively deals with system uncertainties and disturbances, it often suffers from chattering, which can lead to wear and tear in mechanical systems. TOSMC, on the other hand, reduces or eliminates chattering by using higher-order derivatives, resulting in smoother control actions and enhanced system stability. Unlike other control methods, this technique integrates the functions of two different approaches depending on the parameter value representing the strategy’s fractional-order control. When this parameter is set to 1, the proposed technique operates as the conventional TOSMC, thereby merging two controls into one and providing a unique advantage over existing methods. So the fractional-order third-order SMC (FOTOSMC) approach is the main contribution of this paper. This designed algorithm is characterized by ease of realization, does not require the use of an MM of the DFIG, has high robustness, and distinctive performance, is easy to apply, and has a fast DR. This designed algorithm was applied to a DPC-controlled DFIG to control the energy. Therefore, the use of DPC based on FOTOSMC is the second main contribution of the paper. The designed algorithm differs from the algorithms mentioned above. The DPC-FOTOSMC algorithm has many advantages such as simplicity, ease of realization, high robustness, and its high ability to enhance the fineness of stream and energy. In addition to its fast DR, it will make it an effective solution in industrial applications in the future. The efficacy and robustness of the designed DPC-FOTOSMC for the 1.5 MW IG-MRWT is implemented and verified using MATLAB. The effectiveness and efficiency of the DPC-FOTOSMC were verified compared to the traditional approach using variable WS. A comparison of the results was studied in terms of the minimization ratios of RT, THD, energy fluctuations, and the value of both SSE and undershoots of IG-MRWT energy.

The main objectives achieved for this study include the following:

• Increase the effectiveness and efficiency of the TOSMC controller in terms of durability and DR.

• Augment the efficiency and stability of the MRWT-based energy system.

• Overcoming DPC algorithm problems such as low power quality, high THD of current, overshoot, and SSE values.

The manuscript is organized as follows: Sect. 2 outlines the design of the designed power system. Section 3 describes the FO-TOSMC approach. Section 4 details the DPC-FO-TOSMC. Section 5 presents the results and initiates the discussion. Section 6 validates the proposed strategy experimentally on the IG-based MRWT system. Finally, Sect. 7 summarizes the entire paper.

Proposed energy system

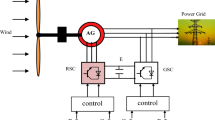
In this part, the studied energy system for generating electrical energy from wind is discussed. This studied energy system is characterized by several positive aspects that increase its importance. In this proposed system, WE was used as the primary source of power generation, which reduces toxic gas emissions. Simplicity and ease of implementation are among the most prominent features of this studied energy system, as it can be implemented on land and at sea. In Fig. 1, the structure of the system proposed for the study is given, as this system is of great importance as it protects the environment and allows overcoming the problem of increasing demand for energy. This system consists of an MRWT turbine, DFIG, two different inverters, and a control. The use of an MRWT turbine to convert WE into mechanical energy makes the studied system of great importance and a promising solution in the energy field.

In this system, an IG generator was used to convert the mechanical energy generated by the MRWT into electrical energy. A generator with a capacity of 1.5 megawatts was used. The stator of the IG is connected directly to the network without using any intermediary, which makes the studied energy system less expensive. In addition, the rotating part of the IG is connected using two inverters to the grid, which allows the power generated and transferred to the grid to be well controlled.

Fig. 1

Proposed power system.

MRWT control

The MPPT-PI strategy is used to control the turbine. This strategy was discussed in detail in⁴³. Using this strategy allows for determining the reference value of Ps. Also, to use the MPPT-PI strategy, the current and torque values ​​are related to the WS.

IG control

As is known, feeding IG from the network requires the use of two converters. In this studied energy system, a grid inverter using a diode was used to simplify the system and facilitate its implementation. The machine inverter is controlled by the proposed approach. In this work, the machine is used to reflect a two-level converter. The focus was on controlling the machine inverter only, without resorting to controlling the network converter, to determine the strength and efficiency of the proposed approach.

To accomplish this proposed energy system in MATLAB, the modeling of the basic components of the studied system must be addressed. In the sub-section, the MM of the turbine is discussed, where the necessary equations that highlight this turbine are given.

MRWT model

MRWT is considered one of the recently used solutions to augment the power gained from WE, as it is a new WT technology that relies on integrating several WTs into one WT. The use of MRWT allows it to defeat the problems and disadvantages of traditional WTs and to augment the power gained from the WE. MRWT was discussed in detail in the work⁹, where the MM for it was given, mentioning its disadvantages and advantages. In MRWT, the power gained from the wind is related to the number of WTs composing it, as the larger the number of WTs, the greater the power gained from the WE. The use of MRWT allows for reducing the size and dimensions of WTs, which allows for minimizing costs and facilitates the completion of WTs on the ground.

The power gained from wind using MRWT can be expressed by Eq. (1), as in this work only two WTs were used to create the MRWT.

$$\:{P}_{t}=\sum\:_{i=1}^{i=2}{P}_{i}$$

(1)

Where, P_t is the total energy of the MRWT and P_i is the power of the WTs (i = 1 and 2).

The torque of the MRWT is related to the power gained and the size and dimensions of the MRWT, so Eq. (2) is used to find this torque. Often, two WTs of different dimensions are used to form an MRWT and thus there are two different torques. Total torque is a sum of torques.

$$\:{T}_{t}=\sum\:_{i=1}^{i=2}{T}_{i}$$

(2)

Where, T_t is the total torque and T_i is the torque of both WT (i = 1 and 2).

In Eq. (3), the expression for each WT torque is shown. As is known, the torque value is affected by the change in WS, the large WTs (R₁ and R₂), the air density (ρ), and the coefficient of power (C_p). In MRWT, the two WTs have different WSs, as the WS of the second WT is not the same as that of the first WT, as it is affected by the distance between the two WTs and the size of the first WT¹⁰.

$$\:\left\{\begin{array}{c}{T}_{2}={C}_{p}.\rho\:\bullet\:\frac{\pi\:\bullet\:{R}_{2}^{5}\bullet\:{V}_{2}^{2}}{2{\lambda\:}_{2}^{3}}\\\:{T}_{1}={C}_{p}.\rho\:\bullet\:\frac{\pi\:\bullet\:{R}_{1}^{5}\bullet\:{V}_{1}^{2}}{2{\lambda\:}_{1}^{3}}\end{array}\right.$$

(3)

Torque is greatly affected by the value of Cp, as the larger the value of Cp, the greater the torque, and vice versa. The expression for Cp can be stated in Eq. (4). Also, the value of Cp is affected by the value of both pitch angle (β) and tip speed ratio (λ).

$$\:{C}_{p}\left(\lambda\:,\beta\:\right)=\frac{0.035}{{\beta\:}^{3}+1}+\frac{1}{0.08\beta\:+\lambda\:}$$

(4)

Using Eq. (3), the expression for the capacities of the two WTs that make up the MRWT is included in Eq. (5)^9,10.

$$\:\left\{\begin{array}{c}{P}_{2}={C}_{p}\left(\lambda\:,\beta\:\right).\frac{\rho\:\bullet\:{S}_{2}\bullet\:{V}_{2}^{3}}{2}\\\:{P}_{1}={C}_{p}\left(\lambda\:,\beta\:\right).\frac{\rho\:\bullet\:{S}_{1}\bullet\:{V}_{1}^{3}}{2}\end{array}\right.$$

(5)

Equation (6) shows the expression for λ for each WT, where the value of this expression is closely related to the value of the WS. The greater the WS, the lower the value of λ and vice versa⁸.

$$\:\left\{\begin{array}{c}{\lambda\:}_{2}=\frac{{R}_{2}.{w}_{2}}{{V}_{2}}\\\:{\lambda\:}_{1}=\frac{{R}_{1}.{w}_{1}}{{V}_{1}}\end{array}\right.$$

(6)

In MRWT, the first WT has a speed that is the same as the WS (V₁ = V). However, the speed of the second WT differs, as its WS is affected by the first WT and the distance between the two WTs (x), so its speed is less than the WS of the first WT. Therefore, Eq. (7) is used to find the WS of the second WT¹⁰.

$$\:{V}_{2}={V}_{1}\left(1-\frac{1-\sqrt{\left(1-{C}_{T}\right)}}{2}\left(1+\frac{2x}{\sqrt{1+4{x}^{2}}}\right)\right)$$

(7)

Where, the distance between the two turbines is 15 m and the C_T value is 0.9.

To feed the generator, a two-level inverter is used. The use of this inverter is necessary, as it is possible to control the quality of the resulting energy. In the next subsection, the MM for this reflector is mentioned.

Generator inverter model

A 2-level inverter is used to achieve RSC. This inverter was used because of its simplicity and ease of realization. The focus was on using this inverter to show the extent of the ability of the DPC-FOTOSMC to enhance energy fineness without resorting to using a multi-level inverter or GSC with a controlled inverter. Figure 2 represents the inverter used to embody the RSC of IG. Note that each leg of this inverter has two switches that work in the opposite direction.

Fig. 2

Two-level inverter.

Where, I_GSC is the output current of the GSC, V_dc is the DC voltage, and I_RSC is the input current of the RSC.

The value of the voltage at the points can be calculated using Eq. (8).

$$\:\left\{\begin{array}{c}{V}_{A}=1/3(2{V}_{Ao}-{V}_{Bo}-{V}_{Co})\\\:{V}_{B}=1/3(2{V}_{Bo}-{V}_{Ao}-{V}_{Co})\\\:{V}_{C}=1/3(2{V}_{Co}-{V}_{Bo}-{V}_{Ao})\end{array}\right.$$

(8)

With:

$$\:{V}_{Ao}={V}_{A}-{V}_{o}=\left\{\begin{array}{c}+\frac{{V}_{dc}}{2}\:\:\:\:\:\:if\:{K}_{1}\:is\:closed\\\:-\frac{{V}_{dc}}{2}\:\:\:\:\:\:if\:{K{\prime\:}}_{1}\:is\:closed\end{array}\right.,\:\:\:{V}_{Bo}={V}_{B}-{V}_{o}=\left\{\begin{array}{c}+\frac{{V}_{dc}}{2}\:\:\:\:\:\:if\:{K}_{2}\:is\:closed\:\\\:-\frac{{V}_{dc}}{2}\:\:\:\:\:\:if\:{K{\prime\:}}_{2}\:is\:closed\end{array}\right.$$

$$\:{V}_{Co}={V}_{C}-{V}_{o}=\left\{\begin{array}{c}+\frac{{V}_{dc}}{2}\:\:\:\:\:\:if\:{K}_{3}\:is\:closed\\\:-\frac{{V}_{dc}}{2}\:\:\:\:\:\:if\:{K{\prime\:}}_{3}\:is\:closed\end{array}\right.$$

The voltages V_A, V_B, and V_C necessarily have a zero sum.

$$\:\left[\begin{array}{c}{V}_{A}\\\:{V}_{B}\\\:{V}_{C}\end{array}\right]=\frac{{V}_{dc}}{6}\left[\begin{array}{ccc}2&\:-1&\:-1\\\:-1&\:2&\:-1\\\:-1&\:-1&\:2\end{array}\right]\left[\begin{array}{c}{F}_{1}\\\:{F}_{2}\\\:{F}_{3}\end{array}\right]$$

(9)

$$\:\text{W}\text{i}\text{t}\text{h}:\:\:{\:\:{F}_{2}=\:{K}_{2}+{K}_{2}^{{\prime\:}}\:,\:\:F}_{1}={K}_{1}+{K}_{1}^{{\prime\:}}\:{,\:F}_{3}=\:{K}_{3}+{K}_{3}^{{\prime\:}}$$

F₁, F₂, and F₃ they are values ​​that can take the value 1 or −1, depending on the condition of the transistors.

The compound voltages of the 3-phase inverter are given by:

$$\:\left\{\begin{array}{c}{V}_{AB}={V}_{ao}-{V}_{bo}=\frac{{V}_{dc}}{2}[{F}_{1}-{F}_{2}]\\\:{V}_{BC}={V}_{bo}-{V}_{co}=\frac{{V}_{dc}}{2}[{F}_{2}-{F}_{3}]\\\:{V}_{AC}={V}_{ao}-{V}_{bo}=\frac{{V}_{dc}}{2}[{F}_{3}-{F}_{1}]\end{array}\right.$$

(10)

This inverter is used in this work to feed the generator, as its use allows great control over the operation of the generator. Therefore, it is necessary to know the MM of the generator used in power generation. In the next subsection, the mathematical modeling of this generator is discussed.

IG model

Traditionally, IG is one of the popular generators in the field of renewable energies due to its advantages. This generator is considered one of the most durable generators, less expensive, and easy to control compared to other types⁴⁴. Also, this generator can operate in variable WSs due to the use of two different inverters to feed the RSC, which gives it an advantage not found in other machines. DFIG is considered the most important and most widespread type of IG in the field of WE for generating power, as this type was used in this article. As is known, Park’s transformation is a method by which the MM of any generator is given, and this transformation was used to give the MM of IG. Equation (11) represents the currents and voltages generated in the d-q axis⁴⁵.

$$\:\left\{\begin{array}{c}{V}_{dr}=\frac{d}{dt}{\varPsi\:}_{dr}+{R}_{r}{I}_{dr}-{w}_{r}{\varPsi\:}_{qr}\\\:{V}_{qr}={R}_{r}{I}_{qr}+{w}_{r}{\varPsi\:}_{dr}+\frac{d}{dt}{\varPsi\:}_{qr}\\\:{V}_{qs}={R}_{s}{I}_{qs}+{w}_{s}{\varPsi\:}_{ds}+\frac{d}{dt}{\varPsi\:}_{qs}\\\:{V}_{ds}={R}_{s}{I}_{ds}+\frac{d}{dt}{\varPsi\:}_{sd}-{w}_{s}{\varPsi\:}_{qs}\end{array}\right.$$

(11)

The machine’s capabilities are largely related to currents and voltages, so Eq. (11) can be used to calculate powers. The latter can be expressed by Eq. (12).

$$\:\left\{\begin{array}{c}{P}_{s}={V}_{qs}{I}_{qs}+{V}_{ds}{I}_{ds}\\\:{Q}_{s}={V}_{qs}{I}_{ds}-{V}_{ds}{I}_{qs}\end{array}\right.$$

(12)

The machine flux is also related to the current, as the machine flux can be calculated by Eq. (13)⁴⁶.

$$\:\left\{\begin{array}{c}{\varPsi\:}_{dr}=M{I}_{ds}+{L}_{r}{I}_{dr}\\\:{\varPsi\:}_{qr}={L}_{r}{I}_{qr}+M{I}_{qs}\\\:{\varPsi\:}_{qs}=M{I}_{qr}+{L}_{s}{I}_{qs}\\\:{\varPsi\:}_{ds}=M{I}_{dr}+{L}_{s}{I}_{ds}\end{array}\right.$$

(13)

Machine torque can be calculated using flux and current, as machine torque is largely related to stream. Equation (14) expresses the torque formula used in this work.

$$\:{T}_{e}=1.5\:p\frac{M}{{L}_{s}}(-{\varPsi\:}_{sd}{I}_{rq}+{\varPsi\:}_{sq}{I}_{rd})$$

(14)

Equation (15) gives the development of the speed of the machine. Using this equation, the operation of the machine can be regulated by using the difference between the torque of the IG and the torque of the load (T_em -T_r). Based on Eq. (15), the machine can be operated as a generator or as a motor, and this difference depends on whether it is negative or positive⁴⁷.

$$\:{{\varvec{T}}_{\varvec{e}\varvec{m}}-\varvec{T}}_{\varvec{r}}=\varvec{f}{\varvec{\Omega\:}}_{\mathbf{g}}+\varvec{J}\frac{\varvec{d}{\varvec{\Omega\:}}_{\mathbf{g}}}{\varvec{d}\varvec{t}}$$

(15)

In the field of control, many suggestions have been designed to control the powers of this generator, the most prominent of these suggestions being the PI regulator. This controller is described by simplicity, low cost, small gain, and fast DR. But this controller is greatly affected by changes in the machine parameters and gives unsatisfactory results. Therefore, to avoid this problem, several solutions have been designed to compensate for the use of this controller. In the next section, a new solution will be discussed that relies on integrating two nonlinear strategies to control energies and augment the performance of the studied energy system.

Designed FO-TOSMC approach

In this section, the FO-TOSMC is discussed in detail, as it is a new nonlinearity approach based on the combination of both fractional calculus and the TOSMC approach. Therefore, FO-TOSMC is a modification of the TOSMC approach represented in Eq. (16). The use of fractional calculus allows for improving performance and increasing durability, as simplicity and ease of use are among the most important features of this approach^42,48.

$$\:u\left(t\right)=k1.sign\left(S\right)+\:k2\int\:sign\left(S\right)dt\:\:\:+k3{\left(\left|S\right|\right)}^{r}.\:sign\left(S\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(16)

Where S is the sliding surface (S = X^*-X); K₁, k₂, and k₃are the gains of the TOSMC approach. Through these gains, the DR can be regulated and changed, as these gains can take negative or positive values ​​depending on the type of system. Also, to calculate these gains, the method of experimentation and simulation can be used, or smart strategies such as the GWO algorithm can be used, as was done in the work⁴².

The proposed FO-TOSMC is described by simplicity, ease of realization, high robustness, outstanding performance, and an acceptable number of gains, which makes it easy to adjust. Also, the FO-TOSMC strategy does not require knowledge of the MM of the system to apply it, which makes it a suitable solution for complex systems. The FO-TOSMC strategy can be expressed by Eq. (17). This equation represents the MM of the proposed approach, as it was obtained based on Eq. (16).

$$\:y\left(t\right)={(k1.sign\left(S\right)+\:k2\int\:sign\left(S\right)dt\:\:\:+k3{\left(\left|s\right|\right)}^{r}.\:sign(S\left)\right)}^{\alpha\:}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(17)

Where, $\:\alpha\:$ represents the fractional calculus technique, where its value should not take the value 0. Therefore, the designed approach condition to be met is α = 0.

r is an approach-specific value that can be taken to be equal to 0.5.

If α = 1, then the designed approach in this case becomes a TOSMC control. So the proposed approach has an advantage that is not found in other controls, as it plays the role of two algorithms at the same time depending on the value of α.

To obtain the proposed control (FOTOSMC), the value of α must not take the values ​​0 or 1. Therefore, the value of α for the proposed approach can be negative or positive, as smart strategies can be used to determine the best value for it.

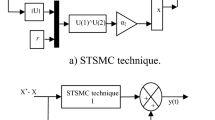
To illustrate and simplify the FOTOSMC strategy performed in this work, Fig. 3 is used, where a diagram of both TOSMC and FOTOSMC is given to show the difference between the two strategies. Figure 3a represents the TOSMC approach while Fig. 3b represents the strategy proposed in this work. Through these forms, the FOTOSMC strategy is completely different from the TOSMC strategy in terms of structure.

Fig. 3

Designed controllers.

Table 1 represents a comparison between the FOTOSMC controller and the PI controller in terms of structure, simplicity, DR, robustness, etc. This table shows that the FOTOSMC controller is completely different from the PI controller in terms of structure and working principle. The FOTOSMC controller is a nonlinear strategy based on the combination of two different strategies: fractional-order control and the TOSMC approach.

Table 1 Comparison of FOTOSMC controller with PI controller.

The gain values ​​of the FOTOSMC approach can be calculated using the experimental and simulation methods, as this method does not require writing complex programs. Also, this method is easy and fast and gives satisfactory results. Also, smart strategies such as GWO can be used to calculate the gains of the FOTOSMC approach.

In the next part, the FOTOSMC approach will be applied to defeat the problems of the DPC of IG, where all the necessary details and equations will be given.

DPC-FO-TOSMC approach

The DPC-FO-TOSMC approach is one of the hybrid strategies proposed in this work to enhance the power fineness and overcome the problems of the DPC of IG. This proposed algorithm is a solution different from the solutions mentioned above, as this algorithm relies on the use of FO-TOSMC to control powers. As mentioned above, the DPC-FOTOSMC strategy is a development of the DPC, where FO-TOSMC type regulators are used in place of traditional regulators, where the outputs of the used controllers are voltage reference values (VRVs). This proposed strategy uses the MSVM technique to convert VRVs ​​into pulses to run the RSC. The MSVM technique was relied upon in this paper for its simplicity and ease of implementation. Also, its ability to improve the THD of current compared to PWM, SVM, and neural SVM techniques is shown in the work done in⁴⁹.

The DPC-FOTOSMC approach is applied to the RSC only, without resorting to controlling the GSC, to demonstrate its ability and robustness. Also, the MPPT is used to determine the reference value for Ps, as using this approach allows the value of current and Ps to be related to the shape of the WS change.

The DPC-FOTOSMC strategy proposed in this part is listed in Fig. 4, where it is noted that this algorithm is simple and that traditional controls (HC) and ST will not work as is the case in DPC. This strategy depends on estimating capacities, where the same estimation equations found in DPC are used.

The DPC-FOTOSMC aims to calculate reference voltage values ​​(V_dr^* and V_qr^*) based on the energy error, where Eq. (18) is used to calculate these values. Equation (18) was written based on Eq. (17), which represents the MM of the proposed controller.

$$\:\left\{\begin{array}{c}{V}_{dr}^{*}={\left(k1.sign\left({e}_{Qs}\right)+\:k2\int\:sign\left({e}_{Qs}\right)dt\:\:\:+k3{\left(\left|{e}_{Qs}\right|\right)}^{r}.\:sign\left({e}_{Qs}\right)\right)}^{\alpha\:}\\\:{V}_{qr}^{*}={\left(k1.sign\left({e}_{Ps}\right)+\:k2\int\:sign\left({e}_{Ps}\right)dt\:\:\:+k3{\left(\left|{e}_{Ps}\right|\right)}^{r}.\:sign\left({e}_{Ps}\right)\right)}^{\alpha\:}\end{array}\right.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(18)

Where, e_Ps and e_Qs are the error powers.

The gain values ​​of the proposed approach used for power control were calculated in this paper using the simulation and experimentation method. This method was relied upon for the ease of obtaining values ​​without much effort. Also, this method is fast and inexpensive, as it does not require writing complex programs as is the case with smart strategies. The company that provided excellent results was selected from among several companies that provided solutions.

The Eq. (18) can be represented by a drawing (Fig. 5) that represents the controls used to determine the reference values ​​and shows the simplicity of the control used and the ease of its realization.

Using the ​​ V_dr^* and V_qr^* values, the operation of the RSC can be controlled, as the quality of these values ​​is related to the competence and efficacy of the FOTOSMC.

Estimating power relates first to estimating stator flux, where voltage and stream are measured to estimate stator flux. Equation (19) is used to estimate stator flux.

Fig. 4

Designed DPC-FOTOSMC approach of IG-MRWT.

Fig. 5

Designed Ps and Qs controllers.

$$\:\left\{\begin{array}{c}{\varPsi\:}_{s\alpha\:}={\int\:}_{0}^{t}({V}_{s}-{R}_{s}{i}_{s\alpha\:})dt\\\:{\varPsi\:}_{s\beta\:}={\int\:}_{0}^{t}({V}_{s}-{R}_{s}{i}_{s\beta\:})dt\end{array}\right.$$

(19)

With:

$$\:\left|{\varPsi\:}_{s}\right|=\sqrt{\left({\varPsi\:}_{s\beta\:}^{2}+{\varPsi\:}_{s\alpha\:}^{2}\right)}$$

(20)

Equation (21) explains the relationship between voltage and flux. This equation can be used to calculate voltage from flux or vice versa.

$$\:\left|\stackrel{-}{{\varPsi\:}_{s}}\right|=\frac{\left|\stackrel{-}{{V}_{s}}\right|}{{w}_{s}}$$

(21)

The flux angle can be determined by Eq. (22), where this angle is important in the proposed control and is used in the Park transform.

$$\:\theta\:r=artg\frac{{{\Psi\:}}_{r\beta\:}}{{{\Psi\:}}_{r\alpha\:}}$$

(22)

Using Eqs. (19), (20), and (21), the capabilities of the proposed DPC-FOTOSMC approach are estimated according to Eq. (23). This equation uses the measured value of the power and the energy error is calculated. The smaller this error is, the better the results.

$$\:\left\{\begin{array}{c}{Q}_{s}=-1.5\left(\frac{{\omega\:}_{s}{{\Psi\:}}_{s}M}{{L}_{s}}{I}_{dr}-\frac{{\omega\:}_{s}{{{\Psi\:}}_{s}}^{2}}{{L}_{s}}\right)\\\:{P}_{s}=-1.5\frac{{\omega\:}_{s}{{\Psi\:}}_{s}M}{{L}_{s}}{I}_{qr}\end{array}\right.$$

(23)

With:

$$\:\sigma\:=1-\frac{{M}^{2}}{{L}_{r}{L}_{s}}$$

(24)

To study the stability of the proposed approach, several strategies can be used to prove the extent of stability. The most prominent of these theories used is Lyapunov’s theory. This theory depends on the calculation of derivation, as it is a mathematical method that requires calculations, which makes it somewhat complicated and the possibility of an error in the calculations is high. Moreover, using this strategy requires skill, which makes its use somewhat complicated, especially in large and complex systems. But there is another method that is simpler than Lyapunov’s theory and does not require complex calculations. This method is known as the Bode curve. The Bode curve is a graphical method by which the stability of controls is studied. It relies on the use of MATLAB to extract the Bode curve.

In this paper, the Bode curve was used to prove the stability of the proposed DPC-FOTOSMC approach. This method was used because it is easy to apply and does not require complex calculations. Also, using the Bode curve does not require knowing the exact MM of the system. The Bode curve can be obtained directly from MATLAB. The Bode curve depends on extracting a curve for both the phase and magnitude (dB) of the approach whose stability is to be proven. According to the values ​​of phase and magnitude (dB), it can be known that the approach is stable or unstable. According to the Bode curve, the approach is stable if the phase (deg) and magnitude (dB) values ​​are negative.

Figure 6 represents a Bode curve for two controls, where the values ​​of phase (deg) and magnitude (dB) are extracted. From this figure, it is noted that the values ​​of phase (deg) and magnitude (dB) change with frequency for two controls. Also, it is noted that the values ​​of phase (deg) and magnitude (dB) are negative, as the range of change of phase (deg) is from 0 to −90 degrees in the case of using the traditional DPC-PI technique and from 180 to −270 degree if the proposed DPC-FOTOSMC approach is used. The magnitude (dB) value changed from 9 to −30 dB if the DPC-PI approach was used. In the case of the proposed DPC-FOTOSMC approach, the value of magnitude (dB) changes from 0 to −120 dB. So, the two approaches have negative values ​​for phase (deg) and magnitude (dB). In the case of the proposed DPC-FOTOSMC approach, the gain at −180° is approximately − 40 dB, so the gain margin is 40 dB. Since the profit margin is positive, this system in the case of using the DPC-FOTOSMC approach is stable.

If using the conventional DPC-PI approach, the measured phase at 0 dB is approximately − 65 deg, so the phase margin is 65 deg. Since the phase margin is positive, this system in the case of using the traditional DPC-PI approach is stable.

Fig. 6

Bode curve for two controllers.

The DPC-FOTOSMC approach proposed in this paper is compared with the DPC approach based on the PI controller using two different WS profiles. In the next part, the proposed approach is implemented and its effectiveness and efficiency in improving power quality and reducing the THD of current are verified.

Simulation results

In this part, the DPC-FOTOSMC approach is realized using MATLAB, with results compared to the DPC based on PI controller. The parameters of the system used are listed in Table 2⁴³. To study the competence of the DPC-FOTOSMC algorithm, a variable WS is used.

Table 2 System parameters.

Test 1: variable WS test

The proposed algorithm is tested in this test using a variable WS as shown in Fig. 7. The results obtained are listed in Fig. 8; Table 3.

Figure 8 shows that the energies follow the references well, with a fast DR for the two controls (Fig. 8a and b). From Fig. 8a, it is noted that the Ps take the same form as the WS as a result of using the MPPT strategy. Also, Ps has negative values ​​that indicate power generation. But the Qs are not affected by changes in WS. The value of the Qs remains constant regardless of time or the value of the WS, as it takes the value of 0 VAR in the presence of fluctuations.

Figure 8c represents the change of the stream as a function of time for the two algorithms. This current has a sinusoidal shape, with its value changing depending on the change in WS.

The THD value of the stream when using the two algorithms is listed in Fig. 8d and e. From these figures, the THD value was 0.85% and 0.49% for DPC and DPC-FOTOSMC, respectively. Therefore, using the DPC-FOTOSMC approach has an advantage in obtaining a good value for THD compared to using DPC. The DPC-FOTOSMC algorithm minimized the THD value by an estimated ratio of 42.35%. This ratio indicates that the fineness of the stream is significantly high if the DPC-FOTOSMC algorithm is used. However, from Fig. 8d and e, it is noted that the amplitude value of the fundamental signal (50 Hz) was better when using the traditional DPC-PI approach compared to the proposed approach. The amplitude value was 2264 A for the proposed DPC-FOTOSMC approach and 2267 A for the traditional approach. Therefore, the amplitude value is considered negative for the approach proposed in this test. This negativity can be attributed to the gains of the proposed DPC-FOTOSMC approach, which can be overcome in the future by using smart strategies such as the GWO technique.

Fig. 7

Variable WS profile.

Fig. 8

First test results.

Figure 9 shows the zoom in the graphical results of the test 1. This figure shows the superiority of the designed approach over the DPC-PI approach in terms of reducing power and stream fluctuations. Therefore, the DPC-FOTOSMC approach can enhance the fineness of stream and energy compared to the DPC-PI approach, making it an effective solution in industrial applications in the future.

Fig. 9

Zoom (First test results).

Table 3 represents the reduction percentages for fluctuations, RT, SSE, and overshoot of IG energy if the two approaches are used. By observing this table, the designed approach has great effectiveness and efficiency in reducing the values ​​of fluctuations, RT, SSE, and overshoot of IG energy compared to the DPC-PI approach. Accordingly, the approach was designed to reduce the values ​​of fluctuation, RT, SSE, and overshoot of Ps by approximately 37.39%, 30.32%, 48.14%, and 50%, respectively, compared to the DPC-PI approach. These ratios make the designed DPC-FOTOSMC approach of great importance in the industrial field.

In the case of Qs, the values ​​of fluctuation, SSE, and overshoot were reduced by 49.17%, 33.33%, and 56.25%, respectively, compared to the DPC-PI approach. However, the designed DPC-FOTOSMC approach provided unsatisfactory time compared to the DPC-PI approach. Therefore, the DPC-PI approach minimized the RT by approximately 20.4% compared to the designed DPC-FOTOSMC approach. This negativity can be attributed to the gains of the Qs controller. This negativity can be defeated in the future by using genetic algorithms to calculate the gains of the designed DPC-FOTOSMC approach.

Table 3 Values of the overshoot, ripples, SSE and RT in the test 1.

The effectiveness and efficiency of the designed algorithm obtained in the first test compared to the DPC approach is confirmed in test 2. The next test is to verify the robustness of the DPC-FOTOSMC-PWM if the IG parameters change.

Test 2: robustness test

The WS used in test 1 is the same as that used in this second test. The second test aims to study the robustness and strength of the designed algorithm compared to the DPC-PI approach in terms of changing IG parameters. In this test, the IG parameters are changed by multiplying the values ​​of the resistors by 2. Also, the values ​​of the machine coils are multiplied by 0.5. The results obtained are listed in Fig. 10; Table 4.

From Fig. 10, it can be seen that even though the IG parameters change, the energies still follow the references well. Changing the IG parameters affects the DPC approach significantly compared to the designed algorithm and this is shown by the augment in the value of fluctuations and the value of THD of the stream. Figure 10a shows that the Ps continues to take the form of a change in WS despite the change in the IG parameters, taking negative values. Also, in Fig. 10b it is noted that the Qs remain constant despite changing the IG parameters.

Figure 10c represents the stream if the IG parameters change of the two controls. This stream continues to take a sinusoidal shape, with its value affected by the change in WS, which is the same as the test 1.

Figure 10d and e represent the THD value if the algorithms used in this work are used. It is noted that the THD value was 1.69% and 1.16% for the DPC-PI and DPC-FOTOSMC approach, respectively. Accordingly, the DPC-FOTOSMC approach significantly minimized the THD value despite changing the IG parameters by an estimated percentage of 31.36% compared to the DPC-PI approach. The ratio of 31.36% shows the competence and strength of the algorithm designed to enhance the fineness of the stream despite changing the IG parameters, which makes it a promising solution. On the other hand, it is noted that the amplitude value of the fundamental signal (50 Hz) was estimated at 2367 A and 2314 A for both the traditional DPC-PI approach and the proposed DPC-FOTOSMC approach, respectively. These values ​​demonstrate the superiority of the traditional DPC-PI approach over the proposed DPC-FOTOSMC approach in terms of amplitude value. Therefore, the amplitude value also remains negative in this test of the proposed DPC-FOTOSMC approach. This negativity can be overcome in the future.

Fig. 10

Second test results.

Figure 11 represents a zoom of the results of the second test. It is noted that the stream and energy fluctuations are lower when using the designed DPC-FOTOSMC approach compared to using DPC-PI technique. This figure highlights the competence and ability of the algorithm designed to enhance the fineness of energy and stream despite changing IG parameters, which gives it an advantage and advantage in the industrial field.

Fig. 11

Zoom (Second test results).

Table 4 shows the numerical values ​​in case the IG parameters change. This table highlights the efficacy and competence of the DPC-FOTOSMC approach in this test compared to DPC-PI technique. It is noted that DPC-FOTOSMC reduced the fluctuation, overshoot, RT, and SSE of Ps by percentages estimated at 44.44%, 81.25%, 32.03%, and 14.33%, respectively, compared to DPC-PI technique. Also, the values ​​of fluctuation, exceed, RT and SSE of Qs were minimized by ratios estimated at 30.87%, 44.44%, and 40%, respectively, compared to DPC-PI technique. Despite this great superiority of the DPC-FOTOSMC technique, it provided a time for Qs greater than the DPC-PI technique. This can be attributed to the gains of the DPC-FOTOSMC, as this drawback can be defeated in the future.

Table 4 Values of the SSE, fluctuations, overshoot, and RT in the second test.

Table 5 represents the extent of change of THD value for two test algorithms. It is noted from this table that the THD value increased significantly in test 2 for the two algorithms, which indicates that it is affected by changing the IG parameters. This increase was greater in the case of using the DPC-PI technique compared to the DPC-FOTOSMC. The difference in THD value between the two tests was estimated at 0.67% and 0.84% for both the designed algorithm and the DPC-PI technique. Therefore, the DPC-FOTOSMC provided a difference for THD that was less than the difference provided by the DPC-PI technique. This obtained result highlights the strength and effectiveness of the DPC-FOTOSMC, making it a promising solution in industrial applications.

Table 5 Study the extent to which the THD value changes in the two tests.

Test 3: steps WS profile test

The third test differs from the previous tests in terms of the shape of the WS used to study the effectiveness and efficiency of the designed DPC-FOTOSMC approach. In this test, WS is used in steps. Figure 12 represents the WS used in this test. The graphical results of this test are represented in Figs. 12 and 13. The numerical results of this test are listed in Table 6.

Figure 1313 represents the power, current, and THD of current for two controls. Figure 13a represents the Ps of two controllers. This power takes negative values and continues to follow the reference well for two controls, which is the same observation in the previous tests. Also, the Ps changes depending on the change in WS and the presence of undulations. The Ps has a fast DR to two controls, with the proposed DPC-FOTOSMC approach preferable to the traditional approach, and this is shown in Table 6.

Figure 13b represents the change in Qs as a function of time for two controls. This capacity is not affected by changes in WS and is the same as observed in previous tests in the presence of ripples. Qs has a fast DR to two controls, with an advantage to the traditional approach over the proposed DPC-FOTOSMC approach.

Figure 13c represents the variation of current as a function of time for two controls. This current remains sinusoidal in this test, with the proposed DPC-FOTOSMC approach having an advantage in terms of quality compared to the traditional approach. The value of the current in this test changes according to the change in WS, as it increases and decreases with increasing and decreasing WS.

Figures 13d and 13e represent the amplitude value of the fundamental signal (50 Hz) and the THD value of the current for two controls. Through these figures, it is observed that the value of the amplitude of the fundamental signal takes approximately the same value for two controls, with an advantage for the traditional approach over the proposed DPCFOTOSMC approach. The THD value for the two controls was 0.47 % and 0.80 % for both the proposed DPC-FOTOSMC approach and the traditional approach, respectively. From these values, it is noted that the proposed DPC-FOTOSMC approach significantly reduced the THD value in this test compared to the traditional approach, which highlights its effectiveness and effectiveness in improving the quality of the current. The proposed DPC-FOTOSMC approach reduces the THD value by an estimated percentage of 41.25 % compared to the traditional approach.

Fig. 12

Steps WS profile.

Fig. 13

Third test results.

Figure 14 represents a Zoom of the results of the third test. From this figure, it is noted that the DPC-FOTOSMC approach significantly reduced the ripples of both current and potential compared to the DPC approach. Therefore, it can be said that the DPC-FOTOSMC approach significantly improves the quality of power and current compared to the DPC approach, which makes it a promising solution in the future for other applications.

Fig. 14

Zoom (Third test results).

Table 6 represents the reduction percentages and values ​​of SSE, fluctuations, overshoot, and RT for two controls. From this table, it is noted that the DPC-FOTOSMC approach provided excellent results compared to the traditional approach. In the case of Ps, the DPC-FOTOSMC approach reduces the value of SSE, fluctuations, overshoot, and RT by percentages estimated at 60.71%, 55.04%, 62.25%, and 8.65%, respectively, compared to the traditional approach. In the case of Qs, the DPC-FOTOSMC approach significantly reduced the value of each SSE, fluctuations, and overshoot, as this reduction was estimated at 43.69%, 27.27%, and 45.45%, respectively, compared to the traditional approach. These percentages prove the effectiveness, efficiency, and high performance of the DPC-FOTOSMC approach in improving the characteristics of the studied system, making it a promising solution that can be relied upon in the future. However, in terms of the RT of the Qs, the DPC-FOTOSMC approach provided unsatisfactory results. This negativity can be attributed to the gain values ​​of the Qs controller, which can be overcome in the future by using smart strategies to calculate the gain values ​​of the DPC-FOTOSMC approach.

Table 6 Values of the SSE, fluctuations, overshoot, and RT in the third test.

Table 7 represents a study of the effect of the values ​​of the amplitude of the fundamental signal (50 Hz) and THD value between the first test and the third test for two controls. From this table, it can be said that the amplitude of the fundamental signal (50 Hz) and THD value are greatly affected by changing the shape of the WS. The THD value for the two controls was noted to have decreased in the third test compared to the first test for the two controls. The difference in the THD value between the first and third tests was estimated at + 0.05% and + 0.02% for both the traditional approach and the proposed DPC-FOTOSMC approach, respectively. Therefore, the percentage decrease in the THD value between the two tests was estimated at 5.88% and 4.08% for both the traditional approach and the proposed DPC-FOTOSMC approach, respectively.

Table 7 also shows that the amplitude value of the fundamental signal (50 Hz) increased significantly in the third test compared to the first test for the two controls. Therefore, the amplitude value is affected by the change in WS. This increase was estimated at 9.79% and 9.87% for both the traditional approach and the proposed DPC-FOTOSMC approach, respectively. So the proposed DPC-FOTOSMC approach provides a higher percentage of increase than the traditional approach, which highlights its performance and the extent of its ability to improve the amplitude value. These results indicate that the proposed DPC-FOTOSMC approach will have great importance in the industrial field in the future.

Table 7 Study the extent to which the amplitude of fundamental signal (50 hz) and THD value changes in test 1 and 3.

Table 8 represents a comparison of the DPC-FOTOSMC with other papers in terms of RT powers. It is noted that the DPC-FOTOSMC has a much better time than several existing strategies. This comparison highlights that the algorithm has a swift DR, which makes it an effective solution in the future in industrial applications such as propulsion and traction systems.

Table 8 A comparison between the DPC-FOTOSMC and some papers in terms of RT power.

Table 9 represents a comparison between some existing works and the proposed DPC-FOTOSMC strategy in terms of the THD of current value. From this table, it is noted that the proposed approach has a much better value for THD than several existing strategies, which makes the proposed DPC-FOTOSMC approach of great importance. This table highlights the effectiveness and strength of the approach in improving the THD value and thus the quality of the current compared to several scientific works.

Table 9 Comparison of the results obtained with other control approaches in terms of the current THD.

Conclusions

In this study, a new algorithm based on the combination of TOSMC controller and fractional calculators was proposed to alleviate the shortcomings of the DPC algorithm of IG-MRWT systems. After removing the traditional controllers, two FOTOSMC controllers are used to command the energy. Also, the PWM algorithm is used to operate the machine inverter based on the reference values ​​of the voltage generated by the FOTOSMC controller. Using both PWM and FOTOSMC makes the DPC algorithm more performing and effective in improving energy quality and increasing the durability of the power system. This algorithm is designed to use power estimation, as it uses the same equations found in the DPC method.

After that, the effectiveness, efficacy, and competence of the algorithm designed using MATLAB was studied, comparing the results with the DPC approach. A variable WS was used to complete this study. The main goal of this algorithm is to enhance power quality and durability. Compared to the DPC strategy, the DPC-FOTOSMC-PWM significantly reduces the THD of the stream by 42.35% and 31.36% in all tests compared to the DPC approach. The use of the designed algorithm allows for improving the power quality by an estimated 37.99% and 44.44% for Ps and 49.17% and 30.87% for Qs in all tests compared to the DPC approach, which ensures high network performance. Also, this approach improved the response time of Ps by an estimated 30.32% and 32.03% compared to the DPC approach. The results show that the designed algorithm has a great ability to enhance the SSE value compared to the DPC approach by ratios estimated at 14.33% and 48.14% for Ps and 40% and 33.33% for Qs in all tests. The algorithm reduces the overshoot of Qs by 56.25% and 44.44% and Ps by 50 and 81.25% compared to the DPC in all tests. As a result of these satisfactory results, the proposed energy system can be safely and efficiently integrated into the grid. Through numerical results, the proposed approach guarantees outstanding performance, making it a future solution in other industrial applications such as photovoltaic systems and traction and propulsion systems.

In the future, experiments will be conducted using real equipment on the algorithm designed to confirm the results and the competence and advantages of this algorithm compared to DPC. Also, intelligent strategies will be used to calculate algorithm gains designed to increase performance and efficiency.