Residual useful life prediction of lithium-ion battery based on accuracy SoH estimation

Abstract

The residual life is one of important performance of lithium-ion battery. Before the life prediction, the SoH (State of Health) data of lithium-ion battery are necessary to be available. In order to improve the accuracy of SoH estimation, electrolyte dynamics is added to the single particle model of lithium-ion battery in this paper. Then, a novel Pade approximation and least squares method are employed to estimate the SoH of lithium-ion batteries. After that, the mapping particle filter is applied to forecast the battery life. MPF can greatly improve the diversity of particles and avoid the operation of resampling. This is the first time that the mapping particle filter has been used to forecast the residual life of lithium-ion batteries. Finally, the experimental data from National Aeronautics and Space Administration is used to prove that the mapping particle filter has a higher precision of prediction than the standard particle filter.

Introduction

Accurate state estimation of lithium-ion batteries (LiBs), including state of charge (SoC) and state of health (SoH), is critical for ensuring the safe and efficient operation of battery-powered systems such as electric vehicles (EVs) and renewable energy storage. Recent advancements in data-driven and model-based approaches have significantly improved the precision and robustness of battery state estimation. For instance, the use of nonlinear autoregressive exogenous (NARX) networks optimized with adaptive weighted square-root cubature Kalman filters has demonstrated remarkable accuracy in dynamic SoC estimation by effectively capturing the nonlinear dynamics of LiBs ¹. Similarly, enhanced methods combining long short-term memory (LSTM) networks with adaptive state update filters have been proposed to improve SoC estimation by incorporating battery parameters and adapting to varying operating conditions ². Further advancements include the integration of extended-input LSTM networks with adaptive singular value decomposition unscented Kalman filters (UKF), which leverage full-cycle current rate and temperature data to achieve highly accurate SoC estimation across diverse operating scenarios ³. Additionally, the development of adaptive strong tracking square-root extended Kalman filters (ASTSEKF) with nonlinear condition adaptability has provided a robust framework for SoC estimation, particularly under complex and dynamic battery operating conditions ⁴. These studies highlight the importance of combining advanced machine learning techniques with adaptive filtering methods to address the challenges of battery state estimation.

The capacity decay of lithium-ion batteries is inevitable due to aging. When the SoH of a lithium-ion battery drops to 0.8, the battery is considered to be failed. The residual life prediction of lithium-ion battery can remind the user to replace the battery in time to ensure an efficient operation for the power system, but the inaccurate life prediction may cause the waste of resources or overuse. The residual life prediction of lithium-ion battery falls into two categories: one is based on the aging mechanism model of lithium-ion battery; the other is based on the historical SoH dataset⁵. The life prediction based on the aging mechanism model is to calculate the cycle times of SoH decaying to 0.8 by simulating the cycle aging process of lithium-ion batteries. There are few related literatures. For example, Yang et al. developed an electrochemical aging model of lithium-ion plating and SEI growth to simulate battery aging and predict the useful life of lithium-ion batteries⁶. Shao et al. studied a discharge capacity prognostics method for lithium-ion batteries based on a simplified electrochemical coupled aging mechanism model, where the solid-phase diffusion process is analyzed by using a simplified electrochemical model, and the particle rupture stress at different C rates is obtained⁷. Considering the impact of fast-charging protocols on battery life, Zhang et al. proposes a life prediction model for lithium-ion batteries that charge with fast-charging protocols in which the charging-based features are extracted from charge data using dilated convolutional network and the discharging-based features extracted from the discharge curve are enhanced using deep neural network⁸. Lithium-ion plating, SEI growth and active material loss were taken into account to predict the residual battery life by Kupper et al.⁹. Safari et al. developed an aging model for Li-ion battery life prediction based on multimodal physics and predicted the battery life¹⁰. Life prediction based on aging mechanism model is an open-loop process without feedback of lithium-ion battery measurement signal. Therefore, life prediction error will increase continuously due to the existence of model error.

The life prediction based on the historical SoH data set is to obtain the empirical decay model by fitting the historical SoH data, and then adopt the appropriate filtering method to improve the residual life prediction accuracy. The acquisition method of historical SoH datasets includes two methods: experimental measurement and online estimation. The experimental measurement method takes a long time with a high cost, which can be overcome by the online estimation method. There are many methods for online SoH estimation. For example, M. Einhorn et al. put forward a SoH estimation approach that can operate at any voltage stage without releasing the battery charge completely. However, it heavily relies on a reliable mapping between SoC and open circuit voltage (OCV)¹¹. Adopting the equivalent circuit model (ECM) and two-state thermal model, Zhang et al.¹² estimated cell SoH and analyzed the convergence of SoH estimates. The research¹³ investigated a parameter identification method based on electrochemical model of lithium-ion battery, analyzes the identifiability of output equation, and obtains the estimation of SoH. In paper¹⁴, a degradation model on account of SPM to estimate the SoH of batteries was established by introducing the formation mechanism of solid-electrolyte interfacial film (SEI). Without the use of voltage and current measurements, the authors of the paper¹⁵ studied the relationship between battery performance and capacity to provide a better improvement in the signal to noise ratio (SNR) of capacity estimation. An entropy-based SoH estimation method was proposed by Kim et al.¹⁶, which regarded the SoH estimation problem as solving recursive least squares (RTLS). Relevance vector machine (RVM) was used to extract characteristics from voltage and current measurements and calculate their correlation with SoH by Hu et al.¹⁷. A data-driven model was adopted to capture the changes in the shape of the charging curve as the battery ages, and the least squares method was used to identify the SoH for the parameters by Sung et al.¹⁸. Liu et al.¹⁹ brought forward a SoH estimation method based on Gaussian Regression Process method to solve the problem, however, in which its classification of data will lead to the increase of measurement noise. A neural network-based SoH estimation method was established by Richardson et al.²⁰, where terminal voltage, temperature, and load are input parameters and SoH is the output parameter.

After obtaining the SoH data set, the next step is to predict the residual life of lithium-ion batteries, and there are many relevant researches. For example, to address the problem of traditional fixed-architecture neural networks often suffering from underfitting or overfitting due to diverse data distributions, Jiang et al proposed the a flexible parallel neural network (FPNN) which integrates modules like inceptionBlock, 3D CNN, 2D CNN, and dual-stream networks²¹. Nuhic et al. combined support vector machine with a data processing method based on load ensemble training to study life prediction of lithium-ion batteries²². Zheng et al. achieved reliable prediction of battery life by combining unscented Kalman filter and correlation vector regression method, which can predict the future residual error of unscented Kalman filter²³. A comprehensive probabilistic approach to predict battery life was introduced by D. Liu et al through combining two health indicators of battery SoH with discharge voltage difference to get direct and indirect life prediction for lithium-ion batteries²⁴. Zhou used a simple statistical regression technique and an optimized correlation vector machine to predict the residual battery life²⁵. Miao et al.²⁶ adopted the improved unscented particle filter to predict battery life on account of historical SoH data, which resulted in an improvement in the prediction accuracy. An improved support vector machine regression particle filter model was used to predict battery life by Dong et al.²⁷, which is more reliable than the standard particle filter. Hu et al.²⁸ predicted the residual battery life by Gauss-Hamilton particle filter and ten-year cycle test results showing that the method captured the uncertainty in life prediction. Up to now, particle filter has been proved to have good accuracy in life prediction of lithium-ion batteries, but standard particle filter (SPF) and its improved version cannot overcome particle degeneracy.

This paper adds the electrolyte dynamics to the single particle model of lithium-ion battery so as to improve the accuracy of SoH estimation. And then, a novel Pade approximation and least squares method were used to estimate the SoH of lithium-ion batteries. To overcome the particle degeneracy and maintain the precision of particle filtering, a mapping particle filter (MPF) method is applied to predict the residual life of lithium-ion battery. Using a series of mappings, the mapping particle filter drives the particles from the prediction to the posterior density for minimizing the divergence between the posterior and intermediate density sequences. Embedding in a reproduced kernel Hilbert space is one of the key advantages of the maps, and thus a practical and efficient Monte Carlo algorithm is implemented. This method can greatly improve the diversity of particles and avoid the resampling process. And it is also the first time that the mapping particle filter has been used to predict the residual life of lithium-ion batteries. Finally, the NASA experimental data and simulation are employed to verify the effectness of SoH estiamtion and residual life prediction.

Methods

This section includes online SoH estimation, principle of mapping particle Filter and algorithm on life prediction of lithium-ion batteries. The details are given as follows:

Online SoH estimation of lithium-ion battery based on electrochemical model

Electrochemical model considering electrolyte dynamics

When the charging and discharging current is large, the electrolyte will produce obvious concentration difference potential, and ignoring the concentration difference potential will adversely affect the accuracy of voltage prediction value. Therefore, in consideration of the electrolyte dynamics, the reaction-diffusion process of lithium ion in the electrodes can be described by the partial differential equation as follows:

$$\begin{aligned} \frac{\partial c^{j}_{s}}{\partial t} = \frac{D^j_s}{r^2_j}\frac{\partial }{\partial r_j}\left( r^2_j\frac{\partial c^{j}_{s}}{\partial r_j}\right) , \end{aligned}$$

(1)

where $c^{j}_{s}$ is the lithium-ion concentration in the active material of electrode; $r_j$ is the radius of the orbicular particle; $D^j_s$ is the diffusivity of lithium ion in the electrodes; j stands for p, n (positive, negative). This model is suitable for the cylindrical lithium-ion battery, and most of the commercial batteries are cylindrical, such as Sony18650, ANR26650 and so on. Equation (1) possesses the Newman boundary conditions as follows:

$$\begin{aligned} \frac{\partial c^{j}_{s}}{\partial r_j}(0,t) =0, \frac{\partial c^{j}_{s}}{\partial r_j}(R^j_s,t) =-\frac{J^j}{D^j_s}. \end{aligned}$$

(2)

Here, $r_j =0$ and $r_j=R^j_s$ signify the central and surfacial positions of a single particle, respectively. $J^j$ is the lithium-ion molar flux in the positive/negative electrode, which is directly independent of the input current. The expression is described as follows:

$$\begin{aligned} J^p=\frac{-I}{a^pL^pFA}, J^n=\frac{+I}{a^nL^nFA}, \end{aligned}$$

(3)

where, F is Faraday constant; A is the surface area of active material in the anode/cathode; $a ^j$ is the specific area, which can be obtained by $a^j=3\epsilon ^j/R^j_s$; $\epsilon ^j$ is the effective volume fraction of the active material. The diffusion process of lithium ion in electrolyte is expressed as follows:

$$\begin{aligned} \frac{\partial c^n_e}{\partial t}(x,t)&=\frac{\partial }{\partial x}\left[ D_e(c^n_e)\frac{\partial c^n_e}{\partial x}(x,t)\right] +\frac{(1-t^0_c)}{\epsilon ^n_eFL^n}I(t),~ \frac{\partial c^{sep}_e}{\partial t}(x,t)=\frac{\partial }{\partial x}\left[ D_e(c^{sep}_e)\frac{\partial c^{sep}_e}{\partial x}(x,t)\right] \nonumber \\ \frac{\partial c^p_e}{\partial t}(x,t)&=\frac{\partial }{\partial x}\left[ D_e(c^p_e)\frac{\partial c^p_e}{\partial x}(x,t)\right] -\frac{(1-t^0_c)}{\epsilon ^p_eFL^p}I(t), \end{aligned}$$

(4)

where, $c^n_e$, $c^p_e$ and $c^{sep}_e$ represent lithium-ion concentration in the electrolyte of cathode, anode and separator, respectively. $t^0_c$ is the number of migrations; $\epsilon ^j_e$ is the effective volume fraction of electrolyte; $L^j$ is the thickness of anode/cathode. Partial differential equation (4) has the following boundary conditions:

$$\begin{aligned} \frac{\partial c^n_e}{\partial x}(0^n,t)&=\frac{\partial c^p_e}{\partial x}(0^p,t)=0 \epsilon ^n_eD_e(L^n)\frac{\partial c^n_e}{\partial x}(L^n,t)=\epsilon ^{sep}_eD_e(0^{sep})\frac{\partial c^{sep}_e}{\partial x}(0^{sep},t) \end{aligned}$$

(5)

$$\begin{aligned} \frac{\partial c^p_e}{\partial x}(L^p,t)&=\frac{\epsilon ^{sep}_eD_e(L^{sep})}{\epsilon ^p_eD_e(L^p)}\frac{\partial c^{sep}_e}{\partial x}(L^{sep},t),~c_e(L^n,t)=c_e(0^{sep},t),~c_e(L^{sep},t)=c_e(L^p,t), \end{aligned}$$

(6)

where, $0^n, 0^p, 0^{sep}, L^{sep}, L^n, L^p$ is the location of boundary. Then terminal voltage output function related with solid potential $\phi ^j _s (x, t)$ is deduced, namely $V(t)=\phi ^p_s-\phi ^n_s$. $\phi ^{j}$ can be expressed as:

$$\begin{aligned} \phi ^{j}_s(x,t)=\bar{\eta }^{j}(t)+\bar{\phi }^{j}_e+U^{j}(\bar{c}^{j}_{ss}(t))+FR^{j}_f\bar{J}^{j}(t) \end{aligned}$$

(7)

$\bar{\eta }^{j}(t)$ is the overpotential, which can be calculated by the following equation:

$$\begin{aligned} \bar{\eta }^{j}(t)=\frac{RT}{\alpha {F}}\sinh ^{-1}\left( \frac{\mp {I}(t)}{2a^{j}L^{j}\bar{i}^{j}_0(t)}\right) . \end{aligned}$$

(8)

The potential of electrolyte $\phi ^{j}_E$ has the following equation:

$$\begin{aligned} \begin{aligned} \frac{\partial \phi ^j_e}{\partial x}(x,t)=&\frac{i^{j}_e(x,t)}{k(c^j_e)}+\frac{2RT}{F}(1-t^0_c)(1+\frac{\textrm{d}\ln {f_{c/a}}}{\textrm{d}\ln {c^j_e}})\frac{\partial \ln {c^j_e}}{\partial x}(x,t)dx\\ \end{aligned} \end{aligned}$$

(9)

where, $i^{j}_e$ is the ion current, $k(c^j_e)$ denotes the specific conductance of electrolyte and $f_{c/a}$ is the average molar activity coefficient in the electrolyte. Assuming $(1+\frac{\textrm{d}\ln {f_{c/a}}}{\textrm{d}\ln {c_e}})$ is an identical value $k_f (t)$. $\phi ^{j}_e$ can be computed by integrating the width between the electrodes by Eq. (9). Then, one get:

$$\begin{aligned} \begin{aligned}&\bar{\phi }^{p}_e(0^p,t)-\bar{\phi }^n_e(0^n,t)=\frac{L^p+2L^{sep}+L^n}{2k(c^j_e)}I(t)+\frac{2RT}{F}(1-t^0_c)k_f(t)[\ln {c^p_e(0^p,t)}-\ln {c^n_e(0^n,t)}]. \end{aligned} \end{aligned}$$

(10)

Therefore, the output voltage V(t) has the following expression:

$$\begin{aligned} \begin{aligned} V(t)&=\frac{RT}{\alpha {F}}\sinh ^{-1}\left( \frac{-I(t)}{2a^pL^pi^p_0}\right) -\frac{RT}{\alpha {F}}\sinh ^{-1}\left( \frac{-I(t)}{2a^nL^ni^n_0}\right) +U^{p} \left( \frac{{c}^{p}_{ss}(t)}{{c}^{p}_{ss,max}}\right) -U^{n}\left( \frac{{c}^{n}_{ss}(t)}{{c}^{n}_{ss,max}}\right) - \left( \frac{R^p_f}{a^pL^p}+\frac{R^n_f}{a^nL^n}\right) I(t)\\&+\frac{2RT}{F}(1-t^0_c)k_f(t)[\ln {c^p_e(0^p,t)}-\ln {c^n_e(0^n,t)}]+\frac{L^p+2L^{sep}+L^n}{2k(c^j_e)}I(t) \end{aligned} \end{aligned}$$

(11)

The last two terms of V(t) are the added concentration potential due to the introduction of liquidics.

In order to facilitate parameter identification, this research introduces a coordinate transformation $\bar{r}_j=r_j/ r_j$. Then Eqs. (1), (2) can be rewritten as:

$$\begin{aligned} \frac{\partial c^{j}_{s}}{\partial t} = \frac{D^j}{R^2_j}\frac{1}{\bar{r}^2_j}\frac{\partial }{\partial \bar{r}_j}(\bar{r}^2_j\frac{\partial c^{j}_{s}}{\partial \bar{r}_j}),~ \frac{\partial c^{j}_{s}}{\partial \bar{r}_j}(0,t) =0, \frac{\partial c^{j}_{s}}{\partial \bar{r}_j}(1,t) =\frac{-R_jJ^j}{D^j} \end{aligned}$$

(12)

To linear equation (12), using coordinate transformation $w^j_s=\bar{r}_jc^j_s$, then equation (12) can be written as:

$$\begin{aligned} \frac{\partial w^{j}_{s}}{\partial t} = \frac{D^j}{R^2_j}\frac{\partial ^2 w^{j}_{s}}{\partial \bar{r}^2_j},~ \frac{\partial w^{j}_{s}}{\partial \bar{r}_j}(0,t) =0, \frac{\partial w^{j}_{s}}{\partial \bar{r}_j}(1,t)-w^j_s(1,t)=\frac{-R_jJ^j}{D^j} \end{aligned}$$

(13)

Then, according to the $i^{j}_0=k^{j}\sqrt{\bar{c}_e c^{j}_{ss}(c^{j}_{ss,max}-c^{j}_{ss})}$, the overpotential (8) can be rewritten as:

$$\begin{aligned} \bar{\eta }^{p}(t)=\frac{RT}{\alpha {F}}\sinh ^{-1}\left( \frac{-I(t)}{2a^pL^pk^p\sqrt{\bar{c}_e{c}^p_{ss}(c^{p}_{ss,max}-c^p_{ss})}}\right) ,~ \bar{\eta }^{n}(t)=\frac{RT}{\alpha {F}}\sinh ^{-1}\left( \frac{I(t)}{2a^nL^nk^n\sqrt{\bar{c}_ec^n_{ss}(c^{n}_{ss,max}-c^n_{ss})}}\right) \end{aligned}$$

(14)

In addition:

$$\begin{aligned} \begin{aligned} R_f=\frac{R^p_f}{a^pL^p}+\frac{R^n_f}{a^nL^n}, R_e=\frac{L^p+2L^{sep}+L^n}{2k(c_e)},~K_f=\frac{2RT}{F}(1-t^0_c)k_f(t) \end{aligned} \end{aligned}$$

(15)

Then:

$$\begin{aligned} \begin{aligned} V(t)=&\frac{RT}{\alpha {F}}\sinh ^{-1}\left( \frac{-I(t)}{2a^pL^pk^p\sqrt{\bar{c}_ec^p_{ss}({c}^p_{ss,max}-c^p_{ss})}}\right) -\frac{RT}{\alpha {F}}\sinh ^{-1} \left( \frac{I(t)}{2a^nL^nk^n\sqrt{\bar{c}_ec^n_{ss}({c}^n_{ss,max}-c^n_{ss})}}\right) \\&+U^{p}\left( \frac{{c}^{p}_{ss}(t)}{{c}^{p}_{ss,max}}\right) -U^{n}\left( \frac{{c}^{n}_{ss}(t)}{{c}^{n}_{ss,max}}\right) -R_fI(t)+R_eI(t)+K_f[\ln {c^p_e(0^p,t)}-\ln {c^n_e(0^n,t)}] \end{aligned} \end{aligned}$$

(16)

For the sake of cutting down the number of variables in V(t) expression, using the principle that the total lithium ions almost does not change in a short time, the following balance equation is achieved:

$$\begin{aligned} \begin{aligned} c_{s s}^{p}(t)=&\frac{1}{\epsilon _{s}^{p} L^{p} A}\left[ n_{L i}(t)-\epsilon _{s}^{n} L^{n} A c_{s s}^{n}(t)\right] ,~ c_{s s, max}^{p}=\frac{n_{L i}(t)}{\epsilon _{s}^{p} L^{p} A},~c_{s s, max}^{n}=\frac{n_{L i}(t)}{\epsilon _{s}^{n} L^{n} A} \end{aligned} \end{aligned}$$

(17)

According to (17), V(t) can be rewritten as:

$$\begin{aligned} \begin{aligned} V(t)=&\frac{RT}{\alpha {F}}\sinh ^{-1}\left( \frac{-I(t)}{E^p\sqrt{G(c_{ss,max}^{n}-c_{s s}^{n}(t))^2}}\right) -\frac{RT}{\alpha {F}}\sinh ^{-1} \left( \frac{I(t)}{E^n\sqrt{\bar{c}_ec^n_{ss}({c}^n_{ss,max}-c^n_{ss})}}\right) \\&+U^{p}(1-\frac{c_{s s}^{n}(t)}{c_{s s, max}^{n}})-U^{n}\left( \frac{{c}^{n}_{ss}(t)}{{c}^{n}_{ss,max}}\right) -R_fI(t)+R_eI(t)+K_f[\ln {c^p_e(0^p,t)}-\ln {c^n_e(0^p,t)}] \end{aligned} \end{aligned}$$

(18)

where, $E^j=2a^jL^jk^j$ and $G=\bar{c}_e\frac{(\epsilon _{s}^{n} L^{n} A)^2}{(\epsilon _{s}^{p} L^{p} A)^2}$. At this point, this research establishes a one-one mapping between V(t)and the concentration at the negative boundary ${c}^{n}_{ss}$. The electrochemical models often work well on constant current profiles, but the models this research considering the electrolyte dynamics can also have good performance when the batteries are under dynamic loads which is important to implement the estimation of SoH and obtain enough accuracy. The next step is to observe the lithium-ion concentration at the negative boundary on account of the measurements such as voltage, current and temperature.

Estimation of lithium-ion concentration at the negative boundary based on the Pade approximation

Introducing $\sigma ^D_n=\frac{R^2_n}{D^n}$ and taking the Laplace transform of (13), then one can get:

$$\begin{aligned} \frac{d^2W^n_s(\bar{r}_n,s)}{d\bar{r}^2_n}-s\sigma ^D_nW^n_s(\bar{r}_n,s)=0 \end{aligned}$$

(19)

The solution of (13) is achieved as follows:

$$\begin{aligned} W^n_s(\bar{r}_n,s)=M^n\frac{\sinh \left( \bar{r}_n\sqrt{s\sigma ^D_n}\right) I(s)}{\sinh \left( \sqrt{s\sigma ^D_n}\right) -\sqrt{s\sigma ^D_n}\cosh {\sqrt{s\sigma ^D_n}}} \end{aligned}$$

(20)

where, $M^n=\frac{R_n}{D^n_sa^nL^nFA}$. Substituting $w^n_s=\bar{r}_nc^n_s$ into (20), at the position $\bar{r}_n=1$, the transport function T(s) from input current I(t) to the surface concentration $c^j_{ss}$ is:

$$\begin{aligned} T(s)=\frac{c^n_{ss}}{I}=M^n\frac{\sinh \left( \sqrt{s\sigma ^D_n}\right) }{\sinh \left( \sqrt{s\sigma ^D_n}\right) -\sqrt{s\sigma ^D_n}\cosh {\sqrt{s\sigma ^D_n}}} \end{aligned}$$

(21)

Since the advantage of Pade approximations is that they inherently preserve poles and zeros, this approximation approach can be utilized to transfer functions (21). The first-order Pade approximation is obtained:

$$\begin{aligned} T(s)\approx -M^n\frac{3/\sigma ^D_n+\frac{2}{7}s}{s+\frac{\sigma ^D_n}{35}s^2} \end{aligned}$$

(22)

Then, applying the inverse Laplace transform to (22):

$$\begin{aligned} \ddot{c}^n_{ss}(t)=-\frac{35}{\sigma ^D_n}\dot{c}^n_{ss}-\frac{105M^n}{(\sigma ^D_n)^2}I(t)-\frac{10M^n}{\sigma ^D_n}\dot{I}(t) \end{aligned}$$

(23)

Regarding the negative electrode, when the input current is constant ($\dot{I}=0$), the assumption of $\ddot{c}^n_{ss}=0$ is feasible. Thus, one have:

$$\begin{aligned} \dot{c}^n_{ss}(t)=\frac{3M^n}{(\sigma ^D_n)}I(t) \end{aligned}$$

(24)

For observing the boundary lithium-ion concentration of the negative electrode, the following boundary state observer is designed:

$$\begin{aligned} \begin{aligned}&\dot{\hat{c}}^n_{ss}(t)=\frac{3M^n}{(\sigma ^D_n)}I(t)-L(\hat{V}(\hat{c}^n_{ss}(t),t)-V(c^n_{ss}(t),t)) \end{aligned} \end{aligned}$$

(25)

When there exists a gain $L>0$, then the boundary observer appearing in equation (25) is convergent. $\hat{V}(\hat{c}^n_{ss}(t),t)$ satisfies:

$$\begin{aligned} \begin{aligned} \hat{V}(\hat{c}^n_{ss}(t),t)&=\frac{RT}{\alpha {F}}\sinh ^{-1}\left( \frac{-I(t)}{E^p\sqrt{G(c_{ss,max}^{n}-\hat{c}_{s s}^{n}(t))^2}}\right) -\frac{RT}{\alpha {F}}\sinh ^{-1} \left( \frac{I(t)}{E^n\sqrt{\bar{c}_e\hat{c}^n_{ss}({c}^n_{ss,max}-\hat{c}^n_{ss})}}\right) \\&+U^{p}(1-\frac{\hat{c}_{s s}^{n}(t)}{c_{s s, max}^{n}})-U^{n}\left( \frac{\hat{c}^{n}_{ss}(t)}{{c}^{n}_{ss,max}}\right) -R_fI(t)+R_eI(t)+K_f[\ln {c^p_e(0^p,t)}-\ln {c^n_e(0^n,t)}] \end{aligned} \end{aligned}$$

(26)

Since the maximum Lithium-ion concentration $c^{n}_{ss,max}$ in the negative electrode has almost no change in a short period of time, $c^{n}_{ss,max}$ can be assumed to be a fixed value around the true value. In addition, the boundary lithium-ion concentration ${c}^n_{ss}$ will change dramatically in a short time, so the boundary lithium-ion concentration plays a remarkable role in the terminal voltage.

Next, the stability of the boundary lithium-ion concentration observer is proved. Introducing variable $\tilde{c}^n_{ss}(t)=c^n_{ss}(t)-\hat{c}^n_{ss}(t)$, then subtracting (25) from (24) yields:

$$\begin{aligned} \begin{aligned} \dot{\tilde{c}}^n_{ss}(t)=-L(V(c^n_{ss}(t),t)-\hat{V}(\hat{c}^n_{ss}(t),t))\\ \end{aligned} \end{aligned}$$

(27)

Using a Lyapunov functional as follows:

$$\begin{aligned} V_L=\frac{1}{2\lambda }(\tilde{c}^n_{ss})^2 \end{aligned}$$

(28)

The derivative of Lyapunov function with respect to time is computed as follows:

$$\begin{aligned} \begin{aligned} V_L=\frac{1}{\lambda }\tilde{c}^n_{ss}\dot{\tilde{c}}^n_{ss}=-\frac{1}{\lambda }\tilde{c}^n_{ss}L(V(t)-\hat{V}(\hat{c}^n_{ss}(t),t)) \end{aligned} \end{aligned}$$

(29)

Since $V(c^n_{ss}, t)$is monotonically increasing with respect to $c^n_{ss}$, one have:

$$\begin{aligned} sign(\tilde{c}^n_{ss})=sign(V(t)-\hat{V}(t)) \end{aligned}$$

(30)

$sign(\cdot )$ means the operation of taking a symbol, then:

$$\begin{aligned} \tilde{c}^n_{ss}=-sign[V(t)-\hat{V}(t)]\times |\tilde{c}^n_{ss}| \end{aligned}$$

(31)

Substituting (31) into (29) obtains:

$$\begin{aligned} \begin{aligned} V_L&=\frac{1}{\lambda }\tilde{c}^n_{ss}\dot{\tilde{c}}^n_{ss}=-\frac{1}{\lambda }L|(V(t)-\hat{V}(\hat{c}^n_{ss}(t),t))|\times |\tilde{c}^n_{ss}|\le 0 \end{aligned} \end{aligned}$$

(32)

Therefore, the boundary concentration observer in (25) is convergent.

SoH estimation based on least square method

Define $\tilde{c}^n_{ss,max}=c^n_{ss,max}-\hat{c}^n_{ss,max}, \tilde{c}^p_{ss,max}=c^p_{ss,max}-\hat{c}^p_{ss,max}$, then the output voltage can be rewritten as:

$$\begin{aligned} \begin{aligned} V(t)&=\frac{RT}{\alpha {F}}\sinh ^{-1}\left( \frac{-I(t)/E^p}{\sqrt{G(\hat{c}^n_{ss,max}+\tilde{c}^n_{ss,max}-\hat{c}^n_{ss})^2}}\right) -\frac{RT}{\alpha {F}}\sinh ^{-1} \left( \frac{I(t)/E^n}{\sqrt{\bar{c}_e\hat{c}^n_{ss}(\hat{c}^n_{ss,max}+\tilde{c}^n_{ss,max}-\hat{c}^n_{ss})}}\right) \\&+U^{p}(1-\frac{c^{n}_{ss}(t)}{\hat{c}^n_{ss,max}+\tilde{c}^n_{ss,max}})-U^{n} \left( \frac{c^{n}_{ss}(t)}{\hat{c}^n_{ss,max}+\tilde{c}^n_{ss,max}}\right) -R_fI(t)+R_eI(t)+K_f[\ln {c^p_e(0^p,t)}-\ln {c^n_e(0^n,t)}]. \end{aligned} \end{aligned}$$

(33)

(33) is expanded by McLaughlin series as follows:

$$\begin{aligned} \begin{aligned} V(t)&=\frac{RT}{\alpha {F}}\sinh ^{-1}\left( \frac{-I(t)/E^p}{\sqrt{G(\hat{c}^p_{ss,max}-{c}^p_{ss})^2}}\right) -\frac{RT}{\alpha {F}}\sinh ^{-1} \left( \frac{I(t)/E^n}{\sqrt{\bar{c}_e\hat{c}^n_{ss}({c}^n_{ss,max}-{c}^n_{ss})}}\right) +U^{p}(1-\frac{c^{n}_{ss}(t)}{\hat{c}^n_{ss,max}})\\&-U^{n}\left( \frac{c^{n}_{ss}(t)}{\hat{c}^n_{ss,max}}\right) -R_fI(t)+R_eI(t)+K_f[\ln {c^p_e(0^p,t)}-\ln {c^n_e(0^n,t)}]+\frac{\partial {V(\hat{c}^n_{ss,max},t)}}{\partial {c^n_{ss,max}}}\tilde{c}^n_{ss,max}+\Delta (c^n_{ss,max}). \end{aligned} \end{aligned}$$

(34)

where, $\Delta (c^n_{ss,max})$ is high-order infinitesimal with respective to $c^n_ {ss, max}$ and can be ignored.

Then:

$$\begin{aligned} \begin{aligned}&V(c^n_{ss,max})-V(\hat{c}^n_{ss,max})=\frac{\partial {V(\hat{c}^n_{ss,max},t)}}{\partial {c^n_{ss,max}}}\tilde{c}^n_{ss,max}. \end{aligned} \end{aligned}$$

(35)

where,

$$\begin{aligned} \begin{aligned} \hat{V}(\hat{c}^n_{ss,max})&=\frac{RT}{\alpha {F}}\sinh ^{-1}\left( \frac{-I(t)/E^n}{\sqrt{G(\hat{c}^n_{ss,max}-{c}^p_{ss})^2}}\right) -\frac{RT}{\alpha {F}}\sinh ^{-1} \left( \frac{I(t)/E^n}{\sqrt{\bar{c}_e\hat{c}^n_{ss}({c}^n_{ss,max}-{c}^n_{ss})}}\right) +U^{p}(1-\frac{c^{n}_{ss}(t)}{\hat{c}^n_{ss,max}})\\&-U^{n}\left( \frac{c^{n}_{ss}(t)}{\hat{c}^n_{ss,max}}\right) -R_fI(t)+R_eI(t)+K_f[\ln {c^p_e(0^p,t)}-\ln {c^n_e(0^n,t)}] \end{aligned} \end{aligned}$$

(36)

The least squares capacity estimator is designed as follows:

$$\begin{aligned} \dot{\hat{c}}^n_{ss,max}=-P\frac{\partial {V(\hat{c}^n_{ss,max},t)}}{\partial {c^n_{ss,max}}}(V(c^n_{ss,max})-V(\hat{c}^n_{ss,max})) \end{aligned}$$

(37)

where, P is a positive scalar, employing Lyapunov function $\frac{1}{2}(\tilde{c}^n_{ss,max})^2$ and observer (37) can easily prove that estimated error ${\tilde{c}}^n_{ss,max}$ is convergent.

After obtaining ${\hat{c}}^n_{ss,max}$, SoH can be calculated as follows:

$$\begin{aligned} SoH=\frac{{\hat{c}}^n_{ss,max}}{{{c}}^n_{ss0,max}} \end{aligned}$$

(38)

where, ${{c}}^n_{ss0,max}$ denotes the initial maximum lithium-ion concentration of the negative electrode.

Principle of mapping particle filter

With the SoH data set obtained, appropriate method should be selected to predict the aging trend and remaining life of lithium-ion batteries. Particle filter is a filtering method based on probability statistics, which is not only suitable for the scene with Gaussian noise, but also effective for the scene with non-Gaussian noise. Particle filter samples the space through particle state realization, which represents the state probability density based on partial noise observation, namely the posterior density. The challenging of particle filter is to recursively express the high probability region of the posterior density with a finite number of particles. Generally, particle filter will show degeneracy, that is, after a number of iterations, the weight will be concentrated on one particle. In the important sampling framework, sampling can be improved by selecting a transitional proposed density that conforms to the current observed value. Since a good selection of proposal density can mitigate filter degradation, the resampling step is still required if the filter is recursively applied. While the application of resampling tends to another problem, namely particle dilution, which reduces particle diversity because only a few particles with higher weight are retained and reproduced during the resampling process. To improve particle diversity, Manuel et al.²⁹ proposed a particle filter using kernel embedded maps, which utilizes a series of maps to pull particles from predicted density to posterior density, minimizing the divergence between posterior and intermediate density sequences. The mapping sequence signifies a gradient flow on the basis of the principle of local optimal transmission. An essential ingredient of the maps is that they are implanted in a reconstituted kernel Hilbert space, which permits a practical and efficient Monte Carlo algorithm. In this paper, this method is used to estimate the residual life of lithium-ion batteries, which is also the first time that the mapping particle filter is applied to the life prediction of lithium-ion batteries.

Sequential Bayesian estimation

This research assumes that the estimation issue consists of a dynamic model X that predicts the state $\textbf{u}$ by the previous state and the observation model Y. This process transforms the state space to the observation space. The system of equations defining the estimation issue is called the state space model, that is:

$$\begin{aligned} \begin{aligned} \textbf{u}_{k}={X}\left( \textbf{u}_{k-1}, \varvec{\eta }_{k}\right) ,~ \textbf{v}_{k}={Y}\left( \textbf{u}_{k}, \varvec{\mu }_{k}\right) \end{aligned} \end{aligned}$$

(39)

where, $\textbf{u}_{k} \in \mathbb {R}^{N_{u}}$ is the state at time k, $\textbf{v}_{k} \in \mathbb {R}^{N_{v}}$ is the observed value, $\varvec{\eta }_{k} \sim p(\varvec{\eta })$ is the model random error and $\varvec{\mu }_{k} \sim p(\varvec{\mu })$ is the observation error. This method is generic independent of the additive, the Gaussian assumptions of the model or the observation error.

Particle flow and optimized transport

The filter requires updating the previous knowledge provided by the predicted density with the observed likelihood. Introducing the concept of homotopy, the prior density $q(\textbf{u})$ can be smoothly converted to the posterior density $p(\textbf{u})$. This can be achieved by a continuous transformation of the parameters, for example $T(\textbf{u}, \lambda ): \mathbb {R}^{N_{u}} \times [0,1] \rightarrow \mathbb {R}, T(\textbf{u}, \lambda )=p(\textbf{u})^{\lambda } q(\textbf{u})^{1-\lambda }$. The parameter $\lambda$ represents a pseudo time ranging from 0 to 1 at a fixed moment in time. Density is expressed in terms of particles, so the transformation can be interpreted as the motion of particles in a fluid, which follows a set of ordinary differential equations:

$$\begin{aligned} \frac{d \textbf{u}_{\lambda }}{d \lambda }=\textbf{V}_{\lambda }\left( \textbf{u}_{\lambda }\right) \end{aligned}$$

(40)

where, $\textbf{u}_{\lambda }$ is the drift field or the velocity field. Here, the flow is the focus of this research, and thus ignoring the diffusion process. Under this flow, the density evolution is given by the Liouville equation:

$$\begin{aligned} \partial _{t} q_{\lambda }+\nabla \cdot \left( \textbf{V}_{\lambda } q_{\lambda }\right) \end{aligned}$$

(41)

Optimal transmission is a promising method for sampling complicated posterior distributions. Set a prior probability density distribution $q(\textbf{u})$ and a target probability density distribution $p(\textbf{z})$, the probability density q is transmitted to p by a mapping $T: \textbf{u} \rightarrow \textbf{z}$. The optimal transmission problem seeks to transform T such that the cost of transporting the density distribution from q to p is minimized. This stands for the classical Munch optimal transmission problem and, under mild conditions, the existence of such an optimal mapping is proved. The thoughts of optimal transmission and particle flow are unified in this research. The local method is applied to find the optimal transmission, where this research needs to obtain a gradient flow. The particle can be advanced from the prior density to the objective density by a series of mappings given by the gradient flow. The mapping in the sequence needs to be as reposeful as possible. Particles show active Lagrangian tracking in gradient flow. At every pseudo time procedure of the mapping operation, the velocity field is selected according to a local optimal transmission criterion.

Implementation of mapping particle filter

Supposing there are a set of equally weighted particles $u^{(1:N_p)}_ {k-1}$ that sample the posterior density of the time $k-1$, the variational mapping is utilized to sample the objective density at the time step k, and the objective density of posterior density is $p (u_k|v_{1:k})$. The mapping method needs only a group of samples of prior density, and it starts with a group of particles unweighted from the prior estimate, that is $\left\{ \textbf{u}_{k, 0}^{(j)}={M}\left( \textbf{u}_{k-1}^{(j)}, \varvec{\eta }_{k}^{(j)}\right) \right\} _{j=1}^{N_{p}}$, where the second subscript represents the mapping iteration. Then the sample points of these predicted densities are pushed to the posterior density by mapping iteration.

Set the particles $u^{(1:N_p)}_ {k-1}$, which are the samples of the middle density of the mapping step $k-1$, the grads of the Kuhr-Becker divergence at the state u is as follows:

$$\begin{aligned} \begin{aligned} \nabla \mathscr {D}_{K L}(\textbf{u})=&-\frac{1}{N_{p}} \sum _{l=1}^{N_{p}}\left[ K\left( \textbf{u}_{k, i-1}^{(l)}, \textbf{u}\right) \nabla \log p\left( \textbf{u}_{k, i-1}^{(l)}\right) +\nabla _{u} K\left( \textbf{u}_{k, i-1}^{(l)}, \textbf{u}\right) \right] \end{aligned} \end{aligned}$$

(42)

The first term of the Kuhl–Baker divergence gradient (42) will push the particle towards the peak of the posterior density. It shows a weighted average of $\nabla \log p$ within the scale of the present particle kernel consisting of the current particle and circumambient particles. The second term in equation (42) are used to divide the particles. If the present particle $\textbf{u}_{k}^{(j)}$ in the range of influence of another particle $\textbf{u}_{k}^{(l)}$, namely in the nuclear scale, So $\nabla _{\textbf{u}_{k, i-1}^{(l)}} K\left( \textbf{u}_{k, i-1}^{(l)}, \textbf{u}_{k, i-1}^{(j)}\right)$ will act as a repulsive force between the particles to separate them. At the i-th mapping, the particle j is transformed into:

$$\begin{aligned} \textbf{u}_{k, i}^{(j)}=\textbf{u}_{k, i-1}^{(j)}-\epsilon \nabla \mathscr {D}_{K L}\left( \textbf{u}_{k, i-1}^{(j)}\right) \end{aligned}$$

(43)

where, $-\nabla \mathscr {D}_{K L}\left( \textbf{u}_{k, i-1}^{(j)}\right)$ is the steepest drop direction of a particle. One problem of sequential Bayesian inference is that there is no exact expression for the posterior density. As the likelihood function is exactly known, there are only a set of particles representing the prior density, not the density itself. The particle of posterior density at time $i-1$ is expressed as:

$$\begin{aligned} p\left( \textbf{u}_{k} \mid \textbf{v}_{1: k-1}\right) \approx \frac{1}{N_{p}} \sum _{j}^{N_{p}} p\left( \textbf{u}_{k} \mid \textbf{u}_{k-1}^{(j)}\right) \end{aligned}$$

(44)

The posterior density can be expressed as follows:

$$\begin{aligned} p\left( \textbf{u}_{k} \mid \textbf{v}_{1: k}\right) \propto \frac{1}{N_{p}} p\left( \textbf{v}_{k} \mid \textbf{u}_{k}\right) \sum _{j}^{N_{p}} p\left( \textbf{u}_{k} \mid \textbf{u}_{k-1}^{(j)}\right) \end{aligned}$$

(45)

Since the set size is finite at time $k-1$, this expression is an approximation of the backward density. In each mapping iteration, all particles move according to Eq. (42). By gradient descent and the corresponding update of $\nabla \mathscr {D}_{K L}$, the successive application of the transformation will converge to the minimum of the Kurl–Baker divergence. The execution process of the mapping particle filter is shown in Table 1.

Table 1 Mapping particle filtering algorithm.

Life prediction of lithium-ion batteries

The premise of applying MPF is to find or build a suitable dynamic model X. The dynamic aging process of lithium-ion batteries is generally established by regression models, such as polynomial fitting and exponential fitting. In this paper, an aging model with exponential growth is used to fit aging curve³⁰. To achieve reliable exponential models, Matlab curve fitting toolbox was used. Choose the following exponential growth model:

$$\begin{aligned} \text {SoH}=a_1\cdot \exp (a_2\cdot k)+a_3\cdot \exp (a_4\cdot k) \end{aligned}$$

(46)

Among them, $a_1$, $a_2$, $a_3$and $a_4$ are model parameters, and the initial values of these parameters can be gotten by fitting the historical SoH estimates. Here, $a_1$and $a_3$ are in connection with the internal impedance, while $a_2$ and $a_4$ are relevant to the aging rate. k is the number of cycles, and SoH is the battery health status. If these parameters are precisely estimated, the model (46) can reliably predict the aging trend and remaining service life of lithium-ion batteries.

The system state equation and output equation can be written as follows:

$$\begin{aligned} & \begin{aligned}&x_{k}=\left[ a_{1,k}; a_{2, k}; a_{3, k}; d_{4, k}\right] \\&{\left\{ \begin{array}{ll}a_{1,k}=a_{1,k-1}+\omega _{a_1} & \omega _{a_1} \sim N\left( 0, \sigma _{a_1}\right) \\ a_{2,k}=a_{2,k-1}+\omega _{a_2} & \omega _{a_2} \sim N\left( 0, \sigma _{a_2}\right) \\ a_{3,k}=a_{3, k-1}+\omega _{a_3} & \omega _{a_3} \sim N\left( 0, \sigma _{a_3}\right) \\ a_{4,k}=a_{4,k-1}+\omega _{a_4} & \omega _{a_4} \sim N\left( 0, \sigma _{a_4}\right) \end{array}\right. } \end{aligned} \end{aligned}$$

(47)

$$\begin{aligned} & \begin{aligned} \text {SoH}_{, k}=a_{1, k} \exp \left( a_{2, k} \cdot k\right) +a_{3,k} \exp \left( a_{4,k} \cdot k\right) ,~ n_{k} \sim N\left( 0, \sigma _{n}\right) \end{aligned} \end{aligned}$$

(48)

where $\text {SoH}_{k}$ is the SoH when the number of cycles is k, and N(0, r) is the Gaussian noise possessing zero mean and standard deviation. The p step prediction value $\text {SoH}_{k+p}$ of SoH is calculated as:

$$\begin{aligned} \begin{aligned} \text {SoH}_{k+p}=\sum _{i=1}^{N} \text {SoH}_{k+p}^{i},~ \text {SoH}_{ k+p}^{i}=a_{1,k}^{i} \exp \left[ a_{2,k}^{i} \cdot (k+P)\right] +a_{3, k}^{i} \exp \left[ a_{4, k}^{i} \cdot (k+P)\right] \end{aligned} \end{aligned}$$

(49)

In this case, the probability distribution function of the predicted value is:

$$\begin{aligned} P\left( \text {SoH}_{k+p} \mid \text {SoH}_{0: k}\right) \approx \sum _{i=1}^{N} \omega _{k}^{i} \delta \left( \text {SoH}_{k+p}-\text {SoH}_{k+p}^{i}\right) \end{aligned}$$

(50)

Results and discussion

In this section, the accuracy of the SoH estimation method is verified firstly through simulation, and then the accuracy of mapping particle filtering (MPF) and standard particle filtering (SPF) in lithium-ion battery life prediction using NASA battery cycle test data under the experimental conditions in Table 2. are compared³¹. Initially, the parameters of the battery model used by this research are identified by the method of particle swarm optimization. The specific parameter identification block diagram In this section, the accuracy of the SoH estimation method is verified firstly through simulation, and then the accuracy of mapping particle filtering (MPF) and standard particle filtering (SPF) in lithium-ion battery life prediction using NASA battery cycle test data are compared³¹. Initially, the parameters of the battery model used by this research are identified by the method of particle swarm optimization. The specific parameter identification block diagram In this section, the accuracy of the SoH estimation method is verified firstly through simulation, and then the accuracy of mapping particle filtering (MPF) and standard particle filtering (SPF) in lithium-ion battery life prediction using NASA battery cycle test data are compared³¹. Initially, the parameters of the battery model used by this research are identified by the method of particle swarm optimization. The specific procedure of parameter identification is described using a block diagram as shown in Fig. 1:

Fig. 1

Procedure of parameter identification by particle swarm optimization.

The procedure begins by initializing the parameters of battery model. Then, one calculates the fitness value of each particle and finds the optimal values for individuals and groups. Next, the speed and position of individual particles are updated. In the judgment step, the error function of the model needs to be calculated and used to identify if the error function is less than the preset value. If yes, the parameter identification is finished, and if no, return to the second step and repeat the same work. In the simulation, 2C/3C constant current is used and 5mV random voltage measurement error is taken into account. The true and estimated values of the initial boundary lithium-ion concentration are $20,000 \text {mol/m}^3$ and $22,500 \text {mol/m}^3$, respectively, while the true and estimated values of the maximum negative lithium-ion concentration are $29,850 \text {mol/m}^3$ and $22,000\text {mol/m}^3$ respectively. Within 10 seconds, the estimated boundary lithium-ion concentration converges rapidly to the true value, as shown in Fig. 2a. Then, the estimated and true values change synchronously over time and maintain a high accuracy. Figure 2b shows the true and estimated value of the maximum negative lithium-ion concentration. The estimated value of the maximum lithium-ion concentration can also be tracked to the true value within 10 seconds and maintains around the true value. The fluctuation of the two estimates is caused by random errors in voltage measurements. Figure 2c shows the relative error of the boundary lithium-ion concentration estimation, and it can be found that the relative error decays to near zero within 10 seconds, which is consistent with the result of Fig. 2b. Figure 2d depicts the error between the real output voltage and the estimated voltage. The voltage estimation error serves as the feedback signal of the state estimation and indirectly characterizes the estimation error of other states. Since the output voltage is a function of the current, the boundary lithium-ion concentration and the maximum lithium-ion concentration, the voltage estimation error approaching zero is equivalent to the estimation of the boundary lithium-ion concentration and the maximum lithium-ion concentration approaching true values. Figure 3a,b)shows the estimated value of SoH and the relative error of the estimated value. It can be found that SoH can also track the true SoH within 10 s, and the stable relative error is less than 0.5%. In conclusion, the SoH estimation method proposed in this paper has a high accuracy.

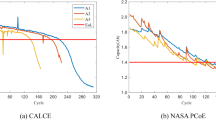
Then, the effectiveness of MPF in lifetime prediction is verified with NASA lithium-ion battery experimental data, mainly using the current, voltage and SoH data of B0005, B0006, B0007 and B0018 batteries. Figure 3c shows the output voltage curve of one battery under different cycles. It can be found that with the increase of cycles, the output voltage curve shifts to the left and the gradient increases when releasing the same amount of electricity. The higher the aging degree, the higher the voltage drop will be, which is also the key to estimate SoH according to the output voltage. Figure 3d shows the aging trend of four kinds of batteries where there are significant differences between them indicating the importance of obtaining the historical SoH data of battery cells. The electrochemical parameters of batteries are obtained by genetic algorithm³². Figures 4 and 5 represent the measured and estimated values of SoH of four batteries. And it can be found that the measured values of SoH have great volatility, which is caused by the loose operation of discharge process or the error of measuring instruments. Although the measured value of SoH is not very accurate, the overall trend of SoH decay is in line with the actual situation. In addition, the estimated value of SoH is highly consistent with the variation trend of the measured values, and the estimation error is maintained within 4%, which indicates that the SoH estimation algorithm in this paper has reliable accuracy. Therefore, the measured value of SoH can be replaced by the real-time SoH estimation to avoid the problem that battery SoH can be only accurately obtained after completing discharge and improving the efficiency of battery life prediction.

The life prediction process is as follows: The SoH value of the 100 cycles is estimated using the method in this chapter; Then, the 100 SoH estimates were fitted in Matlab to obtain the initial aging model parameters. Finally, the mapping particle filter is used to predict the remaining number of cycles when the battery SoH is aged to 80%. Figure 6 represents the battery life prediction results of B0005, B0006, B0007 and B0018, which can be found that the life prediction curve of the mapping particle filter (MPF) is closer to the real aging curve than that of the standard particle filter (SPF). Figure 7a shows the true and estimated number of remaining cycles by bar graph and line graph, respectively. Figure 7b shows the prediction error of the remaining cycle times. It can be found that the lifetime prediction error of MPF is about 2%, while that of SPF is about 7%. Therefore, the lifetime prediction of MPF has high accuracy.

Table 2 Experimental conditions for battery data.

Fig. 2

True and estimated values of boundary lithium-ion concentration (a) and maximum lithium-ion concentration (b); Evaluated error of $c^-_{ss}/c^-_{ss,max}$ (c) and output voltage (d).

Fig. 3

Estimated values (a) and error (b) of SoH; Discharging voltages of different cycles for one battery (c) and aging trends of different batteries (d).

Fig. 4

SoH estimates (a) and estimation error (b) of battery B0005; SoH estimates (c) and estimation error (d) of battery B0006.

Fig. 5

SoH estimates (a) and estimation error (b) of battery B0007; SoH estimates (c) and estimation error (d) of battery B0018.

Fig. 6

Residual life prediction of battery B0005 (a) and battery B0006 (b); Residual life prediction of battery B0007 (c) and battery B0018 (d).

Fig. 7

Prediction of the residual cycles of four batteries (a) and prediction error of the residual cycles of four batteries (b).

Conclusions

In this study, an online estimation method for the state of health (SoH) of lithium-ion batteries was developed based on an electrochemical model that incorporates electrolyte dynamics. Then the residual lifetime of the batteries was subsequently predicted using the mapping particle filter (MPF). Specifically, the Pade approximation method was employed to derive the transfer function between the boundary lithium-ion concentration and the input current, followed by the design of a boundary state estimator to determine the boundary lithium-ion concentration. The SoH was then estimated using the least squares method, and a regression model was applied to fit the SoH data, enabling the extraction of initial parameters for the aging model. The future researches incorporating additional real-world factors such as temperature fluctuations, varying charge-discharge rates, and mechanical stress will be considered and can improve its accuracy and robustness. Besides that, integrating machine learning techniques, such as deep neural networks or reinforcement learning, with the existing model could further refine the SoH estimation and RUL prediction capabilities.