Introduction

With the continuous growth of energy demand, oil exploration and development are facing increasingly severe challenges, and improving drilling efficiency has become a top priority1,2. Steering drilling technology maximizes oil and gas production by adjusting the drill bit direction in real time, and wellbore trajectory prediction, as a core link, has a direct impact on drilling efficiency3,4. However, traditional drilling methods have obvious limitations when dealing with complex geological conditions, and cannot accurately predict wellbore trajectories, which often leads to inefficiency and waste of resources5,6. Therefore, developing accurate wellbore trajectory prediction methods is of great significance for improving directional drilling efficiency, reducing operating costs, and ensuring the efficient development of oil and gas resources.

Yang et al. proposed a longitudinal, torsional, and radial coupling dynamic model of drill pipe, and obtained parameters such as torsional angular displacement and angular velocity in the normal drilling and sliding vibration stages to predict the wellbore trajectory7. While this method accounts for various factors during normal drilling and sliding vibration phases, the influence of drill bit noise compromises the final prediction accuracy. To address this issue, Huang designed an outlier removal mechanism to mitigate its negative impact8. However, comparative simulation results reveal that this method has certain limitations. Zhang et al. proposed an improved trajectory extension model to reduce the trajectory deviation during vertical drilling to control the wellbore trajectory9. However, under complex geological conditions, the formation characteristics are complex and changeable, making it difficult to monitor and adjust in real-time and maintain the ideal deviation, which leads to increased trajectory deviation and affects drilling efficiency and quality. Tian combined a physical model with a GA-BP approach to regressively analyze the BUR of individual bend motor components. This was utilized to predict the wellbore trajectory for the next drilling phase10. Based on space geometry, formation anisotropy theory, and the three-moment formula, Kong et al. established the model of formation variable deviation pressure and formation variable azimuth force to predict wellbore trajectory11. However, these methods are difficult to apply under complex geological conditions. Yan et al. proposed the random forest method to predict angles12. This method only requires data-based prediction of wellbore trajectories without building complex models. However, it is an integrated learning method based on decision trees, which is suitable for static feature data and performs poorly for time-dependent sequence data. Huang et al. predicted the deviation angle and azimuth angle through the LSTM model13. However, the LSTM model faces challenges such as difficulty in hyperparameter tuning and susceptibility to overfitting. Gao et al. proposed a new method combining ridge regularization and SSA to more accurately predict wellbore trajectory. However, this method only considers a single factor affecting the wellbore trajectory14. Therefore, there is an urgent need for a novel wellbore trajectory prediction method to enhance accuracy and applicability.

Hochreiter et al. proposed LSTM in 1997, effectively capturing nonlinear features in data15. Andre Ip et al. used LSTM neural networks to predict the future trajectory of vehicles16; Gou et al. used LSTM neural network to predict the length of a day17; Quan et al. used LSTM to predict pedestrian trajectories18; Bai et al. proposed a dynamic internal LSTM prediction method for predicting key alarm variables in chemical processes19. When the data dimensionality is high, noise is substantial, and the time-series relationships are complex, using independent LSTM models can lead to increased model complexity. This may cause the model to mistakenly learn random fluctuations instead of true patterns, resulting in overfitting the minor variations in the data. To enhance the model’s robustness and reduce the impact of noise, a combined LSTM approach is more effective in capturing the genuine time-series relationships, thereby improving the model’s generalization ability20,21. Yousefzadeh et al. adopted a deep neural network with a variational autoencoder to extract salient features for trajectory optimization. In addition, they combined ConvLSTM and the FMM and proposed the ConvLSTM-FMM method to assist permeability amplification22,23. Mohagheghian et al. used LSTM to predict the drilling strength before the drill bit24. Zhou et al. established a new model based on CNN and LSTM to predict and describe complex keyhole behavior25; Yin et al. proposed a prediction model combining U-Net and LSTM to forecast changes in lake boundaries26; Wu et al. combined CNN and LSTM to achieve more accurate predictions of stock prices27; Lee et al. used a CNN-LSTM model to forecast ship trajectories in different scenarios28; Sahu et al. proposed LSTM and FCNN deep learning methods to classify benign and malicious connections on intrusion datasets29; Ma et al. integrated the LSTM networks with FCNN to program the shape of soft intelligent materials30; Jawed et al. used LSTM-FCNN to analyze EEG signals measured in a resting state with closed eyes31. However, the hyperparameters of these methods are difficult to adjust, and optimization algorithms are needed to optimize them.

In 2023, Mohamed et al. proposed a NOA, which was inspired by the behavior of magpies in finding and storing food. It has strong global search capabilities. By simulating the behavior of magpies in the search space, it can quickly converge to a better solution in a small number of iterations and is suitable for complex nonlinear optimization problems. Abatari et al. used NOA to solve the optimal power flow problem of the power system and applied it to the optimal power flow calculation of IEEE 30-bus and IEEE 118-bus systems32; Xu et al. proposed an improved nonlinear time series prediction method combining VMD and CNN-BiLSTM-AttNTS and NOA to accurately predict short-term wind speed33. ; Zhang et al. designed a multi-layer CNN and developed an improved NOA to optimize the internal parameters of CNN and then predict student grades34.

According to the above-mentioned research, this paper proposes a new steering drilling wellbore trajectory prediction method, named NOA-LSTM-FCNN, which combines NOA, LSTM, and FCNN. This method utilizes the memory units and gate mechanism of LSTM neural networks to handle long-term dependencies in the wellbore trajectory sequence. Outputting the results of the LSTM layer to the FCNN layer enhances the representational capacity of the proposed method. Further optimization is achieved through NOA, enabling the NOA-LSTM-FCNN method to handle complex and large-scale problems while exhibiting a certain degree of adaptability to different scenarios. The proposed method in this paper features automatic hyperparameter optimization, capturing long-term dependencies, improving prediction accuracy and generalization ability, and applies to various types of wellbore trajectory data. Through simulation experiments, compared to traditional prediction methods, this method demonstrates high prediction accuracy, effectively enhancing drilling efficiency, and reducing costs.

The methods of LSTM, FCNN and NOA

Long short-term memory networks (LSTM)

LSTM was first proposed in 1977. When processing long-term data dependencies, it overcomes the gradient vanishing and gradient exploding problems encountered by standard RNNs, effectively controls the reading, writing and deletion of information, and makes the model more flexible and accurate35,36. The basic unit of LSTM includes three main gating mechanisms: input gate, forget gate, and output gate. These three gates work together to determine the storage, update, and output of information. The LSTM structure is shown in Fig. 1. The calculation of the three gates is as follows:

$${{\varvec{f}}_t}=\sigma ({{\varvec{W}}_f} \cdot [{{\varvec{h}}_{t - 1}},{{\varvec{x}}_t}]+{{\varvec{b}}_f})$$
(1)
$${{\varvec{i}}_t}=\sigma ({{\varvec{W}}_i} \cdot [{{\varvec{h}}_{t - 1}},{{\varvec{x}}_t}]+{{\varvec{b}}_i})$$
(2)
$${\tilde {{\varvec{C}}}_t}=tanh({{\varvec{W}}_{\varvec{c}}} \cdot [{{\varvec{h}}_{t - 1}},{{\varvec{x}}_t}]+{{\varvec{b}}_{\varvec{c}}})$$
(3)
$${{\varvec{C}}_t}={{\varvec{f}}_t}*{{\varvec{C}}_{t-1}}+{{\varvec{i}}_t}*{\tilde {{\varvec{C}}}_t}$$
(4)
$${{\varvec{o}}_{\varvec{t}}}=\sigma ({{\varvec{W}}_{\varvec{o}}} \cdot [{{\varvec{h}}_{t - 1}},{{\varvec{x}}_t}]+{{\varvec{b}}_{\varvec{o}}})$$
(5)
$${{\varvec{h}}_t}={{\varvec{o}}_{\varvec{t}}} * tanh({{\varvec{C}}_{\varvec{t}}})$$
(6)

where \({{\varvec{W}}_{\varvec{f}}}\),\({{\varvec{W}}_{\varvec{i}}}\),\({{\varvec{W}}_{\varvec{c}}}\),\({{\varvec{W}}_{\varvec{o}}}\) is the weight matrix of the prediction model; \({{\varvec{b}}_{\varvec{f}}}\),\({{\varvec{b}}_{\varvec{i}}}\),\({{\varvec{b}}_{\varvec{c}}}\),\({{\varvec{b}}_{\varvec{o}}}\) is the bias vector of the prediction model; \({{\varvec{f}}_t}\)is the forgetting gate; \({{\varvec{i}}_t}\) is the input gate; \({{\varvec{o}}_t}\)is the output gate; \({\tilde {{\varvec{C}}}_t}\) is candidate cell states; \({{\varvec{C}}_{t-1}}\) represents the cell state at the previous moment; \(\sigma (x)\) and \(tanh(x)\) is the activation function.

Fig. 1
figure 1

Overall structure of LSTM network.

Full size image

Fully connected neural networks (FCNN)

FCNN is the most basic and common neural network architecture. It consists of an input layer, a hidden layer, an output layer, and multiple neurons (nodes). The neurons in each layer are connected to those in the previous and next layers. The input layer is the first layer of the neural network, responsible for receiving external input data. Each input node corresponds to a feature. The hidden layer is the layer between the input layer and the output layer of the neural network. They process the input data through weighted summation and activation functions. The output layer is the last layer of the neural network, which outputs the final prediction result. Neurons are the basic computing units of FCNN. Each neuron receives input from the previous layer, performs linear transformation through weighting and bias, and then outputs the result through a nonlinear activation function37. Its basic structure is shown in Fig. 2, where \(p=1,2, \cdots\) and \(q=1,2, \cdots\).

First, the input data is passed into the network through the input layer. Then the neurons in each layer are connected to all the neurons in the previous layer, and nonlinear transformation is performed through weighted summation and activation function to extract features layer by layer. Finally, after being processed by multiple hidden layers, the data is passed to the output layer to generate the final prediction result. During the training process, the network evaluates the difference between the prediction and the true value by calculating the loss function and uses the backpropagation algorithm to adjust the weights and biases in the network to minimize the loss value and optimize the prediction ability of the model38,39. FCNN can flexibly adjust the number of layers and neurons. It has a simple structure and can effectively learn complex nonlinear relationships. It is suitable for various prediction tasks.

Fig. 2
figure 2

Basic structure of FCNN.

Full size image

Nutcracker optimizer algorithm (NOA)

In 2023, Mohamed et al. proposed a new optimization method called NOA, inspired by the behavior of magpies in finding and storing food. NOA is a nature-inspired optimization algorithm inspired by the behavior of squirrels collecting and storing food in summer and autumn and retrieving food by recalling storage locations in winter and spring. By simulating this natural process, NOA achieves global optimization and can efficiently solve complex optimization problems. NOA mainly consists of two core strategies: foraging and storage strategy, and cache search and recovery strategy40. The basic framework of NOA is illustrated in Fig. 3.

In the foraging phase, search agents are considered individuals exploring the solution space, where each point in the space represents a potential solution. The search agents assess the quality of each solution by evaluating the objective function value and store high-quality “seed” solutions in the “storage area” to support subsequent optimization. Once the “seed” solutions are transported to the “storage area,” high-quality “seed” solutions are transferred to the “temporary storage points.” Through this hierarchical storage approach, solutions from the “temporary storage points” are prioritized, improving retrieval and application efficiency, and leading to better solutions. This initialization strategy divides the search space, identifies key data points and important areas, and then covers these key data points with a higher probability in the critical regions of the search space. This allows the NOA to quickly discover high-quality solutions with fewer initial data, effectively narrowing the search space and improving search efficiency.

In the cache search stage, NOA introduces a “hierarchical memory strategy” to improve search efficiency. The solutions found during the search process are stored and marked according to priority and hierarchy. The high-quality solutions of the global search are stored at a high level to facilitate the guidance of global exploration; the local solutions are stored at a low level for local optimization. When searching, the algorithm prioritizes the selection of potential high-quality solutions from the high-level memory to avoid blind searches and quickly locate promising areas. In the recovery stage, NOA flexibly adjusts the strategy according to the progress and status of the search. In the early stage of global search, the algorithm prioritizes the recovery of solutions in the high-level memory to guide the search to the potential high-quality area; in the local search stage, it makes more use of the low-level memory to optimize the local solution through in-depth mining. Such a strategy design helps the NOA algorithm to dynamically balance between global exploration and local optimization, continuously improve search results, and gradually approach the optimal solution.

Overall, NOA achieves efficient global optimization capabilities by imitating the behavior of squirrels foraging and storing food, combined with hierarchical memory strategies, and provides an innovative method for solving complex problems.

Fig. 3
figure 3

Basic framework of NOA.

Full size image

The proposed method NOA-LSTM-FCNN

The LSTM layer is used to extract the time-dependent features in the processed well trajectory data, and the FCNN layer is added afterwards to further process these features and generate prediction results. This approach not only comprehensively extracts hidden features and preserves the temporal characteristics of the data but also captures inter-data correlations. However, LSTM-FCNN needs to continuously find the best hyperparameters when setting hyperparameters, and a large number of trial-and-error processes lead to increased computational costs.

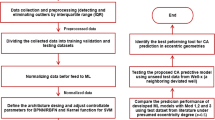
In the construction process of machine learning and deep learning models, the selection of hyperparameters plays a crucial role in model performance. Traditional hyperparameter adjustment methods often rely on manual experience and repeated trials, which are not only time-consuming and labor-intensive but also difficult to ensure that the optimal hyperparameter configuration is found, resulting in high computational costs. The intelligent optimization algorithm (NOA) has a unique advantage. It can efficiently search in the complex hyperparameter space and quickly locate the near-optimal or even optimal hyperparameter combination through continuous iteration and evaluation. This significantly reduces the time cost caused by manual parameter adjustment and improves the efficiency and effectiveness of model development. Therefore, using NOA to optimize the LSTM-FCNN method can automatically find the best hyperparameter combination, thereby effectively reducing computational costs. The flow chart of the proposed method is shown in Fig. 4.

Fig. 4
figure 4

Flowchart of the NOA-LSTM-FCNN method.

Full size image

The main steps are as follows:

  1. (1)

    Import data and preprocess.

The average value method is used to replace the outliers in the data set, and the data set is normalized.

  1. (2)

    Construct the LSTM-FCNN method.

① LSTM first computes a candidate memory, representing new memory content, based on the current input \({{\varvec{x}}_t}\) and the previous time step’s hidden state \({{\varvec{h}}_{t - 1}}\). Then, LSTM uses forget gates and input gates to determine how much of the previous time step’s memory to retain and how much new input information to record, respectively. Finally, LSTM utilizes an output gate to decide which information should be included in the output state.

② Next, the hidden states \({{\varvec{h}}_t}\) outputted by the LSTM layer are further mapped using the FCNN layer, ultimately generating the neural network’s output \({\hat {z}_t}\). As shown in Eq. (7):

$${\hat {z}_t}=f({\varvec{W}} \cdot {{\varvec{h}}_t}+{\varvec{b}})$$
(7)

Where \({\varvec{W}}\) is the weight matrix of the FCNN layer; \({\varvec{b}}\) is the bias vector of the FCNN layer; \(f( \cdot )\) is the activation function.

③ The square of the error between the measured value \({z_t}\) and the LSTM output value \({\hat {z}_t}\) is used as the loss function, as shown in Eq. (8):

$$Loss(\omega ,b)={({z_t} - {\hat {z}_t})^2}={({z_t} - f(\omega \cdot {h_t}+b))^2}$$
(8)

During the training process, the chain rule is used to calculate the error gradient between the predicted output and the true label, and then the gradient is propagated from the output layer back to the input layer, while updating the weights and biases of the gated units. The update of weights and biases is detailed in Eq. (9) and Eq. (10):

$${\omega _{t+1}}={\omega _t} - \alpha \cdot \left( {\left( {\partial Loss(\omega ,b)} \right)/\left( {\partial \omega } \right)} \right)$$
(9)
$${b_{t+1}}={b_t} - \alpha \cdot \left( {\left( {\partial Loss(\omega ,b)} \right)/\left( {\partial b} \right)} \right)$$
(10)

Where \({\omega _t}\) and \({b_t}\) are the weights and bias terms at time t; \({\omega _{t+1}}\) and \({b_{t+1}}\) are the weights and bias terms at the next time step t + 1; \(\alpha\) is the learning rate, indicating the step size along which the weights and bias terms are updated in the direction of the gradient.

  1. (3)

    Automatic optimization of hyperparameters.

The dimension of NOA is the number of hyperparameters that need to be optimized. The RMSE between the predicted value and the actual value is used as the fitness function. The corresponding strategy is used to continuously update the hyperparameters until the current number of iterations is less than the maximum number of iterations. The hyperparameters corresponding to the minimum fitness value are used as the optimal hyperparameters of the model.

  1. (4)

    The NOA-LSTM-FCNN network is trained and predicted.

① Replace the hyperparameters in the NOA-LSTM-FCNN network with the optimal hyperparameters in step (3) and use the training set to train the network. When the number of training times reaches the maximum number of training times, the training ends.

② Use the “predict and update state” function to predict the test set data. This function continuously updates the model’s internal state to ensure accurate predictions on new data.

Data preparation and hyperparameter settings

Data set

The dataset used in this study is sourced from three wells (H21, H22, and H23) in a block of an oilfield in northern China, all of which have complete observational records. The data from each well include features such as deviation, azimuth, tool face angle, well depth, and vertical depth, which are related to the wellbore trajectory.

For Well H21, the designed well depth is 2570 m, and the actual well depth is 2569.87 m. The drill string configuration includes a 311.2 mm PDC bit, Φ216mm drill pipe (1.25°), Φ308mm stabilizer, 203 mm non-magnetic drill collar, 203 mm MWD short section, six 177.8 mm drill collars, nine 158.8 mm drill collars, and 127 mm inclined drill pipe. Data was collected every 20 s, with each data point including deviation, azimuth, tool face angle, well depth, vertical depth, etc. A total of 2000 data points were collected, forming the dataset for Well H21.

For Well H22, the designed well depth is 2390 m, and the actual well depth is 2389.67 m. The drill string configuration includes a 215.9 mm PDC bit, Φ172mm drill pipe (1.25°), Φ212mm stabilizer, float valve, one 158.8 mm non-magnetic drill collar, 172 mm MWD short sections, six 158.8 mm drill collars, nine 127 mm heavy-weight drill pipes, and 127 mm inclined drill pipe. Data was collected every 15 s, with each data point including the same features as those for Well H21. A total of 3000 data points were collected, forming the dataset for Well H22.

For Well H23, the designed well depth is 1170 m, and the actual well depth is 1168.24 m. The drill string configuration includes a 215.9 mm PDC bit, Φ172mm single-bend drill pipe (1.25°), Φ212mm centralizer, Φ165mm variable-thread coupling, one 158.8 mm non-magnetic drill collar, Φ172mm sub, Φ168mm variable-thread coupling, nine 158.8 mm drill collars, and Φ127mm drill pipe. Data was collected every 10 s, with each data point including deviation, azimuth, tool face angle, well depth, vertical depth, etc. A total of 3000 data points were collected, forming the dataset for Well H23.

For the experiment, the data from the three wells was divided into training and testing sets at an 8:2 ratio, with 80% of the data used for training and 20% used for testing. We have modified the corresponding content and highlighted the changes in blue, as detailed on page 6 of the revised manuscript.

Before training the model, the data needs to be preprocessed. For outliers in the data set, the data average of the ten points before and after the outlier is used to replace it. This can ensure the smoothness and continuity of the drilling trajectory data, reduce noise interference, and reflect the real change trend of the data. Normalizing the processed data set and scaling the values of different features to between 0 and 1 can prevent certain features from having too much impact on the model, improve numerical stability, and improve prediction performance. The calculation formula for outlier processing and data normalization is:

$$\bar {z}=\left( {{z_{i-10}}+ \cdots +{z_{i-1}}+{z_{i+1}}+ \cdots +{z_{i+10}}} \right)/20$$
(11)
$$x_{i}^{\prime }=\left( {{x_i}-\bar {x}} \right)/\left( {\left( {1/n} \right) \cdot \sum\limits_{{i=1}}^{n} {\left( {{x_i}-\bar {x}} \right)} } \right),i=1,2,3, \cdots$$
(12)

Where i represents the sequence of the outlier, \({z_i}\) denotes the outlier, \(\bar {z}\) represents the mean value, \(x_{i}^{\prime }\) is the normalized data value, \({x_i}\) is the sample value, \(\bar {x}\) is the sample mean, and n is the total count.

Feature selection

In addition to the well deviation, azimuth and tool face angle, the factors affecting the wellbore trajectory include drilling fluid viscosity, drilling fluid density, drilling fluid flow, flushing pressure, impact force, drilling pressure, drilling speed, rotary torque, direction of closure, closed distance, dogleg, east-west, north-south, vertical section, vertical depth, rock toughness, porosity, and circulation rate. In wellbore trajectory prediction, it is necessary to consider the features that have a significant impact and eliminate those with a smaller impact.

For drilling trajectory data with high dimensions, strong nonlinearity and strong spatiotemporal correlation, mutual information is used to measure the correlation between features41. The theoretical calculation is as follows:

$$I\left( {X,Y} \right)=\sum\limits_{{i=1}}^{n} {\sum\limits_{{j=1}}^{n} {p\left( {{x_i},{y_j}} \right){\text{log}}\left( {\frac{{p\left( {{x_i},{y_j}} \right)}}{{p\left( {{x_i}} \right)p\left( {{y_j}} \right)}}} \right)} }$$
(13)

Where, \((X,Y)\) is a two-dimensional discrete random variable, X and Y are discrete random variables respectively; \(p({x_i},{y_j})\) is the joint distribution law of \((X,Y)\), n is the total number of samples; \(p({x_i})\) and \(p({y_j})\) are the marginal distribution laws of \((X,Y)\), respectively.

When the probability distribution function is difficult to obtain, the k-nearest neighbor nonparametric density estimation method is used to estimate the joint and marginal probability density functions, and then integrate them to obtain the corresponding probability distribution function. Finally, the mutual information is calculated by Eq. (13), and the resulting histogram is shown in Fig. 5. The histogram indicates that drilling speed, drilling pressure, direction of closure, closed distance, dogleg, and vertical depth as input parameters, and deviation angle, azimuth angle, and tool face angle as output parameters, a wellbore trajectory prediction method is constructed.

Fig. 5
figure 5

Histogram of MI values for each feature.

Full size image

Fitness function and evaluation metrics

RMSE serves as a metric reflecting prediction accuracy, providing an intuitive measure of model performance. By minimizing RMSE, we effectively optimize the model to better fit and predict the target variable, thus enhancing its predictive capabilities and generalization performance. Therefore, RMSE is used as a fitness function.

In the prediction algorithm, evaluation metrics are of paramount importance as they not only gauge the accuracy of prediction methods but also guide their optimization and improvement. However, a single metric may not comprehensively reflect the complexity of the problem, often necessitating the consideration of multiple evaluation metrics. Therefore, RMSE, MAPE and R2 were selected as evaluation indicators to measure the performance of the prediction method, the calculation is as follows:

$$RMSE=\sqrt {\frac{{\mathop \sum \nolimits_{{i=1}}^{n} {{\left( {{{\hat {y}}_i} - {y_i}} \right)}^2}}}{n}}$$
(14)
$$MAPE=\frac{1}{n}\mathop \sum \nolimits_{{i=1}}^{n} \left| {\frac{{{{\hat {y}}_i} - {y_i}}}{{{y_i}}}} \right| \times 100\%$$
(15)
$${R^2}=1 - \frac{{\mathop \sum \nolimits_{{i=1}}^{n} {{\left( {{y_i} - {{\hat {y}}_i}} \right)}^2}}}{{\mathop \sum \nolimits_{{i=1}}^{n} {{\left( {{y_i} - \bar {y}} \right)}^2}}}$$
(16)

Where n is the number of predicted samples, \({y_i}\) represents the observed values. \({\hat {y}_i}\) represents the predicted values. \(\bar {y}\) indicates the observed sample mean. The smaller the values of RMSE and MAPE evaluation metrics, the better the predictive performance of the model. The closer the R2 evaluation metric is to 1, the better the model’s performance.

Hyperparameter settings

To evaluate the proposed method’s prediction effect, a comparative analysis was conducted with traditional machine learning methods and deep learning methods, including LR, SVM, BP, CNN, LSTM, and GRU. Since LR does not involve hyperparameter optimization, the hyperparameters of the other models are automatically searched using the NOA optimization algorithm to find the best configuration. Specifically, the key parameters of NOA are set according to experimental experience: the attempt ratio to avoid falling into the local optimum is 0.05, the probability of switching between the cache search phase and the recovery phase is 0.2, and the ratio of exploring other areas of the search space is 0.2. During the optimization process, the number of search agents is set to 30, and the maximum number of function evaluations is 20. The value ranges of the hyperparameter combinations of each model are shown in Table 1. When optimizing the hyperparameters of each model, NOA runs each model 20 times and selects the result with the smallest RMSE value as the best hyperparameter configuration. This section only shows the optimization results of well H21. Well H22 and well H23 use the same optimization method. The optimization results of the SVM hyperparameter regularization parameter C are as follows: The C value of the well deviation angle is 10; The C value of the azimuth angle is 16; the tool face angle is 8. The optimization configuration results of the other models are shown in Tables 2, 3 and 4.

Table 1 The value ranges of the hyperparameter combinations of each model.
Full size table
Table 2 Hyperparameter optimization results of well H21.
Full size table
Table 3 Hyperparameter optimization results of well H22.
Full size table
Table 4 Hyperparameter optimization results of well H23.
Full size table

Experimental results

To verify the effectiveness of the proposed algorithm, Sect. 5 conducts a comparative analysis from two aspects: traditional machine learning methods (LR, SVM, BP) and deep learning methods (CNN, GRU, LSTM). Specifically, Sect. 5.1 shows the comparison results between the proposed algorithm and traditional machine learning methods, Sect. 5.2 shows the comparison results with deep learning methods, and Sect. 5.3 comprehensively compares the performance of the proposed algorithm with conventional machine learning methods and deep learning methods in various evaluation indicators.

The proposed method compared with machine learning method

To validate the effectiveness of the NOA-LSTM-FCNN prediction method, we compared it with traditional machine learning methods such as LR, SVM, and BP, based on the same training dataset. Since LR does not need to perform hyperparameter optimization, only the SVM and BP methods are compared here. The test results for wells H21, H22, and H23 are shown in Figs. 6, 7 and 8.

Fig. 6
figure 6

Predicted results of machine learning for well H21.

Full size image
Fig. 7
figure 7

Predicted results of machine learning for well H22.

Full size image
Fig. 8
figure 8

Predicted results of machine learning for well H23.

Full size image

As can be seen from the figure above, for the deviation angle of Well H21, the predicted curve generated by NOA-SVM has the poorest fit with the true value curve, while the curve generated by NOA-LSTM-FCNN has the best fit. The predicted curves generated by the other two machine learning methods fall between NOA-SVM and NOA-LSTM-FCNN in terms of fit. Regarding the azimuth angle and tool face angle of well H21, and the deviation angle, azimuth angle, and tool face angle of wells H22 and H23, the prediction curve generated by LR has the worst fit to the true value curve, and the curve generated by NOA-LSTM-FCNN is the worst. The best fit. The other two machine learning methods generated prediction curves that were intermediate between NOA-SVM and NOA-LSTM-FCNN in terms of fit.

Based on the analysis above, regarding deviation angle, azimuth angle, and tool face angle of Well H21, all predicted curves generated by LR, NOA-SVM, and NOA-BP exhibit less than ideal fit with the true value curves. Similarly, for Well H22, all predicted curves generated by LR, NOA-SVM, and NOA-BP show a poor fit with the true value curves. Likewise, for Well H23, all predicted curves generated by LR, NOA-SVM, and NOA-BP exhibit significant deviation from the true value curves. From the above analysis, it can be concluded that traditional machine learning methods with hyperparameter optimization can achieve better prediction results.

The proposed method compared with Deep Learning Method

For the comparison of deep learning methods, CNN, GRU, LSTM, and NOA-LSTM-FCNN were selected. Using the same dataset and employing the hyperparameter combinations optimized by NOA as described above for each method, the resulting prediction results are depicted in Figs. 9, 10 and 11.

Fig. 9
figure 9

Predicted results of deep learning for well H21.

Full size image
Fig. 10
figure 10

Predicted results of deep learning for well H22.

Full size image
Fig. 11
figure 11

Predicted Results of Deep Learning for Well H23.

Full size image

By observing Fig. 9, it can be noted that for predicting the deviation angle of the H21 well, the NOA-LSTM-FCNN method exhibits the best predictive performance, while the CNN method performs the worst. The performance of the other methods falls between these two extremes. When predicting the azimuth angle, the CNN method performs poorly, while the NOA-LSTM-FCNN method achieves the best predictive performance. The performance of the other methods is relatively good, closely resembling the true value curve. For predicting the tool face angle, the NOA-LSTM-FCNN method demonstrates the best predictive performance, while the CNN method performs poorly.

Through Fig. 10, it can be observed that for the deviation and azimuth angles of the H22 well, the predictive performance of each method is similar. The NOA-LSTM-FCNN method achieves the best predictive performance. For the prediction of tool face angle, the CNN method has poor prediction effect, the proposed method has the best prediction effect.

According to Fig. 11, for H23 well, the prediction effect of each method is similar, and the predictive results are quite satisfactory.

Therefore, compared to the NOA-CNN, NOA-GRU, and NOA-LSTM methods, the NOA-LSTM-FCNN method achieves better predictive performance for well trajectory prediction.

Evaluation Metrics Prediction results

To provide a comprehensive overview of the performance of the NOA-LSTM-FCNN method, three metrics are used to evaluate the predictive results of the NOA-LSTM-FCNN method on the dataset. As shown in Tables 5, 6 and 7.

Table 5 Evaluation metrics for deviation angle, azimuth angle, and tool face angle prediction of well H21.
Full size table
Table 6 Evaluation metrics for deviation angle, azimuth angle, and tool face angle prediction of well H22.
Full size table
Table 7 Evaluation metrics for deviation angle, azimuth angle, and tool face angle prediction of well H23.
Full size table

It can be seen from Tables 4, 5 and 6 that for the H21 well, the RMSE values of the proposed method for well deviation angle, azimuth angle, and tool face angle are 0.036131°, 0.0020913°, and 0.081527°, respectively; the MAPE values are 0.2702%, 0.0887%, and 0.2087%, respectively; and the R² values are 0.89809, 0.98506, and 0.99706, respectively. For the H22 well, the RMSE values are 0.019605°, 0.012682°, and 3.8406°; the MAPE values are 0.03045%, 0.11065%, and 2.5635%; and the R² values are 0.99416, 0.99757, and 0.99835, respectively. For the H23 well, the RMSE values are 0.0014809°, 3.1052°, and 1.7792°; the MAPE values are 0.18013%, 4.2141%, and 0.42869%; and the R² values are 0.99942, 0.99892, and 0.99474, respectively.

From the results of the prediction evaluation indicators, for well deviation angle, azimuth angle, and tool face angle, the BP method with hyperparameter optimization in machine learning performs the best. In contrast, the LR method yields the lowest accuracy, and the SVM method performs between the two. Compared with other methods, the proposed method has smaller RMSE and MAPE values, and its R² is closer to 1, indicating higher prediction accuracy. Among the deep learning methods, NOA-LSTM-FCNN achieves the best prediction performance, while CNN performs the worst. Therefore, compared to existing machine learning and deep learning methods, the NOA-LSTM-FCNN method demonstrates higher accuracy in wellbore trajectory prediction.

Computational cost

To comprehensively evaluate the effectiveness of the proposed NOA-LSTM-FCNN model, we compared the performance of various models in terms of training time, prediction time, and memory consumption, validating the overall advantages of NOA-LSTM-FCNN for wellbore trajectory prediction tasks. Since there is a strong correlation between the deviation angle, azimuth angle, and tool face angle, and their prediction tasks, output dimensions, and loss functions are identical, we compared and analyzed the computational costs of seven algorithms (LR, NOA-SVM, NOA-BP, NOA-CNN, NOA-LSTM, NOA-GRU, and NOA-LSTM-FCNN) using datasets from Wells H21, H22, and H23, as shown in Figs. 12, 13 and 14.

Fig. 12
figure 12

Training time of each method.

Full size image
Fig. 13
figure 13

Prediction time of each method.

Full size image
Fig. 14
figure 14

Memory consumption of each method.

Full size image

The traditional LR model has extremely low cost in terms of training and prediction time, but due to its simple linear modeling mechanism, it cannot effectively handle complex nonlinear data relationships, resulting in poor prediction accuracy. Although the NOA-SVM model takes longer to train, it performs better in terms of prediction time, and its prediction accuracy is improved compared to the traditional LR model. The NOA-BP model performs moderately in various cost indicators, but its prediction accuracy fails to meet the high requirements of complex well-travel trajectory prediction tasks. The NOA-CNN model has powerful feature extraction capabilities but has obvious disadvantages in terms of cost, such as long training time, average prediction efficiency, and large memory consumption. As algorithms that specialize in processing time series data, the NOA-LSTM and NOA-GRU models can better capture the time characteristics in the well trajectory data and significantly improve the prediction accuracy. However, they are also accompanied by longer training time and larger memory consumption. In contrast, the NOA-LSTM-FCNN model proposed in this article is significantly better than other models in prediction accuracy and achieves an ideal balance between training time and memory consumption, showing good stability and practicality.

Therefore, the NOA-LSTM-FCNN model has obvious advantages in wellbore trajectory prediction scenarios, effectively solving the challenges posed by complex wellbore structures and providing reliable support for practical engineering applications.

Conclusions

In order to improve the accuracy of wellbore trajectory prediction, this article draws on the advantages of NOA, LSTM, and FCNN and proposes a new steerable drilling well trajectory prediction method (NOA-LSTM-FCNN). This method uses LSTM to process well trajectory sequence data; passes the output of LSTM to FCNN to improve expression ability and generalization performance; and then optimizes it through NOA, so that NOA-LSTM-FCNN method can automatically find the best hyperparameter combination and is adaptive. Compared with other methods, the proposed method has higher prediction accuracy, effectively improves drilling efficiency and reduces drilling costs. However, this method has not yet been applied in actual drilling operations. In subsequent research, the number of parameters and training time of this method will be continuously improved and applied in actual drilling activities. In addition, this method can also predict other time series data, such as economic data, stock market data, meteorological data, etc.