Introduction

For the upcoming generation of energy infrastructure, electric power distribution systems are seen as promising ideas 1. Ensuring a constant supply of power and meeting the growing demand are challenging tasks for both developed and developing countries. The reliance on finite petroleum-based resources, coupled with environmental concerns, has intensified interest in renewable energy sources (RESs) 2,3,4. RESs like sun and wind, are a desirable alternative since they are non-polluting, limitless, and scalable when placed close to load centres 5,6. Wind and solar (PV) power generation technologies have grown faster than even the most optimistic forecasts.

Multi-source hybrid energy systems provide consumers greater power quality and dependability than single-source systems 7,8,9,10. This integrated approach makes hybrid systems especially suitable for remote or isolated communities, such as on distant islands. Future distribution networks are expected to incorporate smart grid concepts, with flexible microgrids (MGs) capable of operating reliably across diverse environmental conditions 11. Both grid-connected and standalone applications of these systems are under development, with particular focus on controllers integrated into inverters to support hybrid system functionality 12.

Investigating high-end converter and inverter topologies is one of the many control strategies that are essential to guaranteeing efficient MG functioning 13. High-bandwidth communication systems are necessary for the frequent usage of conventional controllers, such as centralised, master–slave, and droop-based controllers 14,15,16,17. However, these conventional approaches face challenges, such as weak transient responses and instability when dynamic loads are present, as well as limitations in black-start capabilities. Fuzzy-logic controllers, sliding mode control, neuro-fuzzy control, and hierarchical control schemes are some of the methods that have been used to overcome these difficulties 18. However, when large-signal disruptions occur, these techniques frequently fail to provide minimal steady-state tracking error and robustness. Such disturbances—like high startup currents or faults in supercapacitors can lead to disconnection of distributed energy resources (DERs) or damage components. The proposed strategy in this context is thoroughly detailed to overcome these issues. In recent years, advanced modeling techniques like machine learning-based optimization, hybrid control systems, and deep reinforcement learning have become increasingly important in microgrid energy management. Machine learning-based optimization, especially with algorithms such as genetic algorithms, support vector machines, and neural networks, has demonstrated its ability to tackle the complexities of fluctuating energy demands and the variability of renewable energy sources (RES) 19. Hybrid control systems, which integrate both predictive and reactive controls, have been effective in stabilizing microgrid operations by managing various energy sources and ensuring efficient dispatch. Additionally, deep reinforcement learning methods provide a modern approach by learning optimal energy management strategies through ongoing interaction with the system, taking long-term effects into account. However, current research often misses key challenges. Many studies do not adequately address RES uncertainty and are constrained by overly simplified forecasting models. Furthermore, they frequently overlook real-time scheduling and hybridization techniques that could improve system performance in dynamic and unpredictable environments. This research aims to fill these gaps by proposing a hybrid model for a more reliable and adaptive energy management solution 20.

Various research works in the literature have explored unit commitment in renewable energy systems using a range of methods, as outlined in studies 21,22,23,24,25,26,27,28,29,30.

Energy management methods (EMSs) are essential to guaranteeing the PV array, PEMFC, battery bank, and supercapacitor of the DC microgrid function well, claim Alharbi et al. 21. Considering high efficiency and low H2 consumption, the EMS balances the load between the supercapacitor, PV array, PEMFC, and lithium-ion battery. A novel framework for inner-outer layers was created by Lyu et al. 22. Energy Management System (EMS) operational optimisation is the focus of the inner layer, while sizing optimisation is the focus of the outer layer. Its two-layer interaction mechanism is unique in that the outer layer focusses on size assignment and renewal, while the inner layer is constrained by size assignment and notifies the outer layer of the related operating cost.Yu et al. have presented a novel Energy Management System (EMS) for microgrids with multiple energy sources, including hydrogen and fuel cells 23. To improve energy resource efficiency and reduce waste, the EMS uses artificial intelligence algorithms to predict and adapt to sudden changes. A comprehensive analysis of advanced energy management and control in a multi-source/multi-load microgrid has been computed by El Mezdi et al. 24. Electric vehicles (EVs), Li-ion batteries, solar panels, wind turbines, and a DC load are all linked into the microgrid. A DC/AC inverter links them to the AC grid, and power electronic converters link them to a DC bus.A peer-to-peer energy trading system for multi-industrial micro-grids has been presented by Wu et al. 25 to promote the efficient use of local renewable energy resources. Two layers make up the recommended structure.

For an interconnected microgrid, Srivastava and Das 26 offer an interactive class topper optimisation (I-CTO) based energy management scheme that considers demand side management, battery storage systems, renewable energy sources, etc. Rezaei et al. 27 developed a two-layer framework for optimal islanding efficiency of a multi-energy microgrid (MG) coupled with prosumer HRSs. Each HRS has a number of technologies, including electrolysers, solar panels, batteries, and hydrogen storage. They can also share electricity with the MG. In rural, off-grid settlements, Barua et al. 28 evaluated an improved optimisation technique for the energy management of a renewable energy solar/wind microgrid with many diesel generators. By addressing the economic emission dispatch problem with a price penalty component, the main objective is to lower the energy cost and emission level. Tan et al. 29 have introduced an improved data-driven polyhedral uncertainty set based on updated self-organising feature map neural networks doing data clustering. Additionally, a hierarchical structure that eliminates the need for iterations is proposed for implementing the tri-layer energy management of MMGs with a high degree of EV integration. As a result of Wu et al. 30, this study suggests a hierarchical online EMS (HEMS) to run the hybrid hydrogen–electricity storage system (HSS) in a residential microgrid (RMG) affordably.

In reviewing these EMS across various microgrid configurations, several notable drawbacks emerge that underscore the complexities and limitations of current methodologies. Alharbi et al. 21 emphasize efficiency and low hydrogen consumption, yet the challenge remains in balancing rapid, high-demand fluctuations, particularly in systems where multiple energy sources. The inner-outer optimization framework by Lyu et al. 22 offers a two-layer interaction mechanism, yet its high computational requirements can complicate real-time operational effectiveness. Yu et al. 23 introduce AI-driven EMS to manage diverse energy sources, but integrating such algorithms in dynamic microgrids demands continuous recalibration to prevent overfitting to specific patterns, which can limit adaptability to unexpected energy scenarios. El Mezdi et al. 24 discuss multi-source control with varied loads, yet the complexity of coordinating a mix of solar, wind, battery storage, and electric vehicles risks reliability issues if converter systems are not adequately synchronized. Additionally, peer-to-peer energy trading models, such as Wu et al. 25 framework for multi-industrial microgrids, struggle with regulatory and privacy concerns, particularly in decentralized trading environments. Srivastava and Das 26 propose the I-CTO optimization for interconnected microgrids, but scalability and convergence issues may arise as grid size and complexity increase. Rezaei et al. 27 explore optimal islanding in multi-energy microgrids, yet incorporating prosumer-driven energy exchanges with HRSs often leads to stability issues. Furthermore, Barua et al. 28 note the economic emission dispatch for off-grid microgrids, which, while beneficial for remote areas, requires substantial infrastructure investments that may be economically unfeasible. The hierarchical EMS in Tan et al. 29 and Wu et al. 30 indicate advancements in uncertainty handling but are constrained by heavy reliance on data accuracy, which can be problematic in regions lacking comprehensive data infrastructure. These drawbacks highlight the ongoing need for efficient, adaptable, and cost-effective EMS solutions in microgrid environments with diverse and fluctuating energy resources.

Research contribution

The research introduces a new hybrid algorithm that merges QI-NLS-G2O and GRZPNet to achieve optimal energy management in Multi-Energy Microgrids (MEMGs) while addressing the uncertainties associated with Renewable Energy Sources (RES).

This method incorporates off-design performance models for energy conversion devices, which enhances the accuracy of load demand forecasting and energy dispatching in industrial microgrids.

The hybrid approach shows improved performance in system modeling, cost-effective operations, and effective management of energy resources, even in the face of varying uncertainties such as wind and solar generation.

The remainder of this research is listed below; In Section "MG connected system architecture with the suggested controller", the suggested method is carefully explained. Section "Results and discussion" provides the results of the suggested technique’s accomplishments and the comments that follow, while Section “Conclusion” concludes the study.

MG connected system architecture with the suggested controller

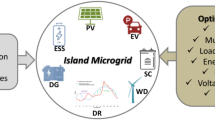
Figure 1 depicts the implementation of the suggested controller within the microgrid (MG) connected system architecture. In addition to a Point of Common Coupling (PCC), which acts as a single connection point for the power and voltage controller (P&V), this system is made up of many radial feeders that are each connected to sensitive and non-sensitive loads. A variety of micro sources, including as photovoltaic (PV) arrays and wind turbines (WT), are also installed on the feeders 31. While sources such as battery require fuel for power generation, renewable sources like WT and PV operate without the need for any fuel, relying on natural energy for electricity production. In the event of a fault, a static switch is used to disconnect the feeder from the utility grid. Additionally, in case of unexpected contingencies, a breaker is employed to prevent system damage. By incorporating MGs and battery storage, the entire system effectively addresses power demand challenges.

Fig. 1
figure 1

MG-connected systems’ architecture using the suggested controller.

Full size image

To prevent excessive discharge, a charge controller is required for the battery. To avoid overcharging, this controller regulates the charging current in addition to setting a limit on the discharge depth. All microgrids (MGs) use the power they generate to charge their batteries and satisfy load demands. The load demand is mostly met by renewable sources, like photovoltaic (PV) arrays and wind turbines (WT), because of their inexpensive cost of generation. In cases where the renewable sources cannot meet the demand, battery is used to address the shortfall. All of the micro sources’ power is used to power the load and charge the battery, as seen in Fig. 232. These relationships can be represented in the following general form:

$$p_{i,load} + p_{i,battery} = p_{i} ,\,\,\,\forall \,i = 1,2, \cdots ,N$$
(1)

where, \(p_{i}\), \(p_{i,load}\), \(p_{i,battery}\),\(N\) represents the output power, power from generator unit \(i\) to serve the load, the power from generator unit \(i\) to charge the battery, number of generators 45,46,47,48.

Fig. 2
figure 2

Flow diagram of the proposed methodology.

Full size image

Modelling of sources

The mathematical models for the battery, wind turbine, and photovoltaic (PV) systems are shown and derived in this subsection as follows:

Modelling of PV array

In order to assess the suggested Maximum Power Point Tracking (MPPT) technique, a two-diode model is utilised to depict the PV arrays’ properties 33. Especially in situations with low irradiance, this method improves performance accuracy and cuts down on computation time34,35. The output current of a PV array made up of strings connected in parallel and modules connected in series can be calculated as follows:36,37

$$i_{pv} n_{para} - i_{01} n_{para} \left[ {\exp \left( {\frac{{v + \mu ir_{se} }}{{\lambda_{1} v_{t} n_{seseries} }}} \right) - 1} \right] - i_{02} n_{para} \left[ {\exp \left( {\frac{{v + \mu ir_{S} }}{{\lambda_{2} v_{t} n_{se} }}} \right) - 1} \right] - \frac{{v + \mu ir_{S} }}{{\mu_{{}} r_{para} }} = i$$
(2)

where, output current as \(i\), output voltage as \(v\), \(r_{se}\) and \(r_{para}\) as resistance in series and parallel, two diodes thermal voltage as \(v_{t}\).

Modelling of wind system

For this study, the mathematical modeling of the horizontal-axis wind turbine (WT) is considered.

$$0.5\,a_{den} \pi \,r^{2} \,n_{w}^{2} b_{c} \left( {\mu ,\delta } \right) = p_{m}$$
(3)

where, air density as \(a_{den}\), radius of the turbine blades as \(r\), speed of the wind as \(n_{wind}^{{}}\), Betz constant is \(b_{c} \left( {\mu ,\delta } \right)\), in theory, up to 59 percent of wind power extracted, according to Betz 38.

$$n\frac{r\omega }{{n_{wind} }} = \mu$$
(4)

where, turbine mechanical angular velocity as \(\omega\).39

$$b_{1} \left( {\frac{{b_{2} }}{{\mu_{i} }} - b_{3} \delta - b_{4} } \right)\,e^{{{\raise0.7ex\hbox{${ - b_{5} }$} \!\mathord{\left/ {\vphantom {{ - b_{5} } {\mu_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\mu_{i} }$}}}} - b_{6} \mu = B_{c} \left( {\mu ,\delta } \right)$$
(5)

where, \(\mu_{i} = \left[ {\frac{1}{\mu + 0.08\delta } - \frac{0.035}{{\delta^{3} + 1}}} \right]^{ - 1}\).

Modelling of battery

The following equations are used to estimate the battery capacity40:

$$\frac{{k_{c} c_{0} \left( {1 - \frac{\theta }{{\theta_{f} }}} \right)^{\varepsilon } }}{{1 + \left( {k_{c} - 1} \right) \times \left( {\left| {\frac{i}{{i_{n} }}} \right|} \right)^{\delta } }} = c\left( {i,\theta } \right)$$
(6)

where, electrolyte temperature as \(\theta\), rated current as \(i_{n}\), constant parameters such as \(\theta_{f}\),\(c_{0}\),\(\varepsilon\),\(\delta\),\(k_{c}\).

$$SOC_{0} - \frac{{q_{e} }}{{c\left( {0,\theta } \right)}},\,q_{e} (t) = \int\limits_{0}^{t} {i_{bat} (t)dt} = SOC$$
(7)

where, \(i_{bat}\) as battery current.

$$SOC_{0} - \frac{{q_{e} }}{{c\left( {i_{fil} ,\theta } \right)}} = DOC;\frac{{i_{bat} }}{{1 + s\tau_{b} }} = i_{fil}$$
(8)

where, battery module discharge average current as \(i_{fil}\).

Multi-objective function of proposed methodology

In addition to meeting load demands, the chosen MG design should minimise fuel expenses and operating and maintenance costs. Consequently, the batteries’ fuel cost functions are integrated into a multi-objective function. Equation (9) represents the expression for this multi-objective function:41

$$F_{obj} = \mathop {\min }\limits_{i = 1}^{4} \left\{ {F(c)} \right\}$$
(9)

where,\(F_{obj}\) as minimize the fuel cost, operation and maintenance cost of the MG connected system, \(F\left( c \right)\) as total fuel cost of MG models.

$$F(c)\, = \,\sum\limits_{i = 1}^{N} {a_{i} + \,b_{i} \,P_{DG,i} \, + \,c_{i} \,P_{DG,i}^{2} }$$
(10)

Load demand prediction and optimal configuration of MG connected system using hybrid technique

In this section, the first step of the suggested hybrid approach is explained. The Gaussian Radius Zone Perceptron Net (GRZPNet) and Quadratic Interpolation and New Local Search for Greylag Goose Optimisation (QI-NLS-G2O) approaches are combined in this strategy. The suggested method seeks to balance the power from renewable sources while satisfying the grid operator’s power demands42. GRZPNet, an artificial neural network, is employed here, with its activation function utilized for the process 43,44. This algorithm develops multivariate, non-linear graphs. Three layers make up the GRZPNet training process: the input layer, hidden layer, and output layer. The hidden layer performs GRZPNet functions, whereas the input layer houses input nodes. A linear combination of the inputs and neurone parameters makes up the output layer, but the transition from the input to the hidden layer is non-linear. Utilising historical power demand data—more especially, data from the preceding year—the network is trained. The demand fluctuation for each hour is represented by the relevant input time intervals.

In the GRZPNet learning phase, load demand is predicted using QI-NLS-G2O. By examining potential solutions in a multi-dimensional search space, it finds the ideal control settings by striking a balance between exploration and exploitation. This approach optimises the learning process by comparing the best local and global solutions. The load demand for each hour serves as the input dataset for GRZPNet, which is trained using the historical demand datasets. Once trained, the network generates optimal demand outputs, reflecting the variation in demand for each hour. The QI-NLS-G2O technique is adopted for training the learning model, as described below.

Steps of QI-NLS-G2O

The learning technique is optimized iteratively using the QI-NLS-G2O algorithm, which effectively fine-tunes the controller, improving both power quality and system reliability in the photovoltaic system.

Step 1: Initialization

Set the input parameters to the controllers’ gain parameter at initialization.

Step 2: Random Generation

The QI-NLS-G2Oalgorithm generates a set of randomly initialized individuals, each representing a potential solution to the problem.

Step 3: Fitness Function

The fitness function is calculated as follows:

$$F = \min \left( {error} \right)$$
(11)

Step 4: Search Space

The QI-NLS-G2Oalgorithm separates individuals into exploration agents and exploitation agents using a dynamic grouping technique. The allocation of solutions to these groups is adjusted iteratively based on the quality of the current best solution.

Step 5: Exploration Phase

The exploration phase plays a crucial role in discovering promising regions within the search space and steering the algorithm away from suboptimal solutions, ultimately guiding it toward the globally optimal solution. Within the exploration phase, individual geese investigate the area around their current position in search of more favourable locations. This process involves an iterative evaluation of potential solutions in the vicinity, to identify the one that yields the best fitness value. The QI-NLS-G2Oalgorithm accomplishes this by utilizing the following equations given as

$$Y\left( {s + 1} \right) = Y^{*} \left( s \right) - D,\left| {F.Y^{*} \left( s \right) - Y\left( s \right)} \right|$$
(12)

where, \(Y\left( s \right)\) denotes the current position of the search agent, \(Y\left( {s + 1} \right)\) denotes the next updated position, \(D\) and \(F\) vectors are given as follows:

$$D = 2dr_{1} - d$$
(13)
$$F = 2r_{2}$$

Here, parameter \(d\) decrease linearly from 2 to 0 across iterations,\(D\) and \(F\) are vectors containing random values within the range [0, 1]. To enhance the exploration capability of the algorithm, three random search agents also explore the search space known as \(Y_{p1} ,\,\,Y_{p2} ,\,\,and\,\,Y_{p3}\) so the algorithm doesn’t depend on the leader’s position only. Then position update of any search agent for \(Y < 1\) is given as

$$Y\left( {s + 1} \right) = u_{1} *Y_{p1} + v*u_{2} *\left( {Y_{p2} - Y_{p3} } \right) + \left( {1 - z} \right)*u_{3} *\left( {Y - Y_{p1} } \right)$$
(14)

where, \(u_{1} ,\,\,u_{2} ,\,\,and\,\,u_{3}\) is between 0 and 2. The \(v\) decreases exponentially expressed as

$$v = 1 - \left( \frac{s}{S} \right)^{2}$$
(15)

For the parameter and decreasing value of \(d\), the position update equation is given as

$$Y\left( {s + 1} \right) = u_{4} *\left| {Y*\left( s \right) - Y\left( s \right)} \right|.e^{{cl.\cos \left( {2\pi l} \right)}} + \left[ {2u_{1} \left( {r_{4} + r_{5} } \right)} \right]*Y*\left( s \right)$$
(16)

where,\(c\) denotes constant parameter, random variable \(l\) with values in [-1, 1], a parameter \(u_{4}\) ranging within [0, 2], and parameters \(r_{4} \,\,and\,\,r_{5}\) both falling within [0, 1].

Step 6: Exploitation Phase

The person with the highest fitness at the conclusion of each iteration is identified as the leader in the QI-NLS-G2Oalgorithm. The QI-NLS-G2Oemploys two different strategies, which are described below, to direct its exploitation activities.

Progressing toward the optimal solution The three best search agents \(Y_{t1} ,\,\,Y_{t2} ,\,\,and\,\,Y_{t3}\) guide other random search agents \(Y\) to update their position towards the best location of prey. Mathematically, it is given as

$$Y_{1} = Y_{t1} - D_{1} \,.\,\left| {F_{1} \,.\,Y_{t1} - Y} \right|$$
(17)
$$Y_{2} = Y_{t2} - D_{2} \,.\,\left| {F_{1} \,.\,Y_{t2} - Y} \right|$$
(18)
$$Y_{3} = Y_{t3} - D_{3} \,.\,\left| {F_{1} \,.\,Y_{t3} - Y} \right|$$
(19)

Then updated position of the population is given as

$$Y\left( {s + 1} \right) = \frac{{Y_{1} + Y_{2} + Y_{3} }}{3}$$
(20)

Exploiting the Region near the Optimal Solution The algorithm prioritizes identifying solutions located near the current best solution (the leader). This is based on the assumption that further improvements may be found in this area. A subset of individuals, designated as \(Y_{f}\), focuses on this localized search. The QI-NLS-G2Oaccomplishes this process using the following equation:

$$Y\left( {s + 1} \right) = Y\left( t \right) + a\left( {1 + v} \right)*u*\left( {Y - Y_{f} } \right)$$
(21)

Step 7: Updating Process

The locations of other search agents are changed by the current positions of the most suitable search agents during the updating procedure, which applies the behavior and saves the first two optimal best solutions.

Step 8: Termination

Repeat steps 3 through 9 until the iteration reaches its maximum capacity. The best algorithmic answers are calculated as a global fitness function of the problem at the end of the iteration, and the position of the associated agent is determined as the global solution of the problem at certain dimensions. Based on the fitness function, the optimal solution is chosen at the termination stage. The best value of the optimization process is represented as \(e_{{}}^{best}\) and \(p_{d}^{best}\). The best dataset of the optimization parameters are defined as follows,

$$\,\left[ {\begin{array}{*{20}c} {e_{{}}^{11} } & {e_{{}}^{12} } & \cdots & {e_{{}}^{1n} } \\ {e_{{}}^{21} } & {e_{{}}^{22} } & \cdots & {e_{{}}^{2n} } \\ \vdots & \vdots & \vdots & \vdots \\ {e_{{}}^{m1} } & {e_{{}}^{m2} } & \cdots & {e_{{}}^{mn} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {p_{d}^{11} } & {p_{d}^{12} } & \ldots & {p_{d}^{1n} } \\ {p_{d}^{21} } & {p_{d}^{22} } & \ldots & {p_{d}^{2n} } \\ \vdots & \vdots & \vdots & \vdots \\ {p_{d}^{m1} } & {p_{d}^{m2} } & \ldots & {p_{d}^{mn} } \\ \end{array} } \right]$$
(22)

It is therefore possible to show the optimal pairing of error signals and power demand.

Steps of GRZPNet

The step by step process of GRZPNet is described as below,

Step 1: The Input Vector

It applies the input vector to the input layer network. The time interval, dc voltage, and current are referred to as the input network and the ideal speed as the output network in the suggested method. After that, the input vector equation is written as

$$V = \left[ {o_{1} \,\,\,o_{2} \cdots \,\,o_{p} \,} \right]^{T}$$
(23)

Here, input vector of the GRZPNet is denoted as \(o\) (Fig. 3).

Fig. 3
figure 3

GRZPNet structure.

Full size image

Step 2: GRZPNet Neurons

To be considered as a single vector, the “prototype” vector is stored in each GRZPNet neurone. Each GRZPNet neurone is compared to its prototype using the input vector, and the neurones’ output falls between 0 and 1 as a measure of similarity. Assuming the input is the same as the prototype, the GRZPNet neuron’s output is 1. Next comes the activation value, which is the neurone response value. “Centre” neurone is where the prototype vector is located.

Step 3: The Output Nodes

The network’s output contains a set of nodes, and each output node determines the score sequence for the related group. In most cases, the highest score category is assigned to inputs in order to classify them. The score determines the cumulative weight for the activation values from each GRZPNet neurone. The output terminal of each radial basis function neurone is connected to the weight value by the sum of the weights; this multiplies the neuron’s activity using its weight before adding the total response. Due to core calculations in each node, each output node has a unique weight for the varying category. The GRZPNet neurones receive a positive weight from the output node, whereas others receive a negative weight.

Results and discussion

In this study, a hybrid approach to power maximisation and overall generation cost minimisation is proposed 49,50. Battery sources and WT have been used to meet the system load needs. With the help of the suggested method, the optimal arrangement of MG sources has been used to meet the rising demand. The MG-connected systems’ load consumption is predicted using the suggested method. Other solution strategies are used to test the performance level of this technique, which is implemented in MATLAB/Simulink.

Figure 4 shows a comparison of actual, forecasted, and generated wind power data over a 24-h period. The actual data, depicted by the green line, varies between 0.7 and 1.1 p.u., reflecting the natural fluctuations in wind energy availability. The forecast data, represented by the pink line, closely tracks the actual data, remaining within the shaded uncertainty band that accounts for possible prediction errors. Notably, around 15:00, there is a peak reaching about 1.2 p.u., emphasizing the dynamic nature of wind power generation and its influence on energy management throughout the day. This variability highlights the importance of precise forecasting and real-time adjustments.

Fig. 4
figure 4

Real, forecast, and generated data for wind power over a 24-h period.

Full size image

Figure 5 shows PV generation data with similar forecast and real data trends. The real data peaks at approximately 1.0 p.u. around noon, indicating peak solar radiation. The forecast data follows closely, and uncertainty is represented by the shaded area. This trend highlights the typical midday peak in PV output due to sunlight availability.

Fig. 5
figure 5

PV generation data with similar forecast and real data trends.

Full size image

Figure 6 shows how the average return values for various models converge over time, highlighting the performance of the proposed model against DDPG, SAC, and TD3 models. The blue line, which represents the proposed model, quickly stabilizes its average return around 3500 after about 4000 iterations, suggesting it achieves optimal performance more swiftly. In contrast, the DDPG, SAC, and TD3 models exhibit slower convergence, emphasizing the proposed model’s enhanced capability to learn and adapt in fewer iterations. This quick convergence is essential for applications that need faster optimization in dynamic environments.

Fig. 6
figure 6

Convergence of different models’ average return values over time.

Full size image

Figure 7 compares seasonal costs under both rated and off-design conditions for various models, highlighting the cost differences between these two operational states. The costs consistently fall between 7000 and 8000 units throughout each season, indicating a stable cost performance. The slight variations between the rated and off-design conditions imply that the proposed model successfully maintains cost efficiency despite seasonal changes or operational differences. This suggests that the model is resilient in managing diverse operational scenarios, ensuring cost optimization and stability in energy management, thereby improving its practical use in real-world microgrid systems.

Fig. 7
figure 7

Seasonal costs under rated and off-design conditions for different models.

Full size image

Scheduling strategy for emergency simulation is shown in Fig. 8. Figure 8(a)—Sudden Decrease in Wind Turbine (WT) Output at 1:00: This chart demonstrates the response of the energy units when a sudden drop in wind turbine output occurs at 1:00. The wind turbine’s output plummets by nearly -2500 kW, simulating an unexpected wind lull or a system failure. To compensate, other units like PV and backup power sources respond by increasing output to stabilize the overall power supply. This shows the microgrid’s ability to adapt to sudden dips in wind generation. Figure 8(b)—Sudden Increase in PV Output at 19:00: Here, PV output spikes unexpectedly around 19:00, reaching around 3000 kW. In this case, the system dynamically reallocates power output among the units to avoid overloading and to maintain system balance. Units like batteries and other flexible sources reduce their output to absorb the surplus from the PV source, demonstrating the system’s capability to manage excess energy generation effectively 51. Figure 8(c)—Sudden Decrease in PV Output at 16:00: This chart shows a sharp reduction in PV output, dropping by approximately -2000 kW at 16:00, likely due to cloud cover or technical issues. The system responds by ramping up power from other sources, such as wind or storage units, to make up for the shortfall. This scenario illustrates the microgrid’s robustness in handling sudden losses in solar generation. Figure 8(d)—Sudden Increase in Wind Turbine Output at 12:00: In this case, there’s a sudden increase in wind output at noon, rising to about 1500 kW. The system adapts by reducing power output from other sources, like PV or backup generation units, to prevent excess supply and potential grid instability. This adaptation reflects the scheduling strategy’s ability to balance varying renewable inputs.

Fig. 8
figure 8

Scheduling strategy for emergency simulation (a) Sudden Decrease in Wind Turbine (WT) Output (b) Sudden Increase in PV Output (c) Sudden Decrease in PV Output (d) Sudden Increase in Wind Turbine Output.

Full size image

Intervals of purchased electricity are shown in Fig. 9. Figure 9 (a)—Daily Electricity Purchase Pattern with Upper and Lower Limits: In this graph, the electricity purchase pattern follows a cyclical demand trend, with the highest purchases occurring during peak hours. The forecast data (green line) aligns closely with the real data (pink line), indicating accurate demand predictions. The system’s purchases fluctuate mostly within the 1000–2500 kW range, constrained by the upper and lower dashed lines. This figure demonstrates the system’s ability to stay within prescribed purchasing limits, minimizing cost and managing demand efficiently. Figure 9(b)—Response to Higher Demand Peaks: This chart reflects a scenario with slightly elevated demand during certain hours, leading to temporary peaks in electricity purchases. Despite these increases, the purchases remain within the upper limit of around 2500 kW. This figure illustrates the system’s adjustment of grid purchases to accommodate higher-than-expected demand while minimizing excessive reliance on the grid. Figure 9(c)—Reduced Electricity Purchases During Lower Demand Hours: In this scenario, the system maintains relatively low electricity purchases, remaining near the lower limit of approximately 1000 kW for most of the day. This suggests a period of lower demand or higher availability of local generation (e.g., from RES). The system efficiently reduces grid purchases during these hours, conserving costs and relying more on internal generation sources. Figure 9(d)—Consistent Purchase Levels with Minor Fluctuations: In this scenario, the system maintains a relatively stable level of electricity purchase throughout the day, with minor fluctuations. The forecast and real data remain well-aligned, and all values stay comfortably within the upper and lower limits. This consistency reflects a balanced approach to grid purchases, with stable demand patterns and reliable forecasting.

Fig. 9
figure 9

Intervals of purchased electricity (a) (b) (c) (d).

Full size image

Intervals of purchased natural gas are shown in Fig. 10. Figure 10 (a)—Stable Natural Gas Purchases with Consistent Demand: In this figure, the natural gas purchase levels remain relatively steady throughout the day, with values closely following the forecast. Both the forecast (green line) and real data (pink line) fluctuate within the 200–500 cubic meters range, ensuring sufficient backup energy. This stability suggests a scenario where the microgrid anticipates consistent demand, allowing for predictable and manageable natural gas purchases. Figure 10 (b)—Increase in Natural Gas Purchases during Peak Demand Periods: This graph shows a scenario where natural gas purchases rise above the typical baseline, approaching the upper limit during peak demand hours. This increase likely compensates for lower RES generation or higher-than-expected demand. The system effectively adjusts its purchases to maintain energy supply within required limits, demonstrating its capacity to respond to peak demands by increasing reliance on natural gas as needed. Figure 10 (c)—Reduced Purchases During Low-Demand Hours: In this case, natural gas purchases remain closer to the lower limit, around 200 cubic meters, for much of the day. This scenario reflects periods of low demand or high-RES availability, allowing the microgrid to minimize natural gas reliance and save costs. The system adapts by reducing its natural gas purchases to only essential levels, ensuring efficient energy management. Figure 10 (d)—Minor Fluctuations within Allowable Limits: This graph presents a situation with minor fluctuations in natural gas purchases throughout the day, consistently staying within the 200–500 cubic meters range. The forecasted and real data remain well-aligned, indicating that the system can maintain stable gas purchasing without significant deviations. This scenario suggests a balanced and controlled approach to natural gas procurement, reflecting steady demand and reliable forecasting.

Fig. 10
figure 10

Intervals of purchased natural gas (a) (b) (c) (d).

Full size image

The efficiency of the suggested approach is assessed by comparing the elapsed time with existing, which is shown in Table 1. The table shows that, in comparison to existing, the suggested methods achieve a shorter computation time. The MCP (Table 2) of the suggested technique is examined using the existing technique to demonstrate the potential of the suggested approach. The estimation of cost accuracy percentage (ECAP) can be used to calculate the suitability of the suggested technique, and Eq. (24) provides specifics on the condition.

$$ECAP = \frac{best - worst}{{best}} \times 100$$
(24)
Table 1 Computational complexity comparison.
Full size table
Table 2 Mean, median and standard deviation of market clearing price (MCP) comparative analysis.
Full size table

Table 3 presents the Cost Average Percentage (CAP) for various existing techniques, indicating that these methods generally maintain a low CAP. In contrast, the proposed approach distinguishes itself by delivering better results under similar load conditions, with its overall cost being significantly lower than that of the other techniques. This highlights the proposed method’s effectiveness in enhancing cost efficiency. Additionally, the State of Charge (SoC) performance comparison in Table 4 further showcases the advantages of the suggested approach. With an impressive SoC value of 97.52%, the proposed method surpasses other existing techniques, which show SoC values of 80%, 55.47%, and 63%, respectively. These findings emphasize the proposed method’s accuracy and reliability in achieving a higher and more stable SoC, thereby ensuring effective energy management. The comparison of both CAP and SoC values offers strong evidence of the proposed model’s superior performance in energy management systems compared to existing techniques.

Table 3 Best, worst and ECAP performance analysis.
Full size table
Table 4 Comparative analysis of SoC using various methods.
Full size table

Conclusion

In this research, a hybrid technique is introduced for system modelling and management of MG connected systems with low cost in industrial grids. Performance testing is done on the suggested hybrid technique using the MATLAB/Simulink working platform. The numerical analysis of the results highlights the superior performance of the proposed technique in both CAP and SoC compared to existing methods. The actual data varies between 0.7 and 1.1 p.u., showing a significant peak around 15:00, where it reaches about 1.2 p.u. This reflects the changes in wind energy availability throughout the day. Likewise, the real data for solar energy peaks at around 1.0 p.u. at noon, which aligns with the highest solar radiation. The forecast data closely follows the real data within the shaded uncertainty band, demonstrating the anticipated trends in both wind and solar energy production, while the uncertainty band emphasizes the variations in energy availability. The proposed technique achieves a CAP value of 47.25%, significantly higher than other methods, indicating its enhanced accuracy and optimization efficiency. In terms of SoC, the proposed method reaches 97.52%, outperforming HMADRL (80%), NEGCN-PFOA (55.471%), SAC (43.09%) and DRL (63%). These substantial differences (19.52% to 34.52%) in SoC underscore the proposed method’s effectiveness in maintaining battery health and efficient energy management, making it more reliable for high-demand applications than the other techniques. Future research can focus on enhancing the proposed technique’s adaptability to diverse load conditions, integrating machine learning for predictive accuracy, and expanding its application to larger, complex energy systems.