Introduction

Spin Hall nano-oscillators (SHNOs) have emerged as promising spintronic devices in recent years, consisting of a ferromagnetic layer (FM) and a non-ferromagnetic (NM) layer1,2,3. When an electric current flows through the NM layer, the spin Hall and Rashba effects4,5,6 generate a pure spin current with a polarization direction perpendicular to both the current flow and the FM/NM interface. Through the spin-transfer torque effect7,8, this spin-orbit torque induces high-frequency oscillations in the magnetization direction of the FM layer9. The anisotropic magnetoresistance (AMR) effect10 subsequently converts these magnetization oscillations into resistance variations, enabling the detection of high-frequency microwave signals at the device terminals.

Compared to spin torque nano-oscillators (STNOs)11, another type of spintronic oscillator, SHNOs offer the advantage of a simpler fabrication process due to fewer patterning and etching steps. This simplicity facilitates the arraying of SHNOs, making the realization of large-scale synchronized arrays more feasible12. As nonlinear oscillators, SHNOs have demonstrated significant potential for future applications13,14,15,16,17,18.

Despite these advantages, two key challenges limit the further development of SHNOs. First, the output power of conventional SHNOs is significantly lower—typically more than three orders of magnitude less than that of STNOs1. This disparity is primarily attributed to the relatively weak AMR effect compared to the giant magnetoresistance (GMR)19 and tunneling magnetoresistance (TMR) effect20, which are more efficient at converting magnetization oscillations into resistance variations. Secondly, due to the characteristics of AMR effect, the derivative of the resistance with the magnetization direction is zero when the magnetization direction of the ferromagnetic layer is perpendicular to the current direction, and the oscillation amplitude of the ferromagnetic layer induced by the spin Hall effect is small, so that the output of the microwave signals is almost undetectable in this case. To achieve effective high-frequency signal output, an external magnetic field is often required21,22,23 to deflect the FM layer’s magnetization direction relative to the current, which is impractical for real-world SHNO applications.

To address these limitations, this paper proposes a field-free SHNO utilizing the GMR effect, with its characteristics analyzed by micromagnetic simulations. It is widely recognized that spin waves dominate large-scale SHNO synchronization due to the weak current coupling strength inherent to the AMR effect24,25. However, the introduction of the GMR effect significantly enhances current coupling strength. Therefore, we have preliminarily investigated the feasibility of achieving synchronization through current coupling in SHNOs and compared the performance of two electrical connection configurations: serial and parallel.

Results and discussions

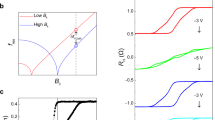
The designed film structure of the SHNO based on the giant magnetoresistance (GMR) effect is illustrated in Fig. 1(a). The multilayer structure comprises sub/IrMn/Co/Cu/Co/Pt from bottom to top, differing from that of conventional SHNOs, with the GMR film replacing the traditional permalloy layer. Notably, the magnetization easy axes of the pinned and free layers in the GMR film are non-parallel, resembling a configuration previously reported in the field of STNOs26, but differing from the structure proposed by J.R. Chen et al.27. As shown in Fig. 1(a), the easy axis of the free layer forms an angle \(\theta\) with the spin current polarization direction (aligned with the y-axis), while the easy axis of the reference layer aligns with the current direction (x-axis).

Fig. 1
figure 1

(a) Film structure of the field-free SHNO with non-parallel easy axis of reference layer and free layer. The current direction is along the easy axis of the reference layer. (b) Schematic drawing of a nano-constriction-based SHNO and narrowest region is 30 nm width. (c) Relationship between the anisotropy magnetoresistance and magnetization angle. (d) Relationship between the giant magnetoresistance and external field after two-steps annealing; inset: hysteresis effect on the magnetoresistance curve without two-steps annealing.

Full size image

In typical GMR and TMR film structures, the magnetic layers contain both free and reference layers. A common fabrication method involves high-temperature annealing (depending on the antiferromagnetic pinning material) along a single direction, resulting in identical magnetic anisotropy orientations for both layers. This configuration, often used in sensors, produces a magnetoresistance curve with a switching shape and significant hysteresis, which is undesirable for sensor applications. To address this, a double annealing process has been developed28. The first annealing step involves a higher temperature and longer duration, such as the classical 350 °C annealing for 1 hour with IrMn as the pinning material. The second step employs a lower temperature and shorter duration, with the annealing direction offset by an angle (e.g., 90° or 45°) from the first step, depending on the device’s specific requirements. This method enables precise adjustment of the free layer’s magnetization easy axis to form a desired angle with the reference layer’s easy axis.

To maintain compatibility with conventional SHNO fabrication processes, the traditional nano-constriction structure29,30,31 is adopted. This choice avoids the excessive shape anisotropy observed in nano-wire SHNOs32, which makes achieving a non-parallel easy-axis configuration between the reference and free layers via annealing particularly challenging. The three-dimensional structure of the proposed SHNO is depicted in Fig. 1(b). It features a round-edged nano-constriction with a curvature radius of 80 nm and a narrowest region width of 30 nm. This design preserves the fabrication simplicity of conventional SHNOs while enabling high-power microwave signal output without requiring an external magnetic field. Next, we will show the working principle of the designed new-type SHNO. For conventional SHNOs:

$$P\sim {\left| {dR} \right|^2}={\left| {d\theta \cdot \frac{{dR}}{{d\theta }}} \right|^2},$$
(1)

Where P represents the output power of the oscillator, \(\:\theta\:\) represents the angle between the magnetization direction of the ferromagnetic layer and the current direction, R represents the resistance of the oscillator, and \(\:d\theta\:\) represents the magnitude of the change in the magnetization orientation of the ferromagnetic layer during the oscillation, which is related to the magnitude of the applied current and material parameters. Under the premise of the same oscillation amplitude, it is the derivative of the resistance about the angle that determines the power of the oscillator. The conventional SHNO utilizes anisotropy magnetoresistance effect to convert the magnetization direction to resistance, the relationship between the anisotropy magnetoresistance and magnetization angle is shown in Fig. 1(c), which can be expressed as \(R={R_\parallel }+{R_ \bot }(1 - {\cos ^2}\theta )\). Obviously when θ = 0° or 90°, the value of \(dR/d\theta\) is 0. Therefore, the conventional SHNO is not able to work without an external field (the derivative of the resistance about the angle equals 0 at the relaxing point in Fig. 1(c)). Besides, the polarization direction of the spin current generated by the spin Hall effect \({\sigma _j}=j \times \vec {z}\) is perpendicular to the current direction and the flow direction of the spin current so it is often necessary to apply a field that is not perpendicular to the current to deflect the magnetization direction of the ferromagnetic layer (the working point in Fig. 1(c)). On the other hand, for the new-type SHNO, we can rewrite (1) as:

$$P\sim {\left| {dR} \right|^2}={\left| {d{m_{Ref}} \cdot \frac{{dR}}{{d{m_{Ref}}}}} \right|^2},$$
(2)

Where \(d{m_{Ref}}\) represents the projection of the normalized magnetization of the ferromagnetic layer in the easy axis of the reference layer. For the SHNO based on giant magnetoresistance with perpendicular easy axis (\(\theta =0^\circ\)), the ideal relationship between the resistance and \({m_{Ref}}\) is shown in Fig. 1(d) (we only consider the hysteresis effect induced by the magnetic anisotropy here). Since the magnetization of the reference layer is along the current (in the direction of the y-axis), the value of \(dR/d{m_{Ref}}\) is highest without external field (the relaxing and working point in Fig. 1(d)). Moreover, the magnetization of the free layer is oriented perpendicular to the drive current direction to achieve a large oscillation amplitude. For other values of the angle \(\theta\), the dynamics are slightly different, but the underlying principle remains consistent. It is crucial to note that a non-parallel configuration of the easy axes is essential for achieving field-free and high-power oscillation. When the easy axes of the free and reference layers are parallel, the resistance change induced by the magnetization precession around the free layer’s easy axis is negligible. As demonstrated by Chen et al.27, under such conditions and without an external magnetic field, the output power offers no significant improvement over conventional AMR-based SHNOs, so it is also necessary to apply external magnetic field nearly perpendicular to the current. While the required external magnetic field is obviously not convenient for practical applications, the method of introducing anisotropy by two-step annealing provides an effective solution to this problem. This approach enables the non-parallel easy-axis configuration without the need for an external field, facilitating field-free operation. Since the resistance change due to the GMR effect is much stronger (one to two orders of magnitude) compared to the AMR effect, the power of the GMR-SHNO can be increased by two to four orders of magnitude theoretically.

We first simulated the current density distribution and Oersted field distribution of the proposed structure using COMSOL Multiphysics [https://www.comsol.com] software. The results indicate that the current distribution differs slightly from that of conventional SHNOs. Due to the presence of additional metal layers, the proportion of current density in the heavy metal layer is reduced, necessitating a higher critical drive current. This issue can be partially mitigated by increasing the thickness of the heavy metal layer and optimizing the resistivity of the GMR layers through adjustments to the thickness of the IrMn and Co layers.

Overall, replacing the traditional NiFe layer with GMR layers has a minimal impact on the oscillator’s resistance. Structurally, the device can be approximated as a GMR element connected in parallel with a Pt layer. In the simulation, the conductivities of the GMR layers and the Pt layer were set to 1.3 MS/m33 and 8.9 MS/m, respectively. As shown in Fig. 2(a), the current density is primarily concentrated in the narrow region of the device.

Fig. 2
figure 2

(a) Current density distribution in the Pt layer when the drive current is 4 mA. (b) Oersted field distribution when the drive current is 4 mA. (c) Average unit magnetization oscillation with time in the three axes of the SHNO. (d) Oscillation power distribution of the main frequency in the free layer when the drive current is 4 mA.

Full size image

Similarly, the Oersted field distribution was calculated for a drive current of 4 mA, as illustrated in Fig. 2(b). These results highlight the localized nature of the field and provide insight into the operational characteristics of the proposed SHNO structure. After obtaining the current density and field distribution, we utilized Mumax334 to simulate the magnetic characteristics of the new-type SHNO, whose material parameters from the literature11,35: exchange stiffness constant \({A_{ex}}=15\)\(\text{p}\text{J}\), saturation magnetization \({M_s}=580\)\(\text{k}\text{A}/\text{m}\), damping factor \(\alpha =0.01\), spin Hall angle \({\theta _{SH}}=0.08\) for Pt25, and the anisotropy energy is set as \({K_u}=10\)\(\text{k}\text{J}/{\text{m}^3}\). To demonstrate the feasibility of this device, we set \(\theta =15^\circ\)at first. We imported the current density distribution and Oersted field distribution obtained from Comsol into Mumax, and then performed a Fourier variation of the magnetization direction in the x-axis to obtain the spatial distribution of the oscillating power, as shown in Fig. 2(d). Similar to the previous studies, the distribution of the oscillation power we obtained is centrosymmetric, while the polarization direction of the spin current is non-parallel to the magnetization direction of the free layer to induce precession36. Obviously, the high-frequency oscillation is mainly concentrated in the narrow region where the current density is the highest, and the average unit magnetization component in the time-domain is shown in Fig. 2(c). Under the influence of anisotropy energy, the magnetization in the z-axis remains almost constant, while the magnetization in the x-axis oscillates with a relatively large amplitude.

Further, we investigated the relationship between the output characteristics and the driving current, where the frequency of the oscillation was calculated using the average magnetization of the x-axis over time. The results obtained from the simulation are shown in Fig. 3(a), which shows that the oscillation frequency decreases with increasing drive current and enhancing the anisotropy energy can improve the frequency tuneability. Consistent with previous studies, SHNO is much less tunable for oscillation frequency than STNO. It is worth mentioning that all the simulations are carried out in the absence of external field. In addition, considering the employment of annealing to achieve the no-parallel magnetization easy axis of the free and reference layers, the time of annealing and the magnitude of the applied magnetic field will have a vital influence on the performance of the oscillator. To simulate this mechanism, we changed the magnetic anisotropy energy and the easy axis angle of the free layer. Firstly, we changed the anisotropy energy from 5 \(\text{k}\text{J}/{\text{m}^3}\) to 15 \(\text{k}\text{J}/{\text{m}^3}\)corresponding to the free layer, which is affected by the annealing conditions, and the simulation results are shown in Fig. 3(b).

Fig. 3
figure 3

The Mumax simulation results of our designed new-type SHNOs. (a) The oscillation frequency changes with the drive current when the anisotropy energy is set as 5,10,15 kJ/m3 respectively. (b) The oscillation frequency changes with the anisotropy energy when the drive current is set as 4 mA.

Full size image

The FMR frequency of the free layer can be expressed as: \({f_{FMR}}=\gamma /2\pi \sqrt {{B_{eff}}({B_{eff}}+{M_s})}\), where \({B_{eff}}\) represents the effective field, which includes the current induced Oersted field, demagnetization field and the anisotropy-induced field, and \({M_s}\) represents the saturation magnetization. The anisotropic field \({B_{ani}}\) is equivalent to the anisotropic energy, which can be expressed by this formula: \({B_{ani}}=2{K_u}/{M_s}<\vec {u},\vec {m}>\vec {u}\),where \(\vec {u}\) represents the direction of anisotropy axis. Therefore, the FMR frequency of the free layer will increase with the increase of anisotropic energy. Although the FMR frequency differs from the oscillation frequency, the relationship between the FMR frequency and the oscillation frequency of SHNO should be consistent. Therefore, if there is no change in the oscillation mode, the increase of anisotropic energy will lead to the increase of the oscillation frequency of SHNO. On the other hand, the effect of the current on the oscillation frequency is a result of the competition between the Oersted field and the anisotropy field. An increase in current leads to a stronger SOT effect, a larger precession cone angle and a decrease in each anisotropic field. In our designed device, this effect dominates and thus ultimately leads to a decrease in the oscillation frequency of the device, which is consistent with previous studies22.

The results suggest that anisotropy energy has a significantly greater impact on the oscillation frequency compared to the drive current. We hypothesize that there is an upper limit to the magnetic anisotropy that can be introduced through annealing. Excessive annealing time for the free layer could also adversely affect the reference layer, potentially compromising the overall performance of the oscillator. Consequently, we propose that optimal annealing conditions exist for this type of oscillator, which could be further validated through future experimental investigations.

Another parameter that is closely related to the annealing is the direction of the anisotropy of the free layer, i.e., the parameter \(\:\theta\:\). The effect of spin orbit torque on the free layer can be expressed as:

$${\tau _{\mathbf{S}\mathbf{H}\mathbf{E}}}=\frac{{{\Theta _{SH}}g{\mu _B}J(x,y)}}{{2e{M_s}^{{^{2}}}L}}{\mathbf{M}_\mathbf{f}} \times ({\mathbf{m}_\mathbf{p}} \times {\mathbf{M}_\mathbf{f}}),$$
(3)

where \({\Theta _{SH}}\) is the spin Hall angle, g is the spectroscopic Lande factor, \({\mu _B}\) is the Bohr magneton, \(J(x,y)\) is the current density distribution, e is the modulus of the electron charge, \({M_s}\) is the saturation magnetization magnitude,\({\mathbf{M}_\mathbf{f}}\)is the magnetization vector for the free layer and \({\mathbf{m}_\mathbf{p}}\) is the spin polarization vector. From this former research27, we know the closer the angle between the magnetization direction of the free layer and the current direction is to 90°, the stronger is the effect of the spin transfer torque, and the bigger is the corresponding oscillation amplitude. From a practical application standpoint, the direction of anisotropy in the free layer is influenced by various factors, including the annealing direction, shape anisotropy, and interlayer coupling. As not all of these parameters can be precisely controlled, we investigated the feasibility of the designed device under different magnetic anisotropy directions. Specifically, we simulated conditions with easy-axis angles of 15°, 27°, and 45°, and the corresponding results are shown in Fig. 4.

Fig. 4
figure 4

Simulation results for different anisotropy direction of the free layer for I = 4 mA and \({K_u}\)= 5 kJ/m3: (a–c) the time domain change of the averaged 3 axis magnetization direction for \(\theta =15^\circ ,27^\circ ,45^\circ\), respectively. Insert picture for (c) the locally amplified time domain change. (d–f) the frequency domain information of the averaged x-axis magnetization for \(\theta =15^\circ ,27^\circ ,45^\circ\), respectively.

Full size image

As shown in Fig. 4, the oscillation amplitude increases when the angle is changed from 15° to 27°, but a significant reduction in oscillation amplitude occurs when the angle is further increased to 45°. In spin-orbit torque (SOT)-driven magnetization dynamics, the damping-like SOT leads to the maximum reduction in effective damping when the magnetization direction of the free layer is orthogonal to the drive current, as demonstrated by numerous simulations and experimental studies27,31,32. However, our simulation results show that the oscillation amplitude at an angle of 27° is greater than that at 15°, which is intriguing and appears to contradict traditional theories.

We speculate that this discrepancy may be closely related to the device structure, with changes in the anisotropy angle potentially altering the oscillation modes. Notably, when the angle exceeds 45°, it becomes nearly impossible to generate an oscillation waveform that aligns with previous experimental results. As the angle increases, we observe the appearance of additional wave peaks, indicating the emergence of multiple oscillation modes. This phenomenon, characterized by multiple oscillatory modes, could explain the observed trend where an increase in angle initially boosts and then reduces the oscillation amplitude for the same drive current. This interesting behavior may enable the SHNO to output signals at multiple frequencies, offering potential for further investigation.

For GMR-based field-free SHNOs, the direction of anisotropy in the reference layer also plays a crucial role. We believe that by optimizing annealing conditions, SHNOs can be fabricated to achieve varying frequencies and power outputs, providing new flexibility in the design and modification of SHNOs.

The synchronization between oscillators has been of great interest for both spin Hall nano-oscillators and spin torque nano-oscillators. The power and linewidth of a single oscillator are poor for practical applications, and the synchronization between multiple oscillators can increase the power by N2 and decrease the linewidth by N− 112,37. In addition, the synchronization can also be employed as a novel method to modulate the working state of the oscillators, which can be applied for neuromorphic computation and computing unit of non-von Neumann architecture.

Recent studies have shown that SHNOs can achieve larger-scale synchronization compared to STNOs considering the strong spin wave coupling and much easier fabrication process, which implies the great potential for SHNOs in the field of synchronization. For STNOs, synchronization based on spin wave38,39, dipolar field40,41, and electrical current42,43,44 has been widely investigated. But for SHNOs, the demonstrated synchronization mechanism is still limited to spin wave synchronization. For conventional SHNOs, multiple oscillators are connected through ferromagnetic materials, and this unique interconnection provides a medium for the propagation of spin waves, so that spin waves play a dominating role for the synchronization. On the other hand, the resistance change in the oscillation process of SHNOs is very small, so the coupling effect of current is often neglected. However, there are unique advantages in synchronization distance and synchronization range for electrical synchronization43. With the improvement of the magneto-resistance ratio, whether electrical synchronization can be realized or not is an important question for the further applications of SHNOs. As an exploratory attempt, we have investigated the feasibility of electrical synchronization between the designed new-type GMR-SHNOs.

In order to study the synchronization of SHNOs, we employed the microspin model45 instead of the original micromagnetic model for much faster computation speed. For microspin model, it is difficult to simulate the propagation spin wave mode of SHNO and define the oscillation area of the device, so we measured the oscillation area from the simulation results of the localized oscillation mode as input to our microspin mode. It is worth mentioning that in order to match the results of the micromagnetic model, we also introduced a small external field in the microspin model to simulate the Oersted field generated by the drive current. Anyway, here we only want to preliminarily explore the feasibility of using current to achieve synchronization by enhancing the coupling strength and figure out the influence of GMR ration and the difference between oscillators on the mutual synchronization.

We employ a simpler micro-spin model to study the electrical synchronization between multiple spin Hall oscillators. As is shown in Fig. 5(a) and Fig. 5(b), we consider two types of electrical connections, series and parallel with a constant current source, and their electrical coupling relations can be expressed by Eq. (4)42 and (5):

Fig. 5
figure 5

(a) Series connection schematic for SHNOs, where \({R_c}=100\)\(\Omega\)in the following simulation. (b) Parallel connection schematic for SHNOs. (c,d) Synchronization simulation for two connected SHNOs with 5% difference: (c) GMR = 10%, series connection, (d) GMR = 10%, parallel connection, insert: the spectrum when I = 7 mA, (e) GMR = 1%, series connection, (f) GMR = 1%, parallel connection.

Full size image
$${I_{couple}}=\frac{{{R_c}}}{{{R_c}+\sum {{R_N}} }} \times {I_0}$$
(4)
$${I_j}=\frac{{{G_j}}}{{\sum\nolimits_{i}^{N} {{G_i}} }} \times {I_0},{G_i}=\frac{1}{{{R_i}}},$$
(5)

Where \({I_0}\) represents the output of the current source, \({I_{couple}}\)represents the drive current for all the SHNOs connected in series, \({R_c}\) represents the load resistance of SHNO series, which is set as 100\(\Omega\) in all the following simulations, \({I_j}\) represents the drive current of the \({j_{th}}\) SHNO connected in parallel, \({G_j}\) represents the electrical conductance of the \({j_{th}}\) SHNO. Firstly, we investigated the feasibility of synchronization between two SHNOs, and the magnetoresistance ratio of the GMR was set to be 10%, considering that the magnetoresistance ratio of GMR prepared by epitaxial growth is able to exceed up to 40%46, and the additional Pt layer could dilute part of the magnetoresistance ratio. The resistance of the SHNO without external field is set as 100\(\Omega\), and we set a 5% difference between the two SHNOs. As can be seen in Fig. 5(c)&(d), the two oscillators are independent of each other at the beginning, and with the increase of the driving current, the two oscillators synchronize successfully. However, when the magnetoresistance ratio is only 1%, as can be seen in Fig. 5(e)&(f), no matter how the drive current is varied, it cannot make the two oscillators synchronized, because at this point the current coupling is too small and the electrical coupling strength is negligible. Interestingly, for the conditions where synchronization is possible, we can observe not only the two oscillation peaks, but also other oscillation peaks before synchronization occurs. This frequency-mixing effect is undoubtedly due to the current coupling, which may be the reason why the mutual synchronization was eventually possible.

After studying the electrical synchronization preliminarily, we further consider a more general situation. In actual fabrication process, there is no method to precisely control the difference between the oscillators, so we try to model this problem using a probabilistic approach and consider the above study only a random case. We set an upper limit for the difference between the oscillators, after which each simulation takes a random value below this limit as the difference between the two oscillators. We repeated this simulation 100 times for different magnetoresistance ratios and different upper limits, and plotted the probability that synchronization could occur as a histogram, as is shown in Fig. 6. In general, the smaller difference between the oscillators and the higher the magnetoresistance ratio, the higher probability of electrical synchronization, whereas when the magnetoresistance ratio is too low, electrical synchronization can hardly be achieved. Interestingly, we found that parallel coupling is easier to achieve electrical synchronization compared to series coupling.

Fig. 6
figure 6

Synchronization percent for 100 times simulation for different conditions for SHNOs connected in series (a) and parallel (b). All the simulations are performed with \({I_{drive}}=10\) mA and \({K_u}\)= 10 kJ/m3. Generally, it is easier for SHNOs connected in parallel to realize synchronization compared with those connected in series.

Full size image

There are many factors that affect the synchronization between oscillators, the most important of which are frequency detuning and coupling strength. In our model, the differences between the oscillators are consistent, so the most important factor affecting the synchronization is the coupling strength. From a qualitative analysis point of view, we suppose that the external impedance has a stronger effect on the series connection compared to the parallel connection, leading to a weaker coupling between the oscillators in series, which is consistent with the previous experimental results on the electrical synchronization47. Considering that most of the large-scale SHNO arrays realized so far employ series connection to achieve spin wave-based synchronization, the parallel-based electrical coupling method could be of great significance for subsequent large-scale 2D synchronized array of SHNOs.

Conclusion

In this paper, we have proposed a novel SHNO design based on the giant magnetoresistance (GMR) effect, which includes a free layer and a reference layer with non-parallel magnetization easy axes, enabling the SHNO to operate normally without the need for an external magnetic field. Thanks to the enhanced magnetoresistance ratio provided by the GMR effect, the power output of the proposed oscillator is significantly increased compared to conventional SHNOs that rely on the anisotropic magnetoresistance (AMR) effect.

We validated the feasibility of the device through micromagnetic simulations and explored the impact of the driving current, as well as the magnitude and orientation of the magnetic anisotropy on the device’s performance. Moreover, we observed that the strength of the current coupling between SHNOs is enhanced, which prompted an investigation into the feasibility of electrical synchronization between two SHNOs. The results showed that electrical synchronization is achievable in both series and parallel configurations; however, when the magnetoresistance ratio is too low, electrical synchronization becomes challenging. Notably, the coupling strength in the parallel configuration was found to be stronger than in the series configuration. The findings presented in this paper offer new insights into the development of SHNOs and demonstrate, through theoretical simulations, the critical role of enhanced resistance ratios in facilitating electrical coupling. These results are of significant importance for the future advancement of SHNO synchronization technologies.

Methods

The validation of this novel device was carried out using the micromagnetic simulation software Mumax with the relevant parameters: exchange stiffness constant \({A_{ex}}=15\)\(\text{p}\text{J}\), saturation magnetization \({M_s}=580\)\(\text{k}\text{A}/\text{m}\), damping factor \(\alpha =0.01\), spin Hall angle \({\theta _{SH}}=0.08\) for Pt, and the anisotropy energy is set as \({K_u}=10\)\(\text{k}\text{J}/{\text{m}^3}\) at first. High-frequency analysis techniques, such as Fourier transforms, were employed to process the resulting data. The current density distribution and the magnetic field generated by the current were simulated using the finite element simulation software Comsol and imported into the Mumax software. The related simulation code has been uploaded to the repository at https://github.com/Lin-Sven/field-free-SHNO.

For the electrical synchronization simulations, the micro-spin model c-MTJ was utilized. Additionally, the Giant Magnetoresistance (GMR) model was implemented to update the resistance and current values during each simulation step, enabling the simulation of electrical synchronization between two oscillators. The study examined the behavior of two oscillators in both series and parallel configurations, demonstrating that electrical synchronization is feasible for GMR-SHNOs. This provides an important step towards scalable synchronization in SHNO-based applications.