Introduction

Advances in spectral imaging technology have led to improved spatial and spectral resolutions in hyperspectral sensors, resulting in more accurate data acquisition. The resultant hyperspectral images (HSIs) offer copious spatial information about observed scenes along with extensive spectral signatures from over hundreds of contiguous spectral bands1. This characteristic makes HSI widely employed across diverse domains, such as environmental monitoring2, mineral exploration3,4, food safety5, precision agriculture6, and military reconnaissance7. In numerous remote sensing applications, HSI classification is a basic problem that necessitates recognizing the various land cover classes and assigning each pixel to a distinct semantic label from HSIs. However, due to the dimensionality dilemma, inevitable noise interference, scarcity of labeled samples, spectral confusion, and spectral variability, properly distinguishing ground objects and classifying HSIs remains a significant challenge8.

To address the challenges associated with hyperspectral image (HSI) classification, researchers have made significant efforts in developing spectral information extraction algorithms aimed at achieving precise pixel-by-pixel recognition. Traditional methods, including k-nearest neighbor (KNN)9, random forest (RF)10, multinomial logistic regression (MLR)11, and support vector machine (SVM)12, have been commonly utilized. However, these approaches often yield suboptimal classification results, primarily because they fail to account for the spatial dependencies inherent in pixel relationships within the spatial domain.

To mitigate the challenges posed by high dimensionality and redundancy in hyperspectral data, dimensionality reduction (DR) techniques, encompassing both feature selection and feature transformation, have been effectively employed13. Feature selection aims to identify a subset of discriminative bands from the original hyperspectral data, enhancing classification accuracy. Various well-established band selection methods have been proposed to reduce dimensionality by selecting relevant features. For instance, Chang et al. introduced the self-mutual information-based band selection (SMI-BS) method to address critical issues in HSI classification14. Similarly, He et al. developed a semi-supervised band selection approach combined with optimal graph learning (BSOG), which merges band selection with local structure learning15. Additionally, Fu et al. proposed the neighboring band grouping and normalized matching filter (NGNMF) method, which effectively reduces dimensionality while retaining essential spectral information16. While these techniques have achieved notable success, many band selection methods depend on a single objective function, which may lead to the exclusion of crucial spectral features and potentially compromise detection accuracy. To overcome this limitation, Ou et al. introduced a multi-objective cuckoo search algorithm (MOCS) for band selection. This approach constructs an unsupervised model that strikes a balance between information content and inter-band correlation, offering a more comprehensive solution to the band selection problem (MOCS-BS)17. Ultimately, a key challenge in hyperspectral band selection is developing an effective criterion that both preserves essential spectral information and minimizes inter-band correlation.

Feature transformation typically aims to map high-dimensional data into a lower-dimensional feature space, facilitating the extraction of relevant information that enhances classification performance18. Several well-established feature transformation methods, grounded in statistical principles, have been developed, including principal component analysis (PCA)19, maximum noise fraction (MNF)20, linear discriminant analysis (LDA)21, independent component analysis (ICA)22, and nonparametric weighted feature extraction (NWFE)23. These techniques offer various strategies for dimensionality reduction in HSIs, each balancing trade-offs between computational efficiency, class separability, feature preservation, and the ability to model complex, nonlinear data structures. However, these methods often fail to account for the intrinsic relationships and structures within the data, leading to suboptimal results when applied in isolation to complex datasets with intricate distributions. As a result, some researchers have shifted their focus to combining dimensionality reduction techniques with spatial-spectral feature extraction methods, aiming to leverage both the spectral and spatial dimensions of hyperspectral data. This integrated approach has shown promise in enhancing classification performance and overcoming the limitations of single-dimensional reduction strategies8,23,24.

To enhance classification accuracy, there has been increasing emphasis on developing spatial-spectral classification methods for HSIs that leverage their inherent nonlinearity and spectral-spatial characteristics. This has led to the development of various spatial feature extraction techniques, including edge-preserving filters (EPF)25,26, Markov random fields (MRF)27, local binary patterns (LBP)28,29, extended morphological profiles (EMP)30, extended multi-attribute profiles (EMAP)31, and two-dimensional singular spectrum analysis (2-D-SSA)8, among others. For example, Li et al. proposed a spectral-spatial feature extraction method based on ensemble empirical mode decomposition (EEMD) for HSI classification, aimed at extracting relevant features while eliminating redundancy32. To incorporate shape-adaptive spatial structural information from hyperspectral scenes into the feature extraction process, Tu et al. developed a novel technique based on 3-D block characteristics sharing (3-D-BCS), which integrates texture and spatial information to enhance classification performance33. More recently, Zhang et al. introduced the spectral-spatial SuperPCA (S3-PCA) algorithm, which efficiently utilizes spatial information through superpixel-based local reconstruction, thereby improving the extraction of both global-local and spectral-spatial features for HSI classification34. Duan et al. proposed a semi-supervised feature extraction method known as the geodesic-based sparse manifold hypergraph (GSMH), which uncovers the complex manifold structure and multivariate relationships of hyperspectral samples35. Although these conventional spatial-spectral feature extraction techniques are valuable, they can be considered shallow models with limited ability to adaptively capture more abstract and discriminative features from HSIs. As a result, these methods often fall short of fully exploiting the potential of hyperspectral data in terms of higher-level, more intricate feature representations.

Over the past decade, deep learning (DL) techniques have been used frequently and remarkably well for HSI classification tasks. DL models, unlike typical manual feature extractors, can autonomously generate abstract and advanced feature representations from HSIs. As a result of the ongoing development of DL methods, numerous complex architectures, including deep belief networks (DBNs), stacked autoencoders (SAEs), recurrent neural networks (RNNs), generative adversarial networks (GANs), convolutional neural networks (CNNs), and graph convolutional networks (GCNs), have been studied for HSI classification36,37,38,39. In particular, CNNs have received lots of attention and exhibited superior performance due to their local perception and parameter sharing properties. For instance, Hu et al. designed a 1-D-CNN with five convolutional layers, and this architecture employs spectral signatures to directly categorize HSIs in the spectral domain, ignoring the spatial correlation of scenes40. Zhao and Du created a spectral-spatial features-based HSI classification framework that simultaneously adopts dimension reduction and the 2-D-CNN model for spectral feature extraction while automatically exploiting high-level spatially-related information41. To tackle the challenge of limited labeled samples in HSI classification, Liu et al. presented a unique semi-supervised CNN by adding skip connection settings42. Yang et al.43 built a two-branch architecture by integrating 2-D and 1-D CNNs to concurrently characterize the discriminative spectral and spatial characteristics from the spectral and spatial domains of HSIs. Meanwhile, more features that were transferred from other data sources were incorporated to boost the classification performance. Furthermore, Chen et al.44 presented a unique 3-D-CNN-based feature extraction model with coupled regularization to exploit the deep spectral-spatial properties of HSIs to mitigate the disparity between high dimensionality and limited training sample availability. These derived features sacrifice computational complexity and time, although they are discriminating and helpful for classification tasks. Based on this, Roy et al.45 used a spectral-spatial 3-D CNN with a spatial 2-D CNN to create a hybrid SN model. In comparison to the original 3-D CNN, the proposed hybrid spectral CNN model clearly decreases complexity while simultaneously combining complementary information from both spectral-level and abstract-level spatial representations. Overall, CNN-based architectures and variants were demonstrated to be some of the most promising methods because of their exceptional capacity to leverage local contextual information. But sequence attributes and global information are difficult for these architecture-based approaches to capture, which causes bottlenecks in HSI classification tasks, particularly when addressing heterogeneous class distributions with spectrally similar features, leading to improving accuracy when working with complicated data might be difficult as a result46.

Recently, researchers have brought a novel model to the domain of image processing called the Vision Transformer (ViT)47, which is frequently employed in natural language processing. Henceforth, HSI classification has frequently examined a few transformer models. For instance, Hong et al.48 created SpectralFormer, a highly adaptable backbone network, to gather local and spectral sequence characteristics from HSIs’ adjacent channels, where a transformer encoder (TE) module with a cross-layer design was developed to lessen the likelihood of losing important data. Qing et al.49 employed the spectral attention mechanism to capture the long-range dependencies in the continuous spectral relationships of HSIs, and this mechanism was then combined with multiple multi-head self-attention modules to create an end-to-end transformer model known as the SAT Net. More recently, Sun et al.46 created a spectral-spatial feature tokenization transformer (SSFTT) model in order to adequately exploit local semantic features and model the interdependencies between contiguous sequences. That same year, Zhang et al.50 constructed a spectral-spatial self-attention network (SSSAN), using spectral and spatial dual-branch subnetworks to adaptively characterize long-range spectral correlations relative to local spectral features and leverage extensive patch-based contextual information pertinent to the central pixel for HSI classification. Transformers outperform CNN-based approaches in terms of global feature extraction while considerably reducing computing costs. However, transformer-based approaches are primarily concerned with extracting long-term semantic information from spectrum sequences while neglecting local feature information. Furthermore, the unavoidable inefficiency induced by either difficulty in parallelization or computationally prohibitive attention continues to limit the applicability of these sequential architectures51.

Mercifully, recent developments in the state space model (SSM) have enabled the capability to compute very long-range dependencies through state transitions in an unprecedentedly efficient manner51. Additionally, the model’s promising properties of linear computational complexity and scalability enable broad application across a variety of domains. Mamba, an efficient substitute for the Transformer, models 1-D sequences along a particular direction by using selective SSMs, a technique that has shown significant promise in problems involving natural language processing52. In 2D visual tasks like object detection and semantic segmentation, Vim53 and VMamba54 demonstrate remarkable efficiency and effectiveness by extending the Mamba model to accommodate vision scenarios involving 2D spatial awareness. They achieve global contextual modeling by introducing a multidirectional scanning mechanism. Subsequently, to address the dual challenges of spectral redundancy and variability that simultaneously emerge in HSI classification, Yao et al.55 built a SpectralMamba model by implementing the techniques of piecewise sequential scanning (PSS) and gated spatial-spectral merging (GSSM). Although Mamba designs have shown great promise in low-dimensional settings, more research is needed to determine how well-suited they are for high-dimensional HSI classification tasks requiring 3D hyperspectral data. In this instance, He et al.56 created 3D-Spectral-Spatial Mamba (3DSS-Mamba), a new global spectral-spatial contextual modeling network grounded in SSM for HSI classification. Significantly, 3DSSMamba successfully overcomes the performance and efficiency constraints of the most sophisticated CNN-based and Transformer-based HSI classification models.

DL-based frameworks outlined previously have achieved notable advancements in HSI classification by adeptly capturing intricate spectral-spatial contextual relationships and long-range dependencies, but HSI applications still grapple with various challenges. One of the most significant issues is that these architectures are prone to “overfitting’ under extremely limited training data, and they typically suffer from quadratic computational cost as the number of hyperparameters and layers grows. Particularly, deep features often lack semantic interpretability compared to handcrafted features, forming a latent representation of high-dimensional data that remains largely opaque. The interpretability of deep learning models still requires significant advancement. To that end, this paper intends to create a shallow model that captures spatial and spectral changes in HSIs while adapting to small sample difficulties.

This study presents an innovative small sample HSI classification architecture called CiSSA_MLTP, which blends circulant singular spectrum analysis (CiSSA) and multiscale local ternary patterns (MLTP). The proposed strategy encompasses three key elements: First, CiSSA extracts and analyzes extensive spatial characteristics from the principal components (PCs), revealing spatial patterns by studying how spectral properties change across different spatial locations. Next, PCA reduces dimensionality to extract global spectral features, which are then combined with the CiSSA features to create the spatial-spectral feature set (SSFS). Additionally, local ternary pattern (LTP) is applied to PCs to analyze and extract local texture variations, spatial patterns, and contrasts at different scales, offering deeper insights into the texture and structure of objects in HSI. Finally, the performance of the SSFS and multiscale LTP features is separately assessed using the SVM classifier.

The following succinctly describes the method’s primary contributions.

  • CiSSA was originally introduced to HSI to characterize more concentrated spatial-spectral features by integrating the dimensionality reduction technique. As far as is known, CiSSA remains an untapped resource for HSI classification tasks.

  • MLTP introduces a valuable dimension to HSI classification by providing detailed local texture features, enhancing robustness against noise, and improving spatial pattern analysis. As far as is known, no research has yet investigated the application of the MLTP to HSI classification tasks.

  • Decision-level fusion merges the classifier ensemble’s results by combining the probability outputs from each pipeline for classification, considering global spectral, global spatial, and local spatial textures to explore pixel interconnections.

  • The suggested technique outperforms a number of cutting-edge techniques, including CNN-based and Transformer-based models, in classification performance. Its benefits are further amplified in situations where there is an acute shortage of training size.

Related methodologies

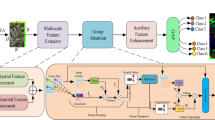
Fig 1 illustrates the comprehensive framework for HSI classification employing the proposed CiSSA_MLTP approach, which encompasses three key components: global spectral feature extraction, extensive spatial feature extraction, and local texture feature extraction at different scales. This framework is demonstrated with the Indian Pines dataset as a case study.

Fig. 1
figure 1

Framework of the presented CiSSA_MLTP architecture for HSI classification.

Full size image

Circulant singular spectrum analysis

CiSSA is a non-parametric subspace decomposition algorithm that breaks down a time-series signal into many single spectrum components57. Its foundation is phase space reconstruction theory. Assume the following: Consider a zero-mean stationary time series \(\{x_t\}\) with T observations. Let \(x=(x_1,\cdots ,x_T)\) denote the vector of these observations. Define L as a positive integer, known as the window length, with the constraint \(1<L<T/2\). CiSSA operates through a four-phase process: embedding, decomposition, grouping, and reconstruction.

Step 1: Embedding. Choose the window length L and transform the univariate time series into a matrix by constructing a trajectory matrix X, where \(N=T-L+1\), as outlined below:

$$\begin{aligned} X=(X_1|\cdots |X_N)=\begin{pmatrix} x_1& x_2& \cdots & x_N \\ x_2& x_3& \cdots & x_{N+1} \\ \vdots & \vdots & \vdots & \vdots \\ x_L& x_{L+1}& \cdots & x_T \end{pmatrix} \end{aligned}$$
(1)

Here, \(X_j=(x_j,\cdots ,x_{j+L-1})\) represents a vector of length L starting at time j. The matrix X is Hankel, meaning that both its columns and rows consist of subseries from the original time series \(\{x_t\}\).

Step 2: Decomposition. The trajectory matrix can be projected onto the space defined by a set of eigenvectors to extract the unobserved components. This involves first constructing a circulant matrix using the sample second moments.

$$\begin{aligned} s_m=\dfrac{1}{T-m}\sum ^{T-m}_{t=1}x_t x_{t-m},m=0,1,\cdots ,L-1 \end{aligned}$$
(2)

The entries of the first row in \(S_C\), denoted as \(\alpha =(\alpha _0,\alpha _1,\cdots ,\alpha _{L-1})\), are specified as follows:

$$\begin{aligned} \alpha _m=\dfrac{L-m}{L}s_m+\dfrac{m}{L}S_{L-m},m=0,1,\cdots ,L-1 \end{aligned}$$
(3)

The eigenvalues of \(S_C\) are represented by \(diag(\lambda _1,\cdots ,\lambda _L)=U^{*}S_CU\), where U is the Fourier matrix and \(U^*\) denotes its conjugate transpose.

The \(k-th\) column of U is the eigenvector corresponding to the eigenvalue \(\lambda _k\), represented as \(u_k=L^{-1/2}(u_{k,1},\cdots ,u_{k,L})\) where \(u_{k,j}=exp\left( -i2\pi (j-1)\dfrac{k-1}{L}\right)\). The eigenvalues \(\lambda _k\) serve as estimates of the spectral density of the time series \(x_t\) at the frequency \(\omega _k=\dfrac{k-1}{L}\), for \(k=1,\cdots ,L\), since

$$\begin{aligned} \lambda _k\simeq \hat{f}\left( \dfrac{k-1}{L}\right) =\sum ^{\infty }_{m=-\infty }s_mexp\left( i2\pi m\dfrac{k-1}{L}\right) \end{aligned}$$
(4)

Hence, there is a direct connection between the eigenvalue \(\lambda _k\) and the frequency \(\omega _k=\dfrac{k-1}{L}\). Consequently, the trajectory matrix X can be decomposed as a sum of rank\(-1\) elementary matrices \(X_k\), such that

$$\begin{aligned} X=\sum ^{L}_{k=1},X_k=\sum ^{L}_{k=1}u_ku^{*}_{k}X \end{aligned}$$
(5)

Step 3: Grouping. The spectral density function exhibits symmetry, \(\lambda _k=\lambda _{L+2-k}\), and the corresponding eigenvectors are complex conjugates, i.e., \(u_k=\bar{u}_{L+2-k}\). This implies that the rank\(\text{-1}\) elementary matrices \(X_k\) and \(X_{L+2-k}\) are related to the same frequency. Consequently, these matrices can be grouped into frequency pairs \(B_k=\{k,L+2-k\}\) for \(k=2,\cdots ,G\), with \(B_1=\{1\}\) and \(B_{\frac{L}{2}+1}\) if L is even. Here, \(G=\left[ \dfrac{L+1}{2}\right]\), where \([\cdot ]\) denotes the integer part.

The elementary matrices based on their associated frequencies can be calculated as:

$$\begin{aligned} \begin{aligned} X_{B_k}&= X_k+X_{L+2-k} \\&= u_ku^*_kX+u_{L+2-k}u^*_{L+2-k}X \\&= (u_ku^*_k+\bar{u}_{k}\bar{u}^*_{k})X \\&= 2\left( \mathscr {R}_{u_k}\mathscr {R}_{u_k}^\prime +\mathscr {J}_{u_k}\mathscr {J}_{u_k}^\prime \right) X \end{aligned} \end{aligned}$$
(6)

Here, \(\mathscr {R}_{u_k}=real(u_k)\) denotes the real part of \(u_k\) and \(\mathscr {J}_{u_k}=imag(u_k)\) denotes the imaginary part of \(u_k\), thus both \(X_k\) and \(X_{B_k}\) are real matrices.

The various elementary frequency groups \(B_k\) with specific unobserved components are associated based on the analysis objectives. The matrix representing a particular unobserved component \(I_j\) is obtained by summing the matrices linked to all the frequencies defining that component, given by:

$$\begin{aligned} X_{I_j}=X_{B_{k1}}+\cdots +X_{B_{kp}} \end{aligned}$$
(7)

Ultimately, the trajectory matrix is reconstructed as:

$$\begin{aligned} X_{I_j}=X_{B_{1}}+\cdots +X_{B_{G}} \end{aligned}$$
(8)

The contribution of a specific frequency group \(B_k\) to the overall matrix is quantified as \(2\lambda _k/\sum \lambda _k\) for \(k=2,\cdots ,G\), and \(\lambda _1/\sum \lambda _k\) for \(k=1\).

Step 4: Reconstruction. In this stage, the matrices \(X_{I_i}=\left( x^{(i)}_{ik}\right)\) obtained in the preceding steps need to be converted into time series of length T, denoted as \(\widetilde{x}^{(j)}=\left( \widetilde{x}^{(j)}_{1},\cdots ,\widetilde{x}^{(j)}_T\right)\). This time series, referred to as the reconstructed series, is derived through diagonal averaging, given by:

$$\begin{aligned} \widetilde{x}^{(j)}_t= \left\{ \begin{array}{ll} \dfrac{1}{t}\sum ^{t}_{i=1}{x}^{(j)}_{i,t-i+1}, 1\le t<L\\ \dfrac{1}{L}\sum ^L_{i=1}{x}^{(j)}_{i,t-i+1}, L\le t<N \\ \dfrac{1}{T-t+1}\sum ^L_{i=t-T+L}{x}^{(j)}_{i,t-i+1}, N< t\le T \end{array}\right. \end{aligned}$$
(9)

It is important to note that the sole parameter required for applying CiSSA is the embedding window L. A general guideline for selecting this parameter is \(L<T/2\); otherwise, the trajectory matrices with a window length L and \(N=T-L+1\) would be equivalent. Additional literature suggests that \(L\le T/3\) to ensure adequate sample second moment estimation. Moreover, L should be sufficiently large to capture complex trends, avoid mixed-frequency components, and be a common multiple of both the seasonal periodicity and the periods of the required oscillatory components.

Local ternary pattern

Tan and Triggs introduced LTP as an extension of LBP. LTP uses a ternary code with three values to achieve greater consistency in uniform and near-uniform regions58. Specifically, gray values within a zone of width \(\pm t\) around a central pixel are quantized to zero; values above \(+t\) are set to \(+1\), and values below \(-t\) are set to \(-1\). LTP can be converted to binary by separating it into positive and negative components. Histograms for these positive and negative parts are created and then concatenated for use. LTP generally outperforms LBP, as it is less sensitive to noise.

The LTP operator for a \(3\times 3\) neighborhood around a central pixel in an image can be calculated using the equation below.

$$\begin{aligned} LBP_8=\sum ^8_{n=1}3^ns^2(x_n-x_{cen}) \end{aligned}$$
(10)
$$\begin{aligned} s(u)= \left\{ \begin{matrix} -1, if\quad u\le x_{cen}-t\\ 1, if\quad u\ge x_{cen}+t\\ 0, if\quad x_{cen}-t<u< x_{cen}+t \end{matrix}\right. \end{aligned}$$
(11)

Here, represents a user-defined threshold, and denotes the number of neighboring pixels surrounding the central pixel.

Fig. 2
figure 2

Formation of local ternary pattern code.

Full size image

To simplify calculations, a ternary pattern is split into two binary patterns as illustrated in Fig 2: the upper and lower patterns. Values of \(-1\) are mapped to 0 in the upper binary pattern and to 1 in the lower binary pattern. Additionally, in the lower pattern, values of 1 from the original window are mapped to 0. The final pattern is constructed by reading the bit pattern from the eastern side of the center pixel and moving counter-clockwise. Subsequently, binary codes are extracted and converted to decimal values for both upper and lower patterns. Lastly, both upper and lower pattern mean, standard deviation, entropy, RMS value, variance, smoothness, kurtosis, and skewness are calculated and concatenated into a single feature vector. The local texture elements such as spots, lines, corners, and edges are captured by these statistical measurements. In addition, the extraction of multi-scale LTP features enhances the ability to capture local scene variations across different scales. This approach leverages the capability of PCA to accentuate spectral differences between pixels, which improves the effectiveness of classification.

Summary of the proposed CiSSA-MLTP

HSIs not only contain fine-grained spectral information but also rich spatial information, with the spatial location of each pixel providing distribution characteristics of the ground objects, which is crucial for land cover classification. However, the classification task becomes particularly complex in the face of challenges such as small sample sizes, high dimensionality, and noise interference. Especially when training samples are extremely limited, accurately identifying various land cover types becomes a significant challenge.

To address this issue, this paper proposes a HSI classification architecture based on CiSSA_MLTP for small sample sizes. This architecture enhances the distinguishability of ground object classification by using a multi-branch approach that integrates global spectral information, temporal variation patterns, spatial co-occurrence features, and multi-scale texture distributions from HSIs. The specific implementation process is shown in Fig 1.

First branch: PCA is used to reduce the dimensionality of the HSI. Then, CiSSA is applied to extract spectral self-similarity, temporal variation, spatial co-occurrence features, and structural features. These features help capture details in terms of temporal changes and spatial structure, thereby improving classification accuracy. This is the primary objective of applying CiSSA to HSI classification tasks for the first time in this paper.

Second branch: PCA dimensionality reduction is performed to extract global spectral features that provide macroscopic differentiation of ground object categories. This process focuses on the overall spectral information of the image, enabling broad differentiation of land cover types.

Third branch: PCA dimensionality reduction is again performed, but LTP is employed to capture texture details, extracting spatial structural features at different scales to assist in distinguishing similar land cover types.

The CiSSA features \(Y^{CiSSA}\) from the first branch and the global spectral features \(Y^{GSF}\) from the second branch are then fused, combining both global and local features to improve the classifier’s adaptability to high-dimensional, complex data. The resulting global-local structural features \(Y^{PCA+CiSSA}\) and multi-scale LTP features \(Y^{LTP}\) are separately fed into SVM classifiers, and a decision-level fusion59 strategy is used to integrate the outputs from each branch, determining the final classification labels. The procedure of CiSSA_MLTP is given in Algorithm 1.

Algorithm 1
figure a

CiSSA_MLTP.

Full size image

Data sets and experiment setup

Hyperspectral datasets

To rigorously evaluate the performance of the CiSSA_MLTP architecture, this section conducts comprehensive experiments using a range of datasets: a low-resolution dataset with class imbalance (Indian Pines, IP), a high spatial resolution dataset (University of Pavia, UP), and a high-resolution dataset with spatial heterogeneity (University of Houston2013, HU). These datasets are accessible for download at https://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes.

Fig. 3
figure 3

Indian Pines dataset. (a) Three-band color composite image. (b) Ground truth map.

Full size image

The IP dataset, acquired by the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) in June 1992, encompasses an agricultural site in Northwestern Indiana. It consists of \(144\times 144\) pixels and 200 spectral channels ranging from 400 to 2500 nm, with 20 bands excluded due to water absorption and low signal-to-noise ratio (SNR). The spatial resolution is 20 m per pixel, and the dataset contains ground truth data classified into 16 crop and vegetation categories, totaling 10,366 labeled pixels. It is notable for its substantial class imbalance in several categories. Fig 3 shows the false-color and ground-truth maps.

Fig. 4
figure 4

Pavia University dataset. (a) Three-band color composite image. (b) Ground truth map.

Full size image

The UP dataset, captured by the Reflective Optics Spectrographic Imaging System (ROSIS) during a 2002 flight over Pavia, Northern Italy, includes \(610 \times 340\) pixels at a 1.3-meter spatial resolution and 103 spectral bands ranging from 430 to 860 nm, excluding 12 noisy bands. It contains 42,776 labeled pixels across 9 urban classes. Fig 4 shows the false-color and ground-truth maps.

Fig. 5
figure 5

Houston2013 dataset. (a) Three-band color composite image. (b) Ground truth map.

Full size image

The HU dataset, acquired by the ITRES-CASI 1500 sensor over the University of Houston campus and surrounding urban areas in June 2012, consists of \(349 \times 1905\) pixels at a 2.5-meter spatial resolution and 144 spectral bands from 364 to 1046 nm. It includes 15 urban land-cover classes with a total of 15,029 labeled pixels. Fig 5 shows the false-color and ground-truth maps.

Experiment setup

Detailed class information for each dataset is systematically presented in Table 1. For each HSI, \(1\%\) of each class’s labeled pixels are randomly chosen for training, while the rest 99% being utilized for testing. To rigorously assess and contrast the categorization performance of different techniques, three standard quantitative indices are utilized: overall accuracy (OA), average accuracy (AA), and kappa coefficient (\(\kappa\)). OA measures the proportion of correctly classified samples versus the total in the test set, AA reflects the average accuracy across all classes, and \(\kappa\) quantifies agreement using the confusion matrix.

Table 1 Number of training and testing samples for IP, UP, and HU datasets.
Full size table

To evaluate the performance and advantages of the CiSSA_MLTP methodology, this section compares it with several advanced state-of-the-art algorithms. This comparison include SVM applied to the initial dataset, spatial-spectral classification utilizing locality-preserving projection combined with local binary pattern and a broad learning system (LPP_LBP_BLS)30, spectral-spatial shared kernel ridge regression (SSSKRR)60, multiscale spatial features with global spectral features derived from PCA (MSF-PCs)8, spectral-spatial feature tokenization transformer (SSFTT)46, central vector oriented self-similarity network (CVSSN)61, adaptive mask sampling and manifold to Euclidean subspace learning (AMS-M2ESL)62, and memory-augmented spectral-spatial Transformer (MASSFormer)63.

  • SVM: A widely used baseline for HSI classification, serving as a fundamental reference for evaluating more advanced algorithms.

  • LPP_LBP_BLS: Combines feature extraction with dimensionality reduction, crucial for high-dimensional data classification, aligning with our approach’s focus on spectral and spatial feature exploitation.

  • SSSKRR: A spectral-spatial shared kernel ridge regression method known for its strong performance in HSI analysis, providing a benchmark for handling both spectral and spatial information.

  • MSF-PCs: A multi-scale fusion approach integrating PCA, segmented-PCA, and 2D singular spectrum analysis, effective in capturing scale-specific features for accurate classification, similar to our method’s multi-scale feature extraction strategy.

  • Recent Deep Learning Models: Including cutting-edge models like SSFTT, CVSSN, AMS-M2ESL, and MASSFormer, these represent the forefront of HSI classification, particularly in spectral and spatial feature adaptation, enabling a comprehensive evaluation of both classification accuracy and computational efficiency.

The eight comparison methods encompass classification techniques that rely solely on spectral information, methods utilizing spectral-spatial features, and approaches that integrate widely adopted convolutional modules or attention mechanisms based on spectral-spatial data. This comprehensive comparison framework allows for a more thorough evaluation of the proposed method’s effectiveness across multiple dimensions.

In the CiSSA_MLTP method, several parameters play a crucial role in optimizing performance. These include:

  • First branch (PCA + CiSSA): The number of PCs, R, the neighborhood window size W, the embedding window size L, are selected to optimize classification accuracy and processing time.

  • Second branch (PCA): The number of PCs, K, is chosen to capture the most significant global spectral features.

  • Third branch (PCA + MLTP): The number of PCs, D, represents the reduced dimensionality of the feature space, the patch size p, the radius r, the number of sample points m, and the number of scales s.

To assess how these parameters affect classification performance, it is necessary to evaluate their impact across three distinct datasets. To facilitate the initial selection of optimal parameters for CiSSA_MLTP, a preliminary fivefold cross-validation approach is employed using a limited subset of training data. This procedure aids in identifying suitable parameter configurations before undertaking more comprehensive evaluations. That is, the dataset was split into five subsets, and the model was trained and tested five times, with each fold using a different subset for testing. This process was repeated, and the optimal parameters were selected based on the average performance across these repetitions to ensure robustness and minimize bias.

In this section, K is set to be \(K = 4\) for the three datasets, R is chosen from the set \(\{3,5,7,9,11,13,15,17,19,21\}\), W is chosen from the interval \(\{3\times 3,5\times 5,7\times 7,9\times 9,11\times 11\}\), and L is chosen from the interval \(\{5\times 5,9\times 9,13\times 13,17\times 17,21\times 21,25\times 25,29\times 29\}\). Here, R is set to be \(R = 21\), and L is set to be \(L = 25\times 25\) for the IP dataset; R is set to be \(R = 13\), and L is set to be \(L=25\times 25\) for the UP dataset; R is set to be \(R = 15\), and L is set to be \(L = 21\times 21\) for the HU dataset. W is set to be \(W = 5\times 5\) for the three datasets. For the IP dataset, D is set to be \(D = 8\), p is set to be \(p = 17\times 17\), r is set to be \(r = 2\), and m is set to be \(m = 8\). For the UP dataset, D is set to be \(D = 9\), p is set to be \(p = 27\times 27\), r is set to be \(r = 2\), and m is set to be \(m = 8\). For the HU dataset, D is set to be \(D = 9\), p is set to be \(p = 25\times 25\), r is set to be \(r = 2\), and m is set to be \(m=8\).

Comparison experiments

Quantitative accuracy analysis

Tables 2, 3 and 4 present detailed quantitative classification results for all methodologies, including class accuracy, OA, AA, and \(\kappa\) for the IP, UP, and HU datasets. To increase the challenge, a random 1% of labeled pixels are designated for training and the remaining for testing. To minimize bias, results averaged over ten trials are reported, with the highest accuracies in each category emphasized in bold.

Table 2 Classification performance of different methodologies on the IP dataset.
Full size table
Fig. 6
figure 6

Classification maps on IP dataset. (a) ground truth map; and the classification results generated by the (b) SVM, (c) LPP_LBP_BLS, (d) SSSKRR, (e) MSF-PCs, (f) SSFTT, (g) CVSSN, (h) AMS-M2ESL, (i) MASSFormer, and (j) CiSSA_MLTP.

Full size image

Overall, SVM underperforms compared to other spatial-spectral algorithms across all datasets, primarily due to its reliance solely on spectral information and disregard for spatial relationships, leading to lower classification accuracy. In contrast, SSSKRR and MSF-PCs achieve competitive accuracy across all datasets, particularly excelling on the UP dataset. LPP_LBP_BLS also performs competitively on the IP and UP datasets, nevertheless its accuracy is lowest on the HU dataset. This lower performance on the HU dataset may be attributed to the small intervals between different land-cover classes and the scattered distribution of classes, resulting in complex classification challenges due to mixed pixels in boundary regions.

Table 3 Classification performance of different methodologies on the UP dataset.
Full size table
Fig. 7
figure 7

Classification maps on UP dataset. (a) ground truth map; and the classification results generated by the (b) SVM, (c) LPP_LBP_BLS, (d) SSSKRR, (e) MSF-PCs, (f) SSFTT, (g) CVSSN, (h) AMS-M2ESL, (i) MASSFormer, and (j) CiSSA_MLTP.

Full size image

For comparisons, SSFTT, CVSSN, and MASSFormer deliver promising land cover predictions on the UP and HU datasets. However, for the IP dataset, these methods show significant variability in accuracy across land cover categories. For example, “Grass-pasture-mowed” and “Oats” categories perform poorly in SSFTT and MASSFormer, likely due to extremely limited training samples-only one labeled sample per category. This scarcity is prone to overfitting and hampers generalization. As shown in Table 2, CVSSN also exhibits low accuracy for these categories, with “Grass-pasture-mowed” and “Oats” achieving only 35.64% and 18.89% accuracy, respectively.

Moreover, the AMS-M2ESL framework demonstrates more consistent classification performance across all three datasets in comparison with alternative methods and attains the highest accuracy across some land cover classes. However, CiSSA_MLTP generally outperforms all other methods. Specifically, CiSSA_MLTP surpasses AMS-M2ESL by 0.06% and 0.08% in OA and \(\kappa\) on the UP dataset, and by 1.41% and 1.52% on the HU dataset. Notably, as compared to the AMS-M2ESL on the IP dataset, CiSSA_MLTP achieves improvements of 5.41% and 6.23% in OA and \(\kappa\), respectively, highlighting its exceptional performance in this dataset.

In general, the superiority of the CiSSA_MLTP algorithm over comparative methods lies in its ability to extract discriminative spatial-spectral features and perform well under small sample conditions. For example, in the IP dataset, when only one sample per class is used for training (e.g., the seventh and ninth land cover types), CiSSA_MLTP achieved classification accuracies of 67.46% and 77.85%, respectively. In contrast, SSFTT and MASSFormer misclassified these types, yielding 0% accuracy, while CVSSN achieved only 35.64% and 18.89% accuracy for the same types. This highlights the algorithm’s robustness in data-scarce scenarios.

Specifically, on three datasets, the confidence intervals for each land cover class, OA, AA, and \(\kappa\) obtained by our proposed method are relatively narrow, further demonstrating the superior stability of our method compared to the comparison algorithms. For instance, on the IP dataset, the confidence intervals for OA and \(\kappa\) are within 0.24%, while the confidence interval for AA is 1.44%. This discrepancy is primarily attributed to the fact that for the seventh and ninth land cover classes, only a single labeled sample is used to train the classifier, which adversely impacted the classifier’s accuracy. For the HU dataset, the confidence intervals for OA, AA, and \(\kappa\) are within 0.74%. In contrast, on the UP dataset, the confidence intervals for OA, AA, and \(\kappa\) are all within 0.08%, further underscoring the robustness of the proposed method.

Table 4 Classification performance of different methodologies on the HU dataset.
Full size table
Fig. 8
figure 8

Classification maps on HU dataset. (a) ground truth map; and the classification results generated by the (b) SVM, (c) LPP_LBP_BLS, (d) SSSKRR, (e) MSF-PCs, (f) SSFTT, (g) CVSSN, (h) AMS-M2ESL, (i) MASSFormer, and (j) CiSSA_MLTP.

Full size image

Qualitative accuracy assessment

For qualitative evaluation, the classification maps produced by various algorithms on the IP, UP, and HU datasets are illustrated in Figs 6, 7 and 8. These visualizations are accompanied by the corresponding ground-truth maps for comparative analysis. Generally, the visual representations of different methods across datasets correlate with the statistical findings presented in Tables 2, 3 and 4. Specifically, for the three datasets, the SVM exhibit numerous salt-and-pepper noise artifacts, particularly noticeable in the challenging class-imbalanced IP dataset, due to the method’s lack of spatial feature extraction capabilities.

Overall, the methods LPP_LBP_BLS, SSSKRR, MSF-PCs, and CVSSN generally yield somewhat smoother visual outcomes with fewer salt-and-pepper artifacts compared to SVM. These methods often produce more continuous homogeneous regions or fewer large misclassified heterogeneous areas. Nevertheless, certain methods exhibit instability issues across the various scenarios. For example, CVSSN applied to the IP dataset and LPP_LBP_BLS on the HU dataset demonstrate some noisy predictions, which contrast markedly with the ground truth maps.

Additionally, SSFTT, AMS-M2ESL, and MASSFormer generate smoother and more precise classification maps, attributed to their advanced spectral-spatial feature extraction capabilities. Unfortunately, these methods occasionally struggle with stability in certain small sample classes. For instance, SSFTT and MASSFormer exhibit significant misclassification in the seventh and ninth land feature categories on the challenging, class-imbalanced IP dataset. In contrast, CiSSA_MLTP provides the cleanest classification map, particularly excelling in boundary regions prone to misclassification, thereby affirming the superior performance of this proposed method.

Parameter analysis

The number of reduced dimensions

The number of PCA significantly influences classification performance. Consequently, prior to extracting CiSSA features, PCA is employed to perform dimensionality reduction and mitigate potential noise. This experiment aims to determine the optimal number of dimensions R for the CiSSA features by evaluating a range of candidate values from 3 to 21, with increments of 2, across the three datasets under consideration.

As depicted in Fig 9, the classification accuracies across each dataset demonstrate a consistent trend with varying R: initially increasing sharply before either declining gradually or stabilizing. Generally, a higher number of PCs correlates with increased execution time for generating CiSSA features. To balance classification accuracy with processing time, the optimal number of PCs is roughly selected as 21 for the IP, and 13 and 15 for the UP and HU datasets, respectively.

Fig. 9
figure 9

Classification performance of CiSSA versus different number of band settings on IP, UP, and HU datasets.

Full size image

Embedding window size

In the CiSSA algorithm, the embedding window size L affects the spatial context captured by each patch. Larger window sizes encompass more complex mixed pixels, impacting the feature extraction and consequently the model performance. Thus, an experiment is performed to identify the optimal L for the three HSIs, using spatial window sizes ranging from \(5\times 5\) to \(29\times 29\) in 4-step increments. The classification outcomes, assessed by OA, AA, and \(\kappa\), are presented in Fig 10. As illustrated, classification accuracy initially increases rapidly with L before stabilizing or decreasing across all three datasets. Given that larger spatial window sizes entail higher computational costs, the optimal window sizes balancing accuracy and processing time are determined to be \(25\times 25\) for the IP and UP datasets, and \(21\times 21\) for the HU dataset.

Fig. 10
figure 10

Classification performance of CiSSA with different embedding windows on IP, UP, and HU datasets.

Full size image

Neighborhood window size

CiSSA is an effective HSI feature extraction technique that captures spatial-spectral information by embedding pixel data into a higher-dimensional space. In CiSSA, the neighborhood window size plays a critical role in determining the spatial extent of local pixel regions considered during feature extraction, impacting both spatial information capture and feature consistency. To identify the optimal neighborhood window size for three hyperspectral datasets, experiments were conducted with neighborhood window sizes ranging from \(3\times 3\) to \(11\times 11\) in 2-step increments, and the classification outcomes, assessed by OA, AA, and \(\kappa\), are presented in Fig 11.

Fig. 11
figure 11

Classification performance of CiSSA with different neighborhood windows on IP, UP, and HU datasets.

Full size image

The results indicate that smaller window sizes extract limited local information, insufficient to capture broader spatial relationships, which hampers classification performance. Conversely, excessively large window sizes may introduce noise and redundancy, complicating the classifier’s ability to distinguish between categories. An optimal window size, around \(5\times 5\) for all three datasets, strikes a balance between spatial feature extraction and noise suppression, maximizing classification accuracy. Thus, the neighborhood window size significantly influences classification effectiveness, and the optimal size is dataset- and task-dependent.

Some other vital settings

This section presents the optimal parameters, including the number of reduced dimensions D, patch size p, and (m, r) for the LTP operator, as detailed in Table 5. Generally, a greater number of selected bands results in increased dimensionality of LTP features, while a larger patch size enhances computational complexity. For the IP dataset, the number of reduced dimensions D is set to 8 with a patch size of \(17\times 17\). For the UP and HU datasets, D is set to 9, with patch sizes of \(27\times 27\) and \(25\times 25\), respectively. Additionally, the impact of the parameter set (m, r) is analyzed, where r defines the radius for selecting circular neighbors and m determines the dimensionality of the LTP histogram. Given that spatially adjacent pixels are likely to belong to the same material, the radius r of the LTP operator should be maintained at a small value. Additionally, increasing m results in greater computational time for the LTP. Considering these factors, the parameter set \((m,r)=(8,2)\) is deemed optimal for balancing classification accuracy and computational efficiency across the three datasets.

Table 5 Optimal parameters of the LTP operator for the SVM classifier using three experimental datasets.
Full size table

Impact of different scale features

The LTP is an effective feature extraction technique for HSIs, capturing local texture information to represent spatial features. In this study, we analyze the impact of multi-scale LTP (MLTP) on classification performance using various neighborhood window sizes, ranging from \(3\times 3\) to \(11\times 11\), with increments of 2. Classification performance is evaluated using OA, AA, and \(\kappa\).

Single-scale feature extraction, using a fixed window size, captures spatial patterns limited to the selected scale. Smaller windows preserve local details but may miss larger-scale relationships, limiting classification accuracy. Larger windows capture broader spatial information but can introduce noise, reducing the classifier’s discriminative power. In contrast, multi-scale LTP combines features from different window sizes, enabling the capture of both fine-grained and global spatial patterns, enhancing classification accuracy and robustness.

As shown in Table 6, at scale 1 (set the neighborhood window size to \(7\times 7\)), classification accuracy is lowest, and execution time is shortest for all three datasets. Increasing the scale improves classification performance, though at the cost of higher execution time due to the added computational steps. For the IP and UP datasets, a scale of 5 provides slight accuracy improvements compared to a scale of 4 but leads to a notable increase in execution time, particularly in the UP dataset. Similarly, for the HU dataset, classification accuracy continues to rise with scale 5 (window sizes \(3\times 3\), \(5\times 5\), \(7\times 7\), \(9\times 9\), and \(11\times 11\)) compared to a scale of 4 (window sizes \(3\times 3\), \(5\times 5\), \(7\times 7\), and \(9\times 9\)), but execution time also increases significantly. To balance accuracy and computational efficiency, we recommend setting the LTP window scale to 4 for hyperspectral data texture feature extraction.

Table 6 Classification results of LTP with single-scale and multi-scale features for small sample sizes on IP, UP, and HU datasets (Optimal results are bolded).
Full size table

Impact of training sample proportion

To thoroughly evaluate the robustness of the nine methods under consideration, this section analyzes their OA and \(\kappa\) across different proportions of labeled samples for all three datasets, as depicted in Fig 12, 1%, 2%, 3%, 4%, and 5% labeled samples were randomly chosen as training for the IP, UP, and HU datasets. Overall, each methodology’s performance improves as the percentage of training samples grows. Specifically, with varying numbers of training samples, SVM performs less well than spatial-spectral-based algorithms. This is because integrating spatial and spectral features can substantially improve classification accuracy of classifier. To rigorously assess the proposed method, this section compares it with recent transformer-based approaches: SSFTT, CVSSN, AMS-M2ESL, and MASSFormer. These methods exhibit superior performance across various training sample proportions on the UP dataset. For the IP and HU datasets, AMS-M2ESL and MASSFormer also deliver competitive results relative to most other methods reviewed. Obviously, the CiSSA_MLTP framework consistently achieves top performance across all datasets and training sample percentages, with particularly notable improvements relative to alternative methods with 1% training samples. This underscores the framework’s exceptional capability to effectively leverage spectral-spatial correlations, represent global spectral features, and capture local texture variations, even with very limited labeled samples.

Fig. 12
figure 12

Classification performance of various methodologies on the IP, UP, and HU datasets with differing proportions of training samples. (a) OA on IP. (b) \(\kappa\) on IP. (c) OA on UP. (d) \(\kappa\) on UP. (e) OA on HU. (f) \(\kappa\) on HU.

Full size image

Time cost comparison

The implementations of SSFTT, CVSSN, AMS-M2ESL, and MASSFormer were executed on a high-performance computing setup featuring an Intel Core i7-13700KF processor, an NVIDIA RTX 4090 GPU, and 64 GB of RAM. In contrast, the proposed CiSSA_MLTP, along with other machine learning-based models, was executed using MATLAB 2016a on a computing system equipped with an AMD Ryzen 77745HX processor, Radeon Graphics (3.60 GHz), and 16 GB of RAM. The corresponding running times for these machine learning models on the IP, UP, and HU datasets are presented in Table 7.

Table 7 Running time in minutes (min) between the contrast methods and the proposed method on three datasets (Optimal results are bolded).
Full size table

As shown in Table 7, SVM demonstrates the shortest execution time across all datasets, as it only relies on spectral features without the need for additional feature extraction steps. In contrast, algorithms such as LPP_LBP_BLS, SSSKRR, and MSF-PCs require more time due to the inclusion of dimensionality reduction or spatial-spectral feature extraction processes. Among all the compared methods, the proposed CiSSA_MLTP consumes the most computational time. This is due to its use of PCA for global spectral feature extraction, CiSSA for spatial co-occurrence feature extraction, and multi-scale LTP for spatial structural feature extraction, all without GPU acceleration.

For the IP dataset, CiSSA_MLTP requires 2.27 minutes more than SVM, yet it yields improvements of over 30.37% in OA, AA, and \(\kappa\). In comparison to LPP_LBP_BLS, CiSSA_MLTP takes 1.18 additional minutes but achieves a 13.16% improvement in these metrics. Although CiSSA_MLTP has a longer runtime, it significantly outperforms the other methods in classification accuracy and visual representation.

Ablation experiment

Ablation experiments were conducted to assess the contributions of different components of the proposed method on the IP, UP, and HU datasets. The model was deconstructed into three modules: global spectral features (GSF) extracted via PCA (second branch of Figure 1), CiSSA feature extraction (first branch of Figure 1), and MLTP feature extraction (third branch of Figure 1). The impact of each module on classification accuracy was evaluated, along with the combined configuration of ’GSF+CiSSA+MLTP’. The results are summarized in Table 8.

Table 8 Ablation study of the proposed method on the IP, UP, and HU datasets (Optimal results are bolded).
Full size table

In the first case, the SVM model using only GSF achieved the lowest classification accuracy across all datasets. In the second case, incorporating CiSSA features significantly improved performance, with OA, AA, and \(\kappa\) increasing by 15.27%, 16.03%, and 17.59% on the IP dataset, and by 11.52%, 13.60%, and 15.98% on the UP dataset, demonstrating the importance of addressing noise and capturing comprehensive spatial-spectral features from HSIs. In the third case, using MLTP further enhanced classification performance by leveraging multi-scale, robust texture features.

In the fourth case, combining GSF and CiSSA led to improvements in OA, AA, and \(\kappa\) on the IP and UP datasets. OA and \(\kappa\) increased by 0.78% and 0.83% on the IP dataset, and OA and AA improved by 0.52% and 0.69% on the UP dataset compared to the second case. However, for the HU dataset, classification accuracy decreased due to complex background noise and feature space expansion from redundant features, which hindered SVM training.

In the fifth case, integrating CiSSA and MLTP resulted in significant improvements in OA, AA, and \(\kappa\) across all datasets, compared to the third case. OA and \(\kappa\) increased by 1.13% and 2.29% on the IP dataset, 2.55% and 3.38% on the UP dataset, and 11.42% and 12.32% on the HU dataset, highlighting the benefits of combining CiSSA’s spatiotemporal features with MLTP’s multi-scale texture differentials.

In the sixth case, combining GSF, CiSSA, and MLTP yielded slightly lower OA and \(\kappa\) on the HU dataset compared to the fifth case but resulted in higher AA. Despite this, the combined configuration still outperformed all other cases, achieving the best classification results on the IP and UP datasets.

Conclusion

In this paper, we introduced a novel framework combining CiSSA and MLBP for small-sample HSI classification, leveraging the fusion of spectral and spatial features to significantly enhance classification performance. Specifically, CiSSA analyzes extensive spatial features in PCA, while PCA extracts global spectral information. By integrating LTP with PCA in another branch, the framework captures fine-grained texture variations, spatial patterns, and contrasts at multiple scales, providing deeper insights into the structure and texture of objects in HSI. A decision-level fusion strategy further integrates the outputs of multiple classifiers, leading to improved classification accuracy.

Through extensive experiments across three prominent HSI datasets, we demonstrated that the CiSSA_MLTP framework substantially enhances the ability to capture spectral-spatial relationships and extract discriminative features. In particular, under small-sample conditions, our approach outperforms state-of-the-art methods. For example, in the IP dataset, using only a single sample per class for training, the CiSSA_MLTP framework achieved classification accuracies of 67.46% and 77.85% for the seventh and ninth land cover types, respectively. In contrast, methods like SSFTT and MASSFormer completely failed, resulting in 0% accuracy, while CVSSN achieved only 35.64% and 18.89% for the same classes. Additionally, with just 1% of labeled data for training, our approach delivered a 20.11% improvement in OA over CVSSN, a 5.41% improvement over AMS-M2ESL, and a 15.95% improvement over MASSFormer. Similar trends were observed across the Pavia University and Houston2013 datasets.

These results underscore the potential of the CiSSA_MLTP framework to address the challenges of small-sample HSI classification, particularly in real-world applications where labeled data is scarce. The proposed approach offers a powerful and efficient solution that advances current HSI classification techniques. Moving forward, we believe this framework could be further extended by exploring additional data augmentation strategies, incorporating advanced fusion techniques, and applying the approach to other remote sensing tasks, such as land-cover change detection or urban mapping.