Introduction

In recent years, the industrial sector has become more committed to reducing its carbon footprint and particularly, plastic-free packaging is gaining industrial interest. From the perspective of the supply chain, plastic packaging is efficient, but as waste, it is likely to cause hazardous effects on the environment. In long-distance transportation, shipping, and handling, corrugated boxes keep products safe. A variety of thicknesses and sizes of corrugated materials can be used to protect fragile or delicate items. Their affordability in comparison to alternative container types has led to their widespread usage. They do not require more workers, sophisticated machinery, or costly apparatus to be deployed. Corrugated boxes have proliferated and are now the most widely used type of shipping container in all areas of transportation and handling of goods.

Sustainability is a critical dynamic in modern businesses, in which, what is required is used to match what is replenished. Corrugated boxes can be effortlessly recycled and reintegrated into the supply chain at the completion of their productive lifespan in a sustainable model. It is widely used in transportation and storage of goods due to its strength and versatility. Old Corrugated Cardboards (OCC) falls under non-hazardous waste, but its bulk and slow decomposition pose environmental challenges. In order to reduce landfill burden, conserve resources, and foster a greener future, it is essential that corrugated waste is recycled sustainably.

On the other hand, a transportation system is an economic framework of facilitating electronic systems, communications, and logistics in order to sustain economic and social activities. The 4-dimensional transportation problems (4-D TPs) have been standardized from the classical transportation problems (TP) and solid transportation problems (3-D TPs). The four sets that define a 4-D TP include a set of known-available sources, a set of targets with known-demands, a set of modes of transportation, and a set of routes1. Thus, a realistic view of contemporary transport systems is presented by a 4-D TP. Since classical TPs (2D, 3D or 4D) are framed in a linear programming framework and are inadequate to handle the existence of uncertainty and fluctuations in today’s competitive market with economies of scale. The relationships between different components of the system are mostly non-linear, which can only be described precisely by a non-linear model. Thus, it is necessary to formulate non-linear transportation problem (NL-TP) to portray fluctuations in today’s competitive market.

A circular economy incorporates revolutionary patterns of manufacturing and usage to guarantee sustained growth over time. It enables us to recycle wastes, cut down on the use of raw materials, maximize resource utilization, and offer it a second chance at life as an entirely novel item. Through the application of the three fundamental concepts of reduce, reuse, and recycle, it also seeks to maximize the use of material resources. This reduces waste, lengthens the lifespan of the product, and builds a more effective and long-lasting manufacturing system. Taking a cue from nature, everything has value and is useable, so waste can be used as another resource. As a result, progress and sustainability are kept in balance.

In order to mitigate the uncertainty embedded in the mathematical modelling of real-life optimization problems, numerous frameworks have been devised over time by various researchers. Fuzzy set theory, stochastic modelling, and rough set approach are few of the pioneered theories available in the literature. An enigmatic instrument for coping with uncertainty and ambiguity, fuzzy set was put forward by Zadeh2. A variety of uncertain theories, namely intuitionistic fuzzy sets3, Neutrosophic fuzzy sets4, complex fuzzy sets5, and Pythagorean fuzzy sets6, have been extrapolated to handle challenging situations involving uncertainty. Later, Fermatean fuzzy set (FFS) was devised by Senapati and Yager7 as an expansion of fuzzy set to deal with uncertainty. In FFS, the sum of the cubes denoting the degree of membership (MD) and non-membership (NMD) is either equal to or less than 1.

Zhang et al.8 devised a bipolar fuzzy set (BFS) that introduced bipolarity in a fuzzy framework. The BFS is characterized by both negative and positive MDs, thus is able to offer a theoretical framework for bipolar aggregation, multi-agent interaction, and resolution of conflicts. In recent years, its ability to incorporate the expertise and consensus of all the concerned professionals and produce more realistic results has made it a vital tool for expressing this ambiguity and uncertainty embedded in real-world optimization issues. Torra9 introduced Hesitant Fuzzy Set (HFS), which permits MD to have a range of possible values, has been found to be an effective structural tool for expressing uncertainty and vagueness.

With respect to the context in which a decision is being established, a decision-maker may possess different perspectives on the same traits. A time-sequential framework is needed to navigate such type of scenarios. As a means of demonstrating the significance of time dimensions, Meng and Li10 introduced the time sequence into the HFS in such a manner that the time sequence framework contains a fixed set of MDs. Variations, fluctuations, and hesitancy of MDs and NMDs with dimensions according to time must be taken into account to better reflect decision-makers’ attitudes.

To reduce the negative effects of OCC on social, economic, and environmental systems, this article developed a green nonlinear transportation system with a circular economy approach. In this nonlinear system, transportation expenses (TE), greenhouse gas emission (GHGE) and transportation time (TT) are optimized. By disuniting the circular economy effect from the proposed model, a sub model is developed. A time sequential Fermatean bipolar hesitant fuzzy set (TS-FBHFS) is developed to illustrate uncertainty along with its multidimensional aspects. Two approaches are used to address the suggested transportation system: the weighted sum technique (WST) and the global criteria method (GCM).

The work carried out in this manuscript is collocated in the following manner: A concise introduction can be found in Section “Introduction”. Section “Literature review, research gap and novelty” is a review of the scientific literature pertaining to the research conducted in the present article. The proposed TS-FBHFS is developed in section “Time-sequential Fermatean bipolar hesitant fuzzy set (TS-FBHFS)”. A non-linear transportation system with circular economy approach under TS-FBHFS for sustainable management of OCC along with a sub-model is devised in section “Mathematical formulation”. The approach to tackle the proposed non-linear transportation system is developed in section “Proposed methodology”. A case study is illustrated to elaborate the proposed model in section “A case study”. Section “Senstivity analysis” deals with the sensitivity analysis. Section “Managerial insights” constitutes the managerial perspectives. The findings, restrictions, and directions for further study are provided in Section “Conclusion”.

Literature review, research gap and novelty

This section discusses the related literature review of studies conducted by researchers around the world. Furthermore, the research gaps identified through a review of relevant literature are deliberated. This part also considers the novel nature of the current work.

Literature review

An overview of the numerous empirical researches on the suggested topic is provided in this review of the literature. The study of the corrugated waste management, 4-D transportation system, non-linear transportation system, circular economy and FFS are all summarised in this section.

Corrugated waste management

The spatial cost-effectiveness of the Swedish waste disposal handling laws is examined by Berglund et al.11. The authors concentrated on the corrugated board case and acknowledged that the various Scandinavian countries have varying economic requirements with regard to the possibilities for recovering and utilizing paper waste. Sotoudehnia et al.12 investigated the possibility of using corrugated cardboard as a feedstock for energy recovery. A study by Zambrano et al.13 evaluated the suitability of OCC for upcycling into tissue paper pulp. Two elemental chlorine-free bleaching sequences were used to study the evolution of OCC fibre physicochemical properties and their impact on tissue properties. Ma et al.14 used the Life Cycle Assessment approach to assess the environmental effects of OCC’ recycling process and examine its life cycle features using a questionnaire survey administered on campus. Yang et al.15 proposed a methodology to extract porous carbon form OCC by utilizing various activators. Lu et al.16 conducted a thorough investigation of the consequences of support type and crystal form in \(Fe\)-based catalysts on the catalytic gasification of OCC. Kim et al.17 investigated how OCC can be catalytically upcycled into lactic acid utilizing lanthanide triflate catalysts. Additionally, chemo catalytic upcycling of OCC into lactic acid was economically analysed. The results suggested that the process has a significant economic benefit. Ketkale and Simske18 investigated a lifecycle and economical assessments of OCC in terms of recycle and reuse in the United States of America. The ecological effects of plastic cushioning against the corrugated cardboard cushioning inserts are evaluated by Silva and Besch19. In order to evaluate paper and cardboard trash in the United States by kind at the federal, state, county, and local levels, Milbrandt et al.20 used statistical and geospatial methodologies. They also intend to serve as a framework for comparable studies conducted in other regions of the world and to advise the efforts by the communities throughout the United States to apply advantageous waste-management practices. Kumar and Verma21 presented a thorough analysis of the thermochemical methods and sludge management strategies used in the pulp and paper industry to generate substrate chemicals.

4-dimensional transportation system

A 4D-TP was put forward by Bera et al.1 that considers the nature of vehicle and the length of the route simultaneously. After that an extensive research has been done by several researchers. Some pioneered works in this direction are as follows: Bera et al.22 developed a 4D-TP that takes hybrid random type-2 parameters for the transportation of breakable goods. A 4D-TP for the supply management of multiple goods with profit and time goals was developed by Samanta et al.23. Jana and Jana24 developed a 4-D TP with fixed charge to supply multi-items by utilizing random type-2 triangular Gaussian fuzzy variables. The devised problem is tackled by employing generalized reduced gradient approach. Two methods were provided by Giri et al.25 to tackle a green, 4-D, fixed-charge TP having several objectives in a Neutrosophic setting. In uncertain fuzzy setting. Akhtar et al.26, Bind et al.27 and Sharma et al.28 developed a 4-DTP to supply goods with multiple goals.

Non-linear transportation system

Gabr29 provided an approach to tackle and analyse quadratic programming problems in an uncertain fuzzy setting. A mathematical framework for a problem related to transportation involving multi-objective objectives, nonlinear transportation cost, and demand with various choices was developed by Maity and Roy30. With interval type-2 fuzzy numbers, Dalman and Bayram31 presented an interactive fuzzy goal methodology to tackle nonlinear problem with multiple objectives. Costs, times, and resources were assumed to be trapezoidal interval type-2 fuzzy numbers. Using fuzzy parameters, Ahmad and Adhami32 proposed a nonlinear transportation system with multiple objectives. The authors employed Neutrosophic programming to solve the nonlinear transportation problem. Using recurrent neural network models, Mansoori and Iffati33 tackled the fuzzy nonlinear programming problem. An overview of existing fuzzy transportation methods and their extensions was presented by Chhibber et al.34. In order to address a non-linear intuitionistic fuzzy transportation and manufacturing problem with multiple goals, Chhibber et al.35 suggested an intuitionistic fuzzy TOPSIS approach. Shivani et al.36 formulated a non-linear solid waste management system for municipal waste by utilizing interval form of rough sets. An inventive approach to a decision assistance system for managing impreciseness associated with a vast volume of human opinion is presented by Hussain and Allah37. It is also shown how to tackle complex real-world applications using an appropriate decision-making technique for the multi-attribute decision making issue utilizing spherical fuzzy settings. A generalization of fuzzy set theory, the Linear Diophantine Fuzzy set was developed by Kannan38. Additionally, they have used the suggested method to show off its usefulness in a numerical example involving the choice of a logistics specialist, which is a crucial choice in emergency logistics optimization.

Fermatean fuzzy set

Several extensions have been proposed based on FFSs to devise imprecise decision framework. In this regard, Rani and Mishra39 developed and analysed interval-valued Fermatean fuzzy set. Akram et al.40 devised 2-tuple linguistic Fermatean fuzzy set as a generalization of FFS to depict realm situations of decision making. Niu et al.41 proposed an expansion of FFS termed as Fermatean cubic fuzzy sets along with its fundamental theory, score function and distance measures. The important attributes of these operators are also examined. As an expansion of FFS, Zhou et al.42 developed dual hesitant Fermatean fuzzy sets with their all-dimensional analysis for COVID-19 vaccine transportation. A Fermatean probabilistic hesitant fuzzy set has been generalized by Qahtan et al.43 as an amplification of a Fermatean probabilistic fuzzy set. The FFS was extended to complex Fermatean fuzzy N-soft sets by Akram et al.44 in an attempt to deal with uncertainty and vagueness in decision making. A Fermatean Neutrosophic set with its fundamental laws and properties was generalized by Saeed et al.45. Chaudhary et al.46 devised time sequential probabilistic Fermatean hesitant fuzzy set as an expansion of FFS by integrating the probabilistic information and time sequential framework along with its application in the sustainable transportation system.

Circular economy

By utilizing circular economy approach, Malinauskaite et al.47 suggested a comprehensive analysis of systems related to waste management of municipalities with waste-to-energy serving as a significant component. The usage of a waste management process based on the creation and application of a waste facility was suggested by Hidlago et al.48. Their integrated technology would primarily produce biogas and syngas. The waste and circularity indicators for Croatia were presented by Luttenberger49 that also examined national policies, targets, accomplishments, and EU recommendations. Finally, actions that would hasten Croatia’s transition to a circular economy, resource efficiency, reduced marine litter in the Adriatic, and a bio economy were also suggested. Hrabec et al.50 offered a strategy that applies contemporary circular economy concepts to assist strategic decision-making in the field of management of municipal waste. The goal of Salmenperä et al.51 was to improve knowledge of the crucial elements that practitioners must contend with as they moved towards a circular economy. The perceptions of two distinct actor groups namely developers and intermediaries were the subject of this investigation. Pamučar et al.52 developed a decision analysis framework with multiple criterions for intelligent transportation system under circular economy concept. Table 1 summarizes a thorough comparison of a number of characteristics between the proposed study and previous comparable works on numerous versions of the transportation system.

Table 1 Comparison of the proposed approach and other TP researches.
Full size table

Research gaps

A comprehensive review of the literature revealed the following research gaps that will be attempted to be filled in this publication.

  • Although several researchers (Rani and Mishra39, Akram et al.40, Niu et al.41, Zhou et al.42, Saeed et al.45, Chaudhary et al.46) have generalized FFS into inimitable fuzzy tools to handle uncertainty. However, integration of FFS with hesitancy and bipolarity under time sequential framework is still a research lacuna available in the literature.

  • Only few authors such as (Meng and Li10, Sharma et al.28, Chaudhary et al.46) utilized time sequences to frame extensions of FFS with hesitancy. But, none of them have incorporated positive and negative MDs and NMDs i.e., bipolarity that exists in real world in a time sequential framework.

  • From the thorough review of literature on non-linear TP, it is evident that researchers like (Maity and Roy30, Dalman and Roy31, Ahmad and Adhami32, Mansoori and Iffati33, Haque et al.53 and Chhibber et al.35) have developed 2D and 3D non-linear transportation system. But, the formulation of non-linear 4D-TP is yet to be framed.

  • It is evident from the recent literature on TP under different generalizations of fuzzy set that a transportation framework for the sustainable management of OCC is not yet developed.

  • In research articles like (Kim et al.17, Ketkale & Simske18, Silva & Besch19, Milbrandt et al.20, Kumar & Verma,21) different approaches to handle OCC have been analysed and suggested. However, a sustainable management system for OCC using non-linear transportation framework with multiple goals is yet to be explored.

Motivation of the study

After conducting a comprehensive review of pertinent prior research and observing a few socioeconomic variables, the motivations for this study are as follows.

  • Improper management of corrugated waste can have detrimental effects on the environment. It emits the methane, a greenhouse gas and takes up significant space in landfills. Since it takes energy, water, and trees to produce fresh cardboard, it also contributes to the depletion of resources. When OCC is improperly disposed of, it can contaminate water and soil, endangering ecosystems and wildlife. Local ecosystems are disrupted by landfills, which draw pests and provide breeding grounds. Recycling helps to reduce carbon emissions. In addition, it uses less energy than producing raw materials. Effective waste management is essential to preventing financial diversion and rising community expenses. Therefore, we have developed a green non-linear transportation architecture with the primary objective of recycling the OCC in order to lessen the hazardous environmental impact of OCC.

  • OCC waste does not have a fixed amount due to a number of activities of generators (who produce) and multiple market scenarios and conditions. This leads to a lack of consistency, incompleteness, and inadequacy of information regarding the management of OCC. It is also true that existing fuzzy set theoretical approaches are not always sufficient to deal with uncertainty in such cases. Thus, we developed a novel extension of fuzzy set theory that allows us to depict uncertainty and imprecision in a wide variety of scenarios.

  • The majority of the system’s relationships are non-linear, and only a non-linear model can accurately capture these linkages. Formulating a non-linear framework is therefore required to depict changes in the present scenario of fierce competition.

Novelty of the study

To fill the lacunae mentioned above, the major highlights of the work carried out in this manuscript are as follows:

  • To address the demerits of various fuzzy extensions, this article develops a fuzzy tool, named TS-FBHFS, which can accommodate the different MDs and NMDs in a time sequential framework. In-depth descriptions of each characteristic of the stated set, including its basic properties as well as a defuzzification methodology are also presented.

  • One may make a big impact and pave the path for a more sustainable future by using appropriate cardboard collection and recycling techniques. In this regard, the article proposes a mathematical framework for green non-linear multi-objective, 4-dimensional transportation problems (GNL-MO-4DTP) under TS-FBHF settings to achieve sustainable management of OCC with circular economy approach.

  • For the first time, circular economy is introduced to the field of transportation as per literature survey.

  • The proposed model seeks to optimize goals, namely overallTE, GHGE, and TT simultaneously in a unified framework for the effective, efficient, and sustainable management of OCC.

  • The suggested methodology includes two different techniques, WST and GCM, and takes into consideration the suggested non-linear transit system for the sustainable management of OCC.

  • In addition, a sub-model without a circular economy framework is developed with the goal of optimizing three objectives namelyTE, GHGE, and TT.

  • Numerous managerial possibilities are also discussed in order to improve the sustainability and efficiency of OCC’s transportation and management.

  • To elucidate the impact of altering model parameters on the outcomes, sensitivity analysis is performed.

Time-sequential Fermatean bipolar hesitant fuzzy set (TS-FBHFS)

In this section, firstly by providing a prime instance, we will discuss the shortcomings of BFSs. The idea of TS-FBHFS is thenthe put forth in this section to outline DM’s viewpoint on various socioeconomic issues that arise in our daily lives. The proposed set is an amalgamation of FFS with HFS and BFS, thereby inheriting the properties of these sets. After that, TS-FBHFS is proposed together with basic operations, and a ranking function for the comparison.

Example 1

Consider the availability of a product in the hands of three inventory managers. They can provide MD and NMD in order to include the expert’s evaluation data.

The assessment values by three inventory managers in the framework of BFS are depicted in the Table 2.

Table 2 Possible forms of positive and negative MD, and NMDs.
Full size table

So, as to incorporate the expert’s evaluation data, MD and NMD can be offered in both positive and negative forms by utilizing the BFS. For 1st inventory manager, \(b_{1} = \left\{ {0.5,0.8, - 0.6, - 0.2} \right\}\) is the representation of information using BFS. Here, sum of positive MD and NMD i.e., 0.5 + 0.8 = 1.3 > 1. Thus, bipolar fuzzy framework is not able to illustrate this scenario. Also, it is evident that Intuitionistic fuzzy set, complex fuzzy set, Pythagorean fuzzy set, FFS, HFS are not able to express this type of scenarios. Moreover, combined evaluation of three inventory managers cannot be predicted in bipolar framework due to the absence of hesitancy. Also, DMs have different pieces of knowledge at different moments.

Therefore, in order to fully characterize such real-world scenarios, it is essential to integrate the theories of BFS, FFS, and HFS beneath the time-sequential framework.

Definition

The structure of TS-FBHFS is mathematically defined as

$${\vec{\mathfrak{f}}} = \left\{ {f,\overrightarrow {{{\mathfrak{m}}^{ + } }} \left( f \right),\overrightarrow {{{\mathfrak{n}}^{ + } }} \left( f \right),\overrightarrow {{{\mathfrak{m}}^{ - } }} \left( f \right),\overrightarrow {{{\mathfrak{n}}^{ - } }} \left( f \right):f \in F} \right\}$$

where \(\overrightarrow {{{\mathfrak{m}}^{ + } }} \left( f \right), \overrightarrow {{{\mathfrak{n}}^{ + } }} \left( f \right)\): \(F \to \left[ {0, 1} \right]\) and \(\overrightarrow {{{\mathfrak{m}}^{ - } }} \left( f \right), \overrightarrow {{{\mathfrak{n}}^{ - } }} \left( f \right)\): \(F \to \left[ { - 1, 0} \right].\) Here, \(F\) is the universal set.

The \(\overrightarrow {{{\mathfrak{m}}^{ + } }} \left( f \right)\) and \(\overrightarrow {{{ }{\mathfrak{n}}^{ + } }} \left( f \right)\) depict sets of the possible positive MDs and NMDs and \(\overrightarrow {{{\mathfrak{m}}^{ - } }} \left( f \right)\) and \(\overrightarrow {{{\mathfrak{n}}^{ - } }} \left( f \right)\) depict sets of the possible negative MDs and NMDs, respectively. Elements of \(\overrightarrow {{{\mathfrak{m}}^{ + } }} \left( f \right),\overrightarrow {{{ }{\mathfrak{n}}^{ + } }} \left( f \right)\), \(\overrightarrow {{{\mathfrak{m}}^{ - } }} \left( f \right) {\text{and}} \overrightarrow {{{\mathfrak{n}}^{ - } }} \left( f \right)\) are arranged in a time-sequential framework.

Additionally, \(\varphi^{ + \left( i \right)} \in\) \(\overrightarrow {{{\mathfrak{m}}^{ + } }} \left( f \right)\), \(\phi^{ - \left( i \right)} \in\) \(\overrightarrow {{{\mathfrak{n}}^{ + } }} \left( f \right)\), \(\varphi^{ - \left( i \right)} \in\) \(\overrightarrow {{{\mathfrak{m}}^{ - } }} \left( f \right)\), \(\phi^{ - \left( i \right)} \in\) \(\overrightarrow {{{\mathfrak{n}}^{ - } }} \left( f \right)\) such that \(0 \le \varphi^{ + \left( i \right)} , \phi^{ + \left( i \right)} \le 1\), \(- 1 \le \varphi^{ - \left( i \right)} , \phi^{ - \left( i \right)} \le 1\), \(0 \le\) \(\left( {{\text{max}}\left\{ {\varphi^{ + \left( i \right)} } \right\}} \right)^{3} + \left( {{\text{max}}\left\{ {\phi^{ + \left( i \right)} } \right\}} \right)^{3} \le 1\) and \(- 1 \le\) \(\left( {{\text{max}}\left\{ {\varphi^{ - \left( i \right)} } \right\}} \right)^{3} + \left( {{\text{max}}\left\{ {\beta^{ - \left( i \right)} } \right\}} \right)^{3} \le 0\).

\({\vec{\mathfrak{f}}} = \left\langle {\overrightarrow {{{\mathfrak{m}}^{ + } }} ,\overrightarrow {{{\mathfrak{n}}^{ + } }} ,\overrightarrow {{{\mathfrak{m}}^{ - } }} ,\overrightarrow {{{\mathfrak{n}}^{ - } }} } \right\rangle\) is termed as time-sequential Fermatean bipolar hesitant element (TS-FBHE).

Example 2

The overall assessment of a product’s availability by three inventory managers by utilizing proposed TS-FBHFS is as follows;

$${\vec{\mathfrak{f}}} = \left\langle {\left\{ {0.5^{\left( 1 \right)} ,0.4^{\left( 2 \right)} ,0.8^{\left( 3 \right)} } \right\},\left\{ {0.8^{\left( 1 \right)} ,0.2^{\left( 2 \right)} ,0.4^{\left( 3 \right)} } \right\},\left\{ { - 0.6^{\left( 1 \right)} , - 0.2^{\left( 2 \right)} , - 0.7^{\left( 3 \right)} } \right\}, \left\{ { - 0.2^{\left( 1 \right)} , - 0.5^{\left( 2 \right)} , - 0.1^{\left( 3 \right)} } \right\}} \right\rangle$$

Here, \(\left\{ {0.5^{\left( 1 \right)} ,0.4^{\left( 2 \right)} ,0.8^{\left( 3 \right)} } \right\}\), \(\left\{ {0.8^{\left( 1 \right)} ,0.2^{\left( 2 \right)} ,0.4^{\left( 3 \right)} } \right\}\) represent the sets of positive MDs and NMDs. Also, \(\left\{ { - 0.6^{\left( 1 \right)} , - 0.2^{\left( 2 \right)} , - 0.7^{\left( 3 \right)} } \right\}, \left\{ { - 0.2^{\left( 1 \right)} , - 0.5^{\left( 2 \right)} , - 0.1^{\left( 3 \right)} } \right\}\) represents the sets of negative MDs and NMDs.

Here, \(\left( {0.5} \right)^{3} + \left( {0.8} \right)^{3} = 0.637 < 1\), due to the property of FFS, we can manage this kind of uncertainty by integrating BFS with FFS.

As a result, we have combined aleatory and epistemic uncertainty within the framework of time-sequences in the form of \({\vec{\mathfrak{f}}} = \left\{ {f,\overrightarrow {{{\mathfrak{m}}^{ + } }} \left( f \right),\overrightarrow {{{\mathfrak{n}}^{ + } }} \left( f \right),\overrightarrow {{{\mathfrak{m}}^{ - } }} \left( f \right),\overrightarrow {{{\mathfrak{n}}^{ - } }} \left( f \right):f \in F} \right\}\). Therefore, TS-FBHFS can overcome shortcomings of BFS and existing extensions of fuzzy set theory.

Fundamental operations

Let \({\vec{\mathfrak{f}}} = \left\langle {\overrightarrow {{{\mathfrak{m}}^{ + } }} ,\overrightarrow {{{\mathfrak{n}}^{ + } }} ,\overrightarrow {{{\mathfrak{m}}^{ - } }} ,\overrightarrow {{{\mathfrak{n}}^{ - } }} } \right\rangle\),\({\vec{\mathfrak{f}}}_{1} = \left\langle {\overrightarrow {{{\mathfrak{m}}_{1}^{ + } }} ,\overrightarrow {{{\mathfrak{n}}_{1}^{ + } }} ,\overrightarrow {{{\mathfrak{m}}_{1}^{ - } }} ,\overrightarrow {{{\mathfrak{n}}_{1}^{ - } }} } \right\rangle\) and \({\vec{\mathfrak{f}}}_{2} = \left\langle {\overrightarrow {{{\mathfrak{m}}_{2}^{ + } }} ,\overrightarrow {{{\mathfrak{n}}_{2}^{ + } }} ,\overrightarrow {{{\mathfrak{m}}_{2}^{ - } }} ,\overrightarrow {{{\mathfrak{n}}_{2}^{ - } }} } \right\rangle\) be three TS-FBHEs, then the fundamental operations are defined as follows:

  1. (i)

    Inclusion

$${\vec{\mathfrak{f}}}_{2} \subseteq {\vec{\mathfrak{f}}}_{1} {\text{ iff }}\forall \varphi_{2}^{ + \left( i \right)} \le \varphi_{1}^{ + \left( i \right)} , \phi_{2}^{ + \left( i \right)} , \ge \phi_{1}^{ + \left( i \right)} ,\varphi_{2}^{ - \left( i \right)} \ge \varphi_{1}^{ - \left( i \right)} ,\phi_{2}^{ - \left( i \right)} \le \phi_{1}^{ + \left( i \right)}$$
$${\vec{\mathfrak{f}}}_{2} = {\vec{\mathfrak{f}}}_{1} {\text{ iff }}\forall \varphi_{2}^{ + \left( i \right)} = \varphi_{1}^{ + \left( i \right)} , \phi_{2}^{ + \left( i \right)} = \phi_{1}^{ + \left( i \right)} ,\varphi_{2}^{ - \left( i \right)} = \varphi_{1}^{ - \left( i \right)} ,\phi_{2}^{ - \left( i \right)} = \phi_{1}^{ + \left( i \right)}$$
  1. (ii)

    Complement

$${\vec{\mathfrak{f}}}^{c} = \bigcup\nolimits_{{\varphi ^{{ + \left( i \right)}} \in {\text{~}}\overrightarrow {{{\mathfrak{m}}^{ + } }} ,~\beta ^{{ + \left( i \right)}} \in {\text{~}}\overrightarrow {{{\mathfrak{n}}^{ + } }} ,{\text{~}}\varphi ^{{ - \left( i \right)}} \in ~\overrightarrow {{{\mathfrak{m}}^{ - } }} ,~\beta ^{{ - \left( i \right)}} \in {\text{~}}\overrightarrow {{{\mathfrak{n}}^{ - } }} }} {\left\langle {\begin{array}{*{20}c} {\left\{ {2 - \varphi ^{{ + \left( i \right)}} } \right\}} \\ {\left\{ {2 - \phi ^{{ + \left( i \right)}} } \right\},} \\ {\left\{ { - 2 - \varphi ^{{ - \left( i \right)}} } \right\},~} \\ {\left\{ { - 2 - \phi ^{{ - \left( i \right)}} } \right\}|} \\ \end{array} } \right\rangle }$$
  1. (iii)

    Union

$${\vec{\mathfrak{f}}}_{1} \cup {\vec{\mathfrak{f}}}_{2} = \bigcup\nolimits_{{\begin{array}{*{20}c} {\varphi_{j}^{ + \left( i \right)} \in \overrightarrow {{{\mathfrak{m}}_{j}^{ + } }} ,\phi_{j}^{ + \left( i \right)} \in \overrightarrow {{{\mathfrak{n}}_{j}^{ + } }} ,\varphi_{j}^{ - \left( i \right)} \in \overrightarrow {{{\mathfrak{m}}_{j}^{ - } }} ,\phi_{j}^{ - \left( i \right)} \in \overrightarrow {{{\mathfrak{n}}_{j}^{ - } }} } \\ {1 \le j \le 2} \\ \end{array} }} {\left\langle {\begin{array}{*{20}c} {\left\{ {\max \left( {\varphi_{1}^{ + \left( i \right)} ,\varphi_{2}^{ + \left( i \right)} } \right)} \right\},\left\{ {{\text{min}}\left( {\phi_{1}^{ + \left( i \right)} ,\phi_{2}^{ + \left( i \right)} } \right)} \right\}} \\ {\left\{ {{\text{min}}\left( {\varphi_{1}^{ - \left( i \right)} ,\varphi_{2}^{ - \left( i \right)} } \right)} \right\},\left\{ {{\text{max}}\left( {\phi_{1}^{ - \left( i \right)} ,\phi_{2}^{ - \left( i \right)} } \right)} \right\}} \\ \end{array} } \right\rangle }$$
  1. (iv)

    Intersection

$${\vec{\mathfrak{f}}}_{1} \cap {\vec{\mathfrak{f}}}_{2} = \bigcup\nolimits_{{\begin{array}{*{20}c} {\varphi_{j}^{ + \left( i \right)} \in \overrightarrow {{{\mathfrak{m}}_{j}^{ + } }} ,\phi_{j}^{ + \left( i \right)} \in \overrightarrow {{{\mathfrak{n}}_{j}^{ + } }} ,\varphi_{j}^{ - \left( i \right)} \in \overrightarrow {{{\mathfrak{m}}_{j}^{ - } }} ,\phi_{j}^{ - \left( i \right)} \in \overrightarrow {{{\mathfrak{n}}_{j}^{ - } }} } \\ {1 \le j \le 2} \\ \end{array} }} {\left\langle {\begin{array}{*{20}c} {\left\{ {\min \left( {\varphi_{1}^{ + \left( i \right)} ,\varphi_{2}^{ + \left( i \right)} } \right)} \right\}, \left\{ {max\left( {\phi_{1}^{ + \left( i \right)} ,\phi_{2}^{ + \left( i \right)} } \right)} \right\}} \\ {\left\{ {max\left( {\varphi_{1}^{ - \left( i \right)} ,\varphi_{2}^{ - \left( i \right)} } \right)} \right\},\left\{ {min\left( {\phi_{1}^{ - \left( i \right)} ,\phi_{2}^{ - \left( i \right)} } \right)} \right\}} \\ \end{array} } \right\rangle }$$
  1. (v)

    Addition

$${\vec{\mathfrak{f}}}_{1} \oplus {\vec{\mathfrak{f}}}_{2} = \bigcup\nolimits_{{\begin{array}{*{20}c} {\varphi_{j}^{ + \left( i \right)} \in \overrightarrow {{{\mathfrak{m}}_{j}^{ + } }} ,\phi_{j}^{ + \left( i \right)} \in \overrightarrow {{{\mathfrak{n}}_{j}^{ + } }} ,\varphi_{j}^{ - \left( i \right)} \in \overrightarrow {{{\mathfrak{m}}_{j}^{ - } }} ,\phi_{j}^{ - \left( i \right)} \in \overrightarrow {{{\mathfrak{n}}_{j}^{ - } }} } \\ {1 \le j \le 2} \\ \end{array} }} {\left\langle {\begin{array}{*{20}c} {\left\{ {\left( {\left( {\varphi_{1}^{ + \left( i \right)} } \right)^{3} + \left( {\varphi_{2}^{ + \left( i \right)} } \right)^{3} - \left( {\varphi_{1}^{ + \left( i \right)} } \right)^{3} \left( {\varphi_{2}^{ + \left( i \right)} } \right)^{3} } \right)^{\frac{2}{3}} } \right\},} \\ {\left\{ {\phi_{1}^{ + \left( i \right)} \phi_{2}^{ + \left( i \right)} } \right\},} \\ {\left\{ { - \varphi_{1}^{ - \left( i \right)} \varphi_{2}^{ - \left( i \right)} } \right\},} \\ {\left\{ { - \left( { - \left( {\phi_{1}^{ - \left( i \right)} } \right)^{3} - \left( {\phi_{2}^{ - \left( i \right)} } \right)^{3} + \left( {\phi_{1}^{ - \left( i \right)} } \right)^{3} \left( {\phi_{2}^{ - \left( i \right)} } \right)^{3} } \right)^{2/3} } \right\} } \\ \end{array} } \right\rangle }$$
  1. (vi)

    Multiplication

$${\vec{\mathfrak{f}}}_{1} \otimes {\vec{\mathfrak{f}}}_{2} = \bigcup\nolimits_{{\begin{array}{*{20}c} {\varphi_{j}^{ + \left( i \right)} \in \overrightarrow {{{\mathfrak{m}}_{j}^{ + } }} ,\phi_{j}^{ + \left( i \right)} \in \overrightarrow {{{\mathfrak{n}}_{j}^{ + } }} ,\varphi_{j}^{ - \left( i \right)} \in \overrightarrow {{{\mathfrak{m}}_{j}^{ - } }} ,\phi_{j}^{ - \left( i \right)} \in \overrightarrow {{{\mathfrak{n}}_{j}^{ - } }} } \\ {1 \le j \le 2} \\ \end{array} }} {\left\langle {\begin{array}{*{20}c} {\left\{ {\varphi_{1}^{ + \left( i \right)} \varphi_{2}^{ + \left( i \right)} } \right\},} \\ {\left\{ {\left( {\left( {\phi_{1}^{ + \left( i \right)} } \right)^{3} + \left( {\phi_{2}^{ + \left( i \right)} } \right)^{3} - \left( {\phi_{1}^{ + \left( i \right)} } \right)^{3} \left( {\phi_{2}^{ + \left( i \right)} } \right)^{3} } \right)^{\frac{2}{3}} } \right\},} \\ {\left\{ { - \left( { - \left( {\varphi_{1}^{ - \left( i \right)} } \right)^{3} - \left( {\varphi_{2}^{ - \left( i \right)} } \right)^{3} + \left( {\varphi_{1}^{ - \left( i \right)} } \right)^{3} \left( {\varphi_{2}^{ - \left( i \right)} } \right)^{3} } \right)^{\frac{2}{3}} } \right\},} \\ {\left\{ { - \phi_{1}^{ - \left( i \right)} \phi_{2}^{ - \left( i \right)} } \right\} } \\ \end{array} } \right\rangle }$$
  1. (vii)

    Exponent

$${\vec{\mathfrak{f}}}^{{\Lambda }} = \bigcup\nolimits_{{\varphi^{ + \left( i \right)} \in { }\overrightarrow {{{\mathfrak{m}}^{ + } }} , \phi^{ + \left( i \right)} \in { }\overrightarrow {{{\mathfrak{n}}^{ + } }} ,{ }\varphi^{ - \left( i \right)} \in \overrightarrow {{{\mathfrak{m}}^{ - } }} , \phi^{ - \left( i \right)} \in { }\overrightarrow {{{\mathfrak{n}}^{ - } }} }} {\left\langle {\begin{array}{*{20}c} {\left\{ {\left( {\varphi^{ + \left( i \right)} } \right)^{{\Lambda }} } \right\},} \\ {\left\{ {\left( {2 - \left( {2 - \left( {\phi^{ + \left( i \right)} } \right)^{3} } \right)^{{\Lambda }} } \right)^{\frac{2}{3}} } \right\},} \\ { \left\{ { - \left( {2 - \left( {2 - \left( { - \varphi^{ - \left( i \right)} } \right)^{3} } \right)^{{\Lambda }} } \right)^{\frac{2}{3}} } \right\}, } \\ {\left\{ { - \left( { - \phi^{ - \left( i \right)} } \right)^{{\Lambda }} } \right\}} \\ \end{array} } \right\rangle }$$
  1. (viii)

    Scalar Multiplication

$${\Lambda }{\vec{\mathfrak{f}}} = \bigcup\nolimits_{{\varphi^{ + \left( i \right)} \in { }\overrightarrow {{{\mathfrak{m}}^{ + } }} , \phi^{ + \left( i \right)} \in { }\overrightarrow {{{\mathfrak{n}}^{ + } }} ,{ }\varphi^{ - \left( i \right)} \in \overrightarrow {{{\mathfrak{m}}^{ - } }} , \phi^{ - \left( i \right)} \in { }\overrightarrow {{{\mathfrak{n}}^{ - } }} }} {\left\langle {\begin{array}{*{20}c} {\left\{ {\left( {2 - \left( {2 - \left( {\varphi^{ + \left( i \right)} } \right)^{3} } \right)^{{\Lambda }} } \right)^{\frac{2}{3}} } \right\},} \\ {\left\{ {\left( {\phi^{ + \left( i \right)} } \right)^{{\Lambda }} } \right\}, } \\ {\left\{ { - \left( { - \varphi^{ - \left( i \right)} } \right)^{{\Lambda }} } \right\}, } \\ {\left\{ { - \left( {2 - \left( {2 - \left( { - \phi^{ - \left( i \right)} } \right)^{3} } \right)^{{\Lambda }} } \right)^{2/3} } \right\}} \\ \end{array} } \right\rangle }$$

Defuzzification function

A defuzzification function for the proposed TS-FBHE is developed in this part. It transforms the time-sequential Fermatean bipolar hesitant information to crisp data, in order to mitigate computational time and complexity. Additionally, two or more TS-FBHEs are ranked with the help of proposed defuzzification function.

The defuzzification function for a TS-FB \({\vec{\mathfrak{f}}} = \left\langle {\overrightarrow {{{\mathfrak{m}}^{ + } }} ,\overrightarrow {{{\mathfrak{n}}^{ + } }} ,\overrightarrow {{{\mathfrak{m}}^{ - } }} ,\overrightarrow {{{\mathfrak{n}}^{ - } }} } \right\rangle\) is stated as

\(\begin{aligned} {\mathfrak{D}}\left( {{\vec{\mathfrak{f}}}} \right) = & f\left( {1 + \frac{2}{{c\left( {\overrightarrow {{{\mathfrak{m}}^{ + } }} } \right) + c\left( {\overrightarrow {{{\mathfrak{m}}^{ + } }} } \right)^{2} }}\sum i\left( {\alpha ^{{ + \left( i \right)}} } \right)^{3} - \frac{2}{{c\left( {\overrightarrow {{{\mathfrak{n}}^{ + } }} } \right) + c\left( {\overrightarrow {{{\mathfrak{n}}^{ + } }} } \right)^{2} }}\sum i\left( {\beta ^{{ + \left( i \right)}} } \right)^{3} } \right. \\ & \;\left. { + \frac{2}{{c\left( {\overrightarrow {{{\mathfrak{m}}^{ - } }} } \right) + c\left( {\overrightarrow {{{\mathfrak{m}}^{ - } }} } \right)^{2} }}\sum i\left( {\alpha ^{{ - \left( i \right)}} } \right)^{3} - \frac{2}{{c\left( {\overrightarrow {{{\mathfrak{n}}^{ - } }} } \right) + c\left( {\overrightarrow {{{\mathfrak{n}}^{ - } }} } \right)^{2} }}\sum i\left( {\beta ^{{ - \left( i \right)}} } \right)^{3} } \right) \\ \end{aligned}\).

Also, the accuracy function is defined as

$$\begin{aligned} {\mathfrak{A}}\left( {{\vec{\mathfrak{f}}}} \right) = & f\left( {1 + \frac{2}{{c\left( {\overrightarrow {{{\mathfrak{m}}^{ + } }} } \right) + c\left( {\overrightarrow {{{\mathfrak{m}}^{ + } }} } \right)^{2} }}\sum i\left( {\alpha ^{{ + \left( i \right)}} } \right)^{3} + \frac{2}{{c\left( {\overrightarrow {{{\mathfrak{n}}^{ + } }} } \right) + c\left( {\overrightarrow {{{\mathfrak{n}}^{ + } }} } \right)^{2} }}\sum i\left( {\beta ^{{ + \left( i \right)}} } \right)^{3} } \right. \\ & \;\left. { + \frac{2}{{c\left( {\overrightarrow {{{\mathfrak{m}}^{ - } }} } \right) + c\left( {\overrightarrow {{{\mathfrak{m}}^{ - } }} } \right)^{2} }}\sum i\left( {\alpha ^{{ - \left( i \right)}} } \right)^{3} + \frac{2}{{c\left( {\overrightarrow {{{\mathfrak{n}}^{ - } }} } \right) + c\left( {\overrightarrow {{{\mathfrak{n}}^{ - } }} } \right)^{2} }}\sum i\left( {\beta ^{{ - \left( i \right)}} } \right)^{3} } \right) \\ \end{aligned}$$

Here,

\(c\left( {\overrightarrow {{{\mathfrak{m}}^{ + } }} } \right)\)

and \(c\left( {\overrightarrow {{{\mathfrak{m}}^{ - } }} } \right)\) denote the cardinality of positive and negative MDs. Similarly, \(c\left( {\overrightarrow {{{\mathfrak{n}}^{ + } }} } \right)\) and \(c\left( {\overrightarrow {{{\mathfrak{n}}^{ - } }} } \right)\) represent the cardinality of positive and negative NMDs, respectively.

Mathematical formulation

The integrated circular economy approach presented in this section addresses the GNLMO-4DTP for the sustainable management of OCC under TS-FBHF circumstances.

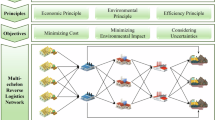
The proposed framework is designed as follows: Firstly, recyclers collect the OCC in cardboard recycling containers from its point of origin, such as various types of industries and landfill sites, and the separated cardboard is transported to a cardboard recycling plant. After collecting OCC from various sources, they are transformed into new corrugated sheets through several steps, such as sorting, shredding, clearing, repulping, forming, drying, and manufacturing. After being reprocessed, these sheets are sold to corrugated box manufacturers for making corrugated containers. Cardboard recycling conserves resources and reduces waste, as well as GHGEs when compared with manufacturing new cardboard. Figure 1 demonstratesthe framework of the proposed non-linear 4D-TP to manage OCC sustainably.

Fig. 1
figure 1

Pictorial depiction of proposed GNLMO-4DTP for sustainable management of corrugated waste.

Full size image

Since, it is not possible to achieve precision for every parameter in this model; the proposed non-linear 4D TPs’ uncertainty is illustrated using the developed TS-FBHFS. Since the OCC units that are offered by the landfill \(\tilde{A}_{c}^{1}\) and commercial establishments \(\tilde{A}_{l}^{2}\) are TS-FBHFE in nature. Additionally, the OCC recycling facility’s capacity \(\tilde{B}_{f}^{3} ,{\text{demand of corrugated sheets }}\tilde{B}_{m}^{4} ,\) and the manufacturer’s method of transportation \(\tilde{E}_{t}\) are considered as TS-FBHFE due to the ambiguity and uncertainty in the era of competitive market. The transit times and costs are regarded to be precise in nature because they are often predetermined. Furthermore, the distance between many routes and the rate of carbon emissions are fixed parameters that cannot be changed.

The proposed non-linear transportation system for sustainable management of OCC aims to optimize three objectives, TE, GHGE and TT as depicted by Eqs. (1–3). The first objective evaluates total transportation expenses during all steps involved in the management of OCC sustainably and it consists of six terms. The first and second terms represent the fixed and variable total TE respectively, for the transit of OCC from \(c{\text{th}}\) commercial industry to \(f{\text{th}}\) corrugated waste recycling facility by \(t{\text{th}}\) mode of transportation via \(r{\text{th}}\) route. Also, third and fourth terms depict the fixed and variable total TE respectively, for the transit of OCC from \(l{\text{th}}\) landfill to \(f{\text{th}}\) corrugated waste recycling facility by \(t{\text{th}}\) mode of transportation via \(r{\text{th}}\) route. Similarly, fifth and sixth terms depict the fixed and variable total TE respectively, for the transit of new corrugated sheets from \(f{\text{th}}\) corrugated waste recycling facility to \(m{\text{th}}\) corrugated box manufacturer by \(t{\text{th}}\) mode of transportation via \(r{\text{th}}\) route.

The second goal aims to optimize total GHGE during the recycling of OCC into new boxes. Here, the first part represent the carbon emission during the various stages in supply chain management. The second part is all about the total penalty of GHGEs at \(f{\text{th}}\) corrugated waste recycling facility during the recycling of used corrugated carboards to new corrugated sheets.

The third goal aims to minimize total TT. The first and second terms depicts the fixed and variable total TT respectively, for the transit of OCC from \(c{\text{th}}\) commercial industry to \(f{\text{th}}\) corrugated waste recycling facility by \(t{\text{th}}\) mode of transportation via \(r{\text{th}}\) route. Also, third and fourth terms depict the fixed and variable total TT respectively, for the transit of OCC from \(l{\text{th}}\) landfill to \(f{\text{th}}\) corrugated waste recycling facility by \(t{\text{th}}\) mode of transportation via \(r{\text{th}}\) route. Moreover, the fixed and variable total TT for the transit of new corrugated sheets from \(f{\text{th}}\) corrugated waste recycling facility to \(m{\text{th}}\) corrugated box manufacturer by \(t{\text{th}}\) mode of transportation via \(r{\text{th}}\) route, respectively are represented by the fifth and sixth terms respectively.

The total availability of OCC at \(c{\text{th}}\) commercial industry and \(l{\text{th}}\) landfill is represented by Eqs. (4) and (5), respectively. Moreover, the demand of OCC at \(f{\text{th}}\) corrugated waste recycling facility is depicted by Eq. (6). Also, demand of corrugated sheets by \(m{\text{th}}\) corrugated box manufacturer is furnished by Eq. (7). Thereafter, capacity of \(t{\text{th}}\) mode of transportation in the recycling process of OCC during transportation of OCC from \(c{\text{th}}\) commercial industry to \(f{\text{th}}\) corrugated waste recycling facility, \(l{\text{th}}\) landfill to \(f{\text{th}}\) corrugated waste recycling facility and \(f{\text{th}}\) corrugated waste recycling facility to \(m{\text{th}}\) corrugated box manufacturer via \(r{\text{th}}\) route is represented by Eqs. (8), (9) and (10) respectively. The Eq. (11) integrates the notion of circular economy in the proposed transportation system.

The following list includes few presumptions that are upheld in the conceptualization of the devised framework:

Assumptions

  • \(\tilde{A}_{c}^{1} > 0,\) \(\tilde{A}_{l}^{2} > 0,\) \(\tilde{B}_{f}^{3} > 0,\) \(\tilde{B}_{m}^{4} > 0,\) and \(\tilde{E}_{t} > 0, \forall f,c,l,m, t\)

  • No damage of OCC, and recycled corrugated sheets.

  • Mode of conveyances and several paths are ideal for the conduction of smooth supply chain.

  • The parameters in the TS-FBHFE form are positive in nature.

  • OCC are collected from \(l{\text{th}}\) landfill and \(c{\text{th}}\) commercial establishment.

Table 3 describes the notations utilized in the development of GNLMO-4DTP. Different nodes, parameters, and decision variables utilized are defined in the Table 2.

Table 3 Notations for proposed non-linear transportation system for the sustainable management of OCC.
Full size table

Model 1

Minimization of total transportation expenses

$$\begin{aligned} Min\;Z_{1} = & \mathop \sum \limits_{c,f,t,r} {\mathfrak{c}}_{cftr}^{13} L_{cfr}^{13} x_{cftr}^{13} + \mathop \sum \limits_{c,f,t,r} {\mathfrak{C}}_{cftr}^{13} L_{cfr}^{13} \left( {x_{cftr}^{13} } \right)^{2} + \mathop \sum \limits_{l,f,t,r,} {\mathfrak{c}}_{lftr}^{23} L_{lfr}^{23} x_{lftr}^{23} \\ & \; + \mathop \sum \limits_{l,f,t,r} {\mathfrak{C}}_{lftr}^{23} L_{lfr}^{23} \left( {x_{lftr}^{23} } \right)^{2} + \mathop \sum \limits_{f,m,t,r} {\mathfrak{c}}_{fmtr}^{34} L_{fmr}^{34} x_{fmtr}^{34} + \mathop \sum \limits_{f,m,t,r} {\mathfrak{C}}_{fmtr}^{34} L_{fmr}^{34} \left( {x_{fmtr}^{34} } \right)^{2} \\ \end{aligned}$$
(1)

Minimization of total greenhouse gas emissions

$$\begin{aligned} {\text{Min}}\;Z_{2} = & \theta _{1} {\mathfrak{e}}_{{CO_{2} }}^{1} \left( {\sum\limits_{{c,f,t,r}} {L_{{cfr}}^{{13}} } x_{{cftr}}^{{13}} + \sum\limits_{{c,f,t,r}} {L_{{cfr}}^{{13}} } \left( {x_{{cftr}}^{{13}} } \right)^{2} + \sum\limits_{{l,f,t,r,}} {L_{{lfr}}^{{23}} } x_{{lftr}}^{{23}} } \right. \\ & \;\left. { + \sum\limits_{{l,f,t,r}} {L_{{lfr}}^{{23}} } \left( {x_{{lftr}}^{{23}} } \right)^{2} + \sum\limits_{{f,m,t,r}} {L_{{fmr}}^{{34}} } x_{{fmtr}}^{{34}} + \sum\limits_{{f,m,t,r}} {L_{{fmr}}^{{34}} } \left( {x_{{fmtr}}^{{34}} } \right)^{2} } \right) \\ & \; + \theta _{2} {\mathfrak{e}}_{{CO_{2} }}^{2} \left( {\sum\limits_{{f,m,t,r}} {L_{{kmr}}^{{34}} } x_{{kmtrw}}^{{34}} + \sum\limits_{{f,m,t,r}} {L_{{fmr}}^{{34}} } \left( {x_{{fmtr}}^{{34}} } \right)^{2} } \right) \\ \end{aligned}$$
(2)

Minimization of total transportation time

$$\begin{aligned} {\text{Min}}\;Z_{3} = & \mathop \sum \limits_{c,f,t,r} {\mathfrak{t}}_{cftr}^{13} L_{cfr}^{13} x_{cftr}^{13} + \mathop \sum \limits_{c,f,t,r} {\mathfrak{T}}_{cftr}^{13} L_{cfr}^{13} \left( {x_{cftr}^{13} } \right)^{2} + \mathop \sum \limits_{l,f,t,r,} {\mathfrak{t}}_{lftr}^{23} L_{lfr}^{23} x_{lftr}^{23} \\ & \; + \mathop \sum \limits_{l,f,t,r} {\mathfrak{T}}_{lftr}^{23} L_{lfr}^{23} \left( {x_{lftr}^{23} } \right)^{2} + \mathop \sum \limits_{f,m,t,r} {\mathfrak{t}}_{fmtr}^{34} L_{fmr}^{34} x_{fmtr}^{34} + \mathop \sum \limits_{f,m,t,r} {\mathfrak{T}}_{fmtr}^{34} L_{fmr}^{34} \left( {x_{fmtr}^{34} } \right)^{2} \\ \end{aligned}$$
(3)
$$\mathop \sum \limits_{c,f,t,r} x_{cftr}^{13} \le \tilde{A}_{c}^{1}$$
(4)
$$\mathop \sum \limits_{l,f,t,r} x_{lftr}^{23} \le \tilde{A}_{l}^{2}$$
(5)
$$\mathop \sum \limits_{c,f,t,r} \left( {x_{cftr}^{13} } \right) + \mathop \sum \limits_{l,f,t,r} \left( {x_{lftr}^{23} } \right) \ge \tilde{B}_{f}^{3}$$
(6)
$$\mathop \sum \limits_{f,b,t,r} x_{fmtr}^{34} \ge \tilde{B}_{m}^{4}$$
(7)
$$\mathop \sum \limits_{f,b,t,r} x_{cftr}^{13} \le \tilde{E}_{t}$$
(8)
$$\mathop \sum \limits_{f,b,t,r} x_{lftr}^{23} \le \tilde{E}_{t}$$
(9)
$$\mathop \sum \limits_{f,b,t,r} x_{fmtr}^{34} \le \tilde{E}_{t}$$
(10)
$$\mathop \sum \limits_{c,f,t,r} x_{cftr}^{13} + \mathop \sum \limits_{l,f,t,r} x_{lftr}^{23} = \mathop \sum \limits_{f,b,t,r} x_{fmtr}^{34}$$
(11)
$$x_{cftr}^{13} \ge 0,x_{lftr}^{23} \ge 0,{ }x_{fmtr}^{34} \ge 0 \forall c,f,l,m,t,r$$
(12)

The following criteria must be fulfilled for the suggested Model 1 to be feasible:

$$\sum \tilde{A}_{c}^{1} \ge \sum \tilde{B}_{f}^{3} ;\sum \tilde{A}_{l}^{2} \ge \sum \tilde{B}_{f}^{3} ;\sum \tilde{E}_{t} \ge \sum \tilde{B}_{f}^{3} ;\sum \tilde{E}_{t} \ge \sum \tilde{B}_{m}^{4} ;$$

Model 2

The devised Model-1 has been generalized to provide a range of specifically designed sub- model by disuniting the effect circular economy approach for OCC management.

$$\begin{gathered} \mathop {\min }\limits_{n = 1,2,3} Z_{n} \hfill \\ {\text{s}}.{\text{t}}.{\text{ constraint }}(4) - ({10), }\& \, ({12}) \hfill \\ \end{gathered}$$

Model-2 is similar to Model-1 except the constraint (11), which defines circular economy and is not a part of this model.

Considering the substantial uncertainty surrounding OCC management, Model-1 has been formulated in the TS-FBHF configuration. The current state of this model makes addressing it a significant challenge. For this framework to be solved invariably, the proposed defuzzification function has been applied.

Model 3: Deterministic version of model 1

$$\mathop {\min }\limits_{n = 1,2,3} Z_{n} = \mathop \sum \limits_{c,f,t,r} x_{cftr}^{13} + \mathop \sum \limits_{l,f,t,r} x_{lftr}^{23} = \mathop \sum \limits_{f,b,t,r} x_{fmtr}^{34}$$
(11)
$$\mathop \sum \limits_{c,f,t,r} x_{cftr}^{13} \le {\mathfrak{D}}\left( {\tilde{A}_{c}^{1} } \right)$$
(13)
$$\mathop \sum \limits_{l,f,t,r} x_{lftr}^{23} \le {\mathfrak{D}}\left( {\tilde{A}_{l}^{2} } \right)$$
(14)
$$\mathop \sum \limits_{c,f,t,r} \left( {x_{cftr}^{13} } \right) + \mathop \sum \limits_{l,f,t,r} \left( {x_{lftr}^{23} } \right) \ge {\mathfrak{D}}\left( {\tilde{B}_{f}^{3} } \right)$$
(15)
$$\mathop \sum \limits_{f,b,t,r} x_{fmtr}^{34} \ge {\mathfrak{D}}\left( {\tilde{B}_{m}^{4} } \right)$$
(16)
$$\mathop \sum \limits_{f,b,t,r} x_{cftr}^{13} \le {\mathfrak{D}}\left( {\tilde{E}_{t} } \right)$$
(17)
$$\mathop \sum \limits_{f,b,t,r} x_{lftr}^{23} \le {\mathfrak{D}}\left( {\tilde{E}_{t} } \right)$$
(18)
$$\mathop \sum \limits_{f,b,t,r} x_{fmtr}^{34} \le {\mathfrak{D}}\left( {\tilde{E}_{t} } \right)$$
(19)
$$\sum {\mathfrak{D}}\left( {\tilde{A}_{c}^{1} } \right) \ge \sum {\mathfrak{D}}\left( {\tilde{B}_{f}^{3} } \right) ;\sum {\mathfrak{D}}\left( {\tilde{A}_{l}^{2} } \right) \ge \sum {\mathfrak{D}}\left( {\tilde{B}_{f}^{3} } \right) ;\sum {\mathfrak{D}}\left( {\tilde{E}_{t} } \right) \ge \sum {\mathfrak{D}}\left( {\tilde{B}_{f}^{3} } \right) ;$$
$$\sum {\mathfrak{D}}\left( {\tilde{E}_{t} } \right) \ge \sum {\mathfrak{D}}\left( {\tilde{B}_{m}^{4} } \right) ;$$

Model 4: Deterministic version of model 2

$$\begin{gathered} \mathop {\min }\limits_{n = 1,2,3} Z_{n} \hfill \\ {\text{s}}.{\text{t}}.{\text{ constraint }}({13)}{-}({19}) \hfill \\ \end{gathered}$$

Proposed methodology

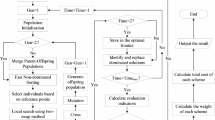
The literature contains numerous techniques for solving optimization problems with multiple goals. Some eminent techniques are Goal programming54, Fuzzy programming55, Fuzzy goal programming56, GCM57, Intuitionistic fuzzy approach58, Weighted goal programming58, WST60, Neutrosophic approach61, Weighted fuzzy goal programming62, Fermatean fuzzy approach63, \(\varepsilon -\) constrained approach64, Sakawa & Nishizaki approach65, and conic scalarization method66. The weighted sum framework explicitly evaluates and weights the criteria, making the decision-making process transparent and understandable. It can be modified to meet the particular needs of a decision-making procedure. Additionally, it can incorporate both qualitative and quantitative factors, such the workplace culture or company image. It is a systematic method for weighing several options and coming to a well-informed conclusion on difficult choices. But there are a few drawbacks to take into account as well. This approach can take a lot of time, particularly if there are a lot of options and requirements to take into account. Subjectivity can also be problematic, particularly if the criteria are not quantifiable, as this might produce inaccurate results. In the GCM, multiple parameters can be set to reflect preferences and provide a general formulation. Using the utopian point, this approach always provides a Pareto optimal solution. Additionally, it uses Minkowski’s Lp metric to measure distance. Minimizing a global criterion is the purpose of this approach. Among all these approaches WST and GCM are opted due to their non-complex, less time consumption procedures. Figure 2 depicts the various aspect of the devised methodology.

Fig. 2
figure 2

A pictorial depiction of the proposed approach.

Full size image

Weighted Sum Technique (WST)

  1. Step 1:

    One by one, deal each goal of the Model 2 or Model 4.

  2. Step 2:

    Calculate the upper and lower bounds for all goals, i.e., \(l_{n} \left( x \right) = min \left\{ {Z_{n} \left( x \right)} \right\}\) and \(u_{n} \left( x \right) = max \left\{ {Z_{n} \left( x \right)} \right\}\).

  3. Step 3:

    Establish the model

    $$Min \phi = \mathop \sum \limits_{n} \omega_{n} \frac{{Z_{n} \left( x \right) - L_{n} }}{{U_{n} }}$$

    Model 2 or Model 4.

    Here, \(\omega_{n}\) are weights given to each objective of Model 2 or Model 4

  4. Step 4:

    Employ Lingo 20.0 to deal the previous stated model.

Global Criterion Method (GCM)

  1. Step 1:

    Assign each objective of the devised non-linear TP, ignoring the rest of the objectives.

  2. Step 2:

    Identify the minimum and maximum limits for all goals.

  3. Step 3:

    Establish the mathematical formulation as

    $$\begin{gathered} {\mathbf{Min}}\;{\varvec{Z}}\left( {\varvec{x}} \right) = \left[ {\mathop \sum \limits_{{{\varvec{n}} = 1}}^{3} \left( {\frac{{Z_{n} \left( X \right) - Z_{n}^{min} }}{{Z_{n}^{max} - Z_{n}^{min} }}} \right)^{4} } \right]^{\frac{1}{4}} \hfill \\ {\text{s}}.{\text{ t}}.{\text{ constraints of model 2 or model4}} \hfill \\ \end{gathered}$$
  4. Step 4:

    Using Lingo 20.0, solve the above problem.

A case study

This section provides a case study in order to elaborate the pertinence of devised model for sustainable management of OCC. Let Ghazipur Landfill (\(L_{1}\)) and Shakir Traders (\(C_{1}\)) a commercial establishment be two sources of OCC. Thereafter, these OCC are supplied to Green-O-Tech (\(F_{1}\)), a paper recycling facility for recycling purpose. Finally, the new corrugated sheets recycled form OCC are sold out to Aaradhya box manufacture \(\left( {M_{1} } \right)\) for the manufacturing of corrugated containers. Table 4 exhibited the availability at commercial establishment (\(\tilde{A}_{c}^{1} )\) and landfill (\(\tilde{A}_{l}^{2}\)), demand of corrugated recycling facility (\(\tilde{B}_{f}^{3} )\) and box manufacturer (\(\tilde{B}_{m}^{4} )\), and capability of mode of conveyances (\(\tilde{E}_{t} )\) as TS-FBHF. Overall, TE, TT, and GHGEs are given in Table 5. Distances of several routes are given in Table 6. The geographical locations of all organizations are depicted by Fig. 3.

Table 4 Availability, demand and capability of mode of conveyances in TS-FBHF form.
Full size table
Table 5 Overall transportation expense, transportation time, and carbon emissions.
Full size table
Table 6 Distance of several routes.
Full size table
Fig. 3
figure 3

Geographical locations for case study (https://www.google.com/maps/@28.5437975,76.9677832,9.67z/data=!4m2!6m1!1s1MH8-Gs2kgxrcHGLOuSy_KC8zRMbdMT8?entry=ttu&g_ep=EgoyMDI0MTAxNi4wIKXMDSoASAFQAw%3D%3D).

Full size image

Here, in both models (with or without circular economy approach), the weights given to three goals TE, GHGE, and TT are 0.4, 0.3, and 0.3 respectively, in case of WST approach.

The suggested non-linear model is empirically implemented under multiple circumstances with LINGO 20.0 software on an Intel Core i5 CPU equipped with 8 GB of RAM, running Microsoft Windows 10. We have two models, a circular economy model and non-circular economy model. First model contains 12 variables, 3 objectives, and 11 constraints. For the 1st objective (TE), number of iterations are 12, total elapsed time is 0.12 s and memory used is 26 kb. In case of 2nd goal (GHGE), number of iterations are 10, total elapsed time is 0.05 s and memory used is 26 kb. For objective 3rd (TT), number of iterations, total elapsed time, and memory used are 9, 0.05 s and 26 kb respectively. For the overall solution of model 1 using WST, number of iterations, total elapsed time, and memory used are 7, 0.05 s and 28 kb respectively. Number of iterations, total elapsed time, and memory used are 76, 0.11 s and 28 kb respectively, when we apply GCM to the model 1.

On the other hand, second model contains 12 variables, 3 goals and 10 constraints. For the 1st objective (TE), number of iterations, total elapsed time, and memory used are 14, 0.06 and 26 kb respectively. In case of 2nd goal (GHGE), number of iterations are 10, total elapsed time is 0.07 s and memory used is 26 kb. For 3rd goal (TT), number of iterations, total elapsed time, and memory used are 9, 0.06 s and 26 kb respectively. For the overall solution of model 2 using WST, number of iterations, total elapsed time, and memory used are 7, 0.03 s and 28 kb respectively. Number of iterations, total elapsed time, and memory used are 31, 0.08 s and 28 kb respectively, when we apply GCM to the model 2.

The methods suggested in section “Proposed methodolgy” have been deployed to tackle the proposed GNLMO-4DTP with an integrated circular economy approach under TS-FBHF parameters. The pareto optimal outcomes for the case study based on Model 1 employing WST and GCM are displayed in Table 7. Despite having the identical inputs, the optimal values found by the two strategies are distinct. From Table 7 it is evident that in case of optimization of first objective and third objective i.e., TE and TT, GCM gives better results. But, in case of second objective WST provides better optimal value. Thus, decision maker will prefer to employ GCM over WST in this GNLMO-4DTP with an integrated circular economy approach under TS-FBHF parameters. Figure 4 compares the results obtained by two methods in case of Model 1.

Table 7 Optimal results of case study based on Model 1(with circular economy).
Full size table
Fig. 4
figure 4

Comparison of result obtained by WST and GCM for GNLMO-4DTP with circular economy approach under TS-FBHF configuration.

Full size image

The suggested methods in section “Proposed methodology” have been deployed to tackle the proposed model GNLMO-4DTP without circular economy approach under TS-FBHF parameters. The Pareto optimal outcomes for the case study based on Model 2 employing WST and GCM are displayed in Table 8. It is evident that in case of optimization of first objective and third objective i.e., TE and TT, WST gives better results. But, in case of second objective GCM, provides better optimal value. Thus, decision maker will prefer to employ WST over GCM in this GNLMO-4DTP without circular economy framework under TS-FBHF settings. Figure 5 compares the results obtained by two methods in case of Model 2.

Table 8 Optimal results of case study based on Model 2 (without circular economy).
Full size table
Fig. 5
figure 5

Comparison of result obtained by WST and GCM for GNLMO-4DTP without circular economy approach under TS-FBHF configuration.

Full size image

Table 9 compares the results obtained for case study based on the proposed GNLMO-4DTP and developed sub model by utilizing WST and GCM. The comparison of optimal values of three objectives in both models is depicted. Although, values of TE, GHGEs and TT are more optimized for model 2 (without circular economy) as compared to model 1(with circular economy) by utilizing both WST and GCM. But, integration of circular economy brings sustainability in the model and reduces the hazardous effect of supply chain on the environment and human lives.

Table 9 Comparison of Results of GNLMO-4DTP.
Full size table

We established a few indices on the basis of which we would assess our work to previous research that has been done in the literature in order to perform a comparison with that earlier research.

  • Type of Transportation Network

    It is possible to manage and visualize transportation networks in a highly precise way with 4-DTP. There are few authors who have worked on 4D-TP (Bera et al.1, Samanta et al.23, Giri et al.25, Bind et al.27, Akhtar et al.26, Sharma et al.28). No consideration has been made for OCC’s transportation or sustainable management. A 3D transportation system has also been developed by Haque et al.53. Furthermore, Ahmad and Adami32, Chibber et al.35, and Sharma et al.63 have employed classical TP, which is insufficient for portraying realistic transportation system circumstances.

  • Depiction of Impreciseness

    Due to the intrinsic uncertainty in non-linear transport networks, it is not necessary for the parameters such as availability, consumer demand, transportation ability, TE, TT, and GHGE to be exact. A number of extensions of fuzzy set theory, including the intuitionistic fuzzy set, Neutrosophic set (Smarandache4), BFS (Zhang et al.8), Complex fuzzy set (Ramot et al.,5), Hesitant fuzzy set (Tora,9), Pythagorean fuzzy set (Yager6), and FFS (Senapati and Yager,7), have been discovered in the scientific literature that demonstrate unpredictability. However, because of certain restrictions, none of the aforementioned can deal with the uncertainty. Our suggested set can be used for any kind of challenge involving unpredictability since it combined BFS, HFS, and FFS into one system with a time sequential framework.

  • Methodology

    The system’s pareto optimum solution will be determined by the type of solution techniques used. The suggested multi-objective model for waste management of OCC can be solved utilizing a variety of approaches. Several classic methods, including GCM57,  Weighted goal programming59,WST60, Goal programming54, ϵ-constrained approach64, Sakawa & Nishizaki approach65, and conic scalarization method66 are available in the literature for solving optimization problems with multiple goals. WST and GCM are the most popular methods among them all due to their straightforward and swift procedures. Compared to other classical and stochastic methods available in the literature, these approaches require less processing time and are less complex.

  • Non-linearity

    The majority of the system’s relationships are irregular, indicating that only a non-linear model can accurately represent them. But only few authors Gabr29, Maity and Roy30, Dalman and Bayram31, Ahmad and Adhami32, Chhibber et al.34, Shivani et al.36, Suzuki, & Arita67, Punyavathi et al.68, Hassan et al.69, and Hubert et al.70 have worked on 2-D, 3-D versions of NL-TP. Thus, it is essential to define non-linear transportation problem (NL-TP) in a 4-D transportation framework to reflect oscillations in today’s competitive market.

  • Application

    Management of solid waste, managing food waste, healthcare waste management, flower waste management, and many other waste management models can be created by integrating our proposed TS-FBHFS framework.

Senstivity analysis

To show the efficacy, applicability, and consistency of our proposed GNLMO-4DTP , we performed a sensitivity analysis to see how well it operates under different scenarios. This section explains the variations and examines the effect of the variations in the TS-FBHF parameter to demonstrate the overall performance of the devised system in the corrugated waste management system. In order to assess the impact of a small modification without compromising the ideal solution, it is extremely challenging to keep the same ideal solution. Using a straightforward methodology, we begin analysing the sensitivity of our GNLMO-4DTP. We demonstrate sensitivity analysis over the availability, demand and capacity constraints associated with proposed non-linear system. The availability constraints namely available amount of corrugated waste in commercial \(\tilde{A}_{c}^{1}\) and landfill \(\tilde{A}_{l}^{2}\) are manipulated. Moreover, capability of corrugated waste at recycling facility \(\tilde{B}_{f}^{3}\), demand of corrugated sheets \(\tilde{B}_{m}^{4}\) and capacity of conveyance \(\tilde{E}_{t}\) are also fluctuated. The parameter ranges are analyzed so that the Pareto optimal solution remains constant. Through this sensitivity analysis, we can comprehend how fluctuations in parameters affect the Pareto optimum solution of the suggested transportation framework.

The parameter changes within the same optimal solution for GNLMO-4DTP with circular economy and TS-FBHFS configuration are analysed in Table 10 and Fig. 6. Furthermore, under TS-FBHFS settings, Table 11 and Fig. 7 analyse changes in various parameters within the range of the ideal solution for GNLMO-4DTP without the influence of circular economy.

Table 10 Range of parameters for GNLMO-4DTP with circular economy.
Full size table
Fig. 6
figure 6

Range of parameters for GNLMO-4DTP with circular economy.

Full size image
Table 11 Range of parameters for GNLMO-4DTP without circular economy.
Full size table
Fig. 7
figure 7

Range of parameters for GNLMO-4DTP without circular economy.

Full size image

Managerial insights

A GNLMO-4DTP with circular economy approach is formulated in this article for managing the OCC under TS-FBHFS configuration. As a result of this study, different public and commercial organizations involved in waste management can gain useful insight into how to manage OCC. The following are some managerial takeaways from this investigation:

  • The proposed model for OCC offers multiple benefits with distinct aspects that can be handled across large regions. The proposed green transportation system for OCC is based on the 3 R’s i.e., recycling, reuse, and recovery as OCC is being decomposed to corrugated sheets which are further utilized to develop corrugated containers of different sizes.

  • A closed loop management system, entitled GNLMO-4DTP has been developed with the goal of recycling or reusing resources and materials back into the production cycle as opposed to throwing them away. Developing a closed loop transportation framework allows wastes to be diminished or eliminated simultaneously.

  • The proposed GNLMO-4DTP integrates circular economy enabling resource optimization, reducing the consumption of raw inputs, and recycling the trash to offer it a second chance at life.

  • Cardboard recycling conserves resources and reduces waste and additionally cuts down GHGEs when compared with manufacturing new cardboard.

Conclusion

In this article, an extended fuzzy tool, called TS-FBHFS is developed that can deal with a set of positive and negative MDs along with NMDs within a dimension of time series. The proposed TS-FBHFS is an amalgamation of FFS, HFS and BFS within a time dimensional series, that can portray numerous types of uncertainties embedded in different optimization issues. a detailed explanation of every attribute of the stated set, including its fundamental features and defuzzification process are also provided. The integration of the proposed set that captures imprecision and uncertainty simultaneously in a time-sequential framework can enhance the accuracy of representing real-world scenarios.

Recycling non-hazardous OCC is crucial to sustainable waste management. The OCC recycling makes a positive environmental impact by cutting down on landfill wastes, preserving resources, and lowering carbon emissions. To fully utilize OCC recycling and create a more sustainable future, individual efforts and government and commercial backing are essential. In this article, the procedure of recycling OCC sustainably at minimum TE, minimum GHGE and minimum total TT has been analysed by developing a non-linear 4-D transportation system with an integrated circular economy approach. The devised transportation system is formulated under TS-FBHF configuration due to the existence of fluctuations of several parameters involved in the formulation. The devised GNLMO-4DTP is also evaluated without the impact of circular economy. The proposed GNLMO-4DTP with TS-FBHF parameters encompasses nonlinear multiple goals to optimize TE, GHGE and TT simultaneously in a single framework and in this regard, the WST and GCM approaches are employed along with proposed defuzzification function to get the ideal compromise solution for all three goals. In case of the proposed model with circular economy framework, GCM outperforms the WST methodology. On the other hand, results obtained by utilizing WST are better than that of GCM in case of model without integration of circular economy. The computing component of the solution makes utilization of the LINGO 20.0 software.

This work has a few shortcomings despite its significant contributions. One of the limitations is that, we have utilized only two approaches namely WST and GCM in order to tackle the proposed non-linear transportation framework. Although, there are several traditional, metaheuristic and fuzzy techniques, including GP, WGP, \(\varepsilon -\) cconstrained approach, Sakawa-Nishizaki approach, conic scalarization approach, genetic algorithm, particle swarm optimization, ant colony optimization, teaching–learning based optimization, and fuzzy programming, genetic methodologies, intuitionistic fuzzy approach, etc. are available in the literature to handle a non-linear transportation framework with multiple objectives. Aside from this, several parameters such as travel expenses, travel time, carbon foot prints and distance of several routes are not taken as uncertain parameters and are precise in nature.

In the future, aside from the non-linear TP, the proposed TS-FBHFS framework can be employed to tackle several mathematical models. There are many ways to formulate problems using the devised framework, including municipal waste management issues, routing problems, decision-making problems with multiple criteria, multi-attribute decisions, and traveling salesman problems. Moreover, several aggregation operators can also be devised to integrate TS-FBHF information. Our green non-linear transportation framework can be reformulated under different forms of carbon policies, probabilistic information, robust ranking function, reverse logistics, etc.