Introduction

In recent years, there has been growing scientific interest in developing and characterising advanced magnetic materials for various technological applications. Soft magnetic ferrites have become a focal point due to their exceptional magnetic properties and diverse uses in power electronics, telecommunications, and high-frequency devices1. Among these, manganese-zinc (Mn-Zn) ferrites are particularly promising because of their low coercivity, high permeability, and good electrical conductivity2. These properties make Mn-Zn ferrites ideal candidates for a wide range of applications, including transformers, inductors, and electromagnetic interference suppression components. The excellent electrical and magnetic characteristics of Mn-Zn ferrites have driven extensive research to improve their performance further and tailor their properties for specific industrial and technological needs.

To enhance the performance of Mn-Zn ferrites, researchers have explored various strategies, including the introduction of dopants or substitutes that can modify the structural and magnetic behaviour of the material3. One promising approach is the incorporation of rare-earth elements, which are renowned for their unique electrical and magnetic properties. Among these, lanthanum (La) has emerged as a particularly effective dopant. The substitution of La in Mn-Zn ferrites has been shown to significantly influence the magnetic and structural properties, offering new avenues for optimising these materials for advanced applications2,4. Lanthanum incorporation modifies the crystal structure, resulting in enhanced superexchange interactions and magnetic anisotropy, which can lead to improved performance in devices operating at high frequencies and temperatures3,5.

While rare-earth doping has been extensively studied in ferrites, recent research on other functional materials has provided insights into similar material enhancements through alternative approaches. For example, the development of oxide nanoparticles and related nanomaterials has led to improvements in material functionality across various applications, including catalysis, sensing, and electronics6. The modification of structural and magnetic properties through dopants in oxide nanomaterials has shown parallels to the effects observed in ferrites, underscoring the importance of studying Mn-Zn ferrites doped with La. Research on functional materials has demonstrated that rare-earth elements can significantly influence the structural, magnetic, and dielectric properties of these materials, making them highly relevant for future technological applications7,8.

In particular, the novelty of this study lies in the systematic exploration of how La doping influences the atomic arrangement, grain morphology, and magnetic interactions within Mn-Zn ferrites. Although several studies have explored rare-earth doping in ferrites, our work extends the understanding of La’s role in modifying the material’s microstructure and magnetization dynamics4,9. By systematically varying the La content and comparing our results with previous studies, we aim to offer new insights into the structure-property relationships that govern the functional performance of La-doped Mn-Zn ferrites.

In this paper, we focus on the structural and magnetic characteristics of La-doped Mn-Zn soft microferrites. The structural properties will be analysed using X-ray diffraction (XRD) to determine phase formation, lattice constants, and crystallite size10. Scanning electron microscopy (SEM) will provide information on grain morphology and size distribution11. To evaluate the magnetic behaviour, vibrating sample magnetometry (VSM) will be employed to measure the magnetic saturation, coercivity, and remanence12. Superconducting quantum interference device (SQUID) magnetometry will also be used for high-precision magnetic measurements, especially at low temperatures13.

The insights gained from this study will contribute to the optimisation of Mn-Zn ferrites for high-frequency and high-temperature applications, potentially improving their usability in inductors, transformers, and other electromagnetic devices. Our findings will provide a clearer understanding of how rare-earth doping, specifically La incorporation, influences the structural and magnetic properties of Mn-Zn ferrites, laying the groundwork for further advancements in this field.

Material and methodology

In this section, we will discuss theoretical concepts that form the basis of our investigation into the structural and magnetic characteristics of lanthanum (La)-substituted manganese-zinc (Mn-Zn) nanoferrites, as well as the methodology used for sample preparation.

The material’s quality significantly impacts the quality of ferrite-based devices. Ferrite properties are greatly influenced by their chemical composition and microstructure, both affected by the manufacturing process. The popularity of synthesizing advanced ceramics as nanoparticles is increasing in material processing technologies12,13,14,15,16. Co-precipitation is a common chemical method for producing nanoparticles17,18, and there are other methods such as solution combustion19, sol-gel auto combustion20,21, spray pyrolysis22, micro-emulsion technology23, and solid-state reaction followed by mechanical milling24,25. In this research, La-doped Mn-Zn nanoferrites were created using the sol-gel auto-combustion process. In this research, La-doped Mn-Zn nanoferrites were created using the sol-gel auto-combustion process due to their cost-effectiveness, ability to produce homogenous products, and scalability for industrial applications26.

Sol-Gel auto combustion method

The La-substituted Mn-Zn nanoferrites were synthesised using the sol-gel auto-combustion process. The materials used included manganese nitrate [Mn (NO3)2.4H2O], and Zinc Nitrate [Zn (NO3)2. 6H2O], Lanthanum Nitrate [La (NO3)3.6H2O], Iron Nitrate [Fe (NO3)3. 9H2O] and Citric Acid [C6H8O7.H2O]. A transparent solution was created by dissolving precise amounts of pure metal nitrates in 40 mL of distilled water. In a separate step, citric acid was dissolved in 40 mL of distilled water and then mixed with ethylene glycol and the nitrate solution. The citric acid served as both a complexant for the metal ions and a fuel. To achieve a high combustion rate, a 1:1 molar ratio of metal nitrates to citric acid was maintained. The pH was adjusted to 7 using an ammonia solution.

The water solution was heated to 80 °C with continuous mechanical stirring at 300 rpm in an open-air atmosphere to allow evaporation until a sticky gel formed as shown in Fig. 1. Once the gel was formed, the temperature was increased to 200 °C at a controlled heating rate of 10 °C/min. A spontaneous combustion occurred, lasting 20–30 s, resulting in fluffy powdered products with blazing flints. The resulting powder was sintered at 450 °C for 4 h in an air atmosphere to ensure phase purity and crystallisation.

The sol-gel auto-combustion method was chosen due to its advantages in synthesizing ferrite nanoparticles, including uniform mixing of reactants at the molecular level, lower processing temperatures, and the ability to control particle size and morphology27. The use of citric acid and ethylene glycol ensures effective chelation and promotes the formation of a homogenous gel. Furthermore, the method is well-suited for creating complex oxide materials with consistent stoichiometry. However, critical parameters such as the heating atmosphere, stirring speed, and combustion dynamics should be optimised and explicitly reported in the manuscript for improved reproducibility.

Fig. 1
figure 1

Synthesis Process of Ferrite Powder using Sol-Gel Auto Combustion Technique.

Full size image

Structural properties

X-ray diffraction (XRD)

X-ray diffraction (XRD) is a widely used technique for the structural characterisation of powder samples. In the θ-2θ scan mode, a monochromatic X-ray beam is directed at the sample surface, with the detector positioned at an angle of 2θ relative to the incident beam28,29,30,31. The recorded spectrum, plotted as intensity vs. 2θ, is based on Bragg’s law of diffraction. To satisfy Bragg’s law, either the wavelength (λ) or angle (θ) must be scanned32,33,34,35,36. By comparing the peak positions with standard data, the phases present in the sample can be identified. Sharper peaks indicate better crystallinity. XRD spectra provide information on average particle size, lattice parameters, and crystal structure. Shifts in peak positions can indicate strain in the sample. For the characterisation of the samples, XRD was performed using Panalytical’s X’PertPro at SAIF PU, Chandigarh.

Transmission electron microscopy

Transmission electron microscopy (TEM) offers high sensitivity for analysing grain size and morphology, providing greater magnification, resolution, and depth of focus compared to an optical microscope. TEM’s approach of complementary imaging and spatial resolution microanalysis enables the examination of the morphology, content, crystal structure, and electrical and/or magnetic structure, as well as the size and shape of nanomaterials on a minuscule scale. By utilising transmitted electrons, TEM can reveal the interior crystal structure through bright and dark field imaging, and enable orientation and crystal identification through selected region electron diffractions. While TEM operates on the same principle as an optical (light) microscope, it utilises electrons instead of light. The shorter wavelength of electrons (200 kV electrons have a wavelength of 0.025 Å) enables high resolution (0.2 nm) and high magnification (a thousand times better than a light microscope).

Magnetic properties

Vibrating sample magnetometer (VSM)

Vibrating Sample Magnetometry (VSM) utilises Faraday’s law of induction to detect the magnetic behaviour of materials by inducing an electromotive force (e.m.f.) in a conductor through a time-varying magnetic flux5. The sample is magnetised under a continuous magnetic field by aligning its magnetic domains, and higher applied fields result in increased magnetization. The sample’s magnetic dipole moment generates a stray field that fluctuates with the sample’s motion, inducing an electric field in the pick-up coils. This induced current, proportional to the sample’s magnetization, is amplified by a lock-in amplifier and analysed using computer software to determine magnetization values and their dependency on the applied magnetic field. For VSM measurements, the powdered sample is weighed, pressed into a quartz container, and mounted on a ceramic rod. Calibration is performed using a nickel (Ni) standard with a known saturation magnetization of 55.01 emu/g at 8 kOe.

Initial permeability and dissipation factor

Permeability describes how a substance interacts with a magnetic field. It is the ratio of magnetic induction (B) to the applied magnetic field (H). Relative permeability (µr) consists of two components: the real part (µ´), which accounts for energy storage, and the imaginary part (µ´´), which accounts for power dissipation37. The loss tangent (tan δµ) represents the inefficiency of magnetic materials, calculated as the ratio of the imaginary part (µ´´) to the real part (µ´). To determine the real component of permeability (µ´) in toroidal ferrite samples, inductance measurements were taken using an LCR Meter Bridge Model.

Results and discussions

The performance of devices based on ferrite depends on their electrical and magnetic characteristics, underscoring the need for a thorough investigation of these properties for practical use. Microstructural factors such as grain size, distribution, density, porosity, and imperfections significantly influence the electrical and magnetic properties of ferrites. This part discusses the empirical findings and elucidates the techniques employed to assess the structural and magnetic properties of the produced samples.

The structural characteristics of all produced samples were examined using X-ray diffraction (XRD) and transmission electron microscopy (TEM). XRD analysis was used to investigate powder crystallinity, phase identification, lattice parameters, and X-ray density. TEM was used to study the structure and morphology of the nanoparticles. The impact of dopant ions (La3+) on microstructural analysis was also explored.

The variation of d.c. resistivity with changes in composition and temperature is investigated in this study. Furthermore, an analysis is conducted on the dielectric constant and loss factor of nanoferrite samples in connection to alternating current frequency and composition. The assessment of experimental data for these properties leads to the derivation of significant conclusions using suitable models, theoretical concepts, and the physical phenomena that impact these properties.

Structural properties of lanthanum substituted Mn-Zn soft nano ferrite

X-ray diffraction

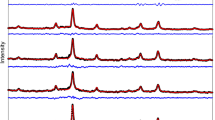
X-ray diffraction (XRD) analysis was performed on all the ferrite samples to study their structural properties and detect the phases present. The XRD measurements were carried out using PANalytical’s X’PertPro X-ray diffractometer located at the Sophisticated Analytical Instrument Facility (SAIF) at Panjab University, Chandigarh. Cu-Kα radiation with a wavelength of 1.54Å was used to irradiate the powdered ferrite samples. The 2-theta (2θ) angle was scanned from around 20° to 80° during the XRD experiments. The resulting 2θ vs. intensity data was obtained and plotted in the form of graphs, as shown in Figs. 2 and 3, and 4.

The X-ray diffraction (XRD) patterns shown in Figs. 2 and 3, and 4 correspond to three different ferrite samples:

  1. 1.

    Mother sample: Mn0.6Zn0.4Fe2O4.

  2. 2.

    La-substituted sample: Mn0.6Zn0.2La0.2Fe2O4.

  3. 3.

    La-substituted sample: Mn0.6Zn0.4La0.2Fe2O4.

All these samples were synthesised using the sol-gel auto-combustion process at a pH of 7 and subsequently sintered at 450 °C for 4 h.

The XRD patterns exhibit several diffraction peaks, and the corresponding (hkl) values associated with these peaks are indexed in the figures. The observed diffraction peaks are characteristic of the spinel crystal structure in all the samples. The absence of any extra diffraction peaks, other than those corresponding to the spinel structure, indicates that all the samples had a single-phase spinel structure, indicating the lanthanum ions were successfully incorporated into the complete spinel crystal lattice without forming any secondary phases or unreacted constituents. This suggests the sol-gel auto-combustion synthesis resulted in a homogeneous La-doped Mn-Zn nanoferrite system. This suggests that the sol-gel auto-combustion process at pH 7 produced pure, single-phase spinel ferrite samples with La3+ substitution.

Fig. 2
figure 2

X-ray diffraction (XRD) pattern of Mn0.6Zn0.4Fe2O4 (Mother Sample) annealed at 450 °C. The characteristic peaks for the (311), (220), (400), (422), (511), and (440) planes confirm the formation of a well-crystallized spinel ferrite structure.

Full size image
Fig. 3
figure 3

X-ray diffraction (XRD) pattern of Mn0.6Zn0.2La0.2Fe2O4 annealed at 450 °C. The indexed peaks for the (311), (220), (400), (422), (511), and (440) planes confirm a spinel structure. A noticeable shift in the (311) plane suggests lattice strain induced by La doping.

Full size image
Fig. 4
figure 4

X-ray diffraction (XRD) pattern of Mn0.6Zn0.4La0.2Fe1.8O4 annealed at 450 °C. Peaks corresponding to the (311), (220), (400), (422), (511), and (440) planes confirm the spinel structure. Reduced intensity of peaks indicates possible partial substitution of Fe by La, affecting crystallinity.

Full size image

Particle size and lattice constant

The XRD patterns show that the (311) diffraction peak, which is characteristic of the spinel phase, exhibits the strongest intensity in all the samples. The other prominent peaks correspond to the (220), (311), (400), (422), (511), and (440) planes, which indicate the formation of a cubic spinel crystal structure. The crystallite size for each composition was determined using the Scherrer formula3, which was applied to the high-intensity (311) peaks. The calculated particle sizes were:

  1. 1.

    Mn0.6Zn0.4Fe2O4 (mother sample): 16 nm.

  2. 2.

    Mn0.6Zn0.2La0.2Fe2O4 (La-substituted): 12 nm.

  3. 3.

    Mn0.6Zn0.4La0.2Fe2O4 (La-substituted): 10 nm.

It was observed that the particle size decreases with the addition of the La dopant. This finding is consistent with the observations reported in the literature38,39,40,41. The variations in the calculated particle sizes and lattice constants for the different compositions are summarized in Table 1.

Table 1 Crystallite size, lattice constant, unit cell volume, and X-ray density for prepared nanoferrites calcined at 450oC.
Full size table

As per the literature27,28,29, the lattice constant aa tends to increase when a smaller ionic radius cation is replaced by a cation with a larger ionic radius. In this instance, the replacement of Zn2+ (ionic radius 0.82 Å) by La3+ (ionic radius 1.22 Å), and the substitution of Fe3+ (ionic radius 0.76 Å) by La3+, should have led to an increase in the lattice constant aa of the La-substituted samples in comparison to the mother sample (Mn0.6Zn0.4Fe2O4). However, the experimental results presented in Table 1 show that the lattice parameter aa is lower for the La-substituted sample Mn0.6Zn0.2La0.2Fe2O4 compared to the mother sample.

The aa lattice parameter is affected by multiple material properties, such as elastic coefficients, thermal expansion, chemical bonding, and electrical conductivity, as well as phase transitions, stacking faults, and dislocation nucleation30. For a long time, determining the effective lattice parameter based on the characteristics of the solution components has been a major focus in solid-state physics and materials science research.

In the present study, the decrease in the aa lattice parameter observed with La substitution, despite La3+ having a larger ionic radius compared to the replaced cations, implies that the behaviour may be influenced by secondary factors. These factors include the possible formation of secondary phases, lattice defects, or microstrains introduced during synthesis. For instance, microstrain arising from non-uniform substitution or charge neutrality adjustments through defect formation (e.g., vacancies) could lead to contraction of the lattice. Additionally, complementary techniques like SEM/TEM with EDS could confirm the presence of secondary phases, while Williamson-Hall (W-H) analysis could help quantify the contribution of microstrain.

The anomalous increase in the lattice parameter for Mn0.6Zn0.4La0.2Fe1.8O4, as observed in Table 1, further suggests that Fe deficiency and structural distortions may play a critical role in modulating the lattice behaviour. This highlights the complex interplay of substitution mechanisms and structural factors in determining the lattice parameter.

X-ray density

The formula for calculating the X-ray density (Dx) involves using the lattice parameter ‘a’ value. The calculation result is the X-ray density (Dx):

$$\:{D}_{x}=\:\frac{8M}{N{a}^{3}}$$

In the spinel lattice, the number 8 indicates the quantity of molecules in a unit cell. The symbol ‘M’ represents the molecular weight of the composition, while ‘N’ denotes Avogadro’s number, and ‘a’ signifies the lattice parameter. According to this equation, the X-ray density of the sample is directly proportional to the molecular weight of the composition and inversely proportional to the third power of the lattice parameter. Table 1 presents the discrepancies in calculated X-ray density values. The data in the table demonstrates that the X-ray density increases for both doped samples, namely Mn0.6Zn0.2La0.2Fe2O4 and Mn0.6Zn0.4La0.2Fe1.8O4 nanoferrites, compared to the undoped sample (pure sample).

Transmission electron microscopy

Transmission electron microscopy (TEM) image for Mn0.6Zn0.2La0.2Fe2O4 nanoparticle sample is shown in Fig. 5. Direct observation of the micrograph indicates that the particles have various forms and morphologies, with a particle size distribution ranging from 10 to 20 nm, and it is consistent with the XRD data.

The prepared nanoparticle samples exhibit noticeable agglomeration. This agglomeration is a sign of the high reactivity of the samples after the heat treatment process. The agglomeration can occur due to two main factors i.e. as the particle size of the magnetic nanoparticles decreases, each particle develops a permanent magnetic moment that is proportional to its volume. This permanent magnetization causes the nanoparticles to agglomerate due to magnetostatic interactions between them. Additionally, the reduced particle size also leads to stronger exchange interactions between the magnetic nanoparticles. These enhanced exchange interactions can further contribute to the observed agglomeration of the nanoparticles.

In other words, the decreasing particle size results in two key effects that promote agglomeration - the development of permanent magnetic moments that magnetically attract the particles, and the strengthening of exchange interactions between the nanoparticles. Both of these factors at the nanoscale can drive the agglomeration of the magnetic nanoparticles30.

Fig. 5
figure 5

TEM images of Mn0.6Zn0.2La0.2Fe2O4 nanoferrites.

Full size image

Magnetic properties of lanthanum substituted Mn-Zn soft nano ferrite

Saturation Magnetization

The magnetic properties of prepared samples were determined at room temperature using a vibrating sample magnetometer (VSM) with an applied field of 20,000 Oe. Hysteresis loop for Mn0.6Zn0.4Fe2O4 (mother sample), Lanthanum substituted Mn0.6Zn0.2La0.2Fe2O4 and Mn0.6Zn0.4La0.2Fe2O4 are shown in Figs. 6, 7 and 8. The saturation magnetization, Ms, coercivity Hc, and retentivity values obtained for the different compositions are shown in Table 2.

Fig. 6
figure 6

Hysteresis loops of for Mn0.6Zn0.4Fe2O4 (mother sample) at 300 K.

Full size image
Fig. 7
figure 7

Hysteresis loops of Lanthanum substituted Mn0.6Zn0.2La0.2Fe2O4 at 300 K.

Full size image
Fig. 8
figure 8

Hysteresis loops of Lanthanum substituted Mn0.6Zn0.4La0.2Fe2O4 at 300 K.

Full size image

The magnetization observed in the samples results from a combination of external and internal factors, such as anisotropy, grain size, and A-B interactions, as discussed in the literature29. Given that the Mn content remains constant across all ferrite compositions, variations in the saturation magnetization (Ms) can be attributed to changes in Zn and Fe concentrations in the spinel lattice. The table data indicates that the saturation magnetization of samples containing the La3+ dopant is lower than that of the undoped (mother) sample. This trend can be clarified by considering the occupation of cation sites and the alterations in exchange interactions caused by La doping. The magnetic properties of Fe3+ ions on the cubic spinel B-sites make the most significant contribution to the overall magnetization. The magnetic moment of the lattice is determined by the disparity in magnetic moments between the B and A sublattices., i.e., M = MB - MA.

The substitution of Zn2+ and Fe3+ by the larger La3+ ions likely alters the cation distribution and the A-B exchange interactions within the spinel structure. This, in turn, leads to a reduction in the net magnetic moment and the observed lower saturation magnetization in the La-doped samples compared to the undoped mother sample. The substitution of Zn²⁺ and Fe³⁺ by the larger La³⁺ ions likely alters the cation distribution and the A-B exchange interactions within the spinel structure. This, in turn, leads to a reduction in the net magnetic moment and the observed lower saturation magnetization in the La-doped samples compared to the undoped mother sample. While the manuscript discusses the weakening of A-B superexchange interactions caused by La substitution, quantitative estimates or comparisons with theoretical values are not included. Incorporating such estimates would provide a stronger interpretation of the magnetic behaviour, offering a deeper understanding of how the superexchange interaction strengths contribute to the observed trends in magnetic properties.

Table 2 Magnetic parameters for all compositions obtained from VSM.
Full size table

In the La-doped sample, the La3+ ion prefers to occupy the octahedral B-site of the spinel structure, while the Fe3+ ion moves to the tetrahedral A-site. This cation redistribution occurs due to the preference of the La3+ ion for the octahedral environment.

The dopant La3+ has a magnetic moment of 0µB, while the Fe3+ ion has a magnetic moment of 5µB. The substitution of the magnetically active Fe3+ at the B-site by the non-magnetic La3+ reduces the net magnetic moment at the B-site. This, in turn, weakens the A-B superexchange interactions30, leading to a decrease in the overall saturation magnetization of the La-doped samples. The difference in the magnetic moments of the A and B sublattices, which is determined by their distinct cation distributions, has been demonstrated in the literature29.

The coercivity results show that the substitution of La for Fe enhances the coercivity. It is noteworthy that the grain size is reduced after the La replacement, as observed in the XRD analysis. The variation in coercivity with grain size is described by the Stoner-Wohlforth theory3. This theory suggests that factors such as magneto-crystalline anisotropy, microstrain, magnetic particle morphology, size distribution, anisotropy, and magnetic domain size all contribute to the observed changes in coercivity.

Comparison between initial permeability with frequency and composition

In Fig. 9 the variation of initial permeability, µ′ (measured with the LCR Meter Bridge) for prepared ferrites was observed for the frequency at room temperature.

Fig. 9
figure 9

Comparison of initial permeability, µ′, for all prepared nanoferrites (calcined at 450 °C) with frequency.

Full size image

The literature28,29,30 has reported the value of initial permeability (µ′) for the mother (undoped) sample. In the present work, it was observed that the La-substituted Mn-Zn ferrites have a higher value of initial permeability compared to the mother (undoped) sample31. These variations in initial permeability (µ′) can be explained by its dependence on various factors. The initial permeability (µ′)13 is proportional to the square of the saturation magnetization (Ms2).

Table 3 Initial permeability, and permeability loss factor, Tanδµ values for La substituted Mn-Zn ferrites i.e., for Mn0.6Zn0.2La0.2Fe2O4 and Mn0.6Zn0.4La0.2Fe2O4 nanoferrites (Calcined at 450oC) as a function of frequency.
Full size table

However, substituting lanthanum (La3+) into Mn-Zn ferrites results in a decrease in saturation magnetization (Ms). These results are evident from Table 3 which suggests that, beyond the reduction in Ms, the magneto-crystalline anisotropy constant (K1) also plays a crucial role in influencing the changes in initial permeability (µ′) due to the La3+ ion substitution. The initial permeability (µ′) of La-substituted Mn-Zn ferrites increases even though the saturation magnetization (Ms) decreases, indicating a decrease in the net anisotropy constant (K1) due to the substitution of Lanthanum (La3+) in the Mn-Zn ferrites. The change in the magneto-crystalline anisotropy constant (K1) can be qualitatively understood by referring to the Single-Ion Anisotropy Model32,33, which takes into account the contributions of different cations to the overall anisotropy of the material.

It is observed from Fig. 9, that the value of initial permeability, µ′ is found to be larger for La substitution for Fe i.e., for Mn0.6Zn0.4La0.2Fe1.8O4 nanoferrites as compared to the La substitution for Zn i.e., for Mn0.6Zn0.2La0.2Fe2O4. nanoferrites. This implies that the value of net anisotropy constant K1, for the La substitution for Fe i.e., for Mn0.6Zn0.4La0.2Fe1.8O4 nanoferrites is small as compared to the La substitution for Zn i.e., for Mn0.6Zn0.2La0.2Fe2O4 nanoferrites.

In the current work, the grain size reduces with the substitution of La in Mn-Zn ferrites, implying that smaller grains include a higher number of domain walls, leading to an increase in permeability15. The high permeability of Mn-Zn nanoferrites concentrates flux density within the coil, increasing inductance16,17.

Comparison between permeability loss factor with frequency

For high-frequency ferrite applications, it is crucial to minimise the loss factor. In this study, the loss factor is significantly lower than previous research on soft ferrites18,19,20. Figure 10 shows how the permeability loss factor (tan δµ) of the produced ferrites varies with frequency at room temperature.

Fig. 10
figure 10

Comparison of permeability loss factor, tanδµ, for all prepared nanoferrites (calcined at 450 °C) with frequency.

Full size image

The observed loss is attributed to domain wall lag relative to the applied alternating field, which is associated with lattice defects. The permeability loss factor, tan δµ, increases with frequency, indicating potential resonance peaks at higher frequencies. At resonance, the applied field transfers the most energy to the lattice, causing a sharp rise in the permeability loss factor. This resonance effect suggests that the imaginary component of initial permeability increases with frequency7. The permeability loss factor, tanδµ, for Mn0.6Zn0.4La0.2Fe1.8O4 nanoferrites is smaller than for Mn0.6Zn0.2La0.2Fe2O4 nanoferrites due to the inverse relationship between the two.

The minimal losses observed are attributed to precise control over the chemical composition and microstructure of the ferrites. For high-frequency magnetic applications, a low permeability loss factor is essential. The samples in this study exhibit low tan δµ values even at higher frequencies, making them suitable for microwave devices and deflection yokes. Low-loss materials are commonly used in the cores of switch-mode power supplies, RF transformers, and inductors.

Conclusion

  1. 1.

    The present study investigated the modifications in lanthanum-substituted Mn-Zn ferrites’ microstructural and magnetic properties. Mn0.6Zn0.4Fe2O4 ferrites were successively substituted with varying amounts of La³⁺ ions to understand the effects on the physical properties.

  2. 2.

    The samples were prepared using the sol-gel auto-combustion method.

  3. 3.

    The structural analysis using XRD and TEM confirmed that the substitution of Fe³⁺ by La³⁺ (Mn0.6Zn0.4La0.2Fe1.8O4) and the substitution of Zn²⁺ by La³⁺ (Mn0.6Zn0.2La0.2Fe2O4) resulted in a single-phase spinel structure, maintaining the basic structure of the Mn0.6Zn0.4Fe2O4 nanoferrites.

  4. 4.

    The average crystallite sizes were 16 nm for the mother sample, 12 nm for La-substituted Mn0.6Zn0.2La0.2Fe2O4, and 10.7 nm for Mn0.6Zn0.4La0.2Fe1.8O4 nanoferrites.

  5. 5.

    The saturation magnetization (Ms) decreased with La doping, attributed to changes in cation distribution and magnetic exchange interactions.

  6. 6.

    The initial permeability of Mn-Zn ferrites increased with La substitution, explained by the changes in saturation magnetization and magnetocrystalline anisotropy constant.

  7. 7.

    The permeability loss factor in La-doped Mn-Zn ferrites at room temperature was 10− 2.

  8. 8.

    This research contributes to several Sustainable Development Goals (SDGs). The enhanced properties of La-doped Mn-Zn ferrites show potential for advanced technological applications in electronics, aligning with SDG 9: Industry, Innovation, and Infrastructure.

  9. 9.

    The sol-gel auto-combustion synthesis method is environmentally friendly, contributing to SDG 12: Responsible Consumption and Production.

  10. 10.

    The improved magnetic properties could have implications for energy-efficient technologies, supporting SDG 7: Affordable and Clean Energy. Future research will focus on optimising the synthesis process.