Introduction

Understanding the thermal properties of the lunar regolith, which is the unconsolidated surface layer of the Moon, is crucial to planning future lunar explorations and colonization efforts1. These properties significantly impact the design of the lunar infrastructure, the heat transfer in the regolith, and the stability of volatile resources trapped within2. Thermal conductivity, which is the ability of the regolith to conduct heat, plays a crucial role in regulating the lunar surface temperature, which experiences extreme fluctuations because of the Moon’s lack of atmosphere.

Numerical modeling of heat transfer in planetary bodies provided insight into the thermal behavior of surface and subsurface and planetary evaluation. The parameter that can significantly influence the results of thermal modeling is thermal conductivity, since it has a wide range of variability because it depends on many factors such as porosity and surface contact3,4.

In the initial stages of lunar exploration, understanding the thermal conductivity of the lunar regolith was based on laboratory analyses of samples returned by missions such as Apollo. Direct measurements of these samples produced thermal conductivity values ranging from 0.01 to 0.05 W m\(^{-1}\) K\(^{-1}\) and provided the first crucial insight into the thermal properties of the lunar surface material5. However, this approach had inherent limitations. Since the analyzes were limited to specific samples collected over the near equatorial region, they could not represent the heterogeneous composition of the lunar surface across different regions. Additionally, the returned samples may not fully reflect the in situ state of the regolith because of potential alterations such as exposure to Earth’s atmosphere. Despite these limitations, the pioneering work of analyzing returned samples laid the groundwork for our understanding of lunar regolith thermal conductivity and paved the way for developing advanced techniques. Active heating experiments with classical line heat sources were conducted during Apollo 15 and Apollo 17 missions6. In these cases, heating experiments were performed at a depth of 0.35 to 2.34 m. The thermal conductivity was found to be in the range of 0.01 to 0.03 W m\(^{-1}\) K\(^{-1}\)for the average bulk densities of 1825 and 1960 kg m\(^{-3}\)for Apollo 15 and Apollo 17, respectively6. These experiments were confined to the equatorial region of the Moon.

Remote sensing techniques have emerged as a powerful tool to overcome the limitations of returned sample-based studies. By analyzing Moon’s thermal emission at microwave frequencies measured by remote sensing methods, thermal conductivity was estimated in vast areas of the lunar surface7. However, these estimates typically hover around 0.1 W m\(^{-1}\) K\(^{-1}\)and represent the global average which is several times higher compared to returned sample-based measurements and are impacted by variations in surface roughness. In this context, in-situ measurements from unexplored locations, such as the high-latitude regions of the Moon, become extremely important to understand the variations in temperature, thermal conductivity, and packing density.

There were several modeling efforts using a combination of physical principles and emperical relationships to predict the thermal conductivity of lunar regolith based on factors such as density, grain size, composition, and temperature1,8,9,10,11,12. The limited data from in-situ measurements, analysis of returned samples, and remote sensing are used for the modeling. More data samples will help to improve the models to get a bigger picture of heat flow through the lunar regolith.

The Chandra’s Surface Thermo-Physical Experiment (ChaSTE) is one of the instruments onboard the Vikram Lander of the Chandrayaan 3 mission aimed at studying the thermal properties of lunar regolith from surface to 100 mm depth in the high-latitude region for the first time. ChaSTE is a thermal probe consisting of temperature sensors spaced at different distances, which was inserted into the lunar regolith in a controlled manner based on telecommands from the Earth station. The ChaSTE had a slow and motorized insertion into the lunar regolith, which minimized regolith disturbance. In this study, we report the first direct measurement of the thermal conductivity of the lunar regolith at ‘Shiv Shakti’ point (69.373 ° S, 32.319 ° E), the landing site of Vikram Lander, at a depth of 80 mm from the surface.

ChaSTE instrument

The ChaSTE Instrument consists of three major modules:

  1. 1.

    Thermal Probe

  2. 2.

    Probe Deployment and Penetration Mechanism

  3. 3.

    Data acquisition, control and interface electronics

Thermal probe

The ChaSTE probe material was a low thermal conductivity composite (cyanate ester) with a thermal conductivity of 0.16 – 0.17 W m\(^{-1}\) K\(^{-1}\) with sufficient mechanical strength to withstand the penetration force. The thermal probe is equipped with 10 Pt-1000 resistance temperature detectors (RTD) of 4 mm diameter that can measure the temperature in the range of 150 to 350 K. 4-wire RTDs were used to account for the resistance of the lead wire. Fig. 1 shows the schematic of the ChaSTE thermal probe. The part of the probe that penetrated into the lunar regolith had a diameter of 20 mm, while the remaining part had 25 mm. The nose cone was 40 mm long. Before penetration, the probe was housed in a sleeve of diameter 36 mm. In addition to the 10 RTD sensors, a foil-type heater with a width of 15 mm was included, which provided the thermal conductivity by active heating13 experiments. The heater was wound over the RTD 9. The nose tip of the probe was made of titanium alloy.

Fig. 1
figure 1

(Top) The ChaSTE probe. (Bottom) The schematic of the probe. The positions of the RTDs and heater on the probe are marked.

Full size image

Probe deployment and penetration mechanism

ChaSTE was kept in a stowed configuration in the +Yaw panel of the Lander during the flight with the hold and release mechanism, developed using a Shape Memory Alloy (SMA). After soft landing of the Lander on the lunar surface, a brushless DC (BLDC) motor-based mechanism was used to deploy the probe from a stowed position to a configuration that was normal to the Lander bottom deck. Once deployed, the probe was mechanically locked in place. The BLDC motor and the ball screw mechanism were then used to slowly insert the probe into the lunar regolith (Fig. 2). The mechanism was designed to provide a stroke of up to 310 mm to achieve the required penetration depth under different possible landing conditions of Lander on the local terrain.

Fig. 2
figure 2

A schematic showing the lander structure (left) with ChaSTE probe being deployed (middle) and penetrated (right) conditions.

Full size image

Data acquisition, control and interface electronics

The electronics module supported temperature measurements with accuracy better than 1 K for a wide temperature range of 150 to 350 K under high vacuum conditions, controlled operations of probe deployment and penetration; heater operation for thermal conductivity experiment; and interfacing the payload and Lander for telemetry and telecommand. The electronics was a microcontroller-based system with a 12-bit analog-to-digital converter (ADC).

Extensive calibration tests have been conducted by measuring the resistance corresponding to temperature variations (by placing the RTDs into the temperature bath at varying temperatures) to the standard and calibrated data acquisition system, and through ChaSTE electronics keeping the electronics in different thermal environments. The gain and offset are derived for the measurement channels. The maximum deviation between the observed temperatures and the measured temperatures after applying the calibration is found to be < 0.4 K.

Data and methodology

Each ChaSTE data packet consisted of voltage counts corresponding to the temperatures measured by the ten RTDs, and other housekeeping parameters for every second. The ChaSTE data were downlinked through the Indian Space Science Data Center (ISSDC)/Indian Deep Space Network (IDSN), Byalalu, India. The binary data thus received were converted to temperatures by applying calibration parameters. The data have been archived in Planetary Data System-4 (PDS-4) format and made available through ISRO’s PRADAN portal (https://pradan.issdc.gov.in/ch3).

Unlike the standard method of thermal conductivity estimation, where a line heat source is used for active heating, the foil-type heater used in the ChaSTE probe required laboratory calibration. Therefore, laboratory experiments were conducted using a similar probe and lunar simulant materials, and a relationship between thermal conductivity (measured with a standard line heat source) and the slope of the transient heating curve of the ChaSTE active heating experiment was established. This relationship is used to invert the measurement of change in temperature observed during the ChaSTE active heating experiment to the absolute thermal conductivity of the lunar regolith. To do this, the measured variation in temperature values was plotted with the natural logarithm of time. The linear portion (since this will be solely dependent on the thermal conductivity) of this curve was selected to estimate the slope where the temperature of the portion of probe (at the heater location) remains the same as that of the regolith around, providing a steady heat flow to regolith after all transients have died out. In addition, the thermal conductivity was estimated using the standard hot wire (line heat source) method. In the next section, the experiment to establish the relationship between slope of the heating curve and conductivity is described in detail, followed by the evaluation of uncertainties.

Laboratory experiments to estimate thermal conductivity of lunar simulant

Laboratory experiments were carried out to estimate the thermal conductivity of the lunar simulant at different vacuum levels within a vacuum chamber (Fig. 3). The chamber is fitted with a rotary vane vacuum pump and two turbomolecular pumps to achieve higher vacuum levels. Water chillers are used to control the temperature of turbomolecular pumps. The test setup has a DC power supply to provide 0.1 W power to the ChaSTE heater while conducting heating experiments and a data acquisition system to acquire the temperature response of the RTDs. The isothermal conditions inside the test set-up is achieved by circulating water at the desired test temperature using another fluid circulator.

Fig. 3
figure 3

Schematic of the test facility showing different units and ChaSTE probe.

Full size image

The experiments were carried out with a one-to-one model of the ChaSTE probe and powdered polyurethane foam14 as lunar simulant, taken in a container placed in a vacuum chamber at various vacuum levels (pressure upto 10\(^{-5}\) mb, after this vacuum level, the thermal conductivity did not change). The simulant container accommodated the ChaSTE probe and a standard hot wire set up to measure the thermal conductivity, as shown in Fig. 4.

The standard hot wire method15 has been used to evaluate the thermal conductivity of the simulant used to calibrate the ChaSTE probe. The hot wire method consists of a central heater wire made of nichrome having dimensions of 50 \(\mu\)m diameter and 100 mm length maintaining an aspect ratio (length/diameter ratio) of 2000 (to assume it as a line heat source in the hot wire method of thermal conductivity measurements) and a thermocouple instrumented parallel to the heater wire at a distance of 2 mm. The experiment to evaluate the thermal conductivity of the simulant is carried out by giving sufficient power input to the heater wire so that the temperature rise measured by the parallel thermocouple is within 10 to 15 K for a test duration of 5 minutes (300 s). The thermal conductivity of the simulant is estimated using the slope as well as the parallel wire method. Both methods gave similar results within the uncertainty limits of the standard hot-wire method apparatus.

The test was carried out for each thermal conductivity of the simulant (the thermal conductivity of the simulant was varied by varying the vacuum level of the simulant) before the thermal characterization test using the ChaSTE probe16. The thermal conductivity data are obtained by carrying out three sets of tests in each test condition. The average data are used for the calibration of the ChaSTE probe.

For each set of heating experiments conducted at fixed pressure, the probe heater was powered at 0.1 W for 2.5 hours. The temperature variation, known as the heating curve, was measured over time. After about 15 minutes of heating, a linear relationship between temperature and the natural logarithm of time (ln(Time)) was established for each heating experiment and the slope (\(S=\frac{dT}{d(\text {ln}(t))}\)) was observed. The thermal conductivity of the simulant was \(\sim\)0.04 W m\(^{-1}\) K\(^{-1}\) in 1 atmosphere and at a high vacuum level of 10\(^{-5}\) mb, it was \(\sim\)0.004 W m\(^{-1}\) K\(^{-1}\). The variation in estimated slope with simulant thermal conductivity from 0.004 W m\(^{-1}\) K\(^{-1}\) to 0.03 W m\(^{-1}\) K\(^{-1}\) is shown in Fig. 5.

Fig. 4
figure 4

The schematic of the container showing the set-up details.

Full size image

The thermal conductivity (k) is found to have a relationship with the slope of the temperature-ln(Time) curve , as reported by17 and as shown in Fig. 5.

$$\begin{aligned} S(k)= -1.40639 \,\text {ln}(k)-3.04346 \end{aligned}$$
(1)

The logarithmic relation (Eq. 1) is the fit to the slope variation with the thermal conductivity. The heating experiment yields a graph of temperature versus ln(Time). S is obtained as the slope. Then k is derived as:

$$\begin{aligned} k=exp\left( -\left( \frac{(S+3.04346)}{1.40639}\right) \right) \end{aligned}$$
(2)
Fig. 5
figure 5

Variation of thermal conductivity with slope for different self-heating curves of ChaSTE lab experiments.

Full size image

Evaluation of uncertainty in thermal conductivity estimation

The total uncertainty in the measurement of thermal conductivity using the ChaSTE probe is estimated by quantifying it from all sources of uncertainty during the experiment. Quantification is done by conducting ground experiments. The critical parameters in the estimation of the thermal conductivity of the lunar regolith are the temperature measurement of the self-heating temperature rise of the heater for the estimation of the slope of the linear portion of the temperature Vs ln(time) curve. The increase in the self-heating temperature of the heater is measured using RTDs, contributing to the uncertainty of 0.40% in the measurements. The repeatability error in slope measurement contributes 1.825% to measurement uncertainty and is estimated by conducting ten experiments under identical conditions. The hot wire method is used as the standard method for evaluating the thermal conductivity of the simulant18 used in ground experiments as part of the calibration of the ChaSTE probe. The hot wire method contributes to the uncertainty of 5 % in the measurements (with 95% confidence level and coverage factor 2). Equipment and accessories, such as the DC power supply, data acquisition system, and lead wire used in the ground experiments, contributed 1% to the uncertainty estimate. Thus, the total uncertainty of the measurement of thermal conductivity using the ChaSTE probe, which accounts for all the sources mentioned above, is estimated to be 7.5% (with a confidence level 95% and coverage factor 2).

In-situ lunar regolith thermal conductivity estimation using ChaSTE experiment

The Chandrayaan 3 lander soft landed on the Moon’s surface (Fig. 6) at 69.373 ° S, 32.319 ° E on August 23, 2023, at 14:34 UTC. The rover rolled out after landing. The ChaSTE payload was released and deployed vertically down. Subsequently, in steps of 2.5 mm per command of the motor-driven penetration, the ChaSTE probe was inserted inside the Lunar regolith. The whole penetration activity was a controlled action that was completed in 29 hours. After inserting the probe, with RTD sensors and a heater, into the regolith, 150 hours of measurements of the temperature profile of the regolith were taken.

Fig. 6
figure 6

Image of Chandrayaan 3 Vikram lander at Shiv Shakti landing site taken by Pragyan rover navigation camera. ChaSTE is seen in the penetrated configuration.

Full size image

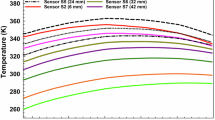
Subsequently, two heating experiments were conducted for the estimation of thermal conductivity, with the heater at a depth of \(\sim\)80 mm from the lunar surface. The power drawn by the heater in these experiments was 0.1 W. During the first experiment, the heater was switched ON, and the surrounding regolith was heated for 3.5 hours, and then the heater was switched OFF. After 10 hours, the heater was turned ON again for 2.5 hours. The temperatures were recorded every second by the RTDs. The temperature measured by RTD 9 during the two heating experiments is shown in Fig. 7 and Fig. 8.

Fig. 7
figure 7

Temperature measured by RTD 9 placed below the heater during the heating experiments.

Full size image
Fig. 8
figure 8

The temperature variation of the RTD 9 during the heater switch ON at a depth of 80 mm for (a) first and (b) second heating experiments.

Full size image
Fig. 9
figure 9

(a, b) Temperature variation with natural logarithm of time for the curves of Fig. 8 (a, b). The portion within the marked region are used for slope estimation.

Full size image

The Fig. 9 (a and b) show temperature variation with the natural logarithm of time for the two experiments. The slopes of the curves were estimated where the relationships are linear (where there are maximum correlations (R\(^2\) > 0.999)) and they were 3.235 K s\(^{-1}\) and 3.130 K s\(^{-1}\), respectively. The slopes were mapped back to the thermal conductivities using the relationship established through ground experiments, as shown in Fig. 5. The estimated thermal conductivities of the ChaSTE conductivity experiments are 0.0115 and 0.0124 W m\(^{-1}\) K\(^{-1}\), with uncertainties of 0.0008 and 0.0009 W m\(^{-1}\) K\(^{-1}\), respectively. The temperature reduction between experiments is observed to be \(\sim\)1 K. The thermal conductivity variation caused by which is within the uncertainty limit of measurements. In the estimation of the uncertainty of the thermal conductivity measurements, the 1 K error in the measurements is accounted for.

Empirical and numerical evaluation of lunar regolith thermal conductivity

Estimation from Empirical Models

As part of the structural qualification testing of the system, ChaSTE was tested by driving the probe into the lunar soil simulant and the loads and motor currents required were noted. Additional penetration tests were conducted by penetrating the probe into the lunar simulant with known packing densities and applying a known amount of loads by mounting the probe in a Universal Test Machine (UTM), capable of providing a range of loads. The penetration forces change drastically with the level of soil compaction or the packing density13. All ChaSTE elements were identical to those used in the ChaSTE system of Chandrayaan 3. The penetration forces were estimated from the penetration motor currents measured during ChaSTE penetration in the lunar regolith for different depths of penetration. The variation of the penetration force with depth measured in the lunar regolith using ChaSTE falls within the curves of the variation of the penetration force with depth for the packing densities of 1930 and 1950 kg m\(^{-3}\).

Fig. 10
figure 10

Thermal conductivity variation of lunar regolith with temperatures estimated using the empirical model. The curves for 1930 and 1950 kg m\(^{-3}\) represent the upper and lower bounds of densities simulated for the location of ChaSTE penetration from the penetration motor current and ground penetration experiments. The temperatures measured are 305 K and 303 K, for the first and second heating experiments, respectively.

Full size image

ChaSTE provided an estimate of the temperature and packing density of the regolith of the ChaSTE penetration point. The variation in thermal conductivity with temperature and packing density has been studied in the literature using a global thermal conductivity model for the lunar regolith9,12. The average packing density evaluated for the ChaSTE penetration point is between 1930 kg m\(^{-3}\) and 1950 kg m\(^{-3}\). The temperatures observed at the beginning of the first and second experiments were 305 K and 303 K, respectively. The thermal conductivity under these conditions using the empirical relations described by12, varies in the range of 0.0118 – 0.012 W m\(^{-1}\) K\(^{-1}\), which is in agreement with the estimated thermal conductivity using the ChaSTE probe, as shown in Fig. 10.

Numerical evaluation of thermal conductivity of moon

The thermal conductivity of the lunar soil medium is determined using numerical studies. An axisymmetric finite element model of the ChaSTE probe was generated with the surrounding soil medium to compute the temperature rise at the heater location, which was then compared with measured temperatures to determine the thermal conductivity of the lunar regolith. The mesh was selected considering the range of thermal diffusivities for the probe and lunar regolith. The numerical model, which contained 0.22 million elements, utilized 2D axisymmetric elements with a refined mesh around the probe region and a biased mesh with additional refinement near the probe boundary. The effective thermal conductivity of the probe (with stacked instrumentation wires) was initially determined using the same numerical thermal model, based on measurements obtained from laboratory experiments with a soil simulant of known thermal conductivity. The thermal model defined known thermophysical properties (density, thermal conductivity, and specific heat) for the probe material and lunar soil, except for the thermal conductivity of the soil. The measured vertical temperature gradient at the Moon penetration site, recorded by the ChaSTE probe prior to the heater powering phase, was specified as the initial temperature boundary condition in the numerical model to determine the thermal conductivity of the lunar soil medium. A constant heater power dissipation of 0.1 W was also specified to simulate heat dissipation during the thermal conductivity experiment. An effective packing density of 1950 kg m\(^{-3}\) was assumed for the surrounding lunar soil medium. Heater temperatures (heating curves) were numerically simulated with a thermal conductivity of 0.0115 W m\(^{-1}\) K\(^{-1}\) and perturbing the thermal conductivity of the soil medium by an order of magnitude. Numerical simulation with a thermal conductivity of 0.0115 W m\(^{-1}\) K\(^{-1}\) for the lunar soil, showed a better agreement with the measured heating curve with maximum temperature deviation of <0.5 °C within 2 hours as shown in Fig. 11. However, for one order lower thermal conductivity, the maximum deviation is \(\sim\)4 °C and for one order higher thermal conductivity, the maximum deviation is \(\sim\)8 °C. The numerical studies provided confidence in the measured thermal conductivity of \(\sim\)0.0115 W m\(^{-1}\) K\(^{-1}\) for the local lunar regolith surrounding the heater location.

Fig. 11
figure 11

Comparison of numerical model computed and ChaSTE measured temperature rise during active heating experiment.

Full size image

Summary and conclusions

In situ measurements of thermal conductivity of the lunar subsurface at the high-latitude landing point Shiv Shakti is estimated for the first time. The thermal probe of ChaSTE on the Chandrayaan 3 Lander was inserted into the lunar regolith with motor-based penetration to minimize the disturbance. The heating experiment to measure the thermal conductivity of the regolith was conducted by turning on the heater and measuring the temperature variation every second. Ground experiments were performed with a probe similar to that in ChaSTE experiment on the Moon and the same power to the heater, by using polyurethane foam powder as the simulant. Polyurethane foam powder is one of the materials with the lowest thermal conductivity under ambient conditions available on Earth. On the surface of the Earth, low density materials show only low thermal conductivity at the same temperature. So thermal conductivity simulants may not be comparable to lunar regolith in terms of density or chemical composition. The ChaSTE probe had ten temperature sensors to measure the temperature variation within 100 mm depth of lunar regolith and one at the heater, where active heating experiments were conducted, was used to evaluate the thermal conductivity. When the steady state is reached or all the transients have died out, the heating rate of the simulant depends only on the thermal conductivity. So, the estimated thermal conductivity is the local thermal conductivity at a depth of 80 mm. By comparing the slopes of the heating curves, the thermal conductivity of the lunar regolith was estimated. During active heating experiments, in this method, the slope is only a function of thermal conductivity when the relationship between temperature and the natural logarithm of time is linear (R\(^2\) > 0.99). By conducting two heating experiments at a depth of 80 mm, the thermal conductivities at the heating location were estimated as 0.0115 and 0.0124 W m\(^{-1}\) K\(^{-1}\), with uncertainties of 0.0008 and 0.0009 W m\(^{-1}\) K\(^{-1}\), respectively.

From the motor current and the penetration experiments conducted on the ground, the average packing density of the lunar regolith that arrived at the ChaSTE penetration location is 1940 kg m\(^{-3}\). The penetration experiments on the ground were conducted by placing the simulant material in a container with varying average packing densities. The average packing density of 1960 kg m\(^{-3}\) was observed at a depth of \(\sim\)2.34 m by the Apollo-17 experiment6. At the ChaSTE penetration location, the average density is 1940 kg m\(^{-3}\) for a depth of 100 mm. A possible reason for the high packing density within 100 mm is that the dust layer may be flown off by the Lander nozzle exhaust during landing. The inferred packing density at the location of the ChaSTE penetration and the measured temperature provided inputs for the empirical models to evaluate the thermal conductivity. The thermal conductivity evaluated using the empirical model (0.0118 – 0.012 W m\(^{-1}\) K\(^{-1}\)) agrees with the values measured by ChaSTE. This gives confidence in using the empirical model to evaluate the thermal conductivity for all possible temperatures for this location. Inserting a probe into the regolith from the Lander platform and measuring the thermal conductivity is an effective way of measuring the thermal conductivity. However, the modification of the regolith by the Lander and the ChaSTE probe was inevitable. Numerical simulations allow us to study the heat transfer in the regolith using available in situ measurements as inputs. The combination of in situ and laboratory experiments provided a unique way of estimating the thermal conductivity of the — hitherto unexplored region of the Moon.