Study on the measurement of high-quality development efficiency and influencing factors in the Yellow River Basin, China

Abstract

Environmental pollution and resource scarcity characterize the Yellow River Basin. Studying the factors of high-quality development efficiency (HQDE) and its spatial correlation in the Yellow River Basin is conducive to promoting the maximization of resource allocation in the Yellow River Basin. In this study, Super-EBM and Malmquist index were used to measure HQDE in the Yellow River Basin and explore its influencing factors. The results show that: (1) HQDE is higher in cities in the upper reaches of the Yellow River Basin than in the middle and lower reaches. Compared with the degree of technology utilization, the growth of HQDE mainly depends on technological progress. (2) The spatial correlation of urban HQDE decreases has been weakened annually. The high-efficiency cities in the upper reaches of the basin are obviously concentrated, while the middle and lower reaches of the confluence have both high- and low-efficiency cities located near each other. (3) HQDE has a negative geographical spillover effect. Regression analysis shows that energy consumption, economic development level, factor endowment, public awareness of environmental protection, and enterprise green level can promote the HQDE, while foreign investment utilization, environmental pollution, and education support have negative impacts on urban HQDE.

Introduction

High-quality development (HQD) is development that meets the growing needs of people for a better life. HQD focuses not only on the speed and scale of economic growth but also on the quality and sustainability of economic development and seeks to achieve comprehensive, coordinated, and sustainable economic and social development in the context of the new era¹. Therefore, promoting regional HQD is crucial. In 2022, the GDP of China’s YRB alone reached 25.39 trillion yuan, accounting for approximately 25% of China’s GDP. However, with the acceleration of economic growth, the contradiction between economic development and the ecological environment in the Yellow River Basin (YRB) is increasingly aggravated, and a series of problems are gradually coming to the fore. In 2022, the exploitation and utilization rate of surface water resources of the Yellow River reaches 83.47%, seriously exceeding its own carrying capacity². And in recent decades, the economic and social development of the basin on the Yellow River water demand has been a continuous growth trend, while the natural water volume has been a decreasing trend. The natural water quantity of the Yellow River has been unable to meet the needs of the economic and social development of the areas along the Yellow River, and the overall water shortage situation is difficult to be fundamentally improved in the short term. The area of soil erosion in the loess basin reaches 255,500 square kilo-meters, accounting for 33.97% of the YRB³. Soil erosion has led to a decline in soil fertility, affecting agricultural production while exacerbating the siltation of river sediments and threatening the safety of downstream flood control. In addition, the economy of the YRB generally shows a pattern of “strong downstream and weak upstream,” with unbalanced economic development⁴. The poor economic ties among provinces and regions⁵, poor sense of coordination and collaboration in regional division of labour⁶, and serious competition in industrial homogenization⁷ have also constrained the overall development of the YRB economy. HQD is of great significance in solving a series of problems faced by the YRB and promoting comprehensive, coordinated, and sustainable economic and social development. Therefore, the promotion of regional HQD is a necessary means to adhere to the concepts of sustainable development and environmental protection^8,9,10.

HQD, as a key path to achieving sustainable regional economic development, not only focuses on the traditional economic growth rate but also emphasizes the efficient use of resources, environmental protection, and the coordinated development of all areas of society. With changes in the global economic situation, especially China’s economic development, which has shifted from high-speed growth to HQD, academic research on HQD has increased in depth. In terms of research content, scholars have mostly analysed the level¹¹, coupling coordination¹², and spatial and temporal evolution of HQD¹³. The main study areas include national areas¹⁴, urban agglomerations¹⁵, watersheds¹⁶, provincial areas¹⁷, and municipal areas¹⁸.

HQDE is an important indicator of the quality and sustainability of regional economic growth. At present, scholars have focused more on the level of HQD, but there is still a need for in-depth research on HQDE. Li et al. analysed the cyclical effects of the industrial structure, environmental regulations, and their interaction terms on HQDE from the perspective of threshold effects and explored possible interaction thresholds for altering the HQDE¹⁹. Sha & Wang used the Malmquist index method to analyse the evolution trend of HQDE in the YRB while applying the entropy value method and the coupling coordination model to conduct coupling coordination analysis²⁰. Chen & Shang applied the DEA model to measure the HQDE of the manufacturing industry in each region of Henan Province²¹. Yang et al. analysed the impact of the combined effect of different influencing factors on the HQDE in the logistics industry through fuzzy set qualitative comparative analysis (fsQCA). The results show that the factors influencing logistics efficiency are multiple and concurrent, and to improve logistics efficiency, practitioners should focus on multifaceted elements instead of a single factor²².

Scholars studying the HQDE tend to also probe its spatial spillover effects. Investigations into the spatial correlation of urban HQDE can analyse the pattern of HQD’s temporal and geographical evolution and spatial agglomeration effects. Thus, the study of the spatial correlation of efficiency in the YRB is quite important and valuable for economic progression. Existing studies often apply the Moran Index and spatial econometric models to measure the geographical overflow effects of HQDE. For example, Liu et al. reported that the spatial correlation between the interprovincial water resource optimization efficiency and HQD coupling coordination in China is significant. The distribution of “low-low” and “high-high” varieties of agglomeration is stable²³. Wang et al. reported an overall fluctuating upward trend in China’s industrial HQD level. Spatially, the efficiency displays a stepwise sequence of diminishing geographic differentiation as one moves inland northwest from the southeast coast²⁴. Innovation in science and technology significantly increases the effectiveness of industrial HQD. Regional variations exist in the influence of industrial HQD in various areas, though²⁵.

Improving the HQDE can be driven by influencing factors. Scholars mainly select economic factors²⁶, environmental factors²⁷, receptivity to external influences²⁸, and policy factors²⁹ to analyse the HQDE. The effects of the same factor on the HQDE vary from region to region. Scholars believe that the connection between excellent economic development and environmental control shows an inverted “U” shape³⁰. Zhang et al. believe that regulation of the environment can support superior economic development, but the synergistic impact on economic development is in a “U”-shaped trend³¹. Hui proposed that, through technical innovation, the digital economy encourages regional manufacturing to establish headquarters³². Shang et al. discovered that while the HQD of the economy is encouraged by the digital economy, the influence on HQD has a significant lag. The first two periods encourage HQD, and the latter phase gradually weakens, showing a non-linear characteristic of first strengthening and then weakening³³. Therefore, regional differences should be taken into account when the role of influencing factors is analysed. Similarly, different factors have different effects on the HQDE in the same region. Yuan et al. reported that the foundational economy and innovation potential of the eastern coastal area had an advantageous and stable influence on superior-quality synergistic growth³⁴. Wang & Yang suggested that the degree of human capital, the degree of urbanization, foreign direct investment, and the size of the economy significantly contributed to the HQD of the urban agglomeration of the Yangtze River Delta³⁵. Obviously, different factors have different impacts in different regions, and different factors in different regions need to be measured separately.

The YRB significantly hinders to ecological security in China but is a vital area for national economic and social growth. Research on the HQDE in the YRB is crucial. Cui et al., based on their data, examined the spatial–temporal coupling properties of the ecological environment and HQD in nine YRB provinces and cities³⁶. Zhang & Li reported that the degree of excellence in agricultural growth in the YRB showed a spatially unbalanced distribution. Regional agricultural development is spatially correlated and shows two types of agglomeration: low-low and high-high³⁷. Yu reported that there exist obvious spatial variations in the effects of factors on the level of HQD in various regions of the YRB. The level of HQD in the YRB clearly varies significantly by location, and there is obvious spatial dependence and heterogeneity³⁸. It is important to examine the mechanism of influence and “prescribe the right medicine” for the sound operation of the city and alleviate the unbalanced development of the region. Yan & Han made it clear that technological inventiveness (TEC) promotes HQD in the manufacturing sector³⁹. Consequently, identifying and analysing the factors influencing the HQDE in the YRB is highly important.

To summarize, there have been many studies on HQD in the YRB, laying a solid theoretical foundation for this study. However, the current research on HQD in the YRB still suffers from the following shortcomings. First, most existing studies focus on the measurement and analysis of HQD levels in different regions. However, the HQDE is a key factor in measuring the effectiveness of various resource inputs under the current level of regional HQD, and only a few scholars have conducted in-depth studies. In addition, there are many cities in the YRB, and the level of development among them is uneven, especially in terms of economic, social, and ecological aspects, which cause an uneven distribution of resources and spatial–temporal dislocation among cities. Therefore, it is necessary to analyse the temporal and spatial differences in the HQDE of cities within the YRB. Second, further research on the driving factors of HQDE in the YRB is needed. The literature mostly explores the drivers of HQDE in the YRB from three aspects: economic, ecological, and social. However, HQDE reflects the comprehensive effectiveness of regional development, which involves not only the government’s policy guidance and macro-control but also the allocation and utilization of energy as a key factor; however, research on the drivers of these two aspects is still lacking.

In view of this, the main contributions of this study are as follows: Firstly, the paper constructs a relatively more comprehensive indicator system based on the perspective of efficiency theory. On the basis of the previous research on the level of HQD, this paper, based on the characteristics of the YRB, adds soil and water factor indicators to the input–output indicator system and systematically analyses the HQDE in the YRB and its spatial and temporal evolution laws. The study effectively solves the problem of improving the efficiency of overall and local HQD, and the results are more scientific. Secondly, this paper discusses the influencing factors of HQDE in the YRB in a more comprehensive way. On the basis of the previous research on HQDE from the economic, ecological, and social aspects, this paper tries to add the social level and the entity variables of the government, the public, and the enterprises to study the factors affecting the HQDE of the YRB, in order to make up for the insufficiency of the research on HQDE of the YRB on both the social and entity levels. Finally, based on the spatial correlation and spillover effect of HQDE in the YRB, sub-regional policies are implemented. This paper reveals the mutual influence mechanism of HQDE between different regions through the spatial correlation and agglomeration characteristics of HQDE in the YRB and proposes differentiated regional development strategies on this basis. The study not only enriches the theoretical research on HQD in the YRB but also provides scientific basis and empirical support for the formulation and implementation of differentiated regional development policies.

The remainder of the paper is roughly arranged as follows: Chapter 2 describes the study methodology and sources of data. Chapter 3 presents the results of the study on HQDE and its geographical correlations and influencing factors. Chapter 4 discusses the research and provides policy recommendations. Chapter 5 provides the conclusions of the study.

Methods and data

Research methodology

Model for measuring the HQDE in the YRB

• (1) Measurement methods

This essay embraces the non-oriented SUPER-EBM model to gauge the HQDE in the YRB under the state of variable scale-back returns, considering unexpected output. The MI index method is chosen to dynamically evaluate the degree of HQDE in cities in the YRB.

The EBM model addresses the drawbacks of conventional DEA techniques, which do not consider slack variables or the original scale information of the projected values of the loss efficiency frontier. Moreover, it can compare various decision-making units that are in frontier positions. Therefore, this paper selects the SUPER-EBM model to quantify the HQDE in the YRB. The calculation formula is as follows:

$$\begin{aligned} \rho^{*} & = \min \frac{{\theta - \varepsilon_{x} \sum\nolimits_{i = 1}^{n} {\frac{{w_{i}^{ - } s_{i}^{ - } }}{{x_{ij} }}} }}{{\varphi + \varepsilon_{y} \sum\nolimits_{r = 1}^{m} {\frac{{w_{r}^{ + } s_{r}^{ + } }}{{y_{rj} }}} - \varepsilon_{z} \sum\nolimits_{p = 1}^{l} {\frac{{w_{p}^{z - } s_{p}^{z - } }}{{z_{pj} }}} }} \\ & \quad \quad s.t.\quad \left\{ {\begin{array}{*{20}l} {\sum\nolimits_{t = 1}^{T} {\sum\nolimits_{j = 1}^{J} {\lambda_{j}^{t} } } x_{ij}^{t} - s_{i}^{ - } \le \theta x_{ij} ,\quad i = 1,2, \ldots ,n} \hfill \\ {\sum\nolimits_{t = 1}^{T} {\sum\nolimits_{j = 1}^{J} {\lambda_{j}^{t} } } y_{rj}^{t} + s_{i}^{ + } \ge \varphi y_{rj} ,\quad r = 1,2, \ldots ,m} \hfill \\ {\sum\nolimits_{t = 1}^{T} {\sum\nolimits_{j = 1}^{J} {\lambda_{j}^{t} } } z_{pj}^{t} - s_{i}^{z - } \le \varphi z_{pj} ,\quad p = 1,2, \ldots ,l} \hfill \\ {\sum\nolimits_{t = 1}^{T} {\sum\nolimits_{j = 1}^{J} {\lambda_{j}^{t} } } = 1} \hfill \\ {\lambda_{j} \ge 0,\quad s_{i}^{ - } \ge 0,\quad s_{r}^{ + } \ge 0,\quad s_{p}^{z - } \ge 0} \hfill \\ \end{array} } \right. \\ \end{aligned}$$

(1)

In the above Eq. (1), ρ^* denotes the value of the HQDE of the decision-making unit. λ_j is the decision unit’s linear combination coefficient j; $x_{ij}^{t} ,y_{rj}^{t}$, and $z_{pj}^{t}$ denote the class i inputs, class r desired outputs, and class p non-desired outputs of the decision unit j in the time period t, respectively; J, n, m, and l represent the number of decision units, inputs, intended results, and unexpected results Correspondingly. $s_{i}^{ - } ,s_{r}^{ + }$, and $s_{p}^{z - }$ represent variables with non-zero slack for inputs of category i (input redundancy), variables with non-zero slack for desired results of category r (desired output shortfalls), and non-zero slack variables for non-desired outputs of category p (non-desired output redundancy), respectively; and $w_{i}^{ - } ,w_{r}^{ + }$, and $w_{p}^{z - }$ are inputs, respectively, indicator weights for both intended and unwanted results, correspondingly; θ denotes the radial planning parameter. ε is an important factor in the EBM model that reflects the share of the non-radial part. It indicates the significance of the non-radial component in the computation of the value of efficiency. The radial model is equivalent to its value is within the range of [0, 1]. A value of 0 indicates radial model, and a value of 1 indicates an SBM model; ε_x, ε_y, and ε_z denote the inputs’ non-radial weights, intended results, and undesirable results, respectively; and $\emptyset$ is the output expansion ratio.

In this paper, the global parametric Malmquist index under the common frontier is chosen to dynamically evaluate the degree of HQDE of cities in the YRB. The global total factor productivity index is built by combining the HQDE ρ above:

$${\text{MI}}^{t,t + 1} \left( {x^{t} ,y^{t} ,z^{t} ;x^{t + 1} ,y^{t + 1} ,z^{t + 1} } \right) = \frac{{\rho^{g,t + 1} \left( {x^{t + 1} ,y^{t + 1} ,z^{t + 1} } \right)}}{{\rho^{g,t} \left( {x^{t} ,y^{t} ,z^{t} } \right)}}$$

(2)

In Eq. (2), $\rho^{g,t} \left( {x^{t} ,y^{t} ,z^{t} } \right)$ denotes the global efficiency value in period t. $\rho^{g,t + 1} \left( {x^{t + 1} ,y^{t + 1} ,z^{t + 1} } \right)$ denotes the global efficiency value in period t + 1. ${\text{MI}}^{t,t + 1}$ denotes the high-quality total factor productivity index from time t to time t + 1. MI = 1 shows no change in HQD effectiveness compared to the previous year; MI > 1 indicates an increase in HQD effectiveness; MI < 1 indicates a decrease in HQD efficiency.

The MI index can be decomposed into a composite technical effectiveness change index (EC) and a technical index of advancement (TC).

$$EC^{t,t + 1} \left( {x^{t} ,y^{t} ,z^{t} ;x^{t + 1} ,y^{t + 1} ,z^{t + 1} } \right) = \frac{{\rho^{t + 1,t + 1} \left( {x^{t + 1} ,y^{t + 1} ,z^{t + 1} } \right)}}{{\rho^{t,t} \left( {x^{t} ,y^{t} ,z^{t} } \right)}}$$

(3)

where $\rho^{t + 1,t + 1} \left( {x^{t} ,y^{t} ,z^{t} } \right)$ denotes the current efficiency value with period t + 1 as the frontier and $\rho^{t,t} \left( {x^{t} ,y^{t} ,z^{t} } \right)$ denotes the current efficiency value with period t as the frontier.

$$\begin{aligned} TC^{t,t + 1} \left( {x^{t} ,y^{t} ,z^{t} ;x^{t + 1} ,y^{t + 1} ,z^{t + 1} } \right) & = \frac{{MI^{t,t + 1} \left( {x^{t} ,y^{t} ,z^{t} ;x^{t + 1} ,y^{t + 1} ,z^{t + 1} } \right)}}{{EC^{t,t + 1} \left( {x^{t} ,y^{t} ,z^{t} ;x^{t + 1} ,y^{t + 1} ,z^{t + 1} } \right)}} \\ & = \frac{{\frac{{\rho^{g,t + 1} \left( {x^{t + 1} ,y^{t + 1} ,z^{t + 1} } \right)}}{{\rho^{g,t} \left( {x^{t} ,y^{t} ,z^{t} } \right)}}}}{{\frac{{\rho^{t + 1,t + 1} \left( {x^{t + 1} ,y^{t + 1} ,z^{t + 1} } \right)}}{{\rho^{t,t} \left( {x^{t} ,y^{t} ,z^{t} } \right)}}}} = \frac{{\frac{{\rho^{g,t + 1} \left( {x^{t + 1} ,y^{t + 1} ,z^{t + 1} } \right)}}{{\rho^{t + 1,t + 1} \left( {x^{t + 1} ,y^{t + 1} ,z^{t + 1} } \right)}}}}{{\frac{{\rho^{g,t} \left( {x^{t} ,y^{t} ,z^{t} } \right)}}{{\rho^{t,t} \left( {x^{t} ,y^{t} ,z^{t} } \right)}}}} \\ \end{aligned}$$

(4)

where $\frac{{\rho^{g,t + 1} \left( {x^{t + 1} ,y^{t + 1} ,z^{t + 1} } \right)}}{{\rho^{t + 1,t + 1} \left( {x^{t + 1} ,y^{t + 1} ,z^{t + 1} } \right)}}$ reflects the distance between the efficiency frontier in period t + 1 and the global efficiency frontier. The t + 1 period frontier is nearer the global frontier when the ratio is higher. A greater ratio suggests that the t-period frontier is closer to the global frontier. $\frac{{\rho^{g,t} \left( {x^{t} ,y^{t} ,z^{t} } \right)}}{{\rho^{t,t} \left( {x^{t} ,y^{t} ,z^{t} } \right)}}$ represents the distance between the t-period frontier and the global frontier. The proportion of the two then depicts the modification during that time t + 1 advancing forward compared to the period t frontier, i.e., the technical progress index.

EC > 1 indicates that the region is moving closer to optimization and towards a more optimal state. EC < 1 indicates that the region is moving away from optimization, that there is room for optimization in its approach to development, and that there is a need to take measures to improve efficiency. TC > 1 indicates that technological innovation and application are effective and that there has been an increase in the region’s technological sophistication. TC < 1 indicates that there has been a regression in the region’s technological sophistication.

• (2) Measurement indicators

The HQDE of cities in the YRB needs scientific evaluation. The efficiency evaluation in this article follows the principles of systematicity, comparability, operability and statistically feasible. In addition, the article constructs an index system founded on the five new development ideas of sharing, openness, greenness, inventiveness, and coordination^{38,40,41,42,43,44}. According to the characteristics of the YRB and drawing on the research of previous scholars on HQD, this paper selects seven indicators on the input side, such as the level of foreign capital utilization⁴⁵, total comprehensive energy consumption⁴⁶ and total water resources⁴⁷. The output side is divided into six desired output indicators, such as the number of patents granted for inventions⁴⁸, total imports and exports⁴⁹, and soil erosion control area⁵⁰; and three undesirable output indicators, such as industrial wastewater emissions⁵¹ and the number of urban registered unemployed people⁵². The specific indicator system is shown in Table 1.

Table 1 Indicator system for measuring the high-quality development efficiency in the Yellow River Basin.

wherein the capitalization of stocks is calculated by the annual fixed asset investment and price index data of each city. The paper refer to the perpetual inventory method, which is calculated by Eq. (5)⁵³.

$$K_{{i,t}} = K_{i,t - 1} \left( {1 - \delta } \right) + I_{{i,t}}$$

(5)

where K_i,t and K_i,t−1 denote the capital stock of the ith city in year t and year t − 1, respectively. I_i,t is the amount of fixed assets invested by the ith city in year t. δ denotes the depreciation rate of fixed assets. After a defined base period and city i are chosen, the above equation is transformed into the following equation by iteration:

$$K_{t} = K_{0} \left( {1 - \delta } \right)^{t} + \mathop \sum \limits_{j = 1}^{t} I_{j} \left( {1 - \delta } \right)^{t - j}$$

(6)

$$K_{0} = I_{0} \left( {1 + g} \right)/\left( {g + \delta } \right)$$

(7)

where I₀ represents the average annual growth rate of the constant price investment amount. The constant price investment amount’s average yearly increase rate is denoted by g. δ is the average capital depreciation rate; in calculating the depreciation rate, this paper speaks of the depreciation rate of 9.6% derived by using the weighting method and substitutes it into the formula⁵⁴.

In addition, the total comprehensive energy consumption is converted according to the indicators “total raw coal consumption” and “total heat supply,” as shown in Eq. (8). Carbon dioxide emissions are converted according to the indicators “total electricity consumption,” “total natural gas supply,” and “liquefied petroleum gas,” as shown in Eq. (9)⁵⁵.

$$E = \mathop \sum \limits_{i = 1}^{n} E_{i,t} \times k_{i,t}$$

(8)

where E is the integrated energy consumption and where n is the number of energy types consumed. E_i,t represents the actual amount of energy consumed by the ith type of energy in year t, and k_i,t represents the discounted standard coal coefficient of the ith type of energy in year t.

$$CO_{2} = \alpha E_{a} + \beta E_{b} + \gamma E_{c}$$

(9)

where E_a, E_b, and E_c denote the total electricity consumption of the whole society, the total natural gas supply, and the total liquefied petroleum gas supply, respectively. α, β, and γ are the carbon emission coefficients of the grid, natural gas, and liquefied petroleum gas, respectively. The carbon emission factors were obtained from the Ministry of Ecology and Environment of the People’s Republic of China and the National Bureau of Statistics of the People’s Republic of China^56,57,58.

Spatial correlation analysis of the HQDE in the YRB

• (1) Spatial weighting matrix

Constructing a spatial weight matrix is a prerequisite for spatial analysis. The neighbour relationships of the 75 cities studied in this paper are incomplete. The indicator “carbon dioxide emissions” has spatial mobility, so the neighbourhood matrix is not suitable for the weight matrix of this paper. HQD encompasses economic, social, environmental, and other aspects, and economic and geographic factors are equally important in the study of HQD in the YRB. This paper draws on the study of Li et al. to construct a nested weight matrix of economic-geographical distances that can consider both economic and geospatial correlations between regions⁵⁹, which is calculated by Eq. (14).

The expression for the spatial weight distribution W is as follows, where W_ij represents the spatial weight coefficients:

$$W_{ij} = \left[ {\begin{array}{*{20}c} {W_{11} } & \cdots & {W_{1n} } \\ \cdots & \ddots & \cdots \\ {W_{n1} } & \cdots & {W_{nn} } \\ \end{array} } \right]$$

(10)

The spatial weight matrix defines W_ij using the idea of geographic proximity:

$$W_{{{\text{ij}}}} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\quad region\,\, i\,\, is\,\, adjacent\,\, to\,\, region\,\, j} \hfill \\ {0,} \hfill & {\quad region\,\, i\,\, is\,\, not\,\, contiguous\,\, with\,\, region\,\, j} \hfill \\ \end{array} \quad i = 1,2, \ldots ,n;\quad j = 1,2, \ldots ,n;} \right.$$

(11)

The geographic distance weight matrix is usually constructed using the inverse of the geographic distance or the square of the inverse of the geographic distance:

$$W_{{{\text{ij}}}} = \frac{1}{{d_{ij} }}\quad {\text{or}}\quad W_{{{\text{ij}}}} = \frac{1}{{d_{ij}^{2} }}$$

(12)

In the above equation, $d_{{{\text{ij}}}} = {\text{arcos}}\left[ {\left( {\sin \varphi_{i} \times \sin \varphi_{j} } \right) + \left( {\cos \varphi_{i} \times \cos \varphi_{j} \times \cos \left( {\Delta \tau } \right)} \right)} \right] \times R$, ϕ_i and ϕ_j denote the latitude and longitude, respectively, of a region (geo-geometric centre or seat of government). Δτ is the difference in longitude between the two regions, and the radius of the Earth is represented by R, which is 3958.761 miles. In practice, row normalization is frequently used in the spatial weight matrix. The diagonal elements of the spatial weight matrix are set to 0, and d_ij = d_ji.

The economic distance weight matrix considers both the spatial correlation of distance and the economy, and the inverse of the absolute value of the difference between the per capita GDP of two spatial units is commonly used to construct the economic distance matrix⁶⁰, as shown in Eq. (13).

$$W_{ij} = \left\{ {\begin{array}{*{20}l} {\frac{1}{{\left| {\overline{{Y_{i} }} - \overline{{Y_{j} }} } \right|}},} \hfill & {\quad i \ne j} \hfill \\ {0,} \hfill & {\quad i = j} \hfill \\ \end{array} } \right.$$

(13)

In the above equation, $\overline{{Y_{i} }}$ and $\overline{{Y_{j} }}$ denote the per capita GDP of the two regions.

The economic-geographic nested weight matrix combines the geographic distance weight matrix with the economic weight matrix, which can accurately demonstrate the comprehensiveness and complexity of spatial effects:

$$W_{q} = W_{d} \times W_{e}$$

(14)

where W_q represents the economic-geographic nested weight matrix, the geographic distance matrix $W_{{\text{d}}} = \frac{1}{{d_{ij}^{2} }}$, and the economic distance matrix $W_{e} = \frac{1}{{\left| {\overline{{Y_{i} }} - \overline{{Y_{j} }} } \right|}}$, where $\overline{{Y_{i} }}$ and $\overline{{Y_{j} }}$ denote the per capita GDP of the two regions.

• (2) Spatial autocorrelation test

The most commonly used metric for spatial correlation tests is Moran’s I, calculated as shown in Eq. (15).

$$Moran^{\prime}s\,I = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \mathop \sum \nolimits_{j = 1}^{n} W_{ij} \left( {x_{i} - \overline{x}} \right)\left( {x_{j} - \overline{x}} \right)}}{{S^{2} \mathop \sum \nolimits_{i = 1}^{n} \mathop \sum \nolimits_{j = 1}^{n} W_{ij} }}$$

(15)

$S^{2} = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left( {x_{i} - \overline{x}} \right)^{2} }$ is the sample variance, and $\overline{x} = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {x_{i} }$. W_ij symbolizes the constructed spatial weight matrix. When the spatial weight matrix is subjected to row normalization, $\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{n} {W_{ij} } } = n$. At this point, Eq. (15) above can be simplified to Eq. (16).

$$Moran^{\prime}s\,I = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \mathop \sum \nolimits_{j = 1}^{n} W_{ij} \left( {x_{i} - \overline{x}} \right)\left( {x_{j} - \overline{x}} \right)}}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {x_{i} - \overline{x}} \right)^{2} }}$$

(16)

The value of the Moran index is located between − 1 and 1, and the larger the value is, the stronger the relationship between regions. If the Moran index is higher than zero, this suggests that there is a phenomenon of aggregation of high values or aggregation of low values. For example, there is a positive spatial correlation when the Moran index is zero; this suggests that the high and low values are randomly distributed without an obvious spatial distribution pattern and there is no spatial autocorrelation. When the Moran index is less than 0, high values in neighbouring regions repel high values and attract low values, and there is a staggered occurrence of high and low values, showing a negative spatial correlation.

Secondly, a Z-test for Moran’s I index is also needed, and the Z value is calculated by Eq. (17).

$$\begin{aligned} Z & = \frac{Moran^{\prime}sI - E\left( I \right)}{{\sqrt {Var\left( I \right)} }} \\ E\left( I \right) & = \frac{ - 1}{{N - 1}},\quad Var\left( I \right) = E\left( {I^{2} } \right) - E\left( I \right)^{2} \\ \end{aligned}$$

(17)

The Z value for the normal distribution function at the 5% significance level that is greater than the crucial value of 1.96 indicates that the values have similar attribute values between neighbouring cities. Otherwise, it indicates that there is no significant spatial correlation between cities.

Analytical model of factors influencing the HQDE in the YRB

• (1) Measurement methods

This paper draws on the idea of the coordinated development of the 3 Es (energy, economy, and environment) proposed in the “Broad Energy Efficiency Strategy” project and refers to the existing relevant research results^61,62. On the basis of the perspective of HQD, an indicator system of influencing factors in the seven dimensions of “energy-economy-environment-society-government-public-enterprise” was constructed^8,63,64,65, and Stata 17.0 is used to study the factors influencing HQDE in the YRB²⁵. Analysis of the external drivers of HQDE in watershed cities must consider spatial dependence to reduce estimation errors within the model. On the basis of the traditional static panel regression (OLS) model, an appropriate spatial econometric model is selected through the LM test, robust LM test, and Hausman test.

• (2) Measurement indicators

This paper combines existing research results with the actual situation in the YRB, selects HQDE as the explained variable, and sets the explanatory variable according to the seven aspects of “energy-economy-society-environment-government-public-enterprise.” The indicator system of HQDE in the YRB is shown in Table 2. To eliminate the effect of heteroskedasticity, the logarithm is taken for the indicators of educational support, public awareness of environmental protection, and enterprise green level, and the financial support indicator was shrunk using Stata.

Table 2 Index system of factors influencing the high-quality development efficiency in the Yellow River Basin.

• (3) Measurement models

This paper chose the ordinary panel regression model and the spatial Durbin model with fixed effects to compare and analyse the influencing factors under different models.

The ordinary panel regression model formula is shown in Eq. (18).

$$\begin{aligned} HE_{it} & = \beta_{1} ECR_{it} + \beta_{2} PGDP_{it} + \beta_{3} IS_{it} + \beta_{4} FI_{it} + \beta_{5} WER_{it} + \beta_{6} UR_{it} \\ & \quad + \beta_{7} CLR_{it} + \beta_{8} FS_{it} + \beta_{9} EI_{it} + \beta_{10} PEA_{it} + \beta_{11} EG_{it} + \mu_{it} \\ \end{aligned}$$

(18)

The spatial Durbin model regression model formula is shown in Eq. (19).

$$\begin{aligned} HE_{it} & = \alpha \mathop \sum \limits_{j = 1}^{n} W_{ij} HE_{jt} + \beta_{1} ECR_{it} + \beta_{2} PGDP_{it} + \beta_{3} IS_{it} + \beta_{4} FI_{it} + \beta_{5} WER_{it} + \beta_{6} UR_{it} + \beta_{7} CLR_{it} \\ & \quad + \beta_{8} FS_{it} + \beta_{9} EI_{it} + \beta_{10} PEA_{it} + \beta_{11} EG_{it} + \theta_{1} \mathop \sum \limits_{j = 1}^{n} W_{ij} ECR_{jt} + \theta_{2} \mathop \sum \limits_{j = 1}^{n} W_{ij} PGDP_{jt} + \theta_{3} \mathop \sum \limits_{j = 1}^{n} W_{ij} IS_{jt} \\ & \quad + \theta_{4} \mathop \sum \limits_{j = 1}^{n} W_{ij} FI_{jt} + \theta_{5} \mathop \sum \limits_{j = 1}^{n} W_{ij} WER_{jt} + \theta_{6} \mathop \sum \limits_{j = 1}^{n} W_{ij} UR_{jt} + \theta_{7} \mathop \sum \limits_{j = 1}^{n} W_{ij} CLR_{jt} + \theta_{8} \mathop \sum \limits_{j = 1}^{n} W_{ij} FS_{jt} \\ & \quad + \theta_{9} \mathop \sum \limits_{j = 1}^{n} W_{ij} EI_{jt} + \theta_{10} \mathop \sum \limits_{j = 1}^{n} W_{ij} PEA_{jt} + \theta_{11} \mathop \sum \limits_{j = 1}^{n} W_{ij} EG_{jt} + \gamma_{i} + \eta_{i} + \mu_{it} \\ \end{aligned}$$

(19)

where HE is the HQDE and W_ijHE is the spatial lag term; ECR is energy consumption; PGDP is economic development level; IS is industrial structure; FI is level of foreign capital utilization; WER is environmental pollution; UR is of urbanization level; CLR is factor endowment; FS is financial support; and EI is educational support; PEA is public awareness of environmental protection; EG is enterprise green level. W_ij denotes the spatial weight matrix, W_ijHE_jt denotes the spatial autocorrelation between the dependent variable HE and the neighbouring city j, and α is its correlation coefficient. $\sum\nolimits_{j = 1}^{n} {x_{jt} }$ denotes the spatial spillover effect of the influencing factor x on city j, and θ is its correlation coefficient. i and j denote the different cities, t denotes the year, γ_i denotes the time effect, η_i denotes the spatial effect, and μ_it denotes the random error term, which obeys the normally distributed random error term.

Study area and data sources

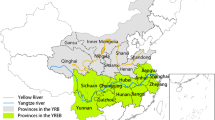
In this study, 75 prefecture-level cities in the YRB were chosen as the study subjects, as shown in Fig. 1. The data span from 2012 to 2022 and were obtained from the China Urban Statistical Yearbook, the Provincial Statistical Yearbook of 8 provinces in the YRB, and the China Urban Construction Statistical Yearbook. Some missing data were filled in using multiple interpolation and random forest methods. For regional comparison, the YRB is divided into three parts: upstream, midstream, and downstream. The upstream includes the cities of Xining, Guyuan, Shizuishan, and Wuzhong, totaling 21 cities. The middle reaches include the cities of Ankang, Baoji, Hanzhong, and Shangluo, totaling 30 cities. The downstream includes Anyang, Hebi, Kaifeng, Puyang, and other cities, totaling 24 cities. The details are shown in Table 3.

Fig. 1

Location map of the Yellow River Basin and the three reaches. This map was created by the authors using ArcGIS software (version 10.2) (https://www.arcgis.com/).

Table 3 The division of prefecture-level cities in the upstream, midstream, and downstream of the Yellow River Basin.

Sichuan Province is located in the upper reaches of the YRB, but there are only a few areas in the basin, such as Ruoergai, where data are difficult to collect. Based on academic rigor, the data are not looked up. Compared with upstream areas such as Qinghai and Gansu, which have similar geographic locations and backgrounds, Sichuan Province has little influence in the HQD of the YRB and focuses mainly on the development of the Yangtze River Basin. Therefore, this paper does not study Sichuan Province. Although the current study discards a few cities in this Sichuan Province, it is a better guarantee for the scientificity of the whole study. However, the collection of data will be strengthened in future scientific research.

Results

Evaluation results of HQDE measurements in the YRB

Results of the static evaluation of the HQDE in the YRB

The measured and average HQDE value for each city in the YRB from 2012 to 2022 are shown in Appendix A. The average HQDE value for each watershed over the past eleven years is shown in Fig. 2. Overall, the change trend of the three river sections in the YRB is basically the same, with a “W”-shaped wave growth trend. At this stage, the cities in the YRB transformed from traditional rough economies to high-density economies, and the effect of resource utilization and economic development pattern adjustment was shown. And 2017–2022 is the 13th Five-Year Plan period of China’s development, and economic development has entered a new normal. Especially after the proposal of ecological protection and HQD of the YRB in 2019, the HQDE of the YRB in this stage increased under the influence of various aspects, such as the implementation of resource environment and regional development policies.

Fig. 2

Changes in the efficiency of high-quality development in the Yellow River Basin over the past eleven years.

Results of the dynamic evaluation of the HQDE in the YRB

This section continues to adopt the practice of Section "Results of the static evaluation of the HQDE in the YRB" by geometrically averaging the data in the time dimension and arithmetic averaging in the regional dimension, respectively. 2012 is the base period of this paper, and the MI index and its decompositions are all 1, so they are omitted. This paper geometrically averages the MI index and its decompositions (EC index and TC index) of the cities in the YRB for 11 years and gives the MI rankings, as shown in Fig. 3.

Fig. 3

MI, EC and TC indices and MI rankings of high-quality development efficiency in Yellow River Basin cities.

As shown in Fig. 3, the MI of all 75 prefecture-level cities shows a steady growth trend. Cities with larger MI rankings are mostly concentrated in provincial capitals and centres such as Jinzhong, Shangqiu, and Bayan Nur. From the perspective of technical efficiency, owing to their efficient resource allocation capacity and mature innovation system. By optimizing the combination of production factors and improving the efficiency of resource utilization, these cities have achieved a reduction in production costs and an increase in output efficiency. From the perspective of technological progress, provincial capitals and provincial central cities, as regional innovation centres, possess strong scientific research strength and technological innovation capabilities. These cities have been able to actively promote the transformation of the industrial structure, driving the improvement of total factor productivity.

The comprehensive evaluation of the efficiency dynamics after arithmetic averaging of the MI index and its factorization index is shown in Fig. 4. From the perspective of the whole basin, the MI index of the YRB showed a fluctuating and upwards trend from 2013 to 2022, with an annual average MI index of 1.132 and a growth rate of 4.59%. The MI index fluctuated greatly from 2013 to 2018, after which the changes in the MI index slowed as a whole and maintained a fluctuating growth trend. From the perspective of index composition, the change in EC was relatively smooth, with an annual average EC of 1.016 and an annual average growth rate of 0.85%, whereas TC had greater increases and decreases, with an annual average TC of 1.113 and an annual average growth rate of 2.97%. TC is significantly greater than EC is, indicating that technological progress is the main factor driving the growth of the MI index. That is, the application and popularization of new technologies is an important driver of MI growth.

Fig. 4

MI, EC and TC indices of the whole Yellow River Basin and sub-basins in the past decade.

In terms of sub-basins, the average annual MI indices of the upstream, midstream, and downstream regions were 1.13, 1.165, and 1.094, with average annual growth rates of 6.8%, 4.72%, and 4.39%, respectively. The growth of the upstream region is significantly higher than that of the midstream and downstream regions. The trends of MI and TC in the upper and lower midstream cities of the watershed are roughly in line with each other, while there are some differences in terms of EC. The driving force for the sustainable growth of the MI index is mainly technological progress. From 2012 to 2022, the slower growth of EC in the basin had little effect on the enhancement of the MI index, which also suggests that technological efficiency needs to be improved, i.e., the management mode needs to be innovated and improved.

Results of spatial correlation analysis on the HQDE of cities in the YRB

Global spatial autocorrelation analysis

In this work, the economic geography weight matrix is constructed on the basis of the geographic coordinates of the cities in the YRB, and the global Moran index values of the HQDE of 75 cities from 2012 to 2022 are measured, as shown in Table 4. The results show that the overall Moran index of the YRB is 0.384, the P value passes the test at the level of 0.01, and the Z value is greater than 1.96. There is a significant positive spatial correlation of the mean efficiency value of the cities in the YRB. In addition, the distribution of the HQDE of each city clearly shows high-value aggregation or low-value aggregation phenomena.

Table 4 Global spatial autocorrelation statements for the last eleven years.

As shown in Table 4, the P value of the Moran index is less than 0.05 in 2012–2018, and the Z-value is greater than 1.96, which is significant at the 0.05 level, in these years. The data indicate that there is a significant spatial correlation in the HQDE of cities in the YRB during these seven years. However, after 2018, the p-values are all greater than 0.05, and the significance level is low. Especially, the probability of its efficiency random distribution is as high as 84.4% in 2020, and the probability of the existence of spatial correlation is only 15.6%. Combined with the Moran index, the Moran index is greater than 0 in all years except 2020, indicating the existence of significant high-value aggregation or low-value aggregation characteristics. Second, the global Moran index shows a fluctuating downwards trend, indicating that the spatial correlation of the HQDE of cities in the YRB gradually weakens from 2012 to 2022. The reason for this may be that large cities and city clusters have comparative advantages in economic development, attracting many key resources, technologies, and labour to produce agglomeration effects. However, with the promotion of the “Belt and Road” and “supply-side reform,” the economic development of developed regions has led to the development of neighbouring regions, which has weakened the agglomeration effect.

Local spatial autocorrelation analysis

The study utilizes ArcGIS 10.6 software to carry out local autocorrelation analysis. The clustering results are shown in Appendix B, and the LISA agglomeration map is shown in Fig. 5.

Fig. 5

LISA agglomeration map of the efficiency of high-quality development of cities in the Yellow River Basin. This map was created by the authors using ArcGIS software (version 10.2) (https://www.arcgis.com/).

Figure 5 depicts the degree of spatial correlation of the HQDE of cities in the YRB in 2013, 2016, 2019, and 2022. Overall, the high-efficiency cluster cities were located mainly in Gansu Province and Ningxia Hui Autonomous Region in the upper reaches of the YRB. These cities have a relatively high concentration of resources and have implemented policies that include industrial restructuring and green development measures, which have contributed to HQDE. The region’s HQDE is more leading and resonant, with significant spatial dependence. The efficiency outliers, “high-low” and “low–high” cities, are located mainly in some cities in Gansu Province in the upper reaches of the Yellow River, some cities in Shaanxi and Shanxi Provinces in the middle reaches of the river, along with some cities in Henan Province in the lower reaches of the river. There is significant spatial heterogeneity in this region, with large differences in HQDE among cities. Some cities in these provinces are overly reliant on traditional industries and are still dominated by heavy industry and mining, and their industrial structures have not been sufficiently transformed, leading to lower HQDE. Cities with low-efficiency clusters are located mainly in Henan, Shanxi and Shandong Provinces in the lower reaches of the YRB. Owing to different stages of development and economic foundations, some cities in lower reaches of the YRB have large differences in development and relatively weak economic ties and cooperation, resulting in a low spatial dependence of HQDE.

In 2022, the local clustering characteristics of the HQDE of cities in the YRB are not significant. Cities in the YRB have different levels of economic development and development priorities. The HQDE measured by the Super-EBM model is the result of multiple input factors and the consideration of desired and non-desired outputs, is affected by various factors, such as economic efficiency and environmental efficiency, and does not converge because of a specific similar influencing factor in neighbouring regions. Therefore, the clustering effect of HQDE is not significant.

Results of the analysis of factors influencing the HQDE in the YRB

The results of the spatial measurement model test are shown in Table 5. The LM test was performed on the residuals under the OLS regression to verify the spatial dependence. The results show that the Moran’s I value passed the 1% significance level test. The estimated coefficients of the LM test and Robust LM test for both the spatial lag and spatial error models are significant, so the paper chooses the spatial Durbin model. LR and Wald tests were subsequently conducted, and the results revealed that they were significant at the 1% level, and the test results passed. The original hypothesis that “there is no serial correlation in the residuals of the model” was rejected, and the spatial Durbin model was not degraded. Therefore, this paper chooses the SDM to analyse the factors influencing HQDE in the YRB. The value of the Hausman test is 15.840, and the corresponding P value is 0.045, which passes the significance test at the 1% level, indicating that the fixed effect model should be chosen.

Table 5 Spatial measurement correlation test results.

Considering the test findings above, this study uses the spatial Durbin model with fixed effects. Using Stata 17.0 software, the thesis conducted regression analysis without considering the spatial impact on the HQDE of the cities in the YRB. It includes OLS regression, SDM regression analysis with individual fixed effects, time fixed effects, and double fixed effects. The outcomes are displayed in Table 6.

Table 6 Test results of the spatial panel model and spatial lag model.

On the basis of the calculation results of the OLS and SDM models, the following conclusions are drawn:

From the overall perspective, the regression coefficient of HE is 1.048 when time effects or individual differences are not taken into account, which is highly significant at the 1% level, indicating that there are significant spatial correlations and spillover effects of the HQDE of YRB cities. The spatial autoregressive coefficients of HE under time fixed and double fixed constraints are negative and significant at the 1% level. That is, the efficiency value HE has a negative spatial spillover effect without considering the time effect and the endowment differences between cities. This suggests that cities with stronger HQD may plunder resources or technology from neighbouring regions, and the uneven distribution of resources may lead to a decline in the efficiency of other regions or industries due to a lack of resources, resulting in a negative spatial spillover effect.

The results of the regression analysis indicate that energy consumption (ECR), economic development level (PGDP), public awareness of environmental protection (PEA), and enterprise green level (EG) have significant positive effects on HQDE, reflecting the key role of these factors in promoting HQD. The level of energy consumption is a direct reflection of industrialization and economic growth and does not necessarily have a negative effect, as higher energy consumption usually represents more dynamic economic activity, which in turn increases the overall HQDE. Higher level of economic development, public awareness of environmental protection, enterprise green level can effectively support higher-quality economic growth, promote sustainable regional development, and contribute positively to the increase in HQDE. The foreign investment utilization (FI), environmental pollution (WER), and education support (EI) have a negative impact on HQD, suggesting that these factors constrain the realization of HQD to some extent. Although foreign investment can bring capital and technology, overreliance on foreign investment may inhibit the innovation drive of local firms, limiting their ability to innovate on their own and lowering the overall HQDE. Educational support is generally considered to have a positive impact on the HQDE; however, the realization of HQD may also be indirectly constrained if educational inputs are insufficient or unevenly distributed. The impact of industrial structure (IS), urbanization level (UR), factor endowment (CLR), and financial support (FS) on HQDE is usually manifested as a long-term effect, and the effects are not directly reflected.

To further explore the robustness of the influencing factors, this paper uses three methods, namely, replacing the control variables, lagging the explanatory variables, and excluding the special year of the epidemic (2019–2022). The industrial structure directly reflects the intrinsic composition and development direction of the regional economy, and the differences in the industrial structures of different cities in the YRB may affect the resource allocation, technological progress, and production efficiency of each region. Therefore, this study chooses to replace the industrial structure to explore the robustness of the model. The regression results when replacing the control variables, lagging the explanatory variables by two periods, and excluding the special year of the epidemic are shown in the “Robustness (1),” “Robustness (2),” “Robustness (3),” and “Robustness (4)” columns, and the results are shown in Table 7. The results of the robustness test show that there is a discrepancy between the results of the significance of the influencing factors and the direction of the estimated coefficients and the above results, but the overall regression results are consistent with the above results, proving that the results are robust.

Table 7 Robustness test results.

Discussions and policy recommendations

Further discussions

HQD is an important strategic direction for the development of the YRB and China at present. In this context, clarifying the HQDE and driving factors of cities in the YRB is highly important for promoting the transformation, upgrading, and green development of cities in the basin. On the basis of previous studies on the level of HQD, this research further constructs the HQDE evaluation index system, which helps to quantitatively reflect the allocation efficiency and utilization effect of resources. Through the study of HQDE, the development status and effectiveness of economic and social fields can be comprehensively and accurately measured and assessed, the flow of resource allocation can be guided in a more efficient and sustainable direction⁶⁶, and a scientific basis for policy formulation can be provided. The study shows that the HQDE in YRB region has a general upward trend during 2012–2022. This is comparable to the results of the study on YRB development by Dou et al.⁶³.

Firstly, the value of urban efficiency in the YRB varies greatly (higher in the upstream area and lower in the middle and downstream areas) spatially, while it converges at the end of the study period, which is in line with the results of Zhang and Feng’s study⁶⁷. Specifically, the upstream area is better protected ecologically due to the abundance of natural resources and the low level of exploitation⁶⁸. Therefore, particular attention should be paid to the development of this area when formulating the HQDE policy⁶⁹. For the downstream region, the same advantages of HQD are evident because of its strong economic base and broad market⁷⁰. The midstream regions may lag behind in HQDE because of its relatively centralized geographical location, lack of resource advantages-upstream, and competitive pressure-downstream⁷¹.

Secondly, there is a geographical correlation between the HQDE values of the cities in the YRB and the clustering of efficient cities. The high-efficiency clusters of HQDE in the cities of the YRB are concentrated mainly in the upstream region of the YRB, and the low-efficiency clusters are concentrated mainly in the midstream and downstream regions of the YRB. This suggests that there is a need to propose different policies for HQDE in different regions. Owing to the large differences in resource endowment, economic structure, and development level among cities, different policy measures have different effects⁷². Therefore, integrating high-quality urban development into the development efficiency model and proposing appropriate development strategies for different cities are crucial for realizing comprehensive and green development. This conclusion is consistent with the studies of Shang and Xue, who suggested that different cities should take advantage of each other’s strengths in order to formulate development strategies that are both realistic and able to stimulate their inner potential⁷³.

Notably, there is a negative spatial spillover effect on the HQDE values of the cities in the YRB, and the research results are similar to those of Fang⁷⁴. This means that a city’s HQDE is affected not only by its own factors but also by the development of neighbouring cities or regions. Because of the fierce resource competition among cities in the upper, middle, and lower YRB regions, which leads to frequent overexploitation of resources and ecological damage, the HQD of a city will limit the HQD of neighbouring regions. Achieving coordinated interregional development by weakening this negative spatial spillover effect is a practical solution for enhancing the HQDE of cities. Meanwhile, Li et al. have revealed that negative spatial spillovers should be minimized to achieve a shift from “non-Pareto improvements” to “Pareto improvements,” which promotes high-quality urban development⁷⁵.

Thirdly, considering both time and space effect conditions, the level of economic development is an important factor influencing the HQDE of YRB. The improvement of the level of economic development has a positive impact on the high-quality development of the Yellow River Basin, which is consistent with the viewpoint of Li et al.⁷⁶. Specifically, economic development not only promotes industrial upgrading and optimizes resource allocation but also enhances the economic strength of the regions in the basin, providing a solid material foundation for ecological protection and infrastructure construction⁷⁷. The positive impact of this solid material foundation on promoting high-quality development has also been confirmed in the field of agriculture⁷⁸. In addition, the improvement of the level of economic development will also increase the investment in the governance and protection of the watershed, promote the restoration of ecosystems and the improvement of environmental quality, and inject a lasting impetus for the high-quality development of the Yellow River Basin⁷⁹. Therefore, accelerating economic development is one of the key paths to promote the high-quality development of the Yellow River Basin⁸⁰.

Fourthly, factor endowment is also an important factor affecting the HQDE in the YRB. This shows that the upgrading of the factor endowment structure can optimize resource allocation, improve production efficiency and innovation capacity, inject strong momentum for HQD, and promote sustained and healthy economic growth⁸¹. In addition, the upper reaches of the YRB are rich in resources, while the middle and lower reaches are more densely populated and have frequent economic activities. This difference in regional factor endowment has caused regional differentiation in the level of economic development and also led to diversity in the efficiency of high-quality urban development⁸². Therefore, when exploring how to achieve HQD in the YRB, we find that optimizing the structure of factor endowment has become a key strategy to promote the region towards HQD.

Additionally, educational support is another key factor affecting HQDE in the YRB. Education support theoretically has a potential positive effect on the HQDE in the YRB. However, due to the lagging of education investment⁸³ and the role of irrational education expenditure structure⁸⁴, education investment can also show a negative effect. On the one hand, the strategic development status of the YRB is relatively secondary, and the impact of education investment on regional development has a lag. Compared with the coastal and other developed cities, it is not very attractive to excellent talents, so the loss of talents makes the positive effect of education not shown⁸⁵. On the other hand, it may be due to the irrational structure of education expenditure, redundancy, or imbalance, which leads to the low conversion rate of education investment, thus restricting the HQD of the YRB⁸⁶. Therefore, strengthening educational support, optimizing the allocation of educational resources, and improving the quality of education are important issues that must be addressed to achieve HQD in the YRB.

Policy recommendations

In conjunction with the above discussion, the following policy recommendations are proposed:

Firstly, implementing differentiated HQDE strategies regionally. The government should formulate targeted policies based on the specific development stages of different regions and cities in the YRB in order to reduce regional differences in HQDE. In upstream regions of the Yellow River, the core of the strategy should be to enhance technological innovation capacity. It should focus on supporting the development of green industries and the application of intelligent technologies, optimizing the industrial structure, and promoting the synergistic development of efficient resource use and ecological protection. In the middle and down reaches, the government should increase financial and policy support and prioritize infrastructure development and environmental governance. It should also strengthen investment in education, science and technology innovation, and ecological protection to enhance the quality and sustainability of regional economic development.

Secondly, strengthening regional coordination and development mechanisms. Through the establishment of a cross-regional resource-sharing platform and coordination mechanism, it will reduce resource competition and negative spatial spillover effects among cities and promote synergistic regional economic development. Meanwhile, it will optimize resource allocation and reduce the damage to the ecological environment caused by over-exploitation of resources.

Thirdly, implementing differentiated resource allocation policies. The upper reaches of the YRB should make full use of their resource advantages and develop resource-intensive industries while focusing on the economical and efficient use of resources; the middle and lower reaches need to optimize their population and economic layout and improve the quality of their populations and economic vitality. The government should also strengthen regional cooperation, and promote the free flow and optimal allocation of factors between regions, so as to achieve coordinated regional economic development.

Fourthly, improving the quality of education. Cultivate more high-quality talents and guide the flow of talents to the YRB to provide intellectual support for regional development. At the same time, the government should also adjust the structure of education expenditure, reduce redundancy and imbalance, and improve the conversion rate of education investment, so as to provide a strong guarantee of talents for the HQD of the YRB.

Conclusion

On the basis of the panel data of 75 cities in the YRB from 2012 to 2022, this paper constructs an HQDE evaluation system and analyses the spatiotemporal characteristics of HQDE in the YRB. This study uses a spatial econometric model to analyse the factors influencing HQDE in the YRB and conducts a robustness test. The following conclusions are obtained:

First, the HQDE in the YRB shows a fluctuating upwards trend, with prominent HQDE in the upstream and downstream reaches of the YRB, lower HQDE in the middle reaches, significant regional differences, and a spatial distribution pattern of “high in the east and low in the west.” In addition, the improvement in the HQDE in the YRB is more dependent on the degree of technological progress, while the role of technological efficiency is smaller. Second, there is a significant spatial correlation of HQDE in the YRB as a whole, but the spatial agglomeration characteristics between cities are gradually weakening. Moreover, there is spatial dependence of HQDE among cities in the basin, with HH agglomerations being concentrated mainly in the upstream basin region of the Yellow River, whereas LL agglomerations are located mainly in the midstream and downstream basin regions. Third, the HQDE of the YRB is affected by a variety of driving factors, such as economic development level, factor endowment, and educational support, which significantly influence the HQDE of the YRB.

The HQDE evaluation and analysis framework proposed in this paper can be used as a tool for governments and scholars to monitor HQDE. The selection of input–output indicators and their influencing factors can also provide a reference for future research. This study has several limitations. For example, there are limitations in the evaluation indicators of HQDE and influencing factors, which are reflected in the fact that this paper does not analyse in depth the differences in endowments of cities in the YRB. In addition, owing to the difficulty of data collection, only the HQDE levels of eight provinces in the YRB are studied; thus, a comprehensive evaluation of the HQDE of the YRB region as a whole is lacking.