Global and local path planning of robots combining ACO and dynamic window algorithm

Abstract

As a key technology, robot path planning is of great significance in safely and efficiently completing tasks. However, faced with the challenges of static and dynamic obstacles in complex environments, traditional path planning methods have limitations in terms of efficiency and adaptability. Therefore, a global and local path planning method combining improved ant colony algorithm and improved dynamic window algorithm is proposed. The optimization ability, convergence efficiency, and obstacle avoidance performance are optimized in complex environments. The innovation is reflected in the proposed cone pheromone initialization, adaptive heuristic factor regulation, and ant colony division of labor strategies, which improve the global search ability and convergence speed of ant colony algorithm. In addition, the path direction angle evaluation function and dynamic velocity sampling optimization are introduced to enhance the obstacle avoidance stability of dynamic window algorithm. The research results showed that the optimization method had the greatest improvement on the basic ant colony algorithm, with an average path reduction of 30.18 and an accuracy increase of 98.46%. In a 20*20 grid map, the improved strategy achieved convergence in the 23rd iteration, with an average path length of only 25.87 during convergence. In a 30*30 grid map, the improved method converged in the 81st iteration, and the path length at convergence was 41.03. In the designed four environments, the smoothness was 0.94, 0.91, 0.79, and 0.65, all of which were better than comparison algorithms. The designed method based on improved dynamic window algorithm can effectively avoid dynamic obstacles. The research not only improves the efficiency and robustness of the path planning algorithm, but also improves the autonomous navigation ability of robots in complex environments, providing more adaptive path planning schemes for industrial automation, service robots, exploration robots and other fields.

Introduction

In today’s society, innovative technologies emerge endlessly, which greatly promote social progress and industrial transformation¹. Robot technology covers many fields such as mechanical engineering, electronic engineering, computer science, and artificial intelligence. For a long time, it has been a key force driving progress in fields such as industrial automation and intelligent manufacturing^2,3. As a core component of robot technology, robot path planning can ensure the safety of robots during task execution, avoid collision with obstacles, and improve the working efficiency⁴. In addition, in a multi-robot system, excellent path planning mechanism can ensure the cooperative work among robots and avoid mutual interference⁵. However, faced with a complex environment, the combination of static and dynamic obstacles puts forward higher requirements for robot path planning⁶. In addition, the robot needs to find the shortest path from the starting point to the end point in a complex static environment. Moreover, when the robot encounters dynamic obstacles, it also needs to quickly re-plan the path to avoid collision^7,8. Traditional robot path planning methods typically rely on accurate maps. It is difficult to maintain the accuracy of the map in the dynamic changing environment. In addition, faced with dynamic obstacles, traditional methods often fail to re-plan paths in time, resulting in increased collision risk⁹. Therefore, the global optimization and local obstacle avoidance problems of robot path planning in complex environment are explored. A two-layer path planning scheme combining Ant Colony Optimization (ACO) and dynamic window algorithm is proposed. The research aims to improve the autonomous navigation ability of robots in static and dynamic environments, and improve the computational efficiency, accuracy and robustness of path planning. The contribution of the research is to improve the ant colony algorithm to support multi-objective optimization and enhance the global search ability, and optimize the dynamic window algorithm to improve the adaptability of the robot to dynamic obstacles. In addition, the advantages of the proposed method in path length, accuracy, and convergence speed are verified through rich experiments, which provide technical support for the application of robots in industrial automation, intelligent transportation, and service robots.

The research is divided into four sections. First, the global robot path planning literature is reviewed to lay the theoretical foundation. Second, the path planning method of improved ACO and dynamic window algorithm is introduced, and its optimization strategy in static and dynamic environment is emphasized. Then, the effectiveness of the proposed method is verified by experiments, and the path length, accuracy, and convergence speed are analyzed. Finally, the research results are summarized, shortcomings are pointed out, and future research directions are proposed.

Related works

Robot path planning is a core issue in the robot technology, which is related to whether robots can efficiently and safely complete tasks. The application of robots is constantly expanding, from manufacturing to service industries, to healthcare, agriculture, exploration, and even households. Robot path planning has attracted more attention from scholars. Aiming at the hierarchical Dubins for multiple unmanned aerial vehicles, J. Fu et al. proposed a multi-layer projection clustering algorithm for unmanned aerial vehicles to reduce the cumulative distance from the target to the cluster center. A straight-line flight judgment method was developed to reduce the computational amount of obstacle avoidance, and improve the adaptive window probabilistic road map algorithm for obstacle avoidance path planning. Combining ant colony system with homotopy probability roadmap framework, the travel agent problem with obstacle constraints was solved¹⁰. P. N. Srinivasu et al. built a temporal difference strategy based on reinforcement learning combined with probability road-map and inverse kinematics methods for precise path planning and real-time workspace mapping in robot assisted surgery. This method optimized the path planning length, improved the surgical efficiency, and promoted the application in the medical field¹¹. J. Qi et al. proposed a multi-objective dynamic fast exploration stochastic strategy based on path designed generation and quadratic programming for robot navigation in unknown dynamic environments. This algorithm could quickly select the best node among candidate nodes while considering path length and smoothness, thereby improving the success rate of robots avoiding unknown obstacles¹². B. Sangiovanni et al. designed a mixed control method to achieve full body collision avoidance in humanoid robot manipulators. A specially trained deep reinforcement learning method was introduced for obstacle avoidance. The traditional motion planning algorithm was improved, effectively achieving collision avoidance¹³. Aiming at the environmental information collection efficiency of intelligent vehicles in unknown scenarios, Y. Xu et al. proposed a hierarchical online information path planning framework that included global action optimization and local path planning. In particular, a lightweight kernel-based Bayesian optimization method was proposed to facilitate efficient information utility evaluation and control action decision making¹⁴. J. Fu et al. proposed a trajectory homotopy optimization framework for dynamic penetration mission planning of multiple unmanned aerial vehicles under hostile obstacles and perceptual constraints. A time-varying mechanism was constructed to adapt to the delayed updates of unknown target search and dynamic trajectory planning, using Gaussian probability fields to predict enemy positions. The dynamic window probabilistic road map method was designed to shorten the planned path. Moreover, a penetration strategy algorithm based on decision tree was developed. The multi-coupling homotopy trajectory was introduced to optimize dynamic obstacle avoidance¹⁵.

In addition, Y. Yang proposed a deep Q-network algorithm to address the multi-robot path planning in unmanned warehouse sorting systems. The Q-learning algorithm, experience replay mechanism, and capacity technology of productive neural networks were combined to obtain target Q-values, reducing randomness in robot path planning and improving the efficiency of multi- robot path planning¹⁶. U. Orozco-Rosas et al. built a learning algorithm that combined Q-learning and artificial potential field approach to address the low efficiency of feasible path planning. The artificial potential field improved the slow convergence speed of Q-learning, effectively enhancing efficiency and path smoothness¹⁷. R. Sarkar et al. built an optimized Genetic Algorithm (GA) based on domain knowledge for the application of GA in robot path planning. Four new genetic operators were used to solve path planning problems with a single objective, effectively improving the accuracy and efficiency of robot path planning while improving the performance of GA¹⁸. P. G. Luan et al. built a novel mixed GA to address the low smoothness in global path planning for robots. The mutation operator was provided with a dynamic mutation rate and a switchable global local search strategy to solve premature problems, reducing computational cost, effectively enhancing path smoothness, and improving efficiency¹⁹.

In summary, existing research has made significant progress in robot path planning, but there are still some limitations. Although reinforcement learning has adaptive capabilities, the convergence speed is slow and its generalization ability to large-scale environments is limited. The optimization-based method performs well in global path planning, but lacks flexibility in dynamic environment and is difficult to adjust the path quickly. Genetic algorithm and probabilistic road map can improve the search efficiency, but there are often problems such as high computational cost and insufficient path smoothness. In addition, most studies have only optimized for specific application scenarios and lack comprehensive adaptability in complex environments. Therefore, a robot path planning method combining ACO and DWA is designed. The study utilizes an improved ACO algorithm for global planning in static environments and a DWA for local planning in dynamic environments. Then, the two methods are organically combined to achieve effective obstacle avoidance and reasonable path planning for robots, which is innovative.

Methods

This section proposes a robot path planning method that combines improved ACO and DWA. Global and local planning strategies are optimized to adapt to static and dynamic environments. This method first utilizes the optimized ACO for global path planning in static environments. Then, the DWA is taken to achieve local obstacle avoidance in dynamic environments, ultimately achieving efficient and safe navigation of robots in complex environments.

Global planning for static environment based on improved ACO algorithm

In a static environment, the obstacle on the robot’s action path remains fixed. When planning the path, a path to the destination can be pre-calculated without frequent updates²⁰. The problem that needs to be considered at this point is how to plan the path to make it the most time-saving and stable problem. Therefore, the study utilizes the ACO to achieve path planning for robots in static environments. The ACO is a heuristic search algorithm that simulates the foraging behavior of ants. It has global optimization capability, which can effectively find the optimal path from the initial position to the endpoint. In addition, the ACO is easy to implement and supports parallel processing, which is suitable for multi-objective optimization problems in global planning. It can improve decision quality by integrating heuristic information^21,22. However, the basic ACO may not be able to escape from local optima due to insufficient randomness or inappropriate pheromone updating strategies, or may lack effective alternative paths for robots when facing obstacles or enclosed areas due to insufficient population diversity²³. Therefore, the study aims to optimize the ACO from multiple aspects, as shown in Fig. 1.

Fig. 1

Improved strategy of ant colony optimization algorithm.

In Fig. 1, the basic ACO is optimized from six aspects. First, pheromone initialization optimization uses cone pheromone distribution to enhance pheromone concentration around target points and accelerate path search. Second, adaptive heuristic factor adjustment can enhance exploration in the early stage and accelerate convergence in the later stage by dynamically adjusting pheromone heuristic factor and expectation heuristic factor. Third, the ant colony partitioning mechanism introduces the division of labor between soldier ants and ant kings to improve search range and convergence efficiency. Fourth, the deadlock detection and rollback strategy records the deadlock area through the tabu table, and sets the rollback mechanism to ensure that the search is not blocked. Fifth, the path smoothing process uses cubic B-spline curve to reduce the path transition and improve the motion smoothness. Finally, the optimization algorithm process is combined with the aforementioned improvements to adjust the execution sequence of the ACO algorithm, so that each optimization strategy can cooperate with each other to achieve efficient and stable path planning.

The first one is pheromone initialization. When the ACO starts running, there are no pheromones in the initial static environment map. Ants will choose nodes closer to themselves or the target node. As the iteration progresses, ants gradually leave pheromones on certain paths, attracting more ants²⁴. However, this process is time-consuming and difficult for ants to fully explore the entire solution space. Therefore, the cone shaped pheromone initialization distribution method is used to modify the pheromone distribution in the static environment initial map, as shown in Eq. (1)²⁵.

$${\tau _0}=\frac{{0.09*\left| {x - y} \right|}}{{len}}+\frac{1}{d}$$

(1)

In Eq. (1), ${\tau _0}$ represents the initial node pheromone concentration. x and y respectively represent the horizontal and vertical coordinates of nodes in the map. $len$ represents the length of the map grid. d represents the Euclidean distance, where the object is a node and a target point. 0.09 is the optimal parameter for changing pheromone initialization, which is obtained from multiple experiments. Equation (1) uses $\frac{{0.09*\left| {x - y} \right|}}{{len}}$ to achieve cone diffusion of pheromones from the initial position to the target position. $\frac{1}{d}$ is taken to enhance the pheromones near the target point, preventing the algorithm from converging too early or not converging for a long time when searching for the target point. The second optimization focuses on the heuristic factors in the ACO algorithm, involving Pheromone Heuristic Factor (PHF) and Expected Heuristic Factor (EHF). The former represents the relative importance of pheromone concentration in ant path selection, while the latter represents the importance of heuristic information (such as the reciprocal of path length) in ant path selection. If both heuristic factors are set too high, the algorithm may prematurely focus on certain paths, leading to rapid convergence to the local optimal solution rather than the global optimal solution. Conversely, if both heuristic factors are set too low, the algorithm may randomly walk in the solution space and find it difficult to converge to any optimal solution^26,27. Therefore, an adaptive heuristic factor is proposed, as shown in Eq. (2).

$$\left\{ \begin{gathered} \alpha ^{\prime} = \alpha + \varsigma \int_{0}^{{\frac{n}{N}}} {Timd\left( {Tim} \right)} \hfill \\ \beta ^{\prime} = \beta + \xi \int_{{0.}}^{{\frac{n}{N}}} {Timd\left( {Tim} \right)} \hfill \\ \end{gathered} \right.$$

(2)

In Eq. (2), $\alpha$ and $\beta$ signify PHF and EHF before adaptive processing. $\alpha ^{\prime}$ and $\beta ^{\prime}$ signify PHF and EHF after adaptive processing. $\varsigma$ and $\xi$ represent adaptive adjustment coefficients of PHF and EHF, respectively. $Tim$ represents the time factor. n and N represent the current number of iterations and the maximum number of iterations, respectively. In the early stages, the number of iterations is small and the upper limit of integration is small, resulting in lower integration values. Therefore, the increment of PHF and EHF after adaptive adjustment is relatively small. This means that PHF and EHF do not change much, allowing pheromone concentrations to remain low, improving the search randomness and avoiding premature convergence of ants to the local optimal solution, and increasing the likelihood of understanding. In the later stage, the number of iterations increases and the upper integral limit becomes larger, which increases the integral value and leads to the gradual increase of PHF and EHF after adaptive adjustment. This means that PHF and EHF are increased, making the role of pheromones more pronounced, reinforcing the preference for a better path, and accelerating convergence. The third optimization focuses on ant colony division of labor. Obstacles in a static environment divide the robot path into different spatial blocks. The optimization ability of a single ant colony is limited in this complex environment²⁸. Therefore, the social division of labor in natural ant colonies is introduced to improve the adaptability and path planning efficiency of ant colonies through different types of ants to perform different tasks. The ant colony is divided into two categories: soldier ant and ant king. The soldier ant is mainly responsible for global path exploration, which has strong randomness and can widely sample path space at the initial search stage to avoid the algorithm falling into local optimal. The ant king is responsible for path optimization and decision making. Its main role is to enhance pheromone guidance, improve path quality, and accelerate convergence. Therefore, in the early stage, a high ratio of soldiers indicates a wide search range and more diverse solutions. In the later stage of the algorithm, the proportion of ant king is gradually increased to strengthen the path optimization and improve the planning stability and efficiency. The ratio between the soldier ant and the ant king is shown in Eq. (3).

$$\Lambda =\frac{{{S^2}}}{{{S^2}+{\theta ^2}}}$$

(3)

In Eq. (3), $\Lambda$ represents the probability of ants transitioning from soldier to ant king ant, which occurs when ants perform convergence tasks. S represents the environmental stimuli that affect ants’ response to specific tasks. $\theta$ represents the sensitivity of ants to task requirements, which is used to determine whether ants should start performing convergence tasks. S and $\theta$ are shown in Eq. (4).

$$\left\{ \begin{gathered} S=\sqrt {2\int_{2}^{{\frac{n}{N}}} {Timd\left( {Tim} \right)} } \hfill \\ \theta =1 - \frac{{\sqrt {\frac{{\sum\limits_{{k=0}}^{m} {\left( {{D_k} - D} \right)} }}{m}} }}{D} \hfill \\ \end{gathered} \right.$$

(4)

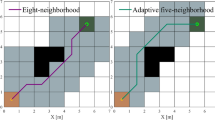
In Eq. (4), ${D_k}$ signifies the path length of the k-th ant. m represents the total number of ants. D represents the average value of the path in all solutions. According to Eq. (4), if S is low, $\Lambda$ is low. The probability of ants changing their identity is low, that is, there are more soldier ants in the ant population, which increases the search range. As the iteration progresses, the S value increases and the $\Lambda$ value also increases, which means that more queens will appear in the ant colony, thereby improving the convergence speed. The fourth optimization focuses on deadlock issues, as shown in Fig. 2.

Fig. 2

Deadlock problem and optimization.

From Fig. 2 (a), when the searching ant encounters a concave obstacle, the ant cannot move forward or search left and right to reach the target point, entering a deadlock state. At this point, when the algorithm detects the surrounding state of ants to confirm that they are in a deadlock, it will set a rollback strategy. Meanwhile, during the rollback process, ants will mark the grid areas that cause deadlocks as tabu areas and load them into the tabu table. Once the ant successfully escapes the deadlock and updates the tabu list, it will continue to perform the search task. However, if the ant falls into a deadlock again due to tabu list restrictions, it will abandon the current search path and set its path as the average value of the paths found by all ants in this iteration. The fifth optimization focuses on smoothing the path. Due to the rasterization of the map and the irregularity of obstacles, the planned path has multiple turning points, making it difficult for robots to move at larger turning points²⁹. Therefore, a cubic B-spline curve method is proposed, determining a series of control points that define the basic curve shape. The control points are adjusted to change the curve shape. Therefore, the smoothed turning points are reduced, the route is shorter, and the quality is better. The sixth optimization summarizes these first five optimizations and improves the algorithm process of basic ACO. Therefore, the optimized ACO flow is shown in Fig. 3.

Fig. 3

Schematic diagram of the optimized ACO flow.

As shown in Fig. 3, after the algorithm starts, the tabu table used to solve the deadlock problem is first initialized. Simultaneously, parameters including pheromones, PHFs, and EHFs are initialized. Subsequently, ants are placed. After completing the division of labor according to the ant colony division strategy, ants search for paths and select the next node. During this process, if the ant encounters a deadlock problem, the grid is marked and the search is abandoned, returning to the ant placement phase for the next search. If there is no deadlock, the pheromone will be updated after completing this search. After completing an iteration, the number of iterations is increased by one. When the maximum iteration is reached, the optimal path is obtained and smoothed to improve the ACO. The improved ACO enhances the pheromone concentration around the target point through cone pheromone initialization, accelerates the initial search efficiency, adapts the inspired factor adjustment to increase the exploration range in the early stage, avoids premature convergence, accelerates optimization in the later stage, and improves the search stability. Moreover, the ant colony division mechanism increases the ratio of soldiers in the initial stage of search to improve the path diversity, and increases the proportion of ant kings in the later stage to accelerate the convergence speed and reduce the algorithm oscillation. The improved ant colony algorithm optimization strategy has increased some computational complexity, such as pheromone updates and path smoothing. However, due to the improved overall convergence speed and reduced overall computation time, it still maintains high computational efficiency in complex environments.

Local planning on the ground of dynamic window algorithm for dynamic environment

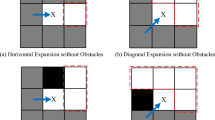
Global path planning enables robots to avoid obstacles and find the optimal path from the initial position to the endpoint in a known static condition. It is usually completed offline, that is, the path calculation is completed before the robot executes the task³⁰. However, static environments can only exist in ideal states. In the real world, the environment is often dynamically changing, with moving obstacles, human, temporarily closed areas, or other unpredictable factors appearing randomly³¹. Therefore, based on the global planning in static environments, the DWA is utilized to achieve local planning. Specifically, global path planning is used to provide robots with a rough task execution direction and target position. Then, local path planning ensures that the robot can respond to changes in real time while maintaining the global goal and safely avoiding obstacles. However, the traditional DWA suffers from path deviation issues. Therefore, it is optimized, as shown in Fig. 4.

Fig. 4

Deviation phenomenon and improvement measures of traditional dynamic window algorithm.

From Fig. 4 (a), the path deviation problem refers to the deviation between local paths and global distances when using DWA to handle dynamic obstacles. In severe cases, it may even turn the optimal path into a non-optimal path. In Fig. 4 (b), the traditional DWA is mainly improved by adding a path direction angle evaluation function. This function can effectively consider the angle difference between the local and the global, enabling the robot to quickly adjust its posture and return to the global path after avoiding dynamic obstacles. The path direction angle evaluation function $Ghead$ is shown in Eq. (5)³².

$$Ghead={180^ \circ } - \vartheta$$

(5)

In Eq. (5), $\vartheta$ represents the angle difference, which is the angle between the center-line of the robot in the local path and the tangent line of the nearest point in the global path direction. The path direction angle evaluation function $Ghead$ is used to measure the Angle difference between the local path and the global path. If the value is large, it indicates that the local path deviates far from the global path, and the trajectory needs to be adjusted to make the robot return to the global path direction as soon as possible. The trajectory evaluation function G in traditional DWA is shown in Eq. (6).

$$G=\varepsilon \left( {a \cdot H+b \cdot D+c \cdot V} \right)$$

(6)

In Eq. (6), $\varepsilon \left( \cdot \right)$ represents the normalization processing function. H represents the robot azimuth evaluation function. D signifies the average distance function between the robot and obstacles. V represents the evaluation function of robot speed. a, b and c respectively represent the weight values of the corresponding three evaluation functions. Therefore, by adding the path direction angle evaluation function $Ghead$ to the trajectory evaluation function G, an optimized trajectory evaluation function is obtained, as displayed in Eq. (7).

$$G^{\prime} = \varepsilon \left( {a \cdot H + b \cdot D + c \cdot V + d \cdot Ghead} \right)$$

(7)

In Eq. (7), d represents the weight of the evaluation function $Ghead$. The improved DWA controls the robot velocity instead of directly controlling its position in space. The velocity space is displayed in Fig. 5.

Fig. 5

Velocity space of the improved dynamic window algorithm.

In Fig. 5, ${V_a}$ represents the velocity space. ${V_d}$ represents the speed that can reach space. ${V_s}$ represents the speed sampling space. ${V_r}$ represents the actual speed. The constraint of the velocity sampling space ${V_s}$ is shown in Eq. (8).

$${V_s}=\left\{ {\left( {v,\omega } \right)\left| {v \in \left[ {{v_{\hbox{min} }},{v_{\hbox{max} }}} \right],w \in \left[ {{w_{\hbox{min} }},{w_{\hbox{max} }}} \right]} \right.} \right\}$$

(8)

In Eq. (8), v and $\omega$ signify the robot velocity and angular velocity. ${v_{\hbox{min} }}$ and ${v_{\hbox{max} }}$ signify the minimum and maximum velocities limited by the robot hardware. Similarly, ${w_{\hbox{min} }}$ and ${w_{\hbox{max} }}$ respectively signify the minimum and maximum angular velocities under hardware limitations. The velocity that can reach space ${V_d}$ is shown in Eq. (9).

$${V_d}=\left\{ {\left( {v,\omega } \right)\left| {v \in \left[ {{v_c} - {{\dot {v}}_b}{T_d},{v_c}+{{\dot {v}}_a}{T_d}} \right],w \in \left[ {{\omega _c} - {{\dot {\omega }}_b}{T_d},{\omega _c}+{{\dot {\omega }}_a}{T_d}} \right]} \right.} \right\}$$

(9)

In Eq. (9), ${v_c}$ represents the current linear velocity. ${\omega _c}$ represents the current angular velocity. ${\dot {v}_b}$ and ${\dot {v}_a}$ respectively represent the maximum linear deceleration and maximum linear acceleration that the robot can achieve, that is, the maximum linear velocity that the robot can reduce and the maximum linear velocity that it can increase per unit time. ${\dot {\omega }_b}$ and ${\dot {\omega }_a}$ respectively represent the maximum angular deceleration and maximum angular acceleration that the robot can achieve. ${T_d}$ represents the sampling period, which is the time interval between the robot control system updating status and making decisions. ${V_a}$ is shown in Eq. (10).

$${V_a}=\left\{ {\left( {v,\omega } \right)\left| {v \leq \sqrt {2 \times dist\left( {v,\omega } \right) \times {{\dot {v}}_b}} \cap w \leq \sqrt {2 \times dist\left( {v,\omega } \right) \times {{\dot {\omega }}_b}} } \right.} \right\}$$

(10)

In Eq. (10), $dist\left( {v,\omega } \right)$ signifies the distance between the trajectory end and the nearest unknown dynamic obstacle. Equation (10) ensures that the distance between the predicted trajectory end and the obstacle must exceed a certain safety threshold. If the distance is below the safety threshold, it is considered unsafe. It needs to be excluded from a set of feasible velocity vectors³³. Combining ${V_s}$, ${V_d}$, and ${V_a}$, ${V_r}$ is obtained, as shown in Eq. (11).

$${V_r}={V_s} \cap {V_d} \cap {V_a}$$

(11)

In Eq. (11), ${V_s}$ defines the velocity range that the robot can sample under kinematic constraints, including the maximum and minimum values of linear and angular velocities. ${V_d}$ considers the current velocity and acceleration/deceleration ability, which defines the velocity range that the robot can actually reach in the next moment. Based on safety constraints, ${V_r}$ defines the velocity range that robots can adopt while avoiding collisions. Therefore, each velocity vector in ${V_r}$ must meet the requirements of kinematics, motor performance, and safety. Within the dynamic window ${V_r}$, the robot can sample multiple velocity pairs $\left( {v,\omega } \right)$ and predict the running trajectory for a certain period of time at these velocities based on the kinematic model. The improved DWA restrains the local path deviation by evaluating the path direction angle, which makes the robot quickly return to the global path direction after obstacle avoidance, and improves the trajectory stability. Moreover, the sub-items of the global path guide the robot to keep a reasonable motion direction and avoid the local optimal problem. Dynamic speed sampling optimization adjusts the speed window according to environmental changes, improves obstacle avoidance flexibility, and makes the path smoother. The additional calculation mainly involves the path direction angle evaluation and sub-item point search, and the calculation complexity does not change much. It can improve the path quality while maintaining good real-time performance, ensuring the reliability of the planning algorithm in dynamic environments.

Finally, the study combines global planning based on improved ACO with local planning based on DWA to obtain the robot global and local path planning method. The method flow is shown in Fig. 6.

Fig. 6

Robot global and local path planning process.

From Fig. 6, the improved ACO is first used to carry out global path planning on the raster map. The global path drives local planning through two core mechanisms. One is to set subentry punctuation sequence at the turning point of the path to provide heading reference for the dynamic window algorithm. The other is to embed the path direction angle evaluation function into the trajectory evaluation system of DWA. To provide phased objectives for local path planning, this research explores setting subtitle points on the global path to correspond to turning points on the path. Then, DWA is used for local path planning of each small segment of the robot on the global path, dynamically avoiding sudden dynamic obstacles under velocity space constraints, and generating collision free trajectories in real time. Moreover, it can also ensure consistency between the direction of motion and the global path, to ensure that the robot can safely move along the global path to adjacent sub-items. The robot follows a planned local path, gradually moving to each sub-point and checking at each point whether it has reached its final destination. If it reaches the final destination, the plan ends and the task is executed. If not, the process continues along the path until the entire path is complete. By integrating global and local planning methods, this paper makes the robot realize accurate and reliable path planning and autonomous navigation in complex environments.

It is worth noting that when the interference of dynamic obstacles causes the original planned global path to fail, the system will trigger the global path re-planning mechanism to ensure that the robot can continue to move to the target point. Specifically, when DWA detects that a local path cannot bypass obstacles, or when the feasibility of the global path decreases (for example, when a sub-entry point deviates three times in a row, or when the path cost exceeds 50% of the original path), the tabu table mechanism will record the currently impassable area and send a re-planning request to the ACO algorithm. The ACO algorithm performs incremental re-planning based on existing path information, adjusting some paths to adapt to new environmental changes without the need to calculate the entire path from scratch, and improving computational efficiency. After the global path is updated, the system resets the sub-target point sequence, and DWA executes a new local path planning, allowing the robot to continue moving along the adjusted path.

Results

To analyze the effectiveness and superiority of the designed method, this section performs experiments on the improved ACO, and path planning for robots. The experimental content contains comparative experiments, ablation experiments, etc.

Performance verification and analysis of improved ACO algorithm

Before the experiment, the experimental configuration and robot parameters are introduced, as displayed in Table 1.

Table 1 Experimental configuration and settings.

From Table 1, MATLAB and PYTHON are used as the main tools for simulation experiments. In the ROS-based inspection robot path planning simulation experiment, the Ubuntu 18.04 is selected as the dependency system for ROS, and GAZEBO and RIVZ software are installed. A robot model constructed by McNaum’s base plate is built in GAZEBO, and RIVZ software is used for 3D visualization to display the motion data, radar data, and environmental data from robots. The improved ACO adopts adaptive adjustment, the colony size is 50 ants, the pheromone evaporation rate is 0.15, the initial concentration is 1 × 10^− 4, and the cone distribution (coefficient 0.09) is introduced to optimize the diffusion. The adaptive heuristic factors are adjusted in [1.2, 3.8] and [2.5, 5.2], respectively, and the update interval is 5 iterations. In the division of ant colonies, the conversion rate of soldier ants is 0.18/ iteration, and the tabu table is 5 × 5 grid. B-splines are used for path smoothing, the distance between control points is less than 3 grids, and the curvature constraint is 0.28 m^− 1. In terms of dynamic window algorithm, the safe distance is 0.35 m and the emergency braking threshold is 0.2 m/s. The evaluation weights for path optimization are 0.45 for path tracking, 0.35 for obstacle avoidance, 0.12 for speed, and 0.08 for heading. The velocity and angular velocity resolutions are 0.01 m/s and 0.05π rad /s, respectively, ensuring the accuracy and stability of path following.

In response to the shortcomings of the traditional ACO, it is optimized. Firstly, the impact of PHF and EHF on the ACO is discussed, as shown in Fig. 7.

Fig. 7

Influence of heuristic factors on ACO algorithm.

In Fig. 7 (a), the PHF and EHF values for combinations 1–7 were (1, 0), (1, 0.5), (1, 1), (1, 2), (1, 5), (1, 10), and (1, 20), respectively. In Fig. 7 (b), the PHF and EHF values for combinations 1–8 were (0, 1), (0.5, 1), (1, 1), (2, 1), (10, 5), (10, 10), (0.1, 0.1), and (0.1, 0.5), respectively. As shown in Fig. 7 (a), if the EHF was small, the search result was poor, and the algorithm took a long time. However, when the EHF was too large, the algorithm stopped prematurely. As shown in Fig. 7 (b), when the PHF increased, the search result was better. If it was too large, the search result was worse. Overall, when the heuristic factor is too high, the algorithm is prone to quickly converge to the local optimal solution, ignoring the search for the global optimal solution. When the heuristic factor is too low, the algorithm search process is too random, making it difficult to find effective solutions. Therefore, it is necessary to improve the heuristic factors in this study. Furthermore, the ablation experiment is conducted, and the experimental plan is displayed in Table 2.

Table 2 Results of ablation experiment.

In Table 2, O1-O6 respectively represent six optimization methods to improve ACO. From Table 2, the average path length planned by the basic ACO algorithm was 36.45, and the path accuracy was 94.64%. When one optimization was added alone, the average path length decreased and the path accuracy increased. For the method 8 with six optimization methods, namely the improved ACO algorithm proposed in this study, the average path length was 30.18, and the path accuracy was 98.46%, which was significantly improved compared with the basic ACO algorithm. In addition, from the computational time results, the introduced different optimization strategies had a small impact on the computational cost, and the overall change was between 3.42s and 3.91s, indicating that each optimization strategy not significantly increased the computational burden. When all optimization strategies were combined, the computational time increased the most, reaching 4.12s. However, compared with the improvement of the basic ACO algorithm, the extra computational cost was acceptable, and the path length was shortened and the path accuracy was improved, which indicated that the comprehensive optimization scheme still maintained a high computational efficiency while improving the planning quality. On this basis, Grid maps of 20*20 and 30*30 are created. The convergence of the basic ACO algorithm³⁴, Max-Min Ant System (MMAS)³⁵, and the optimized ACO is compared. The results are shown in Fig. 8.

Fig. 8

Convergence of different algorithms.

As shown in Fig. 8 (a), in the 20*20 grid map, the ACO converged in the 50th iteration with a mean path length of 28.46. The MMAS algorithm converged in the 29th iteration with a mean path length of 27.46, while the improved ACO algorithm converged at the 23rd iteration with a mean path length of only 25.87. From Fig. 8 (b), in the 30*30 grid map, these three algorithms required more iterations when converging compared with the 20*20 grid map. The ACO algorithm converged at the 120th iteration, the MMAS converged at the 104th iteration, and the improved ACO algorithm converged at the 81st iteration. The distance lengths at convergence were 43.45, 42.46, and 41.03, respectively. In summary, the proposed optimization strategy can effectively improve the convergence speed of ant colony algorithm and shorten the path length. This is mainly due to the fast discovery of high-quality paths during cone pheromone initialization. The dynamic adjustment of adaptive heuristic factors improves global exploration and local convergence capabilities, while the ant colony segmentation mechanism optimizes search efficiency.

Performance verification and analysis of global planning scheme

The designed ACO is adopted for global planning. Four types of static environments are created, namely simple environment, cluttered environment, crowded environment, and maze-like environment, as shown in Fig. 9.

Fig. 9

Map of robot global path planning.

In this scene, each map in Fig. 9 maintained the position of obstacles unchanged. To reduce the impact of randomness, the algorithm runs 30 times with the same initial parameters in each group of maps. Firstly, the path smoothness of ACO, MMAS, and optimized ACO is compared, as displayed in Fig. 10.

Fig. 10

Global path smoothness comparison.

Figure 10 demonstrate the distance smoothness of three algorithms in four types of maps. In Fig. 10 (a), in the simple environment, the average path smoothness of ACO, MMAS, and improved ACO was 0.62, 0.74, and 0.94, respectively. In Fig. 10 (b), in the cluttered environment, the average path smoothness of ACO, MMAS, and improved ACO was 0.53, 0.69, and 0.91, respectively. According to Fig. 10 (c), the average path smoothness of ACO, MMAS, and improved ACO in the crowded environment was 0.56, 0.71, and 0.79, respectively. According to Fig. 10 (d), the average path smoothness of ACO, MMAS, and improved ACO in the maze-like environment was 0.48, 0.51, and 0.65, respectively. The higher the smoothness, the smoother the turning point. The path smoothness of the improved ACO algorithm is better than that of ACO and MMAS in all environments, mainly due to the cubic B-spline curve optimization, which effectively reduces sharp turns in the path and makes the robot travel more smoothly, especially in complex environments. Finally, the optimal path obtained by these three algorithms is shown in Fig. 11.

Fig. 11

Optimal path.

In Fig. 11 (a), the environment was relatively simple with fewer obstacles, and the path differences of these three algorithms were not significant. In Fig. 11 (b), the distribution of obstacles was irregular and chaotic. The global path designed by ACO had five turning points, while the path designed by MMAS had three turning points. The path planned by the optimized ACO had high smoothness and no obvious turning points. In Fig. 11 (c), the environment was relatively crowded, but the planned path was relatively simple. In Fig. 11 (d), at the last corner where the target point was reached, the path planned by the improved ACO was significantly shorter in length and smoother in turns than the path planned by ACO and MMAS. Overall, the improved ACO shows the best performance in different environments. With the support of six optimization schemes, the proposed robot global path planning method is effective and superior.

Performance verification and analysis of local planning scheme

After analyzing the performance of the improved ACO and global path planning method, the study conducts experiments on the local planning method based on the improved DWA. The study first constructs a multi-objective dynamic static combination environment and conducts global path planning to obtain path length, smoothness, and iterations, as displayed in Fig. 12.

Fig. 12

Global planning results in dynamic and static combination environment of multiple targets.

In Fig. 12 (a), the global path of the robot ran from target point 1 to 2, then sequentially from 2 to 3, and finally to target point 4. In Fig. 12 (b), the path length obtained by global planning was 61.34, with a smoothness of 0.64 and 54 iterations. The local path planning performance of dynamic obstacle observation is analyzed, and the results are shown in Fig. 13.

Fig. 13

Local planning results in dynamic and static combination environment of multiple targets.

In Fig. 13 (a), the red dashed line represents the local path that the robot changes after encountering dynamic obstacles in its path. In Fig. 13 (a), when encountering dynamic obstacles, the robot automatically executed an improved DWA to plan a new local path. This not only ensured the continuity and smoothness of path planning, but also guaranteed the navigation safety of the robot in complex environments. In Fig. 13 (b), after local planning, the path length increased to 69.02 due to obstacles, and the smoothness slightly decreased to 0.59. The number of iterations increased to 62, without any significant performance degradation. Overall, the local path planning proposed in the study demonstrates good adaptability, safety, continuity, smoothness, and robustness when facing dynamic obstacles, making it an effective multi-objective path planning solution. The improved path planning method based on the improved A-star algorithm proposed by Z. Lin et al. in the reference³⁵ in 2024 is compared with the method proposed in the study. In addition, the more advanced path planning methods mentioned in references^36,37,38 are also introduced for comparison. The method in reference³⁸ is based on the Fast Exploring Random Tree Star (RRT*) algorithm, which optimizes the global optimality by reducing the redundant nodes in the path and maintaining a constant bending Angle. Reference³⁴ proposes a two-level path planning model, which combines improved ant colony algorithm and conflict resolution strategy. The method mentioned in reference³⁹ is a multi-step ant colony optimization algorithm based on terminal distance index, which is used for path planning of mobile robots. For convenience, the serial number of references is used to represent the method in the experimental results.

Table 3 Comparative experimental results.

In Table 3, path accuracy indicates the spatial matching accuracy between the actual driving path and the global reference path when the robot executes path planning in a dynamic and complex environment. From Table 3, the proposed method showed advantages in the two key indicators, average path length and path accuracy. The average path length was the shortest (71.49) and the path accuracy was the highest (98.24%), indicating that the method had excellent performance in both efficiency and accuracy of path planning. Moreover, the proposed method also had the best performance in computational load and completion time, which were 1.04 MB and 22.7s respectively. In contrast, the methods proposed in references^37,38,39 performed well in some aspects, they were inferior to the research method in terms of path length, accuracy, computational load, and response time. In particular, although the TS-ACCRPP in reference³⁸ had similar accuracy, its computational load and completion time were relatively high. The TDI-MSACO in reference³⁴ showed a balance in path length and accuracy, but had the highest computational load. In summary, the proposed method has significant performance advantages in large and complex Gazebo test environments. Finally, the computational time of different methods under different map sizes and obstacle densities is tested. The computational complexity is compared, as shown in Table 4.

Table 4 Comparison of computational complexity in different environments.

From Table 4, the proposed method showed optimal computational efficiency under all conditions of map scale and obstacle density. Compared with the path planning method proposed in references^34,37,38,39, the computational time of the research method was 0.34s under 20 × 20 low-obstacle environment (10%), and 36.45s under 100 × 100 high-obstacle environment (70%). The computational time increased nonlinearly with the increase of map size and obstacle density. However, through cone pheromone initialization, adaptive heuristic factor adjustment, and ant colony division optimization, the research method can effectively reduce the search complexity, improve the path planning efficiency, and maintain low computational cost and fast convergence speed under different environments.

Discussion

A novel path planning scheme combining improved ant colony algorithm and dynamic window algorithm is proposed to address the challenges of robot path planning in complex environments. Firstly, by improving ACO algorithm to achieve efficient global path planning for static environment, cone pheromone initialization, adaptive heuristic factor regulation and ant colony division of labor strategies are proposed to enhance the global search ability and convergence speed. Secondly, the dynamic window algorithm is combined with the path direction angle evaluation function and dynamic velocity sampling optimization to improve the local obstacle avoidance ability of the robot in the dynamic environment and ensure the rapid regression to the global path after obstacle avoidance. Finally, the experimental verification and performance analysis of the proposed method are carried out. The ablation experiment showed that the mean path length planned by basic ACO was 36.45, and the path accuracy was 94.64%. When a certain optimization was added separately, the mean path length decreased and the accuracy improved. However, the optimized ACO had a mean path length of 30.18, and the path accuracy was 98.46%. In the 20*20 grid map, the ACO converged at the 50th iteration with a path length of 28.46, while the MMAS algorithm converged at the 29th iteration with a path length of 27.46. The optimized ACO converged only at the 23rd iteration with the shortest path length of 25.87. In the 30*30 grid map, ACO, MMAS, and improved ACO converged at the 120th, 104th, and 81st iterations, with path lengths of 43.45, 42.46, and 41.03, respectively. In the 30*30 grid map, the improved ACO algorithm reduced the number of iterations by about 33% and the path length by about 5.6% compared with the original ACO, which proved its superiority in efficiency and accuracy. In addition, the improved ACO exhibited the highest smoothness in all environments. The local path planning scheme can quickly re-plan the path when dynamic obstacles appear. Compared with the pure sampling method, the proposed method performs better on global optimality and path smoothness. Compared with the pure optimization method, the proposed method has more advantages in dynamic adaptability and multi-objective optimization ability. Therefore, the collaborative optimization of global planning and local obstacle avoidance is realized in this study, which is suitable for complex static and dynamic environments, and provides a more adaptive solution for autonomous navigation of robots in industrial automation, intelligent transportation and exploration tasks.

Limitations and future work

There are some limitations in the practical application, which are mainly reflected in the following aspects. The use of simulated environments for experiments can maximize the superiority of the algorithm, but its performance in real environments or experiments related to physical robots may not be adequately tested. Therefore, future research can increase experiments using specific physical robots in real environments (such as industrial production workshops, unmanned warehouse logistics systems, medical assistance robot environments, intelligent transportation systems, or disaster relief scenarios) to verify the adaptability and robustness of the algorithm in real complex environments. The current method does not fully consider the influence of sensor noise and positioning error on path planning performance. In practical robot applications, sensor data is inevitably noisy, and positioning errors may also lead to inaccurate environmental modeling. This may cause the planning result to deviate from the actual optimal path, and even cause collisions. Future research can combine robust optimization algorithms or introduce probability-based methods (such as particle filtering) to improve the robustness of the method in sensor noise and positioning errors. This study does not explore the performance of the algorithm in dynamic environments, particularly in complex or unpredictable moving obstacles such as crowded spaces. Future work can consider introducing dynamic obstacle detection and prediction mechanisms (such as deep learning-based behavior prediction models), combined with real-time path re-planning strategies (such as incremental A or RRT), to enhance the applicability of the algorithm in dynamic environments. The current approach does not provide a detailed analysis of the computing resource requirements of embedded systems, which may limit its real-time application in real mobile robots. In the future, more efficient real-time path planning can be achieved by optimizing the algorithm complexity (such as reducing the state space search range), using parallel computing or hardware acceleration techniques to reduce the computational overhead.

The six ACO optimization strategies proposed in this paper do not provide specific parameter adjustment suggestions for different robot types or environments. For example, how to adjust the weight of the heurist function or the pheromone update rule under different terrains or obstacle densities still needs to be further explored. Future work can analyze the effects of different parameter combinations on algorithm performance through experiments, and provide users with reference manuals for parameter tuning. Current methods do not specify how to effectively integrate it with other key modules of robotic systems, such as sensing and control modules. Future research can develop a modular system architecture, clarify the interface and communication mechanism between modules, and verify its feasibility in real robot systems through experiments. The study only validates simple point robot models, and does not consider robots with complex kinematic constraints, such as car-like robots or humanoid robots. Future work can extend the application of the method by introducing sample-based motion planning methods (such as RRT) or combining trajectory optimization algorithms (such as LQR).

The endurance of mobile robots is an important indicator in practical applications, but the current evaluation does not consider the impact of path planning on energy consumption. Future research can optimize the path planning algorithm by introducing energy consumption models, such as energy consumption calculations based on velocity and acceleration, to maximize battery life while ensuring path safety and efficiency. In this paper, the path planning algorithm for a single robot is optimized to improve its optimization ability, convergence speed, and obstacle avoidance performance in complex environments. However, the path planning for multi-robot collaboration has limitations, mainly reflected in insufficient collaboration mechanisms and communication efficiency, making it difficult to achieve efficient collaboration in complex environments. Future research should focus on developing efficient collaboration strategies and communication mechanisms, exploring task allocation and load balancing to improve the overall performance and efficiency of multi-robot systems.