Model predictive control for quad active bridge DC-DC converter for more electric aircraft applications

Abstract

The isolated multi-port converters quad-active bridge (QAB) presents a unique opportunity to connect multiple sources and loads operating at different power and voltage levels, offering galvanic isolation and shared magnetics as advantages. However, the high number of modulation variables, dynamic response, and overall modeling complexity of QAB converters pose challenges to controller design. Traditional linear controllers often struggle with voltage overshooting and undershooting under abrupt load changes and exhibit limited dynamic performance and coupling among different ports. To address these challenges, this paper introduces a moving discretized control set-model predictive control (MDCS-MPC) strategy for QAB converters. The developed approach predicts phase shift values through the converter model, ensuring fast dynamic performance and eliminating steady-state errors in control variables. The prediction model’s embedded circuit parameters and operating modes enhance performance across various power and terminal voltage ranges. An adaptive step is implemented for quick transitions, significantly reducing computational demands. These analytical findings and the MDCS-MPC strategy are verified through Matlab simulation results and experimental results obtained from the Hardware-in-the-Loop (HIL) real-time Typhoon 602 platform. Both experimental and simulation results demonstrate the effectiveness of the developed strategy, showing superior dynamic response, robustness, and reduced computational requirements. Furthermore, the voltage achieves a very fast dynamic response and exhibits no significant voltage overshoot or undershoot.

Introduction

The increasing demand for more efficient and reliable power conversion systems in more electric aircraft (MEA) applications has spurred significant advancements in power electronics. Among these, the quad active bridge (QAB) converter has emerged as a prominent solution due to its multiport capability, high efficiency, and flexibility in power distribution while preserving galvanic isolation among the ports^1,2,3.

The illustration in Fig. 1 details the components of QAB. The high-frequency transformer (HFT) with multiple terminals plays a critical role in providing galvanic isolation and matching voltage levels across various ports⁴. The bridges, whether half or full, act as the interface between the HFT terminals and the DC ports. QAB is an extension of the dual-active bridge converter (DAB)⁵, featuring an increase in the number of HFT terminals and interconnected bridges that link multiple ports. While a triple-active bridge converter (TAB) expands from two ports to three ports⁶, QAB is designed for four ports^1–7. Significantly, the operational principles applied to DAB can be extended to TAB and QAB converters.

Fig. 1

(a) The topology of QAB converter, (b) Operation waveforms of QAB in the SPS for forward power flow situation (c) Y-equivalent circuit of the QAB converter and possible power transfer paths among the actives bridges, and (d) Δ -equivalent circuit of the QAB converter ^1,2,3.

The theory of voltage angle difference introduces the phase shift modulation (PSM) method, which has been explored in⁸ and⁹ for evaluating the performance of QAB and managing dynamic power. In¹⁰, PSM was integrated into a QAB to improve the reliability of solar generation systems. PSM provides a direct modulation for QAB, resulting in reduced root mean square (rms) currents, zero voltage switching (ZVS), and high power transfer levels when DC voltage aligns with the transformer turns ratio¹¹. While there are alternative modulation methods for QAB, adopting them would increase the computational burden of the controller due to the complexity of the control objective. This paper focuses explicitly on the single-phase shift modulation method for the QAB, which requires a control device with a relatively slower response compared to other controllers.

However, in isolated multiport converter (IMPC) systems, the common magnetic flux of the transformer can lead to power coupling across various ports, which may impact the control performance of the system. The elimination of coupling among the different ports of an IMPC converter is essential for achieving optimal performance^12,13.

The most commonly utilized method for regulating DC-port voltage is proportional-integral (PI) control, known for its ease of implementation¹⁴. However, this approach has slow dynamics and is highly susceptible to changes in the output load. To tackle these challenges and enhance disturbance attenuation capability, two alternative methodologies have been suggested: model-based phase-shift control (MPSC)¹⁵ and virtual direct power control (VDPC)¹⁶. Both approaches necessitate feedforward current data from an output current sensor and an input DC-link voltage. In a study¹⁷, the output current sensor was substituted with a reduced-order observer. Nonetheless, this technique is computationally demanding and entails more precise design, especially for multimodule-based IMPC, where the risk of leakage parameter mismatch is heightened. In another innovation, a dual-loop current controller was introduced¹⁸ to achieve resilient performance against grid voltage disturbance and impedance variation. However, this controller was implemented at the low-frequency ac-dc stage, where control loop delay has the potential to impact overall controller performance. Mou et al.¹¹ introduced a reactive power minimization (RPM) approach for modular multi-active-bridge (MMAB) converters, implementing an open-loop reactive power control structure combined with an active power closed-loop using a linear PI controller. While this strategy is effective for reducing reactive power under steady-state conditions, the inherent limitations of the PI controller restrict its adaptability to dynamic scenarios.

In order to achieve rapid dynamic response and robustness, non-linear control techniques have been introduced. The predictive current mode controller, as proposed in¹⁹, has increased the bandwidth of the outer voltage control loop. However, the circuit still relied on a combination of the PI control method, necessitating additional equipment for compensation. Another study²⁰ discussed the sliding mode control method and compared it with traditional PI control. Despite the sliding mode controller handling transient load changes better than the PI controller, noticeable voltage sag is still apparent in the output voltage comparison. The results suggest that the non-linear control method exhibits less overshoot and faster transient performance than the linear control method. Furthermore, a multi-loop linear control method outlined in²¹ reduces voltage sensitivity to changing load conditions, but its implementation requires multiple control loops, leading to increased complexity. Additionally, a VDPC scheme for DAB converters, which relies less on current sensors, was proposed in²². However, this method still depends on the PI controller and demonstrated limited load current disturbance rejection.

To deal with such a problem, model predictive control (MPC) offers a robust solution that provides rapid dynamic responses, easy integration of constraints, and straightforward digital implementation^23,24,25. For the DAB power converter, the proposed moving discretized control set-model predictive control (MDCS-MPC) algorithm aims to regulate either output voltage^26,27 or output current²⁸ by evaluating and selecting the actuation among various options to minimize the error between the reference and the measured value. The use of finite-control set model-predictive control (FCS-MPC) has been explored in AC power conversion^29,30,31. However, the application of predictive control in multiport DC/DC converters, particularly in QAB converters has not been extensively investigated. Although FCS-MPC methods have been suggested for use in boost converters with a receding horizon in³² and in³³, offering rapid dynamics, these methods resulted in variable switching frequency and required extensive computation. In³⁴, continuous control set model-predictive control (CCS-MPC) was introduced for boost converters, effectively preventing voltage transition overshoot. Nevertheless, the methods as mentioned above are not applicable in QAB.

In^27,28 introduced an MDCS-MPC strategy specifically designed for DAB converters, focusing on precise voltage and current control. Their research demonstrates the effectiveness of MDCS-MPC in achieving robust voltage regulation and fast response times, particularly for applications such as battery charging that demand both voltage and current management. However, while the approach demonstrated advantages for single-port systems, it lacks critical considerations for multi-port converters, where control complexities and cross-port interactions significantly increase. Furthermore, the method in³⁵ does not address adaptive control requirements, resulting in higher computational demands and potentially less efficiency in rapidly changing operational environments. The adaptive step has been integrated for swift transitions, and the MDCS-MPC requires significantly less computational power compared to the FCS-MPC detailed in^2,36.

In^35,37,38, an advanced MDCS-MPC method for DAB converters was introduced. This method demonstrated that predictive modeling can facilitate precise control of both voltage and current while achieving minimal steady-state error. The approach allowed for rapid adjustments to varying power demands, which are essential in high-performance applications. However, the study identified a significant limitation: the computational burden associated with high switching frequencies and multiple prediction horizons, which limits its feasibility for embedded applications or multi-port QAB configurations. Additionally, while MDCS-MPC proved effective for DAB systems, it lacked scalability for QAB systems, which necessitate additional computational resources to handle the complexities of controlling multiple active ports.

Tarisciotti et al.³⁹ further developed the FCS-MPC framework for DAB converters by introducing a flexible cost function and phase-shift modulation, which enhance stability across a broader range of operating conditions. Their approach, which facilitates adaptive power regulation, positions FCS-MPC as a compelling alternative to traditional PI controllers in high-performance applications. However, the authors acknowledged that the method’s reliance on high-frequency switching and multiple prediction steps results in substantial computational demands, which could limit its applicability in real-time, multi-port QAB systems where control efficiency and stability are paramount.

To enhance computational efficiency, Sun et al.⁴⁰ proposed a hybrid modulation scheme within MDCS-MPC aimed at extending the zero-voltage switching (ZVS) range and improving partial load efficiency in three-phase DAB converters. This approach successfully reduced current stress and boosted efficiency, particularly under light-load conditions. However, the hybrid modulation necessitated additional sensing and complex control algorithms, which increased implementation challenges and constrained its scalability for multi-port QAB applications that require simplicity and real-time responsiveness.

To enhance robustness in model predictive approaches, Shen et al.⁴¹ proposed a feedback correction mechanism in FCS-MPC, referred to as FCS-MPCFC. This method addressed model mismatches and environmental disturbances through real-time feedback adjustments, improving the robustness of DAB converters under varying conditions. However, the introduction of feedback correction increased computational complexity. It necessitated careful parameter tuning, presenting challenges for implementation in larger multi-port QAB systems, where it is crucial to maintain accuracy across multiple active ports while managing limited computational resources.

To further reduce computational demand, Zhang et al.⁴² introduced a simplified FCS-MPC strategy that limited the number of candidate voltage vectors assessed at each prediction step. This advancement enabled faster computations, enhancing the feasibility of FCS-MPC for real-time control in power converters. However, Zhang et al. acknowledged that this reduction in computational intensity came with a trade-off: the control accuracy may be compromised, potentially affecting performance in high-power, multi-port QAB systems where precision is crucial, particularly under varying loads and high switching frequencies.

Despite these advancements, a gap remains in balancing computational efficiency, robustness, and dynamic performance, especially for QAB converters in applications like more-electric aircraft, which demand fast, high-frequency control across multiple ports. Addressing this gap, the present study proposes a MDCS-MPC framework optimized for QAB systems. This approach incorporates advanced cost functions and adaptive modulation strategies, demonstrates rapid dynamic performance, eliminates steady-state error in control variables for voltage and current, achieves port decoupling, and efficient computational techniques to provide a scalable and robust solution that meets the rigorous demands of multi-port, high-power applications without compromising control accuracy or stability. The developed method represents a comprehensive solution for high-performance power management in complex converter systems by addressing the limitations identified in previous studies.

Previous research introduced the MDCS-MPC for QAB converters, showcasing its potential to improve dynamic response and mitigate coupling effects in IMPCs through simulation validation [1]. This study expands on that work by incorporating practical experiments using Hardware-in-the-Loop (HIL) testing, thereby providing real-world validation of the developed control scheme.

In addition to experimental verification, the MDCS-MPC algorithm has been enhanced with an adaptive step mechanism, which improves computational efficiency and ensures swift, accurate transitions. This advancement increases both scalability and control precision, setting thedeveloped method apart from traditional PI controllers. The expanded analysis under various load conditions and voltage variations further highlights the robustness and applicability of the control strategy, thereby reinforcing and extending the contributions of the original theoretical study.

The paper is structured as follows: Section "Operation principle of the QAB converter" outlines the topology structure and equivalent circuit model of the QAB converter. Section "Power transmission and operational characteristics of the QAB converter" delves into the power transmission characteristics and small signal modes of the QAB converter. Section "Developed adaptive model predictive control (AMPC)" discusses the developed adaptive model predictive control, including the prediction model, operating principle, adaptive step, proposed cost function, compensation loop for error correction, and the flowchart of the proposed MDCS-MPC. Section "Simulation verification" presents simulation results to validate the effectiveness of the developed control strategy. Section "Experimental evaluation" examines the hardware-in-loop (HIL) experimental results to further validate the developed control strategy. Section "Comparison with existing control methods" discusses a comparison with existing control methods. Finally, Section "Conclusions" presents the conclusions of this work.

Operation principle of the QAB converter

Topology of quad active bridge converters

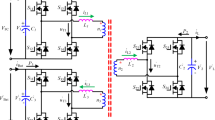
Figure 1a depicts the topology structure of the QAB converter, comprising four DC voltage ports (V₁–V'₄), with v₁–v'₄ symbolizing the four high-frequency AC square wave voltages linked to the high-frequency transformer. The DC-link capacitors for the four DC ports are denoted by C₁–C'₄, while the currents flowing through the power inductors are represented by i_L1–i'_L4. Furthermore, n₁–n₄ correspond to the number of turns in each of the four windings of the high-frequency transformer. T_sh is the switching period. Figure 1b illustrates the operation waveforms of QAB in a forward power flow situation.

MOSFETs serve as switches in the QAB converter, enabling bi-directional current flow across all ports. In each H-bridge, the two switches on the same leg operate in complementary conduction mode. Each H-bridge functions at a fixed switching frequency and maintains a consistent 50% duty cycle. Moreover, the two diagonally opposite switches within each H-bridge are alternately switched ON and OFF, facilitating the desired power flow and switching pattern^43,44.

QAB equivalent circuit and parameter conversion

Based on the TAB converter discussed in⁶, it has been established that the active bridges labeled #2, #3, and #4 within the QAB can be transferred to the primary side at position #1. By considering the AC outputs of the four H-bridges as high-frequency square waves, the equivalent circuit structure of the QAB after this transformation is depicted in Fig. 1c; L_m represents the equivalent magnetizing inductance.

The equivalent inductance voltage parameters are calculated in the Y-type equivalent circuit when converting port j (j = 2 ~ 4) to port #1. This calculation is represented as:

$$v_{j} = \frac{{n_{1} }}{{n_{j} }}v^{\prime}_{j} ,\,\,L_{j} = \left[ {\frac{{n_{1} }}{{n_{j} }}} \right]^{2} L^{\prime}_{j}$$

(1)

Assuming the converter operates at a switching frequency f_s, power is transmitted from port j (j = 2 ~ 4) to port #1. Based on the power derivation of DAB and employing the single-phase shift modulation control strategy, the power expressions for ports j and one can be formulated as follows[1]:

$$P_{j1} = \frac{1}{{T_{sh} }}\int\limits_{0}^{{T_{sh} }} {v_{j} \cdot i\left( \tau \right)d\tau = \frac{{V_{j} \,V_{1} }}{{2\pi^{2} f_{s} L_{j1} }}\varphi_{j1} \left( {\pi - \varphi_{j1} } \right)}$$

(2)

Here, v_j denotes the voltage value of port j after being converted to port #1, L_j represents the equivalent power inductance between port j and port #1, and φ_j1 designates the phase shift angle between them. It is evident that both the phase shift angle and the equivalent inductance L_j influence power transmission between any two ports. Thus, the power calculation formula for any two ports is as follows:

$$P_{ij} = \frac{{V_{i} \,V_{j} \,}}{{2\pi^{2} f_{s} L_{ij} }}\varphi_{ij} \left( {\pi - \left| {\varphi_{ij} } \right|} \right)$$

(3)

Power transmission and operational characteristics of the QAB converter

Power transmission characteristics

The QAB converter operates in a similar manner to the DAB converter, consists of four independent H-bridges (ports), each capable of operating independently. Upon examination of the Δ-equivalent circuit diagram in Fig. 1d, it is evident that a phase shift angle between any two active bridge ports leads to interactive power coupling through the power inductor L_ij.

By analyzing the operating principle of the DAB and implementing an SPS control strategy with the QAB under power-balanced conditions, it becomes possible to obtain high-frequency AC square wave voltage and current waveforms flowing through power inductances L₁ and L_j when transmitting port 1 to ports j = 2, 3, and 4, as shown in Fig. 1b ref ^1,2,3,4. In Fig. 2a, the schematic diagram of power transmission in the QAB illustrates the power flow direction, which is determined by the phase shift angle φ between the ports.

Fig. 2

(a) All possible power path of the QAB converter. (b) Usual balanced condition case, where MV bridge a delivers equal power to the three LV bridges (#2, #3, and #4) (source: bridge #1, load: bridges #2, #3, and #4). (c) Power transmission under unbalanced condition.

By utilizing the single-phase-shift (SPS) control strategy and Eq. (3), we can represent the power transmission expressions for each active bridge as follows[44]:

$$P_{ij} = \frac{{V_{i} V_{j} }}{{2\pi^{2} f_{s} L_{ij} }}\varphi_{ij} \left( {\pi - \left| {\varphi_{ij} } \right|} \right)$$

(4)

After performing the superposition calculation, the power absorbed at port i is:

$$P_{i} = \sum\limits_{j \ne i}^{4} {\frac{{V_{i} V_{j} }}{{2\pi^{2} f_{s} L_{ij} }}\varphi_{ij} \left( {\pi - \left| {\varphi_{ij} } \right|} \right)}$$

(5)

Hence, we can derive the equations for the power at the four ports of the QAB as follows:

$$\left\{ \begin{gathered} P_{1} = \frac{{V_{1} V_{2} \varphi_{21} \left( {\pi - \left| {\varphi_{21} } \right|} \right)}}{{2\pi^{2} f_{s} L_{21} }} + \frac{{V_{1} V_{3} \varphi_{31} \left( {\pi - \left| {\varphi_{31} } \right|} \right)}}{{2\pi^{2} f_{s} L_{31} }} + \frac{{V_{1} V_{4} \varphi_{41} \left( {\pi - \left| {\varphi_{41} } \right|} \right)}}{{2\pi^{2} f_{s} L_{41} }} \hfill \\ P_{2} = \frac{{V_{1} V_{2} \varphi_{12} \left( {\pi - \left| {\varphi_{12} } \right|} \right)}}{{2\pi^{2} f_{s} L_{12} }} + \frac{{V_{2} V_{3} \varphi_{32} \left( {\pi - \left| {\varphi_{32} } \right|} \right)}}{{2\pi^{2} f_{s} L_{32} }} + \frac{{V_{2} V_{4} \varphi_{42} \left( {\pi - \left| {\varphi_{42} } \right|} \right)}}{{2\pi^{2} f_{s} L_{42} }} \hfill \\ P_{3} = \frac{{V_{1} V_{3} \varphi_{13} \left( {\pi - \left| {\varphi_{13} } \right|} \right)}}{{2\pi^{2} f_{s} L_{13} }} + \frac{{V_{2} V_{3} \varphi_{23} \left( {\pi - \left| {\varphi_{23} } \right|} \right)}}{{2\pi^{2} f_{s} L_{23} }} + \frac{{V_{3} V_{4} \varphi_{43} \left( {\pi - \left| {\varphi_{43} } \right|} \right)}}{{2\pi^{2} f_{s} L_{43} }} \hfill \\ P_{4} = \frac{{V_{1} V_{4} \varphi_{14} \left( {\pi - \left| {\varphi_{14} } \right|} \right)}}{{2\pi^{2} f_{s} L_{14} }} + \frac{{V_{2} V_{4} \varphi_{24} \left( {\pi - \left| {\varphi_{24} } \right|} \right)}}{{2\pi^{2} f_{s} L_{24} }} + \frac{{V_{3} V_{4} \varphi_{34} \left( {\pi - \left| {\varphi_{34} } \right|} \right)}}{{2\pi^{2} f_{s} L_{34} }} \hfill \\ \end{gathered} \right.$$

(6)

Based on the power transmission between each port of the QAB converter, its operational states can be classified into power-balanced and power-unbalanced transmission states, as illustrated in Figs. 2b, c, respectively.

In the power-balanced transmission mode, active bridges #2, #3, and #4 exhibit no phase shift angle, such that φ₁₄ = φ₁₃ = φ₁₂. Assuming all port voltages are identical and transformer leakage inductance imbalance is negligible, the power-balanced transmission mode of the QAB can be modeled as three DAB converters operating in a similar manner. Conversely, in the power-unbalanced transmission state, phase shift angles exist between all active bridges #1, #2, #3, and #4, resulting in power coupling interactions among all four ports. In this state, the QAB converter has six distinct power transmission pathways.

Discrete state space average model of QAB Converter

To design the controller, it is essential to first modelling of the QAB converter. The DAB converter can be considered a current source with a controlled average current over one switching cycle⁴⁵. Following this methodology, the average model of the QAB converter can be developed. The average currents of the four ports i_DC2, i_DC3, and i_DC4, denoted as I_DC2, I_DC3, and I_DC4, are functions of the phase shifts and can be expressed as follows, based on Eq. (3):

$$\left\{ \begin{gathered} I_{{{\text{DC2}}}} = \frac{{P_{12} }}{{V_{2} }} = \frac{{V_{in} }}{{2n\pi^{2} f_{s} L_{s} }}\varphi_{12} \left( {\pi - \left| {\varphi_{12} } \right|} \right) \hfill \\ I_{{{\text{DC3}}}} = \frac{{P_{13} }}{{V_{3} }} = \frac{{V_{in} }}{{2n\pi^{2} f_{s} L_{s} }}\varphi_{13} \left( {\pi - \left| {\varphi_{13} } \right|} \right) \hfill \\ I_{{{\text{DC4}}}} = \frac{{P_{14} }}{{V_{4} }} = \frac{{V_{in} }}{{2n\pi^{2} f_{s} L_{s} }}\varphi_{14} \left( {\pi - \left| {\varphi_{14} } \right|} \right) \hfill \\ \end{gathered} \right.$$

(7)

An average equivalent circuit model has been formulated, as shown in Fig. 3. Within this circuit, I₁, I_load2, I_load3, and I_load4 represent the average switching periods of i₁, i_O2, i_O3, and i_O4, respectively. It’s crucial to emphasize that the variations in the DC source voltage have been omitted, leading to I₁ = I_DC1. Consequently, the voltage-stabilizing capacitor C₁ can be removed.

Fig. 3

Average model of the QAB converter [1].

By applying Kirchhoff’s Current Law (KCL) with V₂, V₃, and V₄ as state variables in the average equivalent circuit depicted in Fig. 3, the state space equation of the QAB converter can be defined as follows [28]:

$$\left\{ \begin{gathered} I_{{{\text{DC2}}}} = {\text{f}}_{2} \left( {V_{1} ,V_{3} ,V_{4} ,\varphi_{13} ,\varphi_{14} } \right) = I_{C2} + I_{{{\text{load2}}}} = C_{2} \frac{{dV_{2} }}{dt} + I_{{{\text{load2}}}} \hfill \\ I_{{{\text{DC3}}}} = {\text{f}}_{3} \left( {V_{1} ,V_{2} ,V_{4} ,\varphi_{12} ,\varphi_{14} } \right) = I_{C3} + I_{{{\text{load3}}}} = C_{3} \frac{{dV_{3} }}{dt} + I_{{{\text{load3}}}} \hfill \\ I_{{{\text{DC4}}}} = {\text{f}}_{4} \left( {V_{1} ,V_{2} ,V_{3} ,\varphi_{12} ,\varphi_{13} } \right) = I_{C4} + I_{{{\text{load4}}}} = C_{4} \frac{{dV_{4} }}{dt} + I_{{{\text{load4}}}} \hfill \\ \end{gathered} \right.$$

(8)

To discretize Eq. (8), the Euler method has been employed, yielding the following state-space equation for the discretized QAB converter:

$$\begin{gathered} \left\{ \begin{gathered} V_{2} \left[ {k + 1} \right] = \frac{{I_{{{\text{DC2}}}} \left( {V_{1} ,V_{3} ,V_{4} ,\varphi_{13} ,\varphi_{14} } \right)\left[ k \right] - I_{{{\text{load2}}}} \left[ k \right]}}{{C_{2} f_{s} }} + V_{2} \left[ k \right] \hfill \\ V_{3} \left[ {k + 1} \right] = \frac{{I_{{{\text{DC3}}}} \left( {V_{1} ,V_{2} ,V_{4} ,\varphi_{12} ,\varphi_{14} } \right)\left[ k \right] - I_{{{\text{load3}}}} \left[ k \right]}}{{C_{3} f_{s} }} + V_{3} \left[ k \right] \hfill \\ V_{4} \left[ {k + 1} \right] = \frac{{I_{{{\text{DC4}}}} \left( {V_{1} ,V_{2} ,V_{3} ,\varphi_{12} ,\varphi_{13} } \right)\left[ k \right] - I_{{{\text{load4}}}} \left[ k \right]}}{{C_{4} f_{s} }} + V_{4} \left[ k \right] \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \end{gathered}$$

(9)

To predict the output voltage at time (k + 1), the Euler equation provided in Eq. (9) is utilized to discretize Eq. (8). Consequently, Eqs. (8) and (9) demonstrate that the multiport converter is a nonlinear coupling system with multiple inputs and outputs. However, designing the controller requires additional decoupling links, which significantly increases the system’s computational complexity and can impact its dynamic performance. To address this challenge, this paper proposes MPC, which optimizes the port’s dynamic performance while simultaneously achieving decoupling control of the multiport converter.

Developed adaptive model predictive control (AMPC)

Prediction model

This study employs the DCS-MPC approach as its control method. By utilizing a discrete model, the MPC accurately predicts the voltages and currents of the converter. Consequently, the load current will be assumed to remain relatively constant within a single sampling period based on the QAB converter’s discrete state-space Eq. (9).

$$I_{load} \left[ k \right] = I_{load} \left[ {k + 1} \right]$$

(10)

The output voltage prediction for the time instance (k + 2) is as follows:

$$\left\{ \begin{gathered} V_{2} \left[ {k + 2} \right] = \frac{{I_{{{\text{DC2}}}} \left[ {k + 1} \right] - I_{{{\text{load2}}}} \left[ k \right]}}{{C_{2} f_{s} }} + V_{2} \left[ {k + 1} \right] \hfill \\ V_{3} \left[ {k + 2} \right] = \frac{{I_{{{\text{DC3}}}} \left[ {k + 1} \right] - I_{{{\text{load3}}}} \left[ k \right]}}{{C_{3} f_{s} }} + V_{3} \left[ {k + 1} \right] \hfill \\ V_{4} \left[ {k + 2} \right] = \frac{{I_{{{\text{DC4}}}} \left[ {k + 1} \right] - I_{{{\text{load4}}}} \left[ k \right]}}{{C_{4} f_{s} }} + V_{4} \left[ {k + 1} \right] \hfill \\ \end{gathered} \right.$$

(11)

By substituting the output voltage at time (k + 1) into Eqs. (9)–(11), we have derived the following result:

$$\left\{ \begin{gathered} V_{2} \left[ {k + 2} \right] = \frac{{I_{{{\text{DC2}}}} \left[ {k + 1} \right] + I_{{{\text{DC2}}}} \left[ k \right] - 2I_{{{\text{load2}}}} \left[ k \right]}}{{C_{2} f_{s} }} + V_{2} \left[ k \right] \hfill \\ V_{3} \left[ {k + 2} \right] = \frac{{I_{{{\text{DC3}}}} \left[ {k + 1} \right] + I_{{{\text{DC3}}}} \left[ k \right] - 2I_{{{\text{load3}}}} \left[ k \right]}}{{C_{3} f_{s} }} + V_{3} \left[ k \right] \hfill \\ V_{4} \left[ {k + 2} \right] = \frac{{I_{{{\text{DC4}}}} \left[ {k + 1} \right] + I_{{{\text{DC4}}}} \left[ k \right] - 2I_{{{\text{load4}}}} \left[ k \right]}}{{C_{4} f_{s} }} + V_{4} \left[ k \right] \hfill \\ \end{gathered} \right.$$

(12)

where V₂(k + 2), V₃(k + 2), and V₄(k + 2) represent the predicted voltage at bridges #2, #3, and #4 at time t = (k + 2).

Operating principle and adaptive step

The MDCS-MPC being considered is intended to control the converter’s output voltage V_j (j = 2 ~ 4) using the discretized average model of the QAB in (12). To accomplish this, a preliminary cost function has been introduced in (13) to maintain V_j (j = 2 ~ 4) at their respective reference values of V_j^ref. It is crucial to emphasize that (13) does not represent the final cost function but has been included only for the purpose of illustrating the operational principle of the MDCS-MPC.

$$CF\, = \left( {V_{j}^{{{\text{ref}}}} - V_{j} \left[ {k + 1} \right]} \right)^{2} ,\,\,j \in \left\{ {2,3,} \right.\left. 4 \right\}$$

(13)

The phase shift duty cycle (φ_ij) in Eq. (3) is represented as a continuous function. However, in digital control systems, it must be discretized. The precision of this discretization depends on the control platform employed. δ_d denotes the finest achievable phase shift in a digital control platform [26].

$$\delta_{d} = \frac{{T_{sw} }}{{T_{sh} }}$$

(14)

where T_sw is the sampling time of the controller. As a result, the QAB converter primarily operates within the following range:

$$\varphi_{ij} {\mathbf{ \in }}\left[ {0,{\kern 1pt} {\kern 1pt} 0.5} \right]$$

(15)

The discretization of Eq. (15) involves dividing it into μ_m(= 0.5/δ_d + 1) elements, as outlined in the subsequent array:

$$\varphi_{ij} \in \left\{ {0,\,\delta_{d} ,\,2\delta_{d} ,\,.....,\,0.5} \right\}$$

(16)

An intuitive representation of the MDCS-MPC is shown in Fig. 4. During the control interval from k to k + 1, μ = 5 points are evaluated, centered around the previous working point φ_ij[k] = x. When φ_ij[k + 1] equals x − 2δ_d, x − δ_d, x, x + δ_d, and x + 2δ_d, the output voltage V_j is predicted as V_j⁰[k + 2], V_j¹[k + 2], V_j² [k + 2], V_j³[k + 2] and V_j⁴[k + 2], respectively. The superscript indicates the index of an element in the moving discretized control set.

Fig. 4

Operation principle of the MDCS-MPCs for QAB converter, predictions (black), and best predicted trajectory (blue) for MDCS-MPC. μ is set to be 5 for illustration.

The moving discretized control set during the period k to k + 1 is {x − 2δ_d, x − δ_d, x, x + δ_d, x + 2δ_d}. According to Fig. 4, when φ_ij[k + 1] = x + δ_d, the predicted output voltage V_j³[k + 2] is closest to V_{j_ref}, resulting in the smallest cost function as defined in (13). Therefore, the value x + δ_d is applied to φ_ij at time instance k + 1. The process is repeated in the subsequent control interval, but the moving discretized control set changes to {x − δ_d, x, x + δ_d, x + 2δ_d, x + 3δ_d}. The control set moves with the working point within the domain of (16). During this control interval, φ_ij[k + 2] = x + 3δ_d results in the smallest cost function, and this value is applied at time instance k + 2. This process continues iteratively [27].

While a larger value of μ can enhance transition dynamics, it also increases the computational burden on the real-time digital controller. To mitigate this, an adaptive step for φ_ij is used instead of the finest search step δ_d. The adaptive step δ_adp is defined in Eqs. (17) and (18). The adaptive step δ_adp varies with the output voltage deviation from the reference. When V_j is far from the reference, δ_adp increases. Conversely, when V_j equals the reference, δ_adp becomes δ_d, thus maintaining control accuracy.

$$V_{{{\text{adp}}}} = \left\{ \begin{gathered} \left| {V_{j}^{{{\text{ref}}}} - V_{j} \left[ k \right]} \right|;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{if}} \hfill \\ V_{m} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \,\,\,\,\,\,\,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{if}} \hfill \\ \end{gathered} \right.\left| \begin{gathered} V_{j}^{{{\text{ref}}}} - V_{j} \left[ k \right] \hfill \\ V_{j}^{{{\text{ref}}}} - V_{j} \left[ k \right] \hfill \\ \end{gathered} \right|\begin{array}{*{20}c} \le \\ > \\ \end{array} \begin{array}{*{20}c} {V_{m} } \\ {V_{m} } \\ \end{array}$$

(17)

$$\delta_{{{\text{adp}}}} = \delta_{d} \left( {1 + \xi \,.\,V_{{{\text{adp}}}} } \right)$$

(18)

where ξ is a coefficient determined according to the requirement of transition performance, V_j^ref is the desired output voltage of the multiport converter, j is the number of port, and V_m denotes the maximum value for V_adp.

The benefits of using this adaptive strategy also includes a small computational cost, the utilization of a fixed switching frequency, a fast transient response, and the suppression of steady state error.

Cost function

Taking computational delay into account, the MDCS-MPC employs a prediction horizon of two sampling periods. Consequently, the cost function is proposed as follows:

$$CF\, = \eta_{1} G_{1j} + \eta_{2} G_{2j}$$

(19)

where

$$\left\{ \begin{gathered} G_{{{\text{1j}}}} = \left( {V_{j}^{{{\text{ref}}}} - V_{j} \left[ {k + 2} \right]} \right)^{2} \hfill \\ G_{{{\text{2j}}}} = \left( {V_{j} \left[ {k + 2} \right] - V_{j} \left[ k \right]} \right)^{2} \hfill \\ \end{gathered} \right.$$

(20)

The first term, G₁, is tasked with regulating the output voltage V_j to align with the reference value V_j^ref. Conversely, G₂ is designed to minimize voltage deviations while simultaneously achieving resonance damping and enhancing resistance to sampling noise. When V_j significantly deviates from the reference value, G₁ becomes the predominant factor in the cost function. However, as V_j approaches V_j^ref, the influence of G₂ increases, thereby limiting the variation of V_j. This mechanism effectively prevents V_j from oscillating due to analog-to-digital sampling noise and mitigates oscillations during load transitions. The tuning of weighting factors η₁ and η₂ is critical to the performance of the developed controller. As proposed in¹³, an artificial neural network approach is utilized in this paper to tune the weighting factors in MPC optimally.

Compensation loop for error corrections

There are two primary approaches to enhance prediction accuracy. The first approach involves utilizing a more precise mathematical model of the DAB converter, as investigated in⁴⁶ and⁴⁷. While this method can be effective, it may also result in increased computational complexity due to the use of higher-order models. The second approach involves implementing feedback compensation. Techniques commonly employed in other predictive controls can be effectively applied in the MDCS-MPC, as demonstrated in^{12,19,27,47[52]}. This paper presents a method similar to the approach proposed by Shen et al.⁴¹.

Figure 5 depicts an additional compensation loop designed to correct modeling errors. Within this loop, V_{j_p} represents the predicted output voltage (V_j) based on the ideal QAB model, as described in Eq. (12). V_{j_P}[k + 2] denotes the predicted voltage for the control period from k to k + 1 using MDCS, while V_{j_S} indicates the actual voltage value obtained through sampling. The compensation value for the voltage error is calculated as the weighted sum of the error between the sampled voltage V_{j_S} and the predicted voltage V_{j_P} from the previous two steps. Consequently, the predicted voltage is formulated as shown in Eq. (21).

$$\left\{ \begin{gathered} V_{2\_C} \left[ {k + 2} \right] = \Re_{1} \left( {V_{2\_S} \left[ k \right] - V_{2\_P} \left[ k \right]} \right) + \Re_{2} \left( {V_{2\_S} \left[ {k - 1} \right] - V_{2\_P} \left[ {k - 1} \right]} \right) + V_{2\_P} \left[ {k + 2} \right] \hfill \\ V_{3\_C} \left[ {k + 2} \right] = \Re_{1} \left( {V_{3\_S} \left[ k \right] - V_{3\_P} \left[ k \right]} \right) + \Re_{2} \left( {V_{3\_S} \left[ {k - 1} \right] - V_{3\_P} \left[ {k - 1} \right]} \right) + V_{2\_P} \left[ {k + 2} \right] \hfill \\ V_{4\_C} \left[ {k + 2} \right] = \Re_{1} \left( {V_{4\_S} \left[ k \right] - V_{4\_P} \left[ k \right]} \right) + \Re_{2} \left( {V_{4\_S} \left[ {k - 1} \right] - V_{4\_P} \left[ {k - 1} \right]} \right) + V_{4\_P} \left[ {k + 2} \right] \hfill \\ \end{gathered} \right.$$

(21)

where V_{j_C}[k + 2] is the voltage corrected at [k + 2], V_{j_P} is the predicted output voltage Eq. (12), V_{j_P}[k + 2] is the voltage prediction during the control k to k + 1, V_{j_S} is the measured output voltage, ℜ₁ and ℜ₂ are correction factors. In this study, the weighting coefficients ℜ₁ and ℜ₂ have been empirically calibrated to values of 0.5 and 0.25, respectively [27].

Fig. 5

Block diagram of the developed prediction error compensation loop [28, 52].

Flowchart of developed MDCS-MPC

The flowchart of MDCS-MPC is presented in Fig. 6a. It outlines the step-by-step calculation process of MDCS-MPC during the control period, from k to k + 1. The optimal control variable in MDCS is generated at the end of this process and will be applied at time instance k + 1. The MDCS diagram in Fig. 6 uses μ (= 5) elements, but it can be expanded as per specific requirements. This is done to make it easy to understand the process.

Fig. 6

(a) Flow diagram of developed work [26], (b) Block diagram of the controller implementation.

The evaluation process begins with calculating the adaptive step δ_adp (18). This step determines the distance between two nearby values in MDCS. MDCS slides within the range described in (15), which is centered around the control value φ_ij[k + 1]. This control value is set to be applied at time instance k + 1. After this, the iteration for MDCS-MPC begins.

The predicted bus voltage (V_{j_P}) is calculated using five elements in MDCS. Each voltage prediction is corrected by the compensation loop outlined in Fig. 5. Finally, cost functions (19) are calculated with each corrected voltage prediction value (V_{j_C}) to compare the minimal values.

The element that achieves the minimum cost function CF is then stored in φ_ij[k + 2]. This value is set to be applied at time instance k + 2. The block diagram of the implementation is shown in Fig. 5b.

Simulation verification

In order to validate the converter’s performance and the theoretical analysis, MATLAB/Simulink simulations were carried out using the parameters specified in Table 1. The simulations focused on steady-state operations under balanced conditions, assessed sensitivity to transformer leakage inductance, and evaluated dynamic operation under balanced power conditions. The main objective of these simulations is to ensure the ability to handle unexpected load conditions while maintaining the output voltage at the reference level. Different loads are connected to the output ports of the QAB, and these loads are intentionally activated at random intervals [1].

Table 1 Circuit parameters of the QAB converter model [1].

To evaluate the effectiveness and feasibility of the developed MDCS- MPC strategy, its performance was compared with the PI decoupling control strategy outlined in³, using the same simulation parameters. Detailed parameter configurations can be found in Table 1.

Steady-state performance and soft switching analysis

The simulation results for the QAB converter operating under balanced steady-state conditions are depicted in Figs. 7, 8, 9. In Fig. 7a, the simulation illustrates the DC side voltages for the three outputs on the QAB’s secondary side, demonstrating stabilization at the designated voltage of 150 V, thereby ensuring stable system operation. Conversely, Fig. 7b presents the simulation results under the PI decoupling control strategy. Additionally, Fig. 7c shows the phase shift angles of the H-bridges system, where during the balanced power transmission phase, the phase shift angles φ₁₂, φ₁₃, and φ₁₄ are all equal.

Fig. 7

(a) the DC output voltage of the three secondary sides of the QAB under the developed MDCS-MPC, (b) the DC output voltage of the three secondary sides of the QAB under the PI decoupling control strategy, and (c) the phase shifting ratio of the H-bridges in the system.

Fig. 8

Voltage and current waveforms of the QAB transformer windings at MV and LV ports: (a) Voltage under the developed MDCS-MPC, (b) Inductor currents under the developed MDCS-MPC, (c) Voltage under the PI decoupling control strategy, and (d) Inductor currents under the PI decoupling control strategy.

Fig. 9

Voltage and current waveforms on the semiconductors of the upper and lower switches of the same bridge arm for (a) H-bridge #1, (b) H-bridge #2, (c) H-bridge #3, and (d) H-bridge #4.

Figures 8(a–b) display the high-frequency square wave AC voltage and current waveforms at the primary and secondary sides of the high-frequency transformer, showing a phase shift between the primary and secondary sides without any phase deviation between the bridges on the secondary side. This indicates uniform power transmission from the primary side to the three secondary ports, with equal secondary inductor currents. Additionally, Figs. 8(c–d) illustrate the high-frequency square wave AC voltage and current waveforms at the primary and secondary sides of the high-frequency transformer under the PI decoupling control strategy.

The voltage and current waveforms of the active H-bridge switches of the QAB during the switching process are illustrated in Fig. 9. To assess the soft-switching capability of each H-bridge’s switches under power-balanced transmission conditions, Figs. 9(a–d) were examined. Figure 9a shows that the switches of H-bridge #1 in the QAB achieve ZVS. Similarly, during stable operation, both the upper and lower switches of the same arm in H-bridge #2 achieve ZVS, as shown in Fig. 9b. This pattern is consistently observed in the voltage and current states of the switches in H-bridges #3 and #4, as depicted in Figs. 9c, d, respectively.

The simulation results in Fig. 10 compare waveforms generated under the PI controller and the developed MDCS-MPC to validate the effectiveness of MDCS-MPC in reducing reactive power. The MDCS-MPC approach demonstrates a substantial reduction in reactive power across ports, resulting in optimized waveforms and improved efficiency, particularly under varying load conditions. In contrast, the PI controller leads to significantly higher reactive power levels. Notably, MDCS-MPC achieves zero reactive power at several ports in the QAB converter, enhancing stability in the active power transmission waveform and thus contributing to a more efficient and robust power conversion system.

Fig. 10

Comparison of MDCS-MPC and PI control strategies for active and reactive power in a QAB converter (a) MDCS-MPC approach (b) PI controller.

Dynamic operation

Load disturbance at port #2 on the LV side

The performance of the MDCS-MPC is analyzed at port #2 while maintaining a constant load at the other LV side port. A comparison is made with a traditional PI controller. The test sequence begins with a 100% load condition, followed by a brief no-load period. A 120% load condition is then introduced to assess the controller’s robustness. Subsequently, the converter experiences a load transition from 80 to 50% and returns to a no-load condition.

Figure 11 displays the output voltage comparison between the QAB under the developed MDCS-MPC and the PI controller. The results indicate that under the PI controller, there is a maximum voltage overshoot of 63 V at t = 0.04 s during the transition from 100 to 0% load and a maximum voltage drop of 30 V at t = 0.08 s when transitioning from 0 to 120% load.

Fig. 11

Comparison of port #2 output voltage response to load disturbances: PI controller vs. MDCS-MPC strategy.

In contrast, Fig. 12 illustrates the load current transition, where the PI controller exhibits significant overshoot and undershoot during load changes. Conversely, the developed MDCS-MPC considerably improves the converter’s dynamic response speed and minimizes load voltage fluctuations.

Fig. 12

Dynamic performance of the load current at port #2 with the PI controller and the MDCS-MPC strategy.

Additionally, MDCS-MPC effectively decouples power between ports, preventing power transients at port #2 from causing disturbances at other ports, as shown in Fig. 13.

Fig. 13

Output voltage of ports #3 and #4 when the load disturbance occurs at port #2.

In Fig. 14, the feasibility of power exchange between source port 1 bridge and port #2 on the LV side is evaluated. It is apparent that the power processed by bridge 2 on the LV side varies over time, as does the total power at port #1 (denoted as P₁). Initially, at t = 0 s, the converter operates with balanced power (P₂ = P₃ = P₄). Subsequently, at t = 0.04 s, the operational point of bridge 2 shifts, resulting in a 0% reduction in its power output. As a result, the power processed by the other two bridges remains unchanged, while the power at port #1 decreases by 30%. In the third interval, at t = 0.08 s, the operational point of bridge 2 is adjusted again, leading to a reduction in its power by 120%. This adjustment leaves the power processed by the remaining bridges unchanged, whereas the power at port 1 increases by 40%.

Fig. 14

Dynamic operation of the converter, showing variation in the power flow processed by port #2 for load variation.

Furthermore, at t = 0.12 s, the operational point of bridge 2 undergoes another modification, decreasing its power by 60%. This change does not affect the power processed by the other two bridges, while the power at port #1 experiences a 10% increase. The results indicate that, at t = 0.16 s, the load on port #2 is reduced by 0%. During this phase, the power processed by the other LV side bridges remains stable, and the output voltage is well-regulated. Hence, the efficacy of the described control structure is successfully corroborated.

Load disturbance at port #3 on the LV Side

Figure 15 displays a comparison of the output voltage of the QAB converter under the MDCS-MPC and PI controllers. The results indicate that the MDCS-MPC maintains the desired voltage level with minimal oscillations. It’s noteworthy that the rise time for the MDCS-MPC is significantly faster at 12.902 ms, compared to the PI controller’s 155.443 ms to reach a steady state at the start of the simulation. Additionally, during load changes, the PI controller shows significant overshoot and undershoot, as depicted in the current comparison in Fig. 16. Moreover, the implementation of MDCS-MPC effectively ensures power decoupling between ports, as depicted in Fig. 17, thereby preventing power transients from causing disturbances at other ports.

Fig. 15

Compares the output voltage response at port #3 under various load disturbances between the PI controller and the MDCS-MPC.

Fig. 16

Dynamic performance of the load current at port #3 using the PI controller and the MDCS-MPC strategy.

Fig. 17

Output voltage of ports #2 and #4 when the load disturbance occurs at port #3.

In Fig. 18, we evaluated the possibility of exchanging power between the source port #1 bridge and port #3 on the LV side. As observed, the power processed by bridge 3 on the LV side changes over time, while the total power at port #1 also changes according to port #3 changing. Notably, at t = 0.16 s in port #3, the load is reduced by 0%, and the processed power in the other bridges of the LV side remains constant, with a well-regulated output voltage. This result successfully verifies the performance of the control structure described.

Fig. 18

Dynamic operation of the converter, showing variation in the power flow processed by port #3 for load variation.

Load disturbance at port #4 on the LV side

To assess the impact of load disturbances at port #4 on the LV side, a series of load scenarios were investigated. These scenarios included a reference load of 50%, a 120% load test to evaluate controller stability, transitions from 80 to 50% load, and finally, a no-load state. Figure 19 provides a comparative analysis of the output voltage from the QAB converter under both the MDCS-MPC and PI controllers. The results revealed that, under the PI controller, the voltage at port #4 exhibited specific behaviors during the load transitions. In contrast, Fig. 20 shows that the PI controller experienced significant overshoots and undershoots during these transitions. However, the MDCS-MPC demonstrated improved dynamic response speed and minimized load voltage fluctuations. Additionally, the MDCS-MPC effectively decoupled power between ports, preventing disturbances at load port #4 from affecting other ports, as illustrated in Fig. 21.

Fig. 19

Comparison of port #4 output voltage under load disturbances: PI controller versus MDCS-MPC strategy.

Fig. 20

Dynamic load current performance at port #4: PI controller vs. developed MDCS-MPC strategy.

Fig. 21

Response of output voltage at ports #2 and #3 to a load disturbance at port #4.

Figure 22 explores the capacity for power exchange between the source port #1 bridge and port #4 on the LV side, displaying fluctuating power levels processed by bridge 4 over time, as well as variations in total power at port #1. Initially, at t = 0 s, the converter operates with balanced power (P₂ = P₃), maintaining port #4 at 50% power. Subsequently, at t = 0.04 s, a modification in the bridge 4 operation point increases its power by 12%, while the power through the other two bridges remains unchanged, and port #1 power increases by 15%. During the third phase, at t = 0.08 s, the bridge 4 operation point adjustment leads to a 0% reduction in its power, while the other bridges’ power is steady, and port #1 power decreases by 40%. Furthermore, at t = 0.12 s, an adjustment in the bridge 2 operation point elevates its power by 80%, with unchanged power at the other bridges and a 10% increase in port 1 power.

Fig. 22

Dynamic operation of the converter, showing variation in the power flow processed by port #4 for load variation.

This outcome highlights a 0% load reduction at t = 0.16 s in port #1, maintaining stable power processing in the LV side’s other bridges and a well-regulated output voltage, thereby confirming the control structure’s efficacy.

Responses to load disturbances across All LV-side bridges

Figures 23 and 24 provide a comprehensive analysis of the QAB converter’s performance, illustrating the output voltages and load currents at each port, respectively. The load conditions during the operation period were randomly designed, with different percentages of rated load connected to two ports, loads connected at different times, or all three ports supplying power simultaneously. Examination of the voltage waveform in Fig. 23 reveals minimal oscillations at each port during load changes, with a stable output voltage and an 18 ms rise at each port. The magnified windows in the figure further confirm the consistency of the voltage output. Similarly, the current waveform in Fig. 24 illustrates the individual control capability of the MDCS-MPC strategy, as each port supplies power to the randomly changing loads at different time intervals. The MDCS-MPC controller ensures the converter maintains the desired output current with minimal fluctuations, even during abrupt load changes. Overall, these results demonstrate the superior performance and robustness of the QAB converter under varying load conditions.

Fig. 23

Dynamic response of the output voltage at three ports under the MDCS-MPC during a load disturbance: (a) Load disturbance at port #2, (b) Load disturbance at port #3, and (c) Load disturbance at port #4.

Fig. 24

Load currents at each port of the QAB during a load disturbance under the MDCS-MPC strategy.

Figure 25 illustrates the dynamic results of power exchange between the source port #1 bridge and ports on the LV side, demonstrating the performance of the control structure and the bridge’s ability to process varying amounts of power. The power processed by the LV bridges changes over time, and the total power changes to balance the load. During the first period, the converter operates with unbalanced power (P₂ ≠ P₃ ≠ P₄), causing the LV bridges to process different amounts of power and change their operation points, as shown in Fig. 12. Additionally, a load change (total processed power) is observed. However, as seen in the results, the load is reduced by half, while the processed power on the LV side remains balanced, and the output voltage is well-regulated. These findings confirm the successful performance of the control structure.

Fig. 25

Dynamic operation of the converter, depicting the variation in the power flow processed by the LV bridges due to load variation.

System responses to variations in output voltage reference

Figure 26a illustrates the voltage waveforms of port #2 under the developed control scheme when its voltage increases to 160 V at t = 0.04 s and then decreases to 140 V at t = 0.08 s. The graph demonstrates the precise tracking of the output voltage of port #2 with its reference value, displaying the effectiveness of the control scheme. Moreover, the other port voltages stabilized within 0.01 ms and exhibited a fluctuation amplitude of 0.25 V (± 0.125 V). Similarly, in Figs. 26(b and c), the same reference variation occurs at ports #2 and #3, respectively. Hence, the developed control scheme is highly effective in achieving decoupling across different ports of the QAB converter and can accurately regulate the voltage reference changes.

Fig. 26

Dynamic response to variations in output voltage references: (a) Change in reference voltage at port #2, (b) Change in reference voltage at port #3, and (c) Change in reference voltage at port #4.

Sudden source voltage variation at port #1 and its impact on voltage overshoot at other ports

Figure 27 illustrates the voltage waveform across the ports of a QAB converter under the MDCS-MPC strategy. At t = 0.04 s, the voltage at port #1 experiences a sudden drop from 300 to 280 V, followed by an increase to 320 V at t = 0.08 s. The simulation results of this sudden change in the reference voltage at port #1 indicate that the voltages at ports #2, #3, and #4 remained stable. These results suggest that the MDCS-MPC strategy is effective in maintaining stable voltages across multiple ports of the QAB converter, even during abrupt changes in the reference voltage.

Fig. 27

Dynamic response of the output voltage of each port under the power source disturbance at port #1.

The MDCS-MPC control strategy stabilized the voltage, with no fluctuations observed. The MDCS-MPC demonstrated a fast dynamic response and essentially zero overshoots, with a very short control current adjustment time. These results indicate the effectiveness of the MDCS-MPC strategy.

Experimental evaluation

In order to validate the performance and reliability of the MDCS-MPC system, an experimental investigation was carried out using the Typhoon real-time simulation device HIL 602. The simulated QAB converter employed the same HIL 602, while the control component was designed with a control board incorporating a TMS320F28335 DSP and various interfacing circuits. This control board was directly linked to the HIL 602 for real-time simulation. The key circuit parameters used in the experiment were consistent with those utilized in the simulation, and the control parameters of the MDCS-MPC strategy for the experiments are outlined in Table 2. The test setup, shown in Figs. 28a and 23b, consist of both hardware and a software system, where the developed controller and system were implemented and executed on hardware using the Typhoon real-time simulation. To validate the superiority of the MDCS-MPC approach, an experimental comparison was conducted against the SPS control using the PI decoupling method, as in³.

Table 2 Control parameters.

Fig. 28

(a) HIL real time experimental platform [53]. (b) Process of HIL platform.

Steady-state operation waveforms

The steady-state waveforms are illustrated in Fig. 29, depicting the converter’s operation under steady-state conditions. Figure 29a displays the waveforms of leakage inductance current and voltage on bridges #1 (v₁, i_L1), #2 (v₂, i_L2), #3 (v₃, i_L3), and #4 (v₄, i_L4) for the converter employing the PI decoupling control strategy, showcasing soft switching ZVS on ports #1, #2, #3, and #4. The same waveforms for the MDCS-MPC strategy are presented in Fig. 29b, revealing remarkable similarity to the theoretical waveforms and featuring ZCS.

Fig. 29

Waveforms of leakage inductance current and voltage of the QAB transformer windings at MV and LV ports: (a) PI decoupling control strategy, and (b) MDCS-MPC strategy.

Dynamic operation

In the experimental investigation, the output voltage was tested for load disturbance. During the test, the load at port #2 was increased by 75% before returning to its original value (R₂ = 25 to 6.5 to 25). Figure 30a depicts the voltage waveforms of port #2 and the load current waveform under the developed control scheme. It’s apparent that only the voltage of port #2 experienced an overshoot when the load was disturbed, while the other voltages remained constant. Subsequently, the load current of port #2 was increased to 12.5A and then decreased back to 5A.

Fig. 30

Transient response of the output voltage of each port under load disturbance: (a) Port #2, (b) Port #3, (c) Port #4.

Furthermore, Fig. 30b, c display the corresponding waveforms when similar load disturbances occurred at ports #3 and #4, respectively. Notably, the voltage drop was only observed at the port where the load disturbance occurred, with almost no changes at the other two ports, demonstrating the improved port dynamic control performance offered by the MDCS-MPC strategy. This further validates the superior performance of the developed control scheme in terms of decoupling and anti-interference.

For comparison, we also conducted similar experiments under the PI decoupling control strategy. Figure 31a illustrates the waveforms of port voltages and port #2 load current as the load at port #2 increases by 75% and then returns to its original value. It is observed that the voltage overshoot of port #2 reaches 60 V, and the others are approximately 25 V during the load disturbance at port #2. The response time reaches 0.6 s, and the load current and voltage transients are considerably slower compared to those in Fig. 30 a. Additionally, Figs. 31b,c exhibit the corresponding waveforms when similar load disturbances occurred at ports #3 and #4, respectively. A voltage drop was observed at the port where the load disturbance occurred, with fluctuations occurring at the other two ports. These results emphasize the significant coupling characteristics of the PI decoupling control strategy.

Fig. 31

Transient response of the output voltage at each port under load disturbance using the PI decoupling control strategy: (a) Port #2, (b) Port #3, (c) Port #4.

Furthermore, comparative tests demonstrate that the controller, based on the MDCS-MPC control theory, not only accomplishes power decoupling between ports but also substantially improves the dynamic control performance of QAB ports.

System responses to variations in output voltage reference

The experimental analysis involved examining the variation in reference voltage for each port. Under the MDCS-MPC strategy, Fig. 32a illustrates the port voltages and load current waveforms as the reference voltage of port #2 increases to 200 V and then drops to 100 V. It is apparent that only the voltage at the port with the changing reference closely follows the reference value, while the voltages at the other ports remain steady at their respective reference values of 150 V. Additionally, the load current of port #2 increases from 10 to 15A before returning to 5A. The voltage drops induced by the reference voltage change at port #2 are minimal. Figures 32b, c demonstrate the dynamic waveforms when the reference values of ports #3 and #4 change, respectively. These figures show the accurate tracking of port voltages with their reference values when the reference values change, with only slight fluctuations in the port voltages that do not correspond to their reference values. Figure 32d presents the waveforms when the reference values of ports #3 and #4 change simultaneously. The experimental outcomes confirm that the developed control scheme achieves nearly perfect decoupling when there are variations in the output voltage reference.

Fig. 32

Dynamic response to output voltage reference variations under the developed strategy: (a) Reference voltage change at port #2, (b) Reference voltage change at port #3, (c) Reference voltage change at port #4, (d) Simultaneous reference voltage changes at ports #3 and #4.

For comparison, we conducted similar experiments using the PI decoupling control strategy. Figure 33a shows the port voltages and load current waveforms of port #2 as its reference voltage increases to 200 V and then decreases to 100 V. It is evident that the voltage overshoots of the other ports reach approximately 5 V, which is significantly higher than those observed with the developed control scheme. Figures 33b, c display the dynamic waveforms corresponding to changes in the reference values of ports #3 and #4, respectively. Figure 33d illustrates the waveforms when the reference values of ports #3 and #4 are altered simultaneously. These comparative tests demonstrate that the developed control scheme provides superior decoupling and significantly enhances the system’s response speed.

Fig. 33

Dynamic response to output voltage reference variations under the PI decoupling control strategy: (a) Reference voltage change at port #2, (b) Reference voltage change at port #3, (c) Reference voltage change at port #4, (d) Simultaneous reference voltage changes at ports #3 and #4.

Variation at port #1 and its impact on voltage overshoot at other ports

Another set of comparative experiments was performed under power supply disturbance. When the power supply voltage suddenly drops from 300 to 200 V, followed by an increase to 400 V, the input voltage and port voltage waveforms are depicted in Figs. 34a, b using the PI decoupling method and the MDCS-MPC strategy, respectively. In Fig. 34a, the voltage undershoots at each port are approximately 25 V, with an overshoot of around 35 V under PI decoupling control. However, under the control scheme, each port’s voltage shows only minor fluctuations, as depicted in Fig. 34b. Thus, the control scheme exhibits superior anti-interference performance compared to PI decoupling control regarding power source disturbances.

Fig. 34

Dynamic response to power source disturbance at port #1: (a) PI decoupling control scheme, (b) MDCS-MPC strategy.

To further demonstrate the superiority of the MDCS-MPC strategy, an efficiency comparison was conducted under different operating conditions between the MDCS-MPC and PI decoupling control strategy, as shown in Fig. 35. The results indicate that when the PI decoupling control strategy is employed, the converter reaches a peak efficiency of 94.4% at nominal load. Conversely, with the implementation of MDCS-MPC, the converter accomplishes a peak efficiency of 96.5% at nominal load. These findings confirm the feasibility and effectiveness of the MDCS-MPC approach.

Fig. 35

Efficiency comparison between PI control and MDCS-MPC control as a function of QAB converter output power.

Comparison with existing control methods

To the best of the author’s knowledge, a dedicated MDCS-MPC method for QAB converters has not yet been established in the current literature. Consequently, the MDCS-MPC method is compared with existing MDCS-MPC approaches designed for DAB converters. This comparison assesses various control methods, including the MDCS-MPC approach, based on multiple criteria: the necessity of the control strategy, angle resolution, power topology, cost function design, switching frequency, error tolerance, dynamic performance, parameter sensitivity, decoupling effectiveness, control complexity, and efficiency, as detailed in Table 3.

Table 3 Comparison with state-of-the-art control strategies.

Current control methods for DAB and grid-connected converters each contribute valuable features but also reveal limitations when applied to multi-port systems like QAB converters. López et al.³⁷ introduced MDCS-MPC with precise voltage and current control for DAB, achieving rapid response but at high computational complexity that limits scalability. Tarisciotti et al.³⁵ improved MDCS-MPC for stability with a flexible cost function, yet its high switching frequency demands restrict it to single-port systems. Shen et al.⁴¹ incorporated feedback correction to enhance robustness, but the added complexity makes it less suitable for real-time, multi-port applications. Sun et al.⁴⁰ employed hybrid modulation for ZVS, enhancing efficiency in partial load conditions; however, the need for additional sensing elements increases system complexity.

Other approaches, such as the model-free MDCS-MPC by Sun et al.⁴⁸ and model-free FCS-MPC⁴⁹, simplify control but at the cost of angle resolution and robustness, which are essential for high-performance systems. Zhang et al.⁴² developed a repeat model-based FCS-MPC for grid inverters, improving stability in grid settings but not adaptable to multi-port configurations like QAB. The multi-objective FCS-MPC by Scaglione et al.⁵⁰ supports multi-level inverters but introduces significant computational overhead. Simplified FCS-MPC³⁹ reduces computational load, but sacrifices control precision, making it unsuitable for applications requiring high dynamic performance.

The MDCS-MPC for QAB overcomes these limitations by offering a control design specifically for multi-port systems. It features high-resolution angle control and an optimized cost function that minimizes the need for manual tuning. Additionally, it offers robust error tolerance with adaptive feedback, all within a moderate complexity framework suitable for real-time operation. This approach maintains precise switching frequency control and supports efficient, stable power management across varying loads.

Conclusions

This study has introduced and validated a new MDCS-MPC strategy for QAB DC-DC converters for more electric aircraft applications. This innovative approach has effectively addressed the challenges posed by modulation variables, dynamic response requirements, and overall modeling complexity. Traditional control strategies, such as PI decoupling controllers, often fall short due to their simplistic nature and inability to account for complex converter dynamics. Through comparative analysis under identical simulation conditions and Hardware-in-the-Loop (HIL) experiments on the Typhoon 602 platform, several key conclusions have been drawn.

• 1. Load Disturbance Suppression: The MDCS-MPC strategy significantly reduces coupling between ports and robustly suppresses load disturbances originating from the same port, while the PI decoupling strategy achieves suboptimal decoupling outcomes.

• 2. Reference Voltage Tracking: In response to sudden changes in reference voltage, the MDCS-MPC strategy demonstrates superior decoupling performance, enabling precise tracking of the voltage reference values. Conversely, the PI controller decoupling strategy exhibits slightly inferior performance due to the absence of voltage sample information.

• 3. Source Voltage Disturbance Resistance: The MDCS-MPC strategy effectively resists source voltage disturbances, whereas the PI controller decoupling strategy performs slightly worse in this regard.

• 4. Dynamic Response Speed: The MDCS-MPC strategy exhibits a significantly faster dynamic response compared to the PI controller decoupling strategy. This improvement is attributed to the inclusion of the G₂ term in the cost functions, which plays a crucial role in minimizing oscillatory transient behavior. A substantial reduction in response time is observed, underscoring the effectiveness of the MDCS-MPC strategy.

The HIL real-time experiments on the Typhoon 602 platform further confirmed the practical feasibility and reliability of the MDCS-MPC strategy. The developed control scheme exhibited a fast dynamic response, negligible voltage overshoot or undershoot, and excellent anti-interference performance under various load and source voltage disturbances. Efficiency comparisons indicated that the MDCS-MPC strategy achieved higher efficiency than the PI decoupling control method, solidifying its promise as a superior solution for more electric aircraft applications.