High-step-up quadratic DC–DC converter based on switched capacitor and coupled inductor techniques

Abstract

This paper proposes a non-isolated quadratic high-step-up DC-DC converter. A coupled inductor and a switched capacitor cell are implemented in its structure to increase voltage gain. Balancing the capacitor and the coupled inductor plays the role of the resonant tank, which solves the problem of reverse recovery losses of its diodes. In this structure, soft switching conditions are established for some diodes and MOSFET, which reduces the switching losses of the converter. With a low number of components, the proposed converter achieves a high voltage gain. The diode-capacitor clamp circuit is utilized to reduce the negative effects caused by the leakage inductance and recover the energy stored in it. The performance of the proposed converter is analyzed in the continuous and discontinuous conduction modes. An analysis of design considerations, including inductors and capacitors, is presented. In addition, an analysis of the efficiency of the proposed topology is provided. The proposed topology is compared in terms of voltage gain, voltage/current stress across semiconductor components, and converter efficiency with related topologies. Finally, a 210 W (20 V/420 V) laboratory prototype is presented to verify the proposed converter's mathematical analysis and performance.

Introduction

The issue of energy conversion has been one of the main challenges in the last decade, and engineers are always looking for new ways to provide the required energy. The most important sources are fossil fuels and renewable energy sources. Unlike renewable energy sources, fossil fuels are limited and produce much pollution^1,2. As the output voltage of renewable energy systems is limited, power electronic converters are needed to provide high voltage gain. In the design of these converters, the output voltage gain, the voltage stress across the semiconductor elements, the number of elements, and the efficiency are considered^3,4,5. In order to increase the output voltage gain, a switched capacitor cell and a coupled inductor can be used. In these types of converters, the capacitors of switched capacitor cells are charged in parallel and discharged in series, which increases the voltage gain of the converter. Of course, in this case, the coupled inductor can be used in the mentioned cell structure to improve the diode reverse recovery problem^6,7. Also, the coupled inductor gives the converter higher degrees of freedom to increase output voltage gain and reduce voltage stress across the semiconductor elements⁸. In^9,10,11, a transformer has been used as an isolation technique in those structures. The presence of voltage spikes across semiconductor elements is the main disadvantage of these converters, which is caused by the leakage inductance of the transformer. The number of components used in the structure of the converter is another significant issue for DC-DC converters. The presence of a substantial quantity of components increases the circuit's volume and the construction cost. In addition, each of the elements also includes losses¹².

In^13,14, two symmetrical switched capacitor cells are implemented in order to increase the output voltage gain. In addition, a passive clamp circuit was used to recover the leakage energy and improve the voltage spike across the switch. In¹⁵, a SEPIC DC-DC converter is presented. The structure of this converter includes voltage multiplier cells to increase the output voltage gain. Besides, the passive clamp structure has been used to recover the leakage energy of the coupled inductor. High diode counts and hard switching conditions have reduced converter efficiency.

In^16,17, a diode-capacitor cell and two coupled inductors have been used to increase the output voltage gain. Also, in order to have soft switching conditions, the snubber capacitor is placed parallel to the main power switches. A large number of switches and the presence of a snubber capacitor and two coupled inductors increase the size of the structure of these converters. The DC–DC converter suggested in¹⁸ is based on the conventional boost converter. A switched capacitor cell has been used to increase its voltage gain in this structure; however, it has a low voltage gain. One of the methods to improve the efficiency is the quasi-resonant operation, which is utilized by the converters presented in^19,20. Also, two passive clamp circuits are used in their structure. In^21,22,23,24, the voltage lift technique was utilized to increase voltage gain. In this technique, energy storage elements such as capacitors and inductors are implemented in order to increase the output voltage gain and overcome the parasitic effects of the components. In^25,26,27, the input source and the output terminal do not have a common ground. This method makes these converters unsuitable for PV applications. In some converters, a three-coil coupled inductor has been used to increase the output voltage gain, which has a sizeable magnetic core^27,28,29. In the interleaved DC–DC converter presented in²⁹, two pairs of three-coil inductors and a voltage multiplier cell are utilized to increase the output voltage gain in a cascade structure. Despite the hard switching conditions, the large number of semiconductor elements in this converter has caused an increase in losses and, as a result, a decrease in the converter efficiency.

In this paper, a non-isolated high-step-up DC-DC converter is presented. In order to increase the voltage gain, a coupled inductor and the switched capacitor cell are used in its structure. Due to the presence of the clamp circuit, there is a low voltage stress across the semiconductor components, which increases efficiency and reduces construction costs. The clamp circuit in the proposed structure recovers the leakage energy of the coupled inductor and increases the voltage gain. Additionally, soft switching conditions are established, and the current waveforms flowing through some diodes and MOSFETs are quasi-resonant, which leads to reduced switching losses.

Proposed converter operation principles

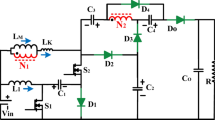
Figure 1 shows the structure of the suggested converter. In order to increase the output voltage gain, the coupled inductor and the switched capacitor technique are used. This structure contains two power switches (S₁, S₂), an inductor (L₁), a coupled inductor, four diodes (D₁, D₂, D₃ and D_O) and four capacitors (C₁, C₂, C₃ and C_O). The input source is V_in, and the output port is V_O. To simplify the steady-state analysis calculations, the following assumptions are considered:

• 1) All components of the converter are considered ideal.

• 2) The coupled inductor is modeled as a leakage inductor (L_K) and a magnetizing inductor (L_m) at the primary side with a coupling coefficient k = L_m/(L_m + L_k) and its turn ratio is n = n₂/n₁.

Fig. 1

Power circuit schematic of the proposed converter.

The key waveform of the suggested converter in Continues Conduction Mode (CCM) is shown in Fig. 2. In the CCM condition, the proposed converter has four operation modes, as shown in Fig. 3a–d. Both power switches are turned on and off simultaneously. So, the control structure of the proposed converter is simple.

Fig. 2

Key waveform of the proposed converter in CCM.

Fig. 3

The equivalent circuits of the operation modes. (a) mode I. (b) mode II. (c) mode III. (d) mode IV. (e) mode V. (CCM operation includes Figures (a–d) and DCM operation includes Figures (a–e)).

Mode I (t₀ < t < t₁): Regarding Fig. 3a, at the beginning of this time interval, switches S₁ and S₂ are simultaneously turned on, such that the power switch S₂ is turned on under ZCS (Zero Current Switching) conditions. In this transient mode, the output diode D_O is forward bias. Because of the influence of the reflected leakage inductance on the secondary side of the coupled inductor, the current passing through diode D_O drops to zero at the end of this time interval, resulting in a low reverse recovery issue.

Mode II (t₁ < t < t₂): In this operation mode, MOSFETs S₁ and S₂ remain in on state from the previous operating mode. Diodes D₂, and D₃ are turned on at ZCS conditions and D₁ and D_O are reversed bias in this mode. The input source charges L₁, and its current level increases linearly. Also, the current of L₁₁ is energized by the input source and C₁, and its current increases. C₂ and C₃ are charged through the secondary side of the coupled inductor. This operation mode ends when D₂ and D₃ are turned off at ZCS conditions. A schematic of the converter in this operational mode is illustrated in Fig. 3b. In this operation mode, the following equations are obtained:

$$ V_{L1}^{II} = V_{in} $$

(1)

$$ \frac{{V_{Lm}^{II} }}{k} = V_{in} + V_{C1} $$

(2)

$$ nV_{Lm}^{II} = V_{C2} = V_{C3} $$

(3)

$$ I_{C1}^{II} = I_{Lk} = I_{Lm} + nI_{L12} $$

(4)

$$ I_{C2}^{II} = I_{C3}^{II} = - \frac{{I_{L12} }}{2} $$

(5)

$$ I_{CO}^{II} = I_{O} $$

(6)

$$ f_{R} = \frac{1}{{T_{R} }} = \frac{1}{{2\pi \sqrt {L_{k} (\,C_{2} |\,|C_{3} )} }} $$

(7)

In order to eliminate the reverse recovery loss of D₂ and D₃ as well as reduce the switch turn-off loss, it is mandatory that the resonant time (T_R) be shorter than the turn-on time of the switching period (T_R < D × T_s) as illustrated in Fig. 2.

Mode III (t₂ < t < t₃): In this transient operation mode, the power switches are in the on state, and all the diodes are reversed bias. Similar to operation mode II, L₁ is charged by V_in, and L₁₁ is charged by V_in and C₁. In addition, the voltages of C₂ and C₃ remain constant. This operation mode ends when the power switches turn off. A schematic of the converter in this operational mode is shown in Fig. 3c. In this operation mode, the following equations are expressed:

$$ V_{L1}^{III} = V_{in} $$

(8)

$$ \frac{{V_{Lm}^{III} }}{k} = V_{in} + V_{C1} $$

(9)

$$ I_{C1}^{III} = I_{Lk} = I_{Lm} $$

(10)

$$ I_{CO}^{III} = I_{O} $$

(11)

Mode IV (t₃ < t < t₄): Regarding Fig. 3d, in this operation mode, D₂, D₃, and the power switches are in off state, and D₁ and D_O are forward biased. C₁ is charged by V_in and L₁. L₁₁, C₂, and C₃ are discharged, and the current passing through L₁₁ decreases. In addition, the input source, L₁₁, C₂, and C₃ charge C_O and supply the power to the output load. In this operation mode, the following equations are obtained:

$$ V_{L1}^{IV} = V_{in} - V_{C1} $$

(12)

$$ V_{O} = V_{in} + V_{C2} + V_{C3} - V_{Lm}^{IV} \left( {n + \frac{1}{k}} \right) $$

(13)

$$ I_{C1}^{IV} = - I_{L1} $$

(14)

$$ I_{C2}^{IV} = I_{C3}^{IV} = \frac{{I_{Lm} }}{n + 1} $$

(15)

$$ I_{CO}^{IV} = I_{O} - I_{C3}^{IV} $$

(16)

Mode V (t₄ < t < t₅): This operation mode corresponds to the DCM condition as shows in Figs. 3e and 4. In this case, D₁ is forward bias, and the rest of the semiconductor elements are in off state. C₁ is charged through the input source and L₁. C_O supplies the output load power. For this operation mode, the following equations are expressed:

$$ V_{L1}^{V} = V_{in} - V_{C1} $$

(17)

$$ I_{CO}^{V} = I_{O} $$

(18)

Fig. 4

Key waveforms of the proposed converter in DCM.

Steady state analysis

Voltage gain in CCM

By applying the volt-second balance principle for L₁ and substituting (1) and (13) into it, the following equation is expressed:

$$ V_{C1} = \frac{1}{1 - D}V_{in} $$

(19)

According to (2) and (19), the following equation is achieved for the voltage across L_m in operation mode II:

$$ V_{Lm}^{II} = \frac{k(2 - D)}{{1 - D}}V_{in} $$

(20)

Using (3) and (20), the following equation is obtained:

$$ V_{C2} = V_{C3} = nV_{Lm}^{II} = \frac{nk(2 - D)}{{1 - D}}V_{in} $$

(21)

By applying the volt-second balance low for L_m and according to (20), the voltage across L_m in operation mode IV is obtained as follows:

$$ V_{Lm}^{IV} = - \frac{kD(2 - D)}{{(1 - D)^{2} }}V_{in} $$

(22)

By substituting (21) and (22) into (12), the following equation for the voltage gain of the converter in CCM condition is calculated:

$$ M_{CCM} = \frac{{V_{O} }}{{V_{in} }} = \frac{{1 + nk(2 - D)^{2} }}{{(1 - D)^{2} }} $$

(23)

In the ideal case, assuming k = 1, the output voltage gain of the converter is expressed as follows:

$$ M_{CCM} = \frac{{V_{O} }}{{V_{in} }} = \frac{{1 + n(2 - D)^{2} }}{{(1 - D)^{2} }} $$

(24)

According to (24), the output current can be derived as:

$$ I_{O} = \frac{{(1 - D)^{2} }}{{1 + n(2 - D)^{2} }}I_{in} $$

(25)

Voltage stress across power semiconductors

Using mode II, the following equations are obtained:

$$ V_{D1} = V_{C1} $$

(26)

$$ V_{DO} = V_{O} + V_{C1} - V_{C3} $$

(27)

According to operation mode IV, the following equations are expressed:

$$ V_{S1} = V_{C1} $$

(28)

$$ V_{S2} = V_{in} - \frac{{V_{Lm}^{IV} }}{k} $$

(29)

$$ V_{D2} = V_{D3} = V_{C2} - nV_{Lm}^{IV} $$

(30)

According to (19), (22), (26), (28), and (29), the following equations are achieved:

$$ V_{D1} = V_{S1} = \frac{1}{1 - D}V_{in} $$

(31)

$$ V_{S2} = \frac{1}{{(1 - D)^{2} }}V_{in} $$

(32)

According to (19), (21), (22), (27), and (30), the following equations can be derived:

$$ V_{D2} = V_{D3} = \frac{nk(2 - D)}{{(1 - D)^{2} }}V_{in} $$

(33)

$$ V_{DO} = \frac{(2 - D)(1 + nk)}{{(1 - D)^{2} }}V_{in} $$

(34)

Current stress of power semiconductors

By applying the ampere-second balance low for C_O, the following equation for the current passing through C₃ in operation mode IV is achieved:

$$ I_{C3}^{IV} = \frac{1}{1 - D}I_{O} $$

(35)

Using (15) and (35), the following equation can be written:

$$ I_{Lm} = \frac{(1 + n)}{{1 - D}}I_{O} $$

(36)

According to (4) and (5), the current passing through C₂ in operation mode II is as follows:

$$ I_{C2}^{II} = \frac{{I_{Lm} - I_{C1}^{II} }}{2n} $$

(37)

By applying the ampere-second balance low for C₂ and according to (35) and (37), the following equation for the current passing through the capacitor C₁ in operation mode II can be obtained as:

$$ I_{C1}^{II} = I_{Lm} + \frac{2n}{D}I_{O} $$

(38)

Now, by substituting (36) into (38), the current passing through capacitor C₁ in operation mode II is achieved as follows:

$$ I_{C1}^{II} = \left( {\frac{1 + n}{{1 - D}} + \frac{2n}{D}} \right)I_{O} $$

(39)

Using (39), the current of C₁ in operation mode IV can be derived as follows:

$$ I_{C1}^{IV} = - D\left( {\frac{1 + n}{{(1 - D)^{2} }} + \frac{2n}{{D(1 - D)}}} \right)I_{O} $$

(40)

According to (36), (37), and (39), the current passing through C₂ in operation mode II is obtained as follows:

$$ I_{C2}^{II} = - \frac{1}{D}I_{O} $$

(41)

Using (14) and (40), inductor current L₁ is expressed as:

$$ I_{L1} = D\left( {\frac{1 + n}{{(1 - D)^{2} }} + \frac{2n}{{D(1 - D)}}} \right)I_{O} $$

(42)

According to operation mode II, it can be written:

$$ I_{S1} = I_{L1} + I_{C1}^{II} $$

(43)

$$ I_{S2} = I_{C1}^{II} $$

(44)

$$ I_{D2} = I_{D3} = - I_{C2}^{II} $$

(45)

According to operation mode IV, it can be written:

$$ I_{D1} = - I_{C1}^{IV} $$

(46)

$$ I_{DO} = I_{C3}^{IV} $$

(47)

Using (39) and (42) into (43), the current stress of S₁ can be obtained as follows:

$$ I_{S1} = \left( {\frac{1 + n}{{(1 - D)^{2} }} + \frac{2n}{{D(1 - D)}}} \right)I_{O} $$

(48)

Using (39) and (44), current stress of S₂ can be obtained as:

$$ I_{S2} = \left( {\frac{1 + n}{{1 - D}} + \frac{2n}{D}} \right)I_{O} $$

(49)

According to (35), (40), (41), (45-47), the following equations are obtained for the current stress of the diodes:

$$ I_{D1} = D\left( {\frac{1 + n}{{(1 - D)^{2} }} + \frac{2n}{{D(1 - D)}}} \right)I_{O} $$

(50)

$$ I_{D2} = I_{D3} = \frac{1}{D}I_{O} $$

(51)

$$ I_{DO} = \frac{1}{1 - D}I_{O} $$

(52)

Voltage gain in DCM

Discontinuous Conduction Mode (DCM) analysis is considered for the condition where the coupled inductor enters the DCM condition. The converter has five operation modes in DCM condition. These operation modes are shown in Fig. 3a-e. Figure 4 shows the key waveform of the suggested converter in DCM condition. According to this figure, by applying the volt-second balance low for L_m, the following equation is achieved:

$$ V_{Lm}^{II} D + V_{Lm}^{IV} \Delta_{1} = 0 $$

(53)

According to (13), (20) and (53), the voltage gain in DCM condition is obtained as:

$$ M_{DCM} = 1 + \frac{2nk(2 - D)}{{1 - D}} + \frac{D(2 - D)(1 + n)}{{\Delta_{1} (1 - D)}} $$

(54)

According to Fig. 4, the average value of the current passing through L_m is expressed as:

$$ I_{Lm} = \frac{{\Delta I_{Lm} }}{2} $$

(55)

According to (20) and (55), the average current passing through L_m is achieved as follows:

$$ I_{Lm} = \frac{kD(2 - D)}{{2f_{S} L_{m} (1 - D)}}V_{in} $$

(56)

By applying the ampere-second balance low for C_O, the following equation is obtained:

$$ I_{CO}^{II} D + I_{CO}^{IV} \Delta_{1} + I_{CO}^{V} (1 - D - \Delta_{1} ) = 0 $$

(57)

According to (6), (16), (18) and (57), the following equation can be written for C₃ in operating mode IV:

$$ I_{C3}^{IV} = \frac{1}{{\Delta_{1} }}I_{O} $$

(58)

According to (15) and (58), the following equation for the average current through L_m is achieved:

$$ I_{Lm} = \frac{1 + n}{{\Delta_{1} }}I_{O} $$

(59)

By substituting (56) into (59), the following equation for Δ₁ can be obtained:

$$ \Delta_{1} = \frac{{2f_{S} L_{m} (1 + n)(1 - D)}}{D(2 - D)R}M_{DCM} $$

(60)

According to (54) and (60), the output voltage gain of the converter in DCM condition is achieved as:

$$ M_{DCM} = \left( {\frac{2 - D}{{1 - D}}} \right)\left( {nk + \sqrt {n^{2} k^{2} + \frac{{D^{2} R}}{{2f_{S} L_{m} }}} } \right) $$

(61)

Using (23), (61), and assuming that the normalized input inductor time constant equals τ = f_sL_m/R, where R represents the load resistance, the boundary conditions between CCM and DCM are as follows:

$$ \tau_{DCM} = {{D^{2} } \mathord{\left/ {\vphantom {{D^{2} } {\left( {2\left( {\frac{{5 - 2D + D^{2} }}{(2 - D)(1 - D)}} \right) - 8} \right)}}} \right. \kern-0pt} {\left( {2\left( {\frac{{5 - 2D + D^{2} }}{(2 - D)(1 - D)}} \right) - 8} \right)}} $$

(62)

According to this equation, the boundary conduction mode (BCM), CCM, and DCM regions for n = 2 can be plotted as shown in Fig. 5.

Fig. 5

The proposed converter CCM and DCM regions.

Non-ideal voltage gain in CCM

The deviation of the non-ideal voltage gain of the proposed converter is influenced by parasitic parameters and leakage inductance. In this analysis, the resistances of the components are considered as follows: inductor and coupled inductor (r_L1, r_L11, r_L12); capacitors (r_C1, r_C2, r_C3, r_CO); switches (r_DS(on)1, r_DS(on)2); diodes (r_D1, r_D2, r_D3, r_DO), along with their forward voltage drops (V_F1, V_F2, V_F3, V_FO). By applying KVL in the loops containing L₁ and L_m the following equations are derived in the operating mode II:

$$ V_{L1}^{II} = V_{in} - r_{L1} I_{L1} - R_{ds1} (I_{L1} + I_{C1}^{II} ) $$

(63)

$$ V_{Lm}^{II} = kV_{in} + kV_{C1} - kI_{C1}^{II} \left( {r_{L11} + r_{C1} + R_{ds1} + R_{ds2} } \right) - kR_{ds1} I_{L1} $$

(64)

$$ V_{C2} + V_{C3} = 2nV_{Lm}^{II} - V_{F2} - V_{F3} - \frac{{V_{O} }}{DR}\left( {r_{C2} + r_{C3} + r_{D2} + r_{D3} } \right) $$

(65)

By substituting (65) into (64), it can be written:

$$ V_{C2} + V_{C3} = 2n\left[ {kV_{in} + kV_{C1} - kI_{C1}^{II} \left( {r_{L11} + r_{C1} + R_{ds1} + R_{ds2} } \right) - kR_{ds1} I_{L1} } \right] - V_{F2} - V_{F3} - \frac{{V_{O} }}{DR}\left( {r_{C2} + r_{C3} + r_{D2} + r_{D3} } \right) $$

(66)

By applying KVL in the loops including inductors L₁ and L_m, the following equations are obtained in the operating mode IV:

$$ V_{L1}^{IV} = V_{in} - V_{C1} - V_{F1} - I_{L1} (r_{L1} + r_{C1} + r_{D1} ) $$

(67)

$$ V_{Lm}^{IV} = \frac{k}{kn + 1}\left[ {V_{in} + V_{C2} + V_{C3} - V_{FO} - V_{O} - I_{Lm} (\frac{{r_{L11} + r_{L12} + r_{C2} + r_{C3} + r_{DO} }}{n + 1})} \right] $$

(68)

By applying the volt-second balance for L₁, the following equation for the voltage across the capacitor C₁ is obtained:

$$ V_{C1} = \frac{{V_{in} }}{1 - D} - I_{L1} \left( {\frac{{r_{L1} + DR_{ds1} }}{1 - D} + r_{C1} + r_{D1} } \right) - \frac{{DR_{ds1} }}{1 - D}I_{C1}^{II} - V_{F1} $$

(69)

By applying the volt-second balance for L_m, the following equation is obtained:

$$ \begin{gathered} V_{in} \left( {\frac{knD + 1}{{1 - D}}} \right) + V_{C1} \frac{{D\left( {kn + 1} \right)}}{1 - D} - I_{C1}^{II} \frac{{D\left( {kn + 1} \right)\left( {r_{L11} + r_{C1} + R_{ds1} + R_{ds2} } \right)}}{1 - D} \hfill \\ - I_{L1} \frac{{D\left( {kn + 1} \right)R_{ds1} }}{1 - D} + V_{C2} + V_{C3} - V_{FO} - I_{Lm} \left( {\frac{{r_{L11} + r_{L12} + r_{C2} + r_{C3} + r_{DO} }}{n + 1}} \right) = V_{O} \hfill \\ \end{gathered} $$

(70)

By substituting (66) into (70), it can be written:

$$ \begin{gathered} \overbrace {{\left[ {\frac{{DR + \left( {r_{C2} + r_{C3} + r_{D2} + r_{D3} } \right)}}{DR}} \right]}}^{{A_{2} }}V_{O} = V_{in} \left( {\frac{knD + 1}{{1 - D}} + 2nk} \right) + V_{C1} \left[ {\frac{{D\left( {kn + 1} \right)}}{1 - D} + 2nk} \right] \\ - I_{C1}^{II} \left[ {\frac{{D\left( {kn + 1} \right)\left( {r_{L11} + r_{C1} + R_{ds1} + R_{ds2} } \right)}}{1 - D} + 2nk\left( {r_{L11} + r_{C1} + R_{ds1} + R_{ds2} } \right)} \right] \\ - I_{L1} \left[ {\frac{{D\left( {kn + 1} \right)R_{ds1} }}{1 - D} + 2nkR_{ds1} } \right] - I_{Lm} \overbrace {{\left[ {\frac{{r_{L11} + r_{L12} + r_{C2} + r_{C3} + r_{DO} }}{n + 1}} \right]}}^{{A_{1} }} \\ - V_{F2} - V_{F3} - V_{FO} \\ \end{gathered} $$

(71)

By substituting (69) into (71), the following equation is obtained:

$$ \begin{gathered} A_{2} V_{O} = V_{in} \overbrace {{\left[ {\frac{knD + 1 + 2nk}{{1 - D}} + \frac{{D\left( {kn + 1} \right)}}{{\left( {1 - D} \right)^{2} }} + 2nk} \right]}}^{{A_{3} }} \\ - I_{L1} \overbrace {{\left[ {\frac{{D\left( {kn + 1} \right)R_{ds1} }}{1 - D} + 2nkR_{ds1} + \left( {\frac{{D\left( {kn + 1} \right)}}{1 - D} + 2nk} \right)\left( {\frac{{r_{L1} + DR_{ds1} }}{1 - D} + r_{C1} + r_{D1} } \right)} \right]}}^{{A_{4} }} \\ - I_{C1}^{II} \overbrace {{\left[ {\frac{{D\left( {kn + 1} \right)\left( {r_{L11} + r_{C1} + R_{ds1} + R_{ds2} } \right)}}{1 - D} + 2nk\left( {r_{L11} + r_{C1} + R_{ds1} + R_{ds2} } \right) + \frac{{D^{2} \left( {kn + 1} \right)R_{ds1} }}{{\left( {1 - D} \right)^{2} }} + \frac{{2nkDR_{ds1} }}{1 - D}} \right]}}^{{A_{5} }} \\ - A_{1} I_{Lm} - V_{F1} \overbrace {{\left[ {\frac{{D\left( {kn + 1} \right)}}{1 - D} + 2nk} \right]}}^{{A_{6} }} - V_{F2} - V_{F3} - V_{FO} \\ \end{gathered} $$

(72)

By simplifying Eq. (72), it can be written:

$$ V_{O} = \frac{{A_{3} }}{{A_{2} }}V_{in} - \frac{{A_{4} }}{{A_{2} }}I_{L1} - \frac{{A_{5} }}{{A_{2} }}I_{C1}^{II} - \frac{{A_{1} }}{{A_{2} }}I_{Lm} - \frac{{A_{6} }}{{A_{2} }}V_{F1} - \frac{1}{{A_{2} }}\left( {V_{F2} + V_{F3} + V_{FO} } \right) $$

(73)

According to (36), (39), and (42), the following equations are expressed:

$$ I_{L1} = D\left( {\frac{1 + n}{{(1 - D)^{2} }} + \frac{2n}{{D(1 - D)}}} \right)\frac{{V_{O} }}{R} $$

(74)

$$ I_{C1}^{II} = \left( {\frac{1 + n}{{1 - D}} + \frac{2n}{D}} \right)\frac{{V_{O} }}{R} $$

(75)

$$ I_{Lm} = \frac{(1 + n)}{{1 - D}}\frac{{V_{O} }}{R} $$

(76)

By substituting (74-76) into (73), it can be written:

$$ \begin{gathered} V_{O} = \frac{{A_{3} }}{{A_{2} }}V_{in} - \frac{{A_{4} D}}{{A_{2} }}\left[ {\frac{1 + n}{{\left( {1 - D} \right)^{2} }} + \frac{2n}{{D\left( {1 - D} \right)}}} \right]\frac{{V_{O} }}{R} - \frac{{A_{5} }}{{A_{2} }}\left[ {\frac{1 + n}{{1 - D}} + \frac{2n}{D}} \right]\frac{{V_{O} }}{R} \\ - \frac{{A_{1} }}{{A_{2} }}\left[ {\frac{1 + n}{{1 - D}}} \right]\frac{{V_{O} }}{R} - \frac{{A_{6} }}{{A_{2} }}V_{F1} - \frac{1}{{A_{2} }}\left( {V_{F2} + V_{F3} + V_{FO} } \right) \\ \end{gathered} $$

(77)

By simplifying (77), the following equation is obtained:

$$ \begin{gathered} V_{O} \overbrace {{\left[ {1 + \frac{{A_{4} D}}{{A_{2} R}}\left[ {\frac{1 + n}{{\left( {1 - D} \right)^{2} }} + \frac{2n}{{D\left( {1 - D} \right)}}} \right] + \frac{{A_{5} }}{{A_{2} R}}\left[ {\frac{1 + n}{{1 - D}} + \frac{2n}{D}} \right] + \frac{{A_{1} }}{{A_{2} R}}\left[ {\frac{1 + n}{{1 - D}}} \right]} \right]}}^{{A_{7} }} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{{A_{2} }}\left[ {A_{3} V_{in} - A_{6} V_{F1} - \left( {V_{F2} + V_{F3} + V_{FO} } \right)} \right] \hfill \\ \end{gathered} $$

(78)

By simplifying (78), the non-ideal output voltage of the proposed converter with the influence of leakage inductance and parasitic resistances of the elements is obtained as follows:

$$ V_{O} = \frac{1}{{A_{2} A_{7} }}\left[ {A_{3} V_{in} - A_{6} V_{F1} - \left( {V_{F2} + V_{F3} + V_{FO} } \right)} \right] $$

(79)

Considering (79) and according to Table 2, the non-ideal voltage gain versus duty cycle D is illustrated in Fig. 6. This figure shows how voltage gain changes with the duty cycle (D) for both an ideal and a non-ideal power converter. The solid red line represents the ideal theoretical case, while the blue dashed line accounts for non-ideal model, assuming an output power of 210 W. Figure 6 is plotted in k = 0.985 and R = 840 Ω. As can be seen, the effect of leakage inductance and parasitic resistances is less at lower duty cycles leading to a comparatively higher efficiency.

Fig. 6

Effect of the leakage inductance and parasitic components on the output voltage gain.

The small inset zooms in on a specific range (around D = 0.5) to highlight the gap between the two models. As expected, the non-ideal case results in a lower voltage gain due to practical factors like parasitic resistances and switching losses. Interestingly, the non-ideal gain peaks sharply at high duty cycles before dropping, indicating potential instability or inefficiency in that region.

Design considerations

Inductor design

The voltage across the inductor is proportional to the current that passes through the inductor per unit of time. So, it can be written as:

$$ V_{L} = L\frac{{\Delta I_{L} }}{\Delta t} $$

(80)

By considering the maximum acceptable current ripple of 20% for inductors L₁ and L_m and according to operation mode II and substituting (1) and (20) into (80), the minimum inductor inductance of L₁ and L_m are obtained from the following equation:

$$ L_{1} > \frac{{DV_{in} }}{{\Delta I_{L} f_{S} }} = \frac{{DV_{in} }}{{20\% I_{L1} f_{S} }} = \frac{{D(1 - D)^{2} R}}{{20\% M\left[ {D(1 + n) + 2n(1 - D)} \right]f_{S} }} $$

(81)

$$ L_{m} > \frac{{D(2 - D)V_{in} }}{{\Delta I_{Lm} (1 - D)f_{S} }} = \frac{{D(2 - D)V_{in} }}{{20\% I_{Lm} (1 - D)f_{S} }} = \frac{D(2 - D)R}{{20\% M(1 + n)f_{S} }} $$

(82)

Capacitor design

The current passing through the capacitor is proportional to the voltage changes across the capacitor per unit of time. So, it can be written as:

$$ I_{C} = C\frac{{\Delta V_{C} }}{\Delta t} $$

(83)

By considering the maximum acceptable ripple of voltage for capacitors usually 1% of the voltage across capacitor C₁) and according to operation mode II and using (39) and (83), the following equation is obtained:

$$ C_{1} > \frac{{(D + 2n - nD)I_{O} }}{{\Delta V_{C1} (1 - D)f_{S} }} = \frac{{(D + 2n - nD)P_{out} }}{{1\% V_{C1} (1 - D)V_{O} f_{S} }} $$

(84)

According to (5), the current passing through C₁ and C₂ is equal in operation mode II. By taking into consideration the maximum acceptable voltage ripple for capacitors (usually 1% of the voltage across capacitor C₂, C₃, and C_O).

And by substituting (6) and (41) into (83), the following equations can be written:

$$ C_{2} > \frac{{I_{O} }}{{\Delta V_{C2} f_{S} }} = \frac{{P_{out} }}{{1\% V_{C2} V_{O} f_{S} }} $$

(85)

$$ C_{3} > \frac{{I_{O} }}{{\Delta V_{C3} f_{S} }} = \frac{{P_{out} }}{{1\% V_{C3} V_{O} f_{S} }} $$

(86)

$$ C_{O} > \frac{{DI_{O} }}{{\Delta V_{CO} f_{S} }} = \frac{{DP_{out} }}{{1\% V_{CO} V_{O} f_{S} }} $$

(87)

Efficiency analysis

In this section, the converter efficiency is investigated by considering the presence of parasitic resistances of the elements. Table 1 shows the RMS values of the current passing through the elements by considering n = 2, D = 0.5, and output resistance R = 840 Ω. Table 2 displays the power loss breakdown across different proposed converter components. In this table, V_F denotes the forward voltage drop of the diode. R_ds and r_D are the on-state resistance of the switch and the diode, respectively. Internal resistances of the capacitor and the inductor are represented by r_C and r_L, respectively. In addition, the power semiconductors specification and their part numbers are provided. Figure 7 shows the power loss distributions of the constituent elements of the suggested converter. According to this figure, the highest share of power losses is related to diode losses, and the lowest is related to capacitor losses. The efficiency and voltage gain curves of the converter versus the duty cycle and for n = 2 are shown in Fig. 8. As shown in this figure, although the voltage gain of the converter increases with the increase of the duty cycle, the efficiency of the converter is acceptable up to a certain range and then decreases. As can be seen, at high-duty cycle ranges, conduction losses increase, and efficiency is reduced.

Table 1 RMS current values of the components.

Table 2 Power losses distribution.

Fig. 7

Power loss distributions of the proposed topology at 210 W output power.

Fig. 8

Efficiency and voltage gain curves versus duty cycle.

Inductor losses: The conduction losses of the inductor and coupled inductor are calculated as following equations:

$$ \left\{ \begin{gathered} p_{L,Cond}^{loss} = r_{L} (I_{L}^{RMS} )^{2} \hfill \\ p_{L1,Cond}^{loss} = 0.01 \times (7)^{2} = 0.49W \hfill \\ p_{L\_Primary,\,Cond}^{loss} = 0.01 \times (5)^{2} = 0.25W \hfill \\ p_{L\_Secondary,\,Cond}^{loss} = 0.022 \times (1.58)^{2} = 0.05W \hfill \\ \end{gathered} \right. $$

(88)

$$ P_{L,Cond\_total}^{loss} = P_{L1,Cond}^{loss} + P_{L\_Primary,Cond}^{loss} + P_{L\_Secondary,Cond}^{loss} = 0.79\,W $$

(89)

The core power losses related to the inductors is calculated as³⁰:

$$ P_{C} = kf_{s}^{\alpha } B_{m}^{\beta } $$

(90)

The power loss (P_C) is expressed in unit W/kg. The parameters α, β and k known as the Steinmetz coefficients, are typically specified by manufacturers for various core materials. For ferrite materials, the values of α can vary from 1 to 2, (1 ≤ α ≤ 2). Based on Faraday's Law, it can be written:

$$ V_{L} = N\frac{d\varphi (t)}{{dt}} = NA_{c} \frac{dB(t)}{{dt}} $$

(91)

The parameter A_c represents the core area as specified by manufacturers for various types of magnetic cores. N is the turns of inductor's windings. Hence, the peak flux density of ΔB for the inductor and the coupled inductor, can be determined as follows:

$$ \left\{ \begin{gathered} \Delta B_{L1} = \frac{1}{{N_{L1} A_{C\_L1} }}\int\limits_{0}^{{DT_{s} }} {V_{L1} dt = } \frac{{V_{L1} DT_{s} }}{{N_{L1} A_{C\_L1} }} = \frac{{V_{L1} D}}{{N_{L1} A_{C\_L1} f_{s} }} \hfill \\ \Delta B_{L\_Primary} = \frac{1}{{N_{L\_Primary} A_{C\_CL} }}\int\limits_{0}^{{DT_{s} }} {V_{L\_Primary} dt = } \frac{{V_{L\_Primary} DT_{s} }}{{N_{L\_Primary} A_{C\_CL} }} = \frac{{V_{L\_Primary} D}}{{N_{L\_Primary} A_{C\_CL} f_{s} }} \hfill \\ \Delta B_{L\_Secondary} = \frac{1}{{N_{L\_Secondary} A_{C\_CL} }}\int\limits_{0}^{{DT_{s} }} {V_{L\_Secondary} dt = } \frac{{V_{L\_Secondary} DT_{s} }}{{N_{L\_Secondary} A_{C\_CL} }} = \frac{{V_{L\_Secondary} D}}{{N_{L\_Secondary} A_{C\_CL} f_{s} }} \hfill \\ \end{gathered} \right. $$

(92)

The core loss in both inductor and coupled inductor can be expressed as P_Core = P_CM, where M represents the mass of the core. Therefore, considering B_m = ΔB/2, the core loss of inductor and coupled inductor is calculated as:

$$ \begin{gathered} P_{Core}^{loos} = kf_{s}^{\alpha } B_{m1}^{\beta } M_{L1} + kf_{s}^{\alpha } B_{m\_Primary}^{\beta } M_{CL} + kf_{s}^{\alpha } B_{m\_Secondary}^{\beta } M_{CL} \\ = kf_{s}^{\alpha } \left[ {B_{m1}^{\beta } M_{L1} + \left( {B_{m\_Primary}^{\beta } + B_{m\_Secondary}^{\beta } } \right)M_{CL} } \right] \\ = kf_{s}^{\alpha } \left[ {\left( {\frac{{V_{L1} D}}{{2N_{L1} A_{C\_L1} f_{s} }}} \right)^{\beta } M_{L1} + \left( {\left( {\frac{{V_{L\_Primary} D}}{{2N_{L\_Primary} A_{C\_CL} f_{s} }}} \right)^{\beta } + \left( {\frac{{V_{L\_Secondary} D}}{{2N_{L\_Secondary} A_{C\_CL} f_{s} }}} \right)^{\beta } } \right)M_{CL} } \right] \\ = 5.597 \, \times \, 10^{ - 4} \times (50 \times 10^{3} )^{1.43} \times \left[ {\left( {0.05618} \right)^{2.85} \times 0.089 + \left( {\left( {0.08498} \right)^{2.85} + \left( {0.08498} \right)^{2.85} } \right) \times 0.215} \right] \\ = 2934.15 \times \left[ {0.000025 + 0.00019 + 0.00019} \right] = 1.19\,W \\ \end{gathered} $$

(93)

The parameters utilized for the calculation of the core losses are as:

k = 5.597 × 10⁻⁴, α = 1.43, β = 2.85, M_L1 = 0.089 kg, M_CL = 0.215, A_{C_L1} = 178mm², A_{c_CL} = 353mm² fs = 50 kHz.

The total power loss of inductors is obtained as follows:

$$ P_{L\_total}^{loss} = P_{L,\,Cond\_total} + P_{Core} = 0.79 + 1.19 = 1.98W $$

(94)

Switch losses: The power losses of the switches are determined as:

$$ \left\{ \begin{gathered} P_{SW}^{loss} = R_{ds} (I_{S}^{RMS} )^{2} + \frac{1}{{2T_{S} }}\left[ {I_{ds(on)} V_{ds} t_{(on)} + I_{ds(off)} V_{ds} t_{(off)} } \right] \hfill \\ P_{SW1}^{loss} = 0.0048 \times (9.78)^{2} + 25 \times 10^{3} \left[ {5.5 \times 23 \times 20 \times 10^{ - 9} + 6 \times 17 \times 37 \times 10^{ - 9} } \right] = 0.62W \hfill \\ P_{SW2}^{loss} = 0.0048 \times (4.89)^{2} + 25 \times 10^{3} \left[ {2.5 \times 35 \times 20 \times 10^{ - 9} + 2.5 \times 35 \times 37 \times 10^{ - 9} } \right] = 0.25W \hfill \\ \end{gathered} \right. $$

(95)

C_OSS is the parasitic capacitor of the switch. P_Coss is obtained as follows³¹:

$$ \left\{ \begin{gathered} P_{Coss} = \frac{1}{2}f_{S} CossV_{DS}^{2} \hfill \\ P_{Coss,S1} = \frac{1}{2}f_{S} C_{OSS,S1} \left( {\frac{{V_{in1} }}{1 - D}} \right)^{2} = \frac{1}{2} \times 50000 \times 476 \times 10^{ - 12} \left( {\frac{20}{{1 - 0.5}}} \right)^{2} = 0.02W \hfill \\ P_{Coss,S2} = \frac{1}{2}f_{S} C_{OSS,S2} \left( {\frac{{V_{in1} }}{{\left( {1 - D} \right)^{2} }}} \right)^{2} = \frac{1}{2} \times 50000 \times 476 \times 10^{ - 12} \left( {\frac{20}{{(1 - 0.5)^{2} }}} \right)^{2} = 0.08W \hfill \\ \end{gathered} \right. $$

(96)

The total power loss of the switches is obtained from the following equation:

$$ P_{SW\_total}^{loss} = P_{SW1}^{loss} + P_{SW2}^{loss} + P_{Coss,S1} + P_{Coss,S2} = 0.62 + 0.25 + 0.02 + 0.08 = 0.97W $$

(97)

Diode losses: The power losses of the diodes are determined as:

$$ \left\{ \begin{gathered} P_{D}^{loss} = V_{F} I_{D\_avg} + (I_{D}^{RMS} )^{2} r_{D} \hfill \\ P_{D1}^{loss} = 0.6 \times 3.45 + (4.89)^{2} \times 0.02 = 2.55W \hfill \\ P_{D2}^{loss} = 0.5 \times 0.49 + (0.7)^{2} \times 0.02 = 0.25W \hfill \\ P_{D3}^{loss} = 0.5 \times 0.49 + (0.7)^{2} \times 0.02 = 0.25W \hfill \\ P_{Do}^{loss} = 0.7 \times 0.49 + (0.7)^{2} \times 0.017 = 0.35W \hfill \\ \end{gathered} \right. $$

(98)

The total power loss of the diodes is obtained from the following equation:

$$ P_{D\_total}^{loss} = P_{D1}^{loss} + P_{D2}^{loss} + P_{D3}^{loss} + P_{Do}^{loss} = 3.4W $$

(99)

Capacitor losses: Losses of the capacitors are determined as follows:

$$ \left\{ \begin{gathered} P_{C}^{loss} = (I_{C}^{RMS} )^{2} \times ESR \hfill \\ P_{C1}^{loss} = (6.91)^{2} \times 0.01 = 0.48W \hfill \\ P_{C2}^{loss} = (1)^{2} \times 0.015 = 0.015W \hfill \\ P_{C3}^{loss} = (1)^{2} \times 0.015 = 0.015W \hfill \\ P_{CO}^{loss} = (0.49)^{2} \times 0.025 = 0.006W \hfill \\ \end{gathered} \right. $$

(100)

The total power loss of the capacitors is obtained as the following equation:

$$ P_{C\_total}^{loss} = P_{C1}^{loss} + P_{C2}^{loss} + P_{C3}^{loss} + P_{CO}^{loss} = 0.51W $$

(101)

Therefore, the total power losses P_Loss is written as:

$$ P_{total}^{loss} = P_{L\_total}^{loss} + P_{SW\_total}^{loss} + P_{D\_total}^{loss} + P_{C\_total}^{loss} = 6.86W $$

(102)

Consequently, the total efficiency of the proposed converter can be calculated as:

$$ \eta_{Converter} = \frac{{P_{o} }}{{P_{o} + P_{total}^{loss} }} \times 100\% = \frac{210}{{210 + 6.86}} \times 100\% = 96.8\% $$

(103)

Dynamic model and control method

The proposed topology consists of six storage elements, where the voltage and current of the components can be derived as follows:

First stage:

$$ V_{L1}^{II} = V_{in} \Rightarrow \frac{{di_{L1} }}{dt} = \frac{{V_{in} }}{{L_{1} }} $$

(104)

$$ V_{Lm}^{II} = k\left( {V_{in} + V_{C1} } \right) \Rightarrow \frac{{di_{Lm} }}{dt} = \frac{{k\left( {V_{in} + V_{C1} } \right)}}{{L_{m} }} $$

(105)

$$ i_{C1}^{II} = i_{Lm} + \frac{2n}{D}I_{O} \Rightarrow \frac{{dv_{C1} }}{dt} = \frac{{i_{Lm} }}{{C_{1} }} + \frac{2n}{{DC_{1} }}I_{O} $$

(106)

$$ i_{C2}^{II} = - \frac{{I_{O} }}{D} \Rightarrow \frac{{dv_{C2} }}{dt} = - \frac{{I_{O} }}{{DC_{2} }} $$

(107)

$$ i_{C3}^{II} = - \frac{{I_{O} }}{D} \Rightarrow \frac{{dv_{C3} }}{dt} = - \frac{{I_{O} }}{{DC_{3} }} $$

(108)

$$ i_{CO}^{II} = I_{O} \Rightarrow \frac{{dv_{CO} }}{dt} = \frac{{I_{O} }}{{C_{O} }} $$

(109)

Second stage:

$$ V_{L1}^{IV} = V_{in} - V_{C1} \Rightarrow \frac{{di_{L1} }}{dt} = \frac{{V_{in} - V_{C1} }}{{L_{1} }} $$

(110)

$$ V_{Lm}^{IV} = \frac{{k\left( {V_{O} - V_{in} - V_{C2} - V_{C3} } \right)}}{n + 1} \Rightarrow \frac{{di_{Lm} }}{dt} = - \frac{{k\left( {V_{O} - V_{in} - V_{C2} - V_{C3} } \right)}}{{\left( {n + 1} \right)L_{m} }} $$

(111)

$$ i_{C1}^{IV} = - i_{L1} \Rightarrow \frac{{dv_{C1} }}{dt} = - \frac{{i_{L1} }}{{C_{1} }} $$

(112)

$$ i_{C2}^{IV} = \frac{{i_{Lm} }}{n + 1} \Rightarrow \frac{{dv_{C2} }}{dt} = \frac{{i_{Lm} }}{{\left( {n + 1} \right)C_{2} }} $$

(113)

$$ i_{C3}^{IV} = \frac{{i_{Lm} }}{n + 1} \Rightarrow \frac{{dv_{C3} }}{dt} = \frac{{i_{Lm} }}{{\left( {n + 1} \right)C_{3} }} $$

(114)

$$ i_{CO}^{IV} = - i_{C3}^{IV} + I_{O} \Rightarrow \frac{{dv_{CO} }}{dt} = - \frac{{i_{Lm} }}{{\left( {n + 1} \right)C_{O} }} + \frac{{I_{O} }}{{C_{O} }} $$

(115)

To derived state space vectors, these equations can be rewritten as follows:

$$ \frac{dx}{{dt}} = X^{II} D + X^{IV} \left( {1 - D} \right) $$

(116)

Therefore, the achieved equations can be stated as follows:

$$ \frac{{di_{L1} }}{dt} = \frac{{V_{in} }}{{L_{1} }} - \frac{{\left( {1 - D} \right)V_{C1} }}{{L_{1} }} $$

(117)

$$ \frac{{di_{Lm} }}{dt} = \frac{k}{{L_{m} }}\left[ {\frac{1 + nD}{{n + 1}}V_{in} + V_{C1} D + \frac{1 - D}{{n + 1}}\left( {V_{C2} + V_{C3} - V_{Co} } \right)} \right] $$

(118)

$$ \frac{{dv_{C1} }}{dt} = \frac{D}{{C_{1} }}i_{Lm} + \frac{{2nV_{Co} }}{{R_{O} C_{1} }} - \frac{1 - D}{{C_{1} }}i_{L1} $$

(119)

$$ \frac{{dv_{C2} }}{dt} = - \frac{{V_{O} }}{{DR_{O} C_{2} }}D + \frac{{\left( {1 - D} \right)}}{{\left( {n + 1} \right)C_{2} }}i_{Lm} \Rightarrow \frac{{dv_{C2} }}{dt} = - \frac{{V_{O} }}{{R_{O} C_{2} }} + \frac{{\left( {1 - D} \right)}}{{\left( {n + 1} \right)C_{2} }}i_{Lm} $$

(120)

$$ \frac{{dv_{C3} }}{dt} = - \frac{{V_{O} }}{{DR_{O} C_{3} }}D + \frac{{\left( {1 - D} \right)}}{{\left( {n + 1} \right)C_{3} }}i_{Lm} \Rightarrow \frac{{dv_{C3} }}{dt} = - \frac{{V_{O} }}{{R_{O} C_{3} }} + \frac{{\left( {1 - D} \right)}}{{\left( {n + 1} \right)C_{3} }}i_{Lm} $$

(121)

$$ \frac{{dv_{Co} }}{dt} = \frac{{V_{Co} }}{{R_{O} C_{O} }}D + \left( { - \frac{{i_{Lm} }}{{\left( {n + 1} \right)C_{O} }} + \frac{{V_{O} }}{{R_{O} C_{O} }}} \right)\left( {1 - D} \right) \Rightarrow \frac{{dv_{Co} }}{dt} = \frac{{V_{Co} }}{{R_{O} C_{O} }} + \frac{{\left( {1 - D} \right)}}{{\left( {n + 1} \right)C_{o} }}i_{Lm} $$

(122)

Dynamic modeling of the proposed converter

For dynamic response analysis, independent storage elements are considered as state variables vector (x). Given that the voltage equations for capacitors C₂ and C₃ are identical, one of them can be excluded to simplify the analysis. In this converter, L₁ , L_m, C₁, C₂, and C_o are selected as state variables. The state variables vector (x), input vector (u), and output vector (y) are considered as follows:

$$ \left\{ \begin{gathered} x^{T} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {i_{L1} } & {i_{Lm} } \\ \end{array} } & {v_{C1} } \\ \end{array} } & {v_{C2} } & {v_{Co} } \\ \end{array} } \right] \hfill \\ u = [V_{in} ] \hfill \\ y^{T} = [V_{o} ] \hfill \\ \end{gathered} \right. $$

(123)

The average state space of the overall system can be displayed as follows

$$ \left\{ \begin{gathered} \mathop x\limits^{ \cdot} = Ax + Bu \hfill \\ y = Cx + Du \hfill \\ \end{gathered} \right. $$

(124)

Equation (124) can be expressed as:

$$ \mathop x\limits^{ \cdot } = \left[ {\begin{array}{*{20}c} 0 & 0 & { - \frac{{\left( {1 - D} \right)}}{{L_{1} }}} & 0 & 0 \\ 0 & 0 & {\frac{kD}{{L_{m} }}} & {\frac{{k\left( {1 - D} \right)}}{{L_{m} \left( {n + 1} \right)}}} & { - \frac{{k\left( {1 - D} \right)}}{{L_{m} \left( {n + 1} \right)}}} \\ { - \frac{1 - D}{{C_{1} }}} & {\frac{D}{{C_{1} }}} & 0 & 0 & {\frac{2n}{{R_{O} C_{1} }}} \\ 0 & {\frac{{\left( {1 - D} \right)}}{{\left( {n + 1} \right)C_{2} }}} & 0 & 0 & { - \frac{1}{{R_{O} C_{2} }}} \\ 0 & {\frac{{\left( {1 - D} \right)}}{{\left( {n + 1} \right)C_{o} }}} & 0 & 0 & {\frac{1}{{R_{o} C_{o} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{L1} } \\ {i_{Lm} } \\ {V_{C1} } \\ {V_{C2} } \\ {V_{Co} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{1} }}} \\ {\frac{{k\left( {1 + nD} \right)}}{{L_{m} \left( {n + 1} \right)}}} \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]V_{in} $$

(125)

$$ y = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{L1} } \\ {i_{Lm} } \\ {V_{C1} } \\ {V_{C2} } \\ {V_{Co} } \\ \end{array} } \right] + \left[ 0 \right]V_{in} $$

(126)

In this case, A, B, C, and D can be written as:

$$ A = \left[ {\begin{array}{*{20}c} 0 & 0 & { - \frac{{\left( {1 - D} \right)}}{{L_{1} }}} & 0 & 0 \\ 0 & 0 & {\frac{kD}{{L_{m} }}} & {\frac{{k\left( {1 - D} \right)}}{{L_{m} \left( {n + 1} \right)}}} & { - \frac{{k\left( {1 - D} \right)}}{{L_{m} \left( {n + 1} \right)}}} \\ { - \frac{1 - D}{{C_{1} }}} & {\frac{D}{{C_{1} }}} & 0 & 0 & {\frac{2n}{{R_{O} C_{1} }}} \\ 0 & {\frac{{\left( {1 - D} \right)}}{{\left( {n + 1} \right)C_{2} }}} & 0 & 0 & { - \frac{1}{{R_{O} C_{2} }}} \\ 0 & {\frac{{\left( {1 - D} \right)}}{{\left( {n + 1} \right)C_{o} }}} & 0 & 0 & {\frac{1}{{R_{o} C_{o} }}} \\ \end{array} } \right] $$

(127)

$$ B = \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{1} }}} \\ {\frac{{k\left( {1 + nD} \right)}}{{L_{m} \left( {n + 1} \right)}}} \\ 0 \\ 0 \\ 0 \\ \end{array} } \right] $$

(128)

$$ C = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right] $$

(129)

$$ D = \left[ 0 \right] $$

(130)

According to the small signal modeling method, state variables, duty cycles, input and output voltages consist of two segments, a DC ($\mathop X\limits^{\_\_} , \, \mathop Y\limits^{\_\_} , \, \mathop U\limits^{\_\_} , \, \mathop D\limits^{\_\_}$) part and an AC ($\tilde{x}, \, \tilde{y}, \, \tilde{u}, \, \tilde{d}$) part.

$$ \left\{ \begin{gathered} x = \mathop X\limits^{\_\_} + \tilde{x} \hfill \\ y = \mathop Y\limits^{\_\_} + \tilde{y} \hfill \\ u = \mathop U\limits^{\_\_} + \tilde{u} \hfill \\ d = \mathop D\limits^{\_\_} + \tilde{d} \hfill \\ \end{gathered} \right. $$

(131)

It is supposed that the AC values are significantly smaller than the DC values ($\mathop X\limits^{\_\_} > > \tilde{x}, \, \mathop Y\limits^{\_\_} > > \tilde{y}, \, \mathop U\limits^{\_\_} > > \tilde{u}, \, \mathop D\limits^{\_\_} > > \tilde{d}$) and do not change considerably during one period. Therefore, the small signal model can be displayed as follows:

$$ \left\{ \begin{gathered} \mathop {{\tilde{\text{x}}}}\limits^{ \cdot } = A^{\prime}{\tilde{\text{x}}} + B^{\prime}{\tilde{\text{u}}} + E^{\prime}\tilde{D} \hfill \\ \hat{y} = C^{\prime}\tilde{x} + D^{\prime}\tilde{u} + F^{\prime}\tilde{D}\, \hfill \\ \end{gathered} \right. $$

(132)

In the small signal analysis, input voltage is short circuited. In (132), $\mathop x\limits^{ \cdot }$, $\widetilde{{\text{u}}}$ and $\mathop y\limits^{ \cdot }$ are the state variables vector, control signals, and output signals, respectively. The new state space vector based on these definitions can be rewrite as follows:

$$ \mathop x\limits^{ \cdot } = \left[ {\begin{array}{*{20}c} 0 & 0 & { - \frac{{\left( {1 - \overline{D}} \right)}}{{L_{1} }}} & 0 & 0 \\ 0 & 0 & {\frac{{k\overline{D}}}{{L_{m} }}} & {\frac{{k\left( {1 - \overline{D}} \right)}}{{L_{m} \left( {n + 1} \right)}}} & { - \frac{{k\left( {1 - \overline{D}} \right)}}{{L_{m} \left( {n + 1} \right)}}} \\ { - \frac{{1 - \overline{D}}}{{C_{1} }}} & {\frac{{\overline{D}}}{{C_{1} }}} & 0 & 0 & {\frac{2n}{{R_{O} C_{1} }}} \\ 0 & {\frac{{\left( {1 - \overline{D}} \right)}}{{\left( {n + 1} \right)C_{2} }}} & 0 & 0 & { - \frac{1}{{R_{O} C_{2} }}} \\ 0 & {\frac{{\left( {1 - \overline{D}} \right)}}{{\left( {n + 1} \right)C_{o} }}} & 0 & 0 & {\frac{1}{{R_{o} C_{o} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\tilde{i}_{L1} } \\ {\tilde{i}_{Lm} } \\ {\tilde{V}_{C1} } \\ {\tilde{V}_{C2} } \\ {\tilde{V}_{Co} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{1} }}} \\ {\frac{{k\left( {1 + n\overline{D}} \right)}}{{L_{m} \left( {n + 1} \right)}}} \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]\tilde{V}_{in} + \left[ {\begin{array}{*{20}c} {\frac{{\overline{I}_{L1} }}{{L_{1} }}} \\ {\frac{{k\overline{V}_{C1} }}{{L_{m} }} - \frac{{k\overline{V}_{C2} }}{{L_{m} \left( {n + 1} \right)}} + \frac{{k\overline{V}_{Co} }}{{L_{m} \left( {n + 1} \right)}}} \\ {\frac{{\overline{I}_{L1} }}{{L_{1} }} + \frac{{\overline{I}_{Lm} }}{{C_{1} }}} \\ { - \frac{{\overline{I}_{Lm} }}{{\left( {n + 1} \right)C_{2} }}} \\ { - \frac{{\overline{I}_{Lm} }}{{\left( {n + 1} \right)C_{O} }}} \\ \end{array} } \right]\tilde{D} $$

(133)

$$ y = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\tilde{i}_{L1} } \\ {\tilde{i}_{Lm} } \\ {\tilde{V}_{C1} } \\ {\tilde{V}_{C2} } \\ {\tilde{V}_{Co} } \\ \end{array} } \right] + \left[ 0 \right]\tilde{V}_{in} + \left[ 0 \right]\tilde{D} $$

(134)

where ${\text{A}}{\prime}$(n × n fixed matrix), ${\text{E}}{\prime}$(n × n fixed matrix), and ${\text{C}}{\prime}$(m × n fixed matrix) are calculated as follows:

$$ A^{\prime} = \left[ {\begin{array}{*{20}c} 0 & 0 & { - \frac{{\left( {1 - \overline{D}} \right)}}{{L_{1} }}} & 0 & 0 \\ 0 & 0 & {\frac{{k\overline{D}}}{{L_{m} }}} & {\frac{{k\left( {1 - \overline{D}} \right)}}{{L_{m} \left( {n + 1} \right)}}} & { - \frac{{k\left( {1 - \overline{D}} \right)}}{{L_{m} \left( {n + 1} \right)}}} \\ { - \frac{{1 - \overline{D}}}{{C_{1} }}} & {\frac{{\overline{D}}}{{C_{1} }}} & 0 & 0 & {\frac{2n}{{R_{O} C_{1} }}} \\ 0 & {\frac{{\left( {1 - \overline{D}} \right)}}{{\left( {n + 1} \right)C_{2} }}} & 0 & 0 & { - \frac{1}{{R_{O} C_{2} }}} \\ 0 & {\frac{{\left( {1 - \overline{D}} \right)}}{{\left( {n + 1} \right)C_{o} }}} & 0 & 0 & {\frac{1}{{R_{o} C_{o} }}} \\ \end{array} } \right] $$

(135)

$$ B^{\prime} = \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{1} }}} \\ {\frac{{k\left( {1 + n\overline{D}} \right)}}{{L_{m} \left( {n + 1} \right)}}} \\ 0 \\ 0 \\ 0 \\ \end{array} } \right] $$

(136)

$$ E^{\prime} = \left[ {\begin{array}{*{20}c} {\frac{{\overline{I}_{L1} }}{{L_{1} }}} \\ {\frac{{k\overline{V}_{C1} }}{{L_{m} }} - \frac{{k\overline{V}_{C2} }}{{L_{m} \left( {n + 1} \right)}} + \frac{{k\overline{V}_{Co} }}{{L_{m} \left( {n + 1} \right)}}} \\ {\frac{{\overline{I}_{L1} }}{{L_{1} }} + \frac{{\overline{I}_{Lm} }}{{C_{1} }}} \\ { - \frac{{\overline{I}_{Lm} }}{{\left( {n + 1} \right)C_{2} }}} \\ { - \frac{{\overline{I}_{Lm} }}{{\left( {n + 1} \right)C_{O} }}} \\ \end{array} } \right] $$

(137)

$$ C^{\prime} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right] $$

(138)

Transfer function of this state-space vector can be expressed as:

$$ G(s) = \frac{{V_{Co} (s)}}{D(s)} = \frac{{8.409e04s^{3} + 1.989e - 07s^{2} + 1.044e14s + 42.65}}{{s^{5} - 361.8s^{4} - 2.164e08s^{3} + 7.794e10s^{2} - 6.994e15s + 2.531e18}} $$

(139)

For this system, by using parameters' values from Table 3, the step response can be modeled in MATLAB. The step-response is shown in Fig. 9. The step response shown in the figure indicates that the system is highly unstable. Initially, the output remains close to zero, but as time progresses, it exhibits an exponential divergence, rapidly growing to an extremely large value (on the order of 10²³). This behavior suggests that the system has at least one unstable pole with a positive real part, leading to an unbounded response. Such instability can arise from inherently unstable open-loop system. To address this issue, a stability analysis should be conducted by examining the system's poles and adjusting the controller parameters potentially through modifying the pole placement strategy to ensure all poles have negative real parts, leading to a stable response.

Table 3 Components' values.

Fig. 9

Step-response of the proposed topology before pole placement strategy.

Pole placement control description

Since the proposed topology is unstable it is required to apply pole-placement strategy, in this case, control diagram is illustrated in Fig. 10. This block diagram represents a state-space control system designed to regulate the output voltage V_CO. The reference input V_CO,ref is processed through an integrator to eliminate steady-state error, with feedback gains k_q and k_x adjusting the control input. Matrices A', C', D, and E' define the system dynamics, ensuring stability and desired performance. The control law combines integral and state feedback to achieve accurate voltage regulation. This structure suggests a pole placement control approach for enhanced system response.

Fig. 10

Schematic of the close-loop control method.

Based on Fig. 10, the following equations can be written:

$$ \tilde{d} = - k_{x} \tilde{x} - k_{q} q $$

(140)

$$ \dot{q} = r - y = r - C^{\prime} \, \tilde{x} $$

(141)

where q is the integrator output and r is the reference signals vector for the output variable. The vector r can be expressed as:

$$ r(t)^{T} = \left[ {V_{Co,ref} } \right] $$

(142)

It can be simplified as follows:

$$ \mathop q\limits^{ \cdot }_{1} (t) = V_{Co,ref} - V_{Co} (t) $$

(143)

In this method, if the control system is complete state controllable, it can be located the closed-loop poles to any suitable location with proper design of the state feedback gain matrix. The controllability matrix of this system is defined as follows:

$$ \Phi _{c} = \left[ {\left. {E^{\prime } } \right|\left. {A^{\prime } E^{\prime } } \right|\left. {A^{{\prime 2}} E^{\prime } } \right|...\left| {A^{{\prime n - 1}} E^{\prime } } \right.} \right] = \left[ {\left. {E^{\prime } } \right|A^{\prime } E^{\prime } } \right] $$

(144)

For this system, if the rank of the controllability matrix Ø_c is complete, then the system is completely controllable.

$$ rank(\Phi_{c} ) = n = 2 $$

(145)

Using Fig. 10 and Eqs. (135), (136), and (137), the open-loop state matrixes change to the matrixes $\tilde{A}^{\prime}$ and $\tilde{E}^{\prime}$ as follows:

$$ \left\{ \begin{gathered} \left[ {\begin{array}{*{20}c} {\dot{\tilde{x}}(t)} \\ {\dot{q}(t)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {A^{\prime}} & 0 \\ { - C^{\prime}} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\tilde{x}(t)} \\ {q(t)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {E^{\prime}} \\ 0 \\ \end{array} } \right]\tilde{D}(t) + \left[ {\begin{array}{*{20}c} 0 \\ I \\ \end{array} } \right]r(t) \, \hfill \\ y(t) = \left[ {\begin{array}{*{20}c} {C^{\prime}} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\tilde{x}(t)} \\ {q(t)} \\ \end{array} } \right] \hfill \\ \end{gathered} \right. $$

(146)

$$ \tilde{A}^{\prime} = \left[ {\begin{array}{*{20}c} {A^{\prime}} & 0 \\ { - C^{\prime}} & 0 \\ \end{array} } \right], \, \tilde{E}^{\prime} = \left[ {\begin{array}{*{20}c} {E^{\prime}} \\ 0 \\ \end{array} } \right] $$

(147)

Now, the new controllability matrix $\overline{{\Phi_{c} }}$ is assumed as follows:

$$ \overline{{\Phi _{c} }} = \left[ {\left. {\hat{E}^{\prime } } \right|\left. {\tilde{A}^{\prime } \tilde{E}^{\prime } } \right|\left. {\tilde{A}^{{\prime 2}} \tilde{E}^{\prime } } \right|...\left| {\tilde{A}^{{\prime n - 1}} \tilde{E}^{\prime } } \right.} \right] = \left[ {\left. {\tilde{E}^{\prime } } \right|\tilde{A}^{\prime } \tilde{E}^{\prime } } \right] $$

(148)

Then, the $\overline{{{\Phi }_{{\text{c}}} }}$ can be written as follows:

$$ \overline{{\Phi_{c} }} = \underbrace {{\left[ {\begin{array}{*{20}c} {E^{\prime}} & {A^{\prime}} \\ 0 & { - C^{\prime}} \\ \end{array} } \right]}}_{M}\left[ {\begin{array}{*{20}c} I & 0 \\ 0 & {\Phi_{c} } \\ \end{array} } \right] $$

(149)

If the following matrix rank is equal to n + m, the defined system will be completely state controlled.

$$ \, rank(M) = n + m = 7 $$

(150)

The fourth eigenvalues of the matrix $\tilde{A}^{\prime}$ are obtained as follows:

$$ eig(\tilde{A^{\prime}}) = \widehat{\lambda } = 1.0e + 04 \, \times \left\{ \begin{gathered} \, 0.0000 \, + \, 0.0000i \hfill \\ \, 1.5651 \, + \, 0.0000i \hfill \\ \, - 1.5650 \, + \, 0.0000i \hfill \\ \, - 0.0001 \, + \, 0.5343i \hfill \\ \, - 0.0001 \, - \, 0.5343i \hfill \\ \, 0.0002 \, + \, 0.0000 \hfill \\ \end{gathered} \right. $$

(151)

As can be seen, two eigenvalues have positive real part. These eigenvalues should be sufficiently shifted to the left side of the jw axis in order to reach the desired location of the converter closed-loop eigenvalues and achieve desired phase margin (PM ≥ 80) and gain margin (GM ≥ 10). The new eigenvalues are determined as follows:

$$ eig(\tilde{A^{\prime}}) = \widehat{\lambda } = 1.0e + 05 \, \times \left\{ \begin{gathered} \, 0.0000 \, + \, 0.0000i \hfill \\ \, - 0.1435 \, + \, 0.0000i \hfill \\ \, - 0.4565 \, + \, 0.0000i \hfill \\ \, - 0.0330 \, + \, 0.0534i \hfill \\ \, - 0.0330 \, - \, 0.0534i \hfill \\ \, - 8.8000 \, + \, 0.0000 \hfill \\ \end{gathered} \right. $$

(152)

Using the formula in MATLAB for placing the eigenvalues by importing the matrixes ($\tilde{A}^{\prime}$ and $\tilde{E}^{\prime}$), and considering the designed places for the closed-loop eigenvalues, this relation can be written:

$$ k = \left[ {k_{x} , \, k_{q} } \right] = place\,(\tilde{A}^{\prime},\,\tilde{E}^{\prime},\,\lambda^{\prime}) $$

(153)

The control coefficients matrixes k_x and k_q are obtained as follows:

$$ k_{x} = \left[ { \, \begin{array}{*{20}c} { - 2.7238} & {1.1290} & {0.2140} & {0.0665} & {381.1460} \\ \end{array} } \right] $$

(154)

$$ k_{q} = \left[ { \, - 1.6225e + 06} \right] $$

(155)

Also, after this control method, the transfer functions are obtained as follows:

$$ G(s) = \frac{{V_{Co} (s)}}{D(s)} = \frac{{ - 1.054e09s^{4} + 1.201e14s^{3} + 5.733e17s^{2} + 2.274e22s - 4.807e10}}{{s^{6} + 9.466e05s^{5} + 5.97e10s^{4} + 9.664e14s^{3} + 5.914e18s^{2} + 2.274e22s - 2.232e09}} $$

(156)

By importing (21) and (22) in (28), the state equations of the control system are written as follows

$$ \left\{ \begin{gathered} \left[ {\begin{array}{*{20}c} {\dot{\tilde{x}}(t)} \\ {\dot{q}(t)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {A^{\prime} - E^{\prime}k_{x} } & { - E^{\prime}k_{q} } \\ { - C^{\prime}} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\tilde{x}(t)} \\ {q(t)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ I \\ \end{array} } \right]r(t) \hfill \\ y(t) = \left[ {\begin{array}{*{20}c} {C^{\prime}} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\tilde{x}(t)} \\ {q(t)} \\ \end{array} } \right] \hfill \\ \end{gathered} \right. $$

(157)

The bode diagram illustrates the frequency response of the system before and after applying the control strategy in Fig. 11. The magnitude plot (top) shows how the system gain varies with frequency, while the phase plot (bottom) depicts the phase shift across different frequencies. Before control (blue line), the phase response and the phase margin was negative (-4.99°), confirming that the system was unstable. The gain margin was infinite, suggesting no gain crossover point, further emphasizing instability. After applying control (red line), the magnitude response was significantly improved, leading to a more stable frequency response. The phase response also became smoother, reducing abrupt shifts. The phase margin increased to 122.92°, and the gain margin became 33.21 dB, ensuring system stability and robustness. Overall, the applied control strategy effectively stabilizes the system by improving margins, leading to a well-conditioned and reliable design.

Fig. 11

Bode plot comparison of the system before and after control implementation. The phase margin (PM) and gain margin (GM) improvements indicate enhanced stability and robustness after applying the control strategy.

Furthermore, the step response of the utilized control strategy is depicted at Fig. 12. This figure shows the step response of the system, which represents how the system's output V_O(s) responds to a step input in D(s). The output starts at zero and rises quickly, indicating a fast transient response. The system overshoots above the final steady-state value (around 1.2 before settling back to 1). Overshoot occurs due to the system's dynamics and can indicate underdamping. The system stabilizes at around 1.5 ms. This suggests a fast response time, which is ideal in many control applications. After the transient response, the output remains close to 1, indicating no steady-state error.

Fig. 12

Step response of the controlled system, showing a smooth transient with minimal overshoot and a fast settling time, demonstrating effective voltage regulation.

Comprehensive comparison

In this section, the proposed converter is compared with some other converters. In Table 4, the voltage gain, the number of elements, normalized voltage stress (NVS) across the main power switch, input and output common ground feature, and the efficiency of the converters at 210 W are gathered and tabulated. In order to make a fair comparison, the value of n = 2 is considered for the turn ratio of all converters. Figure 13a shows the curves of the output voltage gain versus the duty cycle of the suggested structure and other compared converters. Based on this figure, the voltage gain of the suggested converter is higher than the voltage gain of other compared converters for all duty cycle values. Therefore, it can be said that the suggested topology is an high-step-up converter. Figure 13b shows the output voltage gain per the number of elements (Gain/TCC) versus the duty cycle. According to this figure, the output voltage gain of the proposed converter is higher than other converters. Therefore, it can be said that the proposed converter provides a high output voltage gain for a low number of components compared to other references. On the other hand, it can be concluded that the proposed topology components are structured better than the other topologies to provide higher voltage gains. Figure 13c shows the normalized voltage stress across the main power switch. As shown in this figure, the normalized voltage stress across the main power switch of the proposed converter has the lowest value compared to other structures for all duty cycle values.

Table 4 Comparison of the proposed converter with different relevant step-Up DC-DC converters.

Fig. 13

Comparison of the proposed converter with converters mentioned in {R2-6} Table 4 in terms of (a) output voltage gain, (b) Gain/TCC, (c) normalized voltage stress (NVS) across the main power switch, (d) normalized total voltage standing (NTVS).

Furthermore, with an increase in the duty cycle, the normalized voltage stress across the main power switch of the suggested converter decreases. This highlights the superiority of the proposed converter, as the reduction in voltage stress is evident when the duty cycle is raised in relation to the output voltage. As a result, a power switch with low power specifications and low R_ds(on) can be used, which reduces the cost and increases the efficiency. The total normalized voltage stress across the semiconductor elements is shown in Fig. 13d. According to this figure, the total normalized voltage stress of the proposed converter is lower than the structures in^{14,16,17,19,27,28} for all duty cycle values. Furthermore, for D < 0.65, the total normalized voltage stress of the proposed converter is lower than the structures in^24,29. It should be noted that when D > 0.65, conduction losses increase. Moreover, the converter presented in¹⁸ has the lowest total normalized voltage stress compared to the other converters. According to {R2-6} Table 4, the number of components of the proposed converter is equal to the number of components of the structures presented in^13,18,19. Other compared structures have more components than the proposed converter. Another notable advantage of the proposed topology is the establishment of a common ground for both input and output, resulting in reduced electromagnetic interference (EMI) issues. Furthermore, the experimental efficiency of the proposed converter in the output power of 210 W is lower than the efficiency of²⁵ and higher than the efficiency of all other compared converters.

Experimental Results

In this section, to verify the theoretical analysis, the experimental results of the prototype of the suggested converter are presented. The prototype of the proposed converter is shown in Fig. 14. The specifications of the prototype are listed in Table 2. The goal is to convert the input voltage V_in = 20 V to the output voltage V_out = 440 V until the converter delivers 210 W output power. For this purpose, by setting n = 2 and according to (24), the converter's duty cycle should be considered equal to D = 0.5. The switching frequency is considered equal to f_S = 50 kHz. An 840 Ω load is placed on the output port. By considering ΔI_L1 = 1 A and ΔI_Lm = 4.25 A and according to (81) and (82), the minimum inductance values of L₁ and L_m are equal to 200 µH and 140 µH, respectively. Therefore, the inductance values of L₁ and L_m in the prototype are considered equal to 300 µH and 150 µH, respectively. By considering ΔV_C1 = 8 V, ΔV_C2 = ΔV_C3 = 3 V, and ΔV_CO = 0.03 V and according to (84)-(87), the minimum capacity values of C₁, C₂, C₃, and C_O are equal to 4.3 µF, 3.3 µF, 3.3 µF and 166 µF, respectively. So, the capacity values of C₁, C₂, and C₃ are considered equal to 4.7 µF, and the capacitance value of C_O is considered equal to 220 µF. Figure 15a shows the output current and voltage waveforms obtained from the laboratory prototype. It is shown in this figure that the output voltage is equal to 420 V, which proves the statement (24), and the current passing through the output load is equal to 0.5 A. 10 (b) shows the current waveform of L₁. According to this figure, the average current value of L₁ equals 6.96 A, which corresponds to (42). Figure 16 shows the current and voltage waveforms of S₁ and S₂. According to Fig. 16a, the voltage stress of S₁ is equal to 38.5 V. In addition, the waveform of the current passing through it is quasi-resonant. Also, according to Fig. 16b, the voltage stress of S₂ equals 78 V. In addition, as can be seen in this figure, S₂ turns on under ZCS conditions, and the waveform of the current passing through this power switch is also quasi-resonant.

Fig. 14

Laboratory prototype of the proposed converter.

Fig. 15

Experimental results: (a) Voltage and current waveforms of the output load. (b) waveform of the current passing through L₁.

Fig. 16

Voltage and current experimental waveforms of. (a) S₁. (b) S₂.

Figure 17 shows the voltage and current waveforms of D₁, D₂, D₃, and D_O. According to Fig. 17a, the voltage stress of D₁ is equal to 38 V. As shown in Fig. 17b and c, the voltage stress of D₂ and D₃ is equal to 230 V. As evident from the observation, the current waveforms of these diodes reach zero before experiencing reversed or forward biases. This observation substantiates these diodes' ZCS condition. Figure 17d illustrates voltage and current stress across D_O, which is 348 V, and proves the provided mathematical analysis. Figure 18 shows the voltage waveforms of C₁, C₂, and C₃. As shown in this figure, the voltage across C₁, C₂, and C₃ are equal to 39 V, 117 V, and 117 V, respectively.

Fig. 17

Voltage and current experimental waveforms of. (a) D₁. (b) D₂. (c) D₃. (d) D_O.

Fig. 18

Experimental results: Voltage waveforms of. (a) C₁ (b) C₂ (c) C₃.

The control strategy was successfully implemented in an experimental setup to evaluate its performance under varying conditions. Figure 19a illustrates the system's response to input voltage variations, demonstrating a rapid transient response with minimal overshoot. This confirms the controller's effectiveness in maintaining stability.

Fig. 19

Experimental validation of the control strategy under. (a) input voltage variation. (b) load variation.

Figure 19b presents the system's dynamic response to a load variation. Initially, the load resistance is set at 840Ω, and at a certain instant, it is increased to 1000 Ω. The transient region, highlighted in the middle of the figure, shows the system's reaction to this change. The output current (i_O) decreases as expected due to the reduced load current demand, while the output voltage (V_O) remains stable with minimal deviation, confirming the effectiveness of the applied control strategy. The system successfully regulates the voltage despite the load variation, demonstrating the robustness of the proposed control method.

The experimental and theoretical efficiency curves of the proposed converter versus output power are shown in Fig. 20. As depicted, the prototype's efficiency in Vin = 20 V and Pout = 210 W is about 96.3%. Consequently, the proposed converter provides higher efficiency than 95.25% for different output power ranges.

Fig. 20

Experimental and theoretical efficiency of the proposed converter versus output power.

Conclusion

In this paper, a non-isolated quadratic high-step-up DC-DC converter is presented. A coupled inductor and the switched capacitor cell are utilized in this structure to increase the voltage gain. The proposed converter provides high voltage gain with a low number of elements. Low voltage stress across power switches is another advantage of the presented topology, which leads to the selection of MOSFETs with low internal resistance R_ds(on). A diode-capacitor clamp circuit is utilized to reduce the negative effects of leakage inductance and recover stored energy, leading to soft switching conditions for half of the diodes. The combination of these features provides a new topology with a high efficiency of 96.3%, which is recorded at 210W. Steady-state analysis, design consideration, and efficiency analysis are presented in detail. The proposed converter is compared with related structures, and it is observed that the proposed topology has higher efficiency and voltage gain compared to other structures. Finally, to verify the converter's performance qualification and mathematical analysis, a 210 W laboratory prototype is built, and its outcomes are thoroughly examined.